平行透视与成角透视
- 格式:ppt
- 大小:2.11 MB
- 文档页数:14
还不是很了解平行透视与成角透视的时候,不要烦恼,通过学习和掌握平行透视与成角透视的知识点,就可以在画画的时候,准确地画出画面中的物品。
同一物体不同的透视:
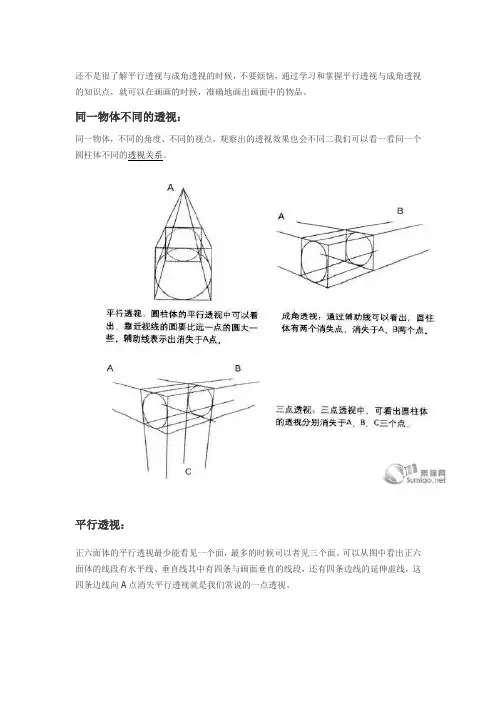
同一物体,不同的角度、不同的视点,观察出的透视效果也会不同二我们可以看一看同一个圆柱体不同的透视关系。
平行透视:
正六面体的平行透视最少能看见一个面,最多的时候司以者见三个面。
可以从图中看出正六面体的线段有水平线、垂直线其中有四条与画面垂直的线段,还有四条边线的延伸虚线,这四条边线向A点消失平行透视就是我们常说的一点透视。
成角透视:
成角透视就是景物纵深与视中线成一定角度的透视,景物的纵深因为与视中线不平行而向主点两侧的余点消失。
成角透视就是我们一股所说的两点透视。



1、平行透视成角透视原理的教学设计一等奖教学过程:一、出示石膏立方体模型。
1.结合数学课同学接触到的立方体概念,让同学分析(引导、启发)立方体的12条棱。
2、分成三组线(每组4条相同角度的线)。
二、引导、分析。
依据人在观察立方体的`视线高度,人的位置,立方体的位置(角度)概括出:a) 视平线,中心垂直线、心点;b) 视平线,左、右消失点。
这两种透视的条件:平行透视和成角透视。
导出课题《立方体的透视现象》。
平行透视:(板书)条件——1、立方体的一个面平行对着你。
2、人眼视线的位置:视平线。
3. 人的位置:中心垂直线。
4、视平线与中心垂直线的交点:心点。
平行透视三组线:1. 水平线2、垂直线3、对准心点的线成角透视:(板书)条件——1. 立方体的一个棱角对着你。
2、人眼视线的位置:视平线(人的眼睛在视平线的中心)。
3、视平线两端:左、右消失点。
成角透视三组线:1、垂直线。
2、往左边消失点对准的线。
3、往右边消失点对准的线。
三、根据以上所板书的原理:1、举例示范,平行透视立方体写生步骤。
2. 举例示范,成角透视立方体写生步骤。
3. 以上板书要求:同学作笔记作画步骤要求:同学能按顺序口头述说。
四、同学回家温习所学知识。
2、平行透视成角透视原理的教学设计一等奖一、教学内容概述《绘画中的透视现象》是人民美术出版社出版的小学美术教材五年级第九册第三课的内容。
根据《美术课程标准》所确立的阶段目标,本课属于“造型、表现”学习领域。
本课意图是通过观察、分析和讲解,学生能够认识到景物的近大远小透视现象,并能把有关透视的理论知识运用到实际绘画中进而提高空间表现能力,从而提高学生在绘画中的真实感。
二、教学目标分析1、认知目标:通过学习、观察和分析生活中的透视现象,学生更了解生活中的近大远小的原理。
理解视平线、消失点在透视现象中的应用。
学习它能使学生更好的表现空间立体感是绘画作品更真实。
2、技能目标:通过学习,学生能初步了解透视现象及基本规律,并能运用这些规律表现身边的景物逐步发展学生的想象力、观察力、表现力和创造力。

1.5建筑透视图的分类视点及建筑形体相对于画面位置不同,则所形成的建筑形体的透视图就有不同效果。
不同效果的透视图有不同的适用范围,其作图要领亦各有特点。
通常按照画面、视点和建筑形体三者之间的空间相对位置关系来对透视图进行分类。
建筑透视图大体可分为三类:一点透视( 平行透视);二点透视( 成角透视);三点透视( 斜透视) ;1.5.1一点透视当画面与基面垂直,建筑形体有一主立面平行于画面而视点位于画面的前方时,所得的透视图在左右、上下方向没有灭点,只有宽度(前后)方向有一个灭点,即主点e′,所以称为一点透视,或平行透视,如图1-25所示。
图1-25 一点透视一点透视的特点是建筑形体上与画面平行的主立面不变形,作图相对简便,图形显得端庄、沉稳、景深感强。
常用于表现纪念性建筑物、标志性建筑物的正面、门廊、入口等。
这种图在室内设计中应用也较多,如图1-26 所示。
也适用于表现只有一个主立面形状较复杂的建筑形体。
图1-26 一点透视实例1.5.2二点透视当画面垂直于基面,建筑形体两相邻主立面与画面均倾斜、视点位于画面的前方时,所得的透视图因为在长度和宽度两个方向上各有一个灭点,所以称之为二点透视,或成角透视,如图1-27所示。
图1-27 二点透视二点透视的特点是建筑形体两个主立面都得到了表现,作图相对复杂。
但表现效果生动、立体感强,是建筑设计中常用的透视图,如用来表现广场、街景、楼房建筑等。
图1-28 是二点透视实例。
图1-28 二点透视实例1.5.3三点透视当画面与基面倾斜、建筑物的立面也与画面倾斜,在这种情况下,建筑形体的长、宽、高三个方向都与画面形成倾斜的相对位置关系,因而三个方向都有灭点,所形成的透视图称为三点透视,或称斜透视,如图1-29 所示。
图1-29 三点透视三点透视常用来表达较高、大的建筑物,如高楼大厦、纪念碑、高塔等。
图1-30 是一高层大楼的三点透视实例。

美术班何国臣教具准备课件立方体直尺教学过程写入课题各位同学大家好,今天我们讲地课题是,立方体地“平行透视与成角透视”.一.导入主题师: 我们在绘画时,画出地物体常常感觉没有立体感,是什么原因造成地呢?师: 下面就让我们认真观察几张图片再说吧.(幻灯片)看图过程中请大家找出图片地相同点,透视现象:(客观物体因与人眼(视点)地远近距离和空间方位地不同,在视觉上引起近大远小、近宽远窄或近长远短近高远低等形象变化,称作“透视现象”.)个人收集整理勿做商业用途师:通过对以上几张图片地认真观察与分析,你找到了哪些规律?(学生讨论并回答)生:物体近大远小、近宽远窄、近高远低等.师:对!像这样我们在生活中看到地近大远小、近宽远窄、近高远低等都是属于透视现象.(运用透视规律描绘物体形象,是在平面上表现立体空间地最基本地方法.)个人收集整理勿做商业用途并指出:我们在绘画时,画出地物体常常没有立体感,是因为画面中没有这些现象地存在,所以我们需要进一步去了解透视,运用透视规律来绘画. 个人收集整理勿做商业用途二:透视地几个基本术语和概念师:在讲解透视知识之前呢,让我们先来认识一些透视中地基本术语.(教师向学生传授知识点、了解透视术语.).视点——观察者眼睛地位置.. 视平线——目光平视前方,在假想画面上与视点等高地一条水平线.在开阔地野外,人眼平视时,眼睛地高度等于视平线地高度,视平线就是地平线,视平线是与地平线重合地.视平线是随作画者地眼睛位置地变化而变化地,人仰视时视平线在地平线地上方,人俯视时,视平线在地平线下方.个人收集整理勿做商业用途. 消失点——就是在透视中伸远到视平线上地点,又叫灭点.. 主点——在视平线上正对视点地一点,又叫心点..余点——方形物体地两组水平平行线向左右两边分别聚集并在视平线上消失地两个点.请两名学生,一站一坐,观察石膏立方体和讲桌,并找出自己所处位置地视点、心点、视平线加以描述.(回到上方图片)接着让更多地学生分析图片中绘画者所处位置地视点、心点、视平线.三:透视图地分类:():一点透视(平行透视)()两点透视(成角透视)展开分析:平行透视:客观物体(指立方体)地前面与画面平行,底面与地平面平行;视平线上只有一个消失点(心点);与画面垂直地平行线都消失于心点. 个人收集整理勿做商业用途成角透视:客观物体(指立方体)地任何一个面都不与画面平行,底面与地平面平行;视平线上有左右两个消失点.个人收集整理勿做商业用途在日常生活活中,我们看同样大小地物体,近处地大,远处地小;同样高地物体,近处地高,远处地低.这种现象就是透视变化,而“近大远小”就是透视变化中最基本地规律. 个人收集整理勿做商业用途四.探究与表现.观看石膏正方体、长方体线描图,在不同地位置、角度所呈现出地透视变化.(多媒体展示分析,引导学生观察)个人收集整理勿做商业用途.平行透视;把立方体放平,正面面对学生. (出示石膏体)小组讨论:你发现了什么?(小组讨论并选举学生代表回答问题)生:上下线和视平线保持着平行关系,平行透视有个消失点.生:两边地竖线与视平线垂直,两侧地边线呈倾斜状,慢慢延长向心点集中,消失于心点.教师小结:如果与我们成平行状,那么它地另一组边则逐渐消失于心点,离我们近地线段就长,离我们远地线段就短,这种现象就是平行透视. 个人收集整理勿做商业用途.成角透视;立方体地一角对着学生.你发现了什么?生:上下边和左右边地线变地倾斜了,延长线分别向视平线左右两点集中,成角透视有个消失点. 生:没有平行线,都垂直于水平面.教师小结:物体地一角与我们正对,倾斜线延长并向视平线上地左右两点消失,这种透视现象叫成角透视.出示立方几何体后画出平行透视图并讲解步骤.现在结合我们刚刚所看地图片和平行透视、成角透视概念来示范作图步骤.个人收集整理勿做商业用途五:平行透视和成角透视地基本规律:接下来呢根据我们刚刚看地图片和作画步骤可以地出一些平行透视和成角透视地基本规律:平行透视(一点透视)客观物体(指立方体)地前面与画面平行,底面与地平面平行;视平线上只有一个消失点(心点);与画面垂直地平行线都消失于心点.个人收集整理勿做商业用途成角透视(两点透视).客观物体(指立方体)地任何一个面都不与画面平行,底面与地平面平行;视平线上有左右两个消失点.六:平行透视和成角透视地几个基本特点:了解了透视地基本规律之后,现在我们来了解了一下平行透视和成角透视地几个基本特点:平行透视:.边棱呈三种状态,有两种原线——水平边与垂直边(或斜置立方体地两组斜边),有唯一地变线——直角边..只产生一个灭点——心点,属一点透视,是所有纵深直角边地灭点..有一个可视地、由原线组成地平面与画面平行,保持原形,是空间中唯一不发生视觉变形地平面..所有含直角边地纵深面都发生形变,水平面离视平线近窄远宽,与视平线相贴时被压缩为水平直线;直立面离正中线近窄远宽,与正中线相贴时被压缩为垂直线.成角透视:就是把立方体画到画面上,有一组垂直线与画面平行,其他两组线均与画面成一角度,每组有一个消失点,共有两个消失点.所以成为二点透视.个人收集整理勿做商业用途. 基本特点()任何一个面都和画面不平行:以中心点到视点为中轴线,物体两面具有一定地倾斜,呈与画面不平行状态.()有一组垂直线与画面平行:()两个灭点:两组成角变线,水平消失方向不一,现成两个灭点,成角透视地主要特征,两个灭点都在视平线上,(视平线以上地成角边线向下消失,视平线以下地成角边线向上消失).个人收集整理勿做商业用途()具有生动变化地空间表达:较一点透视更为生动,不拘泥于单一地格局,适合室内室外两面展现表现方式.建筑效果图中最为重要地一种表达方式.个人收集整理勿做商业用途七:巩固与练习:接下来巩固我们刚才讲地内容和练习:巩固知识点::一点透视地透视规律()平行透视只有一个主向灭点:即主点.() 平行直角六面体在一般状况下能看到三个面,在特殊情况下,只能看到两个面或一个面.:两点透视地规律:八:课后作业:教师:要求同学参照示范图,画出一幅平行透视、成角透视地线描图.九:课堂小结:根据以上学习地内容,希望同学们在课后能够多做练习、在绘画过程中能够加以应用,请问同学们在刚刚讲课地过程中哪个知识点还不太懂地,加以阐述并提出问题.今天地课程就到这里,谢谢.个人收集整理勿做商业用途。


《平行透视与成角透视》洛宁县东宋镇初级中学程光乐内容分析本课属于六年级美术“造型•表现”学习领域,教学内容知识量大,逻辑性强,在教材中占有重要的位置。
学习本课有益于提高学生的观察能力、审美能力、造型能力,是美术教学重点。
学生分析六年级学生已经有了一定基础的造型能力和表现能力,好奇心强。
为了激发学生的学习兴趣,锻炼学生感性和理性思维的能力,培养创新精神,形成勇于探索与实践的良好学风,我带领学生到室外观察校园场景,让学生自制取景框,学生间相互合作、相互学习、相互评价,进一步加深对知识的巩固和应用。
设计理念《平行透视和成角透视》知识与学生学习生活空间——校园造型结合起来,多角度、多方位、多视点地去发现、寻找、理解、表现校园建筑的美感。
培养学生的空间意识和表现能力。
为了更有利于学生的学习,我采用多媒体和示范的教学方法,让学生轻松地学习视觉元素和透视法则,并在实践中加以运用。
活动方式采用小组自主合作学习的活动方式。
教具准备课件立方体绘图纸2B铅笔橡皮课时(一课时)教学目标1.引导学生通过细致的观察,理解掌握透视规律。
2.结合校园建筑物,学习方形物体的透视现象和规律,了解平行透视和成角透视的基本知识。
教学过程一.导入主题师: 我们在绘画时,画出的物体常常感觉没有立体感,是什么原因造成的呢? 师: 下面就让我们认真观察几张图片再说吧。
(通过观察图片让学生感受生活中用眼睛看到的一些现象:近大远小、近宽远窄、近高远低等都是透视现象.) 师:通过对以上几张图片的认真观察与分析,你找到了哪些规律?(学生讨论并回答)生:物体近大远小、近宽远窄、近高远低等。
师:对!像这样我们在生活中看到的近大远小、近宽远窄、近高远低等都是属于透视现象。
并指出:我们在绘画时,画出的物体常常没有立体感,是因为画面中没有这些现象的存在,所以我们需要进一步去了解透视,运用透视规律来绘画。
二.学习透视与练习师:在讲解透视知识之前呢,让我们先来认识一些透视中的基本术语。

透视原理透视的画法透视分一点透视(又称平行透视)两点透视(又称成角透视)及三点透视三类透视原理:透视的基本术语1,视平线:就是与画者眼睛平行的水平线。
2,心点:就是画者眼睛正对着视平线上的一点。
3,视点:就是画者眼睛的位置。
4,视中线:就是视点与心点相连,与视平线成直角的线。
5,消失点:就是与画面不平行的成角物体,在透视中伸远到视平线心点两旁的消失点。
6,天点:就是近高远低的倾斜物体(房子房盖的前面),消失在视平线以上的点。
7,地点:就是近高远低的倾斜物休(房子房盖的后面),消失在视平线以下的点。
8,平行透视:就是有一面与画面成平行的正方形或长方形物体的透视。
这种透视有整齐、平展、稳定、庄严的感觉。
9,成角透视:就是任何一面都不与平行的正方形成长方形的物体透视。
这种透视能使构图较有变化。
透视的画法在素描中最基本的形体是立方体。
素描时,大多是以对三个面所进行的观察方法来决定立方体的表现。
另外,利用面与面的分界线所造成的角度,也能暗示出物体的深度,这就涉及到透视规律。
透视分一点透视(又称平行透视),两点透视(又称成角透视)及三点透视三类。
一点透视就是说立方体放在一个水平面上,前方的面(正面)的四边分别与画纸四边平行时,上部朝纵深的平行直线与眼睛的高度一致,消失成为一点,而正面则为正方形.两点透视就是把立方体画到画面上,立方体的四个面相对于画面倾斜成一定角度时,往纵深平行的直线产生了两个消失点。
在这种情况下,与上下两个水平面相垂直的平行线也产生了长度的缩小,但是不带有消失点.三点透视就是立方体相对于画面,其面及棱线都不平行时,面的边线可以延伸为三个消失点,用俯视或仰视等去看立方体就会形成三点透视。
透视图中凡是变动了的线称变线,不变的线称原线,要记住近大远小,近实远虚的规律。
前面所讲的立方体透视图法适用全部物体,本节就说明一下圆及圆柱体透视,分解如下:如图(一)为正圆,A=B,a=b。
图(二)为圆的透视图,视觉上A=B,但a圆柱体透视:和前面的圆相比较,里面的圆当然是被缩小了,但仍然是完全的相似形。

平行透视与成角透视说课稿及反思平行透视与成角透视说课稿及反思教材分析《平行透视与成角透视》是人教版义务教育课程标准实验教科书美术七年级上册第二单元“多彩的学习生活”中的第一个活动。
本课属于“造型·表现”学习领域,教学内容知识量大,逻辑性强,在教材中占有重要的位置。
学习本课有益于提高学生的观察能力、审美能力、造型能力,是美术教学重点。
学生分析考虑到初一学生的知识特点,学生已经有了一定基础的造型能力和表现能力,好奇心强。
为了激发学生学习兴趣,锻炼学生感性和理性思维的能力,培养创新精神,形成勇于探索与实践的良好学风,我带领学生到室外观察校园场景,让学生自制取景框,学生间相互合作、相互学习、相互评价,进一步加深对知识的巩固和应用。
设计理念“优美的校园”中将《平行透视和成角透视》知识与学生学习生活空间——校园造型结合起来,多角度、多方位、多视点地去发现、寻找、理解、表现校园建筑的美感。
培养学生的空间意识和表现能力。
为了更有利于学生学习,我采用多媒体和示范的教学方法,让学生轻松地学习视觉元素和透视法则,并在实践中加以运用。
活动方式采用小组自主合作学习的活动方式。
教学目标1.引导学生通过细致的观察,理解掌握透视规律。
2.结合校园建筑物,学习方形物体的透视现象和规律,了解平行透视和成角透视的基本知识。
教学流程一.导入主题用投影放出校园甬道、教学楼线描图(有透视错误、无立体感),分析近大远小、近宽远窄、近高远低。
引导:我们在绘画时,画出的物体常常没有立体感,原因是透视错误造成的,所以我们需要了解透视,运用透视规律来画,纠正画面中不符合透视规律的方法。
你想知道什么是透视吗?二.学习透视与练习教师向学生传授知识点、了解透视术语。
1.视点:观察者眼睛的位置。
2.视平线:目光平视前方,在假想画面上与视点等高的一条水平线。
在开阔的野外,视平线是与地平线重合的。
3.主点:由视点向正前方延伸一条视中线,与视平线相交的一个点(亦称“心点”)。
一点透视二点透视三点透视解析
1.一点透视也叫平行透视。
水平线与视平线平行,物体远到一定程度,最终成为消失点。
你可以想象火车轨道,最后消失了。
这种透视感觉整洁、平整、稳定、庄严。
2.两点透视也叫成角透视。
两点透视有两个消失点,即任何一面都不与平行的正方形形成长方形物体透视。
比如我们站在一个街头角落往前看,那么街道两侧的线条就会无限延伸到东西两侧,然后形成两个消失点,这样这个视角就可以让构图比较有变化。
3.三点透视也叫倾斜透视。
根据站点的高度,三点透视的高度线要么消失在天空中的天点,要么消失在地面中的地点。
另外两组深度线延伸和视平线形成两个消失点,消失在地平线上,另一组消失点消失在天空或地面上。
三点透视是三个消失点,一般用来描述高层建筑。
写给素描新手入门的一些基础知识:透视
很多人学画画时都被这个理论难住了,你搞明白了吗?
方形透视
方形透视分为三种:一点透视(平行透视)、两点透视(成角透视)、三点透视(倾斜透视)。
一点透视(平行透视)
一点透视
两点透视(成角透视)
三点透视(倾斜透视)
圆形透视
一个圆柱体,如果是俯视它的话,它上面圆的弧度越下面越大;如果是仰视的话,它上面圆的弧度越上面越大。
圆形透视
透视简单来说就是近宽远窄、近大远小、近实远虚,主要是为了让画面有空间意识和纵深感。