正交试验设计中的方差分析2例题分析

第十一章正交设计试验资料的方差分析在实际工作中，常常需要同时考察3个或3个以上的试验因素，若进行全面试验，则试验的规模将很大，往往因试验条件的限制而难于实施。

正交设计是安排多因素试验、寻求最优水平组合的一种高效率试验设计方法。

第一节、正交设计原理和方法(一) 正交设计的基本概念正交设计是利用正交表来安排多因素试验、分析试验结果的一种设计方法。

它从多因素试验的全部水平组合中挑选部分有代表性的水平组合进行试验，通过对这部分试验结果的分析了解全面试验的情况，找出最优水平组合。

例如，研究氮、磷、钾肥施用量对某小麦品种产量的影响：A因素是氮肥施用量，设A1、A2、A3 3个水平；B因素是磷肥施用量，设B1、B2、B3 3个水平；C因素是钾肥施用量，设C1、C2、C3 3个水平。

这是一个3因素每个因素3水平的试验，各因素的水平之间全部可能的组合有27种。

如果进行全面试验，可以分析各因素的效应，交互作用，也可选出最优水平组合。

但全面试验包含的水平组合数较多，工作量大，由于受试验场地、经费等限制而难于实施。

如果试验的主要目的是寻求最优水平组合，则可利用正交设计来安排试验。

正交设计的基本特点是：用部分试验来代替全面试验，通过对部分试验结果的分析，了解全面试验的情况。

正交试验是用部分试验来代替全面试验，它不可能像全面试验那样对各因素效应、交互作用一一分析；当交互作用存在时，有可能出现交互作用的混杂。

如对于上述3因素每个因素3水平试验，若不考虑交互作用，可利用正交表L9(34)安排，试验方案仅包含9个水平组合，就能反映试验方案包含27个水平组合的全面试验的情况，找出最佳的生产条件。

一、正交设计的基本原理表11-1 33试验的全面试验方案正交设计就是从全面试验点（水平组合）中挑选出有代表性的部分试验点（水平组合）来进行试验。

图1中标有‘9 ’个试验点，就是利用正交表L9(34)从27个试验点中挑选出来的9个试验点。

即：(1)A1B1C1(2)A1B2C2(3)A1B3C3(4)A2B1C2(5)A2B2C3 (6)A2B3C1(7)A3B1C3(8)A3B2C1(9)A3B3C2上述选择，保证了A因素的每个水平与B因素、C 因素的各个水平在试验中各搭配一次。

1．正交试验设计法的基本思想正交试验设计法，就是使用已经造好了的表格--正交表--来安排试验并进行数据分析的一种方法。

它简单易行，计算表格化，使用者能够迅速掌握。

下边通过一个例子来说明正交试验设计法的基本想法。

[例1]为提高某化工产品的转化率，选择了三个有关因素进行条件试验，反应温度(A)，反应时间(B)，用碱量(C)，并确定了它们的试验范围：A：80-90℃B：90-150分钟C：5-7％试验目的是搞清楚因子A、B、C对转化率有什么影响，哪些是主要的，哪些是次要的，从而确定最适生产条件，即温度、时间及用碱量各为多少才能使转化率高。

试制定试验方案。

这里，对因子A，在试验范围内选了三个水平；因子B和C也都取三个水平：A：A l＝80℃，A2＝85℃，A3=90℃B：B l＝90分，B2＝120分，B3=150分C：C l＝5％，C2＝6%，C3＝7%当然，在正交试验设计中，因子可以是定量的，也可以是定性的。

而定量因子各水平间的距离可以相等，也可以不相等。

这个三因子三水平的条件试验，通常有两种试验进行方法：(Ⅰ)取三因子所有水平之间的组合，即A l B l C1，A1B l C2，A1B2C1，……，A3B3C3，共有33=27次试验。

用图表示就是图1 立方体的27个节点。

这种试验法叫做全面试验法。

全面试验对各因子与指标间的关系剖析得比较清楚。

但试验次数太多。

特别是当因子数目多，每个因子的水平数目也多时。

试验量大得惊人。

如选六个因子，每个因子取五个水平时，如欲做全面试验，则需56＝15625次试验，这实际上是不可能实现的。

如果应用正交实验法，只做25次试验就行了。

而且在某种意义上讲，这25次试验代表了15625次试验。

(Ⅱ)简单对比法，即变化一个因素而固定其他因素，如首先固定B、C 于B l、C l，使A变化之：↗A1B1C1→A2↘A3 (好结果)如得出结果A3最好，则固定A于A3，C还是C l，使B变化之：↗B1A3C1→B2 (好结果)↘B3得出结果以B2为最好，则固定B于B2，A于A3，使C变化之：↗C1A3B2→C2 (好结果)↘C3试验结果以C2最好。

8.3.2 考虑交互作用的三水平正交试验的方差分析（因学时有限和正交表太大L27(313)，不讲解！只讲解二水平情况，因为二水平会，三水平自然也会！）例8-4 运动发酵单细胞菌是一种酒精生产菌。

为了确定其发酵培养基的最佳配方，进行了四因素三水平正交试验，试验指标为酒精浓度（g/ml）。

表8-12给出了因素水平表，要求考察交互作用A×B、A×C和A×D。

查附表7可得，本试验应选用L27(313)正交表，表头设计应按照“L27(313)二列间的交互作用表”进行。

本例只考虑一级交互作用（p=1），所以每个三水平交互作用应占(m-1)P=(3-1)1=2列，即A ×B、A×C，和A×D在L27(313)正交表中各占二列。

表8-12 因素水平表表头设计时应避免混杂，试验方案及试验结果见表8-13。

由交互作用表可知，将因素A、B安排在第1、2列之后，第3、4列为A×B交互作用列；再将C安排在第5列后，A×C交互作用在第6、7列；最后将D安排在第9列，则A×D交互作用类落在第8、10列（当然也可将D安排在第8列，则第9、10列为A×D交互作用列）。

表8-13 试验方案及结果分析 L27(313)一、计算（计算过程省略）1.计算各列各水平的K ij 值(K 1j ,K 2j ,K 3j )和K 2ij (K 21j ,K 22j,K 23j ) 各列各水平对应的试验数据之和K 1j ,K 2j ,K 3j ,及其平方和K 21j , K 22j ,K 23j ,列于表8-13中,例如K 1A =∑=91i iX=0.20+0.50*2+1.50+1.10+1.20*2+1.60*2=9.40=K 11 ，K 211= 88.36K 2A =∑=91i i X =0.40+0.50+……+6.15=33.05= K 21 ， K 221=1092.30K 3A =∑=91i i X =0.40+0.30+……+2.80=25.80= K 31 ， K 231 =665.64表示A ×B 的有两列,即第3,4列,计算后可知 K 13 =32.75, K 23 =17.90; K 33 =17.60 K 14 =26.40; K 24 =24.55, K 34 =17.302.计算各列的偏差平方和(S j )及其自由度(f j ) 由式(8-4),可知:S j =CT Q nT K r j m i ij -=-∑=2211 r=n/m=27/3=9;CT=T 2/n=1/27×68.252=172.52所以 S j =9152.17291312=-∑=i ij K ( K 1j 2+K 2j 2+K 3j 2)-172.53S A =S 1=91(K 112 +K 212+K 312)-172.52 =91(88.36+1092.30+665.64)-172.52 =32.62S B =S 2=……=67.90, S 3=……=16.67 , S 4=……=5.14 所以S A ×B =S 3+S 4=21.81S c =S 5=……=2.48, S 6=……=3.04, S 7=……=3.60 所以S A ×C =S 6+S 7=6.64S 8=……=5.13 ; S 10=……=1.21 所以S A ×D =S 8+S 10=6.34 S D =S 9=……=7.43S 11=……=2.33,S 12=……=0.35,S 13=……=0.55 所以S e =S 11+S 12+S 13=3.23因为第j 列的自由度为 f j =m-1=3-1=2,(j=1,2,……13)，所以 f A = f B = f C =f D =2f A ×B = f 3 +f 4=2+2=4, f A ×C = f 6 +f 7 =2+2=4 f A ×D = f 8 +f 10 =2+2=4, f e = f 11 +f 12 +f 13 =2×3=6 验算:① S T 的验算Q T =∑=ni i x 12=0.2²+0.5²+…+2.8²=320.98S T =Q T －CT=320.98-172.52=148.46另外S T =∑=kj j S 1=32.62+67.90+…+0.55=148.45② f T 的验算 f T =n-1=27-1=26另外 f T =13f i =13×(m-1)=13×(3-1)=26 ∴计算过程无误.3.计算方差 V j =jj f SV A =S A /f A =32.62/2=16.31 同理可得V B =33.95,V C =1.24,V D =3.72 V A ×B =5.45,V A ×C =1.66,V A ×D =1.59 Ve=0.538 ∵ejV V 均大于2,且f e =6＞1, ∴无需校正Ve!二、显著性检验 （计算过程省略） 1. 计算 F jF A = V A /Ve=16.31/0.538=30.32, ∵F j =V j /Ve,∴同理可得, F B =63.10, F A ×B =10.13, F C =2.30, F A ×C =3.09 2.查 F ɑF ɑ(f 因,fe)=f ɑ(2,6),F ɑ(f 交,fe)=F ɑ(4,6)当ɑ=0.05时,查得 F 0.05(2,6)=5.14, F 0.05(4,6)=4.53; 当ɑ=0.01时,查得 F 0.01(2,6)=10.92, F 0.01(4,6)=9.15. 3.显著性检验∵F A=30.32和F B=63.10均大于F0.01(2,6)=5.14,∴因素A和B均高度显著(用**表示);又∵F A×B=10.13＞F0.01(4,6)=9.15,∴交互作用A×B也高度显著（用**表示）；又∵F D=6.91,∵介于F0.05(2,6)和F0.01(2,6)之间,∴因素D显著(用*表示);又∵F C=2.30＜F0.05(2,6)=5.14,以及F A×C=3.09和F A×D=2.96均小于F0.05(4,6)=4.53,∴因素C及交互作用A×C和A×D均不显著.根据F值大小,可知各因素及交互作用对试验指标影响的主次顺序为:B,A,A×B,D,A×C,A×D,C.4.列方差分析表表8-14 方差分析表三、最优工艺条件确定因素A、B及交互作用A×B都高度显著，但因在主次顺序中，A ×B排在A、B之后，因此应优先考虑A、B的优水平。

正交试验结果的方差分析方法计算公式和项目试验指标的加和值=,试验指标的平均值与表4-13一样，第j列的(1) I j”水平所对应的试验指标的数值之和(2) II j——“ 2”水平所对应的试验指标的数值之和(3)……(4) k j——同一水平出现的次数。

等于试验的次数除以第j列的水平数.(5)I j/k j——“水平所对应的试验指标的平均”(6)II j/k j——“2”水平所对应的试验指标的平均值(7)……以上各项的计算方法，与“极差法”同，见4.1.7节(8)偏差平方和(4-1)(9) fj ——自由度.fj第j列的水平数－1.(10）Vj——方差.Vj =Sj/fj(4-2)（11）Ve——误差列的方差。

(4-3)（12）Fj——方差之比(4-4)（13）查F分布数值表（见附录6），做显著性检验。

显著性检验结果的具体表示方法与第3章相同。

（14）总的偏差平方和(4-5) （15）总的偏差平方和等于各列的偏差平方和之和。

即(4-6) 式中，m为正交表的列数。

若误差列由5个单列组成，则误差列的偏差平方和S e等于5个单列的偏差平方和之和,即：S e=S e1+S e2+S e3+S e4+S e5；也可用S e= S总－S’来计算，其中：S’为安排有因素或交互作用的各列的偏差平方和之和应引出的结论。

与极差法相比，方差分析方法可以多引出一个结论：各列对试验指标的影响是否显著，在什么水平上显著。

在数理统计上，这是一个很重要的问题。

显著性检验强调试验误差在分析每列对指标影响中所起的作用。

如果某列对指标的影响不显著，那么，讨论试验指标随它的变化趋势是毫无意义的。

因为在某列对指标的影响不显著时，即使从表中的数据可以看出该列水平变化时，对应的试验指标的数值也在以某种“规律”发生变化，但那很可能是由于实验误差所致，将它作为客观规律是不可靠的。

有了各列的显著性检验之后，最后应将影响不显著的交互作用列与原来的“误差列”合并起来，组成新的“误差列”，重新检验各列的显著性。

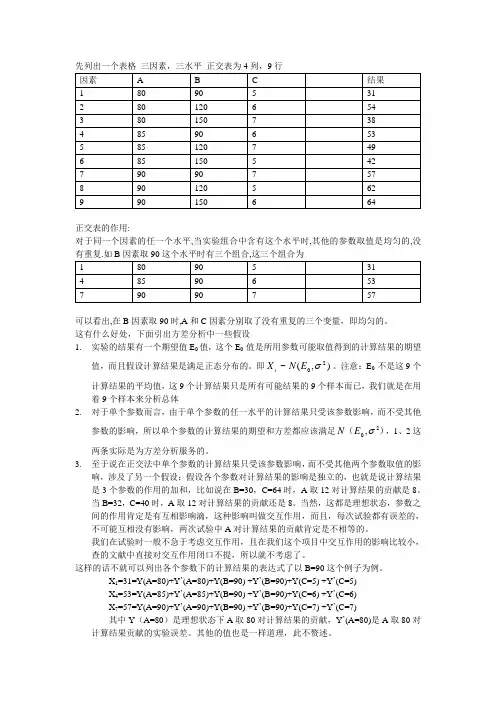
先列出一个表格 三因素，三水平 正交表为4列，9行正交表的作用:对于同一个因素的任一个水平,当实验组合中含有这个水平时,其他的参数取值是均匀的,没有重复.如B 因素取90这个水平时有三个组合,这三个组合为可以看出,在B 因素取90时,A 和C 因素分别取了没有重复的三个变量，即均匀的。

这有什么好处，下面引出方差分析中一些假设1. 实验的结果有一个期望值E 0值，这个E 0 值是所用参数可能取值得到的计算结果的期望值，而且假设计算结果是满足正态分布的。

即),(~20σE N X i 。

注意：E 0 不是这9个计算结果的平均值，这9个计算结果只是所有可能结果的9个样本而已，我们就是在用着9个样本来分析总体2. 对于单个参数而言，由于单个参数的任一水平的计算结果只受该参数影响，而不受其他参数的影响，所以单个参数的计算结果的期望和方差都应该满足）（20,σE N ，1、2这两条实际是为方差分析服务的。

3. 至于说在正交法中单个参数的计算结果只受该参数影响，而不受其他两个参数取值的影响，涉及了另一个假设：假设各个参数对计算结果的影响是独立的，也就是说计算结果是3个参数的作用的加和，比如说在B=30，C=64时，A 取12对计算结果的贡献是8。

当B=32，C=40时，A 取12对计算结果的贡献还是8。

当然，这都是理想状态，参数之间的作用肯定是有互相影响滴，这种影响叫做交互作用，而且，每次试验都有误差的，不可能互相没有影响，两次试验中A 对计算结果的贡献肯定是不相等的。

我们在试验时一般不急于考虑交互作用，且在我们这个项目中交互作用的影响比较小，查的文献中直接对交互作用闭口不提，所以就不考虑了。

这样的话不就可以列出各个参数下的计算结果的表达式了以B=90这个例子为例。

X 1=31=Y(A=80)+Y ’(A=80)+Y(B=90) +Y ’(B=90)+Y(C=5) +Y ’(C=5) X 4=53=Y(A=85)+Y ’(A=85)+Y(B=90) +Y ’(B=90)+Y(C=6) +Y ’(C=6) X 7=57=Y(A=90)+Y ’(A=90)+Y(B=90) +Y ’(B=90)+Y(C=7) +Y ’(C=7)其中Y （A=80）是理想状态下A 取80对计算结果的贡献，Y ’(A=80)是A 取80对计算结果贡献的实验误差。