七年级上8-9单元易错题练习

七年级英语上册Unit9易错题31题汇总1.What’s your (mother) favorite food?2.He always (play) games with us.3.Friday is the (sixth/fifth) day of a week.4.What (be) your favorite sports?5.Do you want (play) basketball with us?6.The storybook is (非常有趣)7.She likes art because it’s relaxing. (对画线部分提问)she like art?8.I like yellow best.(同义句) is yellow.9.The first day of school is interesting. (对画线部分提问)the first day of school?10.What about you? (同义句) ?11.He likes P.E. best at school. (同义句)His P.E. at school.12.你今天上什么科目？you today?13.I think history is interesting.(改为否定句)I think history interesting.14.We have math Friday .It’s difficult interesting .A. on ; andB. on ; butC. in; butD. in; and15.--- ? ---It’s Monday.A. What’s the timeB. What day is it todayC. What’s the date todayD. Is it Monday today16.Mr.Chen teaches math. We all like very much.A. us ,hisB. our ,hisC. us ,himD. our, him17.I don’t like English it’s difficult.A. whyB. butC. andD. because18.Do you have a history lesson the afternoon of Tuesday ?A. inB. atC. onD. for19.Bob and Linda’s favorite subject geography.A. beB. isC. areD. am20.---What you do after dinner?---I do my homework for an hour. A. is B. are C. do D. does21. We play basketball two hours every day.A. forB. onC. inD. to22. 选词的适当形式填空(1)I’m not busy today. I’m . (2)---When do you have music? ---We have them on Wednesday and Friday. (3)Our P.E. lesson at 3:30 on Monday afternoon. (4)YuMei has an art lesson for two .23.Mike needs (a/an) hour to do homework.24.The book are (real) interesting.25. Bob’s and Linda’s favorite subjects geography and history.A. beB. isC. areD. am26.The teacher says math（难但是有用）。

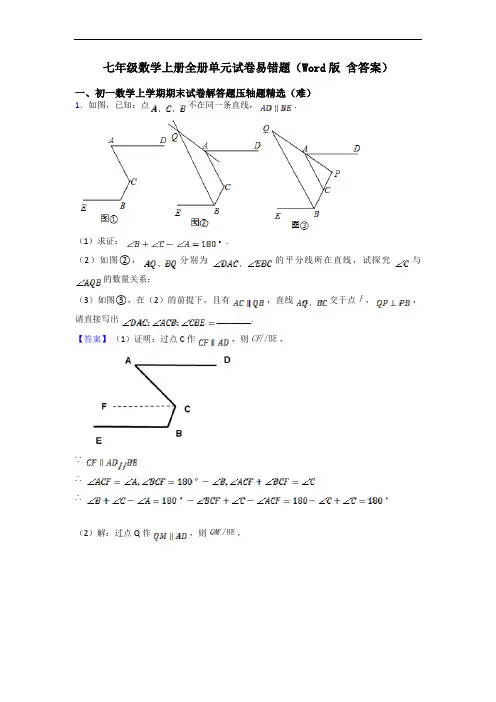
七年级数学上册全册单元试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．如图，已知：点不在同一条直线， .（1）求证： .（2）如图②，分别为的平分线所在直线，试探究与的数量关系；（3）如图③，在（2）的前提下，且有，直线交于点，，请直接写出 ________.【答案】（1）证明：过点C作，则，∵∴∴（2）解：过点Q作，则，∵，∴∵分别为的平分线所在直线∴∴∵∴（3）:1:2:2【解析】【解答】解：（3）∵∴∴∵∴∵∴∴∴∴ .故答案为： .【分析】（1）过点C作，则，再利用平行线的性质求解即可；（2）过点Q作，则，再利用平行线的性质以及角平分线的性质得出，再结合（1）的结论即可得出答案；（3）由（2）的结论可得出，又因为，因此，联立即可求出两角的度数，再结合（1）的结论可得出的度数，再求答案即可.2．点O为直线AB上一点，过点O作射线OC，使∠BOC＝65°，将一直角三角板的直角顶点放在点O处．（1）如图①，将三角板MON的一边ON与射线OB重合时，则∠MOC＝________；（2）如图②，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；（3）将三角板MON绕点O逆时针旋转至图③时，∠NOC＝∠AOM，求∠NOB的度数．【答案】（1）25°（2）解：∠BOC=65°，OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°（3）解：∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解：（1）∠MON=90，∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】（1）根据∠MON和∠BOC的度数可以得到∠MON的度数；（2）根据角平分线的性质，由∠BOC=65°，可以求得∠BOM的度数，然后由∠NOM-90°，可得∠BON的度数，从而得解；（3）由∠BOC=65°，∠NOM=90°，∠NOC= ∠AOM，从而可求得∠NOC的度数，然后由∠BOC=65°，从而得解.3．已知，∠AOB=∠COD=90°，射线OE，FO分别平分∠AOC和∠BOD．（1）当OB和OC重合时，如图（1），求∠EOF的度数；（2）当∠AOB绕点O逆时针旋转至图（2）的位置（0°＜∠BOC＜90°）时，求∠EOF的度数．【答案】（1）解：当OB和OC重合时，∠AOD=∠AOC+∠BOD=180°，又∵射线OE，FO分别平分∠AOC和∠BOD，∴∠COE= ∠AOC，∠BOF= ∠BOD，∴∠EOF=∠COF+∠BOF= （∠AOC+∠BOD）= ×180°=90°（2）解：∵∠AOB=∠COD=90°，∠COE= ∠AOC，∠BOF= ∠BOD，∴∠EOF=∠COE+∠BOF﹣∠BOC= ∠AOC+ ∠BOD﹣∠BOC= （∠AOC+∠BOD）﹣∠BOC= （∠AOB+∠BOC+∠COD+∠BOC）﹣∠BOC= （180°+2∠BOC）﹣∠BOC=90°+∠BOC﹣∠BOC=90°【解析】【分析】（1）由角平分线的性质可得∠COE=∠AOC，∠BOF=∠BOD；由平角的定义可得∠AOC+∠BOD=180°，由角的构成可得∠EOF=∠COE+∠BOF，代入计算即可求解；（2）同理可求解。

第一单元第一课.《在山的那一边》1．注音：痴（chī）想隐秘（mì）凝（níng）成铁青喧（xuān）腾诱（yòu）惑一瞬（shùn）间2．解释：隐秘：隐蔽，不外露一瞬间：一眨眼第二课.《走一步，再走一步》1．注音：训诫（jiè）耸（sǒng）立迂（yūn）回啜(chuò)泣瘦骨嶙峋（lín）（xún）心惊肉跳头晕（yūn）目眩(xuàn)小心翼翼(yì)2．解释：训诫：告诫，教导嶙峋：形容人瘦削头晕目眩：头晕眼睛昏花啜泣：抽噎，抽抽搭搭地哭。

纳罕：惊奇，诧异小心翼翼：谨慎小心，丝毫不敢疏忽的样子。

翼翼，谨慎、严肃。

第三课.《短文两篇》1．注音：收敛（liǎn）宽恕（shǜ）卑（bēi）微零落（luò）一丝不苟（gǒu）聒聒（guō）2．解释：收敛：收拢、合拢聒聒：持续嘈杂，使人厌烦宽恕：宽容，饶恕。

恕，饶恕。

卑微：卑贱，微小，地位低下。

一丝不苟：形容办事认真，连最细微的地方也不马虎。

苟，敷衍了事，马马虎虎。

第四课.《紫藤萝瀑布》1．注音：嚷（rāng）穗（suì）舱（cāng）绽（zhàn）凑（còu）酿（niàng）迸溅（bèng）挑（tiǎo）逗繁（fán）密伫（zhǜ）立凝(níng)望笼（lǒng）罩伶仃（dīng）稀零(líng)忍俊不禁( jīn)仙露琼（qióng）浆盘虬（qúu）卧龙2．解释：忍俊不禁：忍不住笑。

第五课《童趣》1.注音项为之强（jiāng）鹤唳（lì）云端怡（yí）然称快第一单元词语集锦：痴想，隐秘，凝成，铁青，喧腾，诱惑，一瞬间训诫，耸立，迂回，凝视，啜涕，瘦骨嶙峋，心惊肉跳，头晕目眩，小心翼翼收敛，宽恕，卑微，零落，聒聒，断续，一丝不苟终极，迸溅，繁密，伫立，凝望，伶仃，稀零，忍俊不禁，仙露琼浆，蜂围碟阵，盘虬卧龙明察秋毫，怡然称快，怡然自得，庞然大物，夏蚊成雷第二单元第六课《理想》⒈ 给下列加点字注音：倔强（）（）洗濯（）玷污（）诅咒（）碌碌终生（）缀（）连扒（）窃2. 解释下面的词语，并指出加点字的含义。

七年级上册数学全册单元试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．点在线段上， .（1）如图1，，两点同时从，出发，分别以，的速度沿直线向左运动；①在还未到达点时，求的值；②当在右侧时(点与不重合)，取中点，的中点是，求的值；（2）若是直线上一点，且 .求的值.【答案】（1）解：①AP=AC-PC，CQ=CB-QB，∵BC=2AC，P、Q速度分别为1cm/s、2cm/s，∴QB=2PC，∴CQ=2AC-2PC=2AP，∴②设运动秒，分两种情况A: 在右侧，，分别是，的中点，，∴B: 在左侧，，分别是，的中点，，∴（2）解：∵BC=2AC.设AC=x，则BC=2x，∴AB=3x，①当D在A点左侧时，|AD-BD|=BD-AD=AB= CD，∴CD=6x，∴；②当D在AC之间时，|AD-BD|=BD-AD= CD，∴2x+CD-x+CD= CD，x=- CD（不成立），③当D在BC之间时，|AD-BD|=AD-BD= CD，∴x+CD-2x+CD= CD，CD= x，∴；|AD-BD|=BD-AD= CD，∴2x-CD-x-CD= CD，∴CD=；④当D在B的右侧时，|AD-BD|=BD-AD= CD，∴2x-CD-x-CD= CD，CD=6x，∴ .综上所述，的值为或或或【解析】【分析】（1）由线段的和差关系，以及QB=2PC，BC=2AC，即可求解；（2）设AC=x，则BC=2x，∴AB=3x，D点分四种位置进行讨论，①当D在A点左侧时，②当D在AC之间时，③当D在BC之间时，④当D在B的右侧时求解即可.2．如图1，已知∠AOB＝120°，∠COD＝60°，OM在∠AOC内，ON在∠BOD内，∠AOM＝∠AOC，∠BON＝∠BOD．（1）∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时，如图2，∠MON＝________°；（2）∠COD从图2中的位置绕点O逆时针旋转n°（0＜n＜120且n≠60），求∠MON的度数；（3）∠COD从图2中的位置绕点O顺时针旋转n°（0＜n＜120），则n＝________时，∠MON＝2∠BOC．【答案】（1）100（2）解：①当0＜n＜60°时，∠AOC=∠AOB-∠BOC=120°－n，∠BOD=60°－n，∴∠MON=∠MOC+∠COB+∠BON= ∠AOC+n+ ∠BOD= （120°-n）+n+ （60°－n）=100°；②当60°＜n＜120°时，∠AOC=120°－n，∠COD=60°，∠BOD=n-60°，∠MOC= ∠AOC，∠DON= ∠BOD，∴∠MON=∠MOC+∠COD+∠DON= （120°-n）+60°+ （n-60°）=100°．综上所述：∠MON的度数恒为100°（3）解：①当0＜n＜60°时，∠BOC=n，∠MON=2n，∴∠MON= （120°+n）+60°-（60°+n）=100°；解得：n=50°；②当60°＜n＜120°时，∠AOC=360°-（120°+n）=240°－n，∠BOD=60°+n，∴∠MON=360°－∠AOM－∠AOB－∠BON=360°－（240°-n）－120°－（60°+n）=140°，解得：n=70°．综上所述：n=50°或70°【解析】【解答】解：（1）∠MON= ∠AOB+ ∠COD=100°；【分析】（1）由∠AOM＝∠AOC，∠AOC= ∠AOB，∠AOC=∠AOM+∠MOC得出∠MOC= ∠AOB，又∠BON＝∠BOD，从而由∠MON= ∠AOB+ ∠COD即可算出答案；（2）需要分类讨论：①当0＜n＜60°时，根据旋转的性质得出∠AOC=∠AOB-∠BOC=120°－n，∠BOD=60°－n，由∠MON=∠MOC+∠COB+∠BON整体替换再化简即可得出答案；②当60°＜n＜120°时，根据旋转的性质得出∠AOC=120°－n，∠COD=60°，∠BOD=n-60°，∠MOC= ∠AOC，∠DON= ∠BOD，由∠MON=∠MOC+∠COD+∠DON整体替换再化简即可得出答案；（3）分类讨论：①当0＜n＜60°时，∠BOC=n，∠MON=2n，又∠MON=∠MOB+∠BOC-∠NOC = （120°+n）+60°- （60°+n）=100°，从而列出方程，求解得出n的值；②当60°＜n＜120°时，∠BOC=n，∠MON=2n，∠AOC=360°-（120°+n）=240°－n，∠BOD=60°+n，又∠MON=360°－∠AOM－∠AOB－∠BON，从而整体整体代入化简并列出方程，求解即可。

初一数学上册易错题整理完整版有理数易错题练习（一）一．判断⑴ a 与-a 必有一个是负数 .⑵在数轴上，与原点0相距5个单位长度的点所表示的数是5.⑶在数轴上，A 点表示＋1，与A 点距离3个单位长度的点所表示的数是4.⑷在数轴的原点左侧且到原点的距离等于6个单位长度的点所表示的数的绝对值是-6. ⑸ 绝对值小于4.5而大于3的整数是3、4. ⑺ 如果-x =- (-11)，那么x = -11.⑻ 如果四个有理数相乘，积为负数，那么负因数个数是1个.⑼ 若0,a =则0ab=.⑽绝对值等于本身的数是1. 二．填空题⑴若1a -=a -1，则a 的取值范围是： .⑵式子3-5│x │的最 值是 .⑶在数轴上的A 、B 两点分别表示的数为-1和-15，则线段AB 的中点表示的数是 . ⑷水平数轴上的一个数表示的点向右平移6个单位长度得到它的相反数，这个数是________.⑸在数轴上的A 、B 两点分别表示的数为5和7，将A 、B 两点同时向左平移相同的单位长度，得到的两个新的点表示的数互为相反数，则需向左平移 个单位长度.⑹已知│a │=5，│b │=3，│a +b │= a +b ，则a -b 的值为 ；如果│a +b │= -a -b ，则a -b 的值为 .⑺化简-│π-3│= . ⑻如果a ＜b ＜0，那么1a 1b. ⑼在数轴上表示数-113的点和表示152-的点之间的距离为： .⑽11a b⋅=-，则a 、b 的关系是________.⑾若a b ＜0，bc＜0，则ac 0. ⑿一个数的倒数的绝对值等于这个数的相反数，这个数是 . 三.解答题⑴已知a 、b 互为倒数，- c 与2d互为相反数，且│x │=4，求2ab -2c +d +3x 的值.⑵数a 、b 在数轴上的对应点如图，化简：│a -b │+│b -a │+│b │-│a -│a ││.⑶已知│a +5│=1，│b -2│=3，求a -b 的值. ⑷若|a |=4，|b |=2，且|a ＋b |=a ＋b ，求a - b 的值.⑸把下列各式先改写成省略括号的和的形式，再求出各式的值．①(-7)- (-4)- (＋9)＋(＋2)- (-5)； ②(-5) - (＋7)- (-6)＋4．⑹改错(用红笔，只改动横线上的部分)：⑺比较4a和-4a的大小①已知5.0362=25.36，那么50.362=253.6，0.050362=0.02536；②已知7.4273=409.7，那么74.273=4097，0.074273=0.04097；③已知3.412=11.63，那么(34.1)2=116300；④近似数2.40×104精确到百分位，它的有效数字是2，4；⑤已知5.4953=165.9，x3=0.0001659，则x=0.5495．⑻在交换季节之际，商家将两种商品同时售出，甲商品售价1500元，盈利25%，乙商品售价1500元，但亏损25%，问：商家是盈利还是亏本?盈利,盈了多少?亏本，亏了多少元?⑼若x、y是有理数，且|x|-x=0，|y|+y=0，|y|>|x|，化简|x|-|y|-|x+y|.⑽已知abcd≠0,试说明ac、-ad、bc、bd中至少有一个取正值，并且至少有一个取负值.⑾已知a<0，b<0，c>0，判断(a+b)(c-b)和(a+b)(b-c)的大小.⑿已知:1+2+3……+33=17×33，计算1-3+2-6+3-9+4-12+……+31-93+32-96+33-99的值.四．计算下列各题：⑴(-42.75)×(-27.36)-(-72.64)×(+42.75) ⑵12133344⎛⎫---+----⎪⎝⎭⑶77(35)9-÷+⑷523120001999400016342⎛⎫⎛⎫-+-++-⎪ ⎪⎝⎭⎝⎭⑸221.430.57()33⨯-⨯-⑹6(5)(6)()5-÷-÷-⑺91118×18 ⑻-15×12÷6×5 ⑼24221(10.5)2(3)3⎡⎤---⨯÷---⎣⎦⑽-24-(-2)4⑾33(32)32-⨯+⨯有理数易错题练习（二）一．多种情况的问题（考虑问题要全面） （1）已知：,3=x 则x=_______；,5=-x 则x=_______；(2)绝对值不大于4的负整数是________； (3)绝对值小于4.5而大于3的整数是________．(4)在数轴上，与原点相距5个单位长度的点所表示的数是________；(5)在数轴上，A 点表示＋1，与A 点距离3个单位长度的点所表示的数是________；(6) 平方得412的数是____；此题用符号表示：已知,4122=x 则x=_______； (7)若|a|=|b|，则a,b 的关系是________；（8）若|a|=4，|b|=2，且|a ＋b|=a ＋b ，求a －b 的值．二．特值法帮你解决含字母的问题（此方法只适用于选择、填空）有理数中的字母表示 ，从三类数中各取1——2个特值代入检验，做出正确的选择 (1)若a 是负数，则a________－a ；a --是一个________数；（2）已知,x x -=则x 满足________；若,x x =则x 满足________；若x=-x, x 满足________；若=-<2,2a a 化简____ ；(3)有理数a 、b 在数轴上的对应的位置如图所示： 则（ 0-11abA ．a + b ＜0B ．a + b ＞0;C ．a －b = 0D ．a －b ＞0 （4）如果a 、b 互为倒数，c 、d 互为相反数，且,3=m ，则代数式2ab-（c+d ）+m 2=_______。

七年级上册数学全册单元试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．已知：O是直线AB上的一点，是直角，OE平分．（1）如图1．若．求的度数；（2）在图1中，，直接写出的度数（用含a的代数式表示）；（3）将图1中的绕顶点O顺时针旋转至图2的位置，探究和的度数之间的关系．写出你的结论，并说明理由．【答案】（1）解：∵是直角，，，，∵OE平分，，．（2）解：是直角，，，，∵OE平分，，（3）解：，理由是：，OE平分，，，，，即【解析】【分析】（1）根据平角的定义得出∠BOD，∠COB的度数，根据角平分线的定义得出∠BOE=∠BOC=75°，根据角的和差，由∠DOE=∠BOE−∠BOD即可算出答案；（2）根据平角的定义得出∠BOD90°−a ，∠COB180°−a ，根据角平分线的定义得出∠BOE=∠BOC=90°−a，根据角的和差，由∠DOE=∠BOE−∠BOD即可算出答案；（3）∠AOC=2∠DOE ，根据平角的定义得出∠BOC=180°−∠AOC，根据角平分线的定义得出∠BOE=∠BOC=90°−∠AOC ，根据角的和差得出∠BOD=90°−∠BOC=90°−(180°−∠AOC)=∠AOC−90° ，∠DOE=∠BOD+∠BOE，再整体替换即可得出答案。

2．已知线段AB=6．（1）取线段AB的三等分点，这些点连同线段AB的两个端点可以组成多少条线段？求这些线段长度的和；（2）再在线段AB上取两种点：第一种是线段AB的四等分点；第二种是线段AB的六等分点，这些点连同（1）中的三等分点和线段AB的两个端点可以组成多少条线段？求这些线段长度的和。

【答案】（1）解：如图：点C、D为线段AB的三等分点，可以组成的线段为：3+2+1=6（条），∵AB=6，点C、D为线段AB的三等分点，∴AC=CD=DB=2，AD=BC=4，∴这些线段长度的和为：2+2+2+4+4+6=20.（2）解：再在线段AB上取两种点：第一种是线段AB的四等分点D1、D2、D3；第二种是线段AB的六等分点E1、E2，∴这些点连同（1）中的三等分点和线段AB的两个端点可以组成多少条线段共有1+2+3+…+8=36（条）；根据题意以A为原点，AB为正方向，建立数轴，则各点对应的数为：A：0；B：6；C：2；D：4；D1：1.5；D2：3；D3：4.5；E1：1；E2：5；∴①以A、B为端点的线段有7+7+1=15（条），长度和为：6×8=48；②不以A、B为端点，以E1、E2为端点的线段有5+5+1=11（条），长度和为：4×6=24；③不以A、B、E1、E2为端点，以D1、D3为端点的线段有3+3+1=7（条），长度和为：3×4=12；④不以A、B、E1、E2、D1、D3为端点，以C、D为端点的线段有1+1+1=3（条），长度和为：2×2=4；∴这些线段长度的和为：48+24+12+4=88.【解析】【分析】（1）如图，根据线段的三等分点可分别求得每条线段的长度，再由线段的概念先找出所有线段，从而求得它们的和.（2）再在线段AB上取两种点：第一种是线段AB的四等分点D1、D2、D3；第二种是线段AB的六等分点E1、E2；根据线段定义和数线段的规律求得线段条数；根据题意以A为原点，AB为正方向，建立数轴，则各点对应的数为：A：0；B：6；C：2；D：4；D1：1.5；D2：3；D3：4.5；E1：1；E2：5；再分情况讨论，从而求得所有线段条数和这些线段的长度.3．一副三角板OAC、OBD如图（1）放置，（∠BDO=30°、∠CAO=45°）（1）若OM、ON分别平分∠BOA、∠DOC，求∠MON的度数；（2）将三角板OBD从图（1）绕O点顺时针旋转如图（2），若OM、ON分别平分∠BOA、∠DOC，则在旋转过程中∠MON如何变化？（3）若三角板OBD从图（1）绕O点逆时针旋转如图（3），若其它条件不变，则（2）的结论是否成立？（4）若三角板OBD从图（1）绕O点逆时针旋转，其它条件不变，在旋转过程中，∠MON是否一直不变，在备用图中画图说明．【答案】（1）解：∵OM、ON分别平分∠BOA、∠DOC∴∠AOM=∠BOA，∠AON=∠AOC∵∠MON=∠AOM+∠AON=（∠BOA+∠AOC）∵∠BDO=30°、∠CAO=45°∴∠AOB=90°，∠AOC=45°∴∠MON= （90°+45°）=67.5°答：∠MON的度数为67.5°.（2）解：设∠AOM=∠BOM=x，∠CON=∠DON=y，∠AOD=α则：2x+α=90°，2y+α=45°，∴2x+2y+2α=135°，∴∠MON=x+y+α=67.5°（3）解：（2）的结论成立理由：设∠AOM=∠BOM=x，∠CON=∠DON=y，∠AOD=α则：2x-α=90°，2y-α=45°，∴2x+2y-2α=135°，∴∠MON=x+y-α=67.5°∠MON=x+y-α=67.5°（4）解：在变化，有时∠MON=112.5°。

七年级数学上册全册单元测试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．在数轴上、两点分别表示有理数和，我们用表示到之间的距离；例如表示7到3之间的距离.（1）当时，的值为________.（2）如何理解表示的含义？（3）若点、在0到3（含0和3）之间运动，求的最小值和最大值.【答案】（1）5或-3（2）解：∵ = ，∴表示到-2的距离（3）解：∵点、在0到3（含0和3）之间运动，∴0≤a≤3, 0≤b≤3,当时， =0+2=2，此时值最小，故最小值为2；当时， =2+5=7，此时值最大，故最大值为7【解析】【解答】（1）∵，∴a=5或-3；故答案为：5或-3；【分析】（1）此题就是求表示数a的点与表示数1的点之间的距离是4，根据表示数a的点在表示数1的点的右边与左边两种情况考虑即可得出答案；（2）此题就是求表示数b的点与表示数-2的点之间的距离;（3）此题就是求表示数a的点与表示数2的点之间的距离及表示数b的点与表示数-2的点之间的距离和，而0≤a≤3, 0≤b≤3, 借助数轴当时，的值最小；当时，的值最大.2．已知线段AB= ,点P从点A出发沿射线AB以每秒3个单位长度的速度运动,同时点Q 从点B出发沿射线AB以每秒2个单位长度的速度运动,M、N分别为AP、BQ的中点,运动的时间为（1）若求的值,并写出此时P、Q之间的距离；（2）点M、N能否重合为一点,若能,请直接写出此时线段PQ与线段AB之间的数量关系；若不能,说明理由。

【答案】（1）解：设A点表示的数为原点，则B点表示的数为12，P点表示的数为3t，则M点表示的数为 t，点Q表示的数为12+2t，点N表示的数为12+t，M在N左侧，MN=12+t- t=12- t，∵MN= =4，∴12- t=4，解得t=16；此时PQ的距离为 =4M在N右侧，MN= t-12-t-= t-12，∵MN= =4，∴ t-12=4，解得t=32；此时PQ的距离为 =20（2）解：AB的距离为a，则B点表示的数为a，P点表示的数为3t，则M点表示的数为t，点Q表示的数为a+2t，点N表示的数为a+t，∵M，N重合∴ t=a+t，得t=2a，则P点表示的数为3t=6a, Q表示的数为a+2t=5a，∴PQ的距离为a，故PQ=AB【解析】【分析】（1）设A点表示的数为原点，则B点表示的数为12，P点表示的数为3t，则M点表示的数为 t，点Q表示的数为12+2t，点N表示的数为12+t，再根据，分情况讨论即可.（2）AB的距离为a，则B点表示的数为a，P点表示的数为3t，则M点表示的数为 t，点Q表示的数为a+2t，点N表示的数为a+t，根据MN重合可得出a，t之间的关系，即可解出PQ与AB之间的关系.3．如图1，是直线上的点，线段，点分别是线段的中点.（1）求线段的长；（2）若，点在直线上，，求线段的长；（3）若，点在直线上，，请直接写出线段的长________ .（用含的式子表示）【答案】（1）解：∵点分别是线段的中点，∴，∴（2）解：由（1）知由，当点在点左侧时，，当点在点右侧时，；∴OE的长为8cm或18cm.（3）或或【解析】【解答】解：（3）∵E为BC中点，∴BE= ，当点O在点A左边时，OE=16- +b，当点O在线段AE上时，OE=16- -b，当点O在线段BE上时，OE= -(16-b)=b+ -16，当点O在B点右边时，OE=b+ -16，故答案为：或或 .【分析】（1）由中点的定义可得DC= AC，BE= BC，根据DE=DC+CE即可得答案；（2）由中点定义可求出BE的长，分别讨论点O在点A左边和右边两种情况，根据线段间的和差关系求出OE的长即可；（3）分别讨论点O在点A左边、线段AE上、线段BE上和点B 右边的情况，根据线段的和差关系即可得答案.4．如图，OM是∠AOC的平分线，ON是∠BOC的平分线.（1）如图1，当∠AOB＝90°，∠BOC＝60°时，∠MON的度数是多少？为什么？（2）如图2，当∠AOB＝70°，∠BOC＝60°时，∠MON＝________度.（直接写出结果）（3）如图3，当∠AOB＝α，∠BOC＝β时，猜想：∠MON的度数是多少？为什么？【答案】（1）解：如图1，∵∠AOB＝90°，∠BOC＝60°，∴∠AOC＝∠AOB+∠BOC＝90°+60°＝150°，∵OM是∠AOC的平分线，ON是∠BOC的平分线，∴∠MOC＝∠AOC＝75°，∠NOC＝∠BOC＝30°，∴∠MON＝∠MOC﹣∠NOC＝75°﹣30°＝45°；（2）35（3）解：如图3，∵∠AOB＝α，∠BOC＝β，∴∠AOC＝∠AOB+∠BOC＝α+β，∵OM是∠AOC的平分线，ON是∠BOC的平分线，∴∠MOC＝∠AOC＝（α+β），∠NOC＝∠BOC＝β，∴∠MON＝∠MOC﹣∠NOC＝（α+β）﹣β＝α.【解析】【解答】解：（2）如图2，∵∠AOB＝70°，∠BOC＝60°，∴∠AOC＝70°+60°＝130°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC＝65°，∠NOC＝∠BOC＝30°，∴∠MON＝∠MOC﹣∠NOC＝65°﹣30°＝35°.故答案为：35.【分析】（1）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON＝∠MOC﹣∠NOC求出即可；（2）求出∠AOC度数，求出∠MOC和∠NOC的度数，代入∠MON＝∠MOC﹣∠NOC求出即可；（3）表示出∠AOC度数，表示出∠MOC和∠NOC的度数，代入∠MON＝∠MOC﹣∠NOC求出即可.5．我们学过角的平分线的概念类比给出新概念：从一个角的顶点出发把这个角分成1：2的两个角的射线，叫做这个角的三分线显然，一个角的三分线有两条，例如：如图1，若∠BOC=2∠AOC，则OC是∠AOB的一条三分线。

数学七年级上册全册单元试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．如图，数轴上点 A、B 到表示-2 的点的距离都为 6，P 为线段 AB 上任一点，C，D 两点分别从 P，B 同时向 A 点移动，且 C 点运动速度为每秒 2 个单位长度，D 点运动速度为每秒 3 个单位长度，运动时间为 t 秒.（1）A 点表示数为________，B 点表示的数为________，AB=________.（2）若 P 点表示的数是 0，①运动 1 秒后，求 CD 的长度；②当 D 在 BP 上运动时，求线段 AC、CD 之间的数量关系式.（3）若 t=2 秒时，CD=1，请直接写出 P 点表示的数.【答案】（1）-8；4；12（2）解：①运动一秒后，C点为-2，D点为1，所以CD=3；②当点D在BP上运动时， ,此时C在线段AP上，AC=8-2t，CD=2t+4-3t=4-t，所以AC=2CD（3）解：若 t=2秒时，D点为-2，若 CD=1，则 C=-3 或-1，①当 C=-3 时，CP=4，此时 P=1；②当 C=-1 时，P=3.【解析】【解答】解：⑴故答案为：-8;4;12；【分析】（1）由已知数轴上点 A、B 到表示-2 的点的距离都为 6 ，且点A在点B的左边，就可求出点A和点B表示的数，再利用两点间的距离公式求出AB的长。

（2）①由点A、B表示的数及点C、D的运动速度和方向，可得出运动1秒后点C、D分别表示的数，再求出CD的长；②当点D在BP上时，根据t的取值范围，分别用含t的代数式表示出AC、CD的长，就可得出AC、CD的数量关系。

（3）根据t的值及CD的长，就可得出点C表示的数，从而就可求出点P所表示的数。

2．如图1，已知∠AOB=140°，∠AOC=30°，OE是∠AOB内部的一条射线，且OF平分∠AOE．（1）若∠EOB=30°，则∠COF=________；（2）若∠COF=20°，则∠EOB=________；（3）若∠COF=n°，则∠EOB=________（用含n的式子表示）．（4）当射线OE绕点O逆时针旋转到如图2的位置时，请把图补充完整；此时，∠COF与∠EOB有怎样的数量关系？请说明理由．【答案】（1）20°（2）40°（3）80°-2n°（4）如图所示：∠EOB=80°+2∠COF．证明：设∠COF=n°，则∠AOF=∠AOC-∠COF=30°-n°，又∵OF平分∠AOE，∴∠AOE=2∠AOF=60°-2n°．∴∠EOB=∠AOB-∠AOE=140°-（60°-2n°）=（80+2n）°即∠EOB=80°+2∠COF．【解析】【解答】（1）∵∠AOB=140°，∠EOB=30°，∴∠AOE=∠AOB-∠EOB=140°-30°=110°，∵OF平分∠AOE，∴∠AOF= ∠AOE= ×110°=55°，∴∠COF=∠AOF-∠AOC，=55°-30°，=25°；故答案为：25°；（2）∵∠AOC=30°，∠COF=20°，∴∠AOF=∠AOC+∠COF=30°+20°=50°，∵OF平分∠AOE，∴∠AOE=2∠AOF=2×50°=100°，∴∠EOB=∠AOB-∠AOE=140°-100°=40°；故答案为：40°；（3）∵∠AOC=30°，∠COF=n°，∴∠AOF=∠AOC+∠COF=30°+n°，∵OF平分∠AOE，∴∠AOE=2∠AOF=2（30°+n°）=60°+2n°，∴∠EOB=∠AOB-∠AOE=140°-（60°+2n°）=80°-2n°；故答案为：80°-2n°；【分析】（1）根据∠AOE=∠AOB-∠EOB先求出∠AOE，再根据角平分线的定义求出∠AOF，最后根据∠COF=∠AOF-∠AOC解答即可；（2）根据∠AOF=∠AOC+∠COF先求出∠AOF，再根据角平分线的定义求出∠AOE，最后根据∠EOB=∠AOB-∠AOE解答即可；（3）与（2）的思路相同求解即可；（4）设∠COF=n°，先表示出∠AOF，再根据角平分线的定义求出∠AOE，最后根据∠EOB=∠AOB-∠AOE解答即可．3．如图，两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置，PA、PB与直线MN重合，且三角板PAC、三角板PBD均可绕点P逆时针旋转.（1）直接写出∠DPC的度数.（2）如图②，在图①基础上，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为5°/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为1°/秒，（当PA转到与PM重合时，两三角板都停止转动），在旋转过程中，当PC与PB重合时，求旋转的时间是多少？（3）在（2）的条件下，PC、PB、PD三条射线中，当其中一条射线平分另两条射线的夹角时，请直接写出旋转的时间.【答案】（1）解：∠DPC=180°-∠APC-∠BPD=180°-60°-30°=90°故答案为：90°（2）解：设旋转的时间是t秒时PC与PB重合，根据题意列方程得5t-t=30+90解得t=30又∵180÷5=36秒∴30＜36故旋转的时间是30秒时PC与PB重合（3）解：设t秒时其中一条射线平分另两条射线的夹角，分三种情况：①当PD平分∠BPC时，5t-t=90-30，解得t=15②当PC平分∠BPC时，，解得t=26.25③当PB平分∠DPC时，5t-t=90-2×30，解得t=37.5故15秒或26.25秒或37.5秒时其中一条射线平分另两条射线的夹角【解析】【分析】（1）易得∠DPC=180°-∠APC-∠BPD即可求（2）只需设旋转的时间是t 秒时PC与PB重合，列方程解可得（3）一条射线平分另两条射线的夹角，分三种情况：当PD平分∠BPC时；当PC平分∠BPC时；当PB平分∠DPC时，计算每种情况对应的时间即可.4．如图1，在四边形ABCD中，点E为AB延长线上一点，连接并延长交AD延长线于点，， .（1）求证：；（2）如图2，连接交于点，连接，若为的角平分线，为的角平分线，过点作交于点，求证：；（3）在（2）的条件下，若，，求的度数.【答案】（1）证明：，，，，，；（2）证明：过点作为的角平分线，为的角平分线，设由（1）问可知，，，，，，，，，，，，；（3）解：由（2）得，，，，，，，，，，，，，，过点作，【解析】【分析】（1）先根据平行线的判定证明AF∥BC，可得∠FDC=∠DCB，由已知可得∠CBE=∠DCB，由平行线的判定可得结论；（2）先根据垂直得∠HBC=90°=∠CBE+∠ABH，设，则∠ABH ，由平行线和角平分线的定义可推出，；，即可得结论；（3）根据第（2）的结论，可得，由三角形的内角和得，根据已知可得，过点作，由平行线的性质及已知条件可得∠BFE=30°．5．如图 1，射线 OC在∠AOB的内部，图中共有 3个角：∠AOB、∠AOC 和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线 OC是∠AOB的奇妙线.（1）一个角的角平分线________这个角的奇妙线.（填是或不是）；（2）如图 2，若∠MPN＝60°，射线 PQ绕点 P从 PN位置开始，以每秒 10°的速度逆时针旋转，当∠QPN首次等于 180°时停止旋转，设旋转的时间为 t（s）.①当 t为何值时，射线 PM是∠QPN 的奇妙线？②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转，并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.【答案】（1）是（2）解：①∠MPN=60，∠QPM=10t－60，∠QPN=10t(最大角)，当∠MPN=2∠QPM时，60=2(10t－60)，解得t=9；当∠QPN=2∠MPN时，10t =2×60，解得t=12；当∠QPM=2∠MPN时，10t－60=2×60，解得t=18；综上，当t的值是9或12或18时，射线 PM是∠QPN 的奇妙线.②∠QPN=10t，∠QPM=60－10t+5t=60－5t，∠MPN=60+5t(最大角)，当∠QPM=2∠QPN时， 60－5t =2×10t ，解得t= ；当∠MPN=2∠QPN时，60+5t =2×10t，解得t=4；当∠QPN=2∠QPM时，10t =2×(60－5t)，解得t=6；综上，当射线 PQ是∠MPN的奇妙线时 t的值为或4或6.故答案为：(1)是；(2) ①当t的值是9或12或18时，射线PM是∠QPN 的奇妙线；②当射线 PQ是∠MPN的奇妙线时 t的值为或4或6.【解析】【分析】（1）根据奇妙线定义即可求解；（2）①分3种情况，根据奇妙线定义列方程求解即可；②分3种情况，根据奇妙线定义列方程求解即可.6．如图，O为直线AB上一点，∠BOC＝36°.（1）若OD平分∠AOC，∠DOE＝90°，如图（a)所示，求∠AOE的度数：（2）若∠AOD＝∠AOC，∠DOE＝60°，如图(b）所示，求∠AOE的度数：（3）若∠AOD＝∠AOC，∠DOE＝(n≥2，且n为正整数)，如图(c)所示，请用n含的代数式表示∠AOE的度数________(直接写出结果).【答案】（1）解：∵∠BOC＝36°，OD平分∠AOC，∴∠AOD＝∠DOC＝72°，∵∠DOE＝90°，则∠AOE＝90°−72°＝18°；故答案为：18°（2）解：设∠AOD＝x，则∠DOC＝2x，∠BOC＝180°−3x＝36°，解得：x＝48°，∴∠AOE＝60°－x＝60°−48°＝12°（3） .【解析】【解答】（3）设∠AOD＝x，则∠DOC＝（n−1）x，∠BOC＝180°－nx＝36°，解得：x＝，∴∠AOE＝－＝．【分析】（1）利用角平分线的性质得出∠AOD＝∠DOC＝72°，进而得出∠AOE的度数；（2）设∠AOD＝x，则∠DOC＝2x，∠BOC＝180°−3x＝36°，得出x的值，进而得出∠AOE 的度数；（3）利用（2）中作法，得出x与α的关系，进而得出答案．7．如图，E是直线AC上一点，EF是∠AEB的平分线.（1）如图1，若EG是∠BEC的平分线，求∠GEF的度数；（2）如图2，若GE在∠BEC内，且∠CEG=3∠BEG，∠GEF=75°，求∠BEG的度数.（3）如图3，若GE在∠BEC内，且∠CEG=n∠BEG，∠GEF=α，求∠BEG（用含n、α的代数式表示）.【答案】（1）解：∵EF是∠AEB的平分线，∴∠BEF= ∠AEB，∵EG是∠BEC的平分线，∴∠BEG= ∠BEC，∴∠GEF=∠BEF+∠BEG= （∠AEB+∠BEC）=90°（2）解：∵∠GEF=75°，∴∠BEF=75°-∠BEG，∵EF是∠AEB的平分线，∴∠AEB=2∠BEF=150°-2∠BEG，∵∠CEG=3∠BEG，∴∠BEG+3∠BEG+150°-2∠BEG=180°，∴∠BEG=15°（3）解：∵∠GEF=α，∴∠BEF=α-∠BEG，∵EF是∠AEB的平分线，∴∠AEB=2∠BEF=2α-2∠BEG，∵∠CEG=n∠BEG，∴∠BEG+n∠BEG+2α-2∠BEG=180°，∴∠BEG=【解析】【分析】（1）由角平分线的性质可得∠BEF=∠AEB；∠BEG=∠BEC；然后结合图形得∠GEF=∠BEF+∠BEG=（∠AEB+∠BEC），根据平角的意义即可求解；（2）由角的构成可得∠BEF=∠GEF-∠BEG，由角平分线的性质可得∠AEB=2∠BEF=2（∠GEF-∠BEG），由平角的意义可得∠CEG+∠BEG+∠AEB=180°，于是把∠CEG、∠BEG、∠AEB代入等式可得关于∠BEG的方程，解方程即可求解；（3）用（2）的方法可求解。

人教版数学七年级上册全册单元试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．（1）如图①，已知：Rt△ABC中，AB=AC，直线m经过点A，BD⊥m于D，CE⊥m于E，求证：DE=BD+CE；（2）如图②，将(1)中的条件改为：△ABC中，AB=AC，并且∠BDA=∠AEC=∠BAC=α，α为任意锐角或钝角，请问结论DE=BD+CE是否成立？如成立，请证明；若不成立，请说明理由；（3）应用：如图③，在△ABC中，∠BAC是钝角，AB=AC，∠BAD＞∠CAE，∠BDA=∠AEC=∠BAC，直线m与BC的延长线交于点F，若BC=2CF，△ABC的面积是12，求△ABD与△CEF的面积之和．【答案】（1）证明：∵BD⊥直线m，CE⊥直线m，∴∠BDA=∠CEA=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°，∴∠CAE=∠ABD，在△ADB和△CEA中，∴△ADB≌△CEA(AAS)，∴AE=BD，AD=CE，∴DE=AE+AD=BD+CE；（2）解：结论DE=BD+CE成立；理由如下：∵∠BDA=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α，∴∠CAE=∠ABD，在△ADB和△CEA中，∴△ADB≌△CEA(AAS)，∴AE=BD，AD=CE，∴DE=AE+AD=BD+CE；（3）解：∵∠BAD>∠CAE，∠BDA=∠AEC=∠BAC，∴∠CAE=∠ABD，在△ABD和△CEA中，∴△ABD≌△CEA(AAS)，∴S△ABD=S△CEA，设△ABC的底边BC上的高为h，则△ACF的底边CF上的高为h，∴S△ABC= BC•h=12，S△ACF= CF•h，∵BC=2CF，∴S△ACF=6，∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6，∴△ABD与△CEF的面积之和为6．【解析】【分析】（1）根据BD⊥直线m，CE⊥直线m得∠BDA=∠CEA=90°，而∠BAC=90°，根据等角的余角相等得∠CAE=∠ABD，由AAS证得△ADB≌△CEA，则AE=BD，AD=CE，即可得出结论；（2）由∠BDA=∠BAC=α，则∠DBA+∠BAD=∠BAD+∠CAE=180°-α，得出∠CAE=∠ABD，由AAS证得△ADB≌△CEA即可得出答案；（3）由∠BAD＞∠CAE，∠BDA=∠AEC=∠BAC，∴∠CAE=∠ABD，得出∠CAE=∠ABD，由AAS证得△ADB≌△CEA，得出S△ABD=S△CEA，再由不同底等高的两个三角形的面积之比等于底的比，得出S△ACF即可得出结果．2．如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为________；（2）当△PMN所放位置如图②所示时，求证：∠PFD−∠AEM＝90°；（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．【答案】（1）∠PFD＋∠AEM=90°（2）过点P作PG∥AB∵AB∥CD，∴PG∥AB∥CD，∴∠AEM=∠MPG，∠PFD=∠NPG∵∠MPN=90°∴∠NPG－∠MPG=90°∴∠PFD－∠AEM=90°；（3）设AB与PN交于点H∵∠P=90°，∠PEB＝15°∴∠PHE=180°－∠P－∠PEB＝75°∵AB∥CD，∴∠PFO=∠PHE=75°∴∠N=∠PFO－∠DON=45°．【解析】【解答】（1）过点P作PH∥AB∵AB∥CD，∴PH∥AB∥CD，∴∠AEM=∠MPH，∠PFD=∠NPH∵∠MPN=90°∴∠MPH＋∠NPH=90°∴∠PFD＋∠AEM=90°故答案为：∠PFD＋∠AEM=90°；【分析】（1）过点P作PH∥AB，然后根据平行于同一条直线的两直线平行可得PH∥AB∥CD，根据平行线的性质可得∠AEM=∠MPH，∠PFD=∠NPH，然后根据∠MPH＋∠NPH=90°和等量代换即可得出结论；（2）过点P作PG∥AB，然后根据平行于同一条直线的两直线平行可得PG∥AB∥CD，根据平行线的性质可得∠AEM=∠MPG，∠PFD=∠NPG，然后根据∠NPG－∠MPG=90°和等量代换即可证出结论；（3）设AB与PN 交于点H，根据三角形的内角和定理即可求出∠PHE，然后根据平行线的性质可得∠PFO=∠PHE，然后根据三角形外角的性质即可求出结论．3．点A、B在数轴上分别表示实数a、b，A、B两点之间的距离记作AB．当A、B两点中有一点为原点时，不妨设A点在原点．如图①所示，则AB＝OB＝|b|＝|a﹣b|．当A、B两点都不在原点时：⑴如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB﹣OA＝|b|﹣|a|＝b﹣a＝|b﹣a|＝|a﹣b|⑵如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB﹣OA＝|b|﹣|a|＝﹣b﹣(﹣a)＝a﹣b＝|a﹣b|⑶如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB+OA＝|b|+|a|＝a+(﹣b)＝|a﹣b|回答下列问题：（1）综上所述，数轴上A、B两点之间的距离AB＝________．（2）数轴上表示2和﹣4的两点A和B之间的距离AB＝________．（3）数轴上表示x和﹣2的两点A和B之间的距离AB＝________，如果AB＝2，则x的值为________．（4）若代数式|x+2|+|x﹣3|有最小值，则最小值为________．【答案】（1）（2）6（3）；0或－4（4）5【解析】【解答】(1)综上所述，数轴上A、B两点之间的距离 (2)数轴上表示2和－4的两点A和B之间的距离 (3)数轴上表示和－2的两点A和B之间的距离如果，则的值为或由题意可知：当x在−2与3之间时，此时，代数式|x+2|+|x−3|取最小值，最小值为故答案为：（1）；（2）6；（3），0或－4；（4）5.【分析】（1）发现规律：在数轴上两点之间的距离为这两点所表示的数的差的绝对值，故可求解；（2）根据（1），即可直接求出结果；（3）先根据（1）即可表示出AB；当AB=2时，得到方程，解出x的值即可；（4）|x+2|+|x-3|表示数轴上一点到-2与3两点的距离的和，当这点是-2或5或在它们之间时和最小，最小距离是-2与3之间的距离。

七年级上册数学易错题精选及讲解答案集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#有理数部分1．填空：(1)当a________时，a与－a必有一个是负数；(2)在数轴上，与原点0相距5个单位长度的点所表示的数是________；(3)在数轴上，A点表示＋1，与A点距离3个单位长度的点所表示的数是________；(4)在数轴的原点左侧且到原点的距离等于6个单位长度的点所表示的数的绝对值是_______．错解 (1)a为任何有理数；(2)＋5；(3)＋3；(4)－6．2．用“有”、“没有”填空：在有理数集合里，________最大的负数，________最小的正数，________绝对值最小的有理数．错解有，有，没有．3．用“都是”、“都不是”、“不都是”填空：(1)所有的整数________负整数；(2)小学里学过的数________正数；(3)带有“＋”号的数________正数；(4)有理数的绝对值________正数；(5)若|a|＋|b|=0，则a，b________零；(6)比负数大的数________正数．错解 (1)都不是；(2)都是；(3)都是；(4)都是；(5)不都是；(6)都是．4．用“一定”、“不一定”、“一定不”填空：(1)－a________是负数；(2)当a＞b时，________有|a|＞|b|；(3)在数轴上的任意两点，距原点较近的点所表示的数________大于距原点较远的点所表示的数；(4)|x|＋|y|________是正数；(5)一个数________大于它的相反数；(6)一个数________小于或等于它的绝对值；错解 (1)一定；(2)一定；(3)一定不；(4)一定；(5)一定；(6)不一定．5．把下列各数从小到大，用“＜”号连接：并用“＞”连接起来．8．填空：(1)如果－x=－(－11)，那么x=________；(2)绝对值不大于4的负整数是________；(3)绝对值小于而大于3的整数是________．错解 (1)11；(2)－1，－2，－3；(3)4．9．根据所给的条件列出代数式：(1)a，b两数之和除a，b两数绝对值之和；(2)a与b的相反数的和乘以a，b两数差的绝对值；(3)一个分数的分母是x，分子比分母的相反数大6；(4)x，y两数和的相反数乘以x，y两数和的绝对值．10．代数式－|x|的意义是什么错解代数式－|x|的意义是：x的相反数的绝对值．11．用适当的符号(＞、＜、≥、≤)填空：(1)若a是负数，则a________－a；(2)若a是负数，则－a_______0；(3)如果a＞0，且|a|＞|b|，那么a________ b．错解 (1)＞；(2)＜；(3)＜．12．写出绝对值不大于2的整数．错解绝对值不大2的整数有－1，1．13．由|x|=a能推出x=±a吗错解由|x|=a能推出x=±a．如由|x|=3得到x=±3，由|x|=5得到x=±5．14．由|a|=|b|一定能得出a=b吗错解一定能得出a=b．如由|6|=|6|得出6=6，由|－4|=|－4|得－4=－4．15．绝对值小于5的偶数是几错解绝对值小于5的偶数是2，4．16．用代数式表示：比a的相反数大11的数．错解－a－11．17．用语言叙述代数式：－a－3．错解代数式－a－3用语言叙述为：a与3的差的相反数．18．算式－3＋5－7＋2－9如何读错解算式－3＋5－7＋2－9读作：负三、正五、减七、正二、减九．19．把下列各式先改写成省略括号的和的形式，再求出各式的值．(1)(－7)－(－4)－(＋9)＋(＋2)－(－5)；(2)(－5)－(＋7)－(－6)＋4．解(1)(－7)－(－4)－(＋9)＋(＋2)－(－5)=－7－4＋9＋2－5=－5；(2)(－5)－(＋7)－(－6)＋4=5－7＋6－4=8．20．计算下列各题：(2)5－|－5|=10；21．用适当的符号(＞、＜、≥、≤)填空：(1)若b为负数，则a＋b________a；(2)若a＞0，b＜0，则a－b________0；(3)若a为负数，则3－a________3．错解 (1)＞；(2)≥；(3)≥．22．若a为有理数，求a的相反数与a的绝对值的和．错解－a＋|a|=－a＋a=0．23．若|a|=4，|b|=2，且|a＋b|=a＋b，求a－b的值．错解由|a|=4，得a=±4；由|b|=2，得b=±2．当a=4，b=2时，a－b=2；当a=4，b=－2时，a－b=6；当a=－4，b=2时，a－b=－6；当a=－4，b=－2时，a－b=－2．24．列式并计算：－7与－15的绝对值的和．错解 |－7|＋|－15|=7＋15=22．25．用简便方法计算：26．用“都”、“不都”、“都不”填空：(1)如果ab≠0，那么a，b________为零；(2)如果ab＞0，且a＋b＞0，那么a，b________为正数；(3)如果ab＜0，且a＋b＜0，那么a，b________为负数；(4)如果ab=0，且a＋b=0，那么a，b________为零．错解 (1)不都；(2)不都；(3)都；(4)不都．27．填空：(3)a，b为有理数，则－ab是_________；(4)a，b互为相反数，则(a＋b)a是________．错解 (1)负数；(2)正数；(3)负数；(4)正数．28．填空：(1)如果四个有理数相乘，积为负数，那么负因数个数是________；错解 (1)3；(2)b＞0．29．用简便方法计算：解30．比较4a和－4a的大小：错解因为4a是正数，－4a是负数．而正数大于负数，所以4a＞－4a．31．计算下列各题：(5)－15×12÷6×5．解=－48÷(－4)=12；(5)－15×12÷6×5错解因为|a|=|b|，所以a=b．=1＋1＋1=3．34．下列叙述是否正确若不正确，改正过来．(1)平方等于16的数是(±4)2；(2)(－2)3的相反数是－23；错解 (1)正确；(2)正确；(3)正确．35．计算下列各题；(1)－；(2)2×32．解36．已知n为自然数，用“一定”、“不一定”或“一定不”填空：(1)(－1)n＋2________是负数；(2)(－1)2n＋1________是负数；(3)(－1)n＋(－1)n＋1________是零．错解 (1)一定不；(2)不一定；(3)一定不．37．下列各题中的横线处所填写的内容是否正确若不正确，改正过来．(1)有理数a的四次幂是正数，那么a的奇数次幂是负数；(2)有理数a与它的立方相等，那么a=1；(3)有理数a的平方与它的立方相等，那么a=0；(4)若|a|=3，那么a3=9；(5)若x2=9，且x＜0，那么x3=27．38．用“一定”、“不一定”或“一定不”填空：(1)有理数的平方________是正数；(2)一个负数的偶次幂________大于这个数的相反数；(3)小于1的数的平方________小于原数；(4)一个数的立方________小于它的平方．错解 (1)一定；(2)一定；(3)一定；(4)一定不．39．计算下列各题：(1)(－3×2)3＋3×23；(2)－24－(－2)4；(3)－2÷(－4)2；解(1)(－3×2)3＋3×23=－3×23＋3×23=0；(2)－24－(－2)4=0；40．用科学记数法记出下列各数：.000034．错解.14×106；(2)=×10－4．41．判断并改错(只改动横线上的部分)：(1)用四舍五入得到的近似数有4个有效数字．(2)用四舍五入法，把精确到千分位的近似数是．(3)由四舍五入得到的近似数和是一样的．(4)由四舍五入得到的近似数万，它精确到十分位．42．改错(只改动横线上的部分)：(1)已知=，那么=，=；(2)已知=，那么=4097，=；(3)已知=，那么2=116300；(4)近似数×104精确到百分位，它的有效数字是2，4；(5)已知=，x3=，则x=．有理数·错解诊断练习正确答案1．(1)不等于0的有理数；(2)＋5，－5；(3)－2，＋4；(4)6．2．(1)没有；(2)没有；(3)有．3．(1)不都是；(2)不都是；(3)不都是；(4)不都是；(5)都是；(6)不都是．原解错在没有注意“0”这个特殊数(除(1)、(5)两小题外)．4．(1)不一定；(2)不一定；(3)不一定；(4)不一定；(5)不一定；(6)一定．上面5，6，7题的原解错在没有掌握有理数特别是负数大小的比较．8．(1)－11；(2)－1，－2，－3，－4；(3)4，－4．10．x绝对值的相反数．11．(1)＜；(2)＞；(3)＞．12．－2，－1，0，1，2．13．不一定能推出x=±a，例如，若|x|=－2．则x值不存在．14．不一定能得出a=b，如|4|=|－4|，但4≠－4．15．－2，－4，0，2，4．16．－a＋11．17．a的相反数与3的差．18．读作：负三、正五、负七、正二、负九的和，或负三加五减七加二减九．19．(1)原式=－7＋4－9＋2＋5=－5；(2)原式=－5－7＋6＋4=－2．21．＜；＞；＞．22．当a≥0时，－a＋|a|=0，当a＜0时，－a＋|a|=－2a．23．由|a＋b|=a＋b知a＋b≥0，根据这一条件，得a=4，b=2，所以a－b=2；a=4，b=－2，所以a－b=6．24．－7＋|－15|=－7＋15=8．26．(1)都不；(2)都；(3)不都；(4)都．27．(1)正数、负数或零；(2)正数、负数或零；(3)正数、负数或零；(4)0．28．(1)3或1；(2)b≠0．30．当a＞0时，4a＞－4a；当a=0时，4a=－4a；当a＜0时，4a＜－4a．(5)－150．32．当b≠0时，由|a|=|b|得a=b或a=－b，33．由ab＞0得a＞0且b＞0，或a＜0且b＜0，求得原式值为3或－1．34．(1)平方等于16的数是±4；(2)(－2)3的相反数是23；(3)(－5)100．36．(1)不一定；(2)一定；(3)一定．37．(1)负数或正数；(2)a=－1，0，1；(3)a=0，1；(4)a3＝±27；(5)x3＝－27．38．(1)不一定；(2)不一定；(3)不一定；(4)不一定．40．(1)×108；(2)×10-5．41．(1)有3个有效数字；(2)；(3)不一样；(4)千位．42．(1)2536，；(2)409700，；(3)341；(4)百位，有效数字2，4，0；(5)．整式的加减例1 下列说法正确的是（）A. 的指数是0B. 没有系数C. －3是一次单项式D. －3是单项式分析：正确答案应选D。