小学奥数分数求和专题归纳与总结

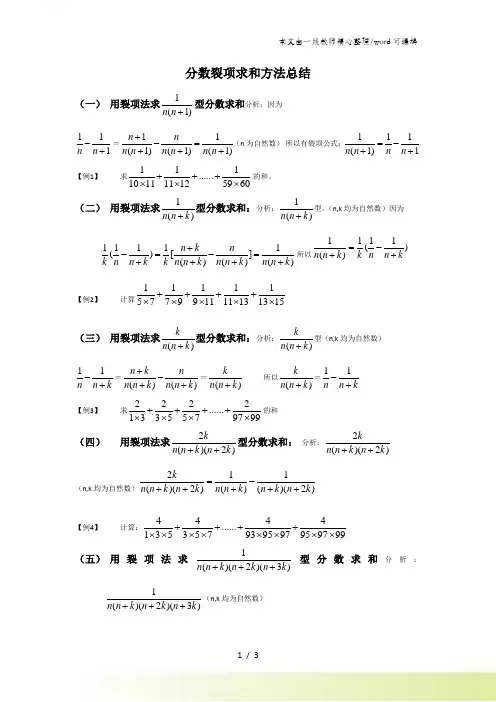
分数裂项求和方法总结（一） 用裂项法求1(1)n n +型分数求和分析：因为 111n n -+＝11(1)(1)(1)n n n n n n n n +-=+++（n 为自然数） 所以有裂项公式：111(1)1n n n n =-++ 【例1】 求111 (101111125960)+++⨯⨯⨯的和。

（二） 用裂项法求1()n n k +型分数求和：分析：1()n n k +型。

（n,k 均为自然数）因为 11111()[]()()()n k n k n n k k n n k n n k n n k +-=-=++++所以1111()()n n k k n n k =-++【例2】 计算11111577991111131315++++⨯⨯⨯⨯⨯（三） 用裂项法求()k n n k +型分数求和：分析：()k n n k +型（n,k 均为自然数） 11n n k -+＝()()n k n n n k n n k +-++＝()k n n k + 所以()k n n k +＝11n n k -+ 【例3】 求2222 (1335579799)++++⨯⨯⨯⨯的和 （四） 用裂项法求2()(2)k n n k n k ++型分数求和： 分析：2()(2)k n n k n k ++ （n,k 均为自然数）211()(2)()()(2)k n n k n k n n k n k n k =-+++++【例4】 计算：4444......135357939597959799++++⨯⨯⨯⨯⨯⨯⨯⨯ （五） 用裂项法求1()(2)(3)n n k n k n k +++型分数求和分析：1()(2)(3)n n k n k n k +++（n,k 均为自然数）【例5】 计算：111......1234234517181920+++⨯⨯⨯⨯⨯⨯⨯⨯⨯（六） 用裂项法求3()(2)(3)k n n k n k n k +++型分数求和： 分析：3()(2)(3)k n n k n k n k +++（n,k 均为自然数） 【例6】 计算：333 (1234234517181920)+++⨯⨯⨯⨯⨯⨯⨯⨯⨯ 【例7】计算：71＋83＋367＋5629＋6337＋7241＋7753＋8429＋883 【分析与解】解答此题时，我们应将分数分成两类来看，一类是把5629、6337、7241、7753这四个分数，可以拆成是两个分数的和。

分数求和分数求和的常用方法：1、公式法，直接运用一些公式来计算，如等差数列求和公式等。

2、图解法，将算式或算式中的某些部分的意思，用图表示出来，从而找出简便方法。

3、裂项法，在计算分数加、减法时，先将其中的一些分数做适当的拆分，使得其中一部分分数可以互相抵消，从而使计算简便。

4、分组法，运用运算定律，将原式重新分组组合，把能凑整或约分化简的部分结合在一起简算。

5、代入法，将算式中的某些部分用字母代替并化简，然后再计算出结果。

典型例题 一、公式法：计算：20081+20082+20083+20084+…+20082006+20082007分析：这道题中相邻两个加数之间相差20081，成等差数列，我们可以运用等差数列求和公式：（首项+末项）×项数÷2来计算。

20081+20082+20083+20084+…+20082006+20082007=（20081＋20082007）×2007÷2=211003二、图解法： 计算：21 ＋41＋81＋161＋321＋641 分析：解法一，先画出线段图：从图中可以看出：21 ＋41＋81＋161＋321＋641=1－641=6463 解法二:观察算式，可以发现后一个加数总是前一个加数的一半。

因此，只要添上一个加数641，就能凑成321，依次向前类推，可以求出算式之和。

21 ＋41＋81＋161＋321＋641=21 ＋41＋81＋161＋321＋（641＋641）－641=21 ＋41＋81＋161＋（321+321）－641……=21×2－641 =6463 解法三：由于题中后一个加数总是前一个加数的一半，根据这一特点，我们可以把原式扩大2倍，然后两式相减，消去一部分。

设x=21＋41＋81＋161＋321＋641①那么，2x=（21＋41＋81＋161＋321＋641）×2 =1+21＋41＋81＋161＋321②用②－①得2x －x=1+21＋41＋81＋161＋321－（21 ＋41＋81＋161＋321＋641）x=6463所以，21 ＋41＋81＋161＋321＋641=6463三、裂项法 1、计算：21+61＋121＋201＋301＋……＋901＋1101 分析：由于每个分数的分子均为1，先分解分母去找规律：2=1×2，6=2×3，12=3×4，20=4×5，30=5×6，……110=10×11，这些分母均为两个连续自然数的乘积。

奥数里的分数应用原理总结1. 介绍奥数是指奥林匹克数学竞赛，是培养学生逻辑思维和数学能力的重要途径之一。

在奥数中，分数应用是一个重要的内容，我们来总结一下奥数里的分数应用原理。

2. 原理介绍分数是数学中的一种表示方法，表示一个整体被划分成若干部分的数。

在奥数中，分数应用主要包括四则运算、比较大小、化简、混合运算等。

2.1 四则运算分数的四则运算包括加法、减法、乘法和除法。

2.1.1 加法和减法两个分数相加或相减，需要满足相同的分母。

具体步骤如下： - 确定两个分数的分母是否相同，如果不同，先通分； - 将两个分数的分子进行对应的加法或减法运算； - 将运算结果的分子写在分数的上方，分母写在分数的下方。

2.1.2 乘法两个分数相乘，直接将两个分数的分子相乘，分母相乘。

具体步骤如下： - 将两个分数的分子相乘，将运算结果的分子写在分数的上方； - 将两个分数的分母相乘，将运算结果的分母写在分数的下方。

2.1.3 除法两个分数相除，可以将除法转化为乘法的形式。

具体步骤如下： - 将被除数的分子乘以除数的分母，将运算结果的分子写在分数的上方； - 将被除数的分母乘以除数的分子，将运算结果的分母写在分数的下方。

2.2 比较大小比较两个分数的大小，可以通过找到两个分数的公共分母进行比较。

具体步骤如下： - 确定两个分数的分母是否相同，如果不同，先通分； - 比较两个分数的分子的大小，如果分子相等，则比较分母的大小，分母越大，分数越小； - 如果分子不相等，比较两个分子的大小，分子越大，分数越大。

2.3 化简分数的化简是指将一个分数约分到最简形式。

具体步骤如下： - 找到分子和分母的最大公约数； - 将分子和分母分别除以最大公约数，得到最简分数。

2.4 混合运算混合运算是指分数与整数的组合运算，包括分数与整数的加减乘除等。

3. 实例分析下面通过一些实例来进一步理解奥数中分数应用的原理。

3.1 实例一：分数的四则运算假设有两个分数：1/3 和 2/5，我们来进行加法运算。

小学五年级奥数练习——分数地综合运算技巧详解（分数地复杂运算、分数地混合运算）一、知识点1．混合运算技巧在分数、小数地四则混合运算中，到底是把分数化作小数，还是把小数化作分数，这影响到运算过程地繁琐与简便程度，也影响到运算结果地精确度。

小数化成分数，或分数化成小数’，有如下几种技巧。

（1）在加减法中，有时遇到分数只能化成循环小数时’，不能把分数化成小数，此时要将包括循环小数在内地所有小数都化为分数；（2）在乘除法中，一般情况下，小数化成分数计算则比较简便；（3）一般情况下，在加减法中，分数化成小数比较方便；（4）在运算中，使用假分数还是带分数，需视情况而定；（5）在计算中经常用到除法’、比、分数、小数、百分数互相之间地变换，把这些常用地数互化成数表对学习非常重要。

2．复杂分数地运算注意点先找出分数线，确定分子部分和分母部分，然后这两部分分别进行计算，每部分地计算结果需要约分地要先约分，再改成“分子部分÷分母部分”地形式，最后求出结果。

3．比和比例地技巧化简比地方法：比地前项和后项同时乘以或除以相同地数（0除外’），最后地比值应写成最简整数比。

具体如下：（1）分数比：可以前项除以后项，在根据比值写出最’简单地整数比。

（2）小数比：可以先利用商不’变地性质将其转化为整数比，然后再化简；（3）整数比：可以根据商不变地性质或像分数约分（前后项同时除以它们’地最大公因数）那样进行化简；4．分数拆分从分母M 地约数中’任意找出两个m 和n ，有)()()()(11n m M n n m M m n m M n m M +++=++=B A 11+=；如10地约’数有：1，10，2，5。

如选1和2，有：)21(102)21(101)21(10)21(1101+++=++=151301+=；另外，a ，b ，c 为M 地约数：)()()()()(11c b a M c c b a M b c b a M a c b a M c b a M ++++++++=++++=5．循环小数循环小数与分数地互化，循环小数之间’简单地加、减法运算，涉及循环小数与分数地’运算主要利用运算定律进行简算。

小学六年级奥数运算部分的分数计算 (4
页)
小学六年级奥数运算部分的分数计算
简介
本文档旨在帮助小学六年级学生进行奥数运算部分的分数计算。

以下将介绍几个常见的分数计算方法。

分数加法
分数加法是将两个或多个分数相加的运算。

要进行分数加法，
必须保持分母相同。

以下是一个示例：
1/4 + 2/4 = 3/4
分数减法
分数减法是将一个分数减去另一个分数的运算。

和分数加法一样，分母必须相同。

以下是一个示例：
3/4 - 1/4 = 2/4
分数乘法
分数乘法是将两个或多个分数相乘的运算。

分数乘法的规则很
简单，只需要将分子相乘得到新的分子，分母相乘得到新的分母。

以下是一个示例：
2/3 * 3/5 = 6/15
分数除法
分数除法是将一个分数除以另一个分数的运算。

分数除法的规
则是将第一个分数的分子乘以第二个分数的倒数。

以下是一个示例：3/4 ÷ 1/2 = 3/4 * 2/1 = 6/4
分数化简
分数化简是将分数转化为最简形式的运算，使分子和分母的公
约数最大化。

例如，将8/12化简为2/3。

将分数化简可以让计算更
简便明了。

总结
通过掌握分数加法、减法、乘法、除法和化简的方法，小学六年级学生可以更好地进行奥数运算部分的分数计算。

以上提供的方法是常见而简单的分数计算技巧，旨在帮助小学六年级的学生更好地理解和应用。

希望能对你有所帮助。

五年级奥数分数求和的技巧
一、把十位数弄清楚
把学习数字的范围缩小到个位和十位数，再把十位数分类好，归类成小于等于6及大于6的两类。

二、个位数的求和运算
对于小于等于6的十位数，在个位上按常规方法做相应的运算，把加法按照数字从右往左从上到下依次排列，就可以更快地把个位数两两相加求和。

三、计算大于6的十位数
当十位数为7，8或者9时，我们可以把它们转换成一个十位数和一个个位数，分别进行记忆，然后把它们分别加上个位数，比如说7可以看做是6+1，8可以看做是6+2，9可以看做是6+3，然后再把6的分数和1、2、3的分数分别加起来就可以了。

四、综合利用技巧
我们可以先把小于等于6的十位数求和，然后把大于6的十位数把它们拆成十位数和个位数进行加减，最后综合处理，就可以较快地求出五年级奥数分数求和的结果了。

小学分数奥数题的知识点在小学奥数的学习中，分数是一个非常重要的知识点。

通过学习和掌握分数的概念和运算规则，可以帮助学生建立数学思维，培养逻辑思维能力。

下面将介绍一些小学分数奥数题的常见知识点。

1. 分数的概念分数是表示一个数与单位整体的关系，由分子和分母两部分组成。

分子表示单位整体的份数，分母表示每份的份数。

例如，1/2表示一个整体分成两份，取其中的一份。

分数中的分子和分母都是整数，分母不能为零。

2. 分数的大小比较在比较两个分数的大小时，可以通过找出它们的公共分母，然后比较分子的大小来判断。

如果两个分数的分母相同，那么分子大的分数就更大；如果两个分数的分母不同，可以通过通分将它们的分母变为相同，再进行比较。

3. 分数的约分和通分对于一个分数，如果分子和分母有公共的因数，可以约去这个公共因数，得到一个与原分数相等的最简分数。

例如，4/8可以约分为1/2。

通分是指将两个或多个分数的分母改成相同的分母。

通分后，可以方便地进行分数的加减运算。

4. 分数的加减运算对于两个分数的加减运算，首先需要将它们的分母通分，然后再按照通分后的分母进行相应的加减操作。

最后再进行约分，得到最简分数。

5. 分数的乘法和除法两个分数的乘法可以直接将它们的分子相乘得到新分子，分母相乘得到新分母。

最后对新分数进行约分。

两个分数的除法可以将除数的分子和被除数的分母相乘得到新分子，除数的分母和被除数的分子相乘得到新分母。

同样地，最后对新分数进行约分。

6. 分数和整数的转换一个自然数可以看作是分母为1的分数，一个整数可以看作是分母为1的分数。

对于一个分数，如果分子和分母相等，那么它可以化简为1。

因此，分数和整数之间可以相互转换。

7. 分数的混合运算混合运算是指将分数与整数进行加减乘除的运算。

在混合运算中，可以先将分数转换为带分数表示，然后按照整数的加减乘除规则进行运算。

通过学习以上的知识点，可以帮助小学生在奥数题中灵活运用分数的概念和运算规则，提高解题能力。

小学六年级数学重要知识总结分数的四则运算技巧在小学六年级的数学学习中，分数的四则运算是一个非常重要的知识点。

掌握了分数的四则运算技巧，不仅可以帮助同学们解决日常生活中的实际问题，还为今后的数学学习打下坚实的基础。

本文将总结分数的四则运算技巧，帮助同学们更好地掌握这一重要知识。

一、分数的加法运算技巧分数的加法运算是指将两个或多个分数相加，得到一个最简分数。

以下是分数加法运算的技巧：1. 分子相同的分数相加：若两个分数的分子相同，直接保持分子不变，分母相加即可。

例如，1/5 + 2/5 = 3/5。

2. 分母相同的分数相加：若两个分数的分母相同，直接保持分母不变，分子相加即可。

例如，3/4 + 5/4 = 8/4 = 2。

3. 分子不同、分母不同的分数相加：首先找到两个分数的公共分母，然后将分数转换为相同分母的分数再相加。

例如，1/3 + 1/4 = 4/12 +3/12 = 7/12。

二、分数的减法运算技巧分数的减法运算是指将两个分数相减，得到一个最简分数。

以下是分数减法运算的技巧：1. 分子相同的分数相减：若两个分数的分子相同，直接保持分子不变，分母相减即可。

例如，3/5 - 1/5 = 2/5。

2. 分母相同的分数相减：若两个分数的分母相同，直接保持分母不变，分子相减即可。

例如，7/8 - 3/8 = 4/8 = 1/2。

3. 分子不同、分母不同的分数相减：首先找到两个分数的公共分母，然后将分数转换为相同分母的分数再相减。

例如，5/6 - 2/3 = 5/6 - 4/6 = 1/6。

三、分数的乘法运算技巧分数的乘法运算是指将两个分数相乘，得到一个最简分数。

以下是分数乘法运算的技巧：1. 将两个分数的分子和分母分别相乘，得到新的分子和分母。

例如，2/3 × 4/5 = (2×4)/(3×5) = 8/15。

2. 如果有整数和分数相乘，先将整数转换为分数，再按照分数相乘的规则进行运算。

小学数学的归纳分数的运算规则与应用解析在小学数学学科中，归纳法是一种重要的思维方法，通过对已有信息的整理和总结，得出普遍规律，从而应用于其他类似的问题中。

而归纳分数的运算规则是数学中的一个重要内容，它涉及了分数的加法、减法、乘法和除法运算。

本文将对归纳分数运算规则进行解析，并探讨其在实际问题中的应用。

一、分数的加法运算规则分数的加法是指将两个分数进行相加，得出其和。

在进行分数的加法运算时，我们应该考虑分子和分母的运算规则。

1. 分子的运算规则：当分数的分母相同时，我们只需将分子相加，分母保持不变。

例如，1/4 + 2/4 = 3/4。

当分数的分母不同时，我们需要通过找到两个分数的公共分母，然后将分子相加，分母保持不变。

例如，1/3 + 1/4 = 4/12 + 3/12 = 7/12。

2. 分母的运算规则：当分数的分母相同时，我们只需将分子相加，分母保持不变。

例如，1/4 + 1/4 = 2/4 = 1/2。

当分数的分母不同时，我们需要找到两个分数的最小公倍数，然后将分母调整为最小公倍数，并将分子相应地调整。

例如，1/2 + 1/3 =3/6 + 2/6 = 5/6。

二、分数的减法运算规则分数的减法与加法类似，我们需要考虑分子和分母的运算规则。

1. 分子的运算规则：当分数的分母相同时，我们只需将分子相减，分母保持不变。

例如，1/2 - 1/2 = 0/2 = 0。

当分数的分母不同时，我们需要通过找到两个分数的公共分母，然后将分子相减，分母保持不变。

例如，3/4 - 1/3 = 9/12 - 4/12 = 5/12。

2. 分母的运算规则：当分数的分母相同时，我们只需将分子相减，分母保持不变。

例如，3/4 - 1/4 = 2/4 = 1/2。

当分数的分母不同时，我们需要找到两个分数的最小公倍数，然后将分母调整为最小公倍数，并将分子相应地调整。

例如，2/3 - 1/4 =8/12 - 3/12 = 5/12。

小学奥数重点知识归纳总结数学作为一门基础学科，对于孩子的综合素质培养具有重要意义。

奥林匹克数学竞赛作为培养学生数学思维和创新能力的重要途径之一，对小学生进行数学启蒙具有重要作用。

在这篇文章中，我将对小学奥数的重点知识进行归纳总结。

一、整数与分数1. 整数的概念与性质整数包括正整数、零和负整数，它们有一系列的性质，如加法、减法、乘法、乘方等运算规则，以及大小比较、绝对值等概念。

2. 分数的概念与性质分数是对一个整体的平均分割，由分子和分母两部分构成，它们有加法、减法、乘法、除法等运算规则，以及约分、比较大小等概念。

3. 整数与分数的转化可以将一个整数转化为相应的分数，也可以将一个分数转化为相应的整数或混合数。

转化时需要注意运算法则和化简。

二、小数与百分数1. 小数的概念与性质小数是指无限不循环小数、无限循环小数和有限小数，它们可以表示实际测量结果。

小数有加法、减法、乘法、除法等运算规则，以及大小比较等概念。

2. 百分数的概念与性质百分数是指以100为基数的分数，常用于表示比例和百分比，它们可以表示实际情况中的比例关系。

百分数有加法、减法、乘法、除法等运算规则，以及比较大小等概念。

3. 小数与百分数的转化可以将一个小数转化为相应的百分数，也可以将一个百分数转化为相应的小数。

转化时需要注意运算法则和移动小数点的位置。

三、几何图形与空间想象1. 图形的基本概念与性质图形包括点、线、线段、角、三角形、四边形、多边形等，它们有不同的性质和特点。

充分理解和掌握这些概念对于解题非常重要。

2. 平面图形的分类与特征平面图形可以分为正方形、长方形、圆、等边三角形等，每种图形都有自己的特征和性质。

熟练掌握它们的特征和相互关系有助于解决与图形相关的问题。

3. 空间图形的认识与探索空间图形包括正方体、长方体、圆柱、圆锥等，它们在现实生活中随处可见。

通过观察和探索，了解它们的性质和特点，有助于培养孩子的空间想象能力。

四、逻辑推理与推理策略1. 逻辑推理的基本思维方式逻辑推理是通过事实和前提推导出结论的思维方式，它要求学生具备辨认条件、推理关系和找出规律的能力。

小学数学竞赛中的分数运算方法在小学数学竞赛中，分数运算是一个常见而且重要的部分。

掌握分数的运算方法，可以帮助学生解决各种与分数相关的问题，提高他们的数学能力和解题技巧。

本文将介绍小学数学竞赛中常见的分数运算方法，包括加法、减法、乘法和除法。

让我们一起来了解吧！一、加法运算在小学数学竞赛中，我们经常会遇到分数的加法运算。

下面是一些基本的加法规则：1. 分母相同的分数相加：只需将分子相加，分母保持不变。

例如，对于两个分数3/4和1/4，它们的和为(3+1)/4=4/4=1。

2. 分母不同的分数相加：首先找到一个公共分母，然后将分数的分子进行相应的倍数调整，最后将分数相加。

例如，对于1/3和1/4这两个分数，可以将它们的分母乘积12作为公共分母，然后将1/3调整为4/12，将1/4调整为3/12，最后相加得到(4+3)/12=7/12。

3. 带分数相加：将带分数转化为假分数，然后按照以上规则进行相加。

例如，对于1 1/2和2/3这两个分数，可以将1 1/2转化为3/2，然后按照以上规则进行相加。

二、减法运算减法运算与加法运算类似，主要区别在于需要注意减数与被减数的顺序以及分数的借位处理。

下面是一些基本的减法规则：1. 分母相同的分数相减：只需将分子相减，分母保持不变。

例如，对于两个分数5/7和2/7，它们的差为(5-2)/7=3/7。

2. 分母不同的分数相减：首先找到一个公共分母，然后将分数的分子进行相应的倍数调整，最后将分数相减。

例如，对于3/4和1/6这两个分数，可以将它们的分母乘积24作为公共分母，然后将3/4调整为18/24，将1/6调整为4/24，最后相减得到(18-4)/24=14/24。

3. 带分数相减：将带分数转化为假分数，然后按照以上规则进行相减。

例如，对于5 1/3和2 2/5这两个分数，可以将5 1/3转化为16/3，然后按照以上规则进行相减。

三、乘法运算乘法运算是数学竞赛中常见的分数运算，下面是一些基本的乘法规则：1. 两个分数相乘：将两个分数的分子相乘得到新的分子，将两个分数的分母相乘得到新的分母。

第 一 讲 小 升 初· 竞 赛 中 的 分 数 问 题知识 导 航在分数式的计算应用问题中，主要包括以下几个方面的题型。

①和(差)倍问题。

具体表现为“已知分数的分子与分母的和(差)，和约分过后的结果，求原分数。

②变化类。

具体表现为“已知分数的分子与分母和(差)的关系，再告诉分子或分母变化后的结果，求原分数。

”③因数分解类。

具体表现为“已知最简真分数的分子与分母的积，求原分数的可能值。

” ④中间分数计算类。

具体表现为“已知某分数在两个分数之间，求该分数的分子与分母的和的最小值。

”……精 典 例 题例1：一个分数约分后是37，若约分前分子与分母的和是40，那么约分前的分数是多少?思路 点 拨想一想：约分后是37 ，你可以想到什么？你有几种方法来解答这个问题？(友情提示：从方程与算术两个角度来思考。

)模 仿 练 习一个分数的分子与分母和是40，约分后是35,那么这个分数原来是多少？例2：一个分数的分子与分母的和是19，加上这个分数的分数单位就是14 ,这个分数是多少？（2006年成都外国语学校奖学金考试数学试题）3/16思路点拨想一想：加上这个分数的分数单位实际是分数中谁发生了变化？想明白后，再结合例1方法来思考一下，相信你能自己解答的！模仿练习一个分数的分子与分母之和是37，若分子减去1，分数值是12,原分数是多少？(2007年成都外国语学校小语种数学试卷)例3：分子、分母相乘的积是2002的最简真分数共有多少个？(2005年成都七中育才东区衔接班招生考试题)思路点拨想一想：满足什么条件的分数才是最简真分数？再想一想对“分子、分母相乘的积是2002”的信息又应该怎样去理解？模仿练习一个最简真分数，分子与分母的积是24，这个真分数是多少？(成都外国语学校2011年“德瑞杯”知识竞赛数学试题)学以致用A级1.一个分数分子与分母的和是72，约分后是27，这个原分数是多少？(2005年成都七中育才东区衔接班招生考试题)2.将分数711 的分子增加77后，如果要求分数的大小不变，分母应变为多少？(2010年成都七中嘉祥外国语学校6年级衔接班试题2)3.一个分数，分子、分母的和是2010，约成最简分数后是760,这个分数是多少？（嘉祥外国语学校2011年5升6招生数学试题）B 级4.某分数分子分母的和为23，若分母增加17，此分数值为14 ，原分数为多少？（成都实验外国语学校“德瑞教育发展基金会”2010年奖学金测试数学A 卷）5.分子与分母的乘积是156的最简真分数有多少个？（2008年成都嘉祥外国语衔接班招生考试题2）6. 一个分数，分子与分母的和是75，若分子加上3，则可约简成58 ,原来的分数是多少? （2007年成都七中育才东区衔接班招生考试题2）C 级7.m,n 为自然数，若34 ＜n m ＜45 ，则m+n 的最小值是多少？（2007年成都七中育才东区衔接班招生考试题2）第 二 讲 分 数 计 算 中 的 拆 分知识 导 航分数计算中的拆分，又叫裂项计算。

六年级奥数分数的速算与巧算介绍本文档旨在介绍六年级奥数中分数的速算与巧算方法。

通过掌握这些方法，学生可以更高效地解决分数相关的计算题目。

分数的基本概念分数由分子和分母组成，表示部分与整体之间的比例关系。

例如，1/2表示将一个整体分成两个相等的部分，其中一个部分为1。

分子表示部分的数量，分母表示整体被分成的块数。

分数的速算方法相同分母的分数相加当两个分数的分母相同，我们只需要将分子相加，分母不变即可。

例如：1/4 + 2/4 = (1+2)/4 = 3/4。

相同分母的分数相减同样，当两个分数的分母相同，我们只需要将分子相减，分母不变即可。

例如：3/4 - 1/4 = (3-1)/4 = 2/4。

不同分母的分数相加与相减当两个分数的分母不同，我们需要找到它们的最小公倍数作为通分的分母。

然后将分子按照最小公倍数进行转换，并进行相应的计算。

例如：1/3 + 1/4 = 4/12 + 3/12 = 7/12。

分数的乘法分数的乘法可以直接将分子相乘，分母相乘得到结果。

例如：2/3 * 3/4 = (2*3)/(3*4) = 6/12。

分数的除法分数的除法可以转换为乘法的倒数计算。

即，将第二个分数的分子与分母交换位置，然后进行乘法计算。

例如：2/3 ÷ 1/4 = 2/3 * 4/1 = 8/3。

分数的巧算方法取整当分子比分母大于等于1时，分数可以通过取整来近似计算。

例如：7/4 可以近似为 2。

转化为小数可以将分数转化为小数进行计算。

例如：1/2 可以转化为 0.5。

分数的倍数关系分数之间存在倍数关系时，可以利用这种关系来进行巧算。

例如：1/2 + 1/4 = 2/4 + 1/4 = 3/4。

约分将分数约分至最简形式，可以更方便进行计算。

例如：4/8 可以约分为 1/2。

结论通过掌握以上分数的速算与巧算方法，六年级的奥数学生可以更快速、准确地解决分数相关的计算题目。

同时，这些方法也可在实际生活中应用到日常计算中。

小学五年级奥数知识点总结与分析
1. 分数与小数
- 分数是指一个数被分为若干等分后的其中一份，通常表示为
a/b的形式，其中a为分子，b为分母。

- 小数是指一个数的整数部分和小数部分以小数点分隔，通常
表示为x.y的形式。

2. 逻辑推理
- 逻辑推理是指根据一些已知条件和逻辑规则，推导出合乎逻
辑的结论的过程。

- 常见逻辑推理题型包括逻辑顺序、推理判断以及选择填空等。

3. 几何图形
- 几何图形是指用线段、角、面、体来表示现实物体或抽象概
念的图形。

- 常见的几何图形包括直线、射线、线段、角、三角形、四边形、圆等。

4. 数字运算
- 数字运算是指对数字进行加减乘除等运算的过程。

- 常见数字运算题型包括四则运算、倍数与约数、分数运算等。

5. 数据统计
- 数据统计是指收集、整理和分析数据的过程。

- 常见的数据统计内容包括平均数、中位数、众数、范围、柱
状图、折线图等。

以上是小学五年级奥数的一些知识点总结与分析，希望对你有
所帮助。

分数求和的技巧在学习数学时，分数求和是一个常见的问题。

对于一些复杂的分数求和题目，可能需要一些技巧和方法来解决。

本文将介绍一些分数求和的技巧，帮助读者更好地理解和解决这类问题。

首先，我们需要了解分数的基本概念。

分数由分子和分母组成，分母表示总份数量，分子表示实际数量。

在求解分数相加时，必须要先将分母统一，然后将分子相加。

例如，如果要计算1/3 + 1/4，首先要找到这两个分数的最小公倍数，即12，然后将两个分数的分子乘以相应的倍数，即4/12 + 3/12 = 7/12。

其次，在分数求和时，可以利用分数的性质进行简化。

对于分数a/b和c/d，如果分母相同，那么可以直接将分子相加得到(a+c)/b；如果分母不同，可以通过通分的方法将分母统一，再进行相加。

另外，如果要计算多个分数的和，可以依次两两相加，逐步求和，这样可以减少出错的可能性，确保计算的准确性。

另一种常见的分数求和技巧是借助整数部分进行计算。

对于带分数的求和，可以先转化为假分数，然后进行相加。

例如，要计算2 1/3 + 3 2/5，可以先将它们转化为假分数，即7/3 + 17/5，然后按照前面介绍的方法进行求和。

此外，有些复杂的分数求和问题可能需要利用最大公约数和最小公倍数的性质来解决。

当分母不同且无法通过通分的方法简化时，可以利用最大公约数将分数进行化简，然后再进行相加。

通过找到适当的最大公约数，可以简化计算过程，提高求解效率。

总的来说，分数求和并不是一件困难的事情，只要掌握一些基本的技巧和方法，就可以轻松应对各种分数求和问题。

通过实践和不断练习，相信读者们可以更加熟练地解决分数求和问题，提高数学解题能力。

希望本文介绍的分数求和技巧对读者有所帮助，谢谢阅读！。

奥数之分数的运算分数是数学中的一种数形式，由分子和分母两个整数通过一个分数线连接而成。

分数的表示方法及应用最早可以追溯到古埃及文明时期。

在数学中，分数的四则运算是基本运算之一，本文将详细介绍奥数中分数的运算方法，包括加减乘除四种运算。

1. 加法运算两个分数相加，需要先将分母化为相同的分母，再对分子进行加法运算。

例如：1/2 + 1/4 = (1×2)/(2×2) + (1×1)/(4×1) = 2/4 + 1/4 = 3/42. 减法运算两个分数相减，同样需要将分母化为相同的分母，再对分子进行减法运算。

例如：3/4 - 1/2 = (3×2)/(4×2) - (1×4)/(2×2) = 6/8 - 4/8 = 2/8 = 1/43. 乘法运算两个分数相乘，只需要将分子与分母分别相乘即可。

例如：1/2 × 2/3 = (1×2)/(2×3) = 2/6 = 1/34. 除法运算两个分数相除，需要将被除数的分子与分母互换位置，再将整个式子视为一个乘法运算。

例如：1/2 ÷ 3/4 = 1/2 × 4/3 = (1×4)/(2×3) = 4/6 = 2/3需要注意的是，分数运算中可能会出现约分的情况，即将分子和分母同时除以一个较大的公因数，化简分数的形式。

例如：2/4 = (2÷2)/(4÷2) = 1/2此外，分数还可以转化为小数或百分数的形式。

将分子除以分母即可得到小数，将小数乘以100即可得到百分数。

例如：3/4 = 0.75 = 75%总结奥数中分数的运算主要包括加减乘除四种基本运算，其中加减运算需要先将分母化为相同的分母再进行计算，乘法运算只需要将分子和分母分别相乘，除法运算需要将被除数转化为一个乘法式，并将除数的分子和分母互换位置后进行计算。