根据张宇高数视频总结的考研数学知识点PPT课件
- 格式:pptx
- 大小:4.56 MB
- 文档页数:26

张宇高数笔记第一章节极限与连续数列收敛(有极限),则:①任何子列都收敛,反之就不是收敛数列。
②它的极限存在且唯一。
③它是有界的。
(收敛一定有界,但有界不一定收敛,可能振荡)④它有保号性。
数列极限存在的解题手段:①夹逼法。
②定积分定义法。
③对于给定递推式的数列求极限:(1)用单调有界证明极限存在,然后让等式两边极限相等解出A 。
(2)先斩后奏解出A ,然后用压缩映象原理列出|x n ?A |<=""> 根据题设条件得出x n+1和x n 的递推关系,然后用③的方法。
⑤充分运用题目中给出的函数关系式:(1)x n+1=f(x n ),f (ξ)=ξ;则x n+1?x n =f (x n )?f(x n?1),|x n+1?ξ|=|f (x n )?f (ξ)| (2)任何|f ′(x )|≤k 的函数,都可由拉氏定理得|f (x 1)?f (x 2)|≤k|x 1?x 2| (3)若知f(x)的单调性,可把x n+1和x n 的大小判断转化为对f (x n+1)和f(x n )的判断。
(4)若给出x n+1=f(x n ),f ′(x )和x 0的初值,则用拉氏定理:|x n+1?x 0|=|f (x n )?f (x 0)|=|f′(ξ)(x n ?x 0)|≤A|(x n ?x 0)|压缩映象⑥对于累加型数列x n =∑f(n,k)n k=1求极限,常用无穷项相加放缩的方式夹逼出来。
函数极限存在(设为A ),则:①左右极限都为A 。
(证明题证极限存在的思路)②唯一性、有界性、保号性。
③?ε>0,?δ>0,当0<|x ?x 0|<δ时,有|f (x )?A |<ε此定义在广义上,ε可以为任何形式,但必须满足“可以任意小”。
重要结论与具体解题技巧:①闭区间上连续的函数必有界;开区间上连续的函数,两端点极限都存在才有界。
②无穷项相加的放缩:n ×u min ≤∑u i ≤n i=1 n ×u max 有限项相加(且u i ≥0)的放缩:1×u max ≤∑u i ≤n i=1 n ×u max ③诸如1x 2之类的形式难以处理,想到用倒代换。

张宇高数18讲数学二知识点总结笔记●1.函数极限与连续1)函数极限的定义及使用●定义●使用●是常数、唯一性、局部有界性、局部保号性●等式脱帽法2)函数极限的计算●化简先行●等价无穷小替换●恒等变形●及时提出极限存在且不为0的因式●洛必达法则●泰勒公式●熟记常用公式●展开原则●无穷小比阶●函数极限的存在性●具体性●若洛必达失效,用夹逼准则●抽象性●单调有界准则●连续与间断●研究位置●无定义点、分段函数的分段点●连续●内点处、端点处●间断●2.数列极限1)数列极限的定义及使用●定义●使用●是常数、唯一性、有界性、保号性●收敛的充要条件2)数列极限的存在性与计算●海涅定理的使用●直接计算法●定义法(先斩后奏法)●单调有界准则●用已知不等式●题设给出条件来推证●夹逼准则●用基本放缩法●题设给出条件来推证●综合题总结●用导数、积分、中值定理综合●用方程列、区间列综合●用极限综合●3.一元微分的概念1)导数定义(导数在一点的问题)●分段函数(或含绝对值函数)在分段点●抽象函数在一点●特指点x_0●泛指点x●四则运算中的特殊点●太复杂的函数●f=f_1+f_2●f=f_1* f_2* f_3* ...*●求导公式无定义的点2)微分定义●4.一元微分的计算1)复合函数求导2)隐函数求导3)反函数求导4)分段函数求导(含绝对值)●在分段点用导数定义●在非分段点用导数公式●对数求导法●幂指函数求导法●参数方程确定的函数求导●高阶导数●归纳法(记公式)●莱布尼茨公式●展开式(记公式)5)难点●计算量大●含参数的讨论●高阶导数●5.一元微分的几何应用1)研究对象●“祖孙三代”●f(x)●具体●抽象●f_n(x) 函数族●f_1·f_2·...·f_n● f'(x) ; \frac{\mathrm{d}[f(x)]}{\mathrm{d}{(x^2)}} ; {f}^{(n)}(x)●\int_{a}^{x}f(x)dx●分段函数(含绝对值)●参数方程●x=x(t), y=y(t)●x=r(\theta)cos\theta,y=r(\theta)sin\theta●隐函数F(x,y)=02)研究内容●切线、法线、截距●极值、单调性●单调性的判别●一阶可导点是极值点的必要条件●判别极值的第1,2,3充分条件●拐点、凹凸性●凹凸性的定义●拐点定义●凹凸性与拐点的判别●判别凹凸性的充分必要条件●二阶可导点是拐点的必要条件●判别拐点的第1,2,3充分条件●6.中值定理、微分等式与微分不等式1)中值定理●确定区间●确定辅助函数●确定使用的定理●零点定理●介值定理●费马定理●罗尔定理●拉格朗日中值定理●泰勒公式●柯西中值定理2)微分等式问题●理论依据●考法3)微分不等式问题●用单调性●用最值●用凹凸性●用拉格朗日中值定理●用柯西中值定理●用带有拉格朗日余项的泰勒公式●7.一元微分物理应用1)物理应用●以“A对B的变化率”为核心写\frac{\mathrm{d}A}{\mathrm{d}B}●8.一元积分的概念与性质1)祖孙三代●\int_{a}^{x}f(x)dx ,f(x),{ f^{'}(x) } 的奇偶性,周期性2)积分比大小●用几何意义●看面积大小●用保号性●做差●看正负3)定积分定义●基本形(能凑成\frac{i}{n})●\lim_{n \to \infty}\sum_{i=1}^n f(0+\frac{1-0}{n}i)\frac{1-0}{n} =\int_{0}^{1}f(x)dx●\lim_{n \to \infty}\sum_{i=0}^{n-1} f(0+\frac{1-0}{n}i)\frac{1-0}{n} =\int_{0}^{1}f(x)dx●放缩形(凑不成\frac{i}{n})●夹逼准则●放缩后再凑\frac{i}{n}●变量形●\lim_{n \to \infty}\sum_{i=1}^n f(0+\frac{x-0}{n}i)\frac{x-0}{n} =\int_{0}^{x}f(x)dx4)反常积分的判敛●概念●判别●9.一元积分的计算1)基本积分公式2)不定积分的计算●凑微分法●思想●方法●常用的凑微分公式●程序●换元法●思想●方法●三角函数代换●恒等变形后作三角代换●跟式代换●倒代换●复杂函数的直接带换●思想●方法●u,v的选取原则●推广公式(表格法)●有理函数的积分●定义●思想●方法3)定积分的计算●区间再现公式●华里士公式●其他常用含三角函数的积分等式●区间简化公式●对称性下的积分问题●定积分分部积分法中的“升阶”降阶“”公式●分段函数的定积分●10.一元积分几何应用1)研究对象●f(x)●f_n(x)●参数方程●x=x(t)●y=y(t)●\frac{\partial f}{\partial x}●\int_{a}^{x}f(x)dx●微分方程的解函数f(x)2)研究内容●面积、旋转体体积、平均值●平面曲线的弧长、旋转曲面的面积(侧面积)●“平面上的曲边梯形”的形心坐标公式●平行截面面积为已知的立体体积●11.积分等式与积分不等式1)积分等式●通过证明某特殊积分等式求某特殊积分●积分形式的中值定理2)积分不等式●用函数的单调性●处理被积函数●已知f(x) \leq g(x),用积分保号性证得\int_{a}^{b}f(x)dx \leq\int_{a}^{b}g(x)dx,a<b●用拉格朗日中值定理●用泰勒公式●用放缩法●用分部积分法●用换元法●用夹逼准则求解一类积分的极限问题●曲边梯形面积的连续化与离散化问题●12.一元积分的物理应用1)位移大小与总路程●位移大小●\int_{t_1}^{t_2}v(t)dt●总路程●\int_{t_1}^{t_2}|v(t)|dt2)变力沿直线做功●W=\int_{a}^{b}F(x)dx3)提取物体做功●W=\rho g\int_{a}^{b}xA(x)dx4)静水压力●P=\rho g\int_{a}^{b}x[f(x)-h(x)]dx5)细杆质心●\bar x=\frac{\int_{a}^{b}x\rho (x)dx}{\int_{a}^{b}\rho (x)dx}6)其他重要应用(微元法总结)●13.多元函数微分学1)概念●极限、连续、偏导数、可微2)复合函数求导法●链式求导规则●全导数●全微分形式不变3)隐函数求导●隐函数存在定理●一个方程的情形●方程组的情形4)多元函数的极值、最值●无条件极值●取极值的必要条件●取极值的充分条件●条件极值与拉氏乘数法5)偏微分方程●已知偏导数(或偏增量)的表达式,求z=f(x,y)●给出变换,化已知偏微分方程为常微分方程,求f(u)●给出变换,化已知偏微分方程为指定偏微分方程及其反问题●14.二重积分1)概念●和式极限●普通对称性●轮换对称性●二重积分比大小●用对称性●用保号性●二重积分中值定理●周期性2)计算●直角坐标系与换序●极坐标系与换序●直极互化3)应用●面积●\iint_{D}dxdy●15.微分方程1)一阶微分方程的求解●能写成 y'=f(x)·g(x)●能写成 y'=f(ax+by+c)●能写成 y'=f(\frac{y}{x})●能写成 \frac{1}{y'}=f(\frac{x}{y})●能写成 y'+p(x)y=q(x)2)二阶可降阶微分方程的求解●能写成 y''=f(x,y')●能写成 y''=f(y,y')3)高阶常系数线性微分方程的求解●能写成 y''+py'+qy=f(x)●能写成 y''+py'+qy=f_1(x)+f_2(x)4)用换元法求解微分方程●用求导公式逆用来换元●用自变量来换元●用因变量来换元●用x,y地位互换来换元5)应用题●用极限、导数定义或积分等式建方程●用几何应用建方程●用曲线切线斜率●用两曲线f(x)与g(x)的公切线斜率●用截距●用面积●用体积●用平均值●用弧长●用侧面积●用曲率●用形心。



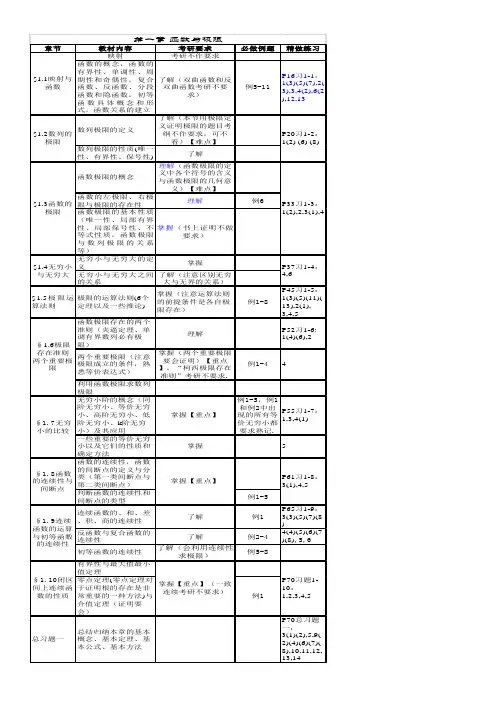


![[考研数学]中值定理](https://uimg.taocdn.com/faea6c2466ec102de2bd960590c69ec3d5bbdb96.webp)
[考研数学]中值定理⽤书:张宇考研数学基础30讲下多为摘录。
条件/表述部分不完全准确(实际上条件归于表述,但为了观察相似的条件所以单独列出了。
)定理的推导(常考证明)和条件细节⾮!常!重!要!可补充内容:证明、⼏何意义、对⽐=总结/不保证对的个⼈理解。
=我先挖个坑在这⾥。
不要让⼏何直观,蒙蔽了我们的双眼。
—柯西有界与最值定理条件:设f(x)在[a,b]上连续,则:表述:m⩽f(x)⩽M。
其中,m,M为f(x)在[a,b]上的最⼩值和最⼤值。
证明:介值定理条件:设f(x)在[a,b]上连续,则:表述:当m⩽µ⩽M时,存在ξ∈[a,b],使得f(ξ)=µ。
证明:(离散)平均值定理条件:设f(x)在[a,b]上连续,则:表述:当a<x1<x2<⋯<x n<b时,在[x1,x n]内⾄少存在⼀个点ξ,使得f(ξ)=f(x1)+f(x2)+⋯+f(x n)n。
证明:借助介值定理证明。
m⩽f(x i)⩽M,(i=1,2,…,n)nm⩽Σf(x i)⩽nMm⩽f(x1)+f(x2)+⋯+f(x n)n⩽M令µ=f(x1)+f(x2)+⋯+f(x n)n,存在ξ∈[x1,x n],使得f(ξ)=µ=f(x1)+f(x2)+⋯+f(x n)n=1n∑ni=1f(x i)平均值定理的ξ常见闭区间。
(函数)零点定理条件:设f(x)在[a,b]上连续,则:表述:当f(a)⋅f(b)<0时,存在ξ∈(a,b),使得f(ξ)=0。
证明:借助介值定理和最值定理推导。
f(a)⋅f(b)<0说明f(a)与f(b)异号故m<0且M>0则m<0<M,存在ξ∈(a,b),使得f(ξ)=0。
前四条有共⽤条件:f(x)在[a,b]上连续。
连续即不间断。
所以端点不是间断点。
出现函数值为零的条件,可以考虑⽤介值定理与零点存在定理做。
延伸:推⼴的零点定理若f(x)在(a,b)上连续,lim,\alpha \cdot \beta< 0 时,则f(x)在(a,b)内⾄少有⼀个根。


2012年张宇考研数学高等数学(下)强化班内部讲义先修课程(高等数学复习导学班)视频地址:新浪微博——宇哥考研:/zhangyumaths 【本讲义参考文献】《考研数学高等数学18讲》,张宇 编著. 中国书籍出版社 《考研数学题源探析经典1000题》,张宇 编著. 北京理工大学出版社第9讲 多元函数微分学从本讲开始进入多元函数的体系,本讲内容是考研绝对的重点,一般会在每年的考试中出至少一个小题(4分)和一个大题(10分左右),有时结合其他知识出综合题.本讲我们只讲多元函数微分学的公共考点,有三个,分别为:1)五个基本概念;2)多元函数微分法;3)多元函数的极值与最值问题。
第一节 多元微分学的五个基本概念1、极限存在性定义 设二元函数f (x , y )定义在区域D 上,点P 0(x 0, y 0)在D 内或者在D 的边界上,如果存在常数A , 对于任给的正数ε,总存在正数δ, 只要点(,)P x y D ∈满足00<PP δ=<,恒有| f (x ,y )−A |<ε 成立, 则称A 为函数f (x , y )当(x , y )→(x 0, y 0)时的极限, 记为0lim (,)x x y y f x y A →→=.这极限也称为二重极限.这里有两点说明.第一,二元函数的极限怎么计算?在考研中这个要求不高.举个例子.【例1】设222222,0(,)0 0xy x y x y f x y x y ⎧+≠00lim (,)x y ⎪+=⎨⎪+=⎩,求f x y →→.【解】因为220|(,)|0xyf x y x y ≤+,由夹逼准则,. 0lim (,)0x y f x y →→=第二,所谓二元函数的极限(二重极限)存在,是指以任何方式趋于时,相应的极限值都为同一个常数),(y x P ),(00y x P A (你是否还记得,在一元函数的极限计算中我们就反复强调:“极限若存在,必唯一”).故,如果以不同方式趋于时,函数趋于不同的值,则可以判定该函数在点的极限值不存在.在考研中这个要求也不高.再举个例子. ),(y x P ),(00y x P ),0y (0x 【例2】设22),(y x xyy x f +=,试证极限不存在. ),(lim 0y x f y x →→【证】这个证明过程比较经典,请记住.当沿着直线),(y x P kx y =趋于点时,有)0,0(=+→=→2200lim y x xy kx y x 2222201lim k kx k x kx x +=+→,结果随的变化而变化,故二重极限不存在. k )y x ,(lim 00y x f →→2. 连续性如果000lim (,)(,)x x y y f x y f x y →→=,则称f (x , y )在点(x 0, y 0)处连续.注意,验证二元函数f (x , y )在某一点(x 0, y 0)是否连续是考研的重点,但是如果不连续,对于多元函数是不讨论间断点的分类的.3. 偏导数存在性(重要!重要!)定义 设函数z = f (x , y )在点(x 0, y 0)的某邻域内有定义, 若极限xy x f y x x f x Δ−Δ+→Δ),(),(lim00000存在, 则称此极限为函数z = f (x , y )在点(x 0, y 0)处对x 的偏导数, 记作00y y x x x z==∂∂, 00y y x x x f ==∂∂, 00x x x y y z ==′, 或00(,)x f x y ′. 于是,00000000000(,)(,)(,)(,'(,)limlim x x x x 0)f x x y f x y f x y f x y f x y x x Δ→→+Δ−−==Δ−x 00000000000(,)(,)(,)(,)'(,)limlim y y y y f x y y f x y f x y f x y f x y y y Δ→→+Δ−−==Δ−y 高阶偏导数 如果函数z =f (x , y )在区域D 内的偏导数(,)x f x y ′、(,)y f x y ′仍具有偏导数, 则它们的偏导数称为函数z =f (x , y )的二阶偏导数. 按照对变量求导次序的不同有如下四个二阶偏导数:22((,)xx z zf x y x x x ∂∂∂′′==∂∂∂, 2((,xy z z )f x y y x x y ∂∂∂′′==∂∂∂∂, 2()(,)yx z z f x y x y y x ∂∂∂′′==∂∂∂∂, 22()(,)yyz zf x y y y y∂∂∂′′==∂∂∂. 其中(,)xyf x y ′′、(,)yx f x y ′′称为二阶混合偏导数.同样可得三阶、四阶、以及n 阶偏导数. 二阶及二阶以上的偏导数统称为高阶偏导数.4. 可微定义 如果函数z = f (x , y )在点(x , y )的全增量Δz = f (x +Δx , y +Δy )−f (x , y ) 可表示为() (z A x B y o ρρΔ=Δ+Δ+=,其中A 、B 不依赖于Δx 、Δy 而仅与x 、y 有关, 则称函数z =f (x , y )在点(x , y )可微, 而称A Δx +B Δy 为函数z =f (x , y )在点(x , y )的全微分, 记作dz , 即dz =A Δx +B Δy .在第三讲中,我们已经详细阐述了一元函数可微的深刻涵义,二元函数的可微概念也是如此(请注意对比,加深理解).(1)写出全增量;000(,)(,z f x x y y f x y =++− 0)(2)写出线性增量A x B y + ,其中0000'(,),'(,)x y A f x y B f x y ==; (3)作极限limx y Δ→Δ→若该极限等于0,则(,)z f x y =在00(,)x y 点可微,否则,就不可微.用形式简单的“线性增量A x B y + ”去代替形式复杂的“全增量z ”,且其误差“()z A x B y −+ ”是o,这就是说,用简单的代替了复杂的,且产生的误差可以忽略不计,这就是可微的真正涵义。
一、函数、极限、连续主要内容:极限的定义与性质,求极限(函数极限、数列极限),无穷小的比较,间断点及其类型.1.函数极限(洛必达法则、等价无穷小代换、泰勒公式)加减运算中等价原则:111111111111,,lim1,,,lim 1,αααββαβαββαααββαβαββ≠-≠-++ 则-则常用的等价代换:()(33332201111sin ,arcsin ,tan ,arctan ,sin arcsin (6633)1ln 1,ln ,1cos .22x x x x x x x x x x x x x x x x x x x x x x αα→--------+-时1,l n 1x x x →- 时 例1 求极限sin lim xx x x x I +→-= 1()6(改1000题数一1.32(17),数二1.65,数三1.43(22))例2 (类1000题数一1.58,数二1.108,数三1.75)()()()()()()2ln 1(),0(),01,0,0,0.1,02x xf x x x f x g x g f f f x +-⎧≠⎪⎪''''==⎨⎪=⎪⎩设具有二阶连续导若求数,()()()401,01,03f f f ⎛⎫'''==-=- ⎪⎝⎭例3设()22lim 1x x x bx e -→+∞⎤+=⎥⎦,试确定,a b 的值 ()2,1a b =-=例4 ()()()1tan sin 20,0lim ,0+x xx xx e x f x f t dtx x --∞→⎧≤=⎨>⎩⎰设,求极限 23e ⎛⎫⎪⎝⎭2.数列极限(夹逼准则、定积分定义、单调有界准则)例5 22212lim 111n n n n n →∞⎛⎫⎛⎫⎛⎫+++= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭12()e例6 求极限2sin sin sin lim 1112n n n n n n n πππ→∞⎛⎫ ⎪+++ ⎪+ ⎪++⎝⎭ 2π⎛⎫ ⎪⎝⎭ (1000题数一1.55,数二1.105,数三1.72)例7 设()()()ln 2,,2f x x x x =+-∈-∞,()1求()f x 在(),2-∞上的最大值,()2若()11ln2,,1,2,n n x x f x n +=== ,求lim n n x →∞()()()111,2lim1n n f x →∞==最大值二、一元函数微分学主要内容:导数的定义,求各类函数的导数(复合函数、隐函数、参数方程、分段函数、高阶导数),性态(单调性、极值与最值、凹凸性与拐点),方程的根,不等式的证明,微分中值定理的证明题.例 设()()()limx af x f x x a x a x a→==-在处连续且存在,则在处()()()()()()()()()()()()()0,00.A f x f xB f x f xC f x f aD f x f x f a '='不可导,但可导不可导,且也不可导可导,且可导,但对不同的可以为也可以不为 1.方程的根例1 证明方程221x x =+有且仅有三个根例2 试求方程()20xe axa =>为常数的根的个数(1000题数二2.122,数三2.110)2.不等式的证明例3()()224201tan 2tanlim nn nn k x x x x x x →∞=≤-≤=∑证明:充分小时,不等式0设求例4 《18讲例题5.11》3.微分中值定理证明例5()[]()[]()()100,1010,12 2.=f x f f f x dx ξξ'∃∈=-⎰设在上有连续的导数,且,证明:使得例6 (1000题数一2.96,数二2.117,数三2.105)()[]()()()()()()222,2100 4.2,20.f x f x f f f f ξξξ'-≤+=⎡⎤⎣⎦''∃-+=设函数在上二阶可导,且,又试证:使得例7(18讲例题4.10的推广)()[]()()()()()()0,10,100,11,,00,1.f x f f m M m Mm M f f ξηξη==>∃∈+=+''设在上连续,在上可导,对任意的,证明:不同的,使得三、一元函数积分学主要内容:不定积分、定积分与反常积分(基本方法、特色方法、判敛),变限积分函数性质(连续性、可导性、奇偶性),定积分的应用,定积分等式与不等式的证明.1.不定积分、定积分、反常积分 例120xe dx ⎡⎤=⎣⎦⎰例2 22202cos sin xt x e dt xdx ππ--⎡⎤+=⎢⎥⎣⎦⎰⎰例3 3111arccos dx x x+∞⎰例4 ()()()20011dxx x αα+∞≥++⎰2.变限积分函数(略)3.定积分有关的等式、不等式的证明题例5()()[][]()()()()()()()()()20,,,0,1,sin 210.bba a f x g x ab a b g x a b f x g x dx f g x dx xdx xπξξ≥∈=>⎰⎰⎰设在上连续,又在区间上证明至少存在一点使利用的结论证明(18讲例8.2)例6.(1000题数一3.137,数二3.175,数三3.153)利用柯西积分不等式()()()()222b b ba a a f x g x dx f x dx g x dx ⎡⎤≤⎢⎥⎣⎦⎰⎰⎰,证明:()()()2222bbaab a fx dx f x dx -'≤⎡⎤⎣⎦⎰⎰,其中()[](),0.f x a b f a =在上有一阶连续导数,例6’.()[]()()()()()()22,0,1,cos sin 1,.babbaaf x a b f x f x dx f x kxdx f x kxdxk ≥=+≤⎰⎰⎰若在上连续,且证明:这里是任意实数例7《18讲例题8.12》。