四川省内江市2016年中考数学试题含答案解析(Word版)
- 格式:doc
- 大小:635.50 KB
- 文档页数:13


四川省内江市 2016年中考数学试卷(解析版)一、选择题(每小题3分,共 1 . — 2016的倒数是( ) 1 A . — 2016 B .— - 2016A 卷(共100分) 36分) C . 20-- D . 2016 2016 9180 000 人次, 2 . 2016年“五一”假期期间,某市接待旅游总人数达到了 科学记数法表示应为( ) 4 5 6 7A . 918X 10B . 9.18X 10C . 9.18X 10D . 9.18X 10 3.将一副直角三角板如图 1放置,使含30。
角的三角板的直角边和含 角的三角板一条直角边在同一条直线上,则/ 1的度数为( ) A . 75 ° B . 65 ° C . 45 ° D . 30 ° 将 9180 000 用4.下列标志既是轴对称图形又是中心对称图形的是 ( )區)輕)◎統C . A . B . 5.下列几何体中,主视图和俯视图都为矩形的是 C .D .6.在函数 X - 3中y = 中, x —4B . X > 3 25名同学参加某比赛,预赛成绩各不相同, :赛,只需要再知道这C .方差D •平均数 A ,B 两地沿同一条公路骑自行车到 C 地,已知A ,C 两地间的 2千米/ 自变量x 的取值范围是( A . X >3 7.某校有 已经知道自己的成绩,能否进入决淫 A .最高分 B .中位数 &甲、乙两人同时分别从 距离为110千米,B ,C 两地间的距离为100千米,甲骑自行车的平均速度比乙快 时,结果两人同时到达 C 地,求两人的平均速度分别为多少.为解决此问题,设乙骑自行 车的平均速度为 A 110 = 100 B 1100 x +2 x X 9.下列命题中,真命题是( A .对角线相等的四边形是矩形 B .对角线互相垂直的四边形是菱形 C .对角线互相平分的四边形是平行四边形 D.对角线互相垂直平分的四边形是正方形 10 .如图 2,点 A ,B ,C 在O O 上,若/ BAC = 45° OB = 2,图中阴影部分的面积为( )C . x > 4D . X >3 且 X M 4取前13名参加决赛,其中一名同学 25名同学成绩的( ) X 千米/时,由题意列出方程,其中正确的是 ( =100 C J10 = 100 _ X 2 . x_2 = X ) A则5小题,共44分) + 3 • tan 30。


四川省内江市2016年中考数学试卷(解析版)A 卷(共100分)一、选择题(每小题3分,共36分)1.-2016的倒数是( )A .-2016B .-12016 C .12016 D .2016 [答案]B[考点]实数的运算。
[解析]非零整数n 的倒数是1n ,故-2016的倒数是12016 =-12016,故选B . 2.2016年“五一”假期期间,某市接待旅游总人数达到了9180 000人次,将9180 000用科学记数法表示应为( )A .918×104B .9.18×105C .9.18×106D .9.18×107[答案]C[考点]科学记数法。
[解析] 把一个大于10的数表示成a ×10n (1≤a <10,n 是正整数)的形式,这种记数的方法叫科学记数法.科学记数法中,a 是由原数的各位数字组成且只有一位整数的数,n 比原数的整数位数少1.故选C .3.将一副直角三角板如图1放置,使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上,则∠1的度数为( )A .75°B .65°C .45°D .30°[答案]A[考点]三角形的内角和、外角定理。
[解析]方法一:∠1的对顶角所在的三角形中另两个角的度数分别为60°,45°,∴∠1=180°-(60°+45°)=75°.方法二:∠1可看作是某个三角形的外角,根据三角形的外角等于与它不相邻的两个内角的和计算. 故选A .4.下列标志既是轴对称图形又是中心对称图形的是( )[答案]A[考点]中心对称与轴对称图形。
[解析]选项B 中的图形是轴对称图形,选项C 中的图形是中心对称图形,选项D 中的图形既不是轴对称图形也不是中心对称图形.只有选项A 中的图形符合题意.故选A .图1 30°45°1 A . B . C . D .5.下列几何体中,主视图和俯视图都为矩形的是( )[答案]B[考点]三视图。

2016年四川省内江市中考真题数学一、选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.-2016的倒数是( )A.-2016B.1 2016 -C.1 2016D.2016解析:乘积是1的两个数互为倒数,-2016的倒数是1 2016 -.答案:B.2. 2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )A.918×104B.9.18×105C.9.18×106D.9.18×107解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.将9 180 000用科学记数法表示为:9.18×106.答案:C.3.将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )A.75°B.65°C.45°D.30°解析:如图,∵∠ACB=∠DFE=90°,∴∠ACB+∠DFE=180°,∴AC∥DF,∴∠2=∠A=45°,∴∠1=∠2+∠D=45°+30°=75°.答案:A.4.下列标志既是轴对称图形又是中心对称图形的是( ) A.B.C.D.解析:根据中心对称图形与轴对称图形的概念判断即可.A、是轴对称图形,是中心对称图形.故正确;B、是轴对称图形,不是中心对称图形.故错误;C、不是轴对称图形,是中心对称图形.故错误;D、是轴对称图形,不是中心对称图形.故错误.答案:A.5.下列几何体中,主视图和俯视图都为矩形的是( )A.B.C.D.解析:A、此几何体的主视图是等腰三角形,俯视图是圆,故此选项错误;B、此几何体的主视图是矩形,俯视图是矩形,故此选项正确;C、此几何体的主视图是矩形,俯视图是圆,故此选项错误;D、此几何体的主视图是梯形,俯视图是矩形,故此选项错误.答案:B.6.在函数y=中,自变量x的取值范围是( )A.x>3B.x≥3C.x>4D.x≥3且x≠4解析:根据分母不能为零,被开方数是非负数,可得x-3≥0且x-4≠0,解得x≥3且x≠4.答案:D.7.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )A.最高分B.中位数C.方差D.平均数解析:某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的中位数.答案:B.8.甲、乙两人同时分别从A,B两地沿同一条公路骑自行车到C地.已知A,C两地间的距离为110千米,B,C两地间的距离为100千米.甲骑自行车的平均速度比乙快2千米/时.结果两人同时到达C地.求两人的平均速度,为解决此问题,设乙骑自行车的平均速度为x千米/时.由题意列出方程.其中正确的是( )A.1101002x x=+B.1101002 x x=+C.1101002x x=-D.1101002 x x=-解析:设乙骑自行车的平均速度为x千米/时,则甲骑自行车的平均速度为(x+2)千米/时,根据题意可得等量关系:甲骑110千米所用时间=乙骑100千米所用时间,根据等量关系可列方程:1101002x x=+.答案:A.9.下列命题中,真命题是( )A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形解析:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;B、对角线互相垂直的平行四边形是菱形;故本选项错误;C、对角线互相平分的四边形是平行四边形;故本选项正确;D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误.答案:C.10.如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )A.π-4B.231π-C.π-2D.22 3π-解析:∵∠BAC=45°,∴∠BOC=90°,∴△OBC是等腰直角三角形,∵OB=2,∴△OBC 的BC =∴BC =∴2190223620OBCOBC S S S ππ⨯=-=-⨯=-V 阴影扇形. 答案:C.11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )C.32D.不能确定解析:如图,∵等边三角形的边长为3,∴高线232AH =⨯=, 11112222ABC S BC AH AB PD BC PE AC PF ==++V g g g g , ∴331111222233AH PD PE PF ⨯=⨯+⨯+⨯g g g g ,∴PD PE PF AH ++==即点P到三角形三边距离之和为2.答案:B.12.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )A.2015 12⎛⎫ ⎪⎝⎭B.2016 12⎛⎫ ⎪⎝⎭C.2016 3⎛⎫⎪⎪⎝⎭D.2015 3⎛⎫⎪⎪⎝⎭解析:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,∴111112 3D E C D sin=︒=,则1 222230B C B E cos=︒=⎝⎭=,同理可得:233133B C⎛⎫⎪=⎪⎝⎭=,故正方形A n B n C n D n的边长是:13n -⎛⎫ ⎪ ⎪⎝⎭,则正方形A2016B 2016C 2016D 2016的边长为:2015⎝⎭.答案:D. 二、填空题(本大题共4小题,每小题5分,共20分)13.分解因式:ax 2-ay 2= .解析:应先提取公因式a ,再对余下的多项式利用平方差公式继续分解.ax 2-ay 2,=a(x 2-y 2),=a(x+y)(x-y).答案:a(x+y)(x-y). 14.化简:29333a a a a a ⎛⎫ ⎪⎝⎭++÷=-- . 解析:原式()293333a a a a a a a a -==+=-++g g . 答案:a.15.如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC=8,BD=6,OE ⊥BC ,垂足为点E ,则OE= .解析:∵四边形ABCD 为菱形,∴AC ⊥BD ,OB=OD=12BD=3,OA=OC=12AC=4, 在Rt △OBC 中,∵OB=3,OC=4,∴5BC ==,∵OE ⊥BC ,∴1122OE BC OB OC =g g , ∴341255OE ⨯==. 答案:125. 16.将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第n 个图形有 个小圆?(用含n 的代数式表示)解析:根据第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,∵6=4+1×2,10=4+2×3,16=4+3×4,24=4+4×5…,∴第n 个图形有:4+n(n+1).答案:4+n(n+1).三、解答题(本大题共5小题,共44分,解答应写出必要的文字说明或推演步骤)17.计算:()10330(201612)tan π--︒--+.解析:原式利用绝对值的代数意义,特殊角的三角函数值,立方根定义,以及零指数幂、负整数指数幂法则计算即可得到结果.答案:原式32123=--+=. 18.如图所示,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF=BD ,连接BF.(1)求证:D 是BC 的中点.解析:(1)根据两直线平行,内错角相等求出∠AFE=∠DCE ,然后利用“角角边”证明△AEF 和△DEC 全等.答案:(1)∵AF ∥BC ,∴∠AFE=∠DCE ,∵点E 为AD 的中点,∴AE=DE ,在△AEF 和△DEC 中,AFE DCE AEF DEC AE DE ∠∠⎧⎪∠∠⎨⎪⎩===,∴△AEF ≌△DEC(AAS).(2)若AB=AC ,试判断四边形AFBD 的形状,并证明你的结论.解析:(2)由(1)知AF 平行等于BD ,易证四边形AFBD 是平行四边形,而AB=AC ,AD 是中线,利用等腰三角形三线合一定理,可证AD ⊥BC ,即∠ADB=90°,那么可证四边形AFBD 是矩形. 答案:(2)若AB=AC ,则四边形AFBD 是矩形.理由如下:∵△AEF ≌△DEC ,∴AF=CD ,∵AF=BD ,∴CD=BD ;∵AF ∥BD ,AF=BD ,∴四边形AFBD 是平行四边形,∵AB=AC ,BD=CD ,∴∠ADB=90°,∴平行四边形AFBD 是矩形.19.某学校为了增强学生体质,决定开设以下体育课外活动项目:A 篮球、B 乒乓球、C 跳绳、D 踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:(1)这次被调查的学生共有人.解析:(1)由题意可知这次被调查的学生共有3620200360÷=(人).答案:(1)200.(2)请你将条形统计图补充完成.解析:(2)首先求得C项目对应人数为:200-20-80-40=60(人),继而可补全条形统计图. 答案:(2)C项目对应人数为:200-20-80-40=60(人).补充如图.(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).解析:(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.答案:(3)列表如下:∵共有12种等可能的情况,恰好选中乙、丙两位同学的有2种, ∴1()2261P ==选中甲、乙. 20.禁渔期间,我渔政船在A 处发现正北方向B 处有一艘可以船只,测得A 、B 两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C 处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).解析:先过点C 作CD ⊥AB ,垂足为点D ,设BD=x 海里,得出AD=(200-x )海里,在Rt △BCD 中,根据45CD tan BD ︒=,求出CD ,再根据BD=CD 求出BD ,在Rt △BCD 中,根据45BD cos BC ︒=,求出BC ,从而得出答案.答案:过点C 作CD ⊥AB ,垂足为点D ,设BD=x 海里,则AD=(200-x)海里,∵∠ABC=45°,∴BD=CD=x ,∵∠BAC=30°, ∴30CD tan AD︒=,在Rt △ACD 中,则)30200CD AD tan x =︒=-g,则)200x x =-,解得,100x =,即100BD =,在Rt △BCD 中,45BD cos BC︒=,解得:1BC =则1452= (海里/时),则该可疑船只的航行速度约为25海里/时. 21.如图,在Rt △ABC 中,∠ABC=90°,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F ,⊙O 是△BEF 的外接圆,∠EBF 的平分线交EF 于点G ,交⊙O 于点H ,连接BD 、FH.(1)试判断BD与⊙O的位置关系,并说明理由.解析:(1)连接OB,证得∠DBO=90°,即可得到BD与⊙O相切.答案:(1)BD与⊙O相切.理由:如图1,连接OB,∵OB=OF,∴∠OBF=∠OFB,∵∠ABC=90°,AD=CD,∴BD=CD,∴∠C=∠DBC,∵∠C=∠BFE,∴∠DBC=∠OBF,∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,∴∠DBO=90°,∴BD与⊙O相切.(2)当AB=BE=1时,求⊙O的面积.解析:(2)由等腰直角三角形的性质得到CF=BF,由于DF垂直平分AC,得到BF,根据勾股定理得到EF的长,根据圆的面积公式即可得到结论.答案:(2)如图2,连接CF ,HE ,∵∠CBF=90°,BC=BF ,∴BF ,∵DF 垂直平分AC ,∴BF ,∴BF=2+1,∴EF ==∵∠CBF=90°,∴EF 是⊙O 的直径,∴⊙O 的面积24124EF π⎛⎫ ⎪+=⎝=⎭g . (3)在(2)的条件下,求HG ·HB 的值.解析:(3)推出△EHF 是等腰直角三角形,求得HF=2EF ,通过△BHF ∽△FHG ,列比例式即可得到结论.答案:(3)∵BH 平分∠CBF , ∴¼»EHHF =, ∴EH=FH ,∴△EHF 是等腰直角三角形,∴2HF EF == ∵∠EFH=∠HBF=45°,∠BHF=∠BHF ,∴△BHF ∽△FHG ,∴HF BH HG HF=,∴22HG HB HF ==g B 卷一、填空题(本大题共4小题,每小题6分,共24分)22.任取不等式组30250k k -≤⎧⎨+⎩>的一个整数解,则能使关于x 的方程:2x+k=-1的解为非负数的概率为 .解析:∵解不等式组30250k k -≤⎧⎨+⎩>的解集为:52-<k ≤3, ∴整数解为:-2,-1,0,1,2,3,关于x 的方程:2x+k=-1的解为:12k x +=-, ∵关于x 的方程:2x+k=-1的解为非负数,∴k+1≤0,解得:k ≤-1,∴能使关于x 的方程:2x+k=-1的解为非负数的为:-1,-2;∴能使关于x 的方程:2x+k=-1的解为非负数的概率为:2613=. 答案:13. 23.如图,点A 在双曲线5y x =上,点B 在双曲线8y x=上,且AB ∥x 轴,则△OAB 的面积等于 .解析:延长AB 交y 轴于点C.12552OAC S =⨯=V ,1284OCB S =⨯=V , 则53242OAB OCB OAC S S S =-=-=V V V . 答案:32. 24.二次函数y=ax 2+bx+c 的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P ,Q 的大小关系是 .解析:∵抛物线的开口向下,∴a <0, ∵02b a->, ∴b >0,∴2a-b <0, ∵12b a-=, ∴b+2a=0,x=-1时,y=a-b+c <0. ∴012b bc --+<,∴3b-2c>0,∵抛物线与y轴的正半轴相交,∴c>0,∴3b+2c>0,∴p=3b-2c,Q=b-2a-3b-2c=-2a-2b-2c,∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-4b<0∴P>Q.答案:P>Q.25.如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是 .解析:如图,点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C″答案:10.二、解答题(本大题共3小题,每小题12分,共36分)26.问题引入:(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=13∠ABC,∠BCO=13∠ACB,∠A=α,则∠BOC= (用α表示)解析:(1)如图①,根据角平分线的定义可得∠OBC=12∠ABC,∠OCB=12∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+12α;如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=120°+13α.答案:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∴∠OBC+∠OCB=12(∠ABC+∠ACB),在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-12(∠ABC+∠ACB)=180°-12(180°-∠A)=90°+12∠A=90°+12α;如图②,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-13(∠ABC+∠ACB)=180°-13(180°-∠A)=120°+13∠A=120°+13α.故答案为90°+12α,120°+13α.拓展研究:(2)如图③,∠CBO=13∠DBC,∠BCO=13∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.解析:(2)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=120°-13α.答案:(2)如图③,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-13(∠DBC+∠ECB)=180°-13(∠A+∠ACB+∠A+ABC)=180°-13(∠A+180°)=120°-13α.故答案为120°-13α.类比研究:(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=1n∠DBC,∠BCO=1n∠ECB,∠A=α,请猜想∠BOC= .解析:(3)根据三角形的内角和等于180°列式整理即可得()11801nBOCn nα-⨯︒∠=-.答案:(3)在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-1n(∠DBC+∠ECB)=180°-1n(∠A+∠ACB+∠A+ABC)=180°-1n(∠A+180°)()11801 nn n α-⨯︒=-.故答案为()11801nn nα-⨯︒-.27.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.(1)若苗圃园的面积为72平方米,求x.解析:(1)根据题意得方程求解即可.答案:(1)根据题意得:(30-2x)x=72,解得:x=3,x=12,∵30-2x≤18,∴x=12.(2)若平行与墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.解析:(2)设苗圃园的面积为y,根据题意得到二次函数解析式y=x(30-2x)=-2x2+30x,根据二次函数的性质求解即可.答案:(2)设苗圃园的面积为y,∴y=x(30-2x)=-2x2+30x,∵a=-2<0,∴苗圃园的面积y有最大值,∴当x=152时,即平行于墙的一边长15>8米,y最大=112.5平方米.(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.解析:(3)由题意得不等式,即可得到结论.答案:(3)由题意得:-2x2+30x≥100,解得:5≤x≤10.28.已知抛物线C:y=x2-3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.(1)求m的值.解析:(1)两图象有一个交点,则对应的方程组有一组解,即△=0,代入计算即可求出m的值.答案:(1)当k=1时,抛物线C与直线l只有一个公共点,∴直线l解析式为y=x,∵23y x x m y x⎧-+⎨⎩==,∴x 2-3x+m=x ,∴x 2-4x+m=0,∴△=16-4m=0,∴m=4.(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y=-3x+b 交于点P ,且 112OA OB OP+=,求b 的值. 解析:(2)作出辅助线,得到△OAC ∽△OPD ,2OP OP OA OB +=,同理2PD PD AC BE+=,AC ,BE 是x 2-(k+3)x+4=0两根,即可.答案:(2)如图,分别过点A ,P ,B 作y 轴的垂线,垂足依次为C ,D ,E ,则△OAC ∽△OPD ,∴OP PD OA AC=. 同理,OP PD BO BE=. ∵112OA OB OP+=, ∴2OP OP OA OB +=.∴2PD PD AC BE+=. ∴112AC BE PD+=, 即2AC BE AC BE PD+=⨯. 解方程组3y kx y x b ⎧⎨-+⎩==, 得3b x k =+, 即3b PD k =+. 由方程组234y kx y x x ⎧⎨-+⎩==消去y ,得x 2-(k+3)x+4=0. ∵AC ,BE 是以上一元二次方程的两根,∴AC+BE=k+3,AC ×BE=4. ∴2343k b k ++=. 解得b=8.(3)在(2)的条件下,设直线l1与y 轴交于点Q ,问:是否在实数k 使S△APQ =S △BPQ ?若存在,求k 的值,若不存在,说明理由.解析:(3)由S △APQ =S △BPQ 得到AC+BE=2PD ,建立方程(k+3)2=16即可.答案:(3)不存在.理由如下:假设存在,当S △APQ =S △BPQ 时,有AP=PB ,于是PD-AC=PE-PD ,即AC+BE=2PD.由(2)可知AC+BE=k+3,83PD k =+,∴8323kk+=⨯+,即(k+3)2=16.解得k=1(舍去k=-7).当k=1时,A,B两点重合,△BQA不存在.∴不存在实数k使S△APQ=S△BPQ.考试高分秘诀是什么?试试这四个方法,特别是中考和高考生谁都想在考试中取得优异的成绩,但要想取得优异的成绩,除了要掌握好相关的知识定理和方法技巧之外,更要学会一些考试技巧。

四川省内江市2016年中考数学试卷(解析版)A卷(共100分)一、选择题(每小题3分,共36分)1.-2016的倒数是( )A.-2016 B.-12016C.12016D.2016[答案]B[解析]非零整数n的倒数是1n ,故-2016的倒数是12016=-12016,故选B.2.2016年“五一”假期期间,某市接待旅游总人数达到了9180 000人次,将9180 000用科学记数法表示应为( )A.918×104B.9.18×105C.9.18×106D.9.18×107[答案]C[解析] 把一个大于10的数表示成a×10n(1≤a<10,n是正整数)的形式,这种记数的方法叫科学记数法.科学记数法中,a是由原数的各位数字组成且只有一位整数的数,n比原数的整数位数少1.故选C.3.将一副直角三角板如图1放置,使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上,则∠1的度数为( )A.75°B.65°C.45°D.30°[答案]A[解析]方法一:∠1的对顶角所在的三角形中另两个角的度数分别为60°,45°,∴∠1=180°-(60°+45°)=75°.方法二:∠1可看作是某个三角形的外角,根据三角形的外角等于与它不相邻的两个内角的和计算.4.下列标志既是轴对称图形又是中心对称图形的是( )[答案]A[解析]选项B 中的图形是轴对称图形,选项C 中的图形是中心对称图形,选项D 中的图形既不是轴对称图形也不是中心对称图形.只有选项A 中的图形符合题意.故选A .5.下列几何体中,主视图和俯视图都为矩形的是( )[答案]B[解析]故选B .6.在函数yx 的取值范围是( ) A .x >3 B .x ≥3 C .x >4D .x ≥3且x ≠4图1 30°45°1 A . B . C . D .A .B .C .D .[解析]欲使根式有意义,则需x-3≥0;欲使分式有意义,则需x-4≠0.∴x的取值范围是30,40.xx-⎧⎨-⎩≥≠解得x≥3且x≠4.故选D.7.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )A.最高分B.中位数C.方差D.平均数[答案]B[解析]这里中位数是预赛成绩排序后第13名同学的成绩,成绩大于中位数则能进入决赛,否则不能.故选B.8.甲、乙两人同时分别从A,B两地沿同一条公路骑自行车到C地,已知A,C两地间的距离为110千米,B,C两地间的距离为100千米,甲骑自行车的平均速度比乙快2千米/时,结果两人同时到达C地,求两人的平均速度分别为多少.为解决此问题,设乙骑自行车的平均速度为x千米/时,由题意列出方程,其中正确的是( )A.1102x+=100xB.1100x=1002x+C.1102x-=100xD.1100x=1002x-[答案]A[解析]依题意可知甲骑自行车的平均速度为(x+2)千米/时.因为他们同时到达C地,即甲行驶110千米所需的时间与乙行驶100千米所需时间相等,所以110=100x.故选A.9.下列命题中,真命题是( ) A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C .对角线互相平分的四边形是平行四边形D .对角线互相垂直平分的四边形是正方形[答案]C[解析]满足选项A 或选项B 中的条件时,不能推出四边形是平行四边形,因此它们都是假命题.由选项D 中的条件只能推出四边形是菱形,因此也是假例题.只有选项C 中的命题是真命题.故选C .10.如图2,点A ,B ,C 在⊙O 上,若∠BAC =45°,OB =2,则图中阴影部分的面积为( )A .π-4B .23π-1C .π-2D .23π-2[答案]C [解析]∵∠O =2∠A =2×45°=90°.∴S 阴影=S 扇形OBC -S △OBC =2902360 -12×2×2=π-2. 故选C .11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )ABC .32D .不能确定 [答案]B[解析]如图,△ABC 是等边三角形,AB =3,点P 是三角形内任意一点,过点P 分别向三边AB ,BC ,CA 作垂线,垂足依次为D ,E ,F ,过点A 作AH ⊥BC 于H .则图2BH =32,AH. 连接PA ,PB ,PC ,则S △PAB +S △PBC +S △PCA =S △ABC . ∴12AB ·PD +12BC ·PE +12CA ·PF =12BC ·AH . ∴PD +PE +PF =AH. 故选B .12.一组正方形按如图3所示的方式放置,其中顶点B 1在y 轴上,顶点C 1,E 1,E 2,C 2,E 3,E 4,C 3……在x 轴上,已知正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3……则正方形A 2016B 2016C 2016D 2016的边长是( )A .(12)2015B .(12)2016C .)2016 D .)2015 [答案] D[解析]易知△B 2C 2E 2∽△C 1D 1E 1,∴2211B C C D =2211B E C E =1111D E C E =tan 30°. ∴B 2C 2=C 1D 1·tan 30.∴C 2D 2. 同理,B 3C 3=C 2D 2·tan 30°=)2; 由此猜想B n C n =n -1. P B ADEF 答案图 C H当n=2016时,B2016C2016=)2015.故选D.二、填空题(每小题5分,共20分)13.分解因式:ax2-ay2=______.[答案]a(x-y)(x+y).[解析]先提取公因式a,再用平方差公式分解.原式=a(x2-y2)=a(x-y)(x+y).故选答案为:a(x-y)(x+y).14.化简:(2a+93a-)÷3aa+=______.[答案]a.[解析]先算小括号,再算除法.原式=(23aa--93a-)÷3aa+=293aa--÷3aa+=(a+3)·3aa+=a.故答案为:a.15.如图4,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=______.[答案]12 5[解析]∵菱形的对角线互相垂直平分,∴OB=3,OC=4,∠BOC=90°.∴BC5.DO CEBA图4∵S △OBC =12OB ·OC ,又S △OBC =12BC ·OE , ∴OB ·OC =BC ·OE ,即3×4=5OE .∴OE =125. 故答案为:125. 16.将一些半径相同的小圆按如图5所示的规律摆放,请仔细观察,第n 个图形有______个小圆.(用含n 的代数式表示)[答案] n 2+n +4 [解析]每个图由外围的4个小圆和中间的“矩形”组成,矩形的面积等于长成宽.由此可知 第1个图中小圆的个数=1×2+4,第2个图中小圆的个数=2×3+4,第3个图中小圆的个数=3×4+4,……第n 个图中小圆的个数=n (n +1)+4=n 2+n +4.故答案为:n 2+n +4.三、解答题(本大题共5小题,共44分)17.(7分)计算:|-3|tan 30(2016-π)0+(12)-1. 解:原式=3-2-1+2 ··············································································· 5分 =3+1-2-1+2 ·········································································································· 6分 =3. ····························································································································· 7分第1个图 第2个图 第3个图 第4个图图518.(9分)如图6所示,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF =BD ,连接BF .(1)求证:D 是BC 的中点;(2)若AB =AC ,试判断四边形AFBD 的形状,并证明你的结论.(1)证明:∵点E 是AD 的中点,∴AE =DE .∵AF ∥BC ,∴∠AFE =∠DCE ,∠FAE =∠CDE .∴△EAF ≌△EDC . ··········································································································· 3分 ∴AF =DC .∵AF =BD ,∴BD =DC ,即D 是BC 的中点. ················································································· 5分(2)四边形AFBD 是矩形.证明如下:∵AF ∥BD ,AF =BD ,∴四边形AFBD 是平行四边形. ···················································································· 7分 ∵AB =AC ,又由(1)可知D 是BC 的中点,∴AD ⊥BC .∴□AFBD 是矩形. ········································································································· 9分19.(9分)某学校为了增强学生体质,决定开放以下体育课外活动项目:A .篮球、B .乒乓球、C .跳绳、D .踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图7(1),图7(2)),请回答下列问题:DC EF B A图6(1)这次被调查的学生共有_______人;(2)请你将条形统计图补充完整;(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).解:(1)由扇形统计图可知:扇形A 的圆心角是36°,所以喜欢A 项目的人数占被调查人数的百分比=36360×100%=10%. ······················· 1分 由条形图可知:喜欢A 类项目的人数有20人,所以被调查的学生共有20÷10%=200(人). ································································ 2分(2)喜欢C 项目的人数=200-(20+80+40)=60(人), ··············································· 3分 因此在条形图中补画高度为60的长方条,如图所示.························································································· 4分(3)画树状图如下:或者列表如下:答案图图7(1) 图7(2)甲 乙 丙 丁 乙 甲 丙 丁 丙 甲 乙 丁 丁甲 乙 丙分 ········································································································································ 7 从树状图或表格中可知,从四名同学中任选两名共有12种结果,每种结果出现的可能性相等,其中选中甲乙两位同学(记为事件A )有2种结果,所以P (A )=212=16. ···········································································································9分 20.(9分)如图8,禁渔期间,我渔政船在A 处发现正北方向B 处有一艘可疑船只,测得A ,B 两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C 处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).解:如图,过点C 作CH ⊥AB 于H ,则△BCH 是等腰直角三角形.设CH =x ,则BH =x ,AH =CH ÷tan 30. ········································································· 2分∵AB =200,∴x =200.∴x =1). ························································································ 4分 ∴BC =. ···················································································· 6分 ∵两船行驶4小时相遇,答案图图8∴可疑船只航行的平均速度=÷4=. ······························ 8分 答:可疑船只航行的平均速度是每小时海里. ······································ 9分21.(10分)如图9,在Rt △ABC 中,∠ABC =90°,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F .⊙O 是△BEF 的外接圆,∠EBF 的平分线交EF 于点G ,交⊙O 于点H ,连接BD ,FH .(1)试判断BD 与⊙O 的位置关系,并说明理由;(2)当AB =BE =1时,求⊙O 的面积;(3)在(2)的条件下,求HG ·HB 的值.(1)直线BD 与⊙O 相切.理由如下:如图,连接OB ,∵BD 是Rt △ABC 斜边上的中线,∴DB =DC .∴∠DBC =∠C .∵OB =OE ,∴∠OBE =∠OEB =∠CED .∵∠C +∠CED =90°,∴∠DBC +∠OBE =90°.∴BD 与⊙O 相切; ········································································································· 3分(2)连接AE .∵AB =BE =1,∴AE∵DF 垂直平分AC ,∴CE =AEBC =1. ··············································· 4分 ∵∠C +∠CAB =90°,∠DFA +∠CAB =90°,答案图 图9∴∠CAB=∠DFA.又∠CBA=∠FBE=90°,AB=BE,∴△CAB≌△FEB.∴BF=BC=1········································································· 5分∴EF2=BE2+BF2=12+(1)2=4+··························································· 6分∴S⊙O=14π·EF2.······················································································· 7分(3)∵AB=BE,∠ABE=90°,∴∠AEB=45°.∵EA=EC,∴∠C=22.5°.···························································································· 8分∴∠H=∠BEG=∠CED=90°-22.5°=67.5°.∵BH平分∠CBF,∴∠EBG=∠HBF=45°.∴∠BGE=∠BFH=67.5°.∴BG=BE=1,BH=BF=1············································································· 9分∴GH=BH-BG∴HB·HG(1=2········································································· 10分B卷一、填空题(每小题6分,共24分)22.任取不等式组30,250kk-⎧⎨+⎩≤>的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的概率为______.[答案]1[解析]不等式组30,250kk-⎧⎨+⎩≤>的解集为-52<k≤3,其整数解为k=-2,-1,0,1,2,3.其中,当k=-2,-1时,方程2x+k=-1的解为非负数.所以所求概率P=26=13.故答案为:1. 23.如图10,点A 在双曲线y =5x 上,点B 在双曲线y =8x上,且AB ∥x 轴,则△OAB 的面积等于______.[答案]32[解析]设点A 的坐标为(a ,5a). ∵AB ∥x 轴,∴点B 的纵坐标为5a. 将y =5a 代入y =8x ,求得x =85a . ∴AB =85a -a =35a . ∴S △OAB =12·35a ·5a =32. 故答案为:32. 24.二次函数y =ax 2+bx +c 的图象如图11所示,且P =|2a +b |+|3b -2c |,Q =|2a -b |-|3b +2c |,则P ,Q 的大小关系是______.[答案]P >Q[解析]∵抛物线的开口向下,∴a <0.∵-2b a =1,∴b >0且a =-2b . ∴|2a +b |=0,|2a -b |=b -2a .∵抛物线与y 轴的正半轴相交,∴c >0.∴|3b +2c |=3b +2c .由图象可知当x =-1时,y <0,即a -b +c <0. ∴-2b -b +c <0,即3b -2c >0.∴|3b -2c |=3b -2c . ∴P =0+3b -2c =3b -2c >0,图11 图10Q=b-2a-(3b+2c)=-(b+2c)<0.∴P>Q.故答案为:P>Q.25.如图12所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是______.[答案]10[解析]作点C关于y轴的对称点C1(-1,0),点C关于x轴的对称点C2,连接C1C2交OA 于点E,交AB于点D,则此时△CDE的周长最小,且最小值等于C1C2的长.∵OA=OB=7,∴CB=6,∠ABC=45°.∵AB垂直平分CC2,∴∠CBC2=90°,C2的坐标为(7,6).在Rt△C1BC2中,C1C210.即△CDE周长的最小值是10.故答案为:10.二、解答题(每小题12分,共36分)26.(12分)问题引入:(1)如图13①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=______(用α表示);如图13②,∠CBO=13∠ABC,∠BCO=13∠ACB,∠A=α,则∠BOC=______(用α表示).(2)如图13③,∠CBO =1∠DBC ,∠BCO =1∠ECB ,∠A =α,请猜想∠BOC =______(用α表示),并说明理由.类比研究:(3)BO ,CO 分别是△ABC 的外角∠DBC ,∠ECB 的n 等分线,它们交于点O ,∠CBO =1n ∠DBC ,∠BCO =1n∠ECB ,∠A =α,请猜想∠BOC =______.解:(1)第一个空填:90°+2α; ··················································································· 2分 第一个空填:90°+3α. ······························································································· 4分 第一空的过程如下:∠BOC =180°-(∠OBC +∠OCB )=180°-12(∠ABC +∠ACB )=180°-12(180°-∠A )=90°+2α. 第二空的过程如下:∠BOC =180°-(∠OBC +∠OCB )=180°-13(∠ABC +∠ACB )=180°-13(180°-∠A )=120°+3α. (2)答案:120°-3α.过程如下: ∠BOC =180°-(∠OBC +∠OCB )=180°-13(∠DBC +∠ECB )=180°-13(180°+∠A )=120°-3α.··························································································································· 8分 (3)答案:120°-3α.过程如下: ∠BOC =180°-(∠OBC +∠OCB )=180°-1n (∠DBC +∠ECB )=180°-1n (180°+∠A )=1n -·180°-nα. ······································································································· 12分 27.(12分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边O C B A 图13②AO图13① O C B A E D 图13③周长为30米的篱笆围成.已知墙长为18米(如图14所示),设这个苗圃园垂直于墙的一边长为x 米.(1)若苗圃园的面积为72平方米,求x ;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x 的取值范围.解:(1)苗圃园与墙平行的一边长为(30-2x )米.依题意可列方程x (30-2x )=72,即x 2-15x +36=0. ········································································· 2分 解得x 1=3,x 2=12. ··································································································· 4分(2)依题意,得8≤30-2x ≤18.解得6≤x ≤11.面积S =x (30-2x )=-2(x -15)2+225(6≤x ≤11). ①当x =152时,S 有最大值,S 最大=2252; ······························································· 6分 ②当x =11时,S 有最小值,S 最小=11×(30-22)=88. ··········································· 8分(3)令x (30-2x )=100,得x 2-15x +50=0.解得x 1=5,x 2=10. ································································································· 10分 ∴x 的取值范围是5≤x ≤10. ························································································· 12分28.(12分)如图15,已知抛物线C :y =x 2-3x +m ,直线l :y =kx (k >0),当k =1时,抛物线C 与直线l 只有一个公共点.(1)求m 的值;(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y =-3x +b 交于点P,且图141OA +1OB =2OP,求b 的值; (3)在(2)的条件下,设直线l 1与y 轴交于点Q ,问:是否存在实数k 使S △APQ =S △BPQ ,若存在,求k 的值;若不存在,说明理由.解:(1)∵当k =1时,抛物线C 与直线l 只有一个公共点,∴方程组23,y x x m y x ⎧=-+⎨=⎩有且只有一组解. ································································· 2分 消去y ,得x 2-4x +m =0,所以此一元二次方程有两个相等的实数根.∴△=0,即(-4)2-4m =0.∴m =4. ························································································································ 4分(2)如图,分别过点A ,P ,B 作y 轴的垂线,垂足依次为C ,D ,E ,则△OAC ∽△OPD ,∴OP OA =PD AC . 同理,OP OB =PD BE . ∵1OA +1OB =2OP ,∴OP OA +OP OB =2. ∴PD AC +PD BE =2. ∴1AC +1BE =2PD ,即AC BE AC BE +=2PD. ·································································· 5分 解方程组,3y kx y x b =⎧⎨=-+⎩得x =3b k +,即PD =3b k +. ··················································· 6分 由方程组2,34y kx y x x =⎧⎨=-+⎩消去y ,得x 2-(k +3)x +4=0.。

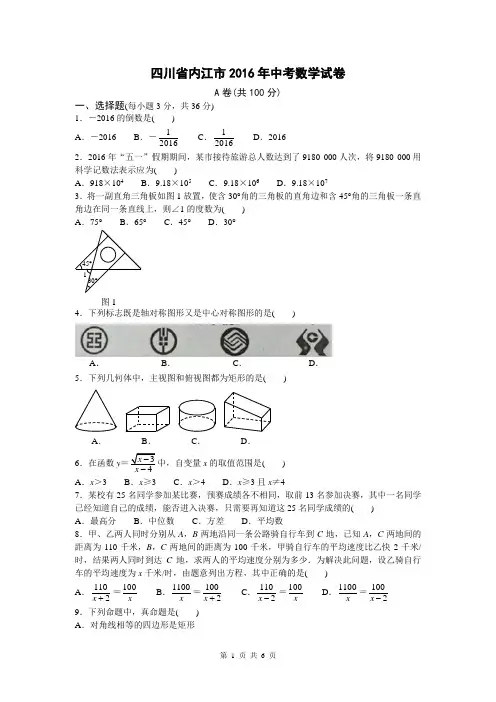
四川省内江市2016年中考数学试卷A 卷(共100分)一、选择题(每小题3分,共36分)1.-2016的倒数是( ) A .-2016 B .-12016 C .12016D .2016 2.2016年“五一”假期期间,某市接待旅游总人数达到了9180 000人次,将9180 000用科学记数法表示应为( )A .918×104B .9.18×105C .9.18×106D .9.18×107 3.将一副直角三角板如图1放置,使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上,则∠1的度数为( ) A .75° B .65° C .45° D .30°4.下列标志既是轴对称图形又是中心对称图形的是( )5.下列几何体中,主视图和俯视图都为矩形的是( )6.在函数yx 的取值范围是( ) A .x >3 B .x ≥3 C .x >4 D .x ≥3且x ≠47.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( ) A .最高分 B .中位数 C .方差 D .平均数8.甲、乙两人同时分别从A ,B 两地沿同一条公路骑自行车到C 地,已知A ,C 两地间的距离为110千米,B ,C 两地间的距离为100千米,甲骑自行车的平均速度比乙快2千米/时,结果两人同时到达C 地,求两人的平均速度分别为多少.为解决此问题,设乙骑自行车的平均速度为x 千米/时,由题意列出方程,其中正确的是( ) A .1102x +=100x B .1100x =1002x + C .1102x -=100xD .1100x =1002x - 9.下列命题中,真命题是( ) A .对角线相等的四边形是矩形图1 30°45°1A .B .C .D .A .B .C .D .B .对角线互相垂直的四边形是菱形C .对角线互相平分的四边形是平行四边形D .对角线互相垂直平分的四边形是正方形10.如图2,点A ,B ,C 在⊙O 上,若∠BAC =45°,OB =2,则图中阴影部分的面积为( ) A .π-4 B .23π-1 C .π-2 D .23π-211.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )ABC .32D .不能确定12.一组正方形按如图3所示的方式放置,其中顶点B 1在y 轴上,顶点C 1,E 1,E 2,C 2,E 3,E 4,C 3……在x 轴上,已知正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3……则正方形A 2016B 2016C 2016D 2016的边长是( ) A .(12)2015 B .(12)2016 C .)2016 D .)2015二、填空题(每小题5分,共20分)13.分解因式:ax 2-ay 2=______.14.化简:(23a a -+93a-)÷3a a +=______. 15.如图4,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =8,BD =6,OE ⊥BC ,垂足为点E ,则OE =______.P BA D EF 答案图C H图216.将一些半径相同的小圆按如图5所示的规律摆放,请仔细观察,第n 个图形有______个小圆.(用含n 的代数式表示)三、解答题(本大题共5小题,共44分)17.(7分)计算:|-3|tan 30°-(2016-π)0+(12)-1.18.(9分)如图6所示,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF =BD ,连接BF . (1)求证:D 是BC 的中点;(2)若AB =AC ,试判断四边形AFBD 的形状,并证明你的结论.19.(9分)某学校为了增强学生体质,决定开放以下体育课外活动项目:A .篮球、B .乒乓球、C .跳绳、D .踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图7(1),图7(2)),请回答下列问题: (1)这次被调查的学生共有_______人; (2)请你将条形统计图补充完整;(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).图7(1)图7(2)D C EFBA 图6D O CEB A 图4 第1个图 第2个图 第3个图 第4个图图520.(9分)如图8,禁渔期间,我渔政船在A 处发现正北方向B 处有一艘可疑船只,测得A ,B 两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C 处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).21.(10分)如图9,在Rt △ABC 中,∠ABC =90°,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F .⊙O 是△BEF 的外接圆,∠EBF 的平分线交EF 于点G ,交⊙O 于点H ,连接BD ,FH .(1)试判断BD 与⊙O 的位置关系,并说明理由; (2)当AB =BE =1时,求⊙O 的面积; (3)在(2)的条件下,求HG ·HB 的值.B 卷一、填空题(每小题6分,共24分)22.任取不等式组30,250k k -⎧⎨+⎩≤>的一个整数解,则能使关于x 的方程:2x +k =-1的解为非负数的概率为______.23.如图10,点A 在双曲线y =5x 上,点B 在双曲线y =8x上,且AB ∥x 轴,则△OAB 的面积等于______.24.二次函数y =ax 2+bx +c 的图象如图11所示,且P =|2a +b |+|3b -2c |,Q =|2a -b |图12图11图10答案图图9答案图图8-|3b +2c |,则P ,Q 的大小关系是______.25.如图12所示,已知点C (1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值是______.二、解答题(每小题12分,共36分)26.(12分)问题引入:(1)如图13①,在△ABC 中,点O 是∠ABC 和∠ACB 平分线的交点,若∠A =α,则∠BOC=______(用α表示);如图13②,∠CBO =13∠ABC ,∠BCO =13∠ACB ,∠A =α,则∠BOC =______(用α表示).(2)如图13③,∠CBO =13∠DBC ,∠BCO =13∠ECB ,∠A =α,请猜想∠BOC =______(用α表示),并说明理由.类比研究:(3)BO ,CO 分别是△ABC 的外角∠DBC ,∠ECB 的n 等分线,它们交于点O ,∠CBO =1n ∠DBC ,∠BCO =1n∠ECB ,∠A =α,请猜想∠BOC =______.27.(12分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图14所示),设这个苗圃园垂直于墙的一边长为x 米.(1)若苗圃园的面积为72平方米,求x ;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x 的取值范围.28.(12分)如图15,已知抛物线C :y =x 2-3x +m ,直线l :y =kx (k >0),当k =1时,抛物线C 与直线l 只有一个公共点. (1)求m 的值;(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y =-3x +b 交于点P ,且1OA+1OB =2OP,求b 的值; (3)在(2)的条件下,设直线l 1与y 轴交于点Q ,问:是否存在实数k 使S △APQ =S △BPQ,若存图14O C BA图13②AO图13①O C B AE D图13③在,求k的值;若不存在,说明理由.。
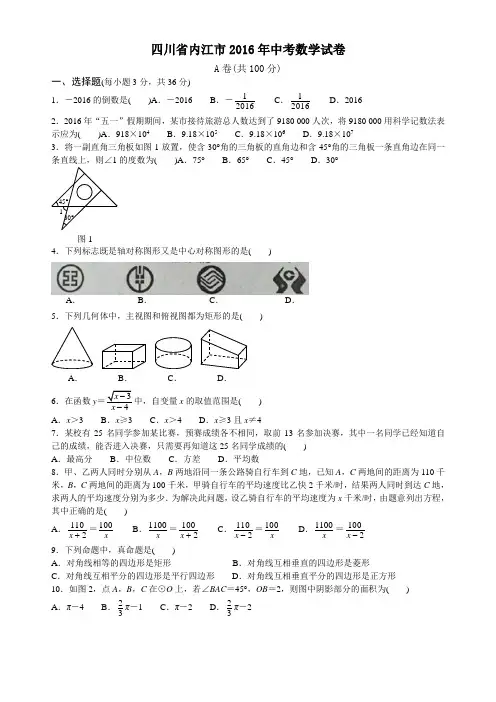
四川省内江市2016年中考数学试卷A卷(共100分)一、选择题(每小题3分,共36分)1.-2016的倒数是( )A.-2016 B.-12016C.12016D.20162.2016年“五一”假期期间,某市接待旅游总人数达到了9180 000人次,将9180 000用科学记数法表示应为( )A.918×104B.9.18×105C.9.18×106D.9.18×1073.将一副直角三角板如图1放置,使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上,则∠1的度数为( )A.75°B.65°C.45°D.30°4.下列标志既是轴对称图形又是中心对称图形的是( )5.下列几何体中,主视图和俯视图都为矩形的是( )6.在函数y=3x-中,自变量x的取值范围是( )A.x>3 B.x≥3 C.x>4 D.x≥3且x≠47.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )A.最高分B.中位数C.方差D.平均数8.甲、乙两人同时分别从A,B两地沿同一条公路骑自行车到C地,已知A,C两地间的距离为110千米,B,C两地间的距离为100千米,甲骑自行车的平均速度比乙快2千米/时,结果两人同时到达C地,求两人的平均速度分别为多少.为解决此问题,设乙骑自行车的平均速度为x千米/时,由题意列出方程,其中正确的是( )A.1102x+=100xB.1100x=1002x+C.1102x-=100xD.1100x=1002x-9.下列命题中,真命题是( )A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形10.如图2,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )A.π-4 B.23π-1 C.π-2 D.23π-2图130°45°1A.B.C.D.A.B.C.D.11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )ABC .32D .不能确定 12.一组正方形按如图3所示的方式放置,其中顶点B 1在y 轴上,顶点C 1,E 1,E 2,C 2,E 3,E 4,C 3……在x 轴上,已知正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3……则正方形A 2016B 2016C 2016D 2016的边长是( )A .(12)2015 B .(12)2016 C .)2016 D .)2015 二、填空题(每小题5分,共20分)13.分解因式:ax 2-ay 2=______.14.化简:(23a a -+93a-)÷3a a +=______. 15.如图4,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =8,BD =6,OE ⊥BC ,垂足为点E ,则OE =______.16.将一些半径相同的小圆按如图5所示的规律摆放,请仔细观察,第n 个图形有______个小圆.(用含n 的代数式表示)三、解答题(本大题共5小题,共44分)17.(7分)计算:|-3|tan 30°-(2016-π)0+(12)-1.图2 DOCEBA 图4 第1个图 第2个图 第3个图 第4个图图518.(9分)如图6所示,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF =BD ,连接BF .(1)求证:D 是BC 的中点;(2)若AB =AC ,试判断四边形AFBD 的形状,并证明你的结论.19.(9分)某学校为了增强学生体质,决定开放以下体育课外活动项目:A .篮球、B .乒乓球、C .跳绳、D .踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图7(1),图7(2)),请回答下列问题:(1)这次被调查的学生共有_______人;(2)请你将条形统计图补充完整;(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).20.(9分)如图8,禁渔期间,我渔政船在A 处发现正北方向B 处有一艘可疑船只,测得A ,B 两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C 处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).图7(1)图7(2)DC EF B A图6图821.(10分)如图9,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.(1)试判断BD与⊙O的位置关系,并说明理由;(2)当AB=BE=1时,求⊙O的面积;(3)在(2)的条件下,求HG·HB的值.图9B卷一、填空题(每小题6分,共24分)22.任取不等式组30,250k k -⎧⎨+⎩≤>的一个整数解,则能使关于x 的方程:2x +k =-1的解为非负数的概率为______.23.如图10,点A 在双曲线y =5x 上,点B 在双曲线y =8x 上,且AB ∥x 轴,则△OAB 的面积等于______.24.二次函数y =ax 2+bx +c 的图象如图11所示,且P =|2a +b |+|3b -2c |,Q =|2a -b |-|3b +2c |,则P ,Q 的大小关系是______.25.如图12所示,已知点C (1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值是______.二、解答题(每小题12分,共36分)26.(12分)问题引入:(1)如图13①,在△ABC 中,点O 是∠ABC 和∠ACB 平分线的交点,若∠A =α,则∠BOC =______(用α表示);如图13②,∠CBO =13∠ABC ,∠BCO =13∠ACB ,∠A =α,则∠BOC =______(用α表示). (2)如图13③,∠CBO =13∠DBC ,∠BCO =13∠ECB ,∠A =α,请猜想∠BOC =______(用α表示),并说明理由.类比研究:(3)BO ,CO 分别是△ABC 的外角∠DBC ,∠ECB 的n 等分线,它们交于点O ,∠CBO =1n ∠DBC ,∠BCO =1n∠ECB ,∠A =α,请猜想∠BOC =______. 27.(12分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图14所示),设这个苗圃园垂直于墙的一边长为x 米.(1)若苗圃园的面积为72平方米,求x ;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x 的取值范围.OC B A 图13②ABCO 图13① O C B A E D 图13③图12图11 图1028.(12分)如图15,已知抛物线C :y =x 2-3x +m ,直线l :y =kx (k >0),当k =1时,抛物线C 与直线l 只有一个公共点.(1)求m 的值;(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y =-3x +b 交于点P ,且1OA +1OB =2OP,求b 的值; (3)在(2)的条件下,设直线l 1与y 轴交于点Q ,问:是否存在实数k 使S △APQ =S △BPQ ,若存在,求k 的值;若不存在,说明理由.四川省内江市2016年中考数学试卷 解析一、选择题(每小题3分,共36分)1.-2016的倒数是( )A .-2016B .-12016 C .12016D .2016 [答案]B答案图图15图14[解析]非零整数n的倒数是1n,故-2016的倒数是12016-=-12016,故选B.2.2016年“五一”假期期间,某市接待旅游总人数达到了9180 000人次,将9180 000用科学记数法表示应为( )A.918×104B.9.18×105C.9.18×106D.9.18×107[答案]C[解析] 把一个大于10的数表示成a×10n(1≤a<10,n是正整数)的形式,这种记数的方法叫科学记数法.科学记数法中,a是由原数的各位数字组成且只有一位整数的数,n比原数的整数位数少1.故选C.3.将一副直角三角板如图1放置,使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上,则∠1的度数为( )A.75°B.65°C.45°D.30°[答案]A[解析]方法一:∠1的对顶角所在的三角形中另两个角的度数分别为60°,45°,∴∠1=180°-(60°+45°)=75°.方法二:∠1可看作是某个三角形的外角,根据三角形的外角等于与它不相邻的两个内角的和计算.故选A.4.下列标志既是轴对称图形又是中心对称图形的是( )[答案]A[解析]选项B中的图形是轴对称图形,选项C中的图形是中心对称图形,选项D中的图形既不是轴对称图形也不是中心对称图形.只有选项A中的图形符合题意.故选A.5.下列几何体中,主视图和俯视图都为矩形的是( )[答案]B选项A 选项B 选项C 选项D主视图三角形矩形矩形梯形俯视图圆(含圆心) 矩形圆矩形故选B.6.在函数y=3x-中,自变量x的取值范围是( )A.x>3 B.x≥3 C.x>4 D.x≥3且x≠4[答案]D[解析]欲使根式有意义,则需x-3≥0;欲使分式有意义,则需x-4≠0.图130°45°1A.B.C.D.A.B.C.D.∴x 的取值范围是30,40.x x -⎧⎨-⎩≥≠解得x ≥3且x ≠4.故选D . 7.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )A .最高分B .中位数C .方差D .平均数[答案]B[解析]这里中位数是预赛成绩排序后第13名同学的成绩,成绩大于中位数则能进入决赛,否则不能. 故选B .8.甲、乙两人同时分别从A ,B 两地沿同一条公路骑自行车到C 地,已知A ,C 两地间的距离为110千米,B ,C 两地间的距离为100千米,甲骑自行车的平均速度比乙快2千米/时,结果两人同时到达C 地,求两人的平均速度分别为多少.为解决此问题,设乙骑自行车的平均速度为x 千米/时,由题意列出方程,其中正确的是( )A .1102x +=100xB .1100x =1002x +C .1102x -=100xD .1100x =1002x - [答案]A[解析]依题意可知甲骑自行车的平均速度为(x +2)千米/时.因为他们同时到达C 地,即甲行驶110千米所需的时间与乙行驶100千米所需时间相等,所以1102x +=100x. 故选A .9.下列命题中,真命题是( )A .对角线相等的四边形是矩形B .对角线互相垂直的四边形是菱形C .对角线互相平分的四边形是平行四边形D .对角线互相垂直平分的四边形是正方形[答案]C[解析]满足选项A 或选项B 中的条件时,不能推出四边形是平行四边形,因此它们都是假命题.由选项D 中的条件只能推出四边形是菱形,因此也是假例题.只有选项C 中的命题是真命题.故选C .10.如图2,点A ,B ,C 在⊙O 上,若∠BAC =45°,OB =2,则图中阴影部分的面积为( )A .π-4B .23π-1C .π-2D .23π-2[答案]C[解析]∵∠O =2∠A =2×45°=90°.∴S 阴影=S 扇形OBC -S △OBC =2902360πg -12×2×2=π-2. 故选C .11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )ABC .32D .不能确定 [答案]B[解析]如图,△ABC 是等边三角形,AB =3,点P 是三角形内任意一点,过点P 分别向三边AB ,BC, 图2CA 作垂线,垂足依次为D ,E ,F ,过点A 作AH ⊥BC 于H .则BH =32,AH. 连接P A ,PB ,PC ,则S △P AB +S △PBC +S △PCA =S △ABC . ∴12AB ·PD +12BC ·PE +12CA ·PF =12BC ·AH . ∴PD +PE +PF =AH. 故选B .12.一组正方形按如图3所示的方式放置,其中顶点B 1在y 轴上,顶点C 1,E 1,E 2,C 2,E 3,E 4,C 3……在x 轴上,已知正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3……则正方形A 2016B 2016C 2016D 2016的边长是( )A .(12)2015 B .(12)2016 C .)2016 D .)2015 [答案] D[解析]易知△B 2C 2E 2∽△C 1D 1E 1,∴2211B C C D =2211B E C E =1111D E C E =tan 30°. ∴B 2C 2=C 1D 1·tan 30°.∴C 2D 2. 同理,B 3C 3=C 2D 2·tan 30°=)2; 由此猜想B n C n =)n -1. 当n =2016时,B 2016C 2016=)2015. 故选D .二、填空题(每小题5分,共20分)13.分解因式:ax 2-ay 2=______.[答案]a (x -y )(x +y ).[解析]先提取公因式a ,再用平方差公式分解.原式=a (x 2-y 2)=a (x -y )(x +y ).故选答案为:a (x -y )(x +y ). P B ADEF 答案图 C H14.化简:(23a a -+93a-)÷3a a +=______. [答案]a .[解析]先算小括号,再算除法.原式=(23a a --93a -)÷3a a +=293a a --÷3a a +=(a +3)·3a a +=a . 故答案为:a .15.如图4,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =8,BD =6,OE ⊥BC ,垂足为点E ,则OE =______.[答案]125[解析]∵菱形的对角线互相垂直平分,∴OB =3,OC =4,∠BOC =90°.∴BC5.∵S △OBC =12OB ·OC ,又S △OBC =12BC ·OE , ∴OB ·OC =BC ·OE ,即3×4=5OE .∴OE =125. 故答案为:125. 16.将一些半径相同的小圆按如图5所示的规律摆放,请仔细观察,第n 个图形有______个小圆.(用含n 的代数式表示)[答案] n 2+n +4 [解析]每个图由外围的4个小圆和中间的“矩形”组成,矩形的面积等于长成宽.由此可知第1个图中小圆的个数=1×2+4,第2个图中小圆的个数=2×3+4,第3个图中小圆的个数=3×4+4,……第n 个图中小圆的个数=n (n +1)+4=n 2+n +4.故答案为:n 2+n +4.三、解答题(本大题共5小题,共44分)17.(7分)计算:|-3|tan 30°-(2016-π)0+(12)-1. 第1个图 第2个图 第3个图 第4个图图5DOC EBA 图4解:原式=3-2-1+2 ································································· 5分 =3+1-2-1+2 ························································································· 6分=3. ········································································································ 7分18.(9分)如图6所示,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF =BD ,连接BF .(1)求证:D 是BC 的中点;(2)若AB =AC ,试判断四边形AFBD 的形状,并证明你的结论.(1)证明:∵点E 是AD 的中点,∴AE =DE .∵AF ∥BC ,∴∠AFE =∠DCE ,∠F AE =∠CDE .∴△EAF ≌△EDC . ····················································································· 3分∴AF =DC .∵AF =BD ,∴BD =DC ,即D 是BC 的中点. ··································································· 5分(2)四边形AFBD 是矩形.证明如下:∵AF ∥BD ,AF =BD ,∴四边形AFBD 是平行四边形. ····································································· 7分∵AB =AC ,又由(1)可知D 是BC 的中点,∴AD ⊥BC .∴□AFBD 是矩形. ····················································································· 9分19.(9分)某学校为了增强学生体质,决定开放以下体育课外活动项目:A .篮球、B .乒乓球、C .跳绳、D .踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图7(1),图7(2)),请回答下列问题:(1)这次被调查的学生共有_______人;(2)请你将条形统计图补充完整;(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).解:(1)由扇形统计图可知:扇形A 的圆心角是36°,所以喜欢A 项目的人数占被调查人数的百分比=36360×100%=10%. ···················· 1分 由条形图可知:喜欢A 类项目的人数有20人,所以被调查的学生共有20÷10%=200(人). ······················································ 2分(2)喜欢C 项目的人数=200-(20+80+40)=60(人), ·········································· 3分图7(1)图7(2)DC EF B A图6因此在条形图中补画高度为60的长方条,如图所示.·········································································· 4分(3)画树状图如下:分 (7)从树状图或表格中可知,从四名同学中任选两名共有12种结果,每种结果出现的可能性相等,其中选中甲乙两位同学(记为事件A )有2种结果,所以P (A )=212=16. ·························································································· 9分20.(9分)如图8,禁渔期间,我渔政船在A 处发现正北方向B 处有一艘可疑船只,测得A ,B两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C 处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).解:如图,过点C 作CH ⊥AB 于H ,则△BCH 是等腰直角三角形.设CH =x ,则BH =x ,AH =CH ÷tan 30°. ·····························································2分∵AB =200,∴x =200.∴x 1). ········································································· 4分 ∴BC x =). ······································································ 6分∵两船行驶4小时相遇,∴可疑船只航行的平均速度=)÷4=). ························ 8分答:可疑船只航行的平均速度是每小时)海里. ································· 9分答案图 甲 乙 丙 丁 乙 甲 丙 丁 丙 甲 乙 丁 丁甲 乙 丙图8答案图21.(10分)如图9,在Rt △ABC 中,∠ABC =90°,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F .⊙O 是△BEF 的外接圆,∠EBF 的平分线交EF 于点G ,交⊙O 于点H ,连接BD ,FH .(1)试判断BD 与⊙O 的位置关系,并说明理由;(2)当AB =BE =1时,求⊙O 的面积;(3)在(2)的条件下,求HG ·HB 的值.(1)直线BD 与⊙O 相切.理由如下:如图,连接OB ,∵BD 是Rt △ABC 斜边上的中线,∴DB =DC .∴∠DBC =∠C .∵OB =OE ,∴∠OBE =∠OEB =∠CED .∵∠C +∠CED =90°,∴∠DBC +∠OBE =90°.∴BD 与⊙O 相切; ······················································································ 3分(2)连接AE .∵AB =BE =1,∴AE.∵DF 垂直平分AC ,∴CE =AE.∴BC =1. ····································· 4分∵∠C +∠CAB =90°,∠DF A +∠CAB =90°,∴∠CAB =∠DF A .又∠CBA =∠FBE =90°,AB =BE ,∴△CAB ≌△FEB .∴BF =BC =1. ························································ 5分∴EF 2=BE 2+BF 2=12+(1)2=4+. ·················································· 6分∴S ⊙O =14π·EF 2. ······································································· 7分 (3)∵AB =BE ,∠ABE =90°,∴∠AEB =45°.∵EA =EC ,∴∠C =22.5°. ··········································································· 8分∴∠H =∠BEG =∠CED =90°-22.5°=67.5°.∵BH 平分∠CBF ,∴∠EBG =∠HBF =45°.∴∠BGE =∠BFH =67.5°. ∴BG =BE =1,BH =BF =1. ································································ 9分∴GH =BH -BG.∴HB ·HG×(1)=2. ························································· 10分B 卷一、填空题(每小题6分,共24分)图9答案图22.任取不等式组30,250k k -⎧⎨+⎩≤>的一个整数解,则能使关于x 的方程:2x +k =-1的解为非负数的概率为______.[答案]13[解析]不等式组30,250k k -⎧⎨+⎩≤>的解集为-52<k ≤3,其整数解为k =-2,-1,0,1,2,3. 其中,当k =-2,-1时,方程2x +k =-1的解为非负数.所以所求概率P =26=13. 故答案为:13. 23.如图10,点A 在双曲线y =5x 上,点B 在双曲线y =8x 上,且AB ∥x 轴,则△OAB 的面积等于______. [答案]32[解析]设点A 的坐标为(a ,5a). ∵AB ∥x 轴,∴点B 的纵坐标为5a . 将y =5a 代入y =8x ,求得x =85a .∴AB =85a -a =35a . ∴S △OAB =12·35a ·5a =32.故答案为:32.24.二次函数y =ax 2+bx +c 的图象如图11所示,且P =|2a +b |+|3b -2c |,Q =|2a -b |-|3b +2c |,则P ,Q 的大小关系是______.[答案]P >Q[解析]∵抛物线的开口向下,∴a <0.∵-2b a=1,∴b >0且a =-2b . ∴|2a +b |=0,|2a -b |=b -2a .∵抛物线与y 轴的正半轴相交,∴c >0.∴|3b +2c |=3b +2c .由图象可知当x =-1时,y <0,即a -b +c <0. ∴-2b -b +c <0,即3b -2c >0.∴|3b -2c |=3b -2c . ∴P =0+3b -2c =3b -2c >0,Q =b -2a -(3b +2c )=-(b +2c )<0.∴P >Q .故答案为:P >Q .25.如图12所示,已知点C (1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值是______.图10图11 图12[答案]10[解析]作点C 关于y 轴的对称点C 1(-1,0),点C 关于x 轴的对称点C 2,连接C 1C 2交OA 于点E ,交AB 于点D ,则此时△CDE 的周长最小,且最小值等于C 1C 2的长.∵OA =OB =7,∴CB =6,∠ABC =45°.∵AB 垂直平分CC 2,∴∠CBC 2=90°,C 2的坐标为(7,6).在Rt △C 1BC 2中,C 1C 2=10.即△CDE 周长的最小值是10.故答案为:10.二、解答题(每小题12分,共36分)26.(12分)问题引入:(1)如图13①,在△ABC 中,点O 是∠ABC 和∠ACB 平分线的交点,若∠A =α,则∠BOC =______(用α表示);如图13②,∠CBO =13∠ABC ,∠BCO =13∠ACB ,∠A =α,则∠BOC =______(用α表示). (2)如图13③,∠CBO =13∠DBC ,∠BCO =13∠ECB ,∠A =α,请猜想∠BOC =______(用α表示),并说明理由.类比研究:(3)BO ,CO 分别是△ABC 的外角∠DBC ,∠ECB 的n 等分线,它们交于点O ,∠CBO =1n ∠DBC ,∠BCO =1n∠ECB ,∠A =α,请猜想∠BOC =______. 解:(1)第一个空填:90°+2α; ······································································ 2分 第一个空填:90°+3α. ················································································ 4分 第一空的过程如下:∠BOC =180°-(∠OBC +∠OCB )=180°-12(∠ABC +∠ACB )=180°-12(180°-∠A )=90°+2α. 第二空的过程如下:∠BOC =180°-(∠OBC +∠OCB )=180°-13(∠ABC +∠ACB )=180°-13(180°-∠OC B A 图13②ABCO 图13① O C B A E D 图13③A )=120°+3α. (2)答案:120°-3α.过程如下: ∠BOC =180°-(∠OBC +∠OCB )=180°-13(∠DBC +∠ECB )=180°-13(180°+∠A )=120°-3α. 8分(3)答案:120°-3α.过程如下: ∠BOC =180°-(∠OBC +∠OCB )=180°-1n (∠DBC +∠ECB )=180°-1n (180°+∠A )=1n n -·180°-nα. ······································································································· 12分 27.(12分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图14所示),设这个苗圃园垂直于墙的一边长为x 米.(1)若苗圃园的面积为72平方米,求x ;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x 的取值范围.解:(1)苗圃园与墙平行的一边长为(30-2x )米.依题意可列方程x (30-2x )=72,即x 2-15x +36=0. ······························································· 2分解得x 1=3,x 2=12. ···················································································· 4分(2)依题意,得8≤30-2x ≤18.解得6≤x ≤11.面积S =x (30-2x )=-2(x -152)2+2252(6≤x ≤11). ①当x =152时,S 有最大值,S 最大=2252; ······················································· 6分 ②当x =11时,S 有最小值,S 最小=11×(30-22)=88. ······································· 8分(3)令x (30-2x )=100,得x 2-15x +50=0.解得x 1=5,x 2=10. ·················································································· 10分∴x 的取值范围是5≤x ≤10. ······································································· 12分28.(12分)如图15,已知抛物线C :y =x 2-3x +m ,直线l :y =kx (k >0),当k =1时,抛物线C 与直线l 只有一个公共点.(1)求m 的值;(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y =-3x +b 交于点P ,且1OA +1OB =2OP,求b 的值; (3)在(2)的条件下,设直线l 1与y 轴交于点Q ,问:是否存在实数k 使S △APQ =S △BPQ ,若存在,求k 的值;若不存在,说明理由.图14解:(1)∵当k =1时,抛物线C 与直线l 只有一个公共点,∴方程组23,y x x m y x⎧=-+⎨=⎩有且只有一组解. ····················································· 2分 消去y ,得x 2-4x +m =0,所以此一元二次方程有两个相等的实数根.∴△=0,即(-4)2-4m =0.∴m =4. ··································································································· 4分(2)如图,分别过点A ,P ,B 作y 轴的垂线,垂足依次为C ,D ,E ,则△OAC ∽△OPD ,∴OP OA =PD AC . 同理,OP OB =PD BE . ∵1OA +1OB =2OP ,∴OP OA +OP OB =2. ∴PD AC +PD BE =2. ∴1AC +1BE =2PD ,即AC BE AC BE +g =2PD. ······················································ 5分 解方程组,3y kx y x b =⎧⎨=-+⎩得x =3b k +,即PD =3b k +. ··········································· 6分 由方程组2,34y kx y x x =⎧⎨=-+⎩消去y ,得x 2-(k +3)x +4=0.∵AC ,BE 是以上一元二次方程的两根,∴AC +BE =k +3,AC ·BE =4. ···································································· 7分 ∴34k +=23bk +. 解得b =8. ································································································ 8分(3)不存在.理由如下: ················································································· 9分 假设存在,则当S △APQ =S △BPQ 时有AP =PB ,于是PD -AC =PE -PD ,即AC +BE =2PD .由(2)可知AC +BE =k +3,PD =83k +, ∴k +3=2×83k +,即(k +3)2=16. 解得k =1(舍去k =-7). ············································································ 11分 当k =1时,A ,B 两点重合,△QAB 不存在.图15答案图。

内江市中考数学试题及答案(3)2016年内江市中考数学试题及答案解:(1)由扇形统计图可知:扇形A的圆心角是36°,所以喜欢A项目的人数占被调查人数的百分比= ×100%=10%. 1分由条形图可知:喜欢A类项目的人数有20人,所以被调查的学生共有20÷10%=200(人). 2分(2)喜欢C项目的人数=200-(20+80+40)=60(人), 3分因此在条形图中补画高度为60的长方条,如图所示.4分(3)画树状图如下:或者列表如下:甲乙丙丁甲甲乙甲丙甲丁乙乙甲乙丙乙丁丙丙甲丙乙丙丁丁丁甲丁乙丁丙分 7从树状图或表格中可知,从四名同学中任选两名共有12种结果,每种结果出现的可能性相等,其中选中甲乙两位同学(记为事件A)有2种结果,所以P(A)= = . 9分20.(9分)如图8,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A,B两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).[考点]三角函数、解决实际问题。
解:如图,过点C作CH⊥AB于H,则△BCH是等腰直角三角形.设CH=x,则BH=x,AH=CH÷ 30°= x. 2分∵AB=200,∴x+ x=200.∴x= =100( -1). 4分∴BC= x=100( - ). 6分∵两船行驶4小时相遇,∴可疑船只航行的平均速度=100( - )÷4=45( - ). 8分答:可疑船只航行的平均速度是每小时45( - )海里. 9分21.(10分)如图9,在△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.(1)试判断BD与⊙O的位置关系,并说明理由;(2)当AB=BE=1时,求⊙O的面积;(3)在(2)的条件下,求HG•HB的值.[考点]切线的性质与判定定理,三角形的全等,直角三角形斜边上中线定理、勾股定理。
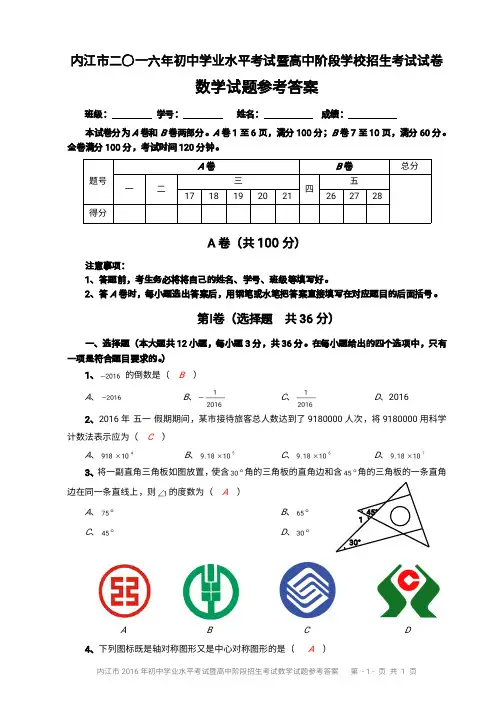
四川省内江市2016年中考数学试卷(解析版)A 卷(共100分)一、选择题(每小题3分,共36分)1.-2016的倒数是( ) A .-2016 B .-12016 C .12016D .2016 [答案]B[解析]非零整数n 的倒数是1n ,故-2016的倒数是12016 =-12016,故选B . 2.2016年“五一”假期期间,某市接待旅游总人数达到了9180 000人次,将9180 000用科学记数法表示应为( )A .918×104B .9.18×105C .9.18×106D .9.18×107 [答案]C[解析] 把一个大于10的数表示成a ×10n (1≤a <10,n 是正整数)的形式,这种记数的方法叫科学记数法.科学记数法中,a 是由原数的各位数字组成且只有一位整数的数,n 比原数的整数位数少1.故选C .3.将一副直角三角板如图1放置,使含30°角的三角板的直角边和含45°角的三角板一条直角边在同一条直线上,则∠1的度数为( ) A .75° B .65° C .45° D .30° [答案]A[解析]方法一:∠1的对顶角所在的三角形中另两个角的度数分别为60°,45°,∴∠1=180°-(60°+45°)=75°.方法二:∠1可看作是某个三角形的外角,根据三角形的外角等于与它不相邻的两个内角的和计算. 故选A .4.下列标志既是轴对称图形又是中心对称图形的是( )[答案]A[解析]选项B 中的图形是轴对称图形,选项C 中的图形是中心对称图形,选项D 中的图形既不是轴对称图形也不是中心对称图形.只有选项A 中的图形符合题意. 故选A .5.下列几何体中,主视图和俯视图都为矩形的是( )图1 30°45°1A .B .C .D .[答案]B6.在函数y中,自变量x的取值范围是( )A.x>3 B.x≥3 C.x>4 D.x≥3且x≠4[答案]D[解析]欲使根式有意义,则需x-3≥0;欲使分式有意义,则需x-4≠0.∴x的取值范围是30,40.xx-⎧⎨-⎩≥≠解得x≥3且x≠4.故选D.7.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )A.最高分B.中位数C.方差D.平均数[答案]B[解析]这里中位数是预赛成绩排序后第13名同学的成绩,成绩大于中位数则能进入决赛,否则不能.故选B.8.甲、乙两人同时分别从A,B两地沿同一条公路骑自行车到C地,已知A,C两地间的距离为110千米,B,C两地间的距离为100千米,甲骑自行车的平均速度比乙快2千米/时,结果两人同时到达C地,求两人的平均速度分别为多少.为解决此问题,设乙骑自行车的平均速度为x千米/时,由题意列出方程,其中正确的是( )A.1102x+=100xB.1100x=1002x+C.1102x-=100x D.1100x=1002x-[答案]A[解析]依题意可知甲骑自行车的平均速度为(x+2)千米/时.因为他们同时到达C地,即甲行驶110千米所需的时间与乙行驶100千米所需时间相等,所以1102x+=100x.故选A.9.下列命题中,真命题是( )A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形[答案]C[解析]满足选项A或选项B中的条件时,不能推出四边形是平行四边形,因此它们都是假命A.B.C.D.题.由选项D中的条件只能推出四边形是菱形,因此也是假例题.只有选项C中的命题是真命题.故选C.10.如图2,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )A.π-4 B.23π-1 C.π-2 D.23π-2[答案]C[解析]∵∠O=2∠A=2×45°=90°.∴S阴影=S扇形OBC-S△OBC=2902360π-12×2×2=π-2.故选C.11.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )ABC.32D.不能确定[答案]B[解析]如图,△ABC是等边三角形,AB=3,点P是三角形内任意一点,过点P分别向三边AB,BC,CA作垂线,垂足依次为D,E,F,过点A作AH⊥BC于H.则BH=32,AH.连接P A,PB,PC,则S△P AB+S△PBC+S△PCA=S△ABC.∴12AB·PD+12BC·PE+12CA·PF=12BC·AH.∴PD+PE+PF=AH.故选B.12.一组正方形按如图3所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……则正方形A2016B2016C2016D2016的边长是( )A.(12)2015B.(12)2016C.)2016D.)2015 PBADEF答案图CH 图2[答案] D[解析]易知△B 2C 2E 2∽△C 1D 1E 1,∴2211B C C D =2211B E C E =1111D EC E =tan 30°. ∴B 2C 2=C 1D 1·tan 30°.∴C 2D 2.同理,B 3C 3=C 2D 2·tan 30°=)2;由此猜想B n C n =)n -1.当n =2016时,B 2016C 2016=)2015.故选D .二、填空题(每小题5分,共20分)13.分解因式:ax 2-ay 2=______. [答案]a (x -y )(x +y ).[解析]先提取公因式a ,再用平方差公式分解. 原式=a (x 2-y 2)=a (x -y )(x +y ). 故选答案为:a (x -y )(x +y ).14.化简:(23a a -+93a-)÷3a a +=______.[答案]a .[解析]先算小括号,再算除法.原式=(23a a --93a -)÷3a a +=293a a --÷3a a +=(a +3)·3a a +=a .故答案为:a .15.如图4,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =8,BD =6,OE ⊥BC ,垂足为点E ,则OE =______.D O CE B A 图4[答案]125[解析]∵菱形的对角线互相垂直平分, ∴OB =3,OC =4,∠BOC =90°. ∴BC5. ∵S △OBC =12OB ·OC ,又S △OBC =12BC ·OE , ∴OB ·OC =BC ·OE ,即3×4=5OE . ∴OE =125. 故答案为:125. 16.将一些半径相同的小圆按如图5所示的规律摆放,请仔细观察,第n 个图形有______个小圆.(用含n 的代数式表示)[答案] n 2+n +4[解析]每个图由外围的4个小圆和中间的“矩形”组成,矩形的面积等于长成宽.由此可知 第1个图中小圆的个数=1×2+4, 第2个图中小圆的个数=2×3+4, 第3个图中小圆的个数=3×4+4, ……第n 个图中小圆的个数=n (n +1)+4=n 2+n +4. 故答案为:n 2+n +4.三、解答题(本大题共5小题,共44分)17.(7分)计算:|-3|·tan 30°-(2016-π)0+(12)-1. 解:原式=3-2-1+2 ································································· 5分=3+1-2-1+2 ························································································· 6分 =3. ········································································································ 7分 18.(9分)如图6所示,△ABC 中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF =BD ,连接BF . (1)求证:D 是BC 的中点;(2)若AB =AC ,试判断四边形AFBD 的形状,并证明你的结论.第1个图 第2个图 第3个图 第4个图图5(1)证明:∵点E 是AD 的中点,∴AE =DE .∵AF ∥BC ,∴∠AFE =∠DCE ,∠F AE =∠CDE . ∴△EAF ≌△EDC . ····················································································· 3分 ∴AF =DC . ∵AF =BD ,∴BD =DC ,即D 是BC 的中点. ··································································· 5分 (2)四边形AFBD 是矩形.证明如下: ∵AF ∥BD ,AF =BD ,∴四边形AFBD 是平行四边形. ····································································· 7分 ∵AB =AC ,又由(1)可知D 是BC 的中点, ∴AD ⊥BC .∴□AFBD 是矩形. ····················································································· 9分 19.(9分)某学校为了增强学生体质,决定开放以下体育课外活动项目:A .篮球、B .乒乓球、C .跳绳、D .踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图7(1),图7(2)),请回答下列问题: (1)这次被调查的学生共有_______人; (2)请你将条形统计图补充完整;(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).解:(1)由扇形统计图可知:扇形A 的圆心角是36°, 所以喜欢A 项目的人数占被调查人数的百分比=36360×100%=10%. ···················· 1分 由条形图可知:喜欢A 类项目的人数有20人, 所以被调查的学生共有20÷10%=200(人). ······················································ 2分 (2)喜欢C 项目的人数=200-(20+80+40)=60(人), ·········································· 3分 因此在条形图中补画高度为60的长方条,如图所示.图7(1)图7(2)D C EF BA 图6·········································································· 4分 (3)画树状图如下:分 (7)从树状图或表格中可知,从四名同学中任选两名共有12种结果,每种结果出现的可能性相等,其中选中甲乙两位同学(记为事件A )有2种结果,所以 P (A )=212=16. ························································································· 9分 20.(9分)如图8,禁渔期间,我渔政船在A 处发现正北方向B 处有一艘可疑船只,测得A ,B两处距离为200海里,可疑船只正沿南偏东45°方向航行.我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).解:如图,过点C 作CH ⊥AB 于H ,则△BCH 是等腰直角三角形.设CH =x ,则BH =x ,AH =CH ÷tan 30°. ····························································· 2分 ∵AB =200,∴x x =200. ∴x 1). ········································································· 4分∴BC x =). ······································································ 6分 ∵两船行驶4小时相遇,答案图图8答案图 甲乙 丙 丁 乙甲 丙 丁 丙甲 乙 丁 丁甲 乙 丙∴可疑船只航行的平均速度=÷4=). ························8分答:可疑船只航行的平均速度是每小时)海里. ································9分21.(10分)如图9,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB 的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.(1)试判断BD与⊙O的位置关系,并说明理由;(2)当AB=BE=1时,求⊙O的面积;(3)在(2)的条件下,求HG·HB的值.(1)直线BD与⊙O相切.理由如下:如图,连接OB,∵BD是Rt△ABC斜边上的中线,∴DB=DC.∴∠DBC=∠C.∵OB=OE,∴∠OBE=∠OEB=∠CED.∵∠C+∠CED=90°,∴∠DBC+∠OBE=90°.∴BD与⊙O相切;······················································································3分(2)连接AE.∵AB=BE=1,∴AE.∵DF垂直平分AC,∴CE=AE.∴BC=1.·····································4分∵∠C+∠CAB=90°,∠DF A+∠CAB=90°,∴∠CAB=∠DF A.又∠CBA=∠FBE=90°,AB=BE,∴△CAB≌△FEB.∴BF=BC=1. ························································5分∴EF2=BE2+BF2=12+(1)2=4+. ··················································6分∴S⊙O=14π·EF2. ·······································································7分(3)∵AB=BE,∠ABE=90°,∴∠AEB=45°.∵EA=EC,∴∠C=22.5°.···········································································8分∴∠H=∠BEG=∠CED=90°-22.5°=67.5°.∵BH平分∠CBF,∴∠EBG=∠HBF=45°.∴∠BGE=∠BFH=67.5°.∴BG=BE=1,BH=BF=1. ································································9分答案图图9∴GH=BH-BG.∴HB·HG(1)=2.························································· 10分B卷一、填空题(每小题6分,共24分)22.任取不等式组30,250kk-⎧⎨+⎩≤>的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的概率为______.[答案]1 3[解析]不等式组30,250kk-⎧⎨+⎩≤>的解集为-52<k≤3,其整数解为k=-2,-1,0,1,2,3.其中,当k=-2,-1时,方程2x+k=-1的解为非负数.所以所求概率P=26=13.故答案为:13.23.如图10,点A在双曲线y=5x上,点B在双曲线y=8x上,且AB∥x轴,则△OAB的面积等于______.[答案]3 2[解析]设点A的坐标为(a,5a ).∵AB∥x轴,∴点B的纵坐标为5a.将y=5a代入y=8x,求得x=85a.∴AB=85a-a=35a.∴S△OAB=12·35a·5a=32.故答案为:32.24.二次函数y =ax 2+bx +c 的图象如图11所示,且P =|2a +b |+|3b -2c |,Q =|2a -b |-|3b +2c |,则P ,Q 的大小关系是______. [答案]P >Q[解析]∵抛物线的开口向下,∴a <0.∵-2ba=1,∴b >0且a =-2b .∴|2a +b |=0,|2a -b |=b -2a .∵抛物线与y 轴的正半轴相交,∴c >0.∴|3b +2c |=3b +2c . 由图象可知当x =-1时,y <0,即a -b +c <0. ∴-2b-b +c <0,即3b -2c >0.∴|3b -2c |=3b -2c . ∴P =0+3b -2c =3b -2c >0,Q =b -2a -(3b +2c )=-(b +2c )<0. ∴P >Q .故答案为:P >Q .25.如图12所示,已知点C (1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值是______. [答案]10[解析]作点C 关于y 轴的对称点C 1(-1,0),点C 关于x 轴的对称点C 2,连接C 1C 2交OA 于点E ,交AB 于点D ,则此时△CDE 的周长最小,且最小值等于C 1C 2的长. ∵OA =OB =7,∴CB =6,∠ABC =45°. ∵AB 垂直平分CC 2, ∴∠CBC 2=90°,C 2的坐标为(7,6). 在Rt △C 1BC 2中,C 1C 210. 即△CDE 周长的最小值是10.故答案为:10.二、解答题(每小题12分,共36分)26.(12分)问题引入:(1)如图13①,在△ABC 中,点O 是∠ABC 和∠ACB 平分线的交点,若∠A =α,则∠BOC图12图11图10=______(用α表示);如图13②,∠CBO =13∠ABC ,∠BCO =13∠ACB ,∠A =α,则∠BOC =______(用α表示).(2)如图13③,∠CBO =13∠DBC ,∠BCO =13∠ECB ,∠A =α,请猜想∠BOC =______(用α表示),并说明理由.类比研究:(3)BO ,CO 分别是△ABC 的外角∠DBC ,∠ECB 的n 等分线,它们交于点O ,∠CBO =1n ∠DBC ,∠BCO =1n∠ECB ,∠A =α,请猜想∠BOC =______.解:(1)第一个空填:90°+2α; ······································································ 2分 第一个空填:90°+3α. ················································································ 4分 第一空的过程如下:∠BOC =180°-(∠OBC +∠OCB )=180°-12(∠ABC +∠ACB )=180°-12(180°-∠A )=90°+2α. 第二空的过程如下:∠BOC =180°-(∠OBC +∠OCB )=180°-13(∠ABC +∠ACB )=180°-13(180°-∠A )=120°+3α. (2)答案:120°-3α.过程如下: ∠BOC =180°-(∠OBC +∠OCB )=180°-13(∠DBC +∠ECB )=180°-13(180°+∠A )=120°-3α. ································································································ 8分 (3)答案:120°-3α.过程如下: ∠BOC =180°-(∠OBC +∠OCB )=180°-1n (∠DBC +∠ECB )=180°-1n (180°+∠A )=1n n -·180°-nα. ···················································································· 12分 27.(12分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图14所示),设这个苗圃园垂直于墙的一边长O C B A 图13②AO图13① O C B A E D 图13③为x 米.(1)若苗圃园的面积为72平方米,求x ;(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;(3)当这个苗圃园的面积不小于100平方米时,直接写出x 的取值范围.解:(1)苗圃园与墙平行的一边长为(30-2x )米.依题意可列方程x (30-2x )=72,即x 2-15x +36=0. ······························································· 2分 解得x 1=3,x 2=12. ···················································································· 4分(2)依题意,得8≤30-2x ≤18.解得6≤x ≤11.面积S =x (30-2x )=-2(x -152)2+2252(6≤x ≤11). ①当x =152时,S 有最大值,S 最大=2252; ······················································· 6分 ②当x =11时,S 有最小值,S 最小=11×(30-22)=88. ······································· 8分(3)令x (30-2x )=100,得x 2-15x +50=0.解得x 1=5,x 2=10. ·················································································· 10分 ∴x 的取值范围是5≤x ≤10. ······································································· 12分28.(12分)如图15,已知抛物线C :y =x 2-3x +m ,直线l :y =kx (k >0),当k =1时,抛物线C 与直线l 只有一个公共点.(1)求m 的值;(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y =-3x +b 交于点P ,且1OA +1OB =2OP,求b 的值; (3)在(2)的条件下,设直线l 1与y 轴交于点Q ,问:是否存在实数k 使S △APQ =S △BPQ ,若存在,求k 的值;若不存在,说明理由.解:(1)∵当k =1时,抛物线C 与直线l 只有一个公共点,∴方程组23,y x x m y x⎧=-+⎨=⎩有且只有一组解. ····················································· 2分答案图图15 图14消去y ,得x 2-4x +m =0,所以此一元二次方程有两个相等的实数根.∴△=0,即(-4)2-4m =0.∴m =4. ··································································································· 4分(2)如图,分别过点A ,P ,B 作y 轴的垂线,垂足依次为C ,D ,E ,则△OAC ∽△OPD ,∴OP OA =PD AC . 同理,OP OB =PD BE . ∵1OA +1OB =2OP ,∴OP OA +OP OB =2. ∴PD AC +PD BE =2. ∴1AC +1BE =2PD ,即AC BE AC BE +=2PD. ····················································· 5分 解方程组,3y kx y x b =⎧⎨=-+⎩得x =3b k +,即PD =3b k +. ··········································· 6分 由方程组2,34y kx y x x =⎧⎨=-+⎩消去y ,得x 2-(k +3)x +4=0.∵AC ,BE 是以上一元二次方程的两根,∴AC +BE =k +3,AC ·BE =4. ···································································· 7分 ∴34k +=23bk +. 解得b =8. ································································································ 8分(3)不存在.理由如下: ················································································· 9分 假设存在,则当S △APQ =S △BPQ 时有AP =PB ,于是PD -AC =PE -PD ,即AC +BE =2PD .由(2)可知AC +BE =k +3,PD =83k +, ∴k +3=2×83k +,即(k +3)2=16. 解得k =1(舍去k =-7). ············································································ 11分 当k =1时,A ,B 两点重合,△QAB 不存在.∴不存在实数k 使S △APQ =S △BPQ . ································································· 12分。