正等轴测图画法练习

正等轴测图一、正等轴测图的轴间角和变形系数1．正等轴测图的投射（影）方向垂直于轴测投影面。

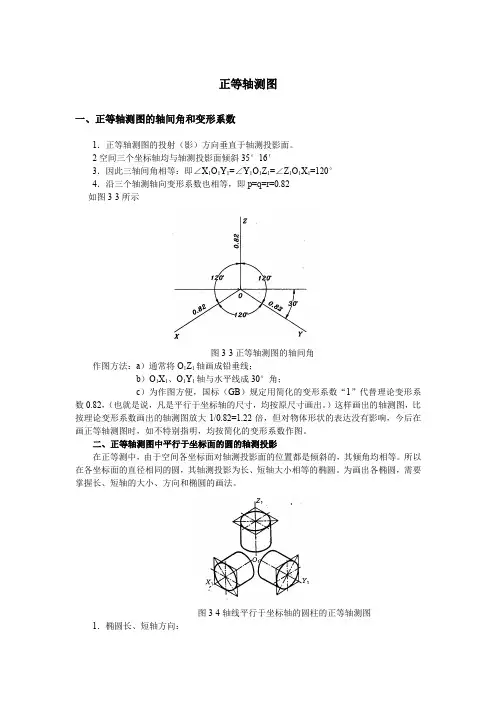
2空间三个坐标轴均与轴测投影面倾斜35°16′3．因此三轴间角相等：即∠X1O1Y1=∠Y1O1Z1=∠Z1O1X1=120°4．沿三个轴测轴向变形系数也相等，即p=q=r=0.82如图3-3所示图3-3正等轴测图的轴间角作图方法：a）通常将O1Z1轴画成铅垂线；b）O1X1、O1Y1轴与水平线成30°角；c）为作图方便，国标（GB）规定用简化的变形系数“1”代替理论变形系数0.82，（也就是说，凡是平行于坐标轴的尺寸，均按原尺寸画出。

）这样画出的轴测图，比按理论变形系数画出的轴测图放大1/0.82=1.22倍，但对物体形状的表达没有影响，今后在画正等轴测图时，如不特别指明，均按简化的变形系数作图。

二、正等轴测图中平行于坐标面的圆的轴测投影在正等测中，由于空间各坐标面对轴测投影面的位置都是倾斜的，其倾角均相等。

所以在各坐标面的直径相同的圆，其轴测投影为长、短轴大小相等的椭圆。

为画出各椭圆，需要掌握长、短轴的大小、方向和椭圆的画法。

图3-4轴线平行于坐标轴的圆柱的正等轴测图1．椭圆长、短轴方向：平行于X1O1Y1坐标面的圆（水平圆）等测为水平椭圆长轴⊥O1Z1轴短轴∥O1Z1轴平行于X1O1Z1坐标面的圆（水平圆）等测为水平椭圆长轴⊥O1Y1轴短轴∥O1Y1轴平行于Y1O1Z1坐标面的圆（水平圆）等测为水平椭圆长轴⊥O1X1轴短轴O1X1轴综上所述：椭圆的长轴⊥与圆所平行的坐标面垂直的那个轴，短轴则平行与该轴测轴。

例如：水平圆的正等测水平椭圆，长轴垂直于圆所平行的水平面垂直的轴测轴Z1轴，短轴则∥Z1轴。

图3-5平行于坐标面的圆的正等轴测图图3-6 2．椭圆长、短轴的大小长轴：是圆内平行于轴测投影面的直径的轴测投影。

因此：（1）在采用变形系数0.82作图时，椭圆长轴大小为d，短轴大小为0.58d。

第三视图和正等轴测图的画法第三视角投影在欧美、日本及港台等地区的教学、设计、生产和商贸中被广泛使用。

近年来，随着与国际社会交流合作的不断深入，第三视角投影在我国的应用日渐广泛。

例如我们毕业生前往就业的外资企业（鸿准、富士康、台积电等）以及对外做出口订单的国内企业大多采用第三视角。

而我们对该方法的学习了解相对匮乏。

本文将结合范例对第三视角的投影和作图规则进行介绍及归纳总结，作为对机械制图知识的补充，以便大家查阅和更为深入的研究。

⑴认识第三视角的空间由来水平投影面H和正立投影面V将三维空间分割为如下第一组图的四部分，可以构成四组投影体系。

如图可以分辨出第三视角投影面位置。

⑵投影面及展开如果将第三视角的两个Ｈ和Ｖ平面取出，再辅助一个侧立投影平面Ｐ，那么就构成了第三角投影体系。

在这个体系中，物体位于三个平面包裹着的内部。

所以，投影平面总是在人和物体之间。

三个投影面得到投影后可以旋转到与Ｖ共面的位置。

下面是一个实例的投影三视图，观察方向分别是：下面是它的展开视图：在主视图中反应的是长和高，右视图中反应的是高和宽，俯视图中反应的是长和宽。

⑶投影规律分析第三视角三视图的仍然符合主和俯视图长对正，主和右视图高平齐，俯和右视图宽相等的“三等”投影规律。

⑷正等轴测图的画法第三视角正等轴测图的轴间角为120度，轴向变形系数都是按照1来近似绘制。

其正等轴测图符合轴测投影规律即:一、实物中与投影轴平行的轮廓线，在轴测图中仍与轴测轴平行；二、实物中相互平行的轮廓线，在轴测图中仍相互平行。

绘制过程中要按轴向1：1进行测量进行。

椭圆和圆角的画法与第一视角的画法并无区别。

总结：第三视角三视图和正等轴测图和第一视角的三视图和正等轴测图在画法操作上并没有多少本质的区别。

但是在看图方向和投影方向是不一样的。

第一视角是人（观察者）->物体->投影平面；而第三视角是人（观察者）->投影平面-> 物体。

在绘制正等轴测图中强调显示的是前视、顶视和右视三个表面。