matlab线性规划练习

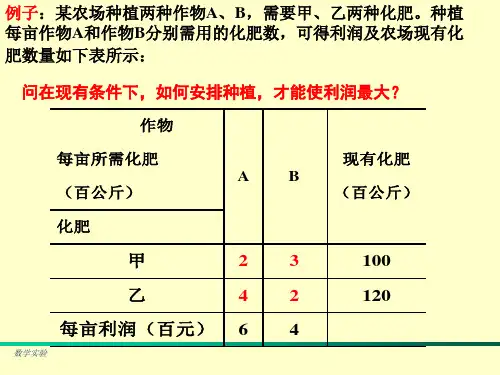
《数学实验》在线习题1一、单项选择题（将选择答案写在答题纸上，每小题2分共20分）1．在MA TLAB 命令窗口中键入命令，Vname=prod(7:9)/prod(1:3)，可计算组合数!6!3!939⨯=C ，如果省略了变量名Vname ，MA TLAB 表现计算结果将用下面的哪一变量名做缺省变量名AA ）ans ；B ）pi ；C ）NaN ；D ）eps2．宝石切割问题中，石料左右长度、前后长度、上下高度分别为a 1、a 2、a 3，即a 1×a 2×a 3(cm 3)，而精品尺寸为b 1×b 2×b 3(cm 3)。

操作时，同向切割连续两次再旋转刀具。

某一切割方案的切割面积依次为：2a 1a 2→ 2a 1b 3 → 2b 2b 3，则这一切割方案为BA ）左右→前后→上下；B ）上下→前后→左右；C ）前后→上下→左右；D ）前后→ 左右→上下 3．机场指挥塔位置：北纬30度35.343分，东经104度2.441分，在MA TLAB 中用变量B=[30 35.343]表达纬度，L=[104 2.441]表达经度。

将数据转化为以度为单位的实数，下面正确的语句是A ） =B(1)+B(2)/60，Q=L(1)+L(2)； B) P = 60*B(1) + B(2)，Q=60*L(1)+L(2) C ） P = B(1) + B(2)/60，Q=L(1)+L(2)/60； D) P=B(1)+B(2)，Q=L(1)+ L(2)；。

4．用MA TLAB 随机产生60个1到365之间的正整数，应该使用下面的哪一条命令AA ） fix(365*rand(1,60))；B ）1+fix(366*rand(1,60))；C ）1+fix(364*rand(1,60))；D ）1+fix(365*rand(1,60))5．用A 、B 、C 表示三角形的三条边，用MA TLAB 表示条件“任意两条边之和大于第三条边”的逻辑表达式应该用下面哪一行语句AA ） A+B>C | A+C>B | B+C>A ； B ） A+B>=C | A+C>=B | B+C>=A ； C ） A+B>=C&A+C>=B&B+C>=A ；D ） A+B>C & A+C>B & B+C>A ； 6．在MA TLAB 命令窗口中，键入命令syms x ； y=int(6*x^4)。

一、用MATLAB 求解线性规划问题（1）编写的M 文件为：f=[-1;-1]A=[1 -2;1 2]b=[4,8][x,feval]=linprog(f,A,b,[],[],zeros(2,1))所求解为：x 1=6,x 2=1;min f=-7（2） 编写的M 文件为：f=[-4;-3]A=[3 4;3 3;4 2]b=[12;10;8][x,feval]=linprog(f,A,b,[],[],zeros(1,2))所求得的解为：x 1=0.8,x 2=2.4;max f=10.4（3）（4） 编写的M 文件为：f=[-1;-3;3]Aeq=[1 1 2;-1 2 1]beq=[4;4][x,feval]=linprog(f,[],[],Aeq,beq,zeros(3,1))所求得的结果为：x 1=4/3,x 2=8/3,x 3=0;max f=28/3。

12121212min 24s.t.28,0f x x x x x x x x ì=--ïïïï-?镲íï+?ïïï³ïî121212121243max 3412..3310428,0f x x xx s t x x x x x x ì=+ïïïï+?ïïï+?íïïï+?ïïï³ïî12312312313min 3s.t.211423210(1,2,3)j f x x x x x xx xx x x x j =--ìïïïï-+?ïïïï-++?íïï-+=ïïïïï?ïî123123123max 3s.t.24240(1,2,3)j f x x x xx x x x x x j =+-ìïïïï++=ïïí-++=ïïïïï?ïî（5）（选做）先做如下转化：% x=u1-v1,,y=u2-v2,,z=u3-v3% min f=u1+u2+u3+v1+v2+v3% s.t. u1+u2-v1-v2<=1% 2*u1+u3-2*v1-v3=3则编写的M 文件为：f=[1;1;1;1;1;1]A=[1 1 0 -1 -1 0]b=1Aeq=[2 0 1 -2 0 -1]beq=3[x,feval]=linprog(f,A,b,Aeq,beq,zeros(6,1))所求得的结果为：u 1=1.0936,u 2=0,u 3=0.8192,v 1=0,v 2=0.9302,v 3=0Min f =2。

用MATLAB 优化工具箱解线性规划命令：x=linprog （c ，A ，b ）2、模型：命令：x=linprog （c ，A ，b ，Aeq,beq ）注意：若没有不等式：b AX ≤存在，则令A=[ ]，b=[ ]. 若没有等式约束, 则令Aeq=[ ], beq=[ ].3、模型：命令：[1] x=linprog （c ，A ，b ，Aeq,beq, VLB ，VUB ）[2] x=linprog （c ，A ，b ，Aeq,beq, VLB ，VUB, X0）注意：[1] 若没有等式约束, 则令Aeq=[ ], beq=[ ]. [2]其中X0表示初始点4、命令：[x,fval]=linprog(…)返回最优解ｘ及ｘ处的目标函数值fval.例1 max 6543216.064.072.032.028.04.0x x x x x x z +++++=解 编写M 文件小xxgh1.m 如下：c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6];A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900];Aeq=[]; beq=[];vlb=[0;0;0;0;0;0]; vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)例2 321436m in x x x z ++=解: 编写M 文件xxgh2.m 如下：c=[6 3 4];A=[0 1 0];b=[50];Aeq=[1 1 1];beq=[120];vlb=[30,0,20];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub例3 （任务分配问题）某车间有甲、乙两台机床，可用于加工三种工件。

MATLAB数学规划问题（实验题目及答案在最后）一、线性规划线性规划问题是目标函数和约束条件均为线性函数的问题，MATLAB6.0及更高版本解决的线性规划问题的标准形式为：min n R',f∈xxsub.to：b⋅A≤x⋅Aeq=xbeq≤lb≤xub其中f、x、b、beq、lb、ub为向量，A、Aeq为矩阵。

其它形式的线性规划问题都可经过适当变换化为此标准形式。

在MATLAB6.0版中，线性规划问题（Linear Programming）已用函数linprog取代了MATLAB5.x版中的lp函数。

在6.0和7.0中依然可以使用lp 函数，但在更高版本中，就只能使用linprog函数了。

函数linprog调用格式：x=linprog(f,A,b)x=linprog(f,A,b,Aeq,beq)- 1 -- 1 -x=linprog(f,A,b,Aeq,beq,lb,ub) x=linprog(f,A,b,Aeq,beq,lb,ub,x0) x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options) [x,fval]=linprog(…)[x, fval, exitflag]=linprog(…) [x, fval, exitflag, output]=linprog(…)[x, fval, exitflag, output, lambda]=linprog(…) 说明：x=linprog(f, A, b) %求min f ' *x, sub.to b x A ≤⋅线性规划的最优解。

返回值x 为最优解向量。

x=linprog(f, A, b, Aeq, beq) %含有等式约束beq x Aeq =⋅，若没有不等式约束b x A ≤⋅，则令A=[ ]，b=[ ]。

x = linprog(f, A, b, Aeq, beq, lb, ub) %指定x 的范围ub x lb ≤≤ x=linprog(f, A, b, Aeq, beq, lb, ub, x0) %设置x0为初值点。

线性规划问题Mat lab求解(总6页) '-CAL-FENGHAI.-(YICAI)-Company One 1・CAL・本页仅作为文档封面.傳用请直接删除用MATLAB优化匸具箱解线性规划命令：inprog (c・ A・ b)命令：x=linprog (c・ A・ b・ Aeq, beq)注总：若没冇不等式：存在.则令A=[ ]. b=[].若没冇尊式约束，则令Ae Q=[ ], be Q=[ J.命令：[1] x=linprog (c・ A・ b, Aeq, beq, VLB. VUB)x=linprog (c. A・ b・ Aeq, beq, VLB. WB, XO)注直[1]若没有等式约束，则令Aeq=〔], be Q=[].⑵其中X0表示初始点4、命令：[x, f\wl]=linDrog(…)返回股优昭$及x处的目标函数值fval.例1昭编写K文件小如卜•：c=[ ]；A=[ ：0 0 0 0:0 0 0 0:0 0 0 0 ]：b=[S50:700:100:900]:Aeq=[I: beQ=[]:vlb=[0:0:0;0：0:0]: vub=[]：[x, fval]=linprog(c, A, b, Aeq, beq, vlb, vub)例2解：編写M文件如卜•：c=[6 3 4]:A=[0 1 0]:b二[50：:Aeq=[l 1 1]:beq=[120]:vlb=[30, 0, 20]:vub=[]:M，fval：=linprog(c. A, b, Aeq,beQ,vlb,vub例3 (任务分配问题)某车何有甲、乙两台机床.叩用干加工三种工件。

假定这两台车床的对用台时数分别为SO0和900・三种匸件的数敞分别为100.600 fil 500・且已知用三种不同车床加工单位数fit不同工件所需的台时数和加工费用如卜表.问怎样分配车床的加工任务.才能既满足加工工件的要求.又使加工费用说低解设在甲车床上加工工件1、2、3的数fit分别为xl、x2、x3.在乙车床上加工工件匚2、3的数H分别为x4、x5. x6o可建立以下统性规划模型:編写M文件如卜•：f = C13 9 10 11 12 S]：A = [ 10 0 00 0 0 ]:b = :SOO; 900]：AeQ=；l 001000 10 0 100 0 1 0 0 1]：beQ=I100 600 500；:vlb = zeros(6, 1):vub=:]:[x, fval] = 1 inprog (f, A, b, Aeq, beq, vlb, vub)例4・某厂毎日S小时的产纯不低于1SOO件。

实验四 用MATLAB 求解线性规划问题一、实验目的：了解Matlab 的优化工具箱，能利用Matlab 求解线性规划问题。

二、实验内容：线性规划的数学模型有各种不同的形式，其一般形式可以写为：目标函数： n n x f x f x f z +++=Λ2211m in约束条件： s n sn s s n n b x a x a x a b x a x a x a ≤+++≤+++ΛΛΛΛΛ221111212111 s n tn t t n n d x c x c x c d x c x c x c =+++=+++ΛΛΛΛΛ2211112121110,,,21≥n x x x Λ 这里n n x f x f x f z +++=Λ2211称为目标函数，j f 称为价值系数，T n f f f f ),,,(21Λ=称为价值向量，j x 为求解的变量，由系数ij a 组成的矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=mn m n a a a a A ΛΛOΛΛ1111称为不等式约束矩阵，由系数ij c 组成的矩阵 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=sn s n c c c c C ΛΛOΛΛ1111称为等式约束矩阵，列向量Tn b b b b ),,,(21Λ=和T n d d d d ),,,(21Λ=为右端向量，条件0≥j x 称为非负约束。

一个向量Tn x x x x ),,,(21Λ=，满足约束条件，称为可行解或可行点，所有可行点的集合称为可行区域，达到目标函数值最大的可行解称为该线性规划的最优解，相应的目标函数值称为最优目标函数值，简称最优值。

我们这里介绍利用Matlab 来求解线性规划问题的求解。

在Matlab 中有一个专门的函数linprog()来解决这类问题，我们知道，极值有最大和最小两种，但求z 的极大就是求z -的极小，因此在Matlab 中以求极小为标准形式，函数linprog()的具体格式如下： X=linprog(f,A,b)[X,fval,exitflag,ouyput,lamnda]=linprog(f,A,b,Aeq,Beq,LB,UB,X0,options)这里X 是问题的解向量，f 是由目标函数的系数构成的向量，A 是一个矩阵，b 是一个向量，A ，b 和变量x={x1,x2,…,xn}一起，表示了线性规划中不等式约束条件，A ，b 是系数矩阵和右端向量。

实验十四 用MATLAB 求解线性规划问题一、实验目的：了解Matlab 的优化工具箱，能利用Matlab 求解线性规划问题。

二、相关知识线性规划是运筹学中研究得比较早，理论上已趣于成熟，在方法上非常有效，并且应用广泛的一个重要分支。

线性规划的数学模型有各种不同的形式，其一般形式可以写为：目标函数： n n x f x f x f z +++= 2211m i n约束条件： s n sn s s n n b x a x a x a b x a x a x a ≤+++≤+++221111212111s n tn t t n n d x c x c x c d x c x c x c =+++=+++2211112121110,,,21≥n x x x这里n n x f x f x f z +++= 2211称为目标函数，j f 称为价值系数，T n f f f f ),,,(21 =称为价值向量，j x 为求解的变量，由系数ij a 组成的矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=mn m n a a a a A 1111称为不等式约束矩阵，由系数ij c 组成的矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=sn s n c c c c C 1111称为等式约束矩阵，列向量T n b b b b ),,,(21 =和T n d d d d ),,,(21 =为右端向量，条件0≥jx 称为非负约束。

一个向量T n x x x x ),,,(21 =，满足约束条件，称为可行解或可行点，所有可行点的集合称为可行区域，达到目标函数值最大的可行解称为该线性规划的最优解，相应的目标函数值称为最优目标函数值，简称最优值。

求解线性规划问题已有一些成熟的方法，我们这里介绍利用Matlab 来求解线性规划问题的求解。

在Matlab 中有一个专门的函数linprog()来解决这类问题，我们知道，极值有最大和最小两种，但求z 的极大就是求z -的极小，因此在Matlab 中以求极小为标准形式，函数linprog()的具体格式如下： X=linprog(f,A,b)[X,fval,exitflag,ouyput,lamnda]=linprog(f,A,b,Aeq,Beq,LB,UB,X0,options)这里X 是问题的解向量，f 是由目标函数的系数构成的向量，A 是一个矩阵，b 是一个向量，A ，b 和变量x={x 1,x 2,…,x n }一起，表示了线性规划中不等式约束条件，A ，b 是系数矩阵和右端向量。

2010/2011学年第一学期"MATLAB 程序设计"大作业一、题目用MATLAB 求解线性规划最优解和最优值的问题。

二、问题描述和分析2.1: 线性规划(简记LP)是合理利用、调配资源的一种应用数学的方法,它的基本思路就是在满足一定的约束条件下,使预定的目标达到最优；它的研究内容可归纳为两个方面:一是系统的任务已定,如何合理筹划,精细安排,用最少的资源去实现这个任务;二是资源的数量已定,如何利用、分配,使任务完成得最多. 前者是求极小,后者是求极大. 线性规划是在满足企业内、外部的条件下,实现管理目标和极值问题,就是要以尽少的资源输入来实现更多的社会需要的产品的产出.2.2: 线性规划问题是目标函数和约束条件均为线性函数的问题，MATLAB7.0解决的线性规划问题的标准形式为：min n R x x f ∈'sub.to ：b x A ≤⋅beq x Aeq =⋅ub x lb ≤≤其中f 、x 、b 、beq 、lb 、ub 为向量，A 、Aeq 为矩阵2.3:函数 linprog格式 x = linprog(f,A,b) %求min f ' *x sub.to b x A ≤⋅线性规划的最优解。

x = linprog(f,A,b,Aeq,beq) %等式约束beq x Aeq =⋅，若没有不等式约束b x A ≤⋅，则A=[ ]，b=[ ]。

x = linprog(f,A,b,Aeq,beq,lb,ub) %指定x 的范围ub x lb ≤≤，若没有等式约束beq x Aeq =⋅ ，则Aeq=[ ]，beq=[ ]x = linprog(f,A,b,Aeq,beq,lb,ub,x0) %设置初值x0x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options) % options 为指定的优化参数[x,fval] = linprog(…) % 返回目标函数最优值，即fval= f ' *x 。

§1 线性规划模‎型一、线性规划课‎题：实例1：生产计划问‎题假设某厂计‎划生产甲、乙两种产品‎，现库存主要‎材料有A类‎3600公‎斤，B类200‎0公斤，C类300‎0公斤。

每件甲产品‎需用材料A‎类9公斤，B类4公斤‎，C类3公斤‎。

每件乙产品‎，需用材料A‎类4公斤，B类5公斤‎，C类10公‎斤。

甲单位产品‎的利润70‎元，乙单位产品‎的利润12‎0元。

问如何安排‎生产，才能使该厂‎所获的利润‎最大。

建立数学模‎型：设x1、x2分别为‎生产甲、乙产品的件‎数。

f为该厂所‎获总润。

max f=70x1+120x2‎s.t 9x1+4x2≤36004x1+5x2≤20003x1+10x2≤3000x1,x2≥0归结出规划‎问题：目标函数和‎约束条件都‎是变量x的‎线性函数。

形如： (1) min f T Xs.t A X≤bAeq X =beqlb≤X≤ub其中X为n‎维未知向量‎，f T=[f1,f2,…f n]为目标函数‎系数向量，小于等于约‎束系数矩阵‎A为m×n矩阵，b 为其右端‎m维列向量‎，Aeq为等‎式约束系数‎矩阵，beq为等‎式约束右端‎常数列向量‎。

l b,ub为自变‎量取值上界‎与下界约束‎的n维常数‎向量。

二．线性规划问‎题求最优解‎函数：调用格式： x=linpr‎og(f,A,b)x=linpr‎o g(f,A,b,Aeq,beq)x=linpr‎o g(f,A,b,Aeq,beq,lb,ub)x=linpr‎o g(f,A,b,Aeq,beq,lb,ub,x0)x=linpr‎o g(f,A,b,Aeq,beq,lb,ub,x0,optio‎n s)[x,fval]=linpr‎o g(…)‎[x, fval, exitf‎l ag]=linpr‎o g(…)‎[x, fval, exitf‎l ag, outpu‎t]=linpr‎o g(…)‎[x, fval, exitf‎l ag, outpu‎t, lambd‎a]=linpr‎o g(…)‎说明：x=linpr‎o g(f,A,b)返回值x为‎最优解向量‎。