计算机仿真技术试卷B

中南大学考试试卷2009 -- 2010 学年 1 学期期末考试试题 时间110分钟计算机仿真技术 课程 32 学时 2 学分 考试形式： 开 卷 专业年级： 自动化06级 总分100分，占总评成绩70% 注：请将答案写在答卷上一 填写下列运算结果（本题12分，每空2分）已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=542031321i A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=581051301i B ,则 (1) A (1:3,3)＝ 305⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(2) B (2:3 ) ＝ []11(3) A ’＝112234305i ⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦(4) B.’＝ 111058305i ⎡⎤⎢⎥⎢⎥⎢⎣⎦+⎥ (5) A.*B ＝ 10931155023225i i +⎡⎤⎢⎥+⎢⎥⎢⎥⎣⎦(6) A*B ＝ 63418415531160312i i i i i +⎡⎤⎢⎥+++⎢⎥⎢⎥+⎣⎦二 判断正误（本题20分，每小题2分）(1) 计算机仿真的三要素为系统、模型和计算机。

（ √ ）(2) 在MATLAB 中，变量名区分字母的大小写，但是MATLAB 提供的标准函数名以及命令名必须用小写字母。

（ × ）(3) MATLAB 中运算符号前带有小点表示执行元素对元素的运算。

（ √ ）(4) 在MATLAB 中，2ⅹ2的矩阵A=[1 2，3 4]是一种正确的输入方式。

（ × ）(5) clc 命令不仅用于清除命令窗口显示的内容同时也删除MATLAB 工作空间中的变量。

（ × ）(6) MATLAB 提供了3种逻辑操作符，其中~表示非。

（ √ ）(7) subplot(211)把屏幕分成两个部分，并把曲线放在左半部分。

（ × ）(8) 数值积分法中，计算步长越小，总误差越小。

（ × ）(9) tf2ss 函数只能将传递函数模型转换成为可控标准型状态方程。

（ √ ）(10) 函数文件中函数名称和文件名可以不同。

控制系统计算机辅助设计综合实验指导实验名称：连续与离散系统校正实验，系统可控性与可观性实验，系统的simulink仿真实验陈茜编实验人：苏建聪学号：200830810122班级：08电气工程及其自动化1班信息工程系实验任务书1. 有一个单位负反馈控制系统，如果控制对象的传递函数为设计要求：① 相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

2. 有一个单位负反馈控制系统，如果控制对象的传递函数为：试设计一个串联滞后校正装置。

设计要求：①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

3. 有一个单位负反馈控制系统，如果控制对象的传递函数为 ()()4+=s s k s G p试设计一个串联超前滞后校正装置，设计要求： ①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

4. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象()()110+=s s s G ，()s G h 为零阶保持器。

用W 变换法设计一超前校正装置D(z)，使系统相位裕度γ≥50°，校验设计后系统的性能指标。

5. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象1)s(0.2s k )(+=s G ο，()s G h 为零阶保持器。

用对数频率法设计D(z)，使系统开环增益k ≥30(1/s)，截止频率ωc ≥15(1/s),相位裕度γ≥50 °1使 s 11se -1(s)-Tsh T G +≈=，求出未校正系统的开环系统的开环传递函数(s)(s)G G (s)0s =G ,的传递函数模型参数。

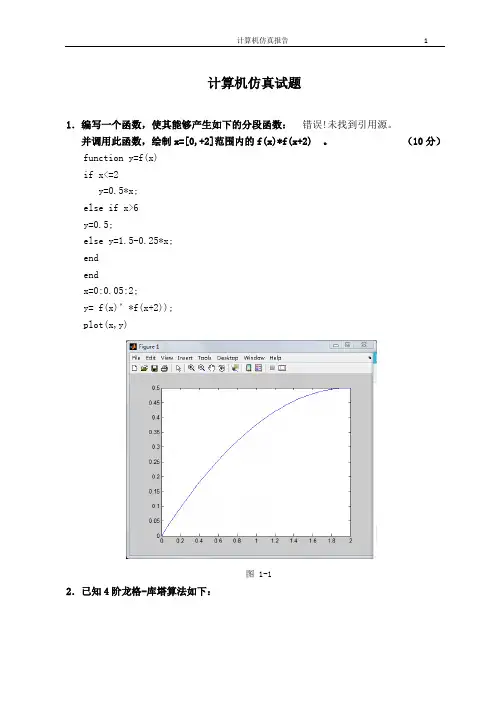
计算机仿真试题1．编写一个函数，使其能够产生如下的分段函数：错误！未找到引用源。

并调用此函数，绘制x=[0,+2]范围内的f(x)*f(x+2) 。

（10分）function y=f(x)if x<=2y=0.5*x;else if x>6y=0.5;else y=1.5-0.25*x;endendx=0:0.05:2;y= f(x)’*f(x+2));plot(x,y)图 1-12．已知4阶龙格-库塔算法如下：试利用该算法求解以下微分方程：（15分）本题可以调用MATLAB函数中龙格-库塔算法函数ode45，首先编写m文件：function dy=func(x,y)dy=-y+1;end再在主窗口调用此文件：[x,y]=ode45('func',[0,5],0)%这里的[0,5]为任取区间，表示方程在此范围的解。

运行结果如下:x =0.00010.00010.00020.00020.00050.00070.00100.00120.00250.00370.00500.00620.01250.01880.02510.0313 0.06270.09410.12550.15690.28190.40690.53190.65690.78190.90691.03191.15691.28191.40691.53191.65691.78191.90692.03192.15692.28192.40692.53192.65692.78192.90693.03193.15693.28193.40693.53193.65693.78193.90694.03194.15694.28194.40694.53194.65694.74274.82854.91425.0000y =0.00010.00010.00020.00020.00050.00070.00100.00120.0025 0.0037 0.0050 0.0062 0.0124 0.0186 0.0248 0.0309 0.0608 0.0898 0.1180 0.1452 0.2457 0.33430.41250.48160.54250.59630.64370.68550.72250.75510.78390.80930.83170.85150.86890.88430.89790.90990.92050.92980.93810.94540.95180.95740.96240.96690.97080.97420.97720.97990.98230.98430.98620.98780.98920.99050.99130.99200.99270.9933为只管起见，我们使用函数命令画出x-y（plot(x,y)）的关系如下图：图1-23．用matlab语言求下列系统的状态方程、传递函数、零极点增益、和部分分式形式的模型参数，并分别写出其相应的数学模型表达式：（15分）（1）G（s）=324327242410355024s s ss s s s+++++++（2）.X=2.25 -5 -1.25 -0.542.25 -4.25 -1.25 -0.2520.25 -0.5 -1.25 -121.25 -1.75 -0.25 -0.75 0X⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦uy= [0 2 0 2] X解：（1）a)求对应状态方程参数：num=[1 07 24 24]; den=[1 10 35 50 24]; [A,B,C,D]=tf2ss(num,den) 运行结果：A =-10 -35 -50 -241 0 0 00 1 0 00 0 1 0B =1C =1 7 24 24D =故，状态方程为：.X = x+ uY=[1 7 24 24]xb)求对应零极点增益模型参数：num=[1 07 24 24]; den=[1 10 35 50 24]; [Z,P,K]=tf2zp(num,den) 运行结果如下： Z =-2.7306 + 2.8531i -2.7306 - 2.8531i -1.5388P = -4.0000 -3.0000 -2.0000 -1.0000K = 1故变换后的零极点模型为： G(s)=c)求对应部分分式型：num=[1 07 24 24]; den=[1 10 35 50 24]; [R,P,H]=residue(num,den) 运行结果如下： R =4.0000 -6.0000 2.0000 1.0000P =-4.0000 -3.0000 -2.0000 -1.0000H = []故变换后的部分分式模型为：11223644)(+++++-+=s s s s s G（2）由题给条件，知：A=[2.25 -5 -1.25 -0.5; 2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75-10 -35 -50 -24 1 0 0 0 0 1 0 0 0 0 1 010 0 0-0.25 -0.75] B=[4;2;2;0] C=[0 2 0 2],D=0 a)求传递函数矩阵： [num,den]=ss2tf(A,B,C,D) 运行结果为： num =0 4.0000 14.0000 22.0000 15.0000 den =1.0000 4.0000 6.2500 5.25002.2500 故，所对应传递函数模型为：25.225.525.641522144)(23423+++++++=s s s s s s s s Gb)求零极点模型：num=[0 4 14 22 15];en=[1 4 6.25 5.25 2.25]; [Z,P,K]=tf2zp(num,den) 运行结果为： Z =-1.0000 + 1.2247i -1.0000 - 1.2247i -1.5000 P =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iK =4.0000故，零极点模型为：)866.05.0()5.1()2247.11)(5.1(4)(2i s s i s s s G ±++±++=c)求对应部分分式模型： [R,P,H]=residue(num,den) 运行结果为： R =4.0000 -0.0000-0.0000 - 2.3094i -0.0000 + 2.3094iP =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iH = []故变换后的部分分式模型为：i s ii s i s s G 866.05.03094.2866.05.03094.25.14)(+++-+-++=4．已知一单位反馈系统开环传递函数为：，试绘制系统Nyquist图，判断闭环系统的稳定性，并求其单位阶跃响应。

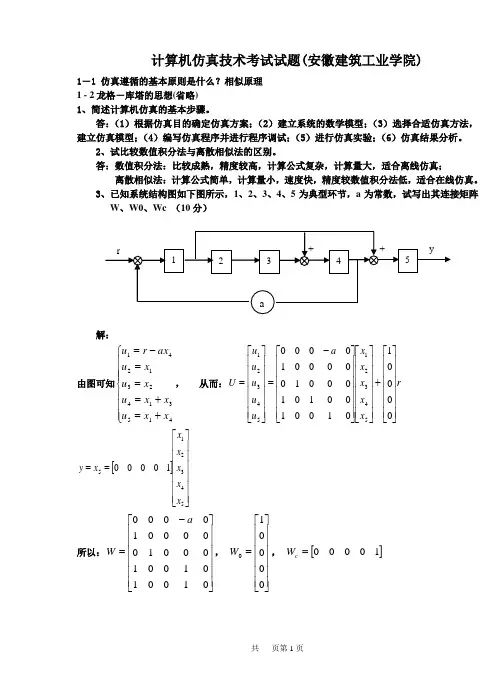
计算机仿真技术考试试题(安徽建筑工业学院)1－1 仿真遵循的基本原则是什么？相似原理 1 - 2龙格－库塔的思想(省略) 1、简述计算机仿真的基本步骤。

答：（1）根据仿真目的确定仿真方案；（2）建立系统的数学模型；（3）选择合适仿真方法，建立仿真模型；（4）编写仿真程序并进行程序调试；（5）进行仿真实验；（6）仿真结果分析。

2、试比较数值积分法与离散相似法的区别。

答：数值积分法：比较成熟，精度较高，计算公式复杂，计算量大，适合离线仿真；离散相似法：计算公式简单，计算量小，速度快，精度较数值积分法低，适合在线仿真。

3、已知系统结构图如下图所示，1、2、3、4、5为典型环节，a 为常数，试写出其连接矩阵W 、W0、Wc （10分）解：由图可知⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+===-=415314231241x x u xx u x u xu ax r u ， 从而：r x x x x x a u u u u u U ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=000010100100101000100000100005432154321[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==54321510000x x x x x x y所以：⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=01001010*******000010000a W ， ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=000010W ， []10000=c W4、已知系统状态空间表达式为[]⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=Xt y t u X X 01)()(012101 ，⎥⎦⎤⎢⎣⎡=11)0(X ，计算步长1.0=h ，输入信号1=u （0≥t ）试采用欧拉法，四阶龙格－库塔法计算h t =时对应的y 值。

（12分）解：⎥⎦⎤⎢⎣⎡=11)0(X ，⎥⎦⎤⎢⎣⎡=2101A ，⎥⎦⎤⎢⎣⎡=01B ，[]01=C 欧拉法：()()⎥⎦⎤⎢⎣⎡=⋅⎪⎪⎭⎫⎝⎛⋅⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=++⎥⎦⎤⎢⎣⎡=+=3.12.11.010*********)0()0(11))0(,0()0()(h Bu AX hX f X h X 2.1)()(==h CX h y 四阶龙格－库塔法： ()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==3201112101)0(,01X f K ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⋅+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎪⎭⎫⎝⎛⋅++=4.31.2013221.011210121.0)0(,21.0012K X f K⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⋅+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎪⎭⎫⎝⎛⋅++=445.3105.2014.31.221.011210121.0)0(,21.0023K X f K()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⋅+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⋅++=8995.32105.201445.3105.21.01121011.0)0(,1.0034K X f K()⎥⎦⎤⎢⎣⎡=++++=3432.12103.1226)0()(4321K K K K hX h X 2103.1)()(==h CX h y5、已知系统传递函数)1(2)()()(+==s s s U s Y s G ，试采用双线性变换法求解系统差分方程，计算步长h ＝0.1s （10分）。

《计算机仿真技术》考试试卷(A卷)班级姓名学号一．填空题。

(每空1分，共20分)1、计算机仿真中系统由_________________、_________________、________________等三个要素组成。

2、常见的系统实验建模法有________________、________________、________________、________________等几种方法。

3、叙述simulink中常见的可变步长的仿真算法有：________________、________________、________________、________________。

(任举四种)4、MA TALB的Comand windows窗口中可以显示workspace中的全部变量的命令是_________________、_________________。

5、计算机仿真算法的算法引起的误差是________________、________________。

6、三维立体绘图中，________________ 是三维曲线绘图命令，________________是三维网格线绘图命令，________________着色表面图绘图命令。

7、符号运算中，泰勒级数计算的函数是________________傅里叶变换的函数________________二．简答题。

(本题5小题，每题8分，共40分)1、计算机仿真的目的和作用2、列举几种计算机仿真软件，并简要介绍一下（要求4种以上）3、matlab主界面主要包括那些窗口，分别有什么样的功能4、局部变量和全局变量之间的区别5、计算机仿真技术中相似性主要包含那几个方面三．编程题 (本题6小题、共40分)根据下面要求，写出程序代码。

1、(5分)设(2E－C-1B)A T=C-1，其中E是4阶单位矩阵，A T是4阶矩阵A的转置。

求矩阵A2、(5分)输入下面的矩阵，求出特征多项式和特征根，并求出特征多项式的微分。

《计算机仿真技术》考试试卷(B 卷)班级 姓名 学号一．填空题。

(每空1分，共20分)1、计算机仿真技术三要素是_______________、_________________、________________。

2、计算机仿真中模型能够代表系统来进行研究，模型主要有________________、________________、________________、________________等几类模型。

3、叙述simulink 中常见的固定步长的仿真算法有：________________、________________、________________、________________。

(任举四种)4、MATALB 主要相似性主要包含以下几种相似_________________、________________、___________________。

5、Simulink 中主要包含_________________、________________、_______________等几种模块。

6、符号运算中，泰勒级数计算的函数是________________，拉普拉斯变换的函数________________，傅里叶级数的计算函数是________________。

二．简答题。

(本题5小题，每题8分，共40分)1、简述根据信号类型分类，计算机仿真主要包含哪几种类型。

2、简述蒙特卡洛法建模的步骤。

3、m 函数文件和m 文本文件之间的区别。

4、叙述三维立体绘图常用的几个绘图指令及其功能。

5、简述matlab 软件的基本组成三．编程题 (本题6小题、共40分)根据下面要求，只需写出程序代码，不需计算结果和图形。

1、(5分)写出右面的矩阵D ，求出其大于4的元素有几个，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=059123107D并通过变量列出其在矩阵的位置和序号2、(5分)求解下面矩阵A 的行列式和逆矩阵，并利用命令取出系数矩阵的逆矩阵的第二行的数据，以小数点后面两位数值的形式显示出来。

2017年中国研究生数学建模竞赛B题（华为公司命题）面向下一代光通信的VCSEL激光器仿真模型友情提示：阅读本题附录3有助于理解本题的相关概念与方法。

随着互联网技术的快速发展，家庭固定网络速度从原来的2Mbps、10Mbps，快速发展到了今天的百兆（100Mbps），甚至千兆（1000Mbps）光纤宽带入户。

“光纤宽带入户”，顾名思义，就是采用光纤来传输信号。

光纤中传输的激光信号具有远高于电信号传输速率的特点(激光信号传输带宽远大于电信号传输带宽)，更适合于未来高速率的传输网络。

工程师们在光纤通信传输系统设计前，往往会通过计算机仿真的方式研究系统设计的指标，以便快速找到最适合的解决方案。

因此在进行系统仿真时，需要准确掌握系统中各个器件的特性以保证仿真模型的精度。

激光器作为光纤通信系统的核心器件是系统仿真中需要考虑的一个重要因素。

与我们生活息息相关的激光器种类繁多，其中的垂直腔面发射激光器（VCSEL: Vertical Cavity Surface Emitting Laser）具有使用简单，功耗较低等特点，一般VCSEL 的工作电流在6mA~8mA。

本题的主要任务，就是得到能准确反映VCSEL激光器特性的数学模型。

激光器输出的光功率强度与器件的温度相关，当器件温度（受激光器自身发热和环境温度的共同影响）改变后，激光器输出的光功率强度也会相应发生变化。

在进行建模时，我们既要准确反映VCSEL激光器特性，还要考虑：1.激光器输出的功率强度与温度的关系——即该激光器可以在多大的外界环境温度范围内使用；2.如何设计激光器参数可以使激光器具有更大的传输带宽（即S21曲线上纵坐标-10dB位置对应的横坐标频率值更大）——即可以实现更快的传输速率。

1问题1：VCSEL的L-I模型L-I 模型，即激光器的工作电流与输出光功率强度关系模型（L ：light ，表示光功率强度，也可以表示为P ；I ：Intensity of current ，表示工作电流）。

计算机仿真1. Matlab 的程序文件和simulink 的模型文件的扩展名分别是________、_______。

2. 四阶龙格-库塔法的局部截断误差为_________________。

（注：步长用h 表示）3. 已知A=[1 2 1;2 3 0;1 0 1];B=[1 2 0;3 5 0;0 1 4],写出下列指令运行的结果：A+B ans=A==B ans=A~=B ans=B./A ans=A*B ans= B*A ans=max(B) ans=4. 控制系统随着时间的改变，状态的变化也是连续的系统称为_______________。

5. 将控制系统状态空间模型转换成零极点模型的语句是_________________。

6. 计算机仿真的三要素为系统、 与计算机。

7. matlab 中最基本的绘图函数是_____________。

二、 综合计算题（第2小题15分，其余每小题10分，共55分）1. 系统结构如下图所示，写出该系统的连接矩阵W 和W 0.并写出连接矩阵非零元素阵W IJ ，其中G i 表示传递函数，,,αβγ表示反馈系数（10分）一、 填空题(每空1分，共15分)A.*B ans=2. （15分）已知',(0)1y y t y =+=，取计算步长0.1h =，试用欧拉法和四阶龙格-库塔法求t=h 时的y 值，并将求得的y 值与精确解()21t y t e t =--比较，并说明造成差异的原因3. （10%）已知系统开环传递函数3243272424()10355024s s s G s s s s s +++=++++，编写函数文件，建立单位负反馈闭环传递函数模型，并求阶跃响应曲线。

4. （10分）下图为非线性环节的仿真子程序框图，试给出符合该框图的非线性环节（用图表示）。

用0i i u u →>表示，0i i u u ←<表示5.（10分）设系统的微分方程为32++=，y为系统输出量，u为系统输入量，试导y y y u出系统的标准状态方程。

计算机仿真技术课内实验题目1． MATLAB 基本操作（1）在MATLAB 中，输入矩阵 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=113011121A ，计算矩阵A 的行列式，A 的逆阵，求矩阵A 中元素的最大值。

（2）在一个途中同时画出cos(x),,sin(x)两条曲线，0<x<9。

2． 连续系统的数学模型表示已知系统的传递函数 1s 3s 1s )s (G +++=，在MATLAB 中建立此系统的模型。

并将这个模型转换为零极点模型和状态空间模型。

求这个系统的阶跃响应和脉冲响应。

3． 离散系统的数学模型表示已知系统的传递函数 3.0s 5.0z 1z )z (G +++=采样周期T=0.2 ，在MA TLAB 中建立此系统的模型。

并将这个模型转换为零极点模型和状态空间模型。

求这个系统的阶跃响应和脉冲响应。

4． 连续系统的数学模型的离散化已知连续系统的传递函数 1s 3s 1s )s (G +++=，在MA TLAB 中建立此系统的模型。

并将这个模型分别取采样周期T=0.2，T=0.1进行离散化，求这个原系统系统和离散化后系统的阶跃响应。

5． 线性系统的频域分析已知系统的传递函数 1s 3s 1s )s (G +++=，画出系统的BODE 图，求出稳定裕度。

画出NYQUIST 和NICHOLS 图，并根据图像对系统的性能给予说明。

6． 线性系统的时域分析已知连续系统的传递函数 5s 3s 5s )s (G +++=，求系统的阶跃响应，并计算系统的上升时间、峰值时间，调整时间、超调量和稳态值。

7． 面向结构图的线性系统的模型已知系统的传递函数 )3s (s 5.0s )s (G 2s 1)s (G 1s 1)s (G 321++=+=+=，求下列系统的表达式（1）G 1(s)+ G 2(s)+ G 3(s) (2) G 1(s)G 2(s) G 3(s) (3) G 1(s)G 2(s)+G 3(s)。

一、数值计算，编程完成以下各题（共20分，每小题5分） 1、脉冲宽度为d ，周期为T 的矩形脉冲的傅里叶级数如下式描述：)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ，41=T d ，2/12/1<<-τ，绘制出函数)(τf 的图形。

解： syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形，求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解：程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下：运行后的最小值点m in x =4.6，m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1，3]区间的图形，并用编程求解该非线性方程0)(=x f 的一个根，设初始点为20=x .解： x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。

《计算机仿真技术》实训实践考核
班级学号姓名成绩
一、考核要求说明
1、本次上机考试时间为120分钟，有6个任务。

2、严格按照题目要求来完成任务，要求每个完成的任务必须生成可执行文件（即exe文件），4个题目放在同一个文件夹下，文件夹以自己的学号+姓名命名。

3、在完成上机考核后将所考题目的程序代码写到答题纸上。

5、考试期间禁止讨论，禁止相互传递内容，如被发现即取消考试资格。

二．考核内容
1、求“0！+1！+2！+3！+ …+10！=”的结果
2、根据图2的形式编写程序（参考教材第四章例题4.19）
图2
3、旅客乘车旅行，可免费携带30公斤行李，超过30公斤的部分每公斤支付托
运费10元，超过50公斤部分则每公斤支付20元托运费。

请编程根据每位旅客行李的重量计算其应付的行李托运费。

4、通过键盘输入一组不重复的数据，请找出其中最小的值及其位置。

5、建立一个对角线上元素为“*”，其余元素为“#”的6*6数组。

6、统计一家商店，在三个月里销售三种商品情况。

要求统计每个月三种商品销售额，三个月里各种商品的销售额以及三个月丽所有商品的销售总额。

（参考例题4.16）
第一个月销售牛奶20箱，洗衣粉100包，衣服50件。

第二个月销售牛奶50箱，洗衣粉80包，衣服40件。

第三个月销售牛奶40箱，洗衣粉110包，衣服60件。

其中牛奶每箱价格为50元，洗衣粉每包价格为5元，衣服每件价格为90元。

月份 牛奶 洗衣粉 衣服
第一个月 20 100 50
第二个月 50 80 40
第三个月 40 110 60。

桂林电子科技大学研究生试卷一、填空（每空1分，共20分）。

1、仿真是指用代替进行实验和研究。

2、为使仿真的结果被证实是真实可靠的，也就是结果是可信的，仿真所遵循的基本原则是相似原理：、和。

3、按照仿真实验时间标尺τ与实际系统的时间标尺t比例来分类，将的仿真称为实时仿真，而τ/t≠1的仿真为非实时仿真。

一般有介入的半实物仿真属于实时仿真，而纯计算机仿真为非实时仿真。

4、凡是系统的输入量是的连续函数，无论其输出量是连续单调函数或是单值或是多值的函数，均称这个系统是连续系统。

用表示的系统可以是非线性或线性系统，而对于表示的系统，只适用于单输入－单输出的线性定常系统，所以表示有一定的局限性。

5、各种数值积分法的截断误差与积分方法的和有关。

是由于的字长是有限制的，计算只能限制在有限位数内，因而产生了舍入误差。

6、对于一个稳定的微分方程，经过转换得到的差分方程的计算结果是稳定的，不同的数值积分方法的计算稳定性相同。

7、按环节离散化就是将系统分成若干个环节，在每个环节的入口处加一个虚拟的，并立即跟一个信号重构过程（加），以便使信号恢复为形式，这时系统实际上已成为一个系统。

当采样周期足够小时，这个采样系统就近似等价于原系统。

二、简述系统仿真的特点（8分）三、线性定常连续系统的数学模型有哪几种形式，分别叙述：1、每种形式数学模型的模型表示；（3分）2、各种数学模型所表示的系统特征是什么？（6分）3、模型之间的相互转化关系是什么？（3分）四、在采样控制系统的数字仿真中，1、画出典型的采样控制系统图；（4分）2、采样控制系统工作的特点；（5分）3、采样控制系统仿真前应处理的问题；（5分）T之间的关系。

（6分）4、如何确定计算步长T和采样控制系统自己固定的采样周期s五、应用MATLAB中的模型表示：1、分别阐述函数ss()、tf()和zpk()的功能；（5分）2、写出sys=tf({-5;[1 -5 6]},{[1 -1];[1 1 0]})的运行结果；（5分）3、写出sys1=ss(sys)的运行结果；（5分）4、写出sys=zpk({[];[2 3]},{1;[0 -1]},[-5;1]) 的运行结果；（5分）六、用图形表示连续调制波形)ty 。

重庆邮电大学第三届计算机仿真大赛赛题1、传统的节、假日（如国庆、五一等）人们都有出行的愿望，或者外出旅行、或者外出购物、或者外出探亲访友等等，但在当前开行车辆数一定的情况下，突然增加的客流总是让人感觉交通服务不太令人满意。

现假设：（1）交通车辆总数一定；（2）车辆运行速度一定；（3）车辆配置相同；（4）影响人们出行舒适感的主要因素：车辆是否拥挤、旅客能否及时上车、车辆是否及时将旅客送达目的地；（5）旅客的一天内的出行时间是随机的，但满足统计分布规律。

请仿真该旅客出行系统（必要时给出合理的假设），向旅客给出出行建议、向交通管理部门给出车辆运行管理建议，以达到保证旅客有尽可能高的舒适度。

2、设人们到售票口购买电影票的平均到达率为每分钟1人，售票员卖一张票平均票20秒（到达间隔与服务时间都为负指数分布）。

问：（1）如果电影开始前2分钟某影迷到达，若他买好票，估计他找到座位大约需1.5分钟，那么他能期望在电影开始前坐好吗？（2）该影迷在电影开始前坐好的概率为多少？（3）为了在电影开始前坐好的把握为90%，他应多早到达？3、Ad Hoc网络中的区域划分和资源分配问题究的热点之一，对于诸如军队和在野外作业的大型公司和集团来说，Ad Hoc网络有着无需基站、无需特定交换和路由节点、随机组建、灵活接入、移动方便等特点，因而具有极大的吸引力。

在Ad Hoc网络中，节点之间的通信均通过无线传输来完成，由于发射功率以及信道（即频率）的限制，节点的覆盖范围有限，当它要与其覆盖范围之外的节点进行通信时，可以通过中间节点转发，如右图所示。

对一个指定区域，用一系列称为一跳覆盖区的小区域将其有重叠地完全覆盖，对每个一跳覆盖区分配一个信道，处于几个一跳覆盖区重叠部分的节点同时使用几个信道工作。

在同一个一跳覆盖区内的用户使用同一个信道相互通信；不同一跳覆盖区的用户之间通过中间节点转发。

如图中，节点A,B间的通信可由路由A-C-D-B或A-C-E-F-B实现。