小学五年级下册数学分数加减简便计算

课题分数的加减混合运算例2 课型新授课时间教学目标1.知识与技能：通过学习、讨论，知道整数加法运算定律、减法的性质同样适用于分数加减法，并能比较熟练地进行分数加减法的简便计算。

2.过程与方法：通过合作交流掌握分数加法的简便运算方法，培养知识迁移、类推的能力以及归纳、概括的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，体会学习的乐趣，养成用简明、灵活的方法解决问题的习惯。

教学重点正确应用加法运算定律进行简算。

教学难点能比较熟练地进行分数加减法的简便计算。

教法引导、分析、归纳、迁移学法自主学习、交流讨论教学准备课件教学过程教学设计个性化调整一、复习引入：53＋36＋47 1.5＋3.8＋6.2计算下面各题，并说出计算的依据。

学生独立完成，集体交流。

式中的字母可以表示什么数？明确：整数加法交换律中，所指的两个数的范围是什么？整数加法结合律中所指的三个数的范围是什么？想一想：这些运算定律对分数加法适用吗？（举例说明）整数加、减法的运算定律对分数加、减法也适用，这节课我们一起学习“整数加法运算定律推广到分数加法。

”板书课题：整数加法的运算定律推广到分数加法。

二、共同探究：1.研究运算定律对分数加法的适用范围。

出示例2、下面每组算式的左右两边有什么样的关系？73+5252+73（32+41）+4332+（41+43）师：这些运算定律中，用字母表示的两个数或三个数，它的范围都包括了什么样的数？（整数和小数，还有分数）（1）在○里填上合适的运算符号，在（）里填上合适的数。

（课件）预习例2并完成下面练习：1.下面各题，怎样简便就怎样算。

16+25+75 86-23-17215+1038+285+917上面各题进行简便计算的根据是什么？用字母怎样表示？2.计算：大胆猜想一下○里应该填什么符号？说说你这样填的理由。

验证规律。

观察这些算式，你发现了什么？（2）组织学生学习，并相互交流。

师：你发现了什么？学生可能会说出：整数加法的交换律、结合律对分数加法同样适用。

五年级下册数学《分数加减混合运算》教案【一】一教学内容分数加减混合运算(二)教材第119 页的内容及第121 页练习二十三第5 ? 8 题。

二教学目标1 .通过教学，使学生理解整数加法的运算定律对分数加法同样适用，并能灵活运用加法运算定律进行简便运算。

2 .培养学生计算的灵活性。

3 .养成认真审题的良好习惯。

三重点难点正确应用加法运算定律进行简算。

四教具准备投影。

五教学过程(一)导入1 .用简便方法计算下面各题，并说出简算的依据。

53 + 36 + 64 + 97 1 . 5 + 3 . 8 + 6 . 22 .全班学生独立完成，并说出加法运算定律的字母表示形式。

3 .老师板书：加法交换律：a + b = b 十a加法结合律：a + b +c = a 十(b +c)(二)教学实施1 .老师设疑：当上面式中的字母表示分数时，这个定律还适用吗?2.出示教材第119 页的例2 ，学生计算两边是否相等，集体交流结果。

提问：① 两组算式的特点各是什么?(两组算式中，左右两边的加数都相同，第一组中加数交换了位置，第二组中改变了加的顺序。

② 这一特点与整数加法的什么运算性质相同?(加法交换律、加法结合律)3 .结论：整数加法的交换律和结合律对分数加法同样适用。

4 .完成教材第119页“做一做”的第l 题及第121 页的第5 、7 题。

学生在教材上填写，集体订正。

5 .完成教材第119 页“做一做”的第2 题。

学生根据数的特点，想想应用什么定律进行简算。

集体订正计算过程，并说出简算的依据。

6 .完成教材第121 页练习二十三的第8 题。

学先计计算出3 个算式的结果：然后让学生观察，找规律，归纳出：(≠0)再应用规律计算 + + + 集体交流计算方法。

(四)思维训练1 .下面各题怎样简便就怎样算。

2 .请将和填在圆圈中，使每条线上的三个数的和都相等。

3 . 计算。

(五)课堂小结本节课，我们研究了如何应用整数加法的运算定律简便计算分数加法。

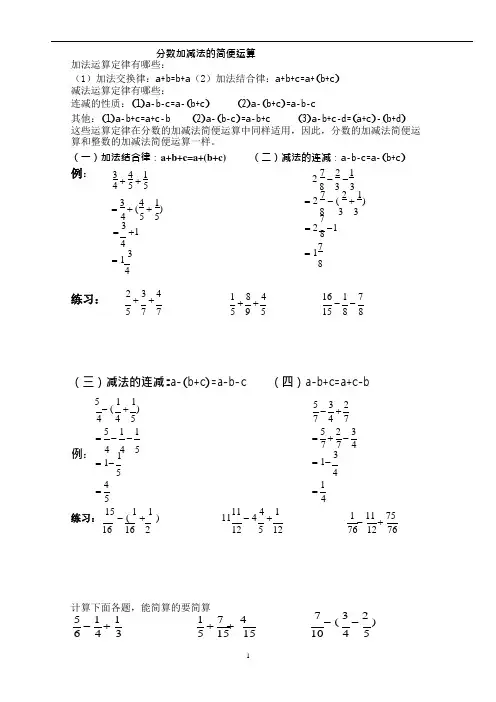
分数加减法的简便运算加法运算定律有哪些：（1）加法交换律：a +b =b +a （2）加法结合律：a +b +c =a +(b +c )减法运算定律有哪些：连减的性质：(1)a -b -c =a -(b +c ) (2)a -(b +c )=a -b -c 其他：(1)a -b +c =a +c -b (2)a -(b -c )=a -b +c (3)a -b +c -d =(a +c )-(b +d ) 这些运算定律在分数的加减法简便运算中同样适用，因此，分数的加减法简便运 算和整数的加减法简便运算一样。

（一）加法结合律：a+b+c=a+(b+c)（二）减法的连减：a -b -c =a -(b +c )例：3 +4 + 1 45 5 2 7 - 2 - 1 8 3 3 = 3 + 4 ( 4 + 1) 5 5 = 2 7 - ( 2 + 1) 8 3 3 7 = 3 +1 = 2 -1 8 4 = 1 3 4练习：2 +3 + 41 + 8 + 4 = 17 816 - 1 - 7 5 7 75 9 515 8 8（三）减法的连减:a -(b +c )=a -b -c（四）a -b +c =a +c -b5- ( 1 + 1) 4 4 5 = 5 - 1 - 1 例： 4 4 5= 1- 15 = 4 55 - 3 + 2 7 4 7 = 5 + 2 - 3 7 7 4 = 1- 34 = 1 4练习： 15 - ( 1 + 1)1111- 4 4 + 1 1 - 11 + 75 16 16 212 5 1276 12 76计算下面各题，能简算的要简算 5 - 1 + 1 1 + 7 + 4 7 - ( 3 - 2) 6 4 3 5 15 1510 4 5米的木头截去 和截去 米，剩下的部分不一样长。

（10 - 5 + 14 - 2 + 9 3 - 7 - 9 9 6 613 9 132 16 16分数乘除法的简便运算（一）乘法结合律：a ×b ×c=a ×(b ×c)例： 5 ⨯ 3 ⨯ 47 8 15（二）乘法分配率：（a+b ）×c=a ×c+b ×ca ×c+b ×c=（a+b ）×c 例： （3 + 1）⨯ 30 （ 2 - 1）⨯ 271 ⨯ 99 + 99 ⨯ 6 5 6 3 97 717 3 173 3 54 变式题：5 × ＋5 ÷4× + ÷ 24 4 248 4 8 3计算下面各题，能简算的要简算。

五年级下册数学分数加减法一、分数加减法的意义。

1. 分数加法的意义。

- 与整数加法的意义相同，都是把两个或两个以上的数合并成一个数的运算。

例如：(1)/(4)+(2)/(4)表示把(1)/(4)和(2)/(4)这两个数合并成一个数。

2. 分数减法的意义。

- 与整数减法的意义相同，已知两个数的和与其中一个加数，求另一个加数的运算。

例如：如果知道(3)/(5)是两个数的和，其中一个加数是(1)/(5)，那么求另一个加数就用减法，即(3)/(5)-(1)/(5)。

二、同分母分数加减法。

1. 计算法则。

- 同分母分数相加减，分母不变，分子相加减。

例如：- (2)/(7)+(3)/(7)=(2 + 3)/(7)=(5)/(7)；- (7)/(9)-(4)/(9)=(7-4)/(9)=(3)/(9)=(1)/(3)（结果能约分的要约成最简分数）。

2. 注意事项。

- 计算结果一定要化成最简分数。

例如，计算(4)/(8)+(1)/(8)=(4 +1)/(8)=(5)/(8)，这里的(5)/(8)已经是最简分数。

如果计算得到(6)/(12)，就需要约分为(1)/(2)。

三、异分母分数加减法。

1. 计算步骤。

- 先通分，将异分母分数化为同分母分数，然后按照同分母分数加减法的法则进行计算。

- 例如计算(1)/(2)+(1)/(3)：- 通分：2和3的最小公倍数是6，(1)/(2)=(1×3)/(2×3)=(3)/(6)，(1)/(3)=(1×2)/(3×2)=(2)/(6)。

- 计算：(3)/(6)+(2)/(6)=(3 + 2)/(6)=(5)/(6)。

- 再如计算(3)/(4)-(1)/(6)：- 通分：4和6的最小公倍数是12，(3)/(4)=(3×3)/(4×3)=(9)/(12)，(1)/(6)=(1×2)/(6×2)=(2)/(12)。

第七课时分数加减法的简便计算
教学目标：使学生掌握分数加减法的简便计算方法并能灵活、合理在进行计算。

教材分析：加法的交换律、结合律，减法的性质，在分数运算中同样适用。

教材首先通过准备题，复习应用加法的运算定律和减法的运算性质，使整数加减法计算简便。

接
着，教学应用加法的地自定笋减法的运算性质，使分数加减计算方便。

教学过程：
一、创设情境营造氛围
1．用简便方法计算P141准备题
2．说明：加法的交换律、结合律和减法的性质在分数运算中同样适用。

应用运算定律和性质可以使计算简便。

二、尝试探索建立模型
1．教学例9
A、出示例9，看一看这三个分数有什么特点？
B、你想怎么计算？你认为这样做简便吗？为什么？
C、反馈。

D、看书P142
2．尝试练习：P142试一试
3．说一说运算定律或性质在加减四则运算中有什么作用？
三、巩固深化拓展延伸
1．用简便方法计算P142、1
2．怎样简便就怎样计算P142、2
3．应用题
4．小结：这节课我们学习了简便计算，你会哪些简便方法？。

分数加减法的简便运算五年级下册一、同分母分数加减法简便运算。

同分母分数相加减，分母不变，分子相加减。

例如：(2)/(5) + (1)/(5) = (3)/(5)，(7)/(8) - (3)/(8) = (4)/(8) = (1)/(2)简便运算方法：如果有多个同分母分数相加或相减，可以先将同分母的分数分别相加减，再进行计算。

例如：(1)/(7) + (3)/(7) + (2)/(7) = ((1)/(7) + (3)/(7)) + (2)/(7) = (4)/(7) + (2)/(7) = (6)/(7)二、异分母分数加减法简便运算。

1. 先通分，将异分母分数化为同分母分数。

通分的方法：找出几个分母的最小公倍数作为公分母，然后根据分数的基本性质，将每个分数的分子和分母同时乘一个适当的数，使它们的分母都变成公分母。

例如：计算(1)/(2) + (1)/(3)，2 和 3 的最小公倍数是 6，通分得到：(3)/(6) + (2)/(6) = (5)/(6)2. 然后按照同分母分数加减法的法则进行计算。

三、分数加减法简便运算的常用技巧。

1. 凑整法：观察算式中分数的特点，将一些分数凑成整数，使计算简便。

例如：(7)/(11) + (2)/(11) + (2)/(11) = (7 + 2 + 2)/(11) = (11)/(11) = 12. 交换律和结合律：在分数加减法运算中，合理运用加法交换律和结合律，可以使计算简便。

例如：(1)/(3) + (2)/(5) + (2)/(3) = ((1)/(3) + (2)/(3)) + (2)/(5) = 1 + (2)/(5) = 1(2)/(5)3. 减法的性质：一个数连续减去几个数，等于这个数减去这几个数的和。

例如：(7)/(8) - (1)/(4) - (1)/(4) = (7)/(8) - ((1)/(4) + (1)/(4)) = (7)/(8) - (2)/(4) = (7)/(8) - (4)/(8) = (3)/(8)4. 去括号法则：如果括号前面是加号，去掉括号后，括号内的符号不变；如果括号前面是减号，去掉括号后，括号内的加号变减号，减号变加号。

第2课时分数加减简便运算【教学内容】分数加法(教材第98~99页的内容及第100~101页练习二十五第5~10题）。

【教学目标】1.通过教学，使学生理解整数加法的运算定律对分数加法同样适用，并能灵活运用加法运算定律进行简算。

2.培养学生计算的灵活性。

3.引导学生养成认真审题的良好习惯。

【重点难点】正确应用加法运算定律进行简算。

【复习导入】1.下面各题，怎样简便就怎样算。

16+25+75 215+1038+285+917要求学生说说：上面各题进行简便计算的根据是什么？用字母怎样表示？引导学生说出：整数加法交换律a+b=b+a整数加法结合律：（a+b）+c=a+(b+c)2.提问：整数加法交换律中，所指的两个数的范围是什么？整数加法结合律中所指的三个数的范围是什么？（使学生明确都是在整数范围内）3.回忆学过的加法，想一想：这些运算定律对分数加法适用吗？（举例说明）揭示课题：整数加、减法的运算定律对分数加、减法也适用，这节课我们一起学习“整数加法运算定律推广到分数加法。

”板书课题：整数加法的运算定律推广到分数加法。

【新课讲授】1.研究运算定律对分数加法的适用范围。

教师：这些运算定律中，用字母表示的两个数或三个数，它的范围都包括了什么样的数？（整数和小数，还有分数）使学生明确，加法运算定律在计算中都可以运用。

（1）教师出示教材第98页例2。

组织学生学习，并相互交流。

教师：你发现了什么？学生可能会说出：整数加法的交换律、结合律对分数加法同样适用。

（2）出示：计算：①51761212++；②23117474+++。

观察这些加数，注意分母和分子有什么特点并讨论怎样可以使计算简便？（把112和712结合起来，27和17结合起来，34和14结合起来，使计算简便）说一说这两道题应用了什么运算定律？（加法的交换律和结合律）①独立练习。

②订正，说说哪里应用了加法交换律，哪里应用了加法结合律。

③归纳，应用加法运算定律，可以把分母相同的分数先加起来，或凑成整数再进行计算比较简便。

五年级下册分数加减混合运算题简算在五年级的数学学习中，分数加减混合运算是一个重要的概念。

通过掌握这种运算方法，学生能够在解决实际问题时更加灵活和准确地进行计算。

本文将介绍五年级下册分数加减混合运算题的简算方法。

一、分数的基本概念在学习分数加减混合运算之前，我们首先需要了解分数的基本概念。

分数由分子和分母组成，分子表示物体或数量的一部分，分母表示总的数量或部分的份数。

例如，分数1/3表示物体或数量的一部分为3份中的1份。

二、分数的加法运算分数的加法运算是指将两个或多个分数进行相加得到一个新的分数。

要进行分数的加法运算，首先需要将分母化为相同的数。

具体步骤如下：1. 找到需要相加的分数，确保它们的分母相同。

2. 如果分母不同，需要找到它们的最小公倍数来将分母化为相同的数。

3. 将分子相加，并保持分母不变，得到新的分子。

4. 确定新的分子和分母是否可以进行约分。

如果可以，进行约分得到最简分数。

例如，计算1/3 + 1/4：首先，找到1/3和1/4的最小公倍数为12，将分母化为12。

1/3 = 4/12，1/4 = 3/12。

然后，将分子相加：4/12 + 3/12 = 7/12。

最后，7/12已经是最简分数，所以1/3 + 1/4 = 7/12。

三、分数的减法运算分数的减法运算是指将一个分数减去另一个分数得到一个新的分数。

要进行分数的减法运算，同样需要将分母化为相同的数。

具体步骤如下：1. 找到需要相减的分数，确保它们的分母相同。

2. 如果分母不同，需要找到它们的最小公倍数来将分母化为相同的数。

3. 将第二个分数的分子取相反数，然后将两个分数的分子相加，并保持分母不变，得到新的分子。

4. 确定新的分子和分母是否可以进行约分。

如果可以，进行约分得到最简分数。

例如，计算3/4 - 1/2：首先，找到3/4和1/2的最小公倍数为4，将分母化为4。

3/4 = 3/4，1/2 = 2/4。

然后，将第二个分数的分子取相反数：-2/4。

教案标题：五年级下册数学教案-4.2 分数加减混合运算-简便计算︳西师大版一、教学目标1. 让学生理解分数加减混合运算的概念，掌握简便计算方法。

2. 培养学生运用数学知识解决实际问题的能力，提高学生的逻辑思维能力。

3. 培养学生良好的学习习惯，激发学生学习数学的兴趣。

二、教学内容1. 分数加减混合运算的概念2. 分数加减混合运算的简便计算方法3. 分数加减混合运算在实际问题中的应用三、教学重点与难点1. 教学重点：分数加减混合运算的简便计算方法2. 教学难点：理解分数加减混合运算的概念，并能熟练运用简便计算方法解决实际问题四、教学方法1. 讲授法：讲解分数加减混合运算的概念和简便计算方法2. 演示法：通过示例演示简便计算方法的应用3. 练习法：布置练习题，让学生巩固所学知识4. 互动法：组织学生进行小组讨论，培养学生的合作意识五、教学过程1. 导入新课：通过回顾分数加减运算的知识，引出分数加减混合运算的概念2. 讲解新课：a. 讲解分数加减混合运算的概念b. 讲解简便计算方法：同分母分数相加减、异分母分数相加减、带分数相加减c. 通过示例演示简便计算方法的应用3. 练习巩固：布置练习题，让学生独立完成，教师巡回指导4. 小组讨论：组织学生进行小组讨论，分享解题心得，培养学生的合作意识5. 课堂小结：总结本节课所学知识，强调重点内容6. 布置作业：布置课后作业，巩固所学知识六、课后反思1. 教师应关注学生的学习情况，及时调整教学方法和进度2. 注重培养学生的逻辑思维能力和解决问题的能力3. 激发学生学习数学的兴趣，提高学生的学习积极性本节课通过讲解分数加减混合运算的概念和简便计算方法，以及实际问题的应用，使学生掌握了分数加减混合运算的知识。

在教学过程中，教师应注重培养学生的逻辑思维能力和解决问题的能力，激发学生学习数学的兴趣，提高学生的学习积极性。

同时，教师应关注学生的学习情况，及时调整教学方法和进度，以确保教学效果。

五年级下册数学分数加减混合运算一、分数加减混合运算的意义。

分数加减混合运算的意义与整数加减混合运算的意义相同，就是把几个分数合并成一个分数的运算，或者求一个分数比另外几个分数的和多（少）多少的运算。

二、分数加减混合运算的运算顺序。

1. 无括号的情况。

- 在没有括号的分数加减混合运算中，按照从左到右的顺序依次计算。

- 例如：(1)/(2)+(1)/(3)-(1)/(4)- 先算(1)/(2)+(1)/(3)=(3)/(6)+(2)/(6)=(5)/(6)；- 再算(5)/(6)-(1)/(4)=(10)/(12)-(3)/(12)=(7)/(12)。

2. 有括号的情况。

- 有括号的分数加减混合运算，先算括号里面的，再算括号外面的。

- 例如：(1)/(2)-((1)/(3)-(1)/(4))- 先算括号里的(1)/(3)-(1)/(4)=(4)/(12)-(3)/(12)=(1)/(12)；- 再算(1)/(2)-(1)/(12)=(6)/(12)-(1)/(12)=(5)/(12)。

三、分数加减混合运算的计算方法。

1. 通分。

- 计算分数加减混合运算时，通常需要先将分数通分，化成同分母分数，再按照同分母分数加减法的法则进行计算。

- 例如：计算(1)/(3)+(1)/(4)-(1)/(6)。

- 3、4、6的最小公倍数是12。

- (1)/(3)=(1×4)/(3×4)=(4)/(12)，(1)/(4)=(1×3)/(4×3)=(3)/(12)，(1)/(6)=(1×2)/(6×2)=(2)/(12)。

- 原式就变为(4)/(12)+(3)/(12)-(2)/(12)=(4 + 3-2)/(12)=(5)/(12)。

2. 简便计算。

- 整数加法的交换律、结合律对于分数加法同样适用。

- 例如：(1)/(5)+(2)/(7)+(4)/(5)。

- 根据加法交换律，可写成(1)/(5)+(4)/(5)+(2)/(7)。

百昇教育五年级数学下册第一单元《分数加减法》日期：一、同分母的分数加减法知识点：在计算同分母的分数加减法中，分母不变，直接用分子相加减。

注意：在计算同分母的分数加减法中，得数如果不是最简分数，我们必须将得数约分，使它成为最简分数。

例5654=510564=2注意：因为510不是最简分数，所以得约分，10和5的最大公因数是5，所以分子和分母同时除以5，最后得数是 2. 例1041059105109=52注意：因为104不是最简分数，必须约分，因为4和10的最大公因数是2，所以分子和分母同时除以2，最后的数是52知识点回顾：如何将一个不是最简的分数化为最简？（将一个非最简分数化为最简，我们就是将这个分数进行约分，一直约到分子和分母互质为止。

所以要将一个分数进行约分，我们必须找到分子和分母的最大公因数，然后用分子和分母同时除以他们的最大公因数。

）练习：1、计算715- 215712- 112 1 - 916911- 71138+ 3816+ 16314+31434+ 342、连线19+ 4927377145+15 1898747+ 671371151114118+78291193922411+511592121ABAB ABBA BA或113、判断对错，并改正（1）47+37=714（2）6 -57-37=577-57-37=527-37=5174、应用题（1）一根铁丝长710米，比另一根铁丝长310米，了；另一根铁丝长多少米？（2）3天修一条路，第一天修了全长的112，第二天修了全长的512，第三天修了全长的几分之几？二、异分母的分数加减法。

在异分母的分数加减法中，可分为三种情况。

分别是分母是互质关系、分母是倍数关系、分母是一般关系（即非互质也非倍数）例：A 代表一个分数的分母，B 代表另一个分数的分母，分母是倍数关系）（即分子都为的倍数）是或的倍数）是（、，分母互质）即分子都为或、1(1111)2(1(11)1(AB A B AB A B A B BAAB ABAB BAB A )3(、A 和B 是一般关系，就找到A 和B 的最小公倍数，进行通分，再加减。