七年级数学三线八角的认识

数学三线八角模型数学中有一种特殊的八角形模型，它被称为数学三线八角模型。

这个模型在数学领域中有着重要的应用，它是由数学三线和八角形组成的。

下面我将详细介绍数学三线和八角形的定义和性质，以及数学三线八角模型的应用。

让我们来了解一下数学三线。

数学三线是指一个多边形内部的三条特殊的直线，它们分别是：内角平分线、中线和高线。

内角平分线是指从多边形内部的一个顶点出发，将相邻两个内角平分成相等的两部分的直线。

中线是指连接多边形的两个不相邻顶点的直线，并且中线的长度等于两个顶点连线长度的一半。

高线是指从多边形的一个顶点向对边的垂直直线。

接下来，我们来了解一下八角形。

八角形是一种具有八个角的多边形。

它有八条边和八个顶点。

八角形是一种特殊的多边形，它具有许多有趣的性质。

例如，八角形的内角和为1080度，每个内角的度数为135度。

此外，八角形的对角线个数为20条，对角线的长度可以通过数学公式计算得出。

有了数学三线和八角形的定义和性质，我们可以将它们结合起来，形成数学三线八角模型。

数学三线八角模型是指通过连接八角形的顶点和边上的特殊直线，形成的一个几何模型。

这个模型具有许多有趣的性质和应用。

数学三线八角模型在几何学中有着重要的应用。

它可以帮助我们研究八角形的特性和性质，推导出八角形的各种公式和定理。

例如，通过数学三线八角模型，我们可以证明八角形的内角和为1080度，每个内角的度数为135度。

这个结论对于解决与八角形相关的几何问题非常有帮助。

数学三线八角模型在数学解题中也有着广泛的应用。

通过运用数学三线八角模型，我们可以解决各种与八角形相关的问题。

例如，给定一个八角形的边长，我们可以利用数学三线八角模型中的定理和公式计算出八角形的面积和周长。

这对于解决实际问题非常有用，如建筑设计中的八角形建筑物的设计和计算。

数学三线八角模型还可以帮助我们研究其他几何形体的特性和性质。

通过将数学三线八角模型应用到其他多边形中，我们可以推导出它们的性质和定理。

2023七年级三线八角课件CATALOGUE 目录•引言•三线八角的定义和性质•基础概念和定理•习题解答和分析•课堂互动与拓展•教学反思和总结01引言1课程背景23学生在小学阶段已经接触过简单的图形知识七年级数学上册第一章已经学习了线段和角本课件是为了帮助学生巩固所学知识并深入理解三线八角相关内容掌握三线八角的概念及基本性质会用符号表示三线八角能利用三线八角解决实际问题课程目标教学内容三线八角的概念及基本性质三线八角的表示方法利用三线八角解决实际问题02三线八角的定义和性质三线八角的定义七年级数学中三线八角是指由同一条直线上的三条线段或射线组成的八个角。

底角: 在三角形中，相邻两边之间的夹角小于90度，这个角叫做底角。

顶角: 在三角形中，相邻两边之间的夹角大于90度，这个角叫做顶角。

等角: 如果两个角的度数相等，那么这两个角叫做等角。

如果两个角是等角，那么它们所对的边也是相等的。

等角对等边 在两条平行线被第三条直线所截的情况下，内错角相等。

内错角相等 在两条平行线被第三条直线所截的情况下，同位角相等。

同位角相等 对顶角相等是指如果两个角是对顶角，那么它们的度数相等。

对顶角相等在几何证明中，三线八角是一种常见的几何图形，常常被用来进行各种几何证明。

在解决一些实际问题时，三线八角也常常被用来作为辅助线或者构造一些几何形状。

03基础概念和定理基础概念射线一个点沿着一定方向无限延伸形成的图形。

直线一个或多个点沿着一定路径无限延伸形成的图形。

线段两个点之间的距离形成的图形。

平行线永远不会相交的两条直线。

相交线两条直线或射线在同一点相遇形成的交点。

定理的证明和解读对顶角相等两个相交的直线或射线在形成两个角，这两个角互为对顶角，它们的大小相等。

三角形内角和为180度一个三角形内的三个角的度数之和等于180度。

四边形内角和为360度一个四边形内的四个角的度数之和等于360度。

定理的应用利用对顶角相等，可以证明两个角是否相等。

第七章 平面图形的认识（二）一、知识点：1、“三线八角”① 如何由线找角：一看线，二看型。

同位角是“F ”型；内错角是“Z ”型；同旁内角是“U ”型。

② 如何由角找线：组成角的三条线中的公共直线就是截线。

2、平行公理：如果两条直线都和第三条直线平行，那么这两条直线也平行。

简述：平行于同一条直线的两条直线平行。

补充定理：如果两条直线都和第三条直线垂直，那么这两条直线也平行。

简述：垂直于同一条直线的两条直线平行。

34、图形平移的性质：图形经过平移，连接各组对应点所得的线段互相平行（或在同一直线上）并且相等。

5、三角形三边之间的关系：三角形的任意两边之和大于第三边；三角形的任意两边之差小于第三边。

若三角形的三边分别为a 、b 、c ，则b a c b a +<<-6、三角形中的主要线段：三角形的高、角平分线、中线。

注意：①三角形的高、角平分线、中线都是线段。

②高、角平分线、中线的应用。

7、三角形的内角和：三角形的3个内角的和等于180°；直角三角形的两个锐角互余；三角形的一个外角等于与它不相邻的两个内角的和；三角形的一个外角大于与它不相邻的任意一个内角。

8、多边形的内角和：n边形的内角和等于（n-2）•180°；任意多边形的外角和等于360°。

第八章幂的运算幂（power）指乘方运算的结果。

a n指将a自乘n次(n个a相乘）。

把a n看作乘方的结果，叫做a的n次幂。

对于任意底数a,b，当ｍ，ｎ为正整数时，有:aｍ•a n=a m+n (同底数幂相乘,底数不变,指数相加)aｍ÷a n=a m-n (同底数幂相除,底数不变,指数相减)(aｍ)n=a mn (幂的乘方,底数不变,指数相乘)(ab)n=a n a n (积的乘方,把积的每一个因式乘方,再把所得的幂相乘)a0=1(a≠0) (任何不等于0的数的0次幂等于1)a-n=1/a n (a≠0) (任何不等于0 的数的-n次幂等于这个数的n次幂的倒数)科学记数法:把一个绝对值大于10(或者小于1)的整数记为a×10n的形式(其中1≤|a|＜10),这种记数法叫做科学记数法.复习知识点：1.乘方的概念:a中，a 叫做底数，求n 个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

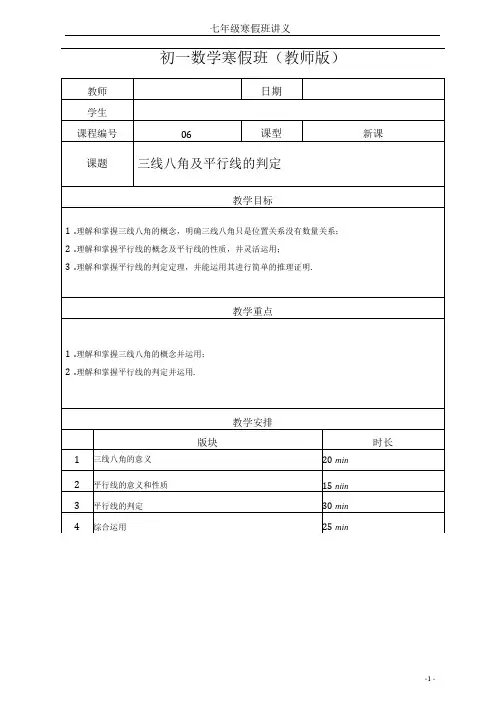
初一数学寒假班（教师版）同位角、内错角、同旁内角（三线八角） 若直线3被直线，所截：（1）同位角：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做 同位角.（如N1和N5）（2）内错角：两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角 叫做内错角.（如N3和N5）（3）同旁内角：两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角.（如N3和N6 ） 注意：三线八角是位置关系，数量上没有确定的关系.模块一：三线八角的意义知识精讲【例1】如图，N2与N3是 角.Z2与N4是 角. N2与N5是 角. Z1与N5是 角. Z3与N5是 角. Z3与N7是 角. N3与N8是 角. N2与N8是 角.【难度】★ 【答案】邻补角、对顶角、同旁内角、同位角、内错用、同位角、同旁内角、内错角. 【解析】考查线八角的角的概念. 【总结】考查三线八角的本概念.【例2】填空(1)/3和N1是两条直线 和 被第三条直线 所截构成的 角. (2)44c3与N7是两条直线 和 被第三条直线 所截构成的 角. (3)/3与N5是两条直线 和 被第三条直线 所截构成的 角. (4)/3与NB 是两条直线 和 被第三条直线 所截构成的 角. (5)Z2与N7是两条直线 和 被第三条直线 所截构成的 角.【难度】★【答案】(1)BC 、DE 、AB 、同位角：(2) BC 、DE 、AC,同位角:(3) BA 、CA. DC 、内错角: (5) DC. AC. DE 、内错角.【解析】考查线八角的角的概念. 【总结】考查三线八角的本概念.例题解析(4) DC. BC 、BA 、同旁内角:【例3】如图，同旁内角有( )对.A. 4对B. 3对C. 2对【难度】★【答案】B【解析】任意两个角都互为同旁内角,共3对.【总结】考查同旁内角的概念.【例4】如图，同位角共有（）对.A. 1对B. 2对C. 3对【难度】★【答案】B【解析】同位角像F形，由F形找同位角.【总结】考查同位角的概念.【例5】如图，是同位角关系的是（）.N2 和N4A. N3 和N4B. N1 和/4C.【难度】★【答案】B【解析】A是内错角：B内错角：C同旁内角.【总结】考查同位角的概念.【例6】如图，内错角共有（）对.A. 1对B. 2对C. 3对【难度】★★【答案】D【解析】NEDB 与/DBC、/EDB 与NDB.4、/FDB 与/DBC、/FDB 与NDBA,共4 对【总结】考查内错角的概念.【例7】如图，同旁内角共有（）对.A. 10 对B. 8 对C. 6 对【难度】★★【答案】C【解析】四边形内有4组，四边形上方和右边各有一组, 共6组.【总结】考查同旁内角的判定.【例8】如图，N1与N2是两条直线—和—被第三条直线所截构成的角.Z3与N4是两条直线和被第三条直线所截构成的角.【难度】★★【答案】AD. BC、AC、内错角：AB. CD、AC、内错角.【解析】内错角像字母Z.【总结】考查内错角的特点及判定.［例9］如图，NC 的同位角有，同旁内角是Z1与N2是 角.直线,空和8被疝）所截，Nd 的内错角是 ZJ 与ZADC 是 角.【难度】★★【答案】Z/WE. NBDE ： ZABC. /DBC 、ZADC. /BDC ； 内错角：NAOE ：同旁内角.【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U. 【总结】考查基本角的特点.【例10］如图，N1的同位角是/， N1的内错角是N , N1的同旁内角是Z, N1的对顶角是N , N1的邻补角是/【难度】★★★【答案】NDEB 、NEBH ： ZAEF. NIBF ； /BEF 、NEBF ；NCFG ； /CFD 、4GFH.【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U, 找的时候要注意找全.【总结】考查基本角的特点及概念.【例11］如图，。

教师可以通过观察学生的解题速度和用时情况，分析学生的解题技巧和熟练程度，为后续教学提供参考。
课堂练习效果评价
详细描述
知识点覆盖程度
做题时间与速度
题目难度评价
01
02
总结词
通过观察学生的问题回答情况，教师可以及时发现学生在知识掌握上的不足和问题，以便及时采取措施进行补救。
详细描述
在七年级数学教学中，学生问题回答情况反馈可以从以下几个方面展开
教学目标
教学目标与要求
三线八角的定义及性质
02
在同一个平面内，不相交的两条直线互相平行。
三线的定义
平行线
当两条直线相交所成的四个角中，有一个角是直角时，两条直线互相垂直。
垂线
既不平行于第一条直线，也不垂直于第二条直线。
第三条线
内错角
在两个平行直线被第三条直线所截的情况下，处于被截直线之间，且分别位于截线的两侧的两个角。
同位角
在两个平行直线被第三条直线所截的情况下，处于被截直线同侧，且分别位于截线的同侧或异侧的两个角。
同旁内角
在两个平行直线被第三条直线所截的情况下，处于被截直线之间，且位于截线的同侧的两个角。
八角的定义
三线八角的基本性质
对顶角相等；等腰三角形两底角相等；三角形三个内角之和等于180度。
等量代换；等角代换；全等三角形的对应边相等，对应角相等。
两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。
三线八角的应用与判定
03
在道路交叉口设置三线八角，用于指示车辆和行人安全行驶和停靠。
指示路标
宣传工具
装饰照明
企业或组织在宣传活动中使用三线八角作为标志，以突出自己的形象和品牌。

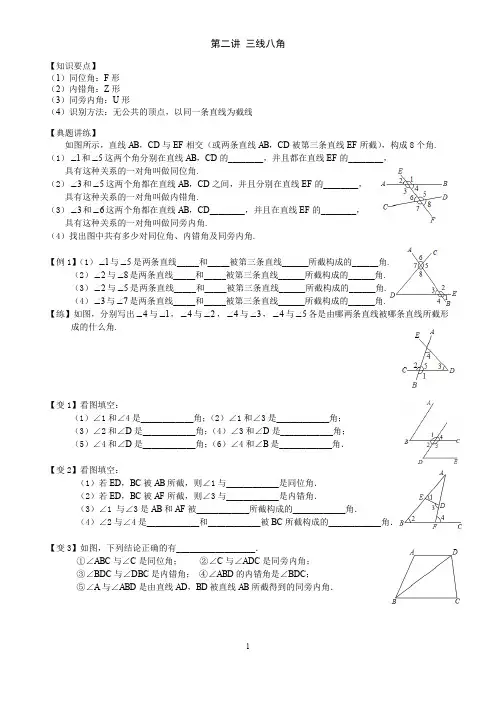
第二讲 三线八角【知识要点】（1）同位角：F 形 （2）内错角：Z 形 （3）同旁内角：U 形（4）识别方法：无公共的顶点，以同一条直线为截线【典题讲练】如图所示，直线AB ，CD 与EF 相交（或两条直线AB ，CD 被第三条直线EF 所截），构成8个角. （1）1∠和5∠这两个角分别在直线AB ，CD 的________，并且都在直线EF 的________，具有这种关系的一对角叫做同位角.（2）3∠和5∠这两个角都在直线AB ，CD 之间，并且分别在直线EF 的________，具有这种关系的一对角叫做内错角.（3）3∠和6∠这两个角都在直线AB ，CD ________，并且在直线EF 的________，具有这种关系的一对角叫做同旁内角.（4）找出图中共有多少对同位角、内错角及同旁内角.【例1】（1）1∠与5∠是两条直线_____和_____被第三条直线______所截构成的______角.（2）2∠与8∠是两条直线_____和_____被第三条直线______所截构成的______角. （3）2∠与5∠是两条直线_____和_____被第三条直线______所截构成的______角. （4）3∠与7∠是两条直线_____和_____被第三条直线______所截构成的______角.【练】如图，分别写出4∠与1∠，4∠与2∠，4∠与3∠，4∠与5∠各是由哪两条直线被哪条直线所截形成的什么角.【变1】看图填空：（1）∠1和∠4是____________角；（2）∠1和∠3是____________角； （3）∠2和∠D 是____________角；（4）∠3和∠D 是____________角； （5）∠4和∠D 是____________角；（6）∠4和∠B 是____________角．【变2】看图填空：（1）若ED ，BC 被AB 所截，则∠1与____________是同位角． （2）若ED ，BC 被AF 所截，则∠3与____________是内错角．（3）∠1 与∠3是AB 和AF 被____________所截构成的____________角．（4）∠2与∠4是____________和____________被BC 所截构成的____________角．【变3】如图，下列结论正确的有__________________．①∠ABC 与∠C 是同位角； ②∠C 与∠ADC 是同旁内角； ③∠BDC 与∠DBC 是内错角； ④∠ABD 的内错角是∠BDC ；⑤∠A 与∠ABD 是由直线AD ，BD 被直线AB 所截得到的同旁内角．【例2】（1）在图中，∠1与∠2是同位角的有__________________．（2）如下左图，与∠B 是同旁内角的角有__________________．（3）如下右图，在∠1，∠2，∠3，∠4中，是内错角的是__________________．（1）如图，AB 是一条直线，下图中∠1和∠2是同位角的是（）．B ．C ．D ．（2）如下左图所示，与∠C 构成同旁内角的有__________________．（3）如上右图，在所标识的角中，是内错角的是（ ）（2）如下中图所示，图中能与∠C 构成同旁内角的有__________个．（3）如下右图，若直线MN 与△ABC 的边AB 、AC 分别交于E 、F ，则图中的内错角有______对．【练】如图，有下列说法：①能与∠DEF 构成内错角的角的个数有2个； ②能与∠BFE 构成同位角的角的个数有2个；③能与∠C 构成同旁内角的角的个数有4个，其中结论正确的是____________.【例4】（1）图中所标出的角中，同位角一共有_______对，内错角一共有_______对，同旁内角一共有_______对．（2）如图所示，同位角一共有_______对，内错角一共有_______对，同旁内角一共有有_______对．【练】（1）如下左图，同位角一共有_______对，内错角一共有_______对，同旁内角一共有有_______对． （2）如下中图，同位角一共有_______对，内错角一共有_______对，同旁内角一共有有_______对． （3）如下右图，直线AB ∥CD ，两相交直线EF 、GH 与AB 、CD 都相交，同位角一共有_______对，内错角一共有_______对，同旁内角一共有有_______对．【拓】如图一共有__________对内错角．【家庭作业】1．如图2－1，填空：（1）∠1和∠2是直线_______和直线_______被直线_______所截形成的__________； （2）∠3和∠4是直线_______和直线_______被直线_______所截形成的__________； （3）∠5和∠8是直线_______和直线_______被直线_______所截形成的__________； （4）∠2和∠7是直线_______和直线_______被直线_______所截形成的__________．2．如图2－2，∠B 的同旁内角有_____________________．3．如图2－3，直线a 、b 、c 两两相交于A 、B 、C 三点，则图中有_______对同位角，_______对内错角，_______对同旁内角.4．如图2－4，直线a 、b 被直线c 所截，∠1＝50°，∠2＝115°. （1）求∠1的同位角的度数；（2）求∠4的内错角的度数；（3）求∠3的同旁内角的度数. 5．如图2－5，直线AB 、AC 被直线DE 所截，构成图中有数字记号的8个角和∠A.请写出这9个角中所有的同位角、内错角、同旁内角.图2-454321cba87654321EDA 图2-3图2-2图2-1c b aFED C B AE D C B A 876543216．如图2－6，△ABC ，直线l 与AB 、BC 分别相交.请写出图中标有数字的四个角和△ABC 的三个角中，共有哪些角是同旁内角，并指出每对同旁内角分别是哪两条直线被哪条直线所截.【补充训练】1、如图所示，图中共有内错角__________对2、如图所示，与∠A 是同旁内角的角共有 _________ 个．3、如图，n 条水平直线（n 为大于1的整数）与一条倾斜直线a 相交.（1）根据上述图形，完成下表：（2）归纳：n 条水平直线与倾斜直线a 相交可得_______条线段，_______对同位角，_______对内错角，_______对同旁内角.图2-6l4321CBA。

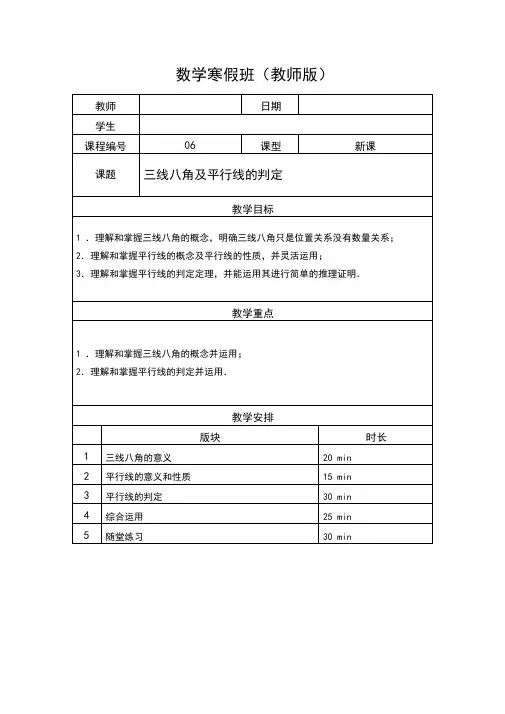
数学寒假班（教师版）模块一：三线八角的意义知识精讲同位角、内错角、同旁内角（三线八角）若直线 a， b 被直线l 所截：（ 1）同位角：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．（如1和5）（ 2）内错角：两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角叫做内错角．（如3和5 ）（ 3）同旁内角：两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角．（如3和6 ）注意：三线八角是位置关系，数量上没有确定的关系． 2 178三线八角及平行线的判定34知∠2 与∠4 是 __ 角． ∠2 与∠5 是 __ 角． ∠1 与∠5 是 __ 角． ∠3 与∠5 是 __ 角． ∠3 与∠7 是 __ 角． ∠3 与∠8 是 __ 角． ∠2 与∠8 是 __ 角．例题解析1】如图，∠______________ 2 与∠ 3 是 角． (1)∠ B 和∠ 1 是两条直线 ___ ___和 __ ___被第三条直线 __ ___ 所截构成的 ___ __ ___(2)ACB 与∠ 7 是两条直线_____ 和 _ ___ 被第三条直线___ _ ___ 所截构成的____ __ ___ (3)∠ 3 与∠ 5 是两条直线 ____ ___和 ____被第三条直线 __所截构成的 __ ___角． (4) 3 与∠ B 是两条直线 ___和 __ __被第三条直线 ___ __所截构成的 __ ___角． (5) 2 与∠ 7 是两条直线 ___和 __ __被第三条直线 __所截构成的 __ ___角．BC 、 DE 、 AB 、同位角；( 2) BC 、 DE 、 AC 、同位角；3) BA 、 CA 、 DC 、内错角； 4) DC 、 BC 、 B A 、同旁内角；5) DC 、 AC 、 DE 、内错角．C3】如图，同旁内角有 ( A ． 4对B ． 3对C ． 2对3 对．2】角角EBD24】如图，同位角共有( )对．A． 1 对B． 2对C． 3对【答案】 BF 形，由 F 形找同位角．5】如图，是同位角关系的是( )．A．∠ 3 和∠ 4 B．∠ 1 和∠ 4【答案】 BA 是内错角；B 内错角；C 同旁内角．6】如图，内错角共有( )对．A． 1 对B． 2对C． 3对【答案】 DEDB 与∠DBC、∠ EDB 与∠DBA、∠ FDB 与∠ DBC、∠ FDB 与∠ DBA，共 4 对7】如图，同旁内角共有( )对．A． 10对B． 8对C． 6对【答案】 C4 组，四边形上方和右边各有一组，共 6 组．8】如图，∠ 1 与∠ 2 是两条直线 _____ 和被第三条直线所截构成的 _____ 角．3 与∠4 是两条直线___ _______ 和被第三条直线______ 所截构成的______ 角．AD、 BC、 AC、内错角； AB、 CD、 AC、内错角．Z．1、平行线的定义同一平面内，不相交的两条直线叫平行线．9】 如图， ∠ C 的同位角有同旁内角是 _________________1 与∠2 是 _____ 角． 直线 AB 和 CD 被 AD 所截， ∠ A 的内错角是 _ _________________ ， ∠ A 与∠ ADC 是 __ 角．ADE 、∠ BDE ；∠ABC 、∠ D BC 、∠ A DC 、∠BDC ；内错角；∠ ADE ；同旁内角． F ，内错角像字母Z ，同旁内角像字母U ．10】如图，∠ 1 的同位角是∠ _____ ，∠ 1的内错角是∠ _____ ，∠ 1 的同旁内角是____ ， ∠ 1 的对顶角是∠ ___ ，∠ 1 的邻补角是∠ _____ ．DEB 、∠ EBH ；∠ AEF 、∠ IBF ；∠ BEF 、∠ EBF ； ∠ CFG ；∠ CFD 、∠ GFH ．F ，内错角像字母 Z ，同旁内角像字母找的时候要注意找全．11】 如图， DC 垂直于 AE ，已知∠ DCE 的同位角是它的一半，∠ B=2∠ ACB ，试判断 △ ABC 的形状．DC ⊥ AE ，∴∠ DCE=90 DCE 的同位角是∠BAC ，由题已知∠ BAC=45 B+∠ ACB=180° -45° =135° 又∵∠ B=2∠ ACB ∴∠ B=90°，∠ ACB=45° ∴△ ABC 为等腰直角三角形模块二：平行线的意义和性质知识精讲2、平行线的基本性质1 ）经过直线外一点，有且只有一条直线与已知直线平行；2）平行线之间的距离处处相等；3）平行于同一条直线的两直线平行（平行的传递性）．4）同一平面内，垂直于同一条直线的两直线平行．5）两条平行线中，任意一条直线上的所有点到另一条直线的距离是一个定值，这个定值叫做这两条平行线间的距离，平行线间的距离处处相等．12】已知直线________________________ a// b ，b //c，那么a c 【答案】平行13】 a、 b、 c 是直线，且a//b， b⊥ c，则a 与 c 的位置关系是．【答案】垂直a∥ b， b⊥ c，∴a⊥ c．14】下列说法中，正确的是（）．A．两直线不相交则平行B．两直线不平行则相交C．若两线段平行，那么它们不相交D．两条线段不相交，那么它们平行【答案】 CA、 B 错； D 错误．15】在同一平面内，有三条直线，其中只有两条是平行的，那么交点有（）．A． 0个B． 1 个C． 2个D． 3个C16】下列说法中，错误的有（）．①若 a 与 c相交， b与 c相交，则 a 与 b 相交；②若 a∥ b， b∥ c，那么a∥ c；③过一点有且只有一条直线与已知直线平行；④在同一平面内，两条直线的位置关系有平行、相交、垂直三种A． 3 个B． 2 个C． 1 个D． 0 个【答案】 Aa 与b 可能平行，错误；②平行线的传递性，正确；③这个点必须不在已知直线上，错误；④在同一平面内，两条直线的位置关系有平行、相交两种，错误．17】如图，按要求画平行线．（ 1）过P 点画AB 的平行线EF；（ 2）过P 点画CD 的平行线MN ．18】如图，点A， B 分别在直线 l1， l2上，（ 1 ）过点 A 画到l 2的垂线段；（ 2）过点 B 画直线 CD∥ l1．模块三：平行线的判定知识精讲平行线的三种判定方法： （ 1 ）两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简单地说，同位角相等，两直线平行．2）两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简单地说，内错角相等，两【答案】∠DCE=∠ A等．CEAB19】如图，请写出能判定CE∥ AB 的一个条件．D20】如图， AB∥ CD， AC⊥BC，∠【答案】25°．AB∥ CD（已知），所以ACE BAC（两直线平行，内错角相等），因为∠BAC =65°（已知），所以BAC =65°，则∠_________ BCD = 度．ACE 65o（等量代换）．E C D ACB 90o（垂直的意义）ACE ACB BCD 180o（邻补角的意义），21】如图，下列说法错误的是（）．A．∠ 1 和∠ 3 是同位角；B．∠C．∠ 1 和∠ 2 是同旁内角；D．∠【答案】 BZ．22】已知，△ ABC 中， DE 垂直于AC 于E，1和∠ 5 是同位角；5和∠ 6 是内错角．1 2365 4△ ACB=90° ，试说明DE△ BC 的理由．E CAD因为∠ACB=90°（已知），所以∠ACB=∠ AED（等量代换），所以 DE ∥ BC（同位角相等，两直线平行）例23】如图，∠5=∠CDA =∠ABC，∠1=∠4，∠2=∠3，∠BAD +∠CDA=180° ，填空：5=∠ CDA（已知）______ // ____ （内错角相等，两直线平行）5=∠ ABC（已知）______ // ____ （同位角相等，两直线平行）2=∠ 3（已知）______ // ____ （内错角相等，两直线平行）BAD+∠ CDA=180° （已知）∴ _____ // ____ （同旁内角互补，两直线平行）∵∠5=∠ CDA（已知），又∵∠ 5 与∠ BCD 互补，∠C DA 与互补（邻补角定义）∴∠B CD=∠ 6（等角的补角相等）∴ _____ // ____ （同位角相等，两直线平行）AD、 BC； AB、CD； AB、C D；AB、CD；∠6；AD、BC．AB⊥ BC，∠1+∠ 2=90° ，∠2=∠ 3，那么BE 与24】如图，DF 平行吗 ?为什么AB⊥ BC（已知），所以∠ ABC=90 °（垂直的意义），即 3 4 90o（角的和差）因为∠2=∠ 3（已知），所以 2 4 90o（等量代换）因为∠1+∠ 2=90°（已知），所以∠1=∠ 4（同角的余角相等），所以 BE∥ DF （同位角相等，两直线平行）1+∠ 3=90° ，试说明 AB//CDE B 2 3CDAFCDGQP1C2MNBCHBAEOD10/ 18所以 GOHAC 、 BC 分别平分∠ QAB 、∠ ABNO 、点 E ， GO ⊥ OH ， OH 平分∠ AOC2=3∠1AC 、 BC 分别平分∠ QAB 、∠ ABN （已知）1∠ QAB ，∠ 2= 1 ∠ ABN （角平分线的意义）B1E所以AOH COH （角平分线的意义）．因为 BOC COA 180o（邻补角的意义），所以∠GOB+∠ HOC=90°（等式性质）因为∠EDO+∠ GOB=90°（已知）所以∠EDO =∠ HOC （同角的余角相等）所以 OH ∥ EF（同位角相等，两直线平行）【总结】本题综合性较强，主要考查平行线的判定定理及同角的余角相等的综合运用，解题时认真分析，找出角度间的关系．29】如图，∠ABE=∠ E+∠ D，试说明A B//CD 的理由．【答案】略D E ECD 180o（三角形内角和等于又 ECD DCB 180o（邻补角的意义）所以∠ DCB=∠ E+∠ D（等式性质）因为∠ABE=∠ E+∠ D（已知）所以∠DCB=∠ ABE（等量代换），所以AB ∥ CD（内错角相等，两直线平行）综合性较强，解题时要认真分考查平行线的判定定理及三角形内角和的综合运用，析1】观察图，下列说法中，正确的是（习题2】如图，能使AB∥ CD 的条件是（）．A. ∠ 1=∠ BC．∠1+∠ 2+∠ B=180B ．∠3=∠AC 选项满足条件．3】一学员在广场上练习驾车，两次拐弯后，行驶的方向与原来的方向相同，这两次 拐弯的角度是（ ）A ．第一次向左拐 30o，第二次向右拐 30oB ．第一次向右拐 50o，第二次向左拐 130oC ．第一次向右拐 50o，第二次向右拐 130oD ．第一次向左拐 50o，第二次向左拐 130o【答案】 A B 向左拐了50°， C 、 D 都朝相反方向开去．4】如图，在下列条件中，能判定AB//CD 的是（）A ．∠ 1=∠ 3B ．∠ 2=∠ 3 CA 错误；B 能推出 AD ∥ BD ； D 错误．5】如图，图中所标号的 8 个角，是∠ C ．∠ 1=∠ 4 D ．∠ 3=∠ 4 A2143DB C1 的同位角的是 ______ ；∠ 3 的内错角是4 的同位角是 ______ ；∠ 6 的内错角是 2；∠ 5；∠ 6、∠ 8；∠ 3、∠ 7； ∠ 4；∠ 5． 习题 6】 如图，已知直线b ⊥ a ，c ⊥ a ．那么直线 b 与 如果不平行，举出反例． b ⊥ a ， c ⊥ a （已知），∴∠ 1=∠ 2=90°（垂直的意义）， ∴ b ∥ c （同位角相等，两直线平行）．76284315c 平行吗？如果平行，请给出证明； bc 1 a7】如图，已知AC⊥ AE， BD⊥ BF，∠1=35°，∠2=35°， AC 与 BD 平行吗 ?AE 与 BF平行吗?为什么?1=35° ，∠2=35°（已知），所以∠ 1=∠ 2（等量代换），因为 AC⊥ AE， BD⊥ BF（已知），所以∠ NBF=∠ BAE（等式性质）所以 AE ∥ BF（同位角相等，两直线平行）FA 8】如图，∠1+∠ 2=180° ． AE 与 FC 会平行吗? 说明理由． D【答案】平行．1+∠ 2=180°（已知），∠2+∠ BDC=180°（邻补角的意义） B1 所以∠ 1=∠ BDC（同角的补角相等）CE 所以 CF ∥ AE（同位角相等，两直线平行）9】根据图完成下列填空（括号内填写定理或公理）1 ）∵∠1= ∠ 4（已知）2）∵∠ ABC +∠ ____ =180°（已知）∴ AB∥ CD（3）∵∠______ =∠ _______ （已知）∴ AD ∥ BC（）4）∵∠5=∠ ______ （已知）∴ AB∥ CD（）1 ） AB ∥ CD、内错角相等，两直线平行；（ 2）∠ BCD 、同旁内角互补，两直线平行；（ 3）∠2=∠ 3、内错角相等，两直线平行；（ 4）∠ ABC 、同位角相等，两直线平行．10】已知DE⊥ BC， FG⊥ BC，∠ DEH=∠ GFC，试说明EH∥ FC 的理由．DE⊥ BC， FG⊥ BC（已知）所以∠ DEC=∠ FGC=90°（垂直的意义）所以∠ GFC+∠ FCG=90°（三角形内角和等于DEH =∠ GFC（已知），所以∠ HEC=所以 EH ∥ FC（内错角相等，两直线平行）AE//BC 的理由．11】已知∠EDC+∠ B=180°，∠EDC=∠ A，试说明【答案】略EDC+∠ B=180°，∠EDC=∠ A（已知）所以∠ A+∠ B=180 °（等量代换）所以 AE ∥ BC（同旁内角互补，两直线平行）习题12】已知：∠ABC＝∠ADC， BF 和DE 分别平分∠ABC 和∠ ADC， 1 2．试说明 DE∥ BF 的理由．BF 和 DE 分别平分∠ABC 和∠ ADC（已11所以 1 ADC ， ABF ABC （角平分线的意义）ABC＝∠ADC（已知），所以∠1=∠ ABF（等式性质）因为∠1=∠ 2（已知），∴∠2=∠ FBA（等量代换）所以 DE ∥ BF（同位角相等，两直线平行）13】已知直线a， b， c被直线 d所截，1 3， 3 4 1800，试说明 a∥ c．所以 a∥ b（同位角相等，两直线平行）因为∠ 3+∠ 4=180°（已知），∠3+∠ 5=180°（邻补角的意义）所以∠ 4=∠ 5（同角的补角相等）所以 b∥ c（同位角相等，两直线平行）所以 a∥ c（平行的传递性）课后作业【作业 1 】下列说法中正确的是（）A．经过一点，有且只有一条直线与已知直线平行B ．两条直线被第三条直线所截，同位角相等C．垂直于同一条直线的两条直线互相垂直D ．两条直线被第三条直线所截，内错角相等，则两条直线平行【难度】★【答案】D【解析】 A 这个点必须是直线外的点，错误； B 同位角相等的前提是两直线平行，错误；C 垂直于同一条直线的两条直线互相平行，错误；故选 D【总结】考查平面内直线的位置关系．2】在同一平面内，若a⊥ b，c⊥ b 则 a 与 c的关系是（）A．平行B．垂直C．相交 D ．以上都不对【答案】 A3】如图，∠ADE 和∠ CED 是（）A．同位角B．内错角C．同旁内角【答案】 BZ．C4】如图，属于内错角的是（）A．∠1 和∠ 2 B．∠ 2 和∠ 3 C．∠1 和∠ 4 D ．∠ 3 和∠ 4DZ．5】下列有关垂直相交的说法：①同一平面内，垂直于同一条直线的两条直线互相平行；②一条直线如果它与两条平行线中的一条垂直，那么它与另一条也垂直；③同一平面内，一条直线不可能与两条相交直线都垂直；其中说法正确个数有（）A． 3个B． 2个C． 1 个D． 0个【答案】BC．6】下列语句：①三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条直线所截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（）A．①、②是正确的命题B．②、③是正确命题C．①、③是正确命题D．以上结论皆错【答案】A90°，即垂直，正确；③这个点必须是直线外的一点，错误，故选A．7】如图，能与构成同旁内角的角有（）A． 5个B． 4个C． 3个D． 2个【答案】AU8】如图，AB⊥ BD， CD⊥ MN，垂足分别是B、 D 点，∠FDC =∠ EBA．1）判断CD 与 AB 的位置关系；2） BE 与 DF 平行吗?为什么 ?1 ）平行（ 2）平行1 ）因为AB⊥ BD， CD⊥ MN（已知），所以CD ∥ AB（垂直于同一条直线的两条直线互相平行）；2）因为∠CDM=∠ ABM 90o（垂直的意义），又∠FDC=所以∠MDF =∠ MBE（等式性质）所以 BE∥ DF（同位角相等，两直线平行）作业9】如图 CD⊥ AB， EF⊥ AB，∠ 1=∠ 2，试说明DG//BC 的理由．CD ⊥ AB， EF⊥ AB（已知），所以EF ∥ CD（垂直于同一条直线的两条直线互相平行）所以∠2=∠ DCB（两直线平行，同位角相等）因为∠2=∠ 1 （已知），所以∠ 1=∠ DCB（等量代换）所以 DG∥ BC（内错角相等，两直线平行）作业10】如图，AB、 CD 被 EF 所截， MG 平分∠ BMN ， NH 平分∠ DNM ，已知∠GMN +∠ HNM =90°，试问：AB∥ CD 吗？请说明理由．MG 平分∠ BMN， NH 平分∠DNM（已知）所以∠BMN=2∠ GMN，∠DNM =2∠ HNM （角平分线的意义）因为∠FMG+∠ HNM =90°（已知）所以∠BMN+∠ DNM =180°（等式性质）所以A B ∥ CD（同旁内角互补，两直线平行）所以 1 A B ， 2 C D （等式性质）B=∠ C ，∠ A=∠ D （已知）， 所以 1 2（等式性质），所以 AE ∥ DF （内错角相等，两直线平行）【总结】 考查平行线的判定定理及三角形内角和定理的综合运用，择性讲解．12】如图，已知：∠ B+∠ D ＝∠BED ． AB 与 CD 平行吗，说明理由．E 作 EF ∥ AB ，则∠ B=∠ BEF （两直线平行，内错角相等） 因为∠ BED =∠ BEF+∠ FED =∠ B+∠ D （已知），所以∠ FED =∠ D （等式性质）所以 CD ∥ EF （内错角相等，两直线平行）所以 AB ∥ CD （平行的传递性） 11】 如图， 因为 A B=∠ C ，∠ B AEB又 AEB 1 180o ， 2 A=∠ D ，试说明 AE//DF ． 180o ， C D CFD 180o （三角形内角和等于CFD 180o （邻补角的意义） 180°) D 综合性较强， 建议老师选。

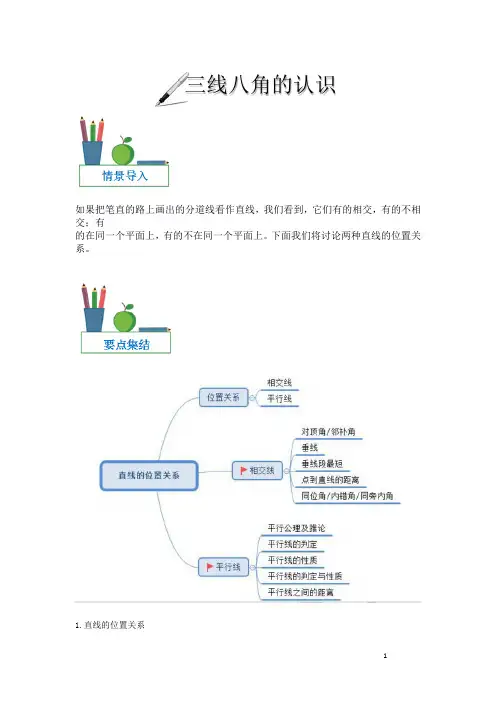
三线八角的认识如果把笔直的路上画出的分道线看作直线，我们看到，它们有的相交，有的不相交；有的在同一个平面上，有的不在同一个平面上。

下面我们将讨论两种直线的位置关系。

1.直线的位置关系在同一平面内，两条直线的位置关系有两种：相交和平行。

（1）相交：在同一平面内，有一个公共交点的两条直线称为相交线。

（2）平行：在同一平面内，永不相交的两条直线叫做平行。

2.对顶角、邻补角一、邻补角：①定义：有公共顶点，且有一条公共边，另一条边互为反向延长线，具有这种位置关系的两个角，互为邻补角。

②性质：位置——互为邻角数量——互为补角（两角之和为 180°）二、对顶角：①定义：有一个公共顶点，并且有一个角的两边分别是另一个角两边的反向延长线，具有这种位置关系的两个角，互为对顶角。

②性质：对顶角相等几何语言：∵∠1+∠2=180°∠2+∠3=180°∴∠1=∠3（同角的补角相等）3.同位角、内错角、同旁内角一、两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角。

如图，直线 a,b 被直线l 所截1、∠1 与∠5 在截线l 的同侧，同在被截直线 a,b 的上方，叫做同位角（位置相同）。

2、∠5 与∠3 在截线l 的两旁（交错），在被截直线 a,b 之间（内），叫做内错角（位置在内且交错）。

3、∠5 与∠4 在截线l 的同侧，在被截直线 a,b 之间（内），叫做同旁内角。

4、三线八角也可以成模型中看出。

同位角是“A”型；内错角是“Z”型；同旁内角是“U”型1. 平面内有两两相交的 4 条直线，如果最多有 m 个交点，最少有 n 个交点，那么 m-n=（）A.3B.4C.5D.62. 平面内三条直线的交点个数可能有（）.A.0,1,2,3 个B.1,3 个C.2,3 个D.1,2,3 个3. 下列说法中，正确的是（）. A．两条不相交的直线叫做平行线B．一条直线的平行线有且只有一条C．在同一平面内，若直线 a∥b，a∥c，则 b∥cD．若两条线段不相交，则它们互相平行4. 下列说法正确的是（）A．不相交的两条线段是平行线B．不相交的两条直线是平行线C．不相交的两条射线是平行线D．在同一平面内，不相交的两条直线是平行线三线八角【典题导入】【亮点题】1. 下列说法中正确的有（）①对顶角的角平分线成一条直线；②相邻二角的角平分线互相垂直；③同旁内角的角平分线互相垂直；④邻补角的角平分线互相垂直．A．1 个B．2 个C．3 个D．4 个2.如图，下列说法中不正确的是（）A．∠1 和∠3 是同旁内角B．∠2 和∠3 是内错角C．∠2 和∠4 是同位角D．∠3 和∠5 是对顶角【小试牛刀】1.下列所示的四个图形中，∠1 和∠2 是同位角的是（）考点A．①②B．②③C．①③D．②④2.某城市有四条直线型主干道分别为l1，l2，l3，l4，l3 和l4 相交，l1 和l2 相互平行且与l3、l4 相交成如图所示的图形，则共可得同旁内角（）对A．4 B．8 C．12 D．163. 如图所示，直线AB，CD 相交于点O，已知∠AOD=160°，则∠BOC 的大小为（）A.20°B.60°C.70°D.1604. 如图，下列各组角中，互为对顶角的是（）. A．∠1 和∠2 B．∠1 和∠3 C．∠2 和∠4 D．∠2 和∠5。

三线八角在实际生活和生产中也有广泛的应用，例如在建筑、机械等领域中都需 要了解直线的位置关系和角度的计算。
02
三线八角的定义和定理
三线八角的定义
七年级数学中，三线八角是常 见的几何概念。
三线八角是指在一个平面内， 有三条直线相交于一点，而每 两条相交的直线都会形成一对 邻补角。
这些角的大小可以用于描述和 证明一些几何关系和定理。
例题二：稍复杂的三线八角问题
总结词
这道例题将三线八角的概念引入到稍微复杂一些的情境中，通过观察和计算，学生可以进一步了解三线八角的 性质和应用。
详细描述
本题以一个稍复杂的图形为例，让学生找出图中所有的三线八角，并比较它们的大小。通过这种形式的题目， 学生可以进一步了解三线八角的性质和应用，为后续的学习打下基础。同时，通过让学生计算两条平行线之间 的距离，可以培养学生的计算能力。
05
三线八角的练习题
练习题一：基础题
总结词
简单基础，涉及知识点较少。
详细描述
本题主要考察学生对三线八角基本概念的理解，包括同位角 、内错角、同旁内角等。学生需根据这些概念判断哪些是同 位角、内错角或同旁内角。
练习题二：提高题
总结词
难度适中，涉及知识点较多。
VS
详细描述
本题不仅要求学生掌握三线八角的基本概 念，还需要理解角之间的位置关系，如平 行线的性质、垂直的定义等。学生需通过 分析图形中的角的位置关系，得出正确答 案。
举例
在三线八角中，如果我们已知两个角分别等于90度和45度，那么我们 可以直接推导出第三个角等于45度。
证明方法二：反证法
总结词
反证法是一种间接证明方法，通过假设相反的结论成立 ，然后推导出矛盾的结论，从而证明原命题的正确性。

的重要性。
02
主题重要性
学习目标
掌握三线八角的定义、性质及判定方法。 能够准确绘制三线八角的基本图形。 能够解决与三线八角相关的几何问题。
02
三线八角基本概念
直线的基本定义
01
02
直线是笔直的、无端点的线，它可以向两个方向无限延伸。在直线上 ，任意两点之间可以确定一条直线。
直线的表示方法：可以用一个小写字母表示一条直线，如“l”，也 可以用两个大写字母表示两条直线，如“AB”。
对角线的性质
对角线把多边形分成几个 三角形，这些三角形是全 等的。
对角线的判定
在四边形ABCD中，如果 AC和BD互相平分，那么 四边形ABCD是平行四边 形。
07
复习与总结
重点知识回顾
角的定义
角是由两条射线或线段共享一个 端点而形成的图形，这个端点叫 做角的顶点，两条射线或线段叫
做角的两边。
角的度量
同位角的性质：两直线平行，同位角相等。
三线八角的性质
内错角的定义及性质
两个角分别在截线的两侧，且夹在两被截线之间，这样的一对角称为内 错角。
内错角的性质：两直线平行，内错角相等。
三线八角的性质
同旁内角的定义及性质 两个角都在截线的同一侧，并且夹在两被截线之间，这样的一对角称为同旁内角。
同旁内角的性质：两直线平行，同旁内角互补。
垂直线的性质证明
垂直线的性质定理
如果一条直线垂直于一个平面，那么 这条直线垂直于该平面上任意一条直 线。
证明过程
通过构造垂线，利用垂线的定义和三 角形的高来进行证明。
对角线的性质证明
对角线的性质定理
在一个n边形中，从任一个顶点出发的对角线有(n-3)条。

4.实践应用，巩固提高
设计富有层次的练习题，让学生在实际操作中巩固所学知识。针对学生的个体差异，实施分层教学，使每个学生都能在原有基础上得到提高。
5.总结反思，拓展延伸
在课堂总结环节，引导学生对所学知识进行梳理，总结三线八角性质的关键点。同时，提出具有挑战性的拓展问题，激发学生的思维，为后续学习奠定基础。
教师设计具有挑战性的问题，引导学生进行自主探究，发现三线八角性质的规律。在此基础上，组织学生进行小组合作交流，分享彼此的发现，互相学习，共同提高。
3.案例解析，深入理解
教师选取具有代表性的例题，进行详细讲解，引导学生通过分析、归纳、总结，掌握三线八角性质的运用。同时，注重培养学生的几何直观，使他们能够运用所学知识解决实际问题。
1.充分了解学生的知识背景，针对学生的个体差异，进行有针对性的教学。
2.注重启发式教学，通过生动形象的语言和直观的教具演示，降低学生对三线八角概念的理解难度。
3.强调几何直观，引导学生通过观察、猜想、验证等方法，发现三线八角性质的规律。
4.注重培养学生的几何逻辑思维，使他们能够运用所学知识解决实际问题。
（二）过程与方法
在本章节的教学过程中，教师将采用以下方法引导学生学习：
1.采用直观演示法，通过生动的实物、模型等展示三线八角的特点，激发学生的学习兴趣。
2.运用任务驱动法，设计富有挑战性的问题，引导学生主动探究、发现三线八角的相关性质。
3.利用小组合作学习法，让学生在讨论、交流中互相学习，培养团队协作能力。
3.揭示课题：“今天我们要学习的是三线八角，它在我们生活中有着广泛的应用，让我们一起探索其中的奥秘。”
（二）讲授新知
在这一环节，我将按照以下步骤进行讲授：
1.讲解三线八角的概念，让学生明确三线八角是由三条线段和四个角组成的几何图形。

初一数学第二学期名校优选小专题02 三线八角识别问题【模型讲解】如图，已知直线a，b被直线c，d所截，直线a，c，d相交于点O，按要求完成下列各小题．(1)在图中的∠1～∠9这9个角中，同位角共有多少对？请你全部写出来；(2)∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？【分析】根据同位角、内错角和同旁内角的特征（同位角形如“F”，内错角形如“Z”，同旁内角形如“U”）判断即可.【解析】解：(1)如题图所示：同位角共有5对：分别是∠1和∠5，∠2和∠3，∠3和∠7，∠4和∠6，∠4和∠9；(2)由三线八角的判断方法∠4和∠5是由c，b，d三线组成，并且构成“U”形图案，所以∠4和∠5是同旁内角，同理可得：∠6和∠8也是同旁内角，故∠6和∠8之间的位置关系与∠4和∠5的相同．【模型演练】1．如图∠1、∠2、∠3、∠4、∠5中，哪些是同位角？哪些是内错角？哪些是同旁内角？2．如图，找出标注角中的同位角、内错角和同旁内角．3．如图所示，指出下列各组角是哪两条直线被哪一条直线所截得的，并说出它们是什么角？1∠和2∠；2∠∠；3∠和5∠；3∠和4∠；4∠和7∠.和6∠；6∠和A4．如图，∠1与∠2，∠3与∠4，分别是什么关系？分别是哪两条直线被哪一条直线所截形成的？5．下列图中∠1与∠2，∠3与∠4分别是哪两条直线被哪一条直线所截而成的？是什么角？6．如图，图中共有多少对同位角，多少对内错角，多少对同旁内角．7．在图中，分别找出一个角与α配对，使两个角成为：(1)同位角；(2)内错角；(3)同旁内角，并指出是由哪条直线截另外两条直线而得．8．如图，试判断∠1与∠2，∠1与∠7，∠1与∠BAD，∠2与∠9，∠2与∠6，∠5与∠8各对角的位置关系．9．如图所示，在标出的7个角中，与∠1是内错角、同旁内角的各有哪几个？与∠5是同位角的有哪几个？10．(1)如果把下图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？(2)如果把下图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠2呢？11．如图所示，(1)∠BED与∠CBE是直线________，________被直线________所截形成的________角；(2)∠A与∠CED是直线________，________被直线________所截形成的________角；(3)∠CBE与∠BEC是直线________，________被直线________所截形成的________角；(4)∠AEB与∠CBE是直线________，________被直线________所截形成的________角．12．如图所示．①∠AED和∠ABC可看成是直线__________、__________被直线__________所截得的__________角；②∠EDB和∠DBC可看成是直线__________、__________被直线__________所截得的__________角；③∠EDC和∠C可看成是直线__________、__________被直线__________所截得的__________角．13．如图：(1)找出直线DC，AC被直线BE所截形成的同旁内角；(2)指出∠DEF与∠CFE是由哪两条直线被哪一条直线所截形成的什么角；(3)试找出图中与∠DAC是同位角的所有角．14．如图：∠1和∠4是AB、_______被_______所截得的________角，∠3和∠5是_______、_____被_______所截得的_________角，∠2和∠5是______、_______被_______所截得的________角，AC、BC被AB所截得的同旁内角是________.15．（1）如果把图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？（2）如果把图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠6呢？16．如图，BE是AB的延长线，指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？（1）∠A和∠D；（2）∠A和∠CBA；（3）∠C和∠CBE．17．复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．（1）如图1，直线1l ，2l 被直线3l 所截，在这个基本图形中，形成了______对同旁内角．（2）如图2，平面内三条直线1l ，2l ，3l 两两相交，交点分别为A 、B 、C ，图中一共有______对同旁内角．（3）平面内四条直线两两相交，最多可以形成______对同旁内角．（4）平面内n 条直线两两相交，最多可以形成______对同旁内角．18．已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置1∠跳到终点位置3∠有两种不同路径，路径1：193∠−−−−→∠−−−→∠同旁内角内错角；路径2：1126103∠−−−→∠−−−→∠−−−→∠−−−−→∠内错角内错角同位角同旁内角.试一试：（1）写出从起始位置1∠跳到终点位置8∠的一种路径；（2）从起始位置1∠依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置8∠？19．探究题：(1)如图1，两条水平的直线被一条竖直的直线所截，同位角有____对，内错角有_____对，同旁内角有_____对；(2)如图2，三条水平的直线被一条竖直的直线所截，同位角有____对，内错角有___对，同旁内角有___对；(3)根据以上探究的结果，n(n 为大于1的整数)条水平直线被一条竖直直线所截，同位角有______对，内错角有_______对，同旁内角有 对．(用含n 的式子表示)答案与解析【模型讲解】如图，已知直线a，b被直线c，d所截，直线a，c，d相交于点O，按要求完成下列各小题．(1)在图中的∠1～∠9这9个角中，同位角共有多少对？请你全部写出来；(2)∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？【分析】根据同位角、内错角和同旁内角的特征（同位角形如“F”，内错角形如“Z”，同旁内角形如“U”）判断即可.【解析】解：(1)如题图所示：同位角共有5对：分别是∠1和∠5，∠2和∠3，∠3和∠7，∠4和∠6，∠4和∠9；(2)由三线八角的判断方法∠4和∠5是由c，b，d三线组成，并且构成“U”形图案，所以∠4和∠5是同旁内角，同理可得：∠6和∠8也是同旁内角，故∠6和∠8之间的位置关系与∠4和∠5的相同．【模型演练】1．如图∠1、∠2、∠3、∠4、∠5中，哪些是同位角？哪些是内错角？哪些是同旁内角？【答案】同位角有∠1和∠5；∠4和∠3；内错角有∠2和∠3；∠1和∠4；同旁内角有∠3和∠5；∠4和∠5；∠4和∠2．【分析】同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．依此即可得出答案．【解析】解：∵∠1和∠5在截线AC同侧，在被截直线BE，CE同方向所成的角；∠4和∠3，在截线CE 的上方，被截直线DB、EB的左侧，∴同位角有∠1和∠5；∠4和∠3，共2对；∵∠2和∠3在截线BD两侧，被截直线AC与CE内部；∠1和∠4在截线BE两侧，被截直线AC与CE 内部，∴内错角有∠2和∠3；∠1和∠4,共2对；∵∠3和∠5在截线CD同侧，被截直线CB与DB内部；∠4和∠5在截线CE同侧，被截直线CB与EB 的内部；∠4和∠2在截线BE同侧，被截直线DB与DE的内部，∴同旁内角有∠3和∠5；∠4和∠5；∠4和∠2，共3对.【点评】本题考查了同位角、内错角、同旁内角，三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．2．如图，找出标注角中的同位角、内错角和同旁内角．【答案】同位角有∠4与∠8、∠4与∠7、∠2与∠3；内错角有∠1与∠3、∠7与∠6、∠6与∠8；同旁内角有∠1与∠4、∠3与∠8，∠1与∠7．【分析】根据同位角：两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧，并且在第三条直线(截线)的同旁，则这样一对角叫做同位角；内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角；同旁内角：两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,结合图形进行分析即可．【解析】同位角有∠4与∠8、∠4与∠7、∠2与∠3；内错角有∠1与∠3、∠7与∠6、∠6与∠8；同旁内角有∠1与∠4、∠3与∠8，∠1与∠7．【点评】本题主要考查了三线八角,解题关键是掌握同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形．3．如图所示，指出下列各组角是哪两条直线被哪一条直线所截得的，并说出它们是什么角？1∠和2∠；2∠∠；3∠和5∠；3∠和4∠；4∠和7∠.和6∠；6∠和A【答案】答案见解析.【分析】根据同位角、内错角和同旁内角的定义进行解答即可.【解析】1∠和2∠是直线ED和直线BD被直线AB所截而产生的同位角；2∠和6∠是直线AB和直线AC被直线BD所截而产生的内错角；∠是直线AB和直线BD被直线AC所截而产生的同位角；6∠和A3∠和5∠是直线ED和直线CD被直线EC所截而产生的同旁内角；3∠和4∠是直线ED和直线BC被直线EC所截而产生的内错角；4∠和7∠是直线BE和直线BC被直线EC所截而产生的同旁内角.【点评】本题考查的是同位角、内错角和同旁内角的定义，熟知三线八角的定义是解题的关键.4．如图，∠1与∠2，∠3与∠4，分别是什么关系？分别是哪两条直线被哪一条直线所截形成的？【答案】∠1与∠2是直线AB、BC被直线AC所截形成的同位角，∠3与∠4是直线AB、AC被直线BC 所截形成的同位角．【分析】同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角．【解析】∠1与∠2是直线AB、BC被直线AC所截形成的同位角，∠3与∠4是直线AB、AC被直线BC所截形成的同位角．【点评】本题考查了同位角的定义，熟练掌握该知识点是本题解题的关键.5．下列图中∠1与∠2，∠3与∠4分别是哪两条直线被哪一条直线所截而成的？是什么角？【答案】图①，∠1与∠2是直线c、d被直线l所截而成的同位角；图②，∠1与∠2是直线AB、CD被直线BC所截而成的同位角；∠3与∠4是直线AB、CD被直线AC所截而成的内错角；图③，∠1与∠2是直线AB、CD被直线AG所截而成的同位角；∠3与∠4是直线AG、CE被直线DC所截而成的内错角；图④，∠1与∠2是直线AD、CB被直线AC所截而成的内错角；∠3与∠4是直线AB、CD被直线AC所截而成的内错角．【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角；内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角；同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角分别进行分析即可．【解析】图①，∠1与∠2是直线c、d被直线l所截而成的同位角；图②，∠1与∠2是直线AB、CD被直线BC所截而成的同位角；∠3与∠4是直线AB、CD被直线AC所截而成的内错角；图③，∠1与∠2是直线AB、CD被直线AG所截而成的同位角；∠3与∠4是直线AG、CE被直线DC所截而成的内错角；图④，∠1与∠2是直线AD、CB被直线AC所截而成的内错角；∠3与∠4是直线AB、CD被直线AC所截而成的内错角．【点评】此题主要考查了三线八角，关键是掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．6．如图，图中共有多少对同位角，多少对内错角，多少对同旁内角．【答案】有6对同位角，4对内错角，4对同旁内角.【分析】利用同位角，内错角，以及同旁内角定义判断即可得到结果．【解析】同位角一共有6对，分别是∠1和∠5，∠2和∠6，∠3和∠7，∠4和∠8，∠7和∠9，∠4和∠9；内错角一共有4对，分别是∠1和∠7，∠4和∠6，∠5和∠9，∠2和∠9；同旁内角一共有4对，分别是∠1和∠6，∠1和∠9，∠4和∠7，∠6和∠9.【点评】解答此题的关键在掌握同位角、内错角和同旁内角的概念，注意同位角在截线的同侧，在被截线的同一方向上；内错角在截线的两侧，在被截线的内侧；同旁内角在截线的同侧，在被截线的内侧．7．在图中，分别找出一个角与α配对，使两个角成为：(1)同位角；(2)内错角；(3)同旁内角，并指出是由哪条直线截另外两条直线而得．【答案】(1)∠3，(2)∠1，(3)∠2，直线EF，GH被直线AB所截得的；或(1)∠6，(2)∠5，(3)∠4，直线DC，AB被直线GH所截得的．【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,结合图形进行分析即可进行分析即可.【解析】解：解:(1)∠α和∠3是同位角,是直线EF、GH被AB所截而成;(2) ∠α和∠1是内错角,是直线EF、GH被AB所截而成;(3) ∠α和∠2是同旁内角,是直线EF、GH被AB所截而成.【点评】本题考查三种角的定义，熟悉掌握同位角，内错角，同旁内角的定义是解题关键.8．如图，试判断∠1与∠2，∠1与∠7，∠1与∠BAD，∠2与∠9，∠2与∠6，∠5与∠8各对角的位置关系．【答案】∠1与∠2是同旁内角，∠1与∠7是同位角，∠1与∠BAD是同旁内角，∠2与∠9没有特殊的位置关系，∠2与∠6是内错角，∠5与∠8是对顶角．【分析】根据同旁内角、同位角、内错角和对顶角的概念即可解答.【解析】由图可知：∠1与∠2是同旁内角.∠1与∠7是同位角.∠1与∠BAD是同旁内角.∠2与∠9没有特殊的位置关系.∠2与∠6是内错角.∠5与∠8是对顶角.【点评】本题考查的知识点是同旁内角、同位角、内错角和对顶角，解题的关键是熟练的掌握同旁内角、同位角、内错角和对顶角.9．如图所示，在标出的7个角中，与∠1是内错角、同旁内角的各有哪几个？与∠5是同位角的有哪几个？【答案】见解析【分析】由于∠1与∠4在截线l1的两旁，又夹在被截的两条直线l4与l5之间，得出它们是内错角，同理，还可找出∠1的另外一个内错角；接下来利用同位角和同旁内角的定义，分别找出∠5的同位角和∠1的同旁内角，即可使问题得解.【解析】与∠1是内错角的有∠4，∠7；与∠1是同旁内角的有∠5，∠6；与∠5是同位角的有∠7.【点评】本题考查的知识点是三线八角的问题，解题关键是熟记同位角、内错角、同旁内角的知识. 10．(1)如果把下图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？(2)如果把下图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠2呢？【答案】（1）∠1与∠2是一对内错角，∠2与∠3是一对同旁内角；（2）∠4与∠5是一对同位角，∠5与∠2是一对同旁内角【分析】根据同位角、同旁内角、内错角的定义进行判断．【解析】（1）∠1与∠2是一对内错角，∠2与∠3是一对同旁内角；（2）∠4与∠5是一对同位角，∠5与∠2是一对同旁内角.【点评】解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．11．如图所示，(1)∠BED与∠CBE是直线________，________被直线________所截形成的________角；(2)∠A与∠CED是直线________，________被直线________所截形成的________角；(3)∠CBE与∠BEC是直线________，________被直线________所截形成的________角；(4)∠AEB与∠CBE是直线________，________被直线________所截形成的________角．【答案】见解析【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角分别进行分析即可．【解析】(1)∠BED与∠CBE是直线DE，CB被直线EB所截成的内错角；(2)∠A与∠CED是直线AD，DE被直线AC所截成的同位角；(3)∠CBE与∠BEC是直线CB，CE被直线BE所截成的同旁内角；(4)∠AEB与∠CBE是直线AE，BC被直线EB所截成的内错角．【点评】本题考查的知识点是同位角，内错角，同旁内角的概念，解题关键是熟记同位角、内错角、同旁内角的位置关系．12．如图所示．①∠AED和∠ABC可看成是直线__________、__________被直线__________所截得的__________角；②∠EDB和∠DBC可看成是直线__________、__________被直线__________所截得的__________角；③∠EDC和∠C可看成是直线__________、__________被直线__________所截得的__________角．【答案】ED；BC；AB；同位；ED；BC；BD；内错；ED；BC；AC；同旁内【解析】解：（1）∠AED和∠ABC可看成是直线ED、BC被直线AB所截得的同位角；（2）∠EDB和∠DBC可看成是直线ED、BC被直线BD所截得的内错角；（3）∠EDC和∠C可看成是直线ED、BC被直线AC所截得的同旁内角．故答案为ED，BC，AB，同位；ED，BC，BD，内错；ED，BC，AC，同旁内．点评：本题考查了同位角、内错角、同旁内角．两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．13．如图：(1)找出直线DC，AC被直线BE所截形成的同旁内角；(2)指出∠DEF与∠CFE是由哪两条直线被哪一条直线所截形成的什么角；(3)试找出图中与∠DAC是同位角的所有角．【答案】(1)∠FBC和∠CFB，∠DFB和∠FBA是直线DC，AC被直线BE所截形成的同旁内角．(2)∠DEF 与∠CFE是由直线AG，DF被直线EF所截形成的内错角．(3)∠DAC的同位角：∠EBH，∠DCH，∠EDF，∠GEF.【解析】试题分析：（1）根据同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角，分别进行分析即可；（2）根据∠DEF与∠CFE的边以及位置特征即可做出判断；（3）根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角进行分析．试题解析：(1)∠FBC和∠CFB，∠DFB和∠FBA是直线DC，AC被直线BE所截形成的同旁内角；(2)∠DEF与∠CFE是由直线AG，DF被直线EF所截形成的内错角；(3)∠DAC的同位角：∠EBH，∠DCH，∠EDF，∠GEF.【点评】此题主要考查了三线八角，关键是掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．14．如图：∠1和∠4是AB、_______被_______所截得的________角，∠3和∠5是_______、_____被_______所截得的_________角，∠2和∠5是______、_______被_______所截得的________角，AC、BC被AB所截得的同旁内角是________.【答案】CD，BE，同位；AB，BC，AC，同旁内AB，CD，AC，内错；∠4和∠5【解析】试题分析：根据图形先确定出三线八角，再根据同位角、内错角和同旁内角的定义即可得出答案．试题解析：∠1和∠4是AB、CD被BE所截得的同位角，∠3和∠5是BC、AB被AC所截得的同旁内角，∠2和∠5是AB、CD被AC所截得的内错角，AC、BC被AB所截得的同旁内角是∠4和∠5.15．（1）如果把图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？（2）如果把图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠6呢？【答案】（1）∠1与∠2是内错角，∠2与∠3是同旁内角；（2）∠4与∠5是同位角，∠5与∠6是对顶角．【解析】试题分析：根据同位角、同旁内角、同位角、对顶角的定义进行判断即可．试题解析：（1）观察图形，根据内错角的定义可知∠1与∠2是内错角，根据同旁内角的定义可知∠2与∠3是同旁内角；（2）根据同位角的定义可知∠4与∠5是同位角，根据对顶角的定义可知∠5与∠6是对顶角．16．如图，BE是AB的延长线，指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？（1）∠A和∠D；（2）∠A和∠CBA；（3）∠C和∠CBE．【答案】见解析【解析】试题分析：（1）（2）同旁内角，“同旁”指在第三条直线的同侧；“内”指在被截两条直线之间．（3）内错角，“内”指在被截两条直线之间；“错”即交错，在第三条直线的两侧．（一个角在第三直线左侧，另一角在第三直线右侧）试题解析：（1）∠A和∠D是由直线AE、CD被直线AD所截形成的，它们是同旁内角；（2）∠A和∠CBA是由直线AD、BC被直线AE所截形成的，它们是同旁内角；（3）∠C和∠CBE是由直线CD、AE被直线BC所截形成的，它们是内错角．17．复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．（1）如图1，直线1l ，2l 被直线3l 所截，在这个基本图形中，形成了______对同旁内角．（2）如图2，平面内三条直线1l ，2l ，3l 两两相交，交点分别为A 、B 、C ，图中一共有______对同旁内角．（3）平面内四条直线两两相交，最多可以形成______对同旁内角．（4）平面内n 条直线两两相交，最多可以形成______对同旁内角． 【答案】（1）2；（2）6；（3）24；（4）()()12n n n --【分析】（1）根据同旁内角的概念找出所有的同旁内角，即可得出答案；（2）根据同旁内角的概念找出所有的同旁内角，即可得出答案；（3）画出四条直线两两相交的图形，然后根据同旁内角的概念找出所有的同旁内角，即可得出答案；（4）根据同旁内角的概念结合前3问的答案找出规律即可得出答案．【解析】（1）如图其中同旁内角有CAB ∠与EBA ∠，DAB ∠与ABF ∠，共2对；故答案是：2；（2）如图其中同旁内角有BAC ∠与BCA ∠，BAC ∠与ABC ∠，ABC ∠与BCA ∠，DAB ∠与ABE ∠，FBC ∠与BCI ∠，ACJ ∠与CAK ∠，共6对，6321=⨯⨯，故答案是：6；（3）如图其中的同位角有BAC ∠与BCA ∠，BAC ∠与ABC ∠，ABC ∠与BCA ∠，CAF ∠与AFE ∠，CAF ∠与ACE ∠，AFE ∠与CEF ∠，ACE ∠与CEF ∠，CED ∠与CDE ∠，CDE ∠与CDE ∠，DCE ∠与CED ∠，IBC ∠与BCD ∠，BCD ∠与CDJ ∠，KDE ∠与DEP ∠，PEF ∠与EFM ∠，AFN ∠与FAG ∠，BAG ∠与ABH ∠，BFE ∠与FBE ∠，FBE ∠与BEF ∠，DAF ∠与ADF ∠，AFD ∠与ADF ∠，IBE ∠与JEB ∠，MFD ∠与FDK ∠，HBM ∠与BFN ∠，IAD ∠与ADJ ∠共24对，24432=⨯⨯，故答案是：24；（4）根据以上规律，平面内n 条直线两两相交，最多可以形成(1)(2)n n n --对同旁内角，故答案是：()()12n n n --．【点评】本题主要结合同旁内角探索规律，掌握同旁内角的概念并找出规律是解题的关键．18．已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置1∠跳到终点位置3∠有两种不同路径，路径1：193∠−−−−→∠−−−→∠同旁内角内错角；路径2：1126103∠−−−→∠−−−→∠−−−→∠−−−−→∠内错角内错角同位角同旁内角.试一试：（1）写出从起始位置1∠跳到终点位置8∠的一种路径；（2）从起始位置1∠依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置8∠？ 【答案】（1）1128∠→∠→∠内错角同旁内角（答案不唯一）；（2）能跳到终点位置8∠.其路径为 1105118∠→∠→∠→∠→∠同位角内错角同旁内角同位角（答案不唯一）【分析】（1）根据同旁内角、内错角和同位角的定义进行选择路径即可；（2）先判断能够到达终点位置，在根据定义给出具体路径即可.【解析】（1）可以是这样的路径：1128∠→∠→∠内错角同旁内角.（答案不唯一）（2）从起始位置1∠依次按同位角内错角同旁内角的顺序跳，能跳到终点位置8∠.其路径为 1105118∠→∠→∠→∠→∠同位角内错角同旁内角同位角（答案不唯一）.【点评】本题考查的是同位角、内错角和同旁内角的定义，熟知这些角的特征是解题的关键.19．探究题：(1)如图1，两条水平的直线被一条竖直的直线所截，同位角有____对，内错角有_____对，同旁内角有_____对；(2)如图2，三条水平的直线被一条竖直的直线所截，同位角有____对，内错角有___对，同旁内角有___对；(3)根据以上探究的结果，n(n 为大于1的整数)条水平直线被一条竖直直线所截，同位角有______对，内错角有_______对，同旁内角有 对．(用含n 的式子表示)【答案】(1)4，2，2；(2)12，6，6；(3)2n (n -1)，n (n -1)，n (n -1)．【分析】根据同位角是两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角，内错角是两个角都在截线的两侧，又分别处在被截的两条直线中间的位置的角，根据同旁内角是两个角都在截线的同旁，又分别处在被截的两条直线中间的位置的角，可得答案．【解析】（1）如图1，两条水平的直线被一条竖直的直线所截，同位角有4对，内错角有2对，同旁内角有2对．故答案为：4，2，2；（2）如图2，三条水平的直线被一条竖直的直线所截，同位角有12对，内错角有6对，同旁内角有6对．故答案为：12，6，6；（3）根据以上探究的结果，n（n为大于1的整数）条水平直线被一条竖直直线所截，同位角有2n（n-1）对，内错角有n（n-1）对，同旁内角有n（n-1）对，故答案为：2n(n-1)，n(n-1)，n(n-1)．【点评】本题考查了同位角、内错角、同旁内角，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．。

同位角、内错角、同旁内角要点一、同位角、内错角、同旁内角的概念1. “三线八角”模型如图，直线AB、CD与直线EF相交(或者说两条直线AB、CD被第三条直线EF所截)，构成八个角，简称为“三线八角”，如图1.图1要点诠释：⑴两条直线AB,CD与同一条直线EF相交．⑵“三线八角”中的每个角是由截线与一条被截线相交而成．2. 同位角、内错角、同旁内角的定义在“三线八角”中，如上图1，（1）同位角：像∠1与∠5，这两个角分别在直线AB、CD的同一方，并且都在直线EF的同侧，具有这种位置关系的一对角叫做同位角.（2）内错角：像∠3与∠5，这两个角都在直线AB、CD之间，并且在直线EF的两侧，像这样的一对角叫做内错角.（3）同旁内角：像∠3和∠6都在直线AB、CD之间，并且在直线EF的同一旁，像这样的一对角叫做同旁内角.要点诠释：(1)“三线八角”是指上面四个角中的一个角与下面四个角中的一个角之间的关系，显然是没有公共顶点的两个角.(2)“三线八角”中共有4对同位角，2对内错角，2对同旁内角1.(1)图3中，∠1、∠2由直线被直线所截而成．(2)图4中，AB为截线，∠D是否属于以AB为截线的三线八角图形中的角？2.如图，(1)DE为截线,∠E与哪个角是同位角?(2)∠B与∠4是同旁内角，则截出这两个角的截线与被截线是哪些直线？(3)∠B和∠E是同位角吗?为什么?【变式】如图所示，下列说法错误的是（）A．∠1和∠3是同位角B．∠1和∠5是同位角C．∠1和∠2是同旁内角D．∠5和∠6是内错角3.如图，用数字标出的八个角中，同位角、内错角、同旁内角分别有哪些？请把它们一一写出来．4.如图∠1、∠2、∠3、∠4、∠5中，哪些是同位角？哪些是内错角？哪些是同旁内角？5.请写出图中的同位角、内错角、同旁内角．答案【答案】(1) EF，CD； AB．（2）不是．解：（1）DE为截线,∠E与∠3是同位角；（2）截出这两个角的截线是直线BC,被截线是直线BF、DE；（3）不是,因为∠B与∠E的两边中任一边没有落在同一直线上,所以∠B和∠E不是同位角. 【答案】B解：内错角：∠1与∠4，∠3与∠5，∠2与∠6，∠4与∠8；同旁内角：∠3与∠6，∠2与∠5，∠2与∠4，∠4与∠5；同位角：∠3与∠7，∠2与∠8，∠4与∠6．【答案】解：同位角：∠5与∠1，∠4与∠3；内错角：∠2与∠3，∠4与∠1；同旁内角：∠4与∠2，∠5与∠3，∠5与∠4.【答案】解：∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8是同位角；∠2与∠8，∠3与∠5是内错角；∠2与∠5，∠3与∠8是同旁内角.。

七年级数学三线八角知识点三线八角是中学数学中常见的一个知识点，也是七年级数学中必须掌握的重点内容。

在这份文章中，我们将详细介绍三线八角的定义、性质以及解题技巧。

一、定义三线八角，顾名思义，就是由三条直线和八个角所组成的图形，如图1所示。

图1其中三条直线相交于一点O，八个角分别为∠AOC、∠AOB、∠BOD、∠EOC、∠EOF、∠FOG、∠GOH和∠BOH，且每两条直线之间的夹角均相等。

二、性质1.每一对相邻的外角互补，即∠AOC+∠BOD+∠EOF+∠GOH=180°。

2.每一对相邻的内角互补，即∠AOB+∠BOH+∠EOC+∠FOG=180°。

3.相邻的外角与其对应的内角互补，即∠AOC+∠EOC=∠AOB+∠BOH=∠BOD+∠FOG=∠EOF+∠GOH =180°。

三、解题技巧对于三线八角的解题，主要是应用它的性质进行推导和运用。

以例题为例：例1 在图2中，∠AOB=30°，∠EOC=110°，则∠BOD和∠EOF的和为多少度？图2解：由三线八角的性质可知，∠AOB+∠BOH+∠EOC+∠FOG=180°。

则∠BOH+∠FOG=180°-∠AOB-∠EOC=180°-30°-110°=40°。

而∠BOD+∠EOF=（180°-∠AOC）÷2+（180°-∠EOC）÷2=(180°-∠BOH)÷2+(180°-∠FOG)÷2=80°。

因此，∠BOD和∠EOF的和为80°。

例2 在图3中，AB//CD，∠BAE=55°，∠CFE=40°，则∠BEF 为多少度？图3解：由三线八角的性质可知，∠AOC+∠EOC=∠AOB+∠BOH=∠BOD+∠FOG=∠EOF+∠GOH =180°。

三线八角教学重点和难点三线八角的意义是重点，能在各种变式的图形中找出这三类角既是重点，也是难点教学过程设计一、从学生原有的认识结构提出问题教师提问：1两条直线相交后产生了几个角?每两个角之间的关系是什么?(除平角外，产生四个角，对顶角相等，邻补角互补)2三条直线之间也可以有什么样的位置关系?(可以让学生用手中的铅笔表示直线)在学生回答的基础上，教师打出投影，(四种情况，如图2—30)(1)三条直线都没有交点(2)两条直线平行被第三条直线所截(3)三条直线两两相交，有三个交点(4)三条直线交于一点上节课是对相交的两条直线所形成的四个角进行研究，今天我们就对三条直线相交后形成的八个角如图2—30(3)进行研究，简称为：三线八角(板书课题)二、三线八角的意义1教师用谈话方式提出问题：在图2—31中，l1和l3(或l2和l3)所形成的四个角是有公共顶点的，而每两个角之间的关系从位置来分，可分为两类：对顶角和邻补角，而上面四个角和下面四个角是没有公共顶点的，那么上面的一个与下面的一个又有什么样的位置关系呢?这就是下面所要研究的问题2分析特点，形成概念(1)同位角的意义先引导学生分析∠1和∠5有什么共同特点?在学生回答的基础上，教师归纳总结出共同特点是：均在直线l3的一侧，且分别在l1和l2的上方，像这样的两个角叫作同位角请同学们指出：图中还有同位角吗?(答：∠2与∠6，∠4与∠8，∠3与∠7)(2)内错角的意义(3)同旁内角的意义(这两种角的教法类似同位角，如果学生要问∠1和∠6，∠1和∠7是什么关系，可以简单说一下，不问也不说)3变式练习，揭露概念本质属性(1)如图2—32，说出以下各对角是哪两条直线被第三条直线所截而得到的?∠1与∠2，∠2与∠4，∠2与∠3答：∠1与∠2是l2、l3被l1所截而得到的一对同旁内角∠2与∠4是直线l2、l1被l3所截而得到的同旁内角∠2与∠3是l2、l1被l3所截而得到的同位角(2)如图2—33，找出下列图中的同位角，内错角和同旁内角答：同位角有：∠2与∠3，∠4与∠7，∠4与∠8；内错角有∠1与∠3，∠6与∠8，∠6与∠7；同旁内角有∠3与∠8，∠1与∠4(3)如图2—34，指出图中∠1与∠2，∠3与∠4的关系答：∠1与∠2是内错角，∠3与∠4也是内错角4正确识别这三类角应注意的问题(1)识别这三类角首先要抓住“三条线”，即：哪两条线被哪一条直线所截(2)抓住“截线”，截线的同侧有哪些角、从中找出同位角和同旁内角，在截线的两侧找内错角三、综合应用，课堂练习1找出如图2—35中的对顶角和邻补角答：对顶角有四对：它们是∠1与∠3，∠2与∠4，∠5与∠6，∠7与∠8；邻补角有∠1与∠2，∠2与∠3，∠3与∠4，∠4与∠1，∠5与∠8，∠8与∠6，∠6与∠7，∠7与∠5(还可以找出图2—35中相等的角，即四对对顶角)2如图2—36，如果∠1=∠2=∠7，那么还有哪些角是相等的答：∠1与∠4是邻补角，∠2与∠5是邻补角，∠3与∠6是邻补角∠7与∠8是邻补角，因为∠1=∠2=∠7，∠2=∠3(对顶角相等)，所以∠1=∠2=∠3=∠7，则∠4=∠5=∠6=∠8(等角的补角相等)3如图2—37中，若∠1=∠2，证明：∠3与∠4是互补的角证明：因为∠1=∠3，(对顶角相等)∠1=∠2，(已知)所以∠2=∠3(等量代换)又因为∠2+∠4=180°所以∠3+∠4=180°(等量代换)即∠3与∠4是互补的角此题在证明的分析中，可以用以下逻辑思考的过程，即“执果索因”法若要证∠3与∠4互补，即证∠3+∠4=180°，但∠4与∠2的和为180°，因此需证∠3=∠2，由于∠3=∠1(对顶角相等)，∠1=∠2是已知，所以∠2=∠3而写出证明过程时，要从先证∠2=∠3出发，最后得到∠3+∠4=180°以上的几何证明题的思考过程是一种常见的方法，它是从要证明结果的出发，探索要得出这个结果时，应具备的条件，只要将条件准备充足，就能得到要求的结果四、小结1教师先提出以下问题：(1)在所学的知识中，直线的位置关系是怎样形成和发展的?(2)学了哪些相互关系的角?(3)寻找同位角、内错角和同旁内角关键应准确找到什么?2在学生回答的基础上，教师指出，(1)(投影)直线位置关系所对应的基本图形结构如图2—38(2)学过六咱相互关系的角①互为余角，②互为补角(邻补角是特殊情形)，③对顶角，④同位角，⑤内错角，⑥同旁内角(3)寻找同位角，同旁内角关键在于准确找到三线(两线被第三线所截)五、作业1选书中习题2以下六个题供选用(1)指出图2—39(1)中，①∠2和∠5的关系是___________；②∠3和∠5的关系是___________；③∠2和____是直线____、______被_____所截，形成的同位角；④∠1和∠4呢?∠3和∠4呢?∠6和∠7是对顶角吗?(2)指出图中2—39(2)中，①∠C和∠D的关系：②∠B和∠GEF的关系；③∠A和∠D的关系；④∠AGE和∠BGE的关系；⑤∠CFD和∠AFB的关系(3)如图2—39(3)，用数学标出的八个角中①同位角有________________；②内错角有________________；③同旁内角有_______________；(4)如图2—39(4)，若∠1=∠2，可推出∠1与∠ADE______________；∠1与∠BDE__________________(5)判断正误：如图2—39(5)，①∠1和∠B是同位角；②∠2和∠B是同位角；③∠2和∠C是内错角；④∠EAD和∠C是内错角；(6)如图2—39(6)，①∠1和∠4是同位角；②∠1和∠5是同位角；③∠2和∠7是内错角；④∠1和∠4是同旁内角；⑤∠1和∠2是同旁内角；板书设计课堂教学设计说明1本教案为1课时45分钟2上节课讨论了两条直线相交以后所形成的四个角，这一节课是进一步讨论三条直线相交后所形成的八个角，所以在教课过程，要运用基本图形结构将所学的知识及其内在联系向学生展示3在讲三线八角概念时，一定要细致地分析、顾名思义，把握住两个关键的环节，“三条线与一条线”，尽量给出变式的图形，让学生分辨清楚4这节课虽然不涉及两条直线平行后被第三条直线所截的问题，但在可能的情况下，将平行线的图形让学生见到，对下一步的学习很有好处，例如，平行四形中的内错角，学生开始接受起来有一定困难，在这一课时中，出现这个基本图形，为以后学习打下基础5在课堂练习中，用到等量代换的公理，建议教师参考小资料，将等量公理补充给学生6本课时对“执果索因”的方法进行了介绍在今后的学习中经过教师多次引导，学生就会建立正确的思维习惯。

找“三线” 识“八角“三线八角”是反映一条直线截两条直线所形成的八个角的位置关系，教材中我们分别称之为同位角、内错角、同旁内角，这条直线叫做截线，两条直线叫做被截线。

在教学中教师反复强调“同位角在截线同旁，在截线同方向；内错角在截线两旁，在被截线之间；同旁内角在截线同旁，在被截线之间。

”但是在实际学习中，学生往往张冠李戴、顾此失彼，除因概念本身牵扯到的线多角多外，笔者认为，主要在于没有找准截线和被截线。

如图，直线c截直线a、b，那么直线c叫做截线，直线a、b叫做被截线。

由定义可知，/1 与/2是同位角，/2与/3是内错角，/2与/4是同旁内角。

然而同时我们还发现，/1 和/2各有一条边都在截线c 上，另两条边分别在被截线b、c上。

/2与/3、/2与/4情况也一样。

于是我们有如下结论：两角的边所在的公共直线即为截线，两角另一边所在的直线为被截线。

下面看例题。

例1 判断图中/1与/2、/2与/3、/1与/3的位置关系？分析：/1的两条边所在的直线为直线a、b,Z2的两条边所在的直线为直线a、c,则公共直线a为截线，直线b、c为被截线。

由于/ 1、/2在直线a同旁，直线b、c右方，故/1与Z2为同旁内角，同理/2与/3为内错角，/1与/3为同旁内解：（略写）。

例2：找出图中同位角、内错角、同旁内角。

分析：图中共有4 条直线，没有说谁是截线被截线，那么任何一条都有可能作为截线。

因此，我们每3 条一组进行组合，共有①②③、①②④、①③④、②③④四组，在①②③中，所有的角都有公共顶点，故无同位角、内错角、同旁内角；在①②④中，直线BE与直线AD BC 都相交，故为BE截线，直线AD BC为被截线；在①③④中3条直线两两相交，那么每条直线均可作为截线；在②③④中，直线AC与直线AD BC都相交，故为AC截线，直线AD BC为被截线。

再根据定义即可求解。

解：①②③中，同位角、内错角、同旁内角均为0对；①②④中，同位角1对即/ EAD与/ EBC内错角0对、同旁内角1对即即/ DAB与/ABC①③④中，若BE为截线，AC BC为被截线时，同位角1对即/EAD 与/ EBC内错角0对、同旁内角1对即/ DAB与/ABC若BC为截线，AB AC为被截线时，同位角0对、内错角0 对、同旁内角1对即/ABC与/ACB若AC为截线，AB BC为被截线时，同位角0对、内错角1 对即/ EAC与/ ACB同旁内角1对即/ BAC与/ ACB②③④中，同位角0对、内错角1对即/DAC与/ACB同旁内角0对；故图中同位角2 对，内错角1 对，同旁内角4 对。

数学七年级下册三线八角一、三线八角的概念。

1. 三线。

- 在平面内，两条直线被第三条直线所截，这里的三条直线就简称为“三线”。

例如直线a、b被直线c所截，直线a、b是被截直线，直线c是截线。

2. 八角。

- 这三条直线相交形成八个角。

根据角的位置关系，可以分为同位角、内错角和同旁内角。

- 以直线a、b被直线c所截为例：- 同位角：在截线c的同侧，并且在被截直线a、b的同一方的两个角。

例如∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8都是同位角。

同位角的形状像字母“F”（可以是倒置、斜置等情况）。

- 内错角：在截线c的两侧，并且在被截直线a、b之间的两个角。

如∠3与∠5，∠4与∠6是内错角。

内错角的形状像字母“Z”（同样可以有不同的放置角度）。

- 同旁内角：在截线c的同侧，并且在被截直线a、b之间的两个角。

像∠3与∠6，∠4与∠5是同旁内角。

同旁内角的形状像字母“U”（也会有不同的摆放形式）。

二、三线八角的识别方法。

1. 先找截线。

- 在复杂的图形中，要准确识别三线八角，首先要确定哪条是截线。

截线是与另外两条直线都相交的直线。

例如在一个三角形和一条直线相交的图形中，如果我们要研究三角形的两条边与这条直线所形成的角的关系，这条直线就是截线。

2. 再根据位置确定角的类型。

- 确定截线后，观察角相对于被截直线和截线的位置。

- 如果角在截线同侧且在被截直线同一方，就是同位角；如果在截线两侧且在被截直线之间，就是内错角；如果在截线同侧且在被截直线之间，就是同旁内角。

三、三线八角的性质在解题中的应用。

1. 平行线下的三线八角性质。

- 如果两条被截直线平行（假设a∥ b，被直线c所截）：- 同位角相等，即∠1=∠5，∠2 = ∠6，∠3=∠7，∠4=∠8。

- 内错角相等，∠3=∠5，∠4=∠6。

- 同旁内角互补，∠3+∠6 = 180^∘，∠4+∠5=180^∘。

- 这些性质可以用来求解角的度数。

例如已知a∥ b，∠1 = 70^∘，求∠5的度数。