ANSYS-Maxwell-2D求解齿槽转矩、饱和电感、饱和磁链的几种方法
- 格式:pdf
- 大小:398.00 KB
- 文档页数:9



ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
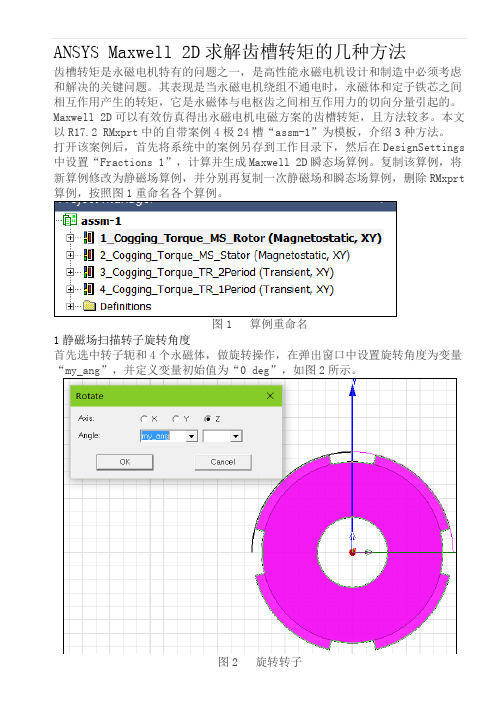
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。

11.2.2.4 LMATRIXLMATRIX宏可以计算任意线圈组中每个线圈的微分电感矩阵和总磁链。
参见《ANSYS理论手册》第5章。
LMATRIX宏用于在静磁场分析的一个“工作点”上计算任意一组导体间的微分电感矩阵和磁链。
“工作点”被定义为在系统上加工作(名义)电流所得到的解,该宏命令既可用于线性求解也可用于非线性求解。
必须用波前求解器来计算“工作点”的解。
LMATRIX宏的计算依赖于对工作点进行求解的过程中建立的多个文件。
该宏在执行求解之前在这些文件前面加一个前缀OPER来重命名文件,并在完成求解后自动保存这些文件。
用户自己也可以保存这些文件的拷贝以进行备份。
该宏命令返回一个N×N+1矩阵参数,N×N部分表示N-绕组系统的微分电感值,此处N表示系统中的线圈数。
N+1列表示总磁链。
第I行表示第I个线圈。
另外,电感矩阵的值还以文本文件的格式输出,以供外部使用。
文件中第一个列表表示每个线圈的磁链。
第二个列表表示微分电感矩阵的上三角部分。
命令:LMATRIXGUI:Main Menu>Solution>-Solve-Electromagnet>-StaticAnalysis-Induct Matrix在调用LMATRIX宏之前,还需要给线圈单元赋一个名义电流值。
对于使用磁矢势(MVP)法或基于棱边元方法进行求解的静磁分析,可以使用BFV、BFA或BFE命令来给线圈单元赋名义电流(以电流密度的方式)。
对于使用简化标势法(RSP)、差分标势法(DSP)和通用标势法(GSP)的静磁分析,可以使用SOURCE36单元的实常数来给线圈单元赋名义电流。
为了使用LMATRIX宏,必须事先用*DIM命令定义一个N阶数组,N为线圈数,数组的每行都表示一个线圈。
数组的值等于线圈在工作点时每匝的名义电流值,且电流值不能为零,当确实有零电流时,可以用一个很小的电流值来近似。
另外,还需用CM命令把每个线圈的单元组合成一个部件。

ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
AoIHKOZ。
mX01jiM。
GCQjxmD。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
PG3z2Zu。
VAY8dQ1。
Wyt3k7x。
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
pz4EOlT。
Y0US14Y。
rS3jYMp。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
W0ppFM8。
Q5qvbs7。
dgJ9Gfx。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
转矩一般有三种施加的方法:第一种,将矩转换成一对一对的力偶,直接施加在对应的节点上面.第二种,在构件中心部位建立一个节点,定义为MASS21单元,然后跟其他受力节点耦合,形成刚性区域,就是用CERIG命令.然后直接加转矩到主节点,即中心节点上面第三种,使用MPC184单元.是在构件中心部位建立一个节点,跟其他受力节点分别形成多根刚性梁,,从而形成刚性面.最后也是直接加载荷到中心节点上面,通过刚性梁来传递载荷.上面三种方法计算的结果基本一致,我做过实验的.只不过是后两种情况都是形成刚性区域,但是CERIG命令是要在小变形或者小旋转才能用,只支持静力,线形分析.而第三种方法适用多种情况,不仅支持大应变,还支持非线形情况。
前言做一个总结意义!!!原因:最近网上有较多的朋友在咨询关于实体加载的方法目的:希望这个问题不再成为大家的疑惑的一部分!!!!!!!!!!!!!!!!一、说说施加方法思路1:矩或扭矩说白了就是矩,所谓矩就是力和力臂的乘积。
施加矩可以等效为施加力;思路2:直接施加弯矩或扭矩,此时需要引入一个具有旋转自由度的节点;二、在ANSYS中实现的方法这里说说3个基本方法,当然可以使用这3个方法的组合方法,组合方法就是对3个基本方法的延伸,但原理仍不变。
方法1:引入mass21,利用cerig命令Ex1:/prep7block,0,1,0,1,0,2k,9,0.5,0.5,2.5mp,ex,1,2e10mp,prxy,1,0.2mp,prxy,1,0.3r,2,1e-6et,1,45et,2,21keyopt,2,3,0lesize,all,0.2vmesh,allksel,s,,,9type,2real,2kmesh,allallselnsel,s,loc,z,2,3NPLOTCERIG,node(0.5,0.5,2.5),ALL,ALL, , , , allsel/SOLUf,node(0.5,0.5,2.5),my,100e3FINISH/SOLnsel,s,loc,z,0d,all,allallselsolve方法2:利用mpc184单元/prep7block,0,1,0,1,0,2mp,ex,1,2e10mp,prxy,1,0.2mp,prxy,1,0.3et,2,184keyopt,2,1,1lesize,all,0.2vmesh,alln,1000,0.5,0.5,2.5type,2mat,2*do,i,1,36e,1000,36+i*enddoallselallsel/SOLUf,node(0.5,0.5,2.5),my,100e3 FINISH/SOLnsel,s,loc,z,0d,all,allallselsolve方法3:使用rbe3命令/prep7block,0,1,0,1,0,2k,9,0.5,0.5,2.5mp,ex,1,2e10mp,prxy,1,0.2mp,prxy,1,0.3r,2,1e-6et,1,45keyopt,2,3,0lesize,all,0.2vmesh,allksel,s,,,9type,2real,2kmesh,allallsel*dim,sla,array,36*do,i,1,36sla(i)=i+36*enddo*dim,sla2,array,36*do,i,1,36sla2(i)=i+36*enddoallselrbe3,node(0.5,0.5,2.5),all,sla,sla2allsel/SOLUf,node(0.5,0.5,2.5),my,100e3FINISH/SOLnsel,s,loc,z,0d,all,allallselsolve三、使用结论方法1和方法2的结果一致,方法3偏大。
ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
【杂谈Maxwell】Maxwell2D等效斜槽1 前言为了抑制振动和噪声,电机采用斜槽是一种常见的结构形式,其的仿真严格来说是一个3D问题,但由于3D仿真时间与资源的限制,采用2D的等效的方式,亦有一定的计算精度,其等效的原理如图1所示,即将轴向分成多个错位段,每段对应一个2D工程,对2D工程的结果进行相加求平均。
原斜槽示意等效斜槽示意图1在ANSYS Maxwell R17版本前,2D等效斜槽是通过对转子初始相位角进行参数化,求解多个工程,然后在后处理中进行处理完成的,在ANSYS Maxwell R17版本起,可以通过一个斜槽的设置,仅求解一个工程即可完成等效,本文对两种方法分别进行讲解。
本文以一台4极24槽永磁电机为例,电机轴向斜1个定子槽,电机的1/4模型如图2所示:图22 R17之前版本整体思路是对转子初始相位角进行参数化,然后在后处理中利用对曲线“统计”中的“平均”得到结果,具体操作如下:(1)在MotionSetup中将转子初始位置设置为一个变量(名称任意),如①所示:图3图4电机的初始角度为7.5°,这里同样将变量的初始值设置为7.5deg ,如图5所示。
图5(2)参数化变量“Ini_deg”图6如图7所示,在①中选择之前设置的初始相位角变量“Ini_deg”,在②选择添加变量的方式为是:个数,③中设置变量的初始值,④中设置变量的结束值,本文斜一个定子槽,对于24槽电机,即360/24=15°,且一般为了与不斜槽的结果做比较,保证结果的相位一直,一般是在初始转子位置角(本例为7.5°)的正负两侧选择起始值,即参数化变量的范围是:开始:(7.5-360/15/2)=0°结束:(7.5+360/15/2)=15°⑤是变量的个数,一般设置为7个或以上就能保证等效的精度,这里设置为7,然后点⑥(这里为了演示,起始之前已经添加好了变量,故Add为灰色,首次添加,Add不是灰的),然后点击⑦图7(3)求解,如图8所示。
齿槽转矩、
一、问题描述
1.齿槽转矩T cog :当永产生的转矩即为T cog ,它是
是永磁电机特有的问题之关键问题。
2.饱和电感:绕组存在导致绕组电感变化。
考虑高电机模型精度有重要意
3.饱和磁链:绕组交链存在饱和现象。
二、基于Maxwell 2d 的求Maxwell 2D 可以有效对于求Tcog,方法很多为模板,介绍3种方法。
打开该案例后,首先Settings 中设置“Fract 算例,将新算例的类型修例,删除RMxprt 算例,按
1.静磁场扫描转子旋转角首先,选中转子轭和4在弹出窗口中将旋转角度弹出的窗口中,定义变量磁链等随电流变化的规律
ANSYS Maxwell 求解
、饱和电感、饱和磁链
永磁电机绕组不通电时,永磁体和定子是永磁体与电枢齿之间相互作用力的之一,是高性能永磁电机设计和制造中在电感,当电机负载不同时,铁心的虑不同负载电流、不同转子角度下的绕意义。
链有磁链,跟电感一样,磁链也受电流求解T cog 的方法
仿真得出永磁电机电磁方案的齿槽转多。
本文以R17.2 RMxprt 中的自带案例
先将系统中的案例另存到工作目录ions 1”,计算并生成Maxwell 2D 修改为静磁场算例,并分别再复制一按照图1重命名各个算例。
图1 算例重命名
角度的方法
个永磁体,做旋转操作(选菜单Edit 度设置为一个新变量“my_ang”(如图量“my_ang”的初值为“0 deg”。
律,则类似地在输入电流的地方,将电链的方法
子铁芯之间相互作用
的切向分量引起的。
T cog 中必须考虑和解决的的磁饱程度会有差异,绕组电感变化,对提流、转子角度的影响,转矩、电感、磁链。
例4极24槽“assm-1”录下,然后在Design 瞬态场算例。
复制该一次静磁场和瞬态场算
t->Arrange->Rotate),图2),并确定;在新(如要求转矩、电感、电流定义为新变量。
)
图2 旋转转子
然后,选中模型中的“Band”区域,选菜单“Maxwell2D->Parameters->Assign-> Torque” 中,定义求解转矩(如要求电感或磁链,则选“…->Matrix…”,另外在此前还要先定义有电流的区域“Excitations->Assign Current”),如图3所示。
图3 定以转矩求解
再在“Analysis”中,添加1个“Setup”,设置迭代精度误差为0.1%。
最后,在“Optimetrics”中选“Add->Optimetric…->Sweep Definitions->Add”,选中变量“my_ang”,设定为线性步长、扫描范围[0 deg ,20 deg]、步长0.2 deg,如图4所示。
(如要求随电流变化的规律,则选定电流变量来进行扫描。
)
图4 Optimetrics扫描范围设置
设置完成后即可求解,然后,在菜单“Maxwell 2D->Results->Create Magnetostatic Report->Rectangular Report”中(静磁场分析报告),查看结果(如图5)。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
(如果是电感或磁链,则默认为1匝,最后要根据实际匝数,对结果进行修正。
)
图5 结果调用界面
重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线
值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
而实际工程中常常会遇到平行充磁的电机,对于平行充磁最常用的处理方式是建立参考坐标系,永磁体的充磁方向参考特定参考坐标系的X轴正方向。
而在上述操作中,参考坐标系无法跟随转子旋转,使用本方法分析平行充磁时的结果将是错误的,因此可以利用第2种方法分析齿槽转矩。
2.静磁场扫描定子旋转角度的方法
打开“2_Cogging_Torque_MS_Stator”算例,首先选择“Stator”和所有的线圈,做旋转操作,设置旋转角度为新变量“my_Stator_ang”,变量初始值为“0 deg”,如图7所示。
图7 旋转定子
按照算例“1_Cogging_Torque_MS_Rotor”的方法,设置“Torque1”和“Setup1”,在“Optimetrics”中设置图8所示扫描范围。
图8 Optimetrics扫描范围设置
求解完成后,查看齿槽转矩结果,如图9、10所示。
图9 齿槽转矩调用界面
图10 扫描转子旋转角度所得齿槽转矩曲线
本方法中,永磁体不旋转,因此充磁方向不改变,分析结果对于任意方式定义的充磁方向均有效。
3.瞬态场求解空载低速旋转转矩多周期仿真的方法
3.1 多周期仿真
打开瞬态场算例“3_Cogging_Torque_TR_2Period”,首先修改模型转速为“1 deg_per_sec”,初始角修改为“-20 deg”,然后在网格划分中设置合理划分规则,再将“Excitations”删除(右键Delete All)(求电感、磁链时不能删!),将求解设置修改为图11所示。
图11 求解设置
本算例中求解2个以上周期,在前面一半时间以“1s”为仿真步长,快速达到稳定;后面一半时间以“0.2s”为仿真步长,得到较高精度。
结果如图12所示。
图12 2周期瞬态场齿槽转矩仿真结果
3.2 单周期仿真
打开瞬态场算例“4_Cogging_Torque_TR_1Period”,设置初始角为“0 deg”,转速为“1deg_per_sec”,求解设置如图13所示
图13 1周期求解设置
本算例求解时长包含1个齿槽转矩周期,结果如图14所示。
图14 1周期瞬态场齿槽转矩仿真结果
4.结果分析
4.1 静磁场仿真结果对比
将静磁场仿真结果导出,并做简单的数据编辑后,导入到同一个结果窗口下,如图15所示,二者结果吻合度较高。
图15 静磁场仿真结果对比
4.2 瞬态场仿真结果对比
将瞬态场仿真结果导出,并做简单的数据编辑后,导入到同一个结果窗口下,如图16所示,2条曲线完全重合。
图16 瞬态场仿真结果对比
4.3 静磁场和瞬态场仿真结果对比
将4个仿真结果完全导入到同一个结果窗口,瞬态场和静磁场结果趋势基本相同,有较小误差。
图17 静磁场和瞬态场仿真结果对比
三、总结
在上述的静磁场计算中,每一步计算都要重新迭代网格,速度较慢,并且需要Optimetrics License支持。
静磁场求解的对象模型默认长度是1m,在后处理中需要做特殊处理。
平行充磁和径向充磁需要区别对待。
而瞬态场的1个周期和2个周期的计算结果相同;另外测试过,转速1deg/sec 和1min/sec的计算结果相同;计算中网格只需要划分一次,且不需要Optimetrics License支持。
四、注意
(1)结果对比的方法是,先将各个结果文件(图形)的数据导出为*.csv文件(可用Excel打开、编辑、做对比曲线),然后修改题头和数值单位,并导入到同一个结果显示窗口中,直接对比。
(2)要求电感、磁链的话:
(a)对于静磁场法,先要添加激励电流(Excitations-> Assign Current),再添加参数矩阵(Parameters->Matrix),所得结果需要进行匝数、串联连接等情况进行校正;
(b)对于瞬态场法,要添加激励线圈(Excitations->Assign Coil)及其匝数,所得结果要根据线圈串联情况进行校正。