六年级趣味数学竞赛

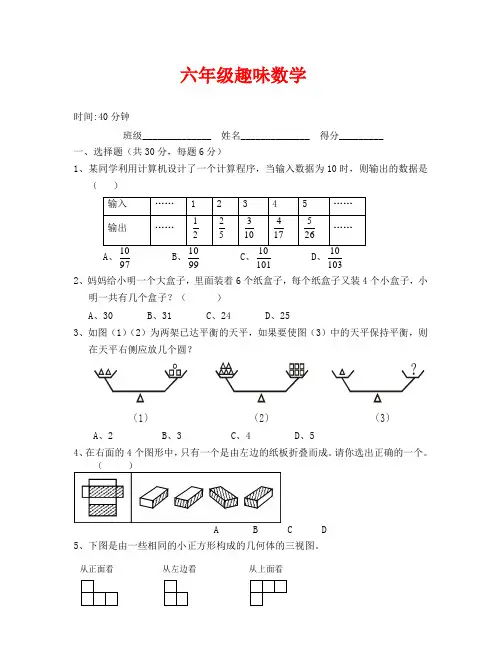
六年级趣味数学时间:40分钟班级______________ 姓名______________ 得分_________一、选择题（共30分，每题6分）1、某同学利用计算机设计了一个计算程序，当输入数据为10时，则输出的数据是（ ） 输入 …… 1 2 3 45 …… 输出…… 21 52 103 174 265 …… A 、97 B 、99 C 、101D 、103 2、妈妈给小明一个大盒子，里面装着6个纸盒子，每个纸盒子又装4个小盒子，小明一共有几个盒子？（ ）A 、30B 、31C 、24D 、253、如图（1）（2）为两架已达平衡的天平，如果要使图（3）中的天平保持平衡，则在天平右侧应放几个圆？？（1）（2）（3）A 、2B 、3C 、4D 、5 4、在右面的4个图形中，只有一个是由左边的纸板折叠而成。

请你选出正确的一个。

（ ）A B C D5、下图是由一些相同的小正方形构成的几何体的三视图。

从左边看 从上面看从正面看有几个正方形（）A、4B、5C、 6D、7二、填空题：（共30分，每题6分）1、直线上有A、B、C、D、E、F、G七个点，则以这些点为端点的线段共有条.2.有27个人到商场去买水喝,遇到商场搞促销,三个空瓶子就可以换一瓶水,问:27个人 ,最少只买_______瓶水,使每个人都有一瓶水喝.3.食堂猛增一群人，炊具只能合伙用。

每人可用一饭碗，菜碗只能两人用。

三人合用一汤碗，55只碗正够分。

请你帮助算一算,共来_________新客人？4．王老太上集市上去卖鸡蛋，第一个人买走蓝子里鸡蛋的一半又一个，第二个人买走剩下鸡蛋的一半又一个，这时蓝子里还剩一个鸡蛋，请问王老太共卖出________个鸡蛋.5、按规律填空: 1，1，2，3，5，8，13，21，（），（）三、解答题（每题8分，共16分）1、井深8米,一只青蛙从井底往上跳,每次跳3米,又滑下2米,那么它要跳几次才能到达井口.(请说明理由)2．三个箱子分别涂有红、黄、蓝三色。

7623222423小学高年级趣味数学竞赛（六年级上册）卷满分：100分 时间：40分钟 班级： 姓名： 成绩：一、智力乐园。

（每空5分，共25分）1.如果x ×145=y ×1514=1，那么5x －2y=（ 1176 ）。

2.有一个分数，分子加5可化简为32，分子减5可化简为187，这个分数是（ ）。

3.一台抽油烟机原价1000元。

降价101后，再涨价101，这台抽油烟机的现价是（990）元。

如果是先涨价101，再降价101，现价是（990）元。

4.一个分数的分子是互为倒数的两个数的积，分母是20以内所有质数的和，这个分数是（771）。

二、计算小英才。

（每小题5分，共25分）21＋61＋121＋201＋301＋421 18 ÷67+6×71+716÷6130(1+21) ×（1+31）×（1+41）×……×（1+71）×（1+81）×（1+91）522÷222 12006×2007＋12007×2008()2006×2008×803三、培优天地。

（每小题10分，共50分）1.有甲、乙两个书架，甲书架有书300本，若把甲书架书的61放到乙书架，则甲、乙两个书架的书的本数相等。

乙书架原来有书多少本？200本2.小马虎将一个数除以5看成是乘5，计算后的结果是1615，正确的答案应该是多少？3.一桶油，连桶共重76千克，用去32的油以后，连桶共重26千克。

原来桶中的油有多少千克？75千克4.实验小学六年级三个班共收集废纸276千克，其中六年一班收集的比六年二班少41，六年二班和六年三班收集废纸的比是8∶9。

三个班各收集废纸多少千克？六一 72千克 六二 96千克 六三108千克5.加工一批零件，每小时加工60个，5小时后还剩下零件总数的52未加工，这批零件共有多少个？ 500个。

第30页/共42页
在广阔的草地上，有一 头牛在吃草。这头牛一年 才吃了草地上一半的草。 问，它要把草地上的草全 部吃光，需要几年？
第31页/共42页
用外观一模一样的钥 匙试开１０把锁，最多 试多少次，就可以分辨 出哪把钥匙配哪把锁的?
第32页/共42页
有一个三位数，在四百 到五百之间，个位数比百 位数大３，十位数比个位 数小５，请问这个三位数 是多少？
第10页/共42页
4.需要多少个五角星才能使天平C保持平衡？
第11页/共42页
5.请唱两首含有数字的 歌曲（中，英文各一首 ）
第12页/共42页
6.一个流浪汉特别喜欢抽烟， 他经常利用捡来的5个烟头的烟 丝卷成一支香烟来抽。今天他拾 了了25个烟头，那么他可以做成 多少支香烟？
第13页/共42页
5 36
第4页/共42页
4.有三个不同的数， 它们的和与它们的积一 样大，这三个数分别是 多少？
第5页/共42页
5.请一笔画出下面图形.
第6页/共42页
6. 请背一一两首含有一九 数字的古一 诗 五
一
四
一
三
第7页/共42页
1.有12粒扣子，要摆成 每边4粒的一个正方形，请 问怎么摆？（在黑板上动 手演示）
第20页/共42页
第21页/共42页
第二环节抢答题
比赛规则是：抢答题要求在主持人念 完题目，宣布“开始”后再进行抢答， 主持人没念完题，抢答的，视为犯规， 扣除相应的分数。争到抢答权的各组 必须在20秒内作答，答题中间隔时超 过20秒视为无法继续回答。各队回答 时必须由一名选手回答，其他选手可 以补充作答，答对一题加10分，答错 或不完整扣10分。
第一环节必答题

返回
15.( 20分)用一根120厘米长的铁丝 围成一个长方体框架，长、宽、 高的比是3:2:1 ，这个长方体的体 积是多少立方厘米
750立方厘米
返回
16.（30分）一个两位数,在它 的前面写上3,所组成的三位数 比原两位数的7倍多24,求原来 的两位数。
46
返回
17.（30分）师徒俩人加工同样多的 零件。当师傅完成了1/2时，徒弟完 成了120个。当师傅完成了任务时， 徒弟完成了 4/5，这批零件共有多 少个
1.2一个数乘以真分数，积小于这
个数。（√ ）
2.2半径２ｃｍ的圆，周长和面积
相等。（×）
3.2一根1米长的绳子，用去它的
1/2 和用去1/2 米，剩下的一样长。
（√ ）
4.2面积相等的两个圆，它们的半
径一定相等。（√ ）
5.2 如果a ：b=3 ：5，那么a=3，
b=5。（×）
6.2 从学校走到电影院，小明用8 分钟，小红用10分钟，小明和小
每人得奖金（340）数
与总脚数之比为2 ：5，那么鸡和兔
D 的头数之比为(
)
A 2 ：5 C 3 ：1
B 1 ：3 D 1 ：1
返回
3.（20分）一位老爷爷说:把我 的年龄加上12，再用4除，然后 减去15，再乘以10，恰好是100 岁。这位老爷爷现在多少岁
5.3 1/4 除以4的倒数，结果是 （ 1 ）。
6.3 甲数是乙数的5/7 ，甲数比乙 数少（ 2/7）.
1.4 某班8名同学，每两名同学 之间都要握一次手，总共需要 握几次手（ 28）次
2.4 甲数的1/3 等于乙数的 1/4， 甲数（ 小于 ）乙数。
3.4 甲数比乙数多1/5，甲数和乙 数的比是（6） ：（5）。

+
六年级趣味竞赛试题
1、你能用直角三角板或直尺找出一个圆的圆心吗？简要地写出你的解决问题的想法或在图中画出你的思路。

(一种方法得5分)
2、找规律填得数。

9×6=54、99×96=9504、999×996=995004、……、那么
99999×99996=（）。

(10分)
3、请你将1、2、3、
4、
5、
6、
7、
8、9这九个不同的数字全部填入下面的方框中，使等式成立。

(10分)
÷÷
4、一块空地上堆放了216块砖（如图3），这个砖堆有两面靠墙。

现在把这个砖堆的表面涂满石灰，被涂上石灰的砖共有____块。

(10分)
5、请你用5个4和恰当的运算符号及括号组成一道算式，使其结果等于24。

这个算式是（ ）。

(10分)
6、一个半圆的周长是51.4厘米，这个半圆的面积是多少平方厘米？（圆周率取3.14）(10分)
7、将一个数乘以5。

所得的乘积减去积的31
后，再除以10，然后依次加上原数的21、31、41
，最后得68，求这个数？(20分)
8、如果ａ*ｂ的含义表示为：ａ×ｂ－ａ＋ｂ。

那么，8＊（6＊4）＊2＝？。

(20分)。

小学人教版六年级趣味数学竞赛试题图文百度文库一、拓展提优试题1．A、B、C、D四个箱子中分别装有一些小球，现将A箱中的部分小球按如下要求转移到其他三个箱子中：该箱中原有几个小球，就再放入几个小球，此后，按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中，此时，四个箱子都各有16个小球，那么开始时装有小球最多的是箱，其中装有小球个．2．某工程队修建一条铁路隧道，当完成任务的时，工程队采用新设备，使修建速度提高了20%，同时为了保养新设备，每天工作时间缩短为原来的，结果，前后共用185天完工，由以上条件可推知，如果不采用新设备，完工共需天．3．王涛将连续的自然数1，2，3，…逐个相加，一直加到某个自然数为止，由于计算时漏加了一个自然数而得到错误的结果2012．那么，他漏加的自然数是．4．李华在买某一商品的时候，将单价中的某一数字“7”错看成了“1”，准备付款189元，实际应付147元，已知商品的单价及购买的数量都是整数，则这种商品的实际单价是元，李华共买了件．5．如图，已知AB＝40cm，图中的曲线是由半径不同的三种半圆弧平滑连接而成，那么阴影部分的面积是cm2．（π取3.14）6．如图，六边形ABCDEF的周长是16厘米，六个角都是120°，若AB＝BC ＝CD＝3厘米，则EF＝厘米．7．如图是甲乙丙三人单独完成某项工程所需天数的统计图，根据图中信息计算，若甲先做2天，接着乙丙两人合作了4天，最后余下的工程由丙1人完成，则完成这项工程共用天．8．在救灾捐款中，某公司有的人各捐200元，有的人各捐100元，其余人各捐50元．该公司人均捐款元．9．甲挖一条水渠，第一天挖了水渠总长度的，第二天挖了剩下水渠长度的，第三天挖了未挖水渠长度的，第四天挖完剩下的100米水渠．那么，这条水渠长米．10．已知A是B的，B是C的，若A+C＝55，则A＝．11．等腰△ABC中，有两个内角的度数比是1：2，则△ABC的内角中，角度最大可以是度．12．能被5和6整除，并且数字中至少有一个6的三位数有个．13．a，b，c是三个互不相等的自然数，且a+b+c＝48，那么a，b，c的乘积最大是．14．甲、乙两人分别从A、B两地同时出发，相向而行，在C点相遇，若在出发时，甲将速度提高，乙将速度每小时提高10千米，二人依然在C点相遇，则乙原来每小时行千米．15．如图，将1个大长方形分成了9个小长方形，其中位于角上的3个小长方形的面积分别为9，15和12，由第4个角上的小长方形的面积等于．【参考答案】一、拓展提优试题1．解：根据最后四个箱子都各有16个小球，所以小球总数为16×4＝64个，最后一次分配达到的效果是，从D中拿出一些小球，使A、B、C中的小球数翻倍，则最后一次分配前，A、B、C中各有小球16÷2＝8个，由于小球的转移不改变总数，所以最后一次分配前，D中有小球64﹣8﹣8﹣8＝40个；于是得到D被分配前的情况：A8，B8，C8，D40；倒数第二次分配达到的效果是，从C中拿出一些小球，使A、B、D中的小球数翻倍，则倒数第二次分配前，A、B中各有小球8÷2＝4个，D中有40÷2＝20个，总数不变，所以最后一次分配前，C中有小球64﹣4﹣4﹣20＝36个，于是得到C被分配前的情况：A4，B4，C36，D20，同样的道理，在B被分配前，A中有小球4÷2＝2个，C中有小球36÷2＝18个，D中有小球20÷2＝10个，B中有小球64﹣2﹣18﹣10＝34个，即B被分配前的情况：A2，B34，C18，D10；再推导一次，在A被分配前，B中有小球34÷2＝17个，C中有小球18÷2＝9个，D中有小球10÷2＝5个，B中有小球64﹣17﹣9﹣5＝33个，即A被分配前的情况：A33，B17，C9，D5；而A被分配前的情况，就是一开始的情况，所以一开始，A箱子装有最多的小球，数量为33个；答：开始时装有小球最多的是A箱，其中装有33小球个；故答案为：A，33．2．解：设计划用x天完成任务，那么原计划每天的工作效率是，提高后每天的工作效率是×（1+20%）＝×＝，前面完成工程的所用时间是天，提高工作效率后所用的实际是（185﹣）×天，所以，+（185﹣）××＝1，+（185﹣）××﹣＝1﹣，（185﹣）××＝，（185﹣）×÷＝÷，185﹣+＝x+，x÷＝185÷，x＝180，答：工程队原计划180天完成任务．故答案为：180．3．解：设这个等差数列和共有n项，则末项也应为n，这个等差数列的和为：（1+n）n÷2＝；经代入数值试算可知：当n＝62时，数列和＝1953，当n＝63时，数列和＝2016，可得：1953＜2012＜2016，所以这个数列共有63项，少加的数为：2016﹣2012＝4．故答案为：4．4．解：189＝3×3×3×7＝27×7147＝3×7×7＝21×7正好是27×7＝189中把27看成21×7＝147所以这种商品的实际单价是21元，卖了7件．故答案为：21，7．5．解：40÷2＝20（厘米）20÷2＝10（厘米）3.14×202﹣3.14×102÷2×4＝1256﹣628＝628（平方厘米）答：阴影部分的面积是628平方厘米．故答案为：628．6．解：如图延长并反向延长AF，BC，DE，分别相交与点G、H、N，因六边形ABCDEF的每个角是120°所以∠G＝∠H＝∠N＝60°所以△GHN，△GAB，△HCD，△EFN都是等边三角形AB＝BC＝CD＝3厘米，△GHN边长是3+3+3＝9（厘米）AN＝9﹣3＝6（厘米）AN＝AF+EFDE＝六边形ABCDEF的周长﹣AB﹣BC﹣CD﹣（AF+EF）＝16﹣3﹣3﹣3﹣6＝1（厘米）EF＝EN＝9﹣3﹣1＝5（厘米）答：EF＝5厘米．故答案为：5．7．解：依题意可知：甲乙丙的工作效率分别为：，，；甲乙工作总量为：×2+×4＝；丙的工作天数为：（1﹣）＝3（天）；共工作2+4+3＝9故答案为：98．解：捐50元人数的分率为：1﹣＝，（200×+100×+50×）÷1＝（20+75+7.5）÷1＝102.5（元）答：该公司人均捐款102.5元．故答案为：102.5．9．解：把这条水渠总长度看作单位“1”，则第一天挖的分率为，第二天挖的分率（1﹣）×＝，第三天挖的分率为（1﹣）×＝，100÷（（1﹣﹣﹣）＝100÷＝350（米）答：这条水渠长350米．故答案为：350．10．解：A是C的×＝，即A＝C，A+C＝55，则：C+C＝55C＝55C＝55÷C＝40A＝40×＝15故答案为：15．11．解：180°×＝180°×＝90°答：角度最大可以是 90度．故答案为：90．12．解：根据分析，分解质因数6＝2×3∴这个三位数能同时被2、3、5整除，而且数字中至少含有一个6∴这个三位数的个位数必须为偶数或0，因被5整除的数个位数必须是0或5，故个位数为0，设此三位数为，按题意a、b中至少有一个数字为6，①a＝6时，则6+b+0 是3的倍数，则b＝0，3，6，9，符合的三位数为：600、630、660、690②b＝6时，则6+a+0 是3的倍数，则a＝3，6，9，符合的三位数为：360、660、960综上所述，符合题意的三位数为：360、660、960、600、630、690故答案为：6．13．解：48÷3＝16，16﹣1＝15，16+1＝17，所以，a，b，c的乘积最大是：15×16×17＝4080．故答案为：4080．14．解：依题意可知：根据甲乙两人的相遇点相同，那么他们的速度比例是不变的．当甲提高时，乙也同样需要提高，而乙提高的是每小时10千米．即10÷＝40千米/小时．故答案为：4015．解：如图，设D的面积为x，9：12＝15：x9x＝12×15x＝x＝20答：第4个角上的小长方形的面积等于20．故答案为：20．。

最新小学六年级下册数学趣味数学竞赛试题图文百度文库一、拓展提优试题1．如图是根据鸡蛋的三个组成部分的质量绘制的扇形统计图，由图可知，蛋壳重量占鸡蛋重量的%，一枚重60克的鸡蛋中，最接近32克的组成部分是．2．从12点开始，经过分钟，时针与分针第一次成90°角；12点之后，时针与分针第二次成90°角的时刻是．3．把一个自然数分解质因数，若所有质因数每个数位上的数字的和等于原数每个数位上的数字的和，则称这样的数为“史密斯书数”如：27＝3×3×3.3+3+3＝2+7，即27是史密斯数，那么，在4，32，58，65，94中，史密斯数有个．4．若A、B、C三种文具分别有38个，78和128个，将每种文具都平均分给学生，分完后剩下2个A，6个B，20个C，则学生最多有人．5．22012的个位数字是．（其中，2n表示n个2相乘）6．若算式（□+121×3.125）÷121的值约等于3.38，则□中应填入的自然数是．7．如图所示的“鱼”形图案中共有个三角形．8．若将算式9×8×7×6×5×4×3×2×1中的一些“×”改成“÷”使得最后的计算结果还是自然数，记为N，则N最小是．9．如图，六边形ABCDEF的周长是16厘米，六个角都是120°，若AB＝BC ＝CD＝3厘米，则EF＝厘米．10．某日是台风天气，雨一直均匀地下着，在雨地里放一个如图1所示的长方体容器，此容器装满雨水需要1小时．请问：雨水要下满如图2所示的三个不同的容器，各需要多长时间？11．甲、乙两人分别从A、B两地同时出发，相向而行．甲、乙的速度比是5：3．两人相遇后继续行进，甲到达B地，乙到达A地后都立即沿原路返回．若两人第二次相遇的地点距第一次相遇的地点50千米，则A、B两地相距千米．12．等腰△ABC中，有两个内角的度数比是1：2，则△ABC的内角中，角度最大可以是度．13．已知x是最简真分数，若它的分子加a，化简得；若它的分母加a，化简得，则x＝．14．小丽做一份希望杯练习题，第一小时做完了全部的，第二小时做完了余下的，第三小时做完了余下的，这时，余下24道题没有做，则这份练习题共有道．15．如图，将1个大长方形分成了9个小长方形，其中位于角上的3个小长方形的面积分别为9，15和12，由第4个角上的小长方形的面积等于．【参考答案】一、拓展提优试题1．解：（1）1﹣32%﹣53%，＝1﹣85%，＝15%；答：蛋壳重量占鸡蛋重量的15%．（2）蛋黄重量：60×32%＝19.2（克），蛋白重量：60×53%＝31.8（克），蛋壳重量：60×15%＝9（克），所以最接近32克的组成部分是蛋白．答：最接近32克的组成部分是蛋白．故答案为：15，蛋白．2．解：分针每分钟走的度数是：360÷60＝6（度），时针每分钟走的度数是：6×5÷60＝0.5（度），第一成直角用的时间是：90÷（6﹣0.5），＝90÷5.5，＝16（分钟），第二次成直角用的时间是：270÷（6﹣0.5），＝270÷5.5，＝49（分钟）．这时的时刻是：12时+49分＝12时49分．故答案为：16，12时49分．3．解：4＝2×2，2+2＝4，所以4是史密斯数；32＝2×2×2×2×2；2+2+2+2+2＝10，而3+2＝5；10≠5，32不是史密斯数；58＝2×29，2+2+9＝13＝13；所以58是史密斯数；65＝5×13；5+1+3＝9；6+5＝11；9≠11，65不是史密斯数；94＝2×472+4+7＝13＝9+4；所以94是史密斯数．史密斯数有4，58，94一共是3个．故答案为：3．4．解：38﹣2＝36（个）78﹣6＝72（个）128﹣20＝108（个）36、48和108的最大公约数是36，所以学生最多有36人．故答案为：36．5．解：2012÷4＝503；没有余数，说明22012的个位数字是6．故答案为：6．6．解：令□＝x，那么：（x+121×3.125）÷121，＝（x+121×3.125）×，＝x+121×3.125×，＝x+3.125；x+3.125≈3.38，x≈0.255，0.255×121＝30.855；x＝30时，x＝×30≈0.248；x＝31时，x＝×31≈0.255；当x＝31时，运算的结果是3.38．故答案为：31．7．解：由一个三角形组成：14个；由两个三角形组成：8个；由三个三角形组成：8个；由四个三角形组成：4个；由六个三角形组成：1个；总共：14+8+8+4+1＝35个．故共有35个三角形．故答案为：35．8．解：根据分析，先分解质因数9＝3×3，8＝2×2×2，6＝2×3，故有：9×8×7×6×5×4×3×2×1＝（3×3）×（2×2×2）×7×（3×2）×5×（2×2）×3×2×1，所以可变换为：9×8×7÷6×5÷4÷3×2×1＝70，此时N最小，为70，故答案是：70．9．解：如图延长并反向延长AF，BC，DE，分别相交与点G、H、N，因六边形ABCDEF的每个角是120°所以∠G＝∠H＝∠N＝60°所以△GHN，△GAB，△HCD，△EFN都是等边三角形AB＝BC＝CD＝3厘米，△GHN边长是3+3+3＝9（厘米）AN＝9﹣3＝6（厘米）AN＝AF+EFDE＝六边形ABCDEF的周长﹣AB﹣BC﹣CD﹣（AF+EF）＝16﹣3﹣3﹣3﹣6＝1（厘米）EF＝EN＝9﹣3﹣1＝5（厘米）答：EF＝5厘米．故答案为：5．10．解：图1所示的长方体容器的容积：10×10×30＝3000（立方厘米）接水口的面积为：10×30＝300（平方厘米）接水口每平方厘米每小时可接水：3000÷300÷1＝10（立方厘米）所以，图①需要：10×10×30÷（10×10×10）＝3（小时）图②需要：（10×10×20+10×10×10）÷（10×10×20）＝1.5（小时）图③需要：2÷2＝1（厘米）3.14×1×1×20÷（3.14×1×10）＝2（小时）答：容器①需要3小时，容器②需要1.5小时，容器③需要2小时．11．解：因为，甲乙的速度比为 5：3；总路程是：5+3＝8；第一次相遇时，两人一共行了AB两地的距离，其中甲行了全程的，相遇地点离A地的距离为AB两地距离的，第二次相遇时，两人一共行了AB两地距离的3倍，则甲行了全程的＝，相遇地点离A地的距离为AB两地距离的2﹣＝，所以，AB两地的距离为：50÷（）＝50÷＝100（千米）答：A、B两地相距100千米．故答案为：100．12．解：180°×＝180°×＝90°答：角度最大可以是 90度．故答案为：90．13．解：设原来的分数x是，则：＝则：b＝3（c+a）＝3c+3a①＝则：4c＝a+b②①代入②可得：4c＝a+3c+3a4c＝4a+3c则：c＝4a③③代入①可得：b＝3c+3a＝3×4a+3a＝15a所以＝＝即x＝．故答案为：．14．解：24÷（1﹣）÷（1﹣）÷（1﹣）＝24÷＝60（道）答：这份练习题共有 60道．故答案为：60．15．解：如图，设D的面积为x，9：12＝15：x9x＝12×15x＝x＝20答：第4个角上的小长方形的面积等于20．故答案为：20．。

抢答题
抢答题
答题要求：
1、每名同学看题之后均可抢答,但 一人不能连续作答。 2、每道题10分，答对加10分，答 错
不扣分。
按照规律填空:
1,1,2,3,5,8,13,21,( ) •按照规律填空:
一根绳子对折2次， 然后从中间剪断，共 剪成几段？
猜数学成语：
3333333…55555555…
22棵
棵2222
返回
13、一来就干（打数学数字）
十
棵2222
返回
14、已知○+△=12，△ +△+
○=15.那么○=? △=?
○=9 △=3
棵2222
返回
15、灭火 （打一数字）
一
返回
16、已知r=3cm,那么这个 半圆的周长和半圆的 弧长相差多少？
6cm
返回
加分题
简便计算： 990+994+998+1002+1006+1010（30分）
数线上哪个点最适合用来表示630?（ ） A 点W B 点Y C 点X D 点Z
有4位小朋友暑假互相通 一次电话，他们一共打了 多少（ ）次电话。
风险题
风险题
1、风险题共16题，已选题别组不能 再选。
2、每道20分，答对加20分，答错 扣20分。
3、每组限选2题。
风险题选题 16
12 3 45 6 7 8 9 10 11 12 13 14 15
1 1 1 （50分） 1 4 4 7 7 11
结束
1、一条公路，甲单独走要8小时， 乙单独要10小时，甲比乙快（ ）%。
32450
返回
2、一张方形的桌子，截去 一个角还剩几个角？

北师大版最新小学人教版六年级趣味数学竞赛试题一、拓展提优试题1．有一口无水的井，用一根绳子测井的深度，将绳对折后垂到井底，绳子的一端高出井口9m；将绳子三折后垂到井底，绳子的一端高出井口2m，则绳长米，井深米．2．（15分）欢欢、乐乐、洋洋参加希望之星决赛，有200位评委为他们投了票，每位评委只投一票．如果欢欢与乐乐所得票数的比是3：2，乐乐与洋洋所得票数的比是6：5，那么欢欢、乐乐、洋洋各得多少票？3．对任意两个数x，y，定义新的运算*为：（其中m是一个确定的数）．如果，那么m＝，2*6＝．4．早晨7点10分，妈妈叫醒小明，让他起床，可小明从镜子中看到的时刻还没有到起床的时刻，他对妈妈说：“还早呢！”小明误以为当时是点分．5．如图所示的“鱼”形图案中共有个三角形．6．甲、乙、丙三人去郊游，甲买了9根火腿，乙买了6个面包，丙买了3瓶矿泉水，乙花的钱是甲的，丙花的钱是乙的，丙根据每人所花钱的多少拿出9元钱分给甲和乙，其中，分给甲元，分给乙元．7．如图，一只玩具蚂蚁从O点出发爬行，设定第n次时，它先向右爬行n个单位，再向上爬行n个单位，达到点A n，然后从点A n出发继续爬行，若点O记为（0，0），点A1记为（1，1），点A2记为（3，3），点A3记为（6，6），…，则点A100记为．8．被11除余7，被7除余5，并且不大于200的所有自然数的和是．9．如图，一个长方形的长和宽的比是5：3．如果长方形的长减少5厘米，宽增加3厘米，那么这个长方形边长一个正方形．原长方形的面积是平方厘米．10．如图，已知AB＝2，BG＝3，GE＝4，DE＝5，△BCG和△EFG的面积和是24，△AGF和△CDG的面积和是51．那么，△ABC和△DEF的面积和是．11．如图所示的点阵图中，图①中有3个点，图②中有7个点，图③中有13个点，图④中有21个点，按此规律，图⑩中有个点．12．从1，2，3，…，2016中任意取出n个数，若取出的数中至少有两个数互质，则n最小是．13．已知x是最简真分数，若它的分子加a，化简得；若它的分母加a，化简得，则x＝．14．如图，将1个大长方形分成了9个小长方形，其中位于角上的3个小长方形的面积分别为9，15和12，由第4个角上的小长方形的面积等于．15．（15分）二进制是计算机技术中广泛采用的一种数制，其中二进制数转换成十进制数的方法如下：那么，将二进制数 11111011111 转化为十进制数，是多少？【参考答案】一、拓展提优试题1．解：（9×2﹣2×3）÷（3﹣2），＝（18﹣6）÷1，＝12÷1，＝12（米），（12+9）×2，＝21×2，＝42（米）．故答案为：42，12．2．解：根据欢欢与乐乐所得票数的比是3：2，乐乐与洋洋所得票数的比是6：5，可以求出欢欢、乐乐、洋洋所得票数的比9：6：5，200×＝90（票）200×＝60（票）200×＝50（票）答：欢欢所得票数是90票，乐乐所得票数是60票，洋洋所得票数是50票．3．解：（1）1*2＝＝，即2m+8＝10，2m＝10﹣8，2m＝2，m＝1，（2）2*6，＝，＝，故答案为：1，．4．解：早晨7点10分，分针指向2，时针指7、8之间，根据对称性可得：与4点50分时的指针指向成轴对称，故小明误以为是4点50分．故答案为：4，50．5．解：由一个三角形组成：14个；由两个三角形组成：8个；由三个三角形组成：8个；由四个三角形组成：4个；由六个三角形组成：1个；总共：14+8+8+4+1＝35个．故共有35个三角形．故答案为：35．6．解：丙花钱是甲的×＝甲：乙：丙＝1：：＝13：12：8（13+12+8）÷3＝11每份：9÷（11﹣8）＝3（元）甲：（13﹣11）×3＝6（元）乙：（12﹣11）×3＝3（元）答：分给甲6元，分给乙3元．故答案为：6，3．7．解：根据分析可知A100记为（1+2+3+…+100，1+2+3+…+100）；因为1+2+3+…+100＝（1+100）×100÷2＝5050，所以A100记为（5050，5050）；故答案为：A100记为（5050，5050）．8．解：不大于200的所有自然数被11除余7的数是：18，29，40，62，73，84，95，106，117，128，139，150，161，172，183，194；不大于200的所有自然数被7除余5的是：12，19，26，33，40，47，54，61，68，75…；同时被11除余7，被7除余5的最小数是40，[11，7]＝77，依次是117、194；满足条件不大于200的所有自然数的和是：40+117+194＝351．故答案为：351．9．解：先求出一份的长：（5+3）÷（5﹣3）＝8÷2＝4（厘米）长是：4×5＝20（厘米）宽是：4×3＝12（厘米）原来的面积是：20×12＝240（平方厘米）；答：原来长方形的面积是240平方厘米．故答案为：240．10．解：作CM⊥AD，垂足为M，作FN⊥AD，垂足为N，设CM＝x，FN＝y．由题意得方程组，解方程组得，所以△ABC与△DEF的面积和是：AB•CM+DE•FN＝×2×8+×5×6＝8+15＝23．故答案为：23．11．解：根据分析得出的规律我们可以得到：图⑩中有3+（4+6+8+10+12+14+16+18+20）＝3+（4+20）×9÷2＝111；故答案为：111．12．解：根据分析，1～2016数中，有奇数1008个，偶数1008个，因为偶数和偶数之间不能互质，故：①n＜1008时，有可能取的n个数都是偶数，就不能出现至少有两个数互质的情况；②n＝1008时，若取的数都是偶数，也不能出现至少有两个数互质的情况；③n≥1009时，则取的n个数里至少有一个为奇数，取出的这个奇数和它相邻的偶数一定互质，综上，n最小是1009．故答案是：1009．13．解：设原来的分数x是，则：＝则：b＝3（c+a）＝3c+3a①＝则：4c＝a+b②①代入②可得：4c＝a+3c+3a4c＝4a+3c则：c＝4a③③代入①可得：b＝3c+3a＝3×4a+3a＝15a所以＝＝即x＝．故答案为：．14．解：如图，设D的面积为x，9：12＝15：x9x＝12×15x＝x＝20答：第4个角上的小长方形的面积等于20．故答案为：20．15．解：（11111011111）2＝1×210+1×29+1×28+1×27+1×26+0×25+1×24+1×23+1×22+1×21+1×20＝1024+512+256+128+64+0+16+8+4+2+1＝（2015）10答：是2015．。

答案：15瓶。
12、代表和平的植物是什么？
13、王某从甲地去乙地，1分钟后， 李某从乙地去甲地。当王某和李某 在途中相遇时，哪一位离甲地较远 一些？
答案：他们相遇时，是在同一 地方，所以两人离甲地同样远
14、有俩根不同的香，香燃完的时 间都是一小时，用什么方法能确定 一段长45分钟的时间?
答案：先点燃三头，等到第一支 香燃完就是半个小时，在点燃第二 支香的另一头，这样再燃完就是15 分钟。30+15=45
15、小华的爸爸1分钟可以剪好5只自 己的指甲。他在5分钟内可以剪好几 只自己的指甲？
答案：20只，包括手指甲和脚指甲
16、企鹅是南极还是北极的特有动物？
17、一只猫吃一只老鼠，用5分钟吃完； 5只猫同时吃5只同样的老鼠 要几分钟吃完？
答： 5分钟
到此结束 谢谢大家
如图，△ABC是等腰直角三角形，D是半圆周的 中点，BC是半圆的直径，已知：AB=BC=10，那 么阴影部分的面积是多少？
猜一数学成语：
一二三四五六七九十 （猜一个字)
答案：口
猜成语： 零存整取 答案：积少成多
猜一数学成语：
7 8 （猜一成语）
答案：七上八下
猜数学成语： 3333333……55555555 ……
答：三五成群
第二环节
抢答题
1、根据下列表述，能确定位置的是 （ ）．
（A）某电影院2排 （B）南京市大桥南路 （C）北偏东30° （D）东经118°，北纬40°
5、甲乙两数，如果甲数的小数点向左移
动一位就相当于乙数的20％。
那么甲数：乙数＝（
）。
6、UFO的中文是？
7、一辆大巴从广州开往韶关，行了一段路程后， 离韶关还有210千米，接着又行了全程的20%， 这时已行路程与未行路程的比是3∶2。广州、韶 关两地相距多少千米？

六年级趣味数学竞赛试题姓名: 得分：一、填空题。

（每空2分，共28分）1．一件上衣原价85元，现在按原价打“八折”出售，现价是（）元。

2．15克盐溶解到650克水中，盐与盐水的比是（）。

3．在比例里，两个外项互为倒数，一个内项是2，另一个内项是（）。

4．从12的因数中选出四个数，组成比例是（）5．圆锥的底面积是30平方厘米，高15厘米，它的体积是（）立方厘米。

6．将一个体积是18立方厘米的圆柱体，削成一个最大的圆锥，这个圆锥体的体积是（）立方厘米，削去部分的体积是（）立方厘米。

7．一根2米长的圆柱形钢材截成两段，表面积增加12.56平方厘米，这段钢材的体积是（）立方厘米。

8．底面直径和高都是6分米的圆柱的体积是（）。

9．一个圆柱的底面半径是2厘米，高是2厘米，如果沿高剪开，它的侧面展开图是（）形，这个图形的周长是（）厘米，面积是（）平方厘米。

10．已知A、B、C三种量的关系是A÷B=C，如果A一定，那么B和C成（）比例关系，如果C一定，A和B成（）比例关系。

二、慎重选择，对号入座。

（ 16分）1．如果3a=4b，那么a∶b＝（）。

①3∶4 ②4∶3 ③3a∶4b 2.一架客机从北京飞往上海，飞行速度和所用的时间（）.①成正比例②成反比例③不成比例3. 商一定，被除数和除数，（）.①成正比例②成反比例③.不一定成比例4．圆柱的体积一定，它的高和（）成反比例。

①底面半径②底面积③底面周长④底面直径5．下面第( )组的两个比不能组成比例① 7:8和14:16 ②0.6:0.2和3:1③19:110 和10:96．圆柱体的底面半径扩大3倍,高不变，体积扩大（）①3倍②9倍③6倍7．把一个棱长4分米的正方体木块削成一个最大的圆柱体，体积是（）立方分米。

①50.24 ②100.48 ③648．把一团圆柱体橡皮泥揉成与它等底的圆锥体，高将（ ） ①扩大3倍 ②缩小3倍③扩大6倍 ④缩小6倍三： 解比例。

一、选择题（每题2分，共20分）1. 下列各数中，质数是（）A. 15B. 17C. 20D. 252. 一个数既是3的倍数，又是5的倍数，这个数最小是（）A. 15B. 30C. 45D. 603. 一个长方形的长是6厘米，宽是4厘米，它的周长是（）A. 16厘米B. 20厘米C. 24厘米D. 28厘米4. 下列各图中，面积最大的是（）A. ①B. ②C. ③D. ④5. 小明和小红分别有10个和8个苹果，他们一共有多少个苹果？（）A. 18个B. 19个C. 20个D. 21个6. 一个三位数，百位和十位上的数字之和是11，个位上的数字是5，这个数最大是（）A. 511B. 515C. 551D. 5157. 下列各数中，既是奇数又是偶数的是（）A. 1B. 2C. 3D. 48. 下列各图形中，既是轴对称图形又是中心对称图形的是（）A. ①B. ②C. ③D. ④9. 一个数的因数有4个，这个数最大是（）A. 4B. 6C. 8D. 1010. 下列各式中，计算错误的是（）A. 3×5+2=17B. 8÷2×3=12C. 6×6÷3=12D. 4×5÷2=10二、填空题（每题2分，共20分）1. 2×5×7=（）2. 3×3×3=（）3. 8×8×8=（）4. 4×5+6=（）5. 12÷3×2=（）6. 7×7×7=（）7. 9×9×9=（）8. 5×5+6=（）9. 12÷3÷2=（）10. 6×6×6=（）三、解答题（每题10分，共30分）1. 小华有20个苹果，小明有比小华少5个苹果，小刚有比小明多3个苹果，请写出小刚有多少个苹果。

2. 一个长方形的长是12厘米，宽是8厘米，请计算它的周长和面积。

小学六年级数学趣味竞赛ห้องสมุดไป่ตู้题
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ；权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊，可是金 子可以 拉着它 的鼻子 走。— —莎士 比
40、学而不思则罔，思而不学则殆。——孔子
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳

一、拓展提优试题1．已知A是B的，B是C的，若A+C＝55，则A＝．2．（15分）一个棱长为6的正方体被切割成若干个棱长为整数的小正方体，若这些小正方体的表面积之和是切割前的大正方体的表面积的倍，求切割成小正方体中，棱长为1的小正方体的个数？3．如图所示的容器中放入底面相等并且高都是3分米的圆柱和圆锥形铁块，根据图1和图2的变化知，圆柱形铁块的体积是立方分米．4．若一个十位数是99的倍数，则a+b＝．5．用1，2，3，4，5，6，7，8，9九个数字组成三个三位数（每个数字只能用1次），使最大的数能被3整除；次大的数被3除余2，且尽可能的大；最小的数被3除余1，且尽可能的小，求这三个三位数．6．根据图中的信息计算：鸡大婶和鸡大叔买的花束中，玫瑰、康乃馨、百合各多少枝？7．一根绳子，第一次剪去全长的，第二次剪去余下部分的30%．若两次剪去的部分比余下的部分多0.4米，则这根绳子原来长米．8．根据图中的信息可知，这本故事书有页页．9．快车和慢车同时从甲、乙两地相对开出，快车每小时行33千米，相遇行了全程的，已知慢车行完全程需要8小时，则甲、乙两地相距千米．10．如图，圆P的直径OA是圆O的半径，OA⊥BC，OA＝10，则阴影部分的面积是．（π取3）11．李华在买某一商品的时候，将单价中的某一数字“7”错看成了“1”，准备付款189元，实际应付147元，已知商品的单价及购买的数量都是整数，则这种商品的实际单价是元，李华共买了件．12．能被5和6整除，并且数字中至少有一个6的三位数有个．13．已知x是最简真分数，若它的分子加a，化简得；若它的分母加a，化简得，则x＝．14．a，b，c是三个互不相等的自然数，且a+b+c＝48，那么a，b，c的乘积最大是．15．小丽做一份希望杯练习题，第一小时做完了全部的，第二小时做完了余下的，第三小时做完了余下的，这时，余下24道题没有做，则这份练习题共有道．16．如图，将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，这根长方体木块原来的体积是立方分米．17．若（n是大于0的自然数），则满足题意的n的值最小是．18．如图，向装有水的圆柱形容器中放入三个半径都是1分米的小球，此时水面没过小球，且水面上升到容器高度的处，则圆柱形容器最多可以装水188.4立方分米．19．（15分）如图，半径分别是15厘米、10厘米、5厘米的圆形齿轮A、B、C为某传动机械的一部分，A匀速转动后带动B匀速转动，而后带动C匀速转动，请问：（1）当A匀速顺时针转动，C是顺时针转动还是逆时针转动？（2）当A转动一圈时，C转动了几圈？20．已知三个分数的和是，并且它们的分母相同，分子的比是2：3：4．那么，这三个分数中最大的是．21．从1开始的n个连续的自然数，如果去掉其中的一个数后，余下的各个数的平均数是，那么去掉的数是．22．有一口无水的井，用一根绳子测井的深度，将绳对折后垂到井底，绳子的一端高出井口9m；将绳子三折后垂到井底，绳子的一端高出井口2m，则绳长米，井深米．23．用底面内半径和高分别是12cm，20cm的空心圆锥和空心圆柱各一个组成如图所示竖放的容器，在这个容器内注入一些细沙，能填满圆锥，还能填部分圆柱，经测量，圆柱部分的沙子高5cm，若将这个容器倒立，则沙子的高度是cm．24．在一个两位数的中间加上小数点，得到一个小数，若这个小数与原来的两位数的和是86.9，则原来两位数是．25．A，B两校的男、女生人数的比分别为8：7和30：31，两校合并后男、女生人数的比是27：26，则A，B两校合并前人数比是．26．若一个长方体，长是宽的2倍，宽是高的2倍，所有棱长之和是56，则此长方体的体积是．27．图中阴影部分的两段圆弧所对应的圆心分别为点A和点C，AE＝4m，点B 是AE的中点，那么阴影部分的周长是m，面积是m2（圆周率π取3）．28．小红整理零钱包时发现，包中有面值为1分，2分，5分的硬币共有25枚，总值为0.60元，则5分的硬币最多有枚．29．若质数a，b满足5a+b＝2027，则a+b＝．30．有两辆火车，车长分别是125米和115米，车速分别是22米/秒和18米/秒，两车相向行驶，从两车车头相遇到车尾分开需要秒．31．定义新运算“*”：a*b＝例如3.5*2＝3.5，1*1.2＝1.2，7*7＝1，则＝．32．如图．从楞长为10的立方体中挖去一个底面半径为2，高为10的圆柱体后，得到的几何体的表面积是，体积是．（π取3）33．一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是．34．如图1是一个正方体的展开图，图2的四个正方体中只有一个是和这个展开图对应的，这个正方体是．（填序号）35．一列快车从甲地开往乙地需要5小时，一列慢车从乙地开往甲地所需时间比快车多，两车同时从甲乙两地相对开出2小时后，慢车停止前进，快车继续行驶40千米后恰与慢车相遇，则甲乙两地相距千米．36．对任意两个数x，y，定义新的运算*为：（其中m是一个确定的数）．如果，那么m＝，2*6＝．37．图中每一个圆的面积都是1平方厘米，则六瓣花形阴影部分的面积是平方厘米．38．早晨7点10分，妈妈叫醒小明，让他起床，可小明从镜子中看到的时刻还没有到起床的时刻，他对妈妈说：“还早呢！”小明误以为当时是点分．39．王涛将连续的自然数1，2，3，…逐个相加，一直加到某个自然数为止，由于计算时漏加了一个自然数而得到错误的结果2012．那么，他漏加的自然数是．40．把一个自然数分解质因数，若所有质因数每个数位上的数字的和等于原数每个数位上的数字的和，则称这样的数为“史密斯书数”如：27＝3×3×3.3+3+3＝2+7，即27是史密斯数，那么，在4，32，58，65，94中，史密斯数有个．【参考答案】一、拓展提优试题1．解：A是C的×＝，即A＝C，A+C＝55，则：C+C＝55C＝55C＝55÷C＝40A＝40×＝15故答案为：15．2．解：大正方体表面积：6×6×6＝216，体积是：6×6×6＝216，切割后小正方体表面积总和是：216×＝720，假设棱长为5的小正方体有1个，那么剩下的小正方体的棱长只能是1，个数是：（63﹣53）÷13＝91（个），这时表面积总和是：52×6+12×6×91＝696≠720，所以不可能有棱长为5的小正方体．（1）同理，棱长为4的小正方体最多为1个，此时，不可能有棱长为3的小正方体，剩下的只能是切割成棱长为2的小正方体或棱长为1的小正方体，设棱长为2的小正方体有a个，棱长为1的小正方体有b个，则解得：（2）棱长为3的小正方体要少于（6÷3）×（6÷3）×（6÷3）＝8个，设棱长为2的小正方体有a个，棱长为1的小正方体有b个，棱长为3的小正方体有c个，化简：由上式可得：b＝9c+24，a＝，当c＝0时，b24＝，a＝24，当c＝1时，b＝33，a＝19.5，（不合题意舍去）当c＝2时，b＝42，a＝15，当c＝3时，b＝51，a＝10.5，（不合题意舍去）当c＝4时，b＝60，a＝6，当c＝5时，b＝69，a＝28.5，（不合题意舍去）当c＝6时，b＝78，a＝﹣3，（不合题意舍去）当c＝7时，a＝负数，（不合题意舍去）所以，棱长为1的小正方体的个数只能是：56或24或42或60个．答：棱长为1的小正方体的个数只能是：56或24或42或60个．3．解：25.7÷（1+1+3）＝25.7÷5＝5.14（立方分米）5.14×3＝15.42（立方分米）答：圆柱形铁块的体积是15.42立方分米．故答案为：15.42．4．解：根据99的整除特性可知：20+16++20+17＝99．．a+b＝8．故答案为：8．5．解：根据分析，最大的数最高位是：9，次大的数最高位是：8，最小的数最高位是1，次大的数倍3除余2，且要尽可能的大，则次大的三位数为：875；最小的数被3除余1，且要尽可能的小，则最小的三位数为：124；剩下的三个数字只有，3，6，9，故最大的三位数为：963．故答案是：963、875、124．6．解：依题意可知：玫瑰与康乃馨和百合的枝数化连比为：10：15：3；购买一份比例的价格为：3×20+15×6+15×10＝300；正好是1倍关系．答：购买玫瑰10枝，康乃馨15枝，百合3枝．7．解：第二次剪求的占全长的：（1）×30%＝＝，0.4÷[（1）]＝0.4÷[]＝＝0.4×15＝6（米）；答：这根绳子原来长6米．故答案为：6．8．解：（10+5）÷（1﹣×2）＝15÷＝25（页）答：这本故事书有25页；故答案为：25．9．解：1﹣＝×8＝（小时）×33＝（千米）÷＝198（千米）答：甲、乙两地相距198千米．故答案为：198．10．解：3×102÷2﹣3×（10÷2）2＝3×100÷2﹣3×25＝150﹣75＝75答：阴影部分的面积是75．故答案为：75．11．解：189＝3×3×3×7＝27×7147＝3×7×7＝21×7正好是27×7＝189中把27看成21×7＝147所以这种商品的实际单价是21元，卖了7件．故答案为：21，7．12．解：根据分析，分解质因数6＝2×3∴这个三位数能同时被2、3、5整除，而且数字中至少含有一个6∴这个三位数的个位数必须为偶数或0，因被5整除的数个位数必须是0或5，故个位数为0，设此三位数为，按题意a、b中至少有一个数字为6，①a＝6时，则6+b+0 是3的倍数，则b＝0，3，6，9，符合的三位数为：600、630、660、690②b＝6时，则6+a+0 是3的倍数，则a＝3，6，9，符合的三位数为：360、660、960综上所述，符合题意的三位数为：360、660、960、600、630、690故答案为：6．13．解：设原来的分数x是，则：＝则：b＝3（c+a）＝3c+3a①＝则：4c＝a+b②①代入②可得：4c＝a+3c+3a4c＝4a+3c则：c＝4a③③代入①可得：b＝3c+3a＝3×4a+3a＝15a所以＝＝即x＝．故答案为：．14．解：48÷3＝16，16﹣1＝15，16+1＝17，所以，a，b，c的乘积最大是：15×16×17＝4080．故答案为：4080．15．解：24÷（1﹣）÷（1﹣）÷（1﹣）＝24÷＝60（道）答：这份练习题共有 60道．故答案为：60．16．解：依题意可知：将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，变面积增加了10个面，那么每一个面的面积为100÷10＝10平方分米．10米＝100分米．体积为：10×100＝1000（立方分米）．故答案为：100017．解：当n＝1时，不等式左边等于，小于，不能满足题意；当n＝2时，不等式左边等于+＝＝，小于，不能满足题意；同理，当n＝3时，不等式左边大于，能满足题意；所以满足题意的n的值最小是3．故答案是：318．解：×3.14×13×3÷（﹣）＝12.56×15＝188.4（立方分米）答：圆柱形容器最多可以装水188.4立方分米．故答案为：188.4．19．解：（1）如图，答：当A匀速顺时针转动，C是顺时针转动．（2）A：B：C＝15：10：5＝3：2：1答：当A转动一圈时，C转动了3圈．20．解：＝＝，答：这三个分数中最大的一个是．故答案为：．21．解：设去掉的数是x，那么去掉一个数后的和是：（1+n）n÷2﹣x＝×（n﹣1）；显然，n﹣1是7的倍数；n＝8、15、22、29、36时，x均为负数，不符合题意．n＝43时，和为946，42×＝912，946﹣912＝34．n＝50时，和为1225，49×＝1064，1225﹣1064＝161＞50，不符合题意．答：去掉的数是34．故答案为：34．22．解：（9×2﹣2×3）÷（3﹣2），＝（18﹣6）÷1，＝12÷1，＝12（米），（12+9）×2，＝21×2，＝42（米）．故答案为：42，12．23．解：据分析可知，沙子的高度为：5+20÷3＝11（厘米）；答：沙子的高度为11厘米．故答案为：11．24．解：根据题意可得：86.9÷（10+1）＝7.9；7.9×10＝79．答：原来两位数是79．故答案为：79．25．解：设A、B两校的男生、女生人数分别为8a、7a、30b、31b，由题意得：（8a+30b）：（7a+31b）＝27：26，27×（7a+31b）＝26×（8a+30b），189a+837b＝208a+780b，837b﹣780b＝208a﹣189a，57b＝19a，所以a＝3b，所以A、B两校合并前人数的比是：（8a+7a）：（30b+31b），＝15a：61b，＝45b：61b，＝（45b÷b）：（61b÷b）＝45：61；答：A，B两校合并前人数比是45：61．故答案为：45：61．26．解：长方体的高是：56÷4÷（1+2+4），＝14÷7，＝2，宽是：2×2＝4，长是：4×2＝8，体积是：8×4×2＝64，答：这个长方体的体积是64．故答案为：64．27．解：阴影部分的周长：4+3×4×2÷4+3×2×2÷4，＝4+6+3，＝13（米）；阴影部分的面积：3×42÷4+3×22÷4﹣2×4，＝12+3﹣8，＝7（平方米）；答：阴影部分的周长是13米，面积是7平方米．故答案为：13、7．28．解：因为0.60元＝60分，设1分，2分，5分的硬币各有x枚、y枚和z枚，则有x+y+z＝25，x+2y+5z＝60，把上面的两个式子相减得出y+4z＝35，要使5分的硬币最大，即Z最大，y最小，因为35是奇数，所以y必须是奇数，当y＝1时，z的值不是整数，当y＝3时，z＝8，所以z＝8；答：5分的硬币最多有8枚；故答案为：8．29．解：依题意可知：两数字和为奇数，那么一定有一个偶数．偶质数是2．当b＝2时，5a+2＝2027，a＝405不符合题意．当a＝2时，10+b＝2027，b＝2017符合题意，a+b＝2+2017＝2019．故答案为：2019．30．解：（125+115）÷（22+18）＝240÷40＝6（秒）；答：从两车头相遇到车尾分开需要6秒钟．故答案为：6．31．解：根据分析可得，，＝，＝2；故答案为：2．32．解：10×10×6﹣3×22×2+2×3×2×10，＝600﹣24+120＝696；10×10×10﹣3×22×10，＝1000﹣120＝880；答：得到的几何体的表面积是696，体积是880．故答案为：696，880．33．解：商是10，除数最大是9，余数最大是8，9×10+8＝98；被除数最大是98．故答案为：98．34．解：如图．图1是一个正方体的展开图，图2的四个正方体中只有一个是和这个展开图对应的，这个正方体是图2①；故答案为：①35．解：慢车行完全程需要：5×（1+），＝5×，＝6（小时）；全程为：40÷[1﹣（+）×2]，＝40÷[1﹣]，＝40÷，＝40×，＝150（千米）；答：甲乙两地相距150千米．故答案为：150．36．解：（1）1*2＝＝，即2m+8＝10，2m＝10﹣8，2m＝2，m＝1，（2）2*6，＝，＝，故答案为：1，．37．解：1×2＝2（平方厘米）；答：六瓣花形阴影部分的面积是2平方厘米．故答案为：2．38．解：早晨7点10分，分针指向2，时针指7、8之间，根据对称性可得：与4点50分时的指针指向成轴对称，故小明误以为是4点50分．故答案为：4，50．39．解：设这个等差数列和共有n项，则末项也应为n，这个等差数列的和为：（1+n）n÷2＝；经代入数值试算可知：当n＝62时，数列和＝1953，当n＝63时，数列和＝2016，可得：1953＜2012＜2016，所以这个数列共有63项，少加的数为：2016﹣2012＝4．故答案为：4．40．解：4＝2×2，2+2＝4，所以4是史密斯数；32＝2×2×2×2×2；2+2+2+2+2＝10，而3+2＝5；10≠5，32不是史密斯数；58＝2×29，2+2+9＝13＝13；所以58是史密斯数；65＝5×13；5+1+3＝9；6+5＝11；9≠11，65不是史密斯数；94＝2×472+4+7＝13＝9+4；所以94是史密斯数．史密斯数有4，58，94一共是3个．故答案为：3．。

六年级数学趣味竞赛班级： 姓名： 分数：一、填空。

（每小题3分）1、有三个连续的两位数，它们的和也是两位数，并且是11的倍数，这三个数分别是（ ）、（ ）、（ ）。

2、时钟从8：45走到9：09，分针旋转了（ ）度。

3、某大楼地下共有4层，地上共有18层，王师傅乘电梯从地下3层升到地上7层，电梯一共升了（ ）层。

4、要从含盐16%的40千克盐水中蒸去水分，制出含盐20%的盐水，应蒸去（ ）千克水。

5、将长70厘米的圆柱体截成3段，表面积增加了234平方厘米，这个圆柱体原来的体积是（ ）立方米。

6、如右图，小明买了6张电影票，他想撕下相连的四张，共有（ ）种不同的撕法。

7、一张纸片第一次把撕成6片，第100次撕后共得小纸片（ ）片。

8、按规律填数： 4、 9、（ ）、43、（ ）、1859、有一种电子钟，每到正点响一次铃，每走9分钟亮一次灯，中午12点整，它既响铃又亮灯，那么下一次既响铃又亮灯是（ ）点钟。

9、如图所示，是一个固定在地面上的雕塑物的正视图，它是由三个实心的正方体组成，棱长分别是1、2、3（单位：米），那么这个雕塑物的表面积是（ ）立方米。

10、如图2的纸片拆成一个正方体，相对两个面上数字和最大是（ ）图1 图2二、判断。

（每题2分）1、同一个圆，周长和半径的比是圆周率：1。

（）2、甲、乙两人各做同样多的零件，甲2.15小时完成，乙2小时18分钟完成，甲比乙的工作效率高。

（）3、某化工厂五月份生产化肥250吨，增产了50吨，增产了25%。

（）4、一根木料锯成4段要12分钟，如果把这根木料锯成8段则要24分钟。

（）5、一个三位数，百位、十位和个位的数字分别是a、b、c，那么这个三位数可记作：100a+10 b + c。

（）三、选择题（每题3分）1、一个圆的直径由4分米增加到5分米，周长增加了（）A. 20%B. 25%C. 50%D. 75%2、正方体边长4厘米，在前、后、左、右、上、下每个面各挖掉一个边长为1厘米的正方体，则剩余物体的表面积是（）平方米。

答案：
１２分
８分 ６分
第一步:小明与弟弟过桥，小明回来，耗时４分；
第二步:小明与爸爸过河，弟弟回来，耗时９分；
第三步:妈妈与爷爷过河，小明回来，耗时１３分；
最后,小明与弟弟过河，耗时3秒，总共耗时29分，多么惊险！
１分 ３分
五、
悖论（一） 一天，萨维尔村理发师 挂出了一块招牌：村里 所有不是自己理发的男 人都由我给他们理发。 于是有人问他：
再见吧，妈妈—— 分母
并肩前进—— 平行
第
一网打尽—— 整除
三
你盼我，我盼你—— 相等
组
一模一样—— 全等
二、农 夫 过 河
有一个农夫，带了一包米，一只鸡和一 只狗准备要过河。当农夫不在时，鸡会 吃米，狗会吃鸡，河边有一艘船，农夫 在船上一次只能带一样东西，请问农夫 该怎么过河？
三 、 只 赢 不 输 的 游 戏
片
请问男说了一句什么话使得这个女生只能将玉照送他？
一、猜谜比赛 二、农夫过河 三、只赢不输的游戏 四、黑夜过桥 五、悖论
一、猜谜比赛
考试作弊—— 假分数
第
一 八分之七（成语）—— 七上八下
七天七夜－－ 周长
组
七六五四三二一—— 倒数
一减一不是零。（打一字）—— 三
第
一笔债务—— 负数
二
马路没弯儿—— 直径
组
双杠—— 等号
1.2.5—— 丢三落四
“您的头发谁给理虔诚的教徒，他在 演说中口口声声说上帝 是无所不能的，什么事 都做得到。一位过路人 问了一句话：
“上帝能创造一块他 自己也举不起来的石 头吗？”
教徒哑口无言
１．我说一句话，
悖论（三）
如果这句话是真