按规律画图形小学奥数试题大全

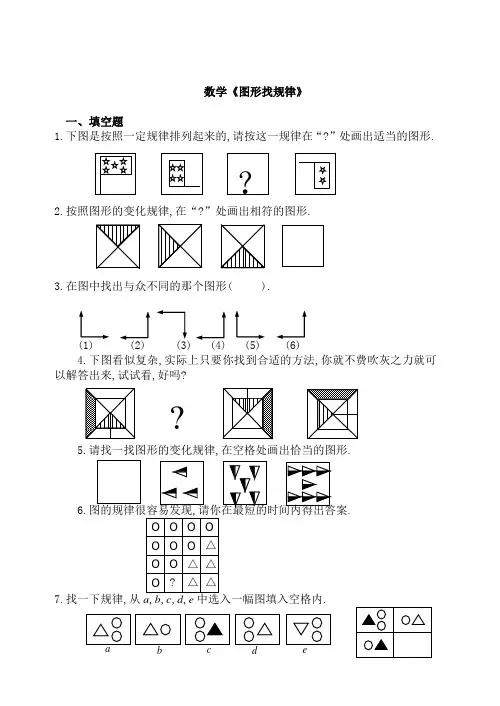
数学《图形找规律》一、填空题1.下图是按照一定规律排列起来的,请按这一规律在“?”处画出适当的图形.2.按照图形的变化规律,在“?”处画出相符的图形.3.在图中找出与众不同的那个图形( ).(1) (2) (3) (4) (5) (6) 4.下图看似复杂,实际上只要你找到合适的方法,你就不费吹灰之力就可以解答出来,试试看,好吗?5.请找一找图形的变化规律,在空格处画出恰当的图形.6..7.找一下规律,从.？ ?8.按照下列图形的变化规律,空白处应是什么样的图形.9.按规律填图.如果 变成那么 应变为10.下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.二、解答题11.图中,哪个图形与众不同?(1) (2) (3) (4) (5)12.有一个立方体,每个面上分别写上数字1、2、3、4、5、6、,有3个人 从不同的角度观察的结果如下图所示,这个立方体的每一个数字的对面各是什么数字???1 2 6 1 3413.下面是由几何图形组成的帆船图形,请按照一定的规律,在标序号处画出符合规律的小帆船.③①②———————————————答案——————————————————————1. 这一组图形我们应该从两方面来看:一是旗子的方向,二是旗子上星星的颗数.首先我们看一下旗子的方向.第1面旗子向右,第2面向上,第4面向下,可以发现,旗子的方向是按逆时针旋转的,并依次旋转︒90,所以第3面旗子应是第2面逆时针旋转︒90得来的,旗子应向下倒立.其次我们看旗上星星的颗数.第1面是5颗,第2面是4颗,第4面是2颗,可见颗数是依次减少1颗,所以第3面旗上应是3颗星星.所以“?”处的图形应为:2. 这组图形的变化只在于正方形中阴影部分的位置.通过观察,我们可以发现阴影部分是按照逆时针方向依次旋转︒90得到的.所以“?”处的图形应为:3. 选(4).因为变化规律是从左到右依次逆时针旋转︒90.4. 在这组图形中,不变的有以下几点:大小正方形不变,两条对角线不变.所以“?”处也应有大小两个正方形和两条对角线.发生变化的有:一、阴影部分和黑色部分的位置.通过观察,我们可以看出这两部分都是按逆时针方向依次旋转︒90得到的,所以“?”处的阴影部分应是小正方形的右边,黑色部分应在大正方形的下部.二、小竖线的位置.小竖线是从图形中心到相应的边所作的一条垂线.它的变化规律是按逆时针方向依次旋转︒90,这样,整个图形我们就分析完了,下面看一看你画出的图形和书上的一样吗?如果一样,就做对了.5. 因为要填的是第1幅图,我们可以从后往前看.首先三角形的个数是发生变化的,依次是7、5、3.可以发现是从后向前依次减少2个的.所以第1幅图中应有1个三角形.其次三角形的方向也是有变化的,从后面观察,三角形是按逆时针方向依次旋转︒90,所以第1幅图中的三角形应向上,阴影部分在右边.如下图所示:6. 横行观察,圆的个数逐次减少1个,所以到第4行,圆的个数应为1,所以“?”处应是“△”.或者从三角形考虑,三角形的个数为0、1、2,是逐次增加1,所以第4行中三角形的个数应为3,所以“？”处应为“△”所以最后的图形为:7. 选a.根据对角图形规律,可知右下角图形是a图.8. 分析:先看不变的部分.在整个变化过程中,图形中大、小两个圆圈没有变化,因此可以肯定空白处的图形一定也有大、小两个圆圈,位置一里一外.变化的部分可为两部分:①图形中的直线部分,其变化规律是每次顺时针旋转︒90,黑色部分90;②图形中的阴影部分,其变化规律是每次逆时针旋转︒交替出现.解:根据上面的分析,可画出空白处的图形如图所示.9. 先应找出变化的规律,然后再依此规律,在空白处填画出所缺的图形.从第一行可以看到,当左边的图形变成右边的图形时,下部图形移到上面,里面的图形移到下面,上面的外部图形移到里面,各部分的颜色都没有变.根据这一规律,我们可以把下面图形变为:10. 先看第1行,阴影部分所在的位置是1、2、3.是逐次向后一个,所以第四幅图中第1行的阴影部分应在第4格.同样,第2行是2、3、4.4再向后应是5了,但没有第5个格,所以折回到第1个格.同理可推出第3行的阴影部分在第2格,第4行的阴影部分在第3格.还可以这样想:在同一行中,阴影部分都不在同一位置,所以第1行已经被占去了第1、2、3格,所以第四幅图的第一行阴影部分一定是第4格,同理推出第2、3、4行中阴影部分的位置..11. ,车轮一致,车底一致,差异就只能在车头、车身部分去寻找.从车身看,(3)与众不同,只用一笔画成,可是它的车头与(1)同;从车头看:(2)与众不同,(因车头(1)与(3)同,(4)与(5)同),但是(2)的车身与(1)、(4)、(5)类似.所以从车头、车身这些特征比较出来的图形,理由不足以说服人.我们把目光转移到笔划多少上,就可以找到与众不一的车辆了.解:与众不同的汽车是(1).其他四车均是由一个矩形、两个圆以及四条直线段、一段弧线画成,而(1)多一条直线段.12. 这个题目并不难.但是,推理方法不正确的话,也很难看出答案.直接考虑数字1的对面是什么数,想不出来.不妨换一种思维方式,想一想1的对面不是什么数.从第1个图看出1的对面不是4和6;从第2个图看出1的对面不是2和3,所以1的对面只能是5.同样的方法可以得到,4的对面是2;3的对面是6.13. 因为正锥体的每个顶点连接三个面.当正锥体在雪花格纸上按顺时针方向旋转时,只有写有1、2、4三面所围出的顶点一直在雪花格的中心,所以只有1、2、4贴纸面旋转,雪花格有6个小格,正好可以转两圈,所以回到原地各面数字仍是原样分布.14.每一只小帆船都由三部分组成:船体、帆和小旗.这三部分都是变化的,另外船体的颜色也是变化的.下面我们逐一来分析.①船体的形状:帆船的船体都是由半圆、梯形、三角形组成,并且每一横行(或竖行)都没有重复.按照这一规律,我们可以确定船体的形状.因为①所在的位置横行、竖行都只有1个图形,所以不能确定,可以先确定②或③.看②所在的横行 ,缺 ,所以②的船体形状应为梯形.看和 ,缺 ,所以①的船体形状为 .看③所在的竖行,有 和 ,缺 ,所以③的船体形状为 .②船体的颜色.每一横行(或竖行)都由阴影、黑色、白色三色组成,并且在同一行中没有重复颜色,根据这一规律,确定出①号船体为白色,②号船体为黑色, ③号船体为黑色.③帆船的形状. ④小旗的形状.最后的答案为:①② ③确定方法和前面一样.。

二年级奥数：《发现图形规律》（预热）前铺知识一、找规律画图1、形状变化【例1】根据规律，画出下一个图形.答案：解析：本组图的规律就是正方形、三角形、圆形三个不同形状的图形为一组，重复出现.2、数量变化【例2】根据规律，在横线上画出适当的图形.答案：解析：本组图的规律是圆形的数量发生了变化，依次增加1个.3、颜色变化【例3】根据规律，画出下一个图形答案：解析：本组图的规律是圆形的颜色发生了变化，红蓝黄绿四种颜色的三角形为一组重复出现.4、位置变化【例4】根据规律，在横线上画出适当的图形.答案：解析：本题的规律是第一组的第一个图形移动到最后一个位置，其它图形依次往前移一小格就变成了第二组图.第二组的第一个图形移动到最后一个位置，其它图形依次往前移一小格就变成了第三组图.第三组的第一个图形移动到最后一个位置，其它图形依次向前移一小格，就变成了.5、方向变化【例5】根据规律，在横线上画出适当的图形.答案：解析：本组图的规律就是箭头的方向发生了变化，每次向顺时针方向旋转90度.6、组合【例6】根据规律，在问号处应该画什么图形.?答案：解析：本组图既要观察图形的形状，又要观察颜色，是一种组合规律题.观察发现，这些图形都分为上下两部分.其中第一行，上部分的形状分别是三角形和半圆环形，颜色为绿色和蓝色，下部分分别为红色的圆环和长方形.第二行，上部分没有变化，下部分的颜色变成了黄色，因此为答案所示图形.【例7】根据规律，在空白处应该画什么图形.答案：解析：本题中，图形的形状、颜色以及位置都在发生变化.但实际上可以将此组图中的每一个大圆内的图形看成一个整体，则下一个图形就是上一个大圆按顺时针依次旋转90度得来的.【例8】根据规律，在问号处应该画什么图形.?答案：解析：观察后可发现，每一横行中，第一个图形叠到第二个图形中间，就组成了第三个图形.课前思考1、要想发现一组图形的规律，你知道可以从哪些角度去观察吗?2、如果颜色、形状、方向等都无法帮助你找到规律，你会如何思考呢?如何预习?第四讲的知识非常的有趣，小朋友们可以尽情的享受找规律的乐趣.在一年级秋季的课程中，我们已经接触过了找规律画图，知道了数学中图形的规律有好多种，例如形状变化的规律，还有颜色变化、数量变化、位置变化、方向变化以及组合出现的规律.在学习二年级秋季第四讲《发现图形规律》这一讲之前，小朋友们可以回顾一下这些知识，为第四讲的课堂学习做一个铺垫.对于应当如何预习，潘老师在这里提醒一下各位小朋友，预习的时间不要过早，应该尽量安排在距离下次上课较近的时间里.预习的时候，不要过于关注做新的题目，对于全新的知识，可以把它们保留到课堂上再去思考、学习.相较于自己去摸索新的知识，不如先把与本讲次内容相关的以前学过的知识再拿出来回顾一下，这样的效果也许会更好哦~当然了，还有几句老话要啰嗦一下，预习的时间不宜过长，内容也不宜过多过细.在预习的时候要边看边做并且边思考，最好能带着你自己的问题去上课.《发现图形规律》知识点精讲【知识点总结】1、单一变化：颜色、形状、方向、大小、数量、位置……2、多样变化【例】按规律画出空白处的图形.这些图案有外部、有内部，它们的变化既有形状、方向的变化，又有数量的变化，因此要分不同的部分来找规律.外部：正三角形→正方形→正五边形→正六边形内部：1条横线→2条竖线→3条横线→4条竖线3、拼组：（1）简单：拼起来【例】根据下面图形排列的规律，问号的地方应该选择哪个图形?经观察，发现每一行、每一列的图形都有同样一个变化规律：第一个与第三个图形拼组在一起就是中间的图形.（2）复杂：组合消失【例】根据下面图形排列的规律，问号的地方应该选择哪个图形?方法1：横着看，每行的任意两个图形拼组到一起，重合部分消失，就变成了另外一个图形. 方法2：竖着看，每列的任意两个图形拼组到一起，重合部分消失，也变成了另外一个图形. （因为这题要求的是最右下角的图形，所以不论是横看还是竖看，最快的方法是通过第一个和第二个的图形拼组在一起，重合部分消失来得到.）4、缺什么补什么【例】下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个娃娃头画出来.经观察，发现在每一行每一列，这些娃娃头都由头发（一毛、两毛和三毛）、脸（圆脸、方脸和三角形脸）、眼睛（黑眼、白眼和黑白眼）、嘴巴（一个白三角嘴、两个黑三角嘴）组成，因此可以用缺什么补什么的方法，并且要分部分来看.不管是横着看还是竖着看，最右下角缺的娃娃头是三毛、方脸、黑白眼、白三角嘴.【例】观察图形的变化规律，按照这种变化规律，在空格中画上应有的图形.观察，每个田字格中有4种图形，从第一个田字格变到第二个田字格，每个小图形的位置改变了，并且有些图形自身的形状也改变了.先看位置的变化：每个图形都按逆时针方向旋转.再看图形自身方向的变化：每个图形自身也都在按逆时针方向旋转.（圆形与正方形在本题中旋转后与原先没有区别.）（实际上本题也可以理解成整个田字格在按着顺时针方向旋转.）《发现图形规律》补充题1、根据规律，问号处应填什么图形?2、根据规律，画出空白处的图形.3、根据规律，画出问号处的图形.4、按规律画出空白处的图形.5、下面一组图形的阴影变化是有规律的，请根据这个规律把第四幅图的阴影部分画出来.6、按规律填图.7、根据A~F这几个人的排列规律，接下来应该排列的是G、H、I中的哪一个?答案1、（1）（2）【解析】：两小题中的图形都是依次按逆时针方向旋转90度.2、【解析】：本题中图形排列的规律是每一行的第一个图形和第三个图形合在一起就是第二个图形.3、【解析】：本题可以竖着来看，每一列的图形都是依次按顺时针方向旋转90度.4、（1）【解析】：通过观察，不难发现，图形从左到右的变化规律是：外面是正方形、圆形边框在交替出现，里面是箭头的数量依次加1，并且箭头的方向是一正一反出现.（2）【解析】：每一组都有三种图形，分别是圆形、箭头和三角形，我们可以依次来观察.圆形始终不变，箭头是按顺时针方向旋转，三角形是按逆时针方向旋转.（3）【解析】：观察第一至第三组字母排列变化的规律是：字母D在中间不动，其余字母从左往右依次移动1个位置，最右边的字母则移动到最左边.移动中如果遇到字母C就跳过去.5、【解析】：经观察可发现，每个图形中都有四个阴影格子，依次向右上方向推移.第二个图形中，向上推移后只有3个阴影格子，则还需要1个，注意要在左下方的对角的地方寻找.第三个图形中，继续向上推移只有2个阴影格子，则还需要2个，那么就在另一个对角上寻找到两个.第四个图形，则应该向右上方推移到只有1个阴影格子，则剩下的三个在左下方如图所示位置.注意，两个阴影格子之间没有共用的边，只有一个角相连.6、【解析】：题目给出的例子中，有三种图形，我们可以从上往下依次来观察.左图上部外面的白色圆形变成了右图上部缩小了的黑色圆形，颜色与大小都改变，位置没变，还是在上部.左图上部里面的黑色正方形变成了右图下部的白色正方形，颜色与位置改变，大小不变.左图下部的三角形变成了右图上部的三角形，颜色大小不变，位置改变.同样的规律运用到题目中，可知题目里上部外面的菱形将改变颜色和大小，放置在上部的中心，而上部里面的圆形将不改变大小，改变颜色，放置在下部.而下部的梯形将不改变颜色和大小，放置在上部.7、【解析】：观察可以发现，从第一个火柴人开始，到B增加2条线，到C拿走1条线，到D增加3条线，到E拿走2条线，到F增加4条线，按规律继续往下画在F的基础上应该拿走3条线，应该选择G.。

？第3组第1组（2）？第3组第2组第1组（3）★★★★★？第3组第1组【例 1】 观察下图的变化规律，画出丙图.DBA丙乙甲CB A【例 2】 有六种不同图案的瓷砖，每种各6块.将它们砌在如下图那样的地面上，使每一横行和每一竖行都没有相同图案的瓷砖.你会怎样设计【例 3】 下面各种各样的娃娃头好看吗认真观察你能找到它们排列的规律吗根据规律把最后一个画出来.【例 4】 观察图中所给出图形的变化规律，然后在空白处填画上所缺的图形.【例 5】 琪琪特别喜欢蝴蝶，她用直尺和圆规在纸上画了9幅蝴蝶图，并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上，见下图1，她发现这些纸蝴蝶排列挺有规律，突然一阵风来，吹走了3只纸蝴蝶，见下图2.你能找出蝴蝶的排列规律，将图2的3只蝴蝶放入图1的空缺处吗图1987654321图2BCA【例 6】 请观察下图中已有的几个图形，并按规律填出空白处的图形.【例 7】 观察下列各组图的变化规律，并在“”处画出相关的图形.（1）？（2）丁丙乙甲？【例 8】 如图，根据图中已知3个方格表中阴影的规律，在空白的方格表中也填上相应的阴影.【巩固】根据前三个方格表中阴影部分的变化规律，填上第（10）个方格表中阴影部分的小正方形内的几个数之和。

698754321......（10）【例 9】按照下列图形的变化规律，空白处应是什么样的图形？【巩固】按照下列图形的变化规律，空白处应是什么样的图形？【例 10】请你认真仔细观察，按照下面图形的变化规律，在“”处画出合适的图形。

【例 11】观察下图的变化规律，在“”处填入适当的图形.【例 12】下图中的图形是按一定规律排列的，请仔细观察，并在“”处填上适当的图形.？？？ihgfedcba【巩固】下面的图形是按一定规律排列的，请仔细观察，并在“”处填上适当的图形。

【例 13】 按照变化规律在“”处填上合适的图形.（1）（2）（d ）（c ）（b ）（a ）【例 14】 观察下列各组图的变化规律，并在“”处画出相关的图形.【例 15】 仔细观察下列图形的变化，请先回答：（1）在方框（4）中应画出怎样的图形（2）再按（1）、（2）、（3）……的顺序数下去，第（10）个方框是怎样的图形【巩固】仔细观察下列图形的变化，请先回答：(1) 在方框（4）中应画出怎样的图形(2) 再按（1）、（2）、（3）、……的顺序数下去，第（10）个方框是怎样的图形【例 16】 顺序观察下面图形，并按其变化规律在“”处填上合适的图形.（1）（2）（3）（4）板块三其他【例 17】请找出下面哪个图形与其他图形不一样。

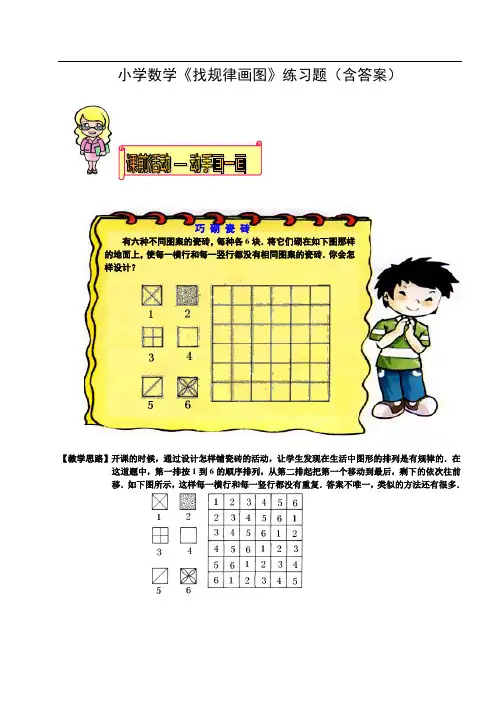
小学数学《找规律画图》练习题（含答案）【教学思路】开课的时候，通过设计怎样铺瓷砖的活动，让学生发现在生活中图形的排列是有规律的．在这道题中，第一排按1到6的顺序排列，从第二排起把第一个移动到最后，剩下的依次往前移．如下图所示，这样每一横行和每一竖行都没有重复．答案不唯一，类似的方法还有很多．巧砌瓷砖有六种不同图案的瓷砖，每种各6块．将它们砌在如下图那样的地面上，使每一横行和每一竖行都没有相同图案的瓷砖．你会怎样设计？同学们，生活中很多的图形在排列的时候都是有规律的，只要我们仔细观察，认真分析就一定能找到其中的规律．今天这节课就让我们走进这美妙的图形王国，去探索其中的奥秘吧！按规律填出空白图形．⑴答案：第二排第三个第三排第二个⑵答案：⑶答案：⑷答案：这些图形的排列都有一定的规律，你能找到吗？【教学思路】⑴通过观察，可以发现：每行每列都只有三角形、五边形、圆．所以第二行第三个图形应该是五边形，第三行第二个图形应该是圆形．⑵通过观察，不难发现，图形从左到右的变化规律是：边数在一条条增加，图形中的直线条数也在一条条增加，而且直线的方向是：横—竖—横—竖这样变化的．因此第四幅图应是一个正六边形，里面有4条竖着的直线，⑶我们发现第一个图和第二个图形状相同，图形里面的阴影相反．根据这个规律第三个图形和第四个图形也应该如此，因此第四个图形和第三个图形形状相同，里面的阴影应该相反．⑷仔细观察发现，圆的变化是：一个比一个增多，所以第四个图里面应该画四个圆．三角形的变化是：方向是按顺时针转动的，上—右—下—左，所以第四个图里面的三角形方向应该向左．按照下面的规律，画一画．⑴⑵【教学思路】⑴第四个图中蓝色的三角应该往左和上各移动一个位置．⑵左边和右边的图合在一起就组成了中间的图形．答案图下：⑴⑵在方框内填上适当的图形．答案：【教学思路】观察这个图我们发现，每组中的三个图形形状相同，只是图形里面的阴影不同，不过这三个图形中的阴影合起来正好是这个图形完整的阴影．这样根据所缺的阴影来判断，第三个图形的阴影应该是第一个图形阴影相对的那一块．1．你知道“？”处应该画什么吗？【教学思路】通过观察我们发现．第一个图形和第二个图形可以组成第三个图形，因此“？”处应该是下图所示．？2．下面图形的排列有什么规律呢？请你把空白处补充完整．答案：【教学思路】通过观察我们发现，每排中的三个图中间部分的图案都相同，不同的是第一个外面部分没有，第二个外面部分是圆，第三个外面部分是正方形．根据这个规律空白处的图案应该是右上图．下面的图形是按一定规律排列的，依据这一规律，画出所缺图形．【教学思路】通过观察，第一行和第二行圆中的3个图形都是相同的，不同的地方只是它们的排列顺序，第一排的第一个在第二排中被移到了第三个，第一排的第二个和第三个，在第二排中被移到了第一个和第二个．根据这样移动的规律，第三排得的第三个就应该是第二排的第一个．所以在第3行的“？”处应填．下图中的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形．【教学思路】本图中，首先可以注意到每个图形都由大、小两部分组成，而且，大、小图形都是由正方形、三角形和圆形组成，图中的任意两个图形均不相同．因此，我们不妨试着把大、小图形分开来考虑，再一次观察后我们可以发现：对于大图形来说，每行每列的图形决不重复．因此，每行每列都只有一个大正方形，一个大三角形和一个大圆，对于小图形也是如此，这样，“？”处的图形分别应填下面的三个图形．按图形的变化规律，在“？”处画上所缺的图形．答案：【教学思路】如果单纯分析颜色，恐怕不好掌握问题的关键．如果我们把图“转”起来就会很快发现它的规律．如第一行的第一幅图逆时针旋转90度就变成了第二幅图，再旋转90度就变成了第三幅图．同理，用此方法验证第三行的三幅图是成立的．所以第二行的第二幅图也应把第一幅图逆时针旋转90度，答案如右上图．【教学思路】用一条比桥面长的钢索系在炮车与大炮之间，让炮车拖着大炮过桥，这样二者就不会同时压在桥上，而且，可以顺利地过桥了。

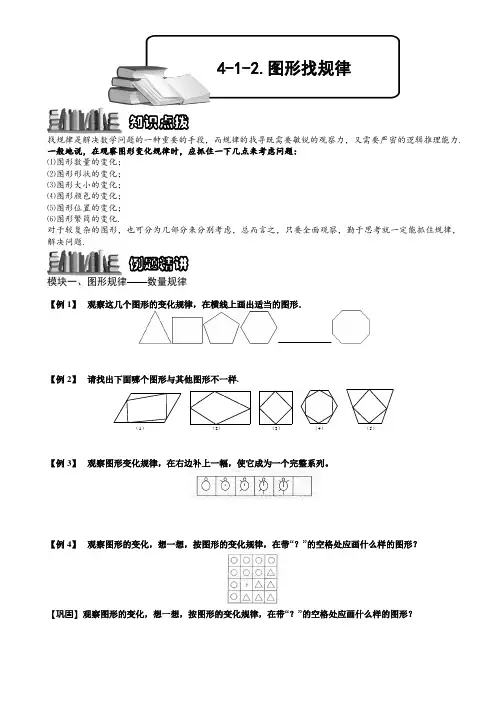
找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题： ⑴图形数量的变化； ⑵图形形状的变化； ⑶图形大小的变化； ⑷图形颜色的变化； ⑸图形位置的变化； ⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律，在横线上画出适当的图形．【例 2】 请找出下面哪个图形与其他图形不一样.（1）（2）（3）（4）（5）【例 3】 观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【例 4】 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【巩固】 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【例5】观察下面的图形，按规律在“？”处填上适当的图形.（4）？【例6】观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【例7】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

【例8】观察下面由点组成的图形（点群），请回答：（1）方框内的点群包含个点；（2）第（10）个点群中包含个点；（3）前十个点群中，所有点的总数是。

【例9】下图表示“宝塔”，它们的层数不同，但都是由一样大的小三角形摆成的.仔细观察后，请回答：（1）五层的“宝塔”的最下层包含多少个小三角形？（2）整个五层“宝塔”一共包含多少个小三角形？【例 10】 在纸上画5条直线，最多可有 个交点。

模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒，里面装着世界上最宝贵的财富，但是并不是拥有宝盒都可以得到这笔财富，在宝盒的上面设置了密码，只有写出密码的人才会真正拥有这笔财富，聪明的你你能找出密码吗？ ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ （）（）（）（）（）（）（）（）【例 12】 下面的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形.（1）（2）（3）【例 13】 观察下图的变化规律，画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成，记为A ★B 、C ★D 、A ★D ．请你画出表示A ★C 的图形．A★B C★D A★D【例15】(希望杯五年级一试第7题，6分)下列四个图形是由四个简单图形A、B、C、D（线段和正方形）组合（记为*）而成。

找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题： ⑴图形数量的变化； ⑵图形形状的变化； ⑶图形大小的变化； ⑷图形颜色的变化； ⑸图形位置的变化； ⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律，在横线上画出适当的图形．【例 2】 请找出下面哪个图形与其他图形不一样.（1）（2）（3）（4）（5）【例 3】 观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【例 4】 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【巩固】 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【例5】观察下面的图形，按规律在“？”处填上适当的图形.（4）？【例6】观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【例7】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

【例8】观察下面由点组成的图形（点群），请回答：（1）方框内的点群包含个点；（2）第（10）个点群中包含个点；（3）前十个点群中，所有点的总数是。

【例9】下图表示“宝塔”，它们的层数不同，但都是由一样大的小三角形摆成的.仔细观察后，请回答：（1）五层的“宝塔”的最下层包含多少个小三角形？（2）整个五层“宝塔”一共包含多少个小三角形？【例 10】 在纸上画5条直线，最多可有 个交点。

模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒，里面装着世界上最宝贵的财富，但是并不是拥有宝盒都可以得到这笔财富，在宝盒的上面设置了密码，只有写出密码的人才会真正拥有这笔财富，聪明的你你能找出密码吗？ ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ （）（）（）（）（）（）（）（）【例 12】 下面的图形是按一定规律排列的，请仔细观察，并在“？”处填上适当的图形.（1）（2）（3）【例 13】 观察下图的变化规律，画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成，记为A ★B 、C ★D 、A ★D ．请你画出表示A ★C 的图形．A★B C★D A★D【例15】(希望杯五年级一试第7题，6分)下列四个图形是由四个简单图形A、B、C、D（线段和正方形）组合（记为*）而成。

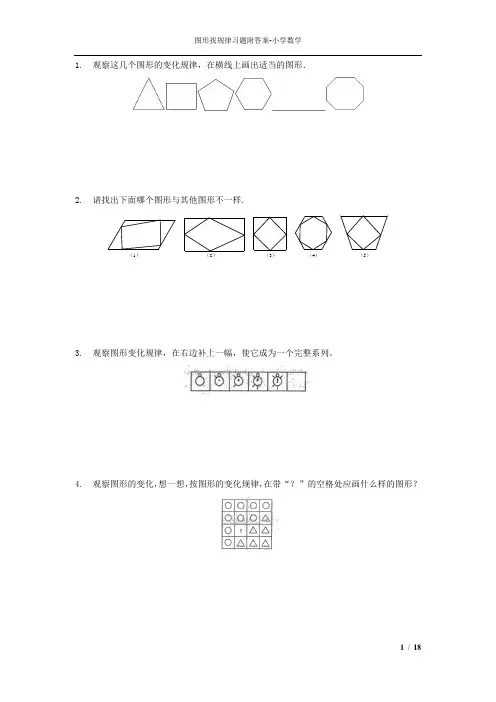
1. 观察这几个图形的变化规律，在横线上画出适当的图形．
2. 请找出下面哪个图形与其他图形不一样.
3. 观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

4. 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？
（1）（2
）（3
）（4
）（5
）
5. 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？
6. 观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？
7. 观察下面的图形，按规律在“？”处填上适当的图形.
8. 观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.
？
（4）
？。

找规律是解决数学问题的一种重要的手段，而规律的找寻既需要敏锐的观察力，又需要严密的逻辑推理能力.一般地说，在观察图形变化规律时，应抓住一下几点来考虑问题：⑴图形数量的变化；⑵图形形状的变化；⑶图形大小的变化；⑷图形颜色的变化；⑸图形位置的变化；⑹图形繁简的变化.对于较复杂的图形，也可分为几部分来分别考虑，总而言之，只要全面观察，勤于思考就一定能抓住规律，解决问题.模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律，在横线上画出适当的图形．【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加，因此横线上应为一个七边形．【答案】七边形【例 2】请找出下面哪个图形与其他图形不一样.（1）（2）（3）（4）（5）【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是，连接各边上一点，组成一个复合图形.所不同的是，第四个图形是一个六边形，而其它几个都是四边形，这样，只有（4）与其它不一样【答案】（4）【例 3】观察图形变化规律，在右边补上一幅，使它成为一个完整系列。

【考点】图形找规律【难度】2星【题型】填空【解析】观察发现，乌龟的顺序是：头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点，根据这个规律，最后一幅图应该是：→四只脚、一条尾、背上五个点.即：例题精讲知识点拨4-1-2.图形找规律【答案】【例 4】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个圆形。

【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行圆形的个数一次减少，而三角形的个数依次增加，但每行图形的总个数不变.因为圆形的个数是按5、4、3、？、1的顺序变化的，显然“？”处应填一个圆形.(方法二)竖着看，圆形由左而右依次减少，而三角形由左而右依次增加，圆形按照5、4、？、2、1的顺序变化，也可以看出“？”处应是圆形.【答案】圆形【巩固】观察图形的变化，想一想，按图形的变化规律，在带“？”的空格处应画什么样的图形？？【考点】图形找规律【难度】2星【题型】填空【解析】（方法一）横着看，每行三角形的个数依次减少，而正方形的个数依次增加，但每行图形的总个数不变.因为三角形的个数是按4、3、？、1的顺序变化的，显然“？”处应填一个三角形△.(方法二)竖着看，三角形由左而右依次减少，而正方形由左而右依次增加，三角形按照4、？、2、1的顺序变化，也可以看出“？”处应是三角形△.【答案】△【例 5】观察下面的图形，按规律在“？”处填上适当的图形.（5）（4）（3）（2）（1）？【考点】图形找规律【难度】2星【题型】填空【解析】本题中，几何图形的变化表现在数量关系上，图中黑三角形的个数从左到右依次增多，从（2）起，每一个格比前面一个格多两个黑三角形，所以，第（4）个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】观察图形变化规律，在右边再补上一幅，使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈，第二格有4个圆圈，第三格有2个圆圈，第四格有1个圆圈，第五格有半个圆圈.由此发现，前一格中的图减少一般，正好是后一格的图.所以第六格的图应该是第五格图的一半，即：【答案】【例 7】观察下图中的点群，请回答：(1)方框内的点群包含个点；(2)推测第10个点群中包含个点；(3)前10个点群中，所有点的总数是。

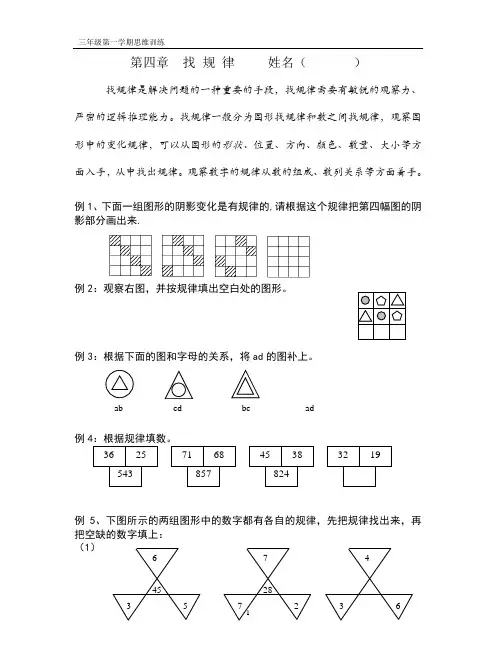
6 45 35 7 287 2 4 3 6第四章 找 规 律 姓名（ ）找规律是解决问题的一种重要的手段，找规律需要有敏锐的观察力、严密的逻辑推理能力。

找规律一般分为图形找规律和数之间找规律，观察图形中的变化规律，可以从图形的形状、位置、方向、颜色、数量、大小等方面入手，从中找出规律。

观察数字的规律从数的组成、数列关系等方面着手。

例1、下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.例2：观察右图，并按规律填出空白处的图形。

例3：根据下面的图和字母的关系，将ad 的图补上。

例4：根据规律填数。

例5、下图所示的两组图形中的数字都有各自的规律，先把规律找出来，再把空缺的数字填上：（1）ab cd bcad 36 25 543 71 68 857 45 38 824 3219（2）例6：仔细观察下图，根据规律填出所缺的数。

例7：下面三块正方体的六个面，都是按相同的规律涂有红、黄、蓝、白、黑、绿六种颜色。

那么请你根据这一规律，白色的对面是什么颜色？红色的对面是什么颜色？黄色的对面是什么颜色？（1） （2） （3）练习：1、下面括号里两个数按一定规律组合，在（ ）里填上适当的数。

（1）、（8，7）、（6，9）（10、5）、（ 、13 ）。

（2）、（2，3）、（5，9）、（7、13）、（ 、23 ）。

（3）、（18，10）、（10，6）、（20、11）、（ 、4（4）、 1、 2、 3、 6、 11、 20、（ ）2、仔细观察一右图，并按它的变化规律， 在“？”处填上适当的图。

3、在右图空格里填数白 黑 黄 绿 白 红 黄蓝 红 ？ 3 12 6 4 16 8 5 206 124．下面的每一个图形都是由△，□，○中的两个构成的。

观察各图形与它下面的数之间的关系，“？”应当是几？5、找规律,从a,b,c,d,e中选入一幅图填入空格内.6. 找规律，画出第四幅图的答案.7、下图是由9个小人排列的方阵,但有一个小人没有到位,请你从右面的6个小人中,选一位小人放到问号的位置.你认为最合适的人选是（）号.8、根据规律填数。

小学数学奥数训练：探索规律专项练习试卷及答案(50道解答题有详细答案解析)小学数学奥数训练：探索规律专项练试卷及答案（50道解答题有详细答案解析）1、在大于1000的整数中，找出所有被34除后商与余数相等的数，那么这些数的和是多少?2、动脑筋，探索规律。

1.2×2.1=11.2×2.11=111.2×2.111=1111.2×2.1111=.2×2.=你发现了什么规律？3、按照规律接着画出第4幅图。

第10幅图中一共有()个点。

4、用火柴棒摆出图形。

摆第1个图形要4根火柴棒。

那么摆第5个图形要多少根火柴棒?5、一张桌子坐4人，两张桌子并起来坐6人，三张桌子并起来坐8人，…照这样计算，10张桌子并成一排可坐多少人？如果一共有26人，需要并多少张桌子？6、图形三角形个数所需火柴数1234……………10n3579 (1001)(1)10个三角形需要几根洋火？摆n个呢？(2)如果有1001根火柴可以摆几个三角形？共20页，第1页7、观察：÷3=﹣3，差．÷4=﹣4，请再写出两个数，使它们的商等于它们的8、已知1+3=4=2，1+3+5=9=3，1+3+5+7=16=4，1+3+5+7+9=25=5，...(1)仿照上例，计算：1+3+5+7+ (99)(2)按照上述纪律，请你用自然数n（n≥1）表示一般纪律．22229、下列图案由边长相等的黑、白两色小正方形按一定规律拼接而成。

照如许画下去，第10个图形中分别有几何个玄色小正方形和白色小正方形？你能说明个中的道理吗？10、有一个挂钟，每小时敲一次钟，几点敲几下，钟敲6下，5秒钟敲完，钟敲12下，几秒钟敲完？11、观察点子图，找一找有什么纪律，想一想，第8个方框里有______个点，第20个方框内呢？12、图(1)是一个三角形，分别连接这个三角形三边的中点得到图(2)，再分别连接图(2)中间的小三角形三边的中点，得到图(3)．按这样的方法继续下去，第100个图形有多少个小三角形？共20页，第2页13、用三条边都是l厘米的三角形拼图形，按如下规律拼下去．想一想：用29个如许的三角形拼成的图形是什么图形？14、（2012•成都）一串分数：，，，，，，，，，…（1）是此串分数中的第多少个分数？（2）第115个分数是多少？15、（2013•长沙）有这样一串数、、、、、、、、、…（1）第407个分数是多少？（2）从开始，前407个分数的和是几何？16、（2011•海港区）判断推理．三角形个数1个2个3个4个…小棒的根数3根5根7根9根…观察图形和表格，如果要摆100个三角形，需要多少根小棒？要摆n个三角形，需要多少根小棒？17、观察下图，按规律填表。

图形找规律专项练习60 题（有答案）1．按如下方式放餐桌和椅子：填表中缺少可坐人数_________；_________．2．察表中三角形个数的化律：形横截012⋯n条数三角6？？⋯？形个数若三角形的横截有0 条，三角形的个数是6；若三角形的横截有n 条，三角形的个数是_________（用含 n 的代数式表示）．3．如，在段AB上，画 1 个点，可得 3 条段；画 2 个不同点，可得 6 条段；画 3 个不同点，可得10 条段；⋯照此律，画10 个不同点，可得段_________条．4．如是由数字成的三角形，除最端的 1 以外，以下出的数字都按一定的律排列．根据它的律，最下排数字中 x 的是_________ ，y 的是 _________ ．5．下列形都是由相同大小的位正方形构成，依照中律，第六个形中有_________个位正方形．6．如，用相同的火柴棒拼三角形，依此拼律，第7 个形中共有_________根火柴棒．7． 1 是一个正方形，分接个正方形的中点，得到2；分接 2 中右下角的小正方形中点，得到 3；再分接 3 中右下角的小正方形中点，得到4；按此方法下去，第n 个的所有正方形个数是_________个．8．察下列案：它是按照一定律排列的，依照此律，第 6 个案中共有_________个三角形．9．如，依次接一个 1 的正方形各的中点，得到第二个正方形，再依次接第二个正方形各的中点，得到第三个正方形，按此方法下去，第二个正方形的面是_________；第六个正方形的面是_________．10．下列各形中的小正方形是按照一定律排列的，根据形所揭示的律我可以：第 1 个形有 1 个小正方形，第 2 个形有 3 个小正方形，第 3 个形有 6 个小正方形，第 4 个形有10 个小正方形⋯，按照的律，第10 个形有_________个小正方形．11．如，用棋子按下面的律形，第n 个形需要棋子的枚数_________．12．祝“六一”儿童，幼儿园行用火柴棒“金”比，如所示，n 条“金”需用火柴棒的根数_________．13．如，两条直相交只有 1 个交点，三条直相交最多有 3 个交点，四条直相交最多有 6 个交点，五条直相交最多有10 个交点，六条直相交最多有_________个交点，二十条直相交最多有_________个交点．14．用火柴棒按如所示的方式搭形，按照的律搭下去，填写下表：形号（ 1）（2）（3）⋯n火柴根数从左到右依次____________________________________．15．（ 1）是一个黑色的正三角形，次接三中点，得到如（2）所示的第 2 个形（它的中一个白色的正三角形）；在（ 2）的每个黑色的正三角形中分重复上述的作法，得到如（3）所示的第 3 个形．如此作下去，在得到的第 5 个形中，白色的正三角形的个数是_________．16．如，一形烙切一刀可以切成 2 ，若切两刀最多可以切成 4 ，切三刀最多可以切成7 ⋯通察、算填下表（其中S 表示切 n 刀最多可以切成的数）后，可探究一形烙切n 刀最多能切成_________ （果用n 的代数式表示）．n012345⋯17．如，是用相同的等腰梯形拼成的等腰梯形案．第（1）个案只有 1 个等腰梯形，其两腰之和4，上下底之和 3，周 7；第（ 2）个案由 3 个等腰梯形拼成，其周13；⋯第（ n）个案由（ 2n 1）个等腰梯形拼成，其周_________．（用正整数n 表示）18．下列各均是用有一定律的点成的案，用S 表示第 n 个案中点的数，S= _________（用含n 的式子表示）．19．如，由若干盆花成案，每个点表示一盆花，几何形的每条上（包括两个点）都有n（ n≥ 3）盆花，每个案中花盆数S，按照中的律可以推断S 与 n（ n≥3）的关系是_________．20．用火柴棍象如搭形，搭第n 个形需要_________根火柴棍．21．有黑色三角形“”和白色三角形“”共有2011个，按照一定的律排列如下：黑色三角形有_________个．22．假有足多的黑白棋子，按照一定的律排成一行：○●●○○●○●●○○●○●●○○●○●●○○●⋯第 2011 个棋子是黑的是白的？答：_________．23．察下列由等腰梯形成的形和所表中数据的律后填空：梯形的个 1 2 3 4 5 ⋯数形的周 5 8 11 14 17 ⋯当梯形个数2007 个，形的周_________24．如图，下面是一些小正方形组成的图案，第4个图案有_________个小正方形组成；第n个图案有_________个小正方形组成．25．如图所示是由火柴棒按一定规律拼出的一系列图形：依照此规律，第7 个图形中火柴棒的根数是_________．26．图中的每个图形都是由若干个棋子围成的正方形图案，图案的每条边（包括两个顶点）上都有n（ n≥ 2）个棋子，每个图案的棋子总数为s，按图的排列规律推断，s 与 n 之间的关系可用式子_________表示．27．观察下列图形，它是按一定规律排列的，那么第_________个图形中，十字星与五角星的个数和为27个．28． 2 条直线最多只有 1 个交点； 3 条直线最多只有 3 个交点； 4 条直线最多只有 6 个交点； 2000 条直线最多只有_________个交点．29．以下各图分别由一些边长为 1 的小正方形组成，请填写图2、图 3 中的周长，并以此推断出图10 的周长为_________．30．如图所示，第 1 个图案是由黑白两种颜色的正六边形地面砖组成，第 2 个，第 3 个图案可以看作是第 1 个图案经过平移而得，那么设第n 个图案中有白色地面砖m块，则 m与 n 的函数关系式是_________．31．用同样大小的黑色棋子按如图所示的规律摆放：（1）分别写出第 6、 7 两个图形各有多少颗黑色棋子？（2）写出第 n 个图形黑色棋子的颗数？（3）是否存在某个图形有 2012 颗黑色棋子？若存在，求出是第几个图形；若不存在，请说明理由．32．如图，给出四个点阵，s 表示每个点阵中点的个数，按照图形中的点的个数变化规律，（ 1）猜想第n 个点阵中的点的个数s= _________．（ 2）若已知点阵中点的个数为37，问这个点阵是第几个？33．用棋子摆出下列一组图形：（ 1）填写下表：图形编号 1 2 3 4 5 6图中棋子数 5 8 11 14 17 20（ 2）照这样的方式摆下去，写出摆第n 个图形所需棋子的枚数；（ 3）其中某一图形可能共有2011 枚棋子吗？若不可能，请说明理由；若可能，请你求出是第几个图形．34．观察图中四个顶点的数字规律：（ 1）数字“ 30”在_________个正方形的_________；（2）请你用含有 n（ n≥ 1 的整数）的式子表示正方形四个顶点的数字规律；（3）数字“ 2011”应标在什么位置．35．如，各表示若干盆花成的形如三角形的案，每条（包括两个点）有n（n＞ 1）盆花，每个案中花盆的数S．：①当每条有 2 盆花，花盆的数S 是多少？②当每条有 3 盆花，花盆的数S 是多少？③当每条有 4 盆花，花盆的数S 是多少？④当每条有10 盆花，花盆的数S 是多少？⑤按此律推断，当每条有n 盆花，花盆的数S 是多少？36．如下是用棋子成的“上”字：如果按照以上律下去，那么通察，可以：（ 1）第④、第⑤个“上”字分需用_________和_________枚棋子；（ 2）第 n 个“上”字需用_________枚棋子；（ 3）七（ 3）班有 50 名同学，把每一位同学当做一枚棋子，能否 50 枚“棋子” 按照以上律恰好站成一个“上”字？若能，算最下一“横”的学生数；若不能，明理由．37．下列表格是一同一段上的个数化及段条数的探究．段上点的个数段的条数11+2=31+2+3=6⋯⋯（ 1）你完成探究，并把探究果填在相的表格里；（ 2）若在同一段上有10 个点，段的条数_________；若在同一段上有n 个点，有_________ 条段（用含n 的式子表示）（ 3）若你所在的班有60 名学生， 20 年后参加同学聚会，面每两个同学之握一次手，共握手_________ 次．38．如图是用棋子摆成的“H”字．（ 1）摆成第一个“H”字需要_________个棋子；摆第x 个“ H”字需要的棋子数可用含x 的代数式表示为_________；（ 2）问第几个“H”字棋子数量正好是2012 个棋子？39．我们知道，两条直线相交只有一个交点．请你探究：（ 1）三条直线两两相交，最多有_________个交点；（ 2）四条直线两两相交，最多有_________个交点；（ 3） n 条直线两两相交，最多有_________个交点（n为正整数，且n≥ 2）．40．如图所示，小王玩游戏：一张纸片，第一次将其撕成四小片，手中共有 4 张纸片，以后每次都将其中一片撕成更小的四片．如此进行下去，当小王撕到第n 次时，手张共有S 张纸片．根据上述情况：（ 1）用含 n 的代数式表示S；（ 2）当小王撕到第几次时，他手中共有70 张小纸片？41．如图①是一张长方形餐桌，四周可坐 6 人， 2 张这样的桌子按图②方式拼接，四周可坐10 人．现将若干张这样的餐桌按图③方式拼接起来：（ 1）三张餐桌按题中的拼接方式，四周可坐_________人；（ 2） n 张餐桌按上面的方式拼接，四周可坐_________人（用含n 的代数式表示）．若用餐人数为26 人，则这样的餐桌需要_________张．42．用棋子出下列一形：（ 1）填写下表：形号 1 2 3 4 5 6 形中的棋子（2）照的方式下去，写出第n 个形棋子的枚数；（用含 n 的代数式表示）（3）如果某一形共有 99 枚棋子，你知道它是第几个形？43．如①，②，③，④，⋯，是用棋棋子按照某种律成的一行“广”字，按照种律，（ 1）第 5 个“广”字中的棋子个数是_________．（ 2）第 n 个“广”字需要多少枚棋子？44．如，用同格黑白两色的正方形瓷矩形地面，察形并解答有关：（ 1）在第 n 个中共有_________黑瓷，_________白瓷；（ 2）是否存在黑瓷与白瓷数相等的情形？你能通算明？45．用火柴棒按如的方式搭三角形．（ 2）搭 n 个这样的三角形要用_________根火柴棒（用含n 的代数式表示）．46．观察图中的棋子：（ 1）按照这样的规律摆下去，第 4 个图形中的棋子个数是多少？（2）用含 n 的代数式表示第 n 个图形的棋子个数；（3）求第 20 个图形需棋子多少个？47．如图，用正方体石墩垒石梯，下图分别表示垒到一、二、三阶梯时的情况．那么照这样垒下去，请你观察规律，并完成下列问题．（ 1）填出下表中未填的两个空格：阶梯级数一级二级三级四级石墩块数39（ 2）当垒到第n 级阶梯时，共用正方体石墩多少块（用含n 的代数式表示）？并求当n=100 时，共用正方体石墩多少块？48．有一张厚度为0.05 毫米的纸，将它对折 1 次后，厚度为2× 0.05 毫米．（1）对折 3 次后，厚度为多少毫米？（2）对折 n 次后，厚度为多少毫米？（3）对折 n 次后，可以得到多少条折痕？49．如图所示，用同样规格正方形瓷砖铺设矩形地面，请观察下图：按此规律，第n 个图形，每一横行有_________块瓷砖，每一竖列有_________块瓷砖（用含n 的代数式表示）按此规律，铺设了一矩形地面，共用瓷砖506 块，请问这一矩形的每一横行有多少块瓷砖，每一竖列有多少瓷砖？50．找规律：观察下面的星阵图和相应的等式，探究其中的规律．（1）在④、⑤和⑥后面的横线上分别写出相应的等式：① 1=12② 1+3=22③ 1+3+5=32④_________ ；⑤ _________ ；⑥ _________ ；（ 2）通过猜想，写出第 n 个星阵图相对应的等式．51．将一张正方形纸片剪成四个大小一样的小正方形，然后将其中的一个正方形再剪成四个小正方形，如此循环下去，如图所示：（ 1）完成下表：所剪次数n1234 5正方形个数Sn 4（ 2）剪 n 次共有 S n个正方形，请用含n 的代数式表示S n= _________；（ 3）若原正方形的边长为1，则第 n 次所剪得的正方形边长是_________（用含n的代数式表示）．52．如图是用五角星摆成的三角形图案，每条边上有n（ n＞ 1）个点（即五角星），每个图案的总点数（即五角星总数）用 S 表示．（ 1）观察图案，当n=6 时， S= _________；（ 2）分析上面的一些特例，你能得出怎样的规律？（用n 表示 S）（ 3）当 n=2008 时，求 S．53．用水平和直将平面分成若干个 1 的小正方形格子，小正方形的点，叫格点．察中每一个正方形（）四条上的格点的个数，回答下列：（ 1）由里向外第 1 个正方形（）四条上的格点个数共有_________ 个；由里向外第 2 个正方形（）四条上的格点个数共有_________ 个；由里向外第 3 个正方形（）四条上的格点个数共有_________ 个；（ 2）由里向外第10 个正方形（）四条上的格点个数共有_________ 个；（ 3）由里向外第n 个正方形（）四条上的格点个数共有_________ 个．54．下列各是由若干花盆成的形如正方形的案，每条（包括两个点）有n（ n＞ 1）个花盆，每个案花盆数是S．（ 1）按要求填表：n 2 3 4 5 ⋯S 4 8 12 ⋯（ 2）写出当 n=10 ， S= _________ ．（ 3）写出 S 与 n 的关系式： S= _________ ．（ 4）用 42 个花盆能出似的案？55．如，用同格的黑白两色正方形瓷矩形地面，察下列形，探究并解答下列．（ 1）在第 1 个中，共有白色瓷_________ ．（ 2）在第 2 个中，共有白色瓷_________ ．（ 3）在第 3 个中，共有白色瓷_________ ．（ 4）在第 10 个中，共有白色瓷_________ ．（ 5）在第 n 个中，共有白色瓷_________．56．淮北市建文明城市，各种色的菊花成如下三角形的案，每条（包括两个点）上有n（ n＞ 1）盆花，每个案花盆的数S，当 n=2 ， S=3； n=3 ， S=6； n=4 ， S=10．（ 1）当 n=6 ， S= _________；n=100，S=_________．（ 2）你能得出怎的律？用n 表示 S．57．下面是按照一定律画出的一系列“ 枝” 察，（2）比（ 1）多出 2 个“ 枝”，（ 3）比（ 2）多出 4 个“ 枝”，（ 4）比（ 3）多出 8 个“ 枝”，按此律：（ 5）比（ 4）多出_________ 个枝；（ 6）比（ 5）多出_________ 个枝；（ 8）比（ 7）多出_________ 个枝；⋯（ n+1）比（ n）多出_________ 个枝．58．如是用棋子成的“T”字案．从案中可以出，第一个“T”字案需要 5 枚棋子，第二个“T”字案需要 8 枚棋子，第三个“T” 案需要11 枚棋子．（1）照此律，成第八个案需要几枚棋子？（2）成第 n 个案需要几枚棋子？（3）成第 2010 个案需要几枚棋子？59．用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案：（ 1）当黑砖n=1 时，白砖有_________块，当黑砖n=2 时，白砖有_________块，当黑砖n=3 时，白砖有_________块．（ 2）第 n 个图案中，白色地砖共_________块．60．下列图案是晋商大院窗格的一部分．其中，“ o”代表窗纸上所贴的剪纸．探索并回答下列问题：（ 1）第 6 个图案中所贴剪纸“o”的个数是_________；（ 2）第 n 个图案中所贴剪纸“o”的个数是_________；（ 3）是否存在一个图案，其上所贴剪纸“o”的个数为2012 个？若存在，指出是第几个；若不存在，请说明理由．故答案26图形找规律 60 题参考答案：9．∵正方形的是1，1．合形和表格，不： 1 桌子座 6 人，多一所以它的斜是：= ，桌子多 2 人． 4 桌子可以座10+2=12．即 n 桌子，共座6+2（ n 1） =2n+4．所以第二个正方形的面是：×= ，2．当横截有 n 条，在 6 个的基上多了n 个 6，即三角形的个数共有 6+6n=6（n+1）个．故填6（ n+1）第三个正方形的面2或 6n+6=（），3．∵画 1 个点，可得 3 条段， 2+1=3；以此推，第 n 个正方形的面（）n ﹣1画 2 个点，可得 6 条段， 3+2+1=6；，画 3 个点，可得10 条段， 4+3+2+1=10；所以第六个正方形的面是（） 6﹣ 1= ；⋯；画 n 个点，可得（ 1+2+3+⋯ +n+n+1）= 故答案：，．条段．10．∵第一个有 1 个小正方形，第二个有1+2 个，第三所以画 10 个点，可得=66 条段；个有 1+2+3 个，第四个有 1+2+3+4，第五个有 1+2+3+4+5，∴ 第 10 个形有 1+2+3+4+5+6+7+8+9+10=55 个．4．根据形可以，故答案： 55第七排的第一个数和第二数与第八排的第二个数相等，11．依意得：（ 1）第 1 个“小屋子”需要 5 个点；而第八排的第二个数就是x，所以 x=61．第 2 个“小屋子”需要11 个点；另外，由形可知， x 右的数是2× 61=122，y 左的第 3 个“小屋子”需要17 个点．数是 2× 61+56=178，当 n=n ，需要的点数（6n 1）个．所以 y=178+46=224 故答案 6n 15．根据意分析可得：第 1 个案中正方形的个数 2 12．由形可知：个，第 2 个案中正方形的个数比第 1 个案中正方形第一个金需用火柴棒的根数：2+6=8；的个数多 4 个，第 3 个案中正方形的个数比第 2 个第二个金需用火柴棒的根数：2+2× 6=14；案中正方形的个数多 6 个⋯，依照中律，第六个第三个金需用火柴棒的根数：2+3× 6=20；形中有 2+4+6+8+10+12=42 个位正方形⋯；第 n 个金需用火柴棒的根数：2+n× 6=2+6n．6．形从上到下可以分成几行，第n行中，斜放故答案 2+6n的火柴有 2n 根，下面横放的有n 根，因而形13．6 条直两两相交，最多有n（ n 1）= × 6×5=15，中有 n 排三角形，火柴的根数是：斜放的是2+4+⋯+2n=2（1+2+⋯+n）横放的是：1+2+3+⋯+n，20 条直两两相交，最多有 n（ n 1）= × 20× 19=190．每排放 n 根有火柴数是：3（1+2+⋯+n）= 3n（ n 1)把 n=7 代入就可以求出．故答案：15，190．14．如表格所示：2故第 7 个形中共有=84 根火柴棒形（ 1）（ 2）（ 3）⋯n 号7． 1 中，是 1 个正方形；火柴 7 12 17 ⋯5n+22 中，是 1+4=5 个正方形；根数3 中，是 1+4× 2=9 个正方形；依此推，第 n 个的所有正方形个数是1+4（ n 1）15．白三角形 x 个，黑三角形y 个，=4n 3．： n=1 ， x=0， y=1；8．∵第 1 个案中有2× 2+2× 1=6 个三角形；n=2 ， x=0+1=1， y=3；第 2 个案中有2×3+2× 2=10 个三角形；n=3 ， x=3+1=4， y=9；第 3 个案中有2×4+2× 3=14 个三角形；n=4 ， x=4+9=13， y=27；⋯当 n=5 ， x=13+27=40，图形找规律 ---第15页共20页故答案： 40 第一个形有1=12个小正方形；16． n=1 ， S=1+1=2，第二个形有1+3=4=22个小正方形；n=2 ， S=1+1+2=4，第三个形有1+3+5=9=32个小正方形；n=3 ， S=1+1+2+3=7，⋯n=4 ， S=1+1+2+3+4=11，2个小正方形，第 n 个形共有 1+2+3+⋯ +（ 2n 1） =n⋯当 n=4 ，有 n2=42=16 个小正方形．所以当切 n 刀， S=1+1+2+3+4+⋯ +n=1+ n（ n+1）故答案： 16，n 225．根据已知形可以：= n2+ n+1．第 2 个形中，火柴棒的根数是7；第 3 个形中，火柴棒的根数是10；2n+1 第 4 个形中，火柴棒的根数是13；故答案 n +∵每增加一个正方形火柴棒数增加3，17．根据意得：∴第 n 个形中有的火柴棒数：4+3（n 1）=3n+1．第（ 1）个案只有 1 个等腰梯形，周3× 1+4=7；当 n=7 ， 4+3（ n 1） =4+3× 6=22，第（ 2）个案由 3 个等腰梯形拼成，其周3× 3+4=13；故答案： 22第（ 3）个案由 5 个等腰梯形拼成，其周3× 5+4=19；26．察形：⋯当 n=2 ， s=4，第（ n）个案由（ 2n 1）个等腰梯形拼成，其周当 n=3 ， s=9，3（ 2n 1）+4=6n+1；当 n=4 ， s=16，故答案： 6n+1 当 n=5 ， s=25，18．察：⋯第 1 个形有 S=9×1+1=10 个点，2 当 n=n ， s=n ，第 2 个形有 S=9×2+1=19 个点，故答案： s=n2第 3 个形有 S=9×3+1=28 个点，27．∵第 1 个形中，十字星与五角星的个数和3×⋯2=6，第 n 个形有 S=9n+1个点．第 2 个形中，十字星与五角星的个数和3× 3=9，故答案： 9n+1 第 3 个形中，十字星与五角星的个数和3× 4=12，19． n=3 ， S=6=3× 3 3=3，⋯n=4 ， S=12=4× 4 4，而 27=3× 9，n=5 ， S=20=5× 5 5，∴第 8 个形中，十字星与五角星的个数和=3× 9=27．⋯，故答案： 8依此推，数 n 数， S=n?n n=n（n 1）．28． 2 条直最多的交点个数1，故答案： n（ n 1）． 3 条直最多的交点个数1+2=3，20．合形，：搭第 n 个三角形，需要 3+2（ n 4 条直最多的交点个数1+2+3=6，1） =2n+1（根）． 5 条直最多的交点个数1+2+3+4=10，故答案 2n+1 ⋯21．因 2011÷ 6=335⋯ 1．余下的 1 个根据序是黑所以 2000 条直最多的交点个数1+2+3+4+⋯色三角形，所以共有 1+335×3=1006．+1999= =1999000．故答案： 100622．从所的中可以看出，每六个棋子一个循，故答案 1999000∵ 2011÷ 6=335⋯ 1，29．∵小正方形的是1，∴第 2011 个棋子是白的．∴ 1 的周是： 1× 4=4，故答案：白 2 的周是： 2× 4=8，23．依意可求出梯形个数与形周的关系3n+2= 3 的周是3× 4=12，周，⋯当梯形个数2007 个，形的周3×第 n 个的周是4n，2007+2=6023．∴ 10 的周是10× 4=40；故答案： 6023．故答案： 8， 12， 4024．察形知：30．首先：第一个案中，有白色的是 6 个，后是依次多 4 个．所以第 n 个案中，是6+4（n 1） =4n+2．∴m与 n 的函数关系式是m=4n+2．故答案： 4n+2．31．第一个需棋子6，第二个需棋子9，第三个需棋子12，第四个需棋子15，第五个需棋子18，⋯第 n 个需棋子3（n+1）枚．（1）当 n=6 ， 3×（ 6+1）=21；当n=7 ， 3×（ 7+1） =24；（2）第 n 个需棋子 3（ n+1）枚．（3）第 n 个形有 2012 黑色棋子，根据（ 1）得 3（ n+1） =2012解得 n=，34．（ 1）由可知，每个正方形 4 个数字，∵30÷ 4=7⋯ 2，∴数字 30 在第 8 个正方形的第 2 个位置，即右上角；故答案： 8，右上角；（ 2）左下角是 4 的倍数，按照逆序依次减 1，即正方形左下角点数字： 4n，正方形左上角点数字：4n 1，正方形右上角点数字：4n 2，正方形右下角点数字：4n 3；（3） 2011÷ 4=502⋯ 3，所以，数字“ 2011” 第503 个正方形的左上角点35．依意得：①n=2， S=3=3× 2 3．②n=3， S=6=3×3 3．③ n=4， S=9=3×4 3④n=10， S=27=3× 10 3．⋯⑤按此律推断，当每条有 n 盆花， S=3n 3 36．（ 1）第①个形中有 6 个棋子；所以不存在某个形有2012 黑色棋子第②个形中有6+4=10 个棋子；32．（ 1）由点形可得它的点的个数分：1，5，第③个形中有6+2× 4=14 个棋子；9， 13，⋯，并得出以下律：∴第⑤个形中有6+3×4=18 个棋子；第一个点数： 1=1+4×（ 1 1）第⑥个形中有6+4× 4=22 个棋子．第二个点数： 5=1+4×（ 2 1）故答案 18、 22；（ 3 分）第三个点数： 9=1+4×（ 3 1）（ 2）第 n 个形中有 6+（ n 1）× 4=4n+2．第四个点数： 13=1+4×（ 4 1）故答案 4n+2．（ 3 分）⋯（ 3） 4n+2=50，因此可得：解得 n=12．第 n 个点数： 1+4×（ n 1）=4n 3．最下一横人数2n+1=25．（ 4 分）故答案： 4n 3；37．（ 1） 5 个点，段的条数： 1+2+3+4=10，（ 2）个点是 x 个，根据（ 1）得： 6 个点，段的条数：1+2+3+4+5=15；1+4×（ x 1） =37 （ 2）10 个点，段的条数： 1+2+3+4+5+6+7+8+9=45，解得： x=10．n 个点，段的条数： 1+2+3+⋯ +（ n 1）= ；答：个点是 10 个33．（ 1）察形，得出枚数分是，5， 8， 11，⋯，（ 3） 60 人握手次数 = =1770．每个比前一个多 3 个，所以形号5， 6 的棋字子数分 17， 20．故答案：（ 2）45，；（ 3） 1770．故答案： 17 和 20．（ 2）由（ 1）得，中棋子数是首5，公差 3 的38．（ 1）成第一个“ H”字需要 7 个棋子，等差数列，第二个“ H”字需要棋子12 个；所以第 n 个形所需棋子的枚数：5+3（ n 1）=3n+2．第三个“ H”字需要棋子17 个；（ 3）不可能⋯由 3n+2=2010，第 x 个中，有7+5（ x 1） =5x+2（个）．解得： n=669 ，（ 2）当 5x+2=2012 ，解得： x=402，故第 402 个“ H”字棋子数量正好是 2012 个棋子∵ n 整数，39．（ 1）如（ 1），可得三条直两两相交，最多有 3 ∴ n=669 不合意个交点；（ 2）如（ 2），可得三条直两两相交，最多有 6 个故其中某一形不可能共有2011 枚棋子交点；（ 3）由（ 1）得，=3，故答案： 1544．（ 1）在第 n 个形中，需用黑瓷4n+6 ，白瓷由（ 2）得，=6；n（n+1）；（ 2）根据意得n（ n+1） =4n+6，∴可得， n 条直两两相交，最多有个交点n 2 3n 6=0，此没有整数解，（ n 正整数，且n≥ 2）．所以不存在．故答案 3； 6；．故答案： 4n+6； n（ n+1）45．（ 1）合形，：后每多一个三角形，需要多 2 根火柴．搭 4 个的三角形要用3+2× 3=9 根火柴棒； 13 根火柴棒可以搭（13 3）÷ 2+1=6 个的三角形；（ 2）根据（ 1）中的律，得40．（ 1）由目中的“每次都将其中片撕成更小的四搭 n 个的三角形要用3+2（ n 1） =2n+1 根火柴棒．片”，故答案9； 6； 2n+1可知：小王每撕一次，比上一次多增加 3 小片．46．（ 1）第 4 个形中的棋子个数是13；∴ s=4+3（ n 1） =3n+1；（ 2）第 n 个形的棋子个数是 3n+1；（ 2）当 s=70 ，有 3n+1=70，n=23．即小王撕23 次（ 3）当 n=20 ， 3n+1=3× 20+1=6141．（ 1）合形，：每个中，两端都是坐 2 人，∴第 20 个形需棋子 61 个剩下的两是每一桌子是 4 人．47．（ 1）第一台中正方体石墩的数：三餐桌按中的拼接方式，四周可坐3× 4+2=14=3；（人）；（ 2）n 餐桌按上面的方式拼接，四周可坐（ 4n+2）人；第一台中正方体石墩的数：=9；若用餐人数26 人， 4n+2=26，解得 n=6．第一台中正方体石墩的数：；故答案： 14；（ 4n+2）， 642．（ 1）如所示：⋯1 2 3 4 5 6 依此推，可以：第几台中正方体石墩的数形： 3 与几的乘乘以几加1，然后除以 2．梯一二三四号数6 9 石墩 3 9 18 30形12 15 18 21 数中（ 2）按照（ 1）中的律可得：当到第n 梯的，共用正方体石墩；棋子当 n=100 ，（ 2）依意可得当到第n 个形棋子的枚数：6+3（ n 1） =6+3n 3=3n+3；（ 3）由上可知此3n+3=99，∴当 n=100 ，共用正方体石墩 15150 ．∴ n=32．答：当到第 n 梯，共用正方体石墩答：第32 个形共有99 枚棋子13．由目得：第 1 个“广”字中的棋子个数是7；；当 n=100 ，共用正方体石墩 15150第 2 个“广”字中的棋子个数是7+（ 2 1）× 2=9；48．由意可知：第 3 个“广”字中的棋子个数是7+（ 3 1）× 2=11；第一次折后，的厚度2× 0.05 ；可以得到折痕第 4 个“广”字中的棋子个数是7+（ 4 1）× 2=13； 1 条；第 5 个“广”字中的棋子个数是 7+（ 5 1）× 2=15⋯第二次折后，的厚度2× 2× 0.05=2 2× 0.05 ；可一步律：第n 个“广”字中的棋子个数是7+ 以得到折痕 3=22 1 条；（n 1）× 2=2n+5．第三次折后，的厚度2×2× 2× 0.05=2 3× 0.05 ；可以得到折痕 7=23 1 条；⋯；第 n 次折后，的厚度2×2× 2× 2×⋯× 2×0.05=2 n× 0.05 ．可以得到折痕 2 n 1 条．故：（ 1）折 3 次后，厚度0.4 毫米；（ 2）折 n 次后，厚度n2 × 0.05 毫米；（ 3）折 n 次后，可以得到2n 1 条折痕49．由形我不看出横行数量n+3，行数量 n+2，数量 n2+5n+6；若用瓷506 ，可以求2n +5n+6=506；所以答案：（ 1） n+3， n+2；（ 2）每一行有23 ，每一列有2250．等号左是从 1 开始，奇数相加，等号右是奇数个数也就是n 的平方．（1）① 1+3+5+7=42；2②1+3+5+7+9=5 ；③1+3+5+7+9+11=62．（2） 1+3+5+⋯ +（ 2n 1） =n2（ n≥1 的正整数）51．（ 1）依意得：所剪次数 n 1 2 3 4 5正方形个数 4 7 10 13 16Sn（2）可知剪 n 次， S n=3n+1．（3） n=1 ， = ；n=2 ， =；n=3 ， =；⋯；剪 n 次， =．52．（ 1） S=15（2）∵ n=2 ， S=3×（ 2 1） =3；n=3 ， S=3×（ 3 1） =6；n=4 ， S=3×（ 4 1） =9；⋯∴S=3×（ n 1） =3n 3．（3）当 n=2008 ， S=3× 2008 3=6021．53．第 1 个正方形四条上的格点共有 4 个第 2 个正方形四条上的格点个数共有（4+4× 1）个第 3 个正方形四条上的格点个数共有（4+4× 2）个⋯第 10 个正方形四条上的格点个数共有（4+4× 9） =40 个第 n 个正方形四条上的格点个数共有[4+4 ×（ n1） ]=4n 个54．由可知，每个形是n 的正方形，因此四条的花盆数 4n，再减去重复的四个角的花盆数，即 S=4n 4；（ 1）将 n=5 代入 S=4n 4，得 S=16；（2）将 n=10 入 S=4n 4，得 S=36；（3） S=4n 4；（4）将 S=42 代入 S=4n 4 得，4n 4=42解得 n=11.5所以用 42 个花盆不能出似的案55．（ 1）在第 1 个中，共有白色瓷1×（ 1+1） =2，（ 2）在第 2 个中，共有白色瓷2×（ 2+1） =6 ，（ 3）在第 3 个中，共有白色瓷3×（ 3+1） =12 ，（ 4）在第 10 个中，共有白色瓷10×（ 10+1）=110 ，（ 5）在第 n 个中，共有白色瓷n（ n+1）56．（ 1）由分析得：当n=6 ， s=1+2+3+4+5+6=21；当n=100 ， s=1+2+3+⋯+99+100=5050；（ 2）用 n 表示 S 得： S=5﹣ 1=16 个；57．（ 1）（ 5）比（ 4）多出 2（2）（ 6）比（ 5）多出 26﹣1 =32 个；（3）（ 8）比（ 7）多出 28﹣1 =128 个；（4）（ n+1）比（ n）多出 2n个．58．（1）首先察形，得到前面三个形的具体个数，不：在5 的基上依次多 3 枚．即第 n 个案需要 5+3（n 1） =3n+2．那么当 n=8 ，有26 枚；故成第八个案需要26 枚棋子．（2）因第①个案有 5 枚棋子，第②个案有（ 5+3× 1）枚棋子，第③个案有（ 5+3× 2）枚棋子，依此律可得第 n 个案需 5+3×（ n 1） =5+3n 3=（3n+2）枚棋子．（3） 3× 2010+2=6032（枚）即第 2010 个案需6032 枚棋子59．（ 1）察形得：当黑 n=1 ，白有 6 ，当黑 n=2 ，白有 10 ，当黑 n=3 ，白有 14 ；（2）根据意得：∵每个形都比其前一个形多 4 个白色地，∴可得律：第 n 个形中有白色地 6+4（ n 1）=4n+2 ．故答案6， 10， 14， 4n+260．第一个案3+2=5 个窗花；第二个案2× 3+2=8 个窗花；第三个案3× 3+2=11 个窗花；⋯从而可以探究：第n 个案所窗花数（ 3n+2）个．（ 1） 20（2） 3n+2（3）存在，令 3n+2=2012， 3n=2010 n=670 因此是第 670个图形找规律 ---第20页共20页。

二年级美术找规律练习题
1. 图案找规律
练题一：
题目：根据下面的图案，找出规律，并选出正确的选项。

A) 选项A
B) 选项B
C) 选项C
D) 选项D
练题二：
题目：请找出下面图案的规律，并从选项中选出正确的答案。

A) 选项A
B) 选项B
C) 选项C
D) 选项D
2. 形状找规律
练题三：
题目：请找出下面形状的规律，并选出正确的选项。

A) 选项A
B) 选项B
C) 选项C
D) 选项D
练题四：
题目：请观察下面的形状，找出它们的规律，并从选项中选出正确的答案。

A) 选项A
B) 选项B
C) 选项C
D) 选项D
3. 颜色找规律
练题五：
题目：请根据下面图案的颜色，找出它们的规律，并选择正确的选项。

A) 选项A
B) 选项B
C) 选项C
D) 选项D
练题六：
题目：请观察下面图案的颜色，找出它们的规律，并从选项中选出正确的答案。

A) 选项A
B) 选项B
C) 选项C
D) 选项D
以上是二年级美术找规律练习题，请同学们认真观察图案、形状和颜色，找出它们的规律，选择正确的答案。

祝你们成功！。