计量经济学数据

名词解释1、 因果效应：在理想化随机对照实验中得到的，某一给定的行为或处理对结果的影响2、 实验数据：来源于为评价某种处理（某项政策）抑或某种因果效应而设计的实验3、 观测数据：通过观察实验之外的实际行为而获得的数据4、 截面数据：对不同个体如工人、消费者、公司或政府机关等在某一特定时间段内收集到的数据5、 时间序列数据：对同一个体（个人、公司、国家等）在多个时期内收集到的数据6、 面板数据：即纵向数据，是多个个体分别在两个或多个时期内观测到的数据7、 离散型随机变量：一些随机变量是离散的连续型随机变量：一些随机变量是连续的8、 期望值：随机变量经过多次重复实验出现的长期平均值，记作E （Y ）9、 期望：Y 的长期平均值，记作μY10、方差：是Y 距离其均值的偏差平方的期望值，记作var （Y ）11、标准差：方差的平方根来表示偏差程度，记作σY12、独立性：两个随机变量X 和Y 中的一个变量无法提供另一个变量的相关信息13、标准正态分布：指那些均值102==σμ、方差的正态分布，记作N （0，1）14、简单随机抽样：n 个对象从总体中抽取，且总体中的每一个个体都有相等的可能性被选入样本15、独立分布：两个随机变量X 和Y 中的一个变量无法提供另一个变量的相关信息，那么这两个变量X 和Y 独立分布 16、偏差：设Y Y E Y Y μμμμ-ˆˆ）（为的一个估计量，则偏差是； 一致性：当样本容量增大时，Y μˆ落入真实值Y μ的微小领域区间内的概率接近于1，即Y Y μμ与ˆ是一致的 有效性：如果Y μˆ的方差比Y μ~更小，那么可以说Y Y μμ~ˆ比更有效 17、最小二乘估计量：21)(m ini -Y ∑=最小化误差m -i Y 平方和的估计量m 18、P 值：即显著性概率，指原假设为真的情况下，抽取到的统计量与原假设之间的差异程度至少等于样本计算值与 原假设之间差异程度的概率19、第一类错误：拒绝了实际上为真的原假设20、一元线性回归模型：i i 10i μββ+X +=Y ；1β代表1X 变化一个单位所导致Y 的变化量21、普通最小二乘（OLS ）估：选择使得估计的回归线与观测数据尽可能接近的回归系数，其中近似程度用给定X 时预 测Y 的误差的平方和来度量22、回归2R ：可以由i X 解释（或预测）的i Y 样本方差的比例，即TSSSSR TSS ESS R -==12 23、最小二乘假设：①给定i X 时误差项i μ的条件均值为零：0)(i i =X μE ；②从联合总体中抽取的，，，，），，（n ...21i i i =Y X 满足独立同分布；③大异常值不存在：即i i Y X 和具有非零有限的四阶距24、1β置信区间：以95%的概率包含1β真值的区间，即在所有可能随机抽取的样本中有95%包含了1β的真值25、同方差：若对于任意i=1，2，...，n ，给定）（条件分布的方差时χμμ=X X i i i i var 为常数且不依赖于χ，则 称误差项i μ是同方差26、异方差：若对于任意i=1，2，...，n ，给定）（条件分布的方差时χμμ=X X i i i i var 为常数且依赖于χ，则称 误差项i μ是异方差27、遗漏变量偏差：指OLS 估计量中存在的偏差，它是在回归变量X 与遗漏变量相关时产生的28、多元回归模型：n ...1i ...i k i k i 22i 110i ，，，=+X ++X +X +=Y μββββ；1β代表在其他影响Y 的因素2X 不变的 前提下，1X 变化一个单位所导致Y 的变化量29、调整2R （2R ）:是2R 的一种修正形式，由于加入新变量后2R 不一定增大，即22ˆ211-k -n 1-n 1Y s s TSS SSR R μ-=⨯-= 30、虚拟变量陷阱：如果有G 个二元变量，且每个观测都只属于其中一类，又如果回归中包含截距项以及所有G 个二 元变量，则会因为完全多重共线性而无法进行回归31、控制变量：回归中保持某些因素不变的回归量32、二次回归模型：i 2i 2i 10i ncome ncome core est μβββ+++=I I S T 33、非线性回归函数：i k i i 2i 1i ...f μ+X X X =），，，（Y ，i=1，...，n ；其中f （k i i 2i 1...X X X ，，，）为非线性回归函数 34、多项式回归模型：i r i r 2i 2i 10i ...μββββ+X ++X +X +=Y35、双对数模型：i i 10i ln ln μββ+X +=Y ）（）（填空题1、 计量经济学提供了利用观测数据（而非实验数据）或者来自现实世界不太完美的实验数据估计因果效应的方法2、 截面数据 是多个个体在同一时间点上收集到的数据；时间序列数据是一个个体在多个时间点上收集到的数据；面板数据 是多个个体分别在多个时间点上收集到的数据3、 随机变量Y 的期望值（也可称为均值，μY ）记作E （Y ），是变量的概率加权平均值；Y 的方差为[]2)(2Y Y E μσ-=Y ,Y 的标准差是方差的平方根4、 两个随机变量X 和Y 的联合概率由它们的联合概率分布所表示；给定X=χ下Y 的条件概率分布是指给定X 取值为χ的条件时，Y 的概率分布5、 正态分布随机变量具有钟形概率密度；若要计算有关正态随机变量的概率，首先需要对其标准化，然后再查阅附录表1的标准正态累积分布表6、 简单随机抽样可以产生n 个随机观测值1Y ，...，n Y ，它们是独立分布的7、 样本均值n 1...Y Y Y Y ，，的估计量；当是总体均值μ为独立分布时，有： ①Y 的抽样分布均值为n 22Y=Y Y σσμ，方差为；②Y 是无偏的；③根据大数定律，Y 是一致的； ④根据中心极限定理，当样本容量较大时，Y 的抽样分布是近似正态的8、 t 统计量可以用来计算和原假设相关的p 值；较小的p 值意味着原假设是错误的9、 Y μ的95%置信区间是指在95%全部可能样本中包含Y μ真值的区间10、样本相关系数是总体相关系数的估计量，它度量了两个变量之间的线性关系—它们的散点图究竟有多近似于一条直线11、总体回归线X X +是10ββ的函数，表示Y 的均值：斜率1β表示X 变化一个单位时对应Y 的预期变化；截距0β决定了回归线的水平（或高低）12、利用样本观测数据(i i Y X ，),i=1，2，... ，n 使用普通最小二乘法可以估计总体回归线；回归截距和斜率的OLS 估计量分别记为10ˆˆββ和 13、2R 和回归标准误差（SER ）度量了i Y 与总体回归线的接近程度；其中2R 的取值范围为0到1；2R 取值较大表明i Y 接近总体回归线；回归标准误差是回归误差的标准差的估计量14、线性回归模型中有三个重要假设：①给定i X 时误差项i μ的条件均值为零：0)(i i =X μE ； ②从联合总体中抽取的，，，，），，（n ...21i i i =Y X 满足独立同分布；③大异常值不存在：即i i Y X 和具有非零有限的四阶距；若这些假设成立，则OLS 估计量10ˆˆββ和是①无偏的②一致的③大样本时服从正态分布 15、对回归系数的假设检验类似于对总体均值的假设检验，都是利用t 统计量来计算p 值，从而确定是接受还是拒绝 原假设；类似于总体均值的置信区间，回归系数的95%置信区间为估计量±1.96标准误差16、如果三个最小二乘假设成立，回归误差同方差并且服从正态分布，则利用同方差适用标准误差计算的t 统计量在原假设下服从学生t 分布；当样本容量足够大时，学生t 分布和正态分布之间的差异可忽略不计17、若遗漏变量（1）与回归中的回归变量相关；（2）是Y 的决定因素之一，则会产生遗漏变量偏差（同时满足）18、多元回归模型是包含多个回归变量的线性回归模型，，，k 21...X X X ，每个回归变量都对应一个回归系数 ，，，，k 21...βββ其中系数1β表示在其他回归变量不变的情况下，1X 变化一个单位时Y 的预期变化，其他回归系数的解释与之类似19、可通过OLS 估计多元回归中的系数；当满足四个最小二乘假设时，OLS 估计量是无偏一致估计量，并且在i 大样本 下服从正态分布①给定i k i i 2i 1...μ时，，，X X X 的条件均值为零，即0...k i i 2i 1i =X X X ），，，（μE ；②从联合分布中抽取的i Y ),...i k i i 2i 1，，，，（X X X =1，...，n 满足独立同分布； ③不存在大异常值，即具有及，，i k i i 1...Y X X 非零有限四阶距； ④不存在完全多重共线性20、在多元回归中，当某个回归变量是其他回归变量的完全线性组合时就产生了完全多重共线性，通常是有选择回归变量时的错误引起的，因此处理完全多重共线性的方法是改变回归变量集21、回归标准误差、22R R 及都表示多元回归模型的拟合优度22、当系数涉及多个约束时的假设称为联合假设，可利用F 统计量进行检验23、在非线性回归中，总体回归函数的斜率依赖于一个或多个解释变量的取值24、两个变量的乘积项称为交互项，在回归中加入交互项可以使其中一个变量的回归斜率依赖于另一个变量的取值计算题P41 2.2 使用表2-2中的概率密度计算E（Y）和E（X）Pr（X=0）=0.30 Pr（X=1）=0.70Pr（Y=0）=0.20 Pr（Y=1）=0.78E（X）=0*0.30+1*0.70=0.70E（Y）=0*0.22+1*0.78=0.782.6下面的表格给出了基于2008年美国适龄人口从业状况和接受大学教育的联合分布（1）E（Y）=0*0.046+1*0.954=0.954（2）失业率=Pr（Y=0）=0.046（3）E（Y丨X=1）=0*Pr（Y=0丨X=1）+1*Pr（Y=1丨X=1）=0.332/0.341=0.9736E（Y丨X=0）=0*Pr（Y=0丨X=0）+1*Pr（Y=1丨X=0）=0.622/0.659=0.94385（4）大学毕业生的失业率=1-E（Y丨X=1）=1-0.9736=0.0264非大学毕业生的失业率=1-E（Y丨X=0）=1-0.94385=0.5615（5）Pr（X=1丨Y=0）=0.009/0.046=0.196Pr（X=0丨Y=0）=0.037/0.046=0.804（6）P（X=Xi，Y=Yi）=P（X=Xi）*P（Y=Yi）独立反之不独立P71 3.8对1000个随机抽取的高三学生安排一项新版的SAT测试。

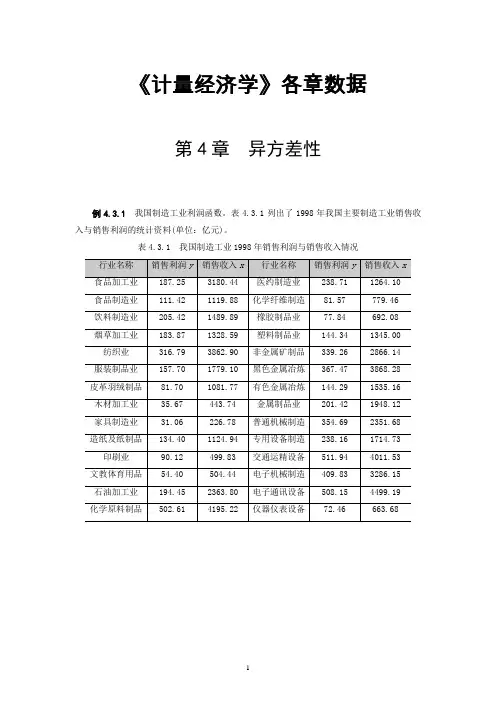
《计量经济学》各章数据第4章异方差性例4.3.1我国制造工业利润函数。

表4.3.1列出了1998年我国主要制造工业销售收入与销售利润的统计资料(单位：亿元)。

表4.3.1 我国制造工业1998年销售利润与销售收入情况4.5 案例分析——中国农村居民人均消费函数中国农村居民人均消费支出主要由人均纯收入来决定。

农村人均纯收入除了从事农业经营的收入外，还包括非农经营收入，即从事其他产业的经营性收入及工资性收入、财产收入和转移支付收入等。

试根据表4.5.1数据，建立我国农村居民人均消费函数（采用对数模型）：u X b X b b Y +++=22110ln ln ln其中，Y 表示农村人均消费支出，1X 表示从事农业经营的收入，2X 表示其他收入。

表4.5.1 中国2001年各地区农村居民家庭人均纯收入与消费支出（单位：元）资料来源：《中国农村住户调查年鉴》（2002），《中国统计年鉴》（2002）思考与练习10．建立住房支出模型:t t t u x b b y ++=10，样本数据如表1下（其中：y 是住房支出，x 是收入，单位：千美元）：表1 住房支出与收入数据(1)用最小二乘法估计10,b b 的估计值、标准差、拟合优度。

(2)用Goldfeld-Quandt 检验异方差性（假设分组时不去掉任何样本值），取05.0=α。

(3)如果存在异方差性，假设222t t x σσ=，用加权最小二乘法重新估计10,b b 的估计值、标准差、拟合优度。

11．试根据表2中消费(y )与收入(x )的数据完成以下问题：(1)估计回归模型：t t t u x b b y ++=10；(2)检验异方差性（可用怀特检验、戈德菲尔德——匡特检验）；(3)选用适当的方法修正异方差性。

表2 消费与收入数据12．考虑表3中的数据。

(1)估计OLS 回归方程：t t t u x b b y ++=10表3 样本数据(2)估计：tttttttu x b b y σσσσ++=11分析两个回归方程的结果。

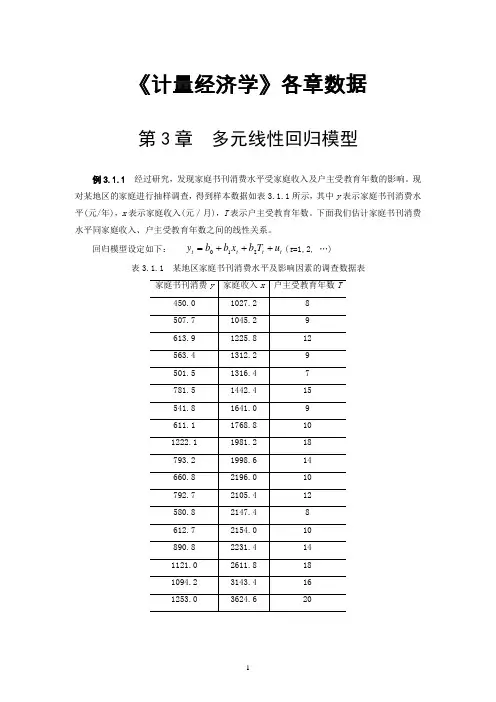
《计量经济学》各章数据第3章 多元线性回归模型例3.1.1 经过研究，发现家庭书刊消费水平受家庭收入及户主受教育年数的影响。

现对某地区的家庭进行抽样调查，得到样本数据如表3.1.1所示，其中y 表示家庭书刊消费水平(元/年)，x 表示家庭收入(元／月)，T 表示户主受教育年数。

下面我们估计家庭书刊消费水平同家庭收入、户主受教育年数之间的线性关系。

回归模型设定如下： t t t t u T b x b b y +++=210(t =1,2, …)表3.1.1 某地区家庭书刊消费水平及影响因素的调查数据表例3.4.1根据表3.4.1给出的中国1980-2003年间总产出(用国内生产总值GDP度量，单位：亿元)，劳动投入L(用从业人员度量，单位为万人)，以及资本投入K(用全社会固定投资度量，单位：亿元)，试建立我国的柯布——道格拉斯生产函数。

表3.4.1 1980-2003年中国GDP、劳动投入与资本投入数据例3.4.2 某硫酸厂生产的硫酸透明度一直达不到优质要求，经分析透明度低与硫酸中金属杂质的含量太高有关。

影响透明度的主要金属杂质是铁、钙、铅、镁等。

通过正交试验的方法发现铁是影响硫酸透明度的最主要原因。

测量了47组样本值，数据见表3.4.3。

试建立硫酸透明度(y)与铁杂质含量(x)的回归模型。

表3.4.3 硫酸透明度(y)与铁杂质含量(x)数据例3.4.3假设某企业在15年中每年的产量Y(件)和总成本X(元)的统计资料表3.4.7所示，试估计该企业的总成本函数模型。

表3.4.7 某企业15年中每年总产量与总成本统计资料3.6.1 案例1——中国经济增长影响因素分析根据表3.6.1给出的1980-2003年间总产出(用国内生产总值GDP度量，单位：亿元)，最终消费CS(单位：亿元)，投资总额I(用固定资产投资总额度量，单位：亿元)，出口总额（单位：亿元）统计数据，试对中国经济增长影响因素进行回归分析。

计量经济学〔第4版〕数据表表某社区家庭每个月收入与花费支出统计表每个月家庭可支配收入X〔元〕800110014001700200023002600290032003500每5616388691023125414081650196920902299月5947489131100130914521738199121342321家6278149241144136415511749204621782530庭6388479791155139715951804206822662629消93510121210140816501848210123542860费96810451243147416721881218924862871支1078125414961683192522332552出1122129814961716196922442585Y1155133115621749202122992640〔元〕11881364157317712035231012101408160618042101143016501870211214851716194722002002合计242049501149516445193052387025025214502128515510表参数预计的计算表1800638-1350-94512756151822500892836640000407044 21100935-1050-64868029511025004197741210000874225 314001155-750-42832092556250018309819600001334025417001254-450-32914800520250010817528900001572516520001408-150-175262352250030590400000019824646230016501506710065225004502529000027225007260019254503421539452025001170326760000370562582900206875048536382556250023532284100004276624932002266105068371725511025004666265134756 10350025301350947127858518225008969986400900乞降2150015829497475074250003354955均匀21501583表中国各地域居民家庭人均整年可支配收入与人均整年花费性支出〔元〕地域可支配收入花费支出地域可支配收入花费支出X Y X Y北京湖北天津湖南河北广东山西广西内蒙古海南辽宁重庆吉林四川黑龙江贵州上海云南江苏西藏浙江陕西安徽甘肃福建青海江西宁夏山东新疆河南资料根源：?中国统计年鉴?〔2021〕。

计量经济学数据计量经济学是经济学的一个重要分支，主要研究经济现象的量化分析和经济模型的构建。

在计量经济学研究中，数据是至关重要的，它提供了对经济现象进行分析和验证的基础。

本文将介绍计量经济学数据的标准格式和一些常用的数据类型。

一、计量经济学数据的标准格式计量经济学数据通常以表格的形式呈现，其中包括以下几个主要部份：1. 变量名称：表格的第一行通常是变量名称，用于标识每一列数据所代表的经济变量。

例如，可以包括GDP（国内生产总值）、CPI（消费者物价指数）、投资等。

2. 时间序列：表格的第一列通常是时间序列，用于标识每一行数据所对应的时间点。

时间序列可以按照不同的频率进行分类，如年度数据、季度数据、月度数据等。

3. 数据值：表格的其他单元格中填写了相应的数据值，代表了每一个变量在不同时间点上的观测值。

数据可以是实数，也可以是离散的分类变量。

4. 单位：表格的第一列下方通常注明了数据的单位，用于说明数据所代表的具体含义，如货币单位、百分比等。

5. 数据来源：表格的最底部通常注明了数据的来源，包括调查机构、统计局等。

这有助于保证数据的可信度和可重复性。

二、常用的计量经济学数据类型在计量经济学研究中，常用的数据类型包括以下几种：1. 时间序列数据：时间序列数据是按照时间顺序罗列的一系列观测值，用于分析经济变量随时间的变化趋势和周期性。

例如，GDP的年度数据就是一种时间序列数据。

2. 截面数据：截面数据是在某一特定时间点上对不同个体进行观测得到的数据，用于分析不同个体之间的差异和关系。

例如，不同地区的失业率数据就是一种截面数据。

3. 面板数据：面板数据是时间序列数据和截面数据的结合，既包括对不同个体的多次观测，也包括对同一时间点的多个个体观测。

面板数据可以用于分析个体特征和时间效应对经济变量的影响。

4. 横截面时间序列数据：横截面时间序列数据是对多个个体在多个时间点上的观测数据，既包括截面数据的横截面特征，也包括时间序列数据的时间特征。

Panel Data 分析的基本框架
线性模型 非线性模型
Panel Data 分析的基本框架：线性模 型
线性模型： （1）单变量模型 （2）联立方程模型 （3）带测量误差模型 （4）伪Panel Data
Panel Data 分析的基本框架：线性
模型之单变量模型
（1） 固定效应和固定系数模型（Fixed Effect Models and Fixed Coefficient Models）：通常采用OLS估计。固 定效应包括时间效应以及时间和个体效应，并可以进一 步放宽条件，允许在有异方差、自相关性和等相关矩阵 块情况下，用GLS估计。 （2）误差成分模型（Error Components Models）：最 常用的Panel Data模型。针对不同情况，通常可以用OLS 估计、GLS估计、内部估计（Within Estimator）和FGLS 估计，并检验误差成分中的个体效应以及个体和时间效 应，同时将自相关和异方差情况也纳入该模型框架中。
平行数据的含义
所谓平行数据，是指在时间序列上取多个 截面，在这些截面上同时选取样本观测值 所构成的样本数据。 面板数据是同时在时间和截面空间上取得 的二维数据。从横截面上看，是由若干个 体在某一时刻构成的截面观测值，从纵剖 面上看是一个时间序列。
平行数据研究的应用和发展
最早是Mundlak（1961）、Balestra和 Nerlove （1966）把Panel Data引入到经济计量中。从此 以后，大量关于Panel Data的分析方法、研究文 章如雨后春笋般出现在经济学、管理学、社会 学、心理学等领域。从1990年到目前为止，已 有近1000篇有关 Panel Data理论性和应用性的文 章发表，Panel Data 研究成为近十年来经济计量 学的一个热点。

计量经济学数据类型
“计量经济学”是指利用经济学理论和数学统计方法来研究实际的经济问题。

数据是计量经济学研究的重要基础，计量经济学中常见的数据类型如下：
1. 时间序列数据：时间序列数据是按时间顺序排列的数据，例如经济指标、股票价格、汇率等。

应用：基于时间序列数据进行趋势预测和时间序列分析，例如预测未来的经济增长率、通货膨胀率、利率等。

2. 横截面数据：横截面数据是在相同时间点上针对不同个体所收集的数据，例如收入、教育程度、职业等。

应用：基于横截面数据进行个体变量的比较分析，例如探讨收入水平与教育程度的关系、职业类型与收入的关系等。

3. 面板数据：面板数据是同时包含时间序列和横截面数据的数据，例如企业的经济数据、家庭调查数据等。

应用：基于面板数据进行个体和时间变量的研究，例如探讨企业投资和利润的关系、家庭收支变化的影响因素等。

4. 实验数据：实验数据是通过对特定因素进行控制来获取的数据，例如经济政策的实验数据、招聘决策的实验数据等。

应用：基于实验数据进行因果关系的分析，例如探讨各种政策对实体经济的影响、探讨招聘流程中不同因素对应聘者选择和工作表现的影响等。

以上数据类型及其应用是计量经济学研究中常见的基础。

在实际应用中，根据实际问题和数据可用性，研究者可以将不同类型的数据进行组合分析，以获取更深入的结论。

1、截面数据：截面数据是许多不同的观察对象在同一时间点上的取值的统计数据集合，可理解为对一个随机变量重复抽样获得的数据。

2、时间序列数据：时间序列数据是同一观察对象在不同时间点上的取值的统计序列，可理解为随时间变化而生成的数据。

3、虚变量数据：虚拟变量数据是人为设定的虚拟变量的取值。

是表征政策、条件等影响研究对象的定性因素的人工变量，其取值一般只取“0”或“1”。

4、内生变量与外生变量：内生变量是由模型系统决定同时可能也对模型系统产生影响的变量，是具有某种概率分布的随机变量，外生变量是不由模型系统决定但对模型系统产生影响的变量，是确定性的变量。

5、总体回归函数：是指在给定X i 下Y 分布的总体均值与X i 所形成的函数关系（或者说将 总体被解释变量的条件期望表示为解释变量的某种函数）6、最大似然估计法（ML ）: 又叫最大或然法，指用产生该样本概率最大的原则去确定样本 回归函数的方法。

7、OLS 估计法：指根据使估计的剩余平方和最小的原则来确定样本回归函数的方法。

8、残差平方和：用RSS 表示，用以度量实际值与拟合值之间的差异，是由除解释变量之外 的其他因素引起的被解释变量变化的部分。

9、拟合优度检验：指检验模型对样本观测值的拟合程度，用2R 表示，该值越接近1表示拟合程度越好。

10、多元线性回归模型：在现实经济活动中往往存在一个变量受到其他多个变量影响的现象，表现在线性回归模型中有多个解释变量，这样的模型被称做多元线性回归模型，多元是指多个解释变量。

11、调整的可决系数：又叫调整的决定系数，是一个用于描述多个解释变量对被解释变量的联合影响程度的统计量，克服了2R 随解释变量的增加而增大的缺陷，与2R 的关系为2211(1)1n R R n k -=----。

12、偏回归系数：在多元回归模型中，每一个解释变量前的参数即为偏回归系数，它测度了当其他解释变量保持不变时，该变量增加1单位对被解释变量带来的平均影响程度。

数据集概述：计量经济学导论伍德里奇数据集是一个包含了多个经济指标的样本数据集，用于开展计量经济学研究和统计推断。

该数据集是经济计量学领域中常用的数据集之一，可用于分析各种经济现象之间的相互关系和影响。

本篇文章将介绍数据集的基本情况、样本选择的原因和意义，以及数据预处理和结果分析的方法。

数据集特点：计量经济学导论伍德里奇数据集包含了多个经济指标的时间序列数据，包括国内生产总值、失业率、消费支出、投资额等。

这些指标涵盖了宏观经济领域的多个方面，可以用于分析各种经济现象之间的相互关系和影响。

数据集的时间跨度较长，包含了多个年份的数据，为研究经济变化提供了丰富的样本。

此外，数据集还提供了不同年份的季节调整数据，方便了对经济指标进行更准确的统计分析。

样本选择原因和意义：本篇文章选择计量经济学导论伍德里奇数据集作为研究样本的原因和意义在于，该数据集包含了多个重要的宏观经济指标，可以用于分析宏观经济现象之间的相互关系和影响。

通过对该数据集进行深入分析和挖掘，可以更好地了解经济运行规律和趋势，为政策制定和预测提供更有价值的参考依据。

此外，该数据集还可以用于检验计量经济学模型的准确性和适用性，为经济学的理论研究和应用提供有力的支持。

数据预处理：在进行数据分析之前，需要对数据进行预处理，包括缺失值填充、异常值处理和数据清洗等。

在本篇文章中，我们采用了以下方法进行数据预处理：1. 缺失值填充：对于缺失的数据，我们采用了均值插补的方法进行了填充。

2. 异常值处理：通过对数据进行箱型图观察，剔除了明显异常的数据点。

3. 数据清洗：对不符合要求的数据进行了清洗，如去除无效样本和不符合研究目的的数据。

结果分析：通过对预处理后的数据进行统计分析，我们发现了一些有趣的结论：1. 国内生产总值和失业率之间存在负相关关系，即当失业率上升时，国内生产总值也相应下降。

这可能是由于失业率上升时，消费者和投资者的信心受到影响，导致需求下降，进而影响到经济增长。

计量经济学数据引言：计量经济学是经济学中的一个分支，它运用数理统计学和经济学的原理，通过收集和分析经济数据来研究经济现象和经济政策的影响。

在计量经济学中，数据的质量和准确性对于研究结果的可靠性至关重要。

本文将介绍计量经济学中常用的数据类型、数据来源、数据处理和数据分析方法。

一、数据类型在计量经济学中，数据可以分为两种类型：横截面数据和时间序列数据。

1. 横截面数据：横截面数据是在某个特定时间点上对不同个体进行观察和测量的数据。

例如，我们可以通过调查收集到某一年份不同家庭的收入、教育水平、家庭规模等信息。

2. 时间序列数据：时间序列数据是在一段时间内对同一事物进行观察和测量的数据。

例如，我们可以通过统计机构的报告获得过去几年某个国家的GDP增长率、失业率等信息。

二、数据来源计量经济学的数据可以从多个来源获取，常见的数据来源包括：1. 统计机构：各国的统计机构通常会发布各种经济指标和统计数据，如国内生产总值（GDP）、劳动力市场数据、物价指数等。

这些数据通常经过严格的调查和统计，具有较高的可靠性。

2. 调查数据：研究人员可以通过设计并实施调查来收集经济数据。

例如，通过问卷调查收集企业的生产成本、消费者的购买意愿等数据。

调查数据的质量和准确性取决于样本的选择和问卷设计等因素。

3. 学术研究：研究人员在进行学术研究时，通常会使用已有的学术文献和研究成果中的数据。

这些数据通常经过严格的检验和验证，具有较高的可信度。

三、数据处理在计量经济学中，数据处理是非常重要的一步，它包括数据清洗、数据转换和数据标准化等过程。

1. 数据清洗：数据清洗是指对收集到的原始数据进行筛选和清理，去除异常值、缺失值和错误值等。

这样可以提高数据的质量和准确性，确保后续分析的可靠性。

2. 数据转换：数据转换是指对原始数据进行变换，使其符合模型假设和分析的要求。

常见的数据转换包括对数转换、差分运算等。

3. 数据标准化：数据标准化是指将不同尺度和单位的数据转化为统一的尺度和单位，以便进行比较和分析。

举例说明计量经济学模型常用的数据类型
计量经济学模型是经济学领域的一种常用模型，它可以用来研究特定问题，如特定国家的经济增长模式、因果关系等，以帮助决策者为经济政策形成更准确的建议。

计量经济学模型又被称为回归模型，因为它借助数据可用于实施回归分析，以获得该经济系统的定量分析和经济预测。

计量经济学模型的数据类型主要包括定量数据和定性数据。

定量数据是指数据的变量是符号数字表示的，如利率、消费和出口量等；定性数据是指数据的变量以文字或符号图形表示，如行政区划、居住地点、性别等。

另外，还有指标数据，指标数据是指以定量或定性来表示某一变量的活动，了解该变量与特定因素之间的关联。

比如，该变量可能与特定政策之间的关系，也可能与某一行业的重要指标有关。

最后，也有结构数据。

结构数据是指查看某一特定变量的特定类型的数据，它关注变量的变化——如绝对值大小、增长率、趋势等，而不关注实际的数值。

总之，计量经济学模型的数据类型主要有定量数据、定性数据、指标数据和结构数据，这些数据有助于经济学家分析和预测特定经济系统的状况，并帮助决策者采取有效的行动，以提高经济系统的效率。

计量经济学（第3版）例题和习题数据表表2.1.1 某社区家庭每月收入与消费支出统计表表2.3.1 参数估计的计算表表2.6.1 中国各地区城镇居民家庭人均全年可支配收入与人均全年消费性支出（元）资料来源：《中国统计年鉴》（2007）。

表2.6.3 中国居民总量消费支出与收入资料单位：亿元年份GDP CONS CPI TAX GDPC X Y 19783605.6 1759.1 46.21519.28 7802.5 6678.83806.7 19794092.6 2011.5 47.07537.828694.2 7551.64273.2 19804592.9 2331.2 50.62571.70 9073.7 7944.24605.5 19815008.8 2627.9 51.90629.899651.8 8438.05063.9 19825590.0 2902.9 52.95700.02 10557.3 9235.25482.4 19836216.2 3231.1 54.00775.5911510.8 10074.65983.2 19847362.7 3742.0 55.47947.35 13272.8 11565.06745.7 19859076.7 4687.4 60.652040.79 14966.8 11601.77729.2 198610508.5 5302.1 64.572090.37 16273.7 13036.58210.9 198712277.4 6126.1 69.302140.36 17716.3 14627.78840.0 198815388.6 7868.1 82.302390.47 18698.7 15794.09560.5 198917311.3 8812.6 97.002727.40 17847.4 15035.59085.5 199019347.8 9450.9 100.002821.86 19347.8 16525.99450.9 199122577.4 10730.6 103.422990.17 21830.9 18939.610375.8 199227565.2 13000.1 110.033296.91 25053.0 22056.511815.3 199336938.1 16412.1 126.204255.30 29269.1 25897.313004.7 199450217.4 21844.2 156.655126.88 32056.2 28783.413944.2 199563216.9 28369.7 183.416038.04 34467.5 31175.415467.9 199674163.6 33955.9 198.666909.82 37331.9 33853.717092.5 199781658.5 36921.5 204.218234.04 39988.5 35956.218080.6 199886531.6 39229.3 202.599262.80 42713.1 38140.919364.1 199991125.0 41920.4 199.7210682.58 45625.8 40277.020989.3 200098749.0 45854.6 200.5512581.51 49238.0 42964.622863.9 2001108972.4 49213.2 201.9415301.38 53962.5 46385.424370.1 2002120350.3 52571.3 200.3217636.45 60078.0 51274.026243.2 2003136398.8 56834.4 202.7320017.31 67282.2 57408.128035.0 2004160280.4 63833.5 210.6324165.68 76096.3 64623.130306.2 2005188692.1 71217.5 214.4228778.54 88002.1 74580.433214.4 2006221170.5 80120.5 217.6534809.72 101616.3 85623.136811.2资料来源：根据《中国统计年鉴》（2001，2007）整理。

面板数据模型1．面板数据定义。

时间序列数据或截面数据都是一维数据。

例如时间序列数据是变量按时间得到的数据；截面数据是变量在截面空间上的数据。

面板数据（panel data）也称时间序列截面数据（time series and cross section data）或混合数据（pool data）。

面板数据是同时在时间和截面空间上取得的二维数据。

面板数据示意图见图1。

面板数据从横截面（cross section）上看，是由若干个体（entity, unit, individual）在某一时刻构成的截面观测值，从纵剖面（longitudinal section）上看是一个时间序列。

面板数据用双下标变量表示。

例如y i t, i = 1, 2, …, N; t = 1, 2, …, TN表示面板数据中含有N个个体。

T表示时间序列的最大长度。

若固定t不变，y i ., ( i= 1, 2, …, N)是横截面上的N个随机变量；若固定i不变，y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列（个体）。

图1 N=7，T=50的面板数据示意图例如1990-2000年30个省份的农业总产值数据。

固定在某一年份上，它是由30个农业总产总值数字组成的截面数据；固定在某一省份上，它是由11年农业总产值数据组成的一个时间序列。

面板数据由30个个体组成。

共有330个观测值。

对于面板数据y i t, i = 1, 2, …, N; t = 1, 2, …, T来说，如果从横截面上看，每个变量都有观测值，从纵剖面上看，每一期都有观测值，则称此面板数据为平衡面板数据（balanced panel data）。

若在面板数据中丢失若干个观测值，则称此面板数据为非平衡面板数据（unbalanced panel data）。

注意：EViwes 3.1、4.1、5.0既允许用平衡面板数据也允许用非平衡面板数据估计模型。

计量经济学数据一、引言计量经济学是经济学中的重要分支，通过运用统计学方法和数学模型来分析经济现象和经济关系。

在计量经济学研究中，数据是不可或缺的基础，它们用于验证经济理论、检验经济假设以及预测经济变量的未来走势。

本文将详细介绍计量经济学中常用的数据类型和标准格式，以及一些常见的数据来源。

二、数据类型1. 交叉面板数据交叉面板数据是计量经济学中常用的数据类型之一，它包含多个个体（如企业、家庭、国家等）在多个时间点上的观测数据。

这些数据通常以表格的形式呈现，其中行表示个体，列表示时间点。

交叉面板数据可以用于分析个体之间的差异以及时间序列的变化。

2. 时间序列数据时间序列数据是按照时间顺序排列的一系列观测值。

这种数据类型常用于分析经济变量随时间的变化趋势。

时间序列数据可以是连续的（如每月的销售额）或离散的（如每年的GDP增长率），并且可以包含多个变量。

3. 截面数据截面数据是在某一时间点上对多个个体进行的观测。

与交叉面板数据不同的是，截面数据只包含一个时间点的观测值。

截面数据常用于比较不同个体之间的差异，例如不同国家的人均收入。

三、数据格式1. CSV格式CSV（逗号分隔值）是一种常见的数据格式，它使用逗号将数据字段分隔开。

每一行代表一个观测值，每一列代表一个变量。

CSV格式的数据可以使用文本编辑器或电子表格软件进行查看和编辑。

2. Excel格式Excel是一种广泛使用的电子表格软件，它可以存储和处理各种类型的数据。

Excel格式的数据以工作表的形式组织，其中每个单元格可以包含一个数据值。

Excel还提供了丰富的数据分析和可视化功能，方便计量经济学研究的进行。

3. 数据库格式数据库是一种用于存储和管理大量数据的系统。

常见的数据库管理系统包括MySQL、Oracle和SQL Server等。

数据库可以以表的形式组织数据，每个表包含多个字段和记录。

计量经济学研究中常用的数据可以通过SQL查询语言从数据库中提取。

计量经济学横截面数据举例子什么是计量经济学计量经济学是使用统计方法分析经济数据；通常分析非实验数据。

计量经济分析的典型目标1.估计经济变量之间的关系；2.检验经济理论和假设；3.预测经济变量；4.评估和执行政府和企业政策经济模型可能是微观或宏观模型；经常使用优化行为，平衡建模；建立经济变量之间的关系例如：需求方程，定价方程…例1.1犯罪的经济模式在一篇开创性的文章中，诺贝尔奖获得者加里·贝克尔提出了一个效用最大化框架来描述个人参与犯罪。

某些犯罪有明确的经济回报，但大多数犯罪行为都有成本。

犯罪的机会成本妨碍了罪犯参与其他活动，如合法就业。

此外，还有与被抓的可能性相关的成本，如果被定罪，还有与监禁相关的成本。

从贝克尔的观点来看，从事非法活动的决定是一种资源分配，考虑到竞争活动的利益和成本。

在一般假设下，我们可以推导出一个等式，描述犯罪活动中花费的时间是各种因素的函数。

我们可以表示这样一个函数y=f（x1，x2，x3，x4，x5，x6，x7），（1.1）犯罪的经济模型（Becker（1968））基于效用最大化推导犯罪活动方程y=f（x1，x2，x3，x4，x5，x6，x7），（1.1）y→在犯罪活动中花费的时间x1→犯罪活动的“工资”；x2→合法就业工资；x3→其他收入；x4→被抓住的概率；x5→如果被抓住，定罪的概率；x6→预期句子；x7→年龄未指定关系的功能形式；在没有经济模型的情况下，这个方程可以假设例1.2工作培训和工作效率考虑在第1.1节开头提出的问题。

一位劳动经济学家想研究工作培训对工人生产力的影响。

在这种情况下，形式理论几乎没有必要。

基本的经济学知识足以认识到教育、经验和培训等因素会影响工人的生产力。

此外，经济学家也很清楚，工人的工资与他们的生产力相称。

这种简单的推理导致了一个模型，比如：工资=f（教育、经验、培训）（1.2）岗位培训模式与员工生产力额外培训对工人生产力有什么影响？正式经济理论并不需要推导方程式：工资=f（教育、经验、培训）工资→小时工资；教育→正规教育年限；经验丰富→多年的工作经验；培训→工作培训周其他因素也可能相关，但这些是最重要的犯罪活动的计量经济模型必须指定功能形式；变量可能必须用其他量来近似犯罪=β0+β1工资+β2其他收入+β3频率+β4频率转换+β5平均值+β6年龄+u犯罪→犯罪活动的量度工资→合法就业工资；其他收入→其他收入；频率→先前逮捕的频率；频率转换→定罪频率；犯罪活动的量度→定罪后的平均刑期；年龄→年龄；u→犯罪活动的不可观察的决定因素举例：道德品质，犯罪活动的工资，家庭背景…职业培训与工人生产率的计量经济学模型工资=β0+β1教育+β2经验+β3培训+u工资→小时工资；教育→正规教育年限；经验丰富→多年的工作经验；u→工作培训周；不可观察的工资决定因素举例：先天能力，教育质量，家庭背景…大多数计量经济学研究的是误差的说明经济计量模型可用于假设检验例如，参数β3表示培训对工资的影响这种影响有多大？它和零不同吗？经济计量分析需要数据不同类型的经济数据集截面数据；时间序列数据；合并横截面；面板/纵向数据计量经济学方法取决于所用数据的性质使用不适当的方法可能会导致误导性的结果横断面数据集在给定时间点/给定时期内的个人、家庭、公司、城市、州、国家或其他利益单位的样本横断面观察或多或少是独立的例如，从总体中进行纯随机抽样有时，纯粹的随机抽样是违反的，例如单位拒绝在调查中作出答复，或如果抽样的特点是聚类应用微观经济学中常见的横截面数据工资和其他特征的横截面数据集指标变量（1=是，0=否）观察数；小时工资关于增长率和国家特征的横截面数据人均实际国内生产总值增长率政府消费占国内生产总值的百分比；成人中等教育率时间序列数据一个或几个变量随时间的变化：比如股票价格，货币供应量，消费者价格指数，国内生产总值，年谋杀率，汽车销售…时间序列观测值通常是串行相关的观察结果的顺序传达了重要信息数据频率：每日、每周、每月、每季度、每年…时间序列的典型特征：趋势与季节性典型应用：应用宏观经济学和金融学最低工资及相关变量的时间序列数据给定年份的平均最低工资平均覆盖率；失业率；国民生产总值合并横截面两个或多个横截面组合在一个数据集中横截面是相互独立绘制的通常用于评估政策变化的汇总横截面例子：•评估房产税变化对房价的影响•1993年房价随机抽样•1995年新的随机房价样本•前后比较（1993年：改革前，1995年：改革后）住宅价格综合截面图房产税；房屋面积（平方英尺）卫生间数量；改革前；改革后面板或纵向数据相同的横截面单位会随着时间的推移而变化面板数据具有横截面和时间序列维度面板数据可以用来解释时不变的不可观测现象面板数据可用于建模滞后响应例子：•城市犯罪统计；每个城市在两年内进行观察•可对不可观测的时不变城市特征进行建模•警察对犯罪率的影响可能表现出时滞城市犯罪统计两年小组数据每个城市都有两个时间序列1986年警察人数；1990年警察人数因果关系与平等概念X对y因果关系的定义：“如果变量x改变了，变量y如何变化但所有其他相关因素都保持不变。

计量经济学数据计量经济学数据是指在计量经济学研究中所使用的各种数据。

计量经济学是一门研究经济现象和经济理论之间关系的学科，通过收集、整理和分析数据来验证经济理论的有效性和准确性。

在计量经济学研究中，数据的选择和使用非常关键。

合适的数据可以帮助研究者更好地理解经济现象，验证经济理论，并提出相应的政策建议。

下面将介绍计量经济学研究中常用的数据类型和数据来源。

1. 宏观经济数据：宏观经济数据是指一国或一地区整体经济活动的数据，包括国内生产总值（GDP）、失业率、通货膨胀率、消费者物价指数等。

这些数据通常由国家统计局或中央银行等机构发布，可以通过官方网站或相关报告获取。

2. 行业数据：行业数据是指特定行业的经济活动数据，如制造业、金融业、房地产业等。

这些数据可以通过行业协会、商业数据库或专业研究机构获取。

3. 个体数据：个体数据是指个别经济主体的数据，如个人、家庭、企业等。

个体数据常用于研究特定经济行为或个体之间的关系。

个体数据可以通过调查问卷、实地访谈、企业报告等方式获取。

4. 时间序列数据：时间序列数据是指同一经济变量在不同时间点上的观测值，如股票价格、利率、汇率等。

时间序列数据可以通过金融市场报价、央行公告等途径获取。

5. 横截面数据：横截面数据是指在同一时间点上对不同经济主体进行观测得到的数据，如不同城市的房价、不同企业的利润等。

横截面数据可以通过调查问卷、企业报告等方式获取。

在计量经济学研究中，数据的质量和可靠性非常重要。

为了确保数据的准确性和可比性，研究者通常需要进行数据清洗和处理，包括删除异常值、填补缺失值、调整单位等。

此外，还需要对数据进行统计分析，如描述性统计、回归分析等，以得出科学的结论。

总之，计量经济学数据是进行计量经济学研究的基础和支撑。

通过合理选择和使用各种类型的数据，研究者可以深入理解经济现象，验证经济理论，并为实际政策制定提供有力的依据。

注意：实验报告的题可以从以下题目中选择，也可以自己命题，自己命题要与金融专业知识相关。

第一部分多元线性回归1、经研究发现，家庭书刊消费受家庭收入及户主受教育年数的影响，表中为对某地区部分(1) 建立家庭书刊消费的计量经济模型；（2）利用样本数据估计模型的参数；（3）检验户主受教育年数对家庭书刊消费是否有显著影响；（4）分析所估计模型的经济意义和作用2某地区城镇居民人均全年耐用消费品支出、人均年可支配收入及耐用消费品价格指数的统计资料如表所示：利用表中数据，建立该地区城镇居民人均全年耐用消费品支出关于人均年可支配收入和耐用消费品价格指数的回归模型，进行回归分析，并检验人均年可支配收入及耐用消费品价格指数对城镇居民人均全年耐用消费品支出是否有显著影响。

3、下表给出的是1960—1982年间7个OECD 国家的能源需求指数（Y ）、实际GDP 指数（X1）、(1)建立能源需求与收入和价格之间的对数需求函数t t t tu X X Y +++=2ln 1ln ln 210βββ，解释各回归系数的意义，用P 值检验所估计回归系数是否显著。

(2) 再建立能源需求与收入和价格之间的线性回归模型 u X X Y t t t +++=21210βββ，解释各回归系数的意义，用P 值检验所估计回归系数是否显著。

(3 )比较所建立的两个模型，如果两个模型结论不同，你将选择哪个模型，为什么？4、考虑以下“期望扩充菲利普斯曲线（Expectations-augmented Phillips curve ）”模型：t t t t u X X Y +++=33221βββ其中：t Y =实际通货膨胀率（%）；t X 2=失业率（%）；t X 3=预期的通货膨胀率（%） 下表为某国的有关数据，表1. 1970-1982年某国实际通货膨胀率Y (%)，23（1）对此模型作估计,并作出经济学和计量经济学的说明。

（2）根据此模型所估计结果，作计量经济学的检验。