管理运筹学案例分析

管理运筹学案例分析产品产量预测一、问题的提出2007年，山西潞安矿业集团与哈密煤业集团进行重组，成立了潞安新疆煤化工（集团）有限公司。

潞安新疆公司成立后，大力加快新项目建设。

通过技术改造和加强管理，使煤炭产量、销售收入、利润、职工收入等得到了大幅提高，2007年生产煤炭506万吨，2008年煤炭产量726万吨，2009年煤炭产量956万吨。

三年每月产量见下表，请预测2010年每月产量。

表1 2007—2009年每月产量表单位：万吨二、分析与建立模型1、根据2007—2009年的煤炭产量数据，可做出下图：表2 2007—2009年每月产量折线图由上图可看出，2007—2009年的煤炭产量数据具有明显的季节性因素和总体上升趋势。

因此，我们采取用体现时间序列的趋势和季节因素的预测方法。

（一）、用移动平均法来消除季节因素和不规则因素影响1、取n=12；2、将12个月的平均值作为消除季节和不规则因素影响后受趋势因素影响的数值；3、计算“中心移动平均值”；4、计算每月与不规则因素的指标值。

表3 平均值表5、计算月份指数；6、调整月份指数。

表4 调整（后）的月份指数（二）、去掉时间序列中的月份因素将原来的时间序列的每一个数据值除以相应的月份指数。

表5 消除月份因素后的时间序列表三、计算结果及分析确定消除季节因素后的时间序列的趋势。

求解趋势直线方程。

设直线方程为：T t =b0+b1 tT t为求每t 时期煤炭产量；b0为趋势直线纵轴上的截距；b1为趋势直线的斜率。

求得：四、一点思考新疆的煤矿生产企业产能只是企业要考虑的部分因素，因国家产业政策以及新疆距离内地需经河西走廊，因此，企业不仅要考虑产能，更多的要考虑运输问题，从某种意义上来说，东疆地区煤炭生产企业不是“以销定产”，而是“以运定产”，也就是说，物流运输方案是企业管理人员要认真思考的问题。

本案例可以结合物流运输远近及运输工具的选择作进一步的运筹分析，以使得煤炭生产企业真正实现科学合理决策。

案例3-1产品混合问题TJ公司生产3中坚果什锦产品，分销给遍布东南地区的食品连锁店。

产品有3个品种，分别是普通型、高级型和假日型，不同品种的区别就是各种坚果的比例不同。

普通型的产品含有15%的杏仁，25%的巴西果，25%的榛子，10%的核桃，25%的胡桃。

高级型的产品各种坚果均含20%。

假日型的产品含25%的杏仁，15%的巴西果，15%的榛子，25%的核桃，20%的胡桃。

TJ公司的会计对包装材料费用、售价等数值进行分析后预测，每磅普通型产品的利润是1.65美元，每磅高级型产品的利润是2.00美元，每磅假日型产品的利润是2.25美元。

这些数值没有包括坚果的价格，因为它们的价格变化非常大。

客户的订单如下：因为对产品的需求在不断增加，预计TJ公司将会获得大于其生产能力的订单。

TJ公司的目的在于合理安排坚果产品的类型，使公司的利润最大；公司不用的坚果都捐献给当地的慈善机构。

还有，无论盈利与否，公司都将满足已经签署的订单。

管理报告分析TJ公司的问题，并准备一个报告向TJ公司总经理简要介绍一下你的观点。

报告的内容必须包括以下几个方面：（1）普通型、高级型和假日型坚果产品的成本。

（2）最优生产组合和总利润。

（3）如果还可以购买一些坚果，分析如何才能使产品的利润增加。

（4）思考公司是否应该从一个供应商那里再以1000美元的价格购入1000磅的杏仁。

（5）如果TJ不必满足全部的已签订单，公司会增加的利润量。

案例3-2投资战略J.D.威廉姆斯公司是一个投资咨询公司，为大量的客户管理高达1.2亿美元的资金。

公司运用一个很有价值的模型，为每个客户安排投资量，分贝在股票增长基金、收入基金和货币市场基金。

为了保证客户投资的多元化，公司对这3种投资的数额加以限制。

一般来说，投资在股票方面的资金应该占总投资的20%-40%，投资在收入基金上的资金应该确保在20%-50%之间，货币市场方面的投资至少应该占30%。

此外，公司还尝试着投入了风险承受能力指数，以迎合不同投资者的需求。

管理运筹学案例
1.生产计划优化：某家汽车制造公司需要优化其生产计划，以降低成本和提高效率。

管理运筹学通过分析生产流程和数据，建立数学模型来帮助公司优化生产计划。

2. 集装箱装载优化：一家货运公司需要将不同尺寸和重量的物
品装入集装箱，以最大程度地利用空间和降低成本。

管理运筹学通过建立装载模型和运算方法，帮助公司实现最优化装载。

3. 供应链管理：一家服装公司需要优化其供应链，以降低库存
成本、提高订单响应速度和提高客户满意度。

管理运筹学通过分析供应链的各个环节，建立数学模型和算法，帮助公司优化供应链管理。

4. 机场货物分配优化：某个机场需要优化货物分配，以最大程
度地利用仓库和车辆容量，降低运输成本和提高效率。

管理运筹学通过建立货物分配模型和运算方法，帮助机场实现最优化货物分配。

5. 人力资源管理：一家公司需要优化其人力资源管理，以提高
员工的工作效率和满意度，降低人事成本。

管理运筹学通过建立人力资源管理模型和算法，帮助公司实现最优化人力资源管理。

6. 投资组合优化：一家投资公司需要优化其投资组合，以实现
最大化收益和最小化风险。

管理运筹学通过建立投资组合模型和算法，帮助公司实现最优化投资组合。

7. 网络规划优化：一家电信公司需要优化其网络规划，以提高
网络效率和降低成本。

管理运筹学通过建立网络规划模型和算法，帮助公司实现最优化网络规划。

8. 排班优化：一家医院需要优化其医护人员排班，以提高工作效率和员工满意度。

管理运筹学通过建立排班模型和算法，帮助医院实现最优化排班。

案例2.1 -----产品定价决策案例背景介绍夏洛特·罗斯坦是克雷布罗索夫特公司的创建人，也是主要股东和CE0，近期她必须考虑对她公司的新产品Brainet软件的价格做出一个合适的战略定位，因为计算机软件市场形势变化多端无测，使得该决策变得非常困难。

根据对软件产品成本及市场的估计，她可以以50元/套的价格销售使收入最大化，或者以40元/套的价格销售，使市场份额最大化，当然还有第三个选择，那就是以45元/套销售，使二者兼得。

成本核算方面：新产品Brainet软件已投入了80万元的前期费用，估计每年还需要花费5万元用于支持和运送CD到需要软件硬拷贝的顾客那里。

市场需求方面：公司已得到了一些IT行业的的相关数据，并从基础数据中整理出三种价格策略在其他公司的竟争影响下（激烈、中等、温和）不同的销售量对应的概率。

表2.1.1 高价格下销售量的概率请在以下三种情况下做出能在一年内收回成本的最佳定价决策。

情况1. 市场竟争水平状况完全不能确定，公司如何做定价决策。

情况2. 公司从过去的经验来看，总结了一些简单的先验概率，即面对激烈竞争的可能性是20%，70％的可能性是中等水平的竞争，10％的可能是温和的竞争，公司又该如何决策。

情况3. 在情况2的基础上，好的助手杰妮和瑞杰又联系过她们的营销调查公司，营销调查公司说他们能够在一星期内提供关于推出Brainet面临的竞争状况和销售结果的研究报告。

而根据营销调查公司以往的预测：对于竟争激烈的情况，他们有80％的概率能够准确预测，有15%的概率预测为中等竞争水平。

对于中等竟争水平的情况，他们有80%的概率能够准确预测，有15％的概率预测为激烈竟争。

最后，对于温和竞争的情况，他们有90％的概率能够准确预测，有7％的概率预测为中等竟争水平，有3％的概率预测为激烈竞争。

”那么Cbrosoft是否应当花2000元进行营销调查？总的最优策略是什么？案例2.1 -----产品定价决策决策过程该决策问题的“自然状态”是市场的三种竟争状况：激烈、中等、温和；案例中需要作出的决策是在三种可选的软件产品市场销售价格方案：50元/套、45元/套、40元/套中确定一种最合适的方案。

管理运筹学案例设计管理运筹学是管理科学中一个重要的分支，通过运用数学、统计学和计算机科学等方法，对管理中的决策问题进行建模、分析和优化。

本文将介绍几个管理运筹学的案例，以帮助读者更好地理解其在实际管理中的应用。

案例一：生产调度优化某工厂生产多个产品，每个产品的生产需要不同的资源和时间。

工厂需要合理安排生产顺序，使得生产效率最大化，成本最小化。

通过管理运筹学的方法，可以建立数学模型来优化生产调度。

首先，我们需要确定每个产品的生产时间和资源需求。

然后，可以使用线性规划等数学方法，设计一个优化模型，以最小化总生产成本为目标函数，同时满足资源约束和交付期限。

案例二：库存管理优化某零售商经营多种商品，需要合理管理库存以满足需求，同时最小化库存成本。

通过管理运筹学的方法，可以建立库存管理模型来优化库存水平。

一种常见的方法是使用动态规划来确定最佳订货数量和补货时机，以最小化库存持有成本和缺货成本的总和。

通过对需求的预测和货架管理的优化，可以实现库存管理的最优化。

案例三：运输路线优化一家物流公司需要合理安排货物的运输路线，以最小化运输成本和时间。

通过管理运筹学的方法，可以设计运输路线优化模型，来寻找最佳的配送方案。

运输路线优化模型可以利用图论和网络优化方法，来确定最短路径和最优运输方案。

通过考虑货物的数量、目的地和运输方式等因素，可以制定最佳的运输策略，实现成本和效率的最优平衡。

结语管理运筹学是管理决策中的重要工具，可以帮助管理者在复杂的环境中做出最佳决策。

通过上述案例的介绍，我们可以看到管理运筹学在生产调度、库存管理和运输路线优化等方面的实际应用。

希望本文能够帮助读者更好地理解管理运筹学的概念和方法，从而在实际管理中取得更好的效果。

综合案例分析案例1 广告分析火烈鸟烤肉饭店是一家位于佛罗里达的面向高消费阶层的一家饭店。

为了帮助计划下一季度的广告宣传计划，该饭店雇佣了HJ广告公司。

饭店的管理层要求HJ推荐如何将广告预算分配在电视、广播和报纸上。

总的广告预算费用是279000美元。

在与火烈鸟烤肉饭店管理层的一次会议上，HJ顾问提供了以下信息：关于每种广告媒体在行业内的宣传率、每则广告能达到的新受众数以及各自的广告成本。

广告媒体每则广告的宣传率每则广告能达到的新受众数成本（美元）电视90 4000 10000广播25 2000 3000报纸10 1000 1000 宣传率被视作衡量广告对现有客户和潜在新客户的价值。

它是图像、消息反馈、可视和可闻形象等的函数。

正如预料的那样，最贵的电视广告有最大的宣传率，同时可到达最多的潜在新客户。

在这一点上，HJ顾问指出，关于每种媒体的宣传率和到达率的数据只在最初的几次广告应用中有效。

例如电视，它的90的宣传率和达到4000个潜在客户的数据只在头10次广告中有效，10次以后，电视广告的效用值会下降。

HJ顾问指出第10次以后播出的广告，宣传率降到55，同时到达的潜在客户数也降到1500。

对于广播媒体，上表中的数据在头15次广告中是有效的，第15次以后，宣传率降到20，能到达的潜在客户数降为1200。

类似地，对于报纸，上表中的数据在头20次广告中是有效的，第20次以后，宣传率降为5，能到达的潜在客户数降为800。

火烈鸟公司管理层接受了最大化各种媒体的总宣传率作为这次广告运动的目标。

由于管理层很在意吸引新的客户，因此希望这次广告活动至少能到达100000个新客户。

为了平衡广告宣传活动以及充分利用广告媒体，火烈鸟公司管理团队还采纳了以下方针：●广播广告的运用次数至少是电视广告的2倍；●电视广告不能运用超过20次；●电视广告的预算至少为140000美元；●广播广告的预算最多不能超过99000美元；●报纸广告的预算至少为30000美元。

管理运筹学lindo案例分析（a）Lindo的数据分析及习题(a)灵敏性分析（Range,Ctrl+R）用该命令产生当前模型的灵敏性分析报告：研究当目标函数的费用系数和约束右端项在什么范围（此时假定其它系数不变）时，最优基保持不变。

灵敏性分析是在求解模型时作出的，因此在求解模型时灵敏性分析是激活状态,但是默认是不激活的。

为了激活灵敏性分析，运行LINGO|Options…,选择General Solver Tab, 在Dual Computations列表框中,选择Prices and Ranges选项。

灵敏性分析耗费相当多的求解时间,因此当速度很关键时，就没有必要激活它。

下面我们看一个简单的具体例子。

例5。

1某家具公司制造书桌、餐桌和椅子，所用的资源有三种：木料、木工和漆工。

生产数据如下表所示:用DESKS、TABLES和CHAIRS分别表示三种产品的生产量,建立LP模型。

max=60*desks+30＊tables+20*chairs；8＊desks+6＊tables+chairs〈=48;4＊desks+2*tables+1。

5*chairs〈=20；2＊desks+1。

5＊tables+.5*chairs<=8;tables<=5;求解这个模型，并激活灵敏性分析。

这时，查看报告窗口（Reports Window）,可以看到如下结果. Global optimal solution found at iteration: 3Objective value: 280.0000Variable Value Reduced CostDESKS 2。

000000 0。

000000TABLES 0.000000 5。

000000CHAIRS 8。

000000 0.000000Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0。

秋季流行服饰与衣料的准备（五人）目从办公室的十层大楼里，凯瑟琳·拉里俯视着下面忙忙碌碌的人流，在充塞着黄色出租车的街道以及乱放着一些买热狗的摊位的人行道上，成群的纽约人来来往往，好不热闹。

在这闷热的暑天里，她注视着各类女性的穿衣时尚，心里想的却是这些人在秋季将会选择怎样的款式。

这并非是她的一时的灵感，而是她工作的重要的一部分因为她拥有并经营着一家妇女精品时装公司――时尚隧道（TrendLines）公司。

今天对她来说是很重要的，因为她将与生产部经理泰德·罗森碰面，一起商讨下一个月秋季生产线的生产计划，特别是在一定的生产能力的基础上确定要各种服装的生产量。

制定下个月的周密的生产计划对于秋季的销售是至关重要的，因为这些产品在9 月份将会上市，而妇女们通常在服装一上市时就会购买大部分的秋天的服饰。

凯瑟琳回转身，走到宽大的玻璃台旁去看铺上面的大量的资料及设计图。

她扫视着6个月以前就设计出来的服装图样，各种样式所需要的材料，以及在时装展上通过消费者调研取得的各种样式的需求预测。

现在，她还记得当时是如何设汁图样并将样品在纽约，米兰和巴黎的服装展上展出，那些天可真是既兴奋而又痛苦。

最后，她付给六个设计者的总酬金为$860,000。

除此外，每次时装展的费用为$2,700,000，包括雇用职业模特、发型师、化妆师，以及衣服的裁制与缝纫、展台背景的设计、模特的走步与排练、会场的租用。

她研究着衣服的样式和所需的材料。

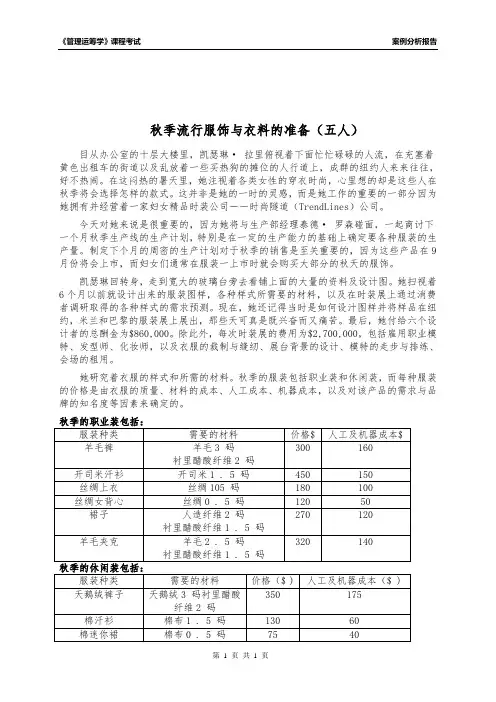
秋季的服装包括职业装和休闲装，而每种服装的价格是由衣服的质量、材料的成本、人工成本、机器成本，以及对该产品的需求与品牌的知名度等因素来确定的。

她知道已经为下个月采购了下面的这些材料：羊毛45,000码、开司米28,000码、丝绸18,000码、人造纤维30,000码、天鹅绒20,000码、棉布30,000码。

各种材料的价格如下图所示：多余的材料（不包括下脚料）可以运回给衣料供应商，并得到全额的偿还。

第一部分一、案例名称: 北方印染公司应如何合理使用技术培训费。

二、案例目的: 确定培养方案, 使企业增加的产值最多。

三、案例分析: 由案例给出的信息, 可以设十三个变量, 分别为x1、x2.x3.x4.x5.x6.x7、x8、x9、x10、x11.x12.x13。

其分别代表的含义是, 第一年由高中生培养初级工的人数, 第二年由高中生培养初级工的人数, 第三年由高中生培养初级工的人数, 由高中生培养中级工的人数, 由高中生培养高级工的人数, 第一年由初级工培养中级工的人数, 第二年由初级工培养中级工的人数, 第三年由初级工培养中级工的人数,第一年由初级工培养高级工的人数, 第二年由初级工培养高级工的人数, 第一年由中级工培养高级工的人数, 第二年由中级工培养高级工的人数, 第三年由中级工培养高级工的人数。

为了更加直观的各个变量的含义, 可以用如下表格展现各个变量的含义, 以便于理解和分析。

根据培养一名初级工在高中毕业后需要一年, 费用为1000元；培养一名中级工, 高中毕业后第一年费用为3000元；培养一名高级工, 高中毕业后第一年费用为3000元；由初级工培养为中级工需一年且费用为2800元；由初级工培养为高级工第一年且费用为2000元；由中级工培养为高级工需一年且费用为3600元。

并且根据第一年的投资为55万。

可以列出如下约束条件:1000x1+3000x4+3000x5+2800x6+2000x9+3600x11≤550000。

根据培养一名初级工在高中毕业后需要一年, 费用为1000元；培养一名中级工, 高中毕业后第二年费用为3000元；培养一名高级工, 高中毕业后第一年费用为2000元；由中级工培养为高级工需一年且费用为3600元；由初级工培养为中级工需一年且费用为2800元；由初级工培养为高级工第一年且费用为2000元；由中级工培养为高级工需一年且费用为3600元。

并且根据第二年的投资为45万。

运筹学案例的分析一、案例背景介绍本案例涉及一家制造业公司，该公司生产和销售汽车零部件。

由于市场竞争激烈，公司面临着多个挑战，如供应链管理、生产调度和库存管理等方面存在问题。

为了解决这些问题，公司决定运用运筹学方法进行分析和优化。

二、问题分析1. 供应链管理问题公司的供应链管理存在一些瓶颈，如供应商选择、物流运输和库存管理等方面存在问题。

如何优化供应链，降低成本，提高效率是一个亟待解决的问题。

2. 生产调度问题公司的生产线存在一些瓶颈，导致生产效率低下和交货周期延长。

如何优化生产调度，提高生产效率，缩短交货周期是公司急需解决的问题。

3. 库存管理问题公司面临着库存管理方面的挑战，如库存过高、库存周转率低等问题。

如何优化库存管理，降低库存成本，提高库存周转率是公司亟需解决的问题。

三、运筹学方法的应用为了解决上述问题，公司决定运用运筹学方法进行分析和优化。

具体应用如下：1. 供应链管理优化通过对供应链进行建模和分析，确定关键节点和瓶颈环节，优化供应商选择和物流运输方案，以降低成本和提高效率。

同时，建立合理的库存管理模型，通过合理的库存控制策略，降低库存成本，提高库存周转率。

2. 生产调度优化通过对生产线进行建模和分析，确定生产瓶颈和瓶颈环节，优化生产调度方案，提高生产效率和缩短交货周期。

同时，建立合理的生产计划和排程模型，通过合理的生产计划和排程策略，提高生产效率和减少交货周期。

3. 库存管理优化通过对库存管理进行建模和分析，确定库存管理的关键指标和影响因素，优化库存管理策略，降低库存成本和提高库存周转率。

同时，建立合理的库存控制模型和库存管理系统，通过合理的库存控制和管理策略，降低库存成本和提高库存周转率。

四、数据分析和模型建立为了进行运筹学分析和优化，公司需要收集相关的数据，并建立相应的模型。

数据可以包括供应链的各个环节的成本、时间和效率等指标，生产线的各个环节的生产能力和效率等指标，以及库存管理的各个环节的库存成本和库存周转率等指标。

管理运筹学案例分析案例背景在当今的商业环境中，管理运筹学扮演着至关重要的角色。

通过运用数学模型和分析技术，管理运筹学帮助企业有效地利用资源、提高效率和降低成本。

本文将通过一个实际案例来说明管理运筹学在企业管理中的应用和重要性。

案例描述ABC公司是一家制造业企业，面临着生产线的调度和管理难题。

公司生产多种不同产品，每种产品需要经过不同的加工工序，而每个工序的加工时间和资源消耗也不同。

在生产线上，不同的产品需要按照特定的顺序进行生产，以确保生产效率最大化。

然而，由于订单量的波动和资源限制，公司经常遇到生产调度不当、生产效率低下的问题。

问题分析ABC公司的管理团队意识到需要寻找一种方法来优化生产线的调度，提高生产效率。

他们决定运用管理运筹学的方法来解决这一问题。

通过建立数学模型和运用优化算法，他们希望找到一个最优的生产调度方案，使得生产效率达到最高，同时满足订单需求和资源限制。

解决方案ABC公司首先对生产线的各个工序进行了详细的分析和测量，确定了每个产品在每个工序的加工时间和资源消耗。

然后，他们建立了一个数学模型，以最小化总生产时间和成本为优化目标，同时考虑到订单优先级和资源限制等约束条件。

通过运用线性规划和整数规划等数学优化方法，ABC公司得到了一个最优的生产调度方案。

他们调整了各个工序的生产顺序，合理安排了各种产品的生产数量，最大限度地提高了生产效率，减少了生产时间和成本。

成果评估经过实际实施和运用，ABC公司发现新的生产调度方案确实带来了显著的效益。

生产效率得到了提高，订单交付时间缩短，生产成本也减少了。

公司不仅提高了客户满意度，还降低了生产的风险和压力。

结论通过本案例的分析，我们可以看到管理运筹学在企业管理中的重要性和价值。

通过运用数学模型和优化算法，企业可以找到最佳的决策方案，提高效率、降低成本、增加利润。

管理运筹学不仅可以帮助企业解决实际问题，还可以提升企业的竞争力和可持续发展能力。

以上是对管理运筹学在实际案例中的分析和应用，希望能够给企业管理者带来启发和借鉴。

《管理运筹学》案例题解案例1：北方化工厂月生产计划安排解：设每月生产产品i （i=1，2，3，4，5）的数量为X i ，价格为P 1i ，Y j 为原材料j 的数量，价格为P 2j ，a ij 为产品i 中原材料j 所需的数量百分比，则：510.6j i ij i Y X a ==∑总成本：TC=∑=1512j j j P Y总销售收入为：511i i i TI X P ==∑目标函数为：MAX TP （总利润）=TI-TC 约束条件为：1030248002151⨯⨯⨯≤∑=j j Y X 1+X 3=0.7∑=51i i XX 2≤0.05∑=51i i XX 3+X 4≤X 1 Y 3≤4000 X i ≥0,i=1,2,3,4,5 应用计算工具求解得到： X 1=19639.94kg X 2=0kg X 3=7855.97kg X 4=11783.96kg X 5=0kg最优解为：348286.39元案例2：石华建设监理工程师配置问题解：设X i 表示工地i 在标准施工期需要配备的监理工程师，Y j 表示工地j 在高峰施工期需要配备的监理工程师。

约束条件为： X 1≥5 X 2≥4 X 3≥4 X 4≥3 X 5≥3 X 6≥2 X 7≥2 Y 1+Y 2≥14 Y 2+Y 3≥13 Y 3+Y 4≥11 Y 4+Y 5≥10 Y 5+Y 6≥9 Y 6+Y 7≥7 Y 7+Y 1≥14Y j ≥ X i （i=j ，i=1,2,…,7） 总成本Y 为：Y=∑=+71)12/353/7(i i i Y X解得X 1=5；X 2=4；X 3=4；X 4=3；X 5=3；X 6=2；X 7=2；1Y =9；2Y =5；3Y =8；4Y =3；5Y =7；6Y =2；7Y =5; 总成本Y=167.案例3：北方印染公司应如何合理使用技术培训费解：变量的设置如下表所示，其中X ij为第i类培训方式在第j年培训的人数：第一年第二年第三年1.高中生升初级工X11X12X132.高中生升中级工X213.高中生升高级工X314.初级工升中级工X41X42X435.初级工升高级工X51X526.中级工升高级工X61X62X63则每年年底培养出来的初级工、中级工和高级工人数分别为：第一年底第二年底第三年底初级工X11X12X13中级工X41X42X21 +X43高级工X61X51 +X62X31 +X52+X63则第一年的成本TC1为：1000X11+3000X21+3000X31+2800X41+2000X51+3600 X61≤550000；第二年的成本TC2为：1000X12+3000X21+2000X31+2800X42+（3200 X51+2000X52）+3600X62≤450000；第三年的成本TC3为：1000X13+1000X21+4000X31+2800X43+3200 X52+3600X63≤500000；总成本TC= TC1 +TC2 +TC3≤1500000;其他约束条件为：X41 +X42 +X43+X51 +X52≤226；X61+X62 +X63≤560；X1j≤90 （j=1，2，3）；X21 +X41≤80；X21 +X42≤80；X 21 +X 43≤80； X 31 +X 51+X 61≤80； X 31 +X 51+X 52+X 62≤80； X 31 +X 52+X 63≤80；以下计算因培训而增加的产值Max TO=(X 11+ X 12+ X 13) + 4(X 41 +X 42 +X 21 +X 43) +5.5(X 61 +X 51 +X 62 +X 31 +X 52+X 63); 利用计算机求解：X 11=38；X 41=80；X 42=59；X 43=77；X 61=80；X 62=79；X 63=79；其余变量都为0； TO=2211案例4：光明制造厂经营报告书设直径4.76、6、8、10和12的钢管的需求量分别是1x ,x 2,3x ,4x ,5x 。

高校管理学专业运筹学模型求解案例分析在高校管理学专业中，运筹学模型是一种重要的分析工具，可用于解决各种与运营和决策相关的问题。

本文将通过一个案例分析，探讨如何应用运筹学模型来解决高校管理中的实际问题。

案例背景：某高校图书馆的座位管理某高校图书馆在高峰期常常出现座位不足的情况，为了更好地满足师生们的学习需求，图书馆决定引入运筹学模型来优化座位管理。

具体问题是如何合理安排学生的座位，以最大化座位利用率，并且保证每个学生都能找到合适的座位。

问题分析与模型建立：首先，我们需要了解座位的数量和类型。

经过调研，图书馆共有A、B、C三类座位，分别具有不同的特点和使用规则。

A类座位可供单人使用，B类座位可供两人使用，C类座位可供小组使用。

我们将座位数量分别记为a、b、c。

在分配座位时，我们应该满足三个条件：1.每个学生都能找到座位；2.座位利用率最大化；3.尽量减少学生之间的距离。

为了解决这个问题，我们可以建立一个数学模型。

假设有n个学生需要找座位，他们的座位偏好可以用一个矩阵D来表示。

矩阵D的第i行第j列表示学生i对座位j的偏好程度，偏好程度越高表示学生i更喜欢座位j。

同时，我们可以定义一个二值变量X，表示座位的使用情况。

如果座位i被使用，则Xi=1；否则，Xi=0。

基于这些假设，我们可以得到以下的线性规划模型：最大化∑(∑(Dij*Xj))约束条件：∑(Xj) >= n （每个学生都能找到座位）∑(Xj) <= a （A类座位数量限制）∑(2*Xj) <= b （B类座位数量限制）∑(k*Xj) <= c （C类座位数量限制）其中k是小组的人数，可以根据实际情况调整。

通过以上的模型，我们可以根据学生们的座位偏好和座位类型的限制，以最优化的方式进行座位分配。

除了满足每个学生找到座位的基本需求外，我们还可以通过调整偏好程度的权重来平衡座位利用率和学生之间的距离。

结果分析与优化：在应用运筹学模型求解后，我们可以得到最优解。