6数列-1981-2018年历年数学联赛48套真题WORD版分类汇编含详细答案

1981年~2018年全国高中数学联赛一试一试题分类汇编1、会合部分2018A1、设会合A 1,2,3, ,99，会合B 2x|xA ，会合C x|2x A ，则会合BC 的元素个数为 ◆答案：24★分析：由条件知， B C 2,4,6, ,48，故B C 的元素个数为 24。

2018B1、设会合A 2,0,1,8，会合B2a|aA ，则会合AB 的所有元素之和是◆答案：31★分析:易知B 4,0,2,16 ，所以AB 0,1,2,4,8,16 ，元素之和为 31.2018B 三、（此题满分 50分）设会合A 1,2, ,n ，X,Y 均为A 的非空子集（同意XY ）．X中的最大元与Y 中的最小元分别记为 maxX,minY ．求知足maxX minY 的有序会合对(X,Y) 的数量。

★分析:先计算知足maxX minY 的有序会合对(X,Y)的数量.对给定的m maxX ，会合X 是会合1,2, ,m 1的随意一个子集与m 的并，故共有2m1种取法.又mminY ，故Y 是m,m1,m2, ,n 的随意一个非空子集，共有2n1m1种取法.所以，知足maxXminY 的有序会合对(X,Y)的数量是：nnn2m12n1m12n2m1n12n1m1m1m1(X,Y)有2n12n1 2n2个，于是知足maxX minY 的有序会合对因为有序会合对1(X,Y)的数量是2n2n2n2n14n2n n1 12017B二、（此题满分40分）给定正整数m，证明：存在正整数k，使得可将正整数集N分拆为k个互不订交的子集A1,A2, ,A k，每个子集A i中均不存在4个数a,b,c,d（能够相同），满足abcdm．★证明：取k m1，令A i{xx i(modm1),x N}，i1,2,,m1设a,b,c,d A i，则ab cd iii i0(modm1)，故m1ab cd，而m1m，所以在A i中不存在4个数a,b,c,d，知足ab cdm2017B四、（此题满分50分）。

⎣
⎦
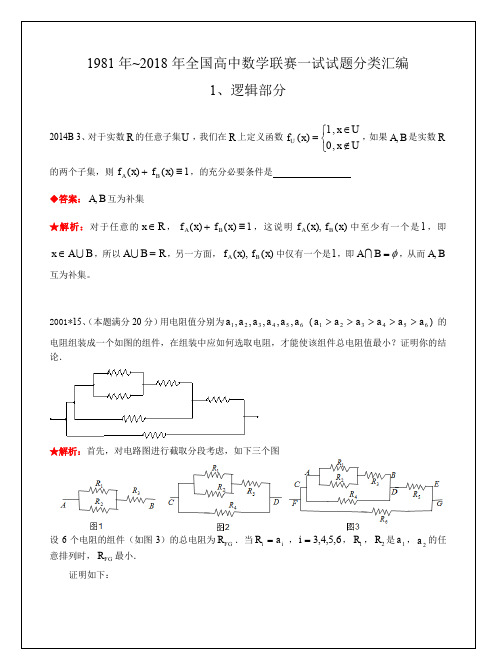
图1 图2 图3
∆内不难看出，这里的10个正六边形的直径为1，它们可以被看做10只“抽屉”，对于三角形ABC 部和边界上任取11个点，根据抽屉原理，至少有一个正六边形包含两个点。

而在这个正六边形中，任意两点间的距离不超过1，这样便证明了我们所要的结论。

图5
11个点中存在两个点，他们间的距离严格小于1
()(n n d
P P n >02.n P P P ≤≤,8均成立13
k +即可半径画圆，这个圆覆盖上述d n
P P >0102.n P P P P P P ≤≤为半径画k 上任意一点
P P>‥‥‥‥‥‥‥‥‥‥‥50 n
该排列为“好排列”
的边都是偶数条．所以这种密码锁的所有不同的密码设置方法
图1 图2
第二步构造一种取法，共取走11个棋子，余下的棋子没有五子连珠。

如图2，只要取出有标号位置的棋子，则余下的棋子不可能五子连珠。

★解析：在表1中，取0,4,14,24,34====---i i i i i i i i x x x x (25,,2,1 =i )，其余各数均取24
1
，25
任意白色。

1981年~2018年全国高中数学联赛二试试题分类汇编组合与构造1981-2018年历年数学联赛48套真题2017A 三、（本题满分50分）将3333⨯方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等。

若相邻两个小方格的颜色不同，则称他们的公共边为“分割边”。

试求分割边条数的最小值。

★解析：记分割边的条数为L .首先，将方格纸按如图所示分成三 个区域，分别染成三种颜色，粗线上均为分割边，此时共有56条 分割边，即56=L 。

下面证明56≥L .将方格纸的行从上至下依次记为1A ,2A ,33,A ,列从左至右依次记为1B ,2B ,33,B ,行i A 中方格出现的颜色数记为()i A n ，列i B 中方格出现的颜色数记为()i B n ，三种颜色分别记为1c ，2c ，3c ， 对于一种颜色j c ，设()i c n 是表示含有j c 色方格的函数与列数之和.记()⎩⎨⎧=色方格中不含色方格中含有，，j i j i j i c A c A c A 01,ξ，同理定义()⎩⎨⎧=色方格中不含色方格中含有，，j i j i j i c B c B c B 01,ξ，则()()()()()()()()()()∑∑∑∑∑∑=======+=+=+313313133131331,,,,j i j jjijii j jijii iic n c B c A c B c A B n A n ξξξξ①由于染j c 色的方格有36333312=⨯个，设含有j c 色方格的行有a 个，列有b 个，则j c 色方格一定在这a 行和b 列的交叉方格中，因此363≥ab .从而()3836322>≥≥+=ab b a c n i 即()39≥i c n . ,3,2,1=j ②由于在行i A 中有()i A n 种颜色的方格，因此至少有()1-i A n 条分割边，同理在行i B 中有()i B n 种颜色的方格，因此至少有()1-i B n 条分割边，于是，()()()()()()()()66661131331331331-=-+≥-+-≥∑∑∑∑====j j i i i i i i i c n B n A n B n A n L ③下面分两种情形讨论.⑴当有一行或有一列全部方格同色时，不妨设有一行全为1c 色，从而方格纸的33列中均含有1c 的方格，由于1c 的方格有363个，故至少有11行中含有1c 色方格。

1981年~2018年全国高中数学联赛试题分类汇编不定方程部分2011B 一、（本题满分40分）求所有三元整数组(,,)x y z ，使其满足333320111515x y z xyz x y ⎧++-=⎪≥⎨⎪≥⎩★解析：由20113333=-++xyz z y x ，得()()()()[]4022222=-+-+-++x z z y y x z y x ①因220114022⨯=，且()()()0222≡-+-+-x z z y y x ()2mod ，所以①等价于()()()⎩⎨⎧=-+-+-=++40221222x z z y y x z y x ②或()()()⎩⎨⎧=-+-+-=++22011222x z z y y x z y x ③对方程组②，消去z 得()()()40221212222=-++-++-y x y x y x ，即67022=--++y x xy y x ④⑴若15=x ，15=y ，则67064522<=--++y x xy y x 与④矛盾；⑵若16≥x ，15≥y ，则670690434256))(1(2>=+≥+-+y x y x 与④矛盾；⑶若15≥x ，16≥y ，则670690434256))(1(2>=+≥+-+y x x y 与④矛盾；综上方程组②无解；对方程组③，由()()()2222=-+-+-x z z y y x 可得y x -，z y -，x z -中有两个为1，一个为0。

⑴若1=-y x ，1=-z y ，0=-x z ，则z x y ==+1或z x y ==-1，z x y ==+1代入③的第一个方程，无解；z x y ==-1代入③的第一个方程，解得671=y ，670==z x ⑵若1=-y x ，0=-z y ，1=-x z ，同理可得671=x ，670==z y ⑶若0=-y x ，1=-z y ，1=-x z ，同理可得671=z ，670==y x 综上，满足条件的三元数组为()670,670,671，()670,671,670，()671,670,6702010AB 8、方程2010=++z y x 满足z y x ≤≤的正整数解),,(z y x 的个数是◆答案：336675★解析：首先易知2010=++z y x 的正整数解的个数为1004200922009⨯=C .把2010=++z y x 满足z y x ≤≤的正整数解分为三类：（1）z y x ,,均相等的正整数解的个数显然为1；（2）z y x ,,中有且仅有2个相等的正整数解的个数，易知为1003；(3)设z y x ,,两两均不相等的正整数解为k .易知100420096100331⨯=+⨯+k ，所以110033*********-⨯-⨯=k 200410052006123200910052006-⨯=-⨯+-⨯=，即3356713343351003=-⨯=k .从而满足z y x ≤≤的正整数解的个数为33667533567110031=++.2010B 二、（本题满分40分）设m 和n 是大于1的整数，求证：11111112(1)().1m m n m m mk k j j m m k j i n n C n C i m -+===⎧⎫+++=+-⎨⎬+⎩⎭∑∑∑ ★证明：11101)m m j j m j q Cq +++=+=∑由（得到1110(1),mm m j j m j q q C q +++=+-=∑1,2,,q n = 分别将代入上式得：11021,m m j m j C ++=-=∑1110322,m m m j j m j C +++=-=∑ 1110(1)(1),m m m j j m j n n C n +++=--=-∑1110(1).m m m j j m j n n C n +++=+-=∑n 将上面个等式两边分别相加得到：1101(1)1(),m n m j j m j i n Ci ++==+-=∑∑（20分）11111(1)(1)1(1),m n n m j j m m j i i n n n Ci m i -+===++-=+++∑∑∑（）11111112(1)().1m m n m m m k k j j m m k j i n n C n C i m -+===⎧⎫+++=+-⎨⎬+⎩⎭∑∑∑ （40分）2008A B5、方程组⎪⎩⎪⎨⎧=+++=+=++000y xz yz xy z xyz z y x 的有理数解),,(z y x 的个数为（）A.1 B.2 C.3 D.4◆答案：B★解析：若0z =，则00.x y xy y +=⎧⎨+=⎩，解得00x y =⎧⎨=⎩，或11.x y =-⎧⎨=⎩，若0z ≠，则由0xyz z +=得1xy =-．①由0x y z ++=得z x y =--．②将②式代入0xy yz xz y +++=得220x y xy y ++-=．③由①式得1x y=-，代入③式化简得3(1)(1)0y y y ---=.易知310y y --=无有理数根，故1y =，由①式得1x =-，由②式得0z =，与0z ≠矛盾，故该方程组共有两组有理数解0,0,0x y z =⎧⎪=⎨⎪=⎩或1,1,0.x y z =-⎧⎪=⎨⎪=⎩2008B 二、（本题满分50分）求满足下列关系式组2222,50,x y z z y z ⎧+=⎨<≤+⎩的正整数解组(,,)x y z 的个数．★解析：令r y z =-，由条件知050r <≤，方程化为222()2x z r z ++=，即2222x zr r z ++=．（1）因0y z r -=>，故22222z x y z x =+->，从而z x >．设0p z x =->．因此（1）化为22220zp p zr r -+++=．（2）下分r 为奇偶讨论，（ⅰ）当r 为奇数时，由（2）知p 为奇数．令121r r =+，121p p =+，代入（2）得221111112()10p p zp zr r r +-++++=．（3）（3）式明显无整数解．故当r 为奇数时，原方程无正整数解．（ⅱ）当r 为偶数时，设12r r =，由方程（2）知p 也为偶数．从而可设12p p =，代入（2）化简得2211110p zp zr r -++=．（4）由（4）式有221111()0z p r p r -=+>，故11p r >，从而可设11p r a =+，则（4）可化为2211()0r a za r +-+=，2211220r ar za a +-+=．（5）因21122r z r a a=++为整数，故212a r ，又1122()z z x p r a >-==+，因此22111()2()r a r za r a a ++=>+，得2212a r <，即1a <．因此，对给定的11,2,,25r =⋅⋅⋅，解的个数恰是满足条件1a <的212r 的正因数a 的个数1()N r ．因212r 不是完全平方数，从而1()N r 为212r 的正因数的个数21(2)r σ的一半．即211()(2)/2N r r σ=．由题设条件，1125r ≤≤．而25以内有质数9个：2，3，5，7，11，13，17，19，23．将25以内的数分为以下八组：012341{2,2,2,2,2}A =，2{23,25,27,211}A =⨯⨯⨯⨯，223{23,25}A =⨯⨯，34{23}A =⨯，25{23}A =⨯，1{3,5,7,11,13,17,19,23}B =，222{3,5}B =，3{35,37}B =⨯⨯，从而易知012341()(2)(2)(2)(2)(2)1234515N A N N N N N =++++=++++=，2()(23)46424N A N =⨯⨯=⨯=，3()9218N A =⨯=，4()12N A =，5()10N A =，1()3824N B =⨯=，2()5210N B =⨯=，3()9218N B =⨯=，将以上数相加，共131个．因此解的个数共131．2006*11、方程()()20052004422006200611x x x x x=+++++ 的实数解的个数为◆答案：1★解析：200520044220062006)1)(1(x x x x x =+++++ 24200420051()(1)2006x x x x x ⇔+++++= 35200520052003200111112006x x x x x x x x ⇔++++++++=。

1981年~2018年全国高中数学联赛一试试题分类汇编2、函数与方程部分2018A 5、设)(x f 是定义在R 上的以2为周期的偶函数，在区间[]1,0上严格递减，且满足1)(=πf ，2)2(=πf ，则不等式组⎩⎨⎧≤≤≤≤2)(121x f x 的解集为 ◆答案：[]ππ28,2--★解析：由)(x f 为偶函数及在区间[]1,0上严格递减知，)(x f 在[]0,1-上递增，结合周期性知，)(x f 在[]2,1上递增，又1)()2(==-ππf f ，2)2()2()28(==-=-πππf f f ， 所以不等式等价于)28()()2(ππ-≤≤-f x f f ，又22821<-<-<ππ 所以ππ282-<<-x ，即不等式的解集为[]ππ28,2--2018A ，B 9、（本题满分16分）已知定义在+R 上的函数)(x f 为⎩⎨⎧--=x x x f 41log )(39,90,>≤<x x ，设c b a ,,是三个互不相同的实数，满足)()()(c f b f a f ==，求abc 的取值范围。

★解析：不妨设c b a <<，由于)(x f 在(]3,0上递减，在[]9,3上递增，在[)+∞,9上递减，且0)3(=f ，1)9(=f ，结合图像知：()3,0∈a ，()9,3∈b ，()+∞∈,9c ，且()1,0)()()(∈==c f b f a f 。

由)()(b f a f =得2log log 33=+b a ，即9=ab ，此时c abc 9=，又c c f -=4)(，由140<-<c 得()16,9∈c ，所以()144,819∈=c abc 。

2018B 7、设)(x f 是定义在R 上的以2为周期的偶函数，在区间[]2,1上严格递减，且满足1)(=πf ，0)2(=πf ，则不等式组⎩⎨⎧≤≤≤≤1)(010x f x 的解集为◆答案：[]ππ--4,62★解析：由)(x f 为偶函数及在区间[]2,1上严格递减知，)(x f 在[]1,2--上递增，结合周期性知，)(x f 在[]1,0上递增，又1)()4(==-ππf f ，0)2()62(==-ππf f ，所以不等式等价于)4()()62(ππ-≤≤-f x f f ，又14620<-<-<ππ，即不等式的解集为[]ππ--4,62.2017A1、设)(x f 是定义在R 上函数，对任意的实数x 有1)4()3(-=-⋅+x f x f ，又当70<≤x 时，)9(log )(2x x f -=，则)100(-f 的值为 ◆答案： 21-★解析：由条件知，1)()7(-=+x f x f ，即1)14()7(-=++x f x f ，故)14()(+=x f x f ，即函数)(x f 的周期为14，所以21)5(1)2()100(-=-=-=-f f f2017B 3、设)(x f 是定义在R 上的函数，若2)(x x f +是奇函数，xx f 2)(+是偶函数，则)1(f 的值为 ◆答案：74-★解析：由条件知，2(1)1((1)(1))(1)1f f f +=--+-=---，1(1)2(1)2f f +=-+， 两式相加消去(1)f -，可知：12(1)32f +=-，即7(1)4f =-.2016A 3、正实数u ，v ，w 均不等于1，若5log log =+w vw v u ，3log log =+v u w v ，则v w log 的值为 ◆答案：54★解析：令a v u =log ，b w v =log ，则a u v 1log =，bv w 1log =，ab a w v v vw v u u u +=•+=log log log log 条件化为5=++b ab a ，311=+b a ，由此可得45=ab ，因此54log log log ==•=u v u v w w ．2016A 10、（本题满分20分）已知)(x f 是R 上的奇函数，1)1(=f ，且对任意0<x ，均有)()1(x xf x x f =-。