当前位置：文档之家 › 计算机中的信息表示

计算机中的信息表示

  • 格式：ppt
  • 大小：459.00 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

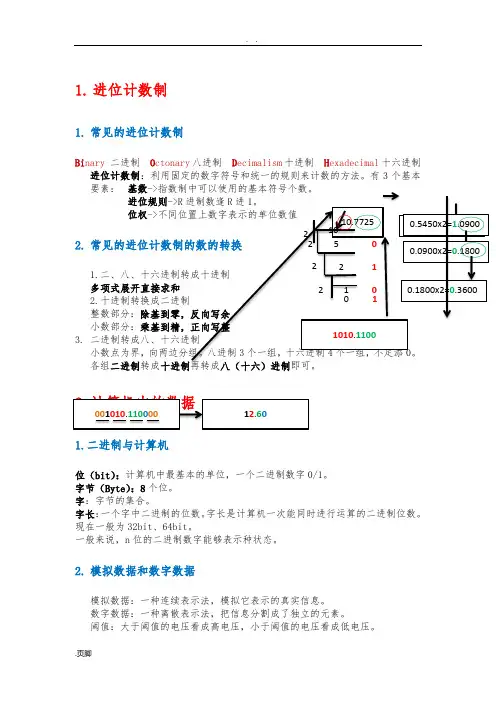
计算机中的信息表示

计算机中的信息表示

1. 进位计数制1. 常见的进位计数制Bi nary 二进制 O ctonary 八进制 D ecimalism 十进制 H exadecimal 十六进制进位计数制：利用固定的数字符号和统一的规则来计数的方法。

有3个基本要素： 基数->指数制中可以使用的基本符号个数。

进位规则->R 进制数逢R 进1。

位权->不同位置上数字表示的单位数值 2. 常见的进位计数制的数的转换 1.二、八、十六进制转成十进制多项式展开直接求和 2.十进制转换成二进制整数部分：除基到零，反向写余小数部分：乘基到精，正向写整 3. 二进制转成八、十六进制小数点为界，向两边分组。

八进制3个一组，十六进制4个一组，不足添0。

各组二进制转成十进制再转成八（十六）进制即可。

2.计算机中的数据 1.二进制与计算机位（bit ）：计算机中最基本的单位，一个二进制数字0/1。

字节（Byte ）：8个位。

字：字节的集合。

字长：一个字中二进制的位数。

字长是计算机一次能同时进行运算的二进制位数。

现在一般为32bit 、64bit 。

一般来说，n 位的二进制数字能够表示种状态。

2. 模拟数据和数字数据模拟数据：一种连续表示法，模拟它表示的真实信息。

数字数据：一种离散表示法，把信息分割成了独立的元素。

阈值：大于阈值的电压看成高电压，小于阈值的电压看成低电压。

10.7725 10 2 5 0 2 2 1 2 1 0 2 0 1 1010.1100 0.7725x2=1.5450 0.5450x2=1.0900 0.0900x2=0.18000.1800x2=0.3600 001010.110000 12.60计算机不能处理模拟数据，要对模拟数据进行数字化。

3. 数据及其分类数值、文本、音频、视频、图像、图形。

4. 数值型数据的表示机器数：一个数在计算机中的表示形式。

机器数有位数限制，多余的位数将被截断，少的位数将被填充。

（机器数的）真值：带有正负号的数。

计算机中信息表示

计算机中信息表示

计算机中信息表⽰1、概述现在的我们⽆时⽆刻不在接触计算机，即常说的电脑。

计算机能⼲很多事，⽐如浏览⽹页、看视频、玩游戏、办公等，实现这些功能都需要计算机有信息存储和处理的能⼒。

现代计算机的信息存储和处理都以⼆进制为基础，简单来说我们在电脑上看到的信息(⽐如⽂字、图⽚、⾳频、视频)都是以⼆进制表⽰的形式存储在计算机上或被计算机以⼆进制这种形式处理的。

⽐如我们在计算机上的记事本中写⽇记，写⼊的是中⽂，在计算机中是以⼆进制编码(01010......)存储的，同时会给这些⼆进制编码指定⼀种解释⽅式，⽐如GB2312编码等，这样⽇记显⽰在屏幕上的才是中⽂。

为什么计算机选择⼆进制存储和处理信息？主要原因是⼆进制容易被电⼦元件表⽰、存储和传输，⽐如可以以电压⾼低表⽰0/1，或以磁场的⽅法顺时针和逆时针表⽰0/1等。

我们⽇常使⽤⼗进制表⽰数字，原因是每个⼈都有⼗个⼿指或⼗个脚趾，使⽤⼗进制符合我们⼤部分⼈的认知，也⽅便⽇常使⽤。

1.1 计算机存储和表⽰的基本单位计算机中存储和表⽰数据的基本单位是位 (bit)，和我们平常在⼗进制中所说的位概念相同，⽐如个位、⼗位、百位等。

⼆进制中每位的取值范围是0或者1。

计算机中每8位代表⼀个字节(byte)，即 1byte = 8bit，这是计算机中的常⽤存储⼤⼩单位。

⽐字节⼤的还有KB、MB、GB、TB、PB、EB，其换算关系如下：1KB = 1024B，1MB = 1024KB，1GB = 1024MB，1TB = 1024GB，1PB = 1024TB，1EB = 1024PB。

’需要注意两个问题：1. B和b的区别，⼤写B代表字节，⼩写b代表⽐特位。

⽐如1KB = 8Kb，常见的⽹速10Mbps，代表每秒10Mb，即⼤约1MB/s；2. 标准换算关系是 1KB = 1024B，但在⼀般⾮正式计算中为了⽅便计算，使⽤1KB = 1000B，其他的依此类推。

⽐如新买的电脑的磁盘或U盘，标称⼤⼩和实际⼤⼩不符合1024的换算关系，原因就是在⼯程制造中⼀般使⽤1000的换算⽐例，⽽计算机使⽤的1024的换算⽐例，所以会导致存在⼀定的偏差。

2计算机信息表示

2计算机信息表示
✓ 定点整数：小数点固定在表示数值的最低位之后 ✓ 定点小数：小数点固定在符号位和数值位之间
41
计算机编码_数值
小数的表示
✓ 浮点数：小数点的位置不固定。由阶码和尾数组 成
✓ 阶码：指数部分，是一个整数 ✓ 尾数：数的有效数值，整数或纯小数两种形式
42
计算机编码_字符
字符编码
✓ 如何表示A、B、C等字母？ ✓ 如何表示句号、逗号等？ ✓ 如何表示回车、换行等？
9
1001
11
不同数制值之间的关系
12
二进制运算
算术运算规则： 0+0=0 0+1=1 0*0=0 0*1=0
1+0=1 1*0=0
1+1=10 1*1=1
110 ＋ 011
1001
011 ＋ 011
110
13
二进制运算
逻辑运算规则： 与 / ：或 / ： 非:
0
1
0
1
110001 011111
✓ 一个字节可有256个值 ✓ 可存放一个半角英文字符（ASCII码）。两
个或四个字节存放一个汉字编码
26
数据的计算机存储
位： b 字节：B
1B＝8b
1KB = 1024 B＝210B 1MB = 1024KB ＝220B 1GB = 1024MB ＝230B 1TB = 1024GB ＝240B
5
1 数制
数制(number system)
✓ 用一组固定的数字（数码符号）和一套 统一的规则来表示数值的方法。也叫计 数制
6
数制
几种常用进位计数制。
✓ 十位制(Decimal notation) D –十个手指 ✓ 24进制（一天）；60进制（秒、分、时） ✓ 二进制(Binary notation) B ✓ 八进制(Octal notation) O ✓ 十六进制数(Hexadecimal notation) H ✓ 古巴比伦人-60进制 ✓ 玛雅人-20进制

计算机中的信息表示

计算机中的信息表示

64O： 64O
第3章 计算机中的信息表示 Nhomakorabea2. 二进制转化成八进制
原则：三位一组法。 原则：三位一组法。 整数部分： 进行分组。 整数部分：从右向左进行分组。 进行分组，不足3位补零。 小数部分： 小数部分：从左向右进行分组，不足3位补零。 110 101 111 . 010 10 0 B=657.24O =657.24O 6 5 7 2 4
无符号整数的表示
无符号整数指的是计数系统中只有大于等于 无符号整数指的是计数系统中只有大于等于0的 只有大于等于0 因此，不需要表示符号。 数，没有负数 ，因此，不需要表示符号。 例如：用8位二进制表示整数的范围： 二进制表示整数的范围 表示整数的范围： 例如： 0000 0000～1111 1111 0000～ 对应的十进制整数的范围： 对应的十进制整数的范围： 0 ～ 255
第3章 计算机中的信息表示
二、八、十六进制之间的转换
1. 八进制转换成二进制 八进制转换成二进制
原则： 一分为三法。 原则： 一分为三法。 位二进制码。 每 1 个八进制数对应 3 位二进制码。 27.461O 27.461O ： 2 7. 4 6 1 010 111 100 110 001B 001B 6 110 4 100B 100B
后边补两个零
第3章 计算机中的信息表示
八进制与二进制的对应关系
八进制 0 1 2 3 011 4 100 5 101 6 110 7 111
二进制
000 001 010
第3章 计算机中的信息表示
十六进制与二进制的对应关系
十六进制 二进制 十六进制 二进制 0 0000 8 1000 1 0001 9 1001 2 0010 A 1010 3 0011 B 1011 4 0100 C 1100 5 0101 D 1101 6 0110 E 1110 7 0111 F 1111

第5讲-信息在计算机中的表示

第5讲-信息在计算机中的表示

第5讲信息在计算机中的表示计算机中进行处理的信息也称为数据。

数据在计算机中均以二进制形式存放，并用它们的组合表示不同类型的信息。

本节介绍各种形式的数据在计算机中的存储。

一、进位计数制数制，即进位计数制，是指用统一的符号规则来表示数值的方法。

数制中的术语：1．基数（基）：在采用进位计数的数字系统中，如果只用r个基本符号（例如0、1、2、……、r-1）表示数值，则称其为基r数制，r称为该数制的“基数”，在进位计数制中常用“基数”来区别不同的进制。

2．位权（权）：任何一个进制的数都是由一串数码表示的，其中每一位数码所表示的实际大小与它所在的位置有关，由位置决定的值叫位权。

各数位的权都是基数的幂，即权＝（基）i。

其中i为数码所在位的编号，从小数点向左依次为0、1、2、3、……；自小数点向右依次为-1、-2、-3、……。

3．按权展开式：某数位的数值等于该位的系数和权的乘积。

对任何一种进位计数制表示的数都可以写出按其权展开的多项式之和，任意一个r进制数N可表示为：N=an-1×rn-1+an-2×rn-2+…+a1×r1+a0×r0+a-1×r-1+…+a-m×r-m其中：ai是数码，r是基数，ri是权；不同的基数，表示是不同的进制数。

（一）十进制数十进制数的主要特点：1．基数是10。

有10个数码（数符）构成，即0、1、2、3、4、5、6、7、8、9。

2．进位规则是“逢十进一”。

当基数为M时，便是“逢M进一”。

3．各数位的权为10的幂。

4．任意一个十进制数，如527 可表示为（527 ）10 、[527]10 或527D 。

有时表示十进制数后的下标10 或D 也可以省略。

5．一般地说，任意一个十进制N 可表达为以下形式：[N]10 ＝an-1×10n-1+an-2×10n-2+…+a1×101+a0×100+a-1×10-1+…+a-m ×10-m 例：1234.56＝21123106105104103102101--⨯+⨯+⨯+⨯+⨯+⨯＝1000+200+60+7+0.5+0.06（二）二进制数二进制数的特点：1．基数是2。

计算机中信息的表示

计算机中信息的表示

计算机中信息的表示
1信息或数据都是以二进制编码的方式存储在计算机中
2.存储单位从小到大: 位(bit)、字节( Byte) 千字节( KB) 兆宇节( MB)、吉字节(GB) 太字节(TB)
3、存储容量单位的换算：
1B =8bit 或1Byte=8bit ；1KB= 1024B ；1MB= 1024KB ；IGB= 1024MB ；1TB= 1024GB
注： 一个英文字母（不区分大小写）
占一个字节
一个阿拉伯数学
一个符号
占两个字节：一个汉字
1、文件名命名格式: 主文件名.
扩展名
注意: 文件夹的命名没有扩展名
2、文件夹名、主文件名可以是数字、字母、符号和汉字组成，但不能出现下列字符：
\ 、/、:、*、?、“、”、<、>、｜。

英语字母不区分大小写，支持长文件名，最长可达255 个字
符。

3、同一磁盘下同一文件夹内，不能出现两个同类型同文件名的文件。

4、常见的文件类型：。

计算机组成原理第02章 计算机中的信息表示

计算机组成原理第02章 计算机中的信息表示

2.1 数值型数据的表示方法
2.1.2 带符号数的表示 2. 补码表示法 ⑴ 补码定义 ·通式 [X]补=M+X (mod M) 数X对模M 的补 数称作其补码 X>0， 作为正常溢出量可以舍去。 若X>0，则模 M 作为正常溢出量可以舍去。 因而正数的补码就是其本身， 因而正数的补码就是其本身，形式上与原码 相同。 相同。
2.1 数值型数据的表示方法
2.1.3 数的定点表示与浮点表示 2. 浮点表示法 浮点数格式(原理性) ⑴ 浮点数格式(原理性) N =±RE×M 其中： 其中： N ：真值 RE ：比例因子 E ：阶码 R ：阶码的底 M ：尾数 一般采取规格化的约定 一般采取规格化 规格化的约定
Ef Em
…
E2 E1 Mf M1 M2
2.1 数值型数据的表示方法
2.1.3 数的定点表示与浮点表示 ⑵ 带符号定点整数 设代码序列为： ……X 设代码序列为：XnXn-1……X1X0 ，Xn为符号位
原码 典型值 真值 最大正数 非零最小正数
2n-1 1
补码 真值
2n-1 1 -2n -1
代码序列
01…… ……11 …… 00…… ……01 ……
第2章 计算机中的信息表示
重点：定点、浮点数的表示； 重点：定点、浮点数的表示；操作码扩展技 术；指令系统的设计 难点：浮点数的IEEE754格式表示， 难点：浮点数的IEEE754格式表示，定点和 IEEE754格式表示 浮点数的表示范围，浮点数的规格化问题， 浮点数的表示范围，浮点数的规格化问题， 操作码扩展技术，指令系统的设计 操作码扩展技术，
2.1 数值型数据的表示方法
2.1.2 带符号数的表示 3. 反码表示法 若定点小数的反码序列为X ·若定点小数的反码序列为X0.X1X2……Xn,则 X X 1>X≥0 [X]反= 0>X≥2-2-n+X 0>X≥-1 若定点整数的反码序列为X ·若定点整数的反码序列为XnXn-1……X1X0,则 X X 2n>X≥0 [X]反= 0>X≥2n+1-1+X 0>X≥-2n

计算机的信息表示方式

计算机的信息表示方式

存 取 命 令
内存储器
输出设备
处理 结果
数据信息 控制信息
输 入 命 令 控制器
存 数
取 数
运算 命令
运算器 输出命令
微 负责数据的算术运算和逻辑运算，即数 据的加工处理。

控制器：负责对程序规定的控制信息进行分析、
控制并协调输入、输出操作或内存访问。 输入设备：负责把用户的程序和数据输入到计算 机的存储器中。如键盘、鼠标、扫描仪。 输出设备：负责从计算机中取出程序执行结果或 其它信息，供用户查看。如显示器 存储器： 是实现记忆功能的部件。负责存储程 序和数据。包括内存和外存（硬盘）。
二进制数的运算（补充）
分类 算术运算、逻辑运算 1、二进制的算术运算 2、二进制的逻辑运算 计算机中信息的表示方法 加、减、乘 与、或、非、异或
一、概念：
1、数据：是指能够识别的物理符号，不仅包括数字、字母、 文字和其他特殊符号组成的文本数据，还包括图形、图象、动 画等多媒体数据。 2、信息：是指数据经过加工后得到的有价值的知识。
1.4 数据的编码 从计算机键盘出入的各种数据是字符形式的，计算机中只处 理二进制数据，必须进行编码。 1.4.1 ASCII码
ASCII码由7位二进制构成，总计128种符号。最前位为“0。
二、 微型计算机系统的基本组成
计算机系统是由硬件系统和软件系统两大部分 组成的。 硬件系统:运算器、控制器、存储器、输入和输 出设备五个部分。 软件系统是指实现算法的程序、数据及其文档， 包括系统软件和应用软件。 计算机系统的组成如下图所示。

1、CPU
CPU（Central Processing Unit）就是
系统的中央处理器，主要功能是执行程序指令、完成

计算机——信息表示及存储

计算机——信息表示及存储

信息表示及存储数据是反映客观事物属性的记录，是信息的具体表现形式。

数据经过加工处理之后，就成为信息；而信息需要经过数字化转变成数据才能存储和传输。

数据信息分为数值型和非数值型。

计算机能够区分不同的信息，是因为它们采用了不同的编码规则。

1、数制数制（也称计数制）是指用一组固定的符号和统一的规则来计数的方法。

十进制（十进位计数制）：生活常用二进制：计算机中使用除此之外还有八进制，十六进制.（1）四个概念数码：数制中表示基本数大小的不同数字符号。

基数：数制中使用数码的个数位权：数制中每个位置的价值标识（后缀）：为了区分不同的进制，在数字后面加上相应的字母或者括号加上数字下标。

比如（66）10。

和66D都表示十进制数：66规则：进位规则，多进制就满多少进！借位规则，多少进制（向高位）借一位就当多少十进制下：8+2=10 10-3=7 9+2=11八进制下：6+2＝10 6+3=11 10-2=6二进制下：1+1=10 10- |=|十六进制下：8+2=A 11-2= F 8+8=10练习：判断102B 1Q ABCDF H 是否正确（××√）6+3=11判断几进制（八进制）（2）进制转换①十进制→R进制整数：除以R反向取余小数：乘以R正向取整（取整变0）例：20.625 D=10100.101 B二进制66.5 D=102.4 Q八进制30.5 D=1E.8 H十六进制练习：29.125 D=11101.001 B二进制②R进制→十进制乘权求和法：每一位的值乘以对应的价值（位权）标位数时注意两点：①从个位开始标，小数和整数方开②位权是0指数开始例：10110.011 B=22.375 D10110.011＝1＊2⁴＋0＊2³＋1＊2²＋1＊2¹＋0＊2⁰＋0＊2⁻¹＋1＊2⁻²＋1＊2⁻³＝16＋0＋4＋2＋0＋0＋1/4＋1/8＝22.37516.6 Q=14.75 D16.6=1*81+6*80+6*8-1=8+6+3/4=14.758A.4 H = 138.25 D8A.4=8*161+A*160+4*16-1=128+A+1/4=138.25练习：1010.101B=10.625D1010.101=1*23+0*22+1*21+0*20+1*2-1+0*2-2+1*2-3 =8+0+2+0+1/2+0+1/8=10.625③8421拼素法：二进制→十进制例：25D=11001 B25＝16＋8＋1＝1100110110B =22D10110＝16＋4＋2＝22练习：1011B=11D1011＝8＋2＋1＝1135 D = 1000 1135＝32＋2＋1＝100011④二进制→八进制/十六进制分组转换法：二进制→八进制：3位转成1位二进制→+六进制：4位转成1位注意两点：①以小数点为界，整数和小数方开②整数位数不够在前面添0，小数位数不够在后面添0.例：10101,1B=25.4Q10101.1=010 101 . 100= 2 5 . 4=25.4110l01.1101 B= 35. D H110101.1101=0011 0101 . 1101= 3 5 . D=35.D练习：110001,11B=61.6Q110001. 11＝110 001. 11O＝6 1 . 6＝61. 6⑤八进制/十六进制→二进制还组转换法：八进制→二进制：1位还成3位(4 2 1)十六进制→二进制：1位还成4位(8 4 2 1)例：16.32Q =1110.01101 B1=001 6=110 . 3=011 2=010=00110.011010F.3DH = 1111.00 111101 BF=15=1101 . 3=0011 D=13=1101=1101.00111101练习：ABC.DH=101010111100.1101 BA=10=1010 B=11=1011 C=12=1100 . D=13=1101=101010111100.1101⑥八进制←→十六进制以二进制为桥八进制（十六进制）→二进制→十六进制（八进制）例：56.3Q=2E.6H①Q→B (1→3) ②B→H (4→1)5=101 101110.0116=110 0010=23=011 1110=E0110=6练习：3D.2H=75.1Q①H→B (1→4) ②B→Q (3→1)3=0011 00111101.0010D=13=1101 111=72=0010 101=5001=1⑦小数点位移对于二进制，小数点左移几位数变为原来的R-n倍。

计算机中信息的表示及存储形式

计算机中信息的表示及存储形式

计算机中信息的表⽰及存储形式计算机内部均采⽤⼆进制来表⽰各种信息。

⼀、数的位置计数法及进制的概念①数制只采⽤R个基本符号——基R数制，R称为数制的“基数”。

②数制中每⼀位（e.g.⼗进制的个⼗百千位等）对应的单位称为“权”，权即以R为底的幂。

③每⼀位数的数值=数码×权，数码为0~R-1。

⼆、数制之间的转换① R转⼗按权展开求和。

②⼗转R整数部分采⽤除基数取余法，⼩数部分采⽤乘基数取整法。

【个⼈理解】⼩数部分权值的指数为负——R-1，除相当于乘以R。

可带⼊公式：数值=数码×权，数码即为待求量。

三、计算机中数的表⽰（定点数，原码，反码，补码）①计算机中数据分为数值数据和⾮数值数据，数值数据分为⽆符号数和有符号数。

⽆符号数多⽤于表⽰字符、地址以及逻辑值等。

有符号数的最⾼位作为符号位，“0”表⽰正，“1”表⽰负，即把符号数值化，这样的数称为“机器数”，机器数对应的原来有正负号的数称为“真值”。

有符号数分为定点数和浮点数。

定点数分为定点整数（纯整数）和定点⼩数（纯⼩数）。

②机器数三种表⽰形式——原码、反码、补码原码：整数X的原码为，符号位为0表⽰正，为1表⽰负，数值部分就是X的绝对值的⼆进制数。

反码：正数的反码与原码相同；对负数，符号位不变，其数值位（X的绝对值位）按位取反。

补码：正数补码与原码相同，对负数，符号位不变，数值位（X的绝对值位）按位取反后在最低位加1。

补码运算简单⽅便，符号位可作为数据的⼀位参与运算，不必单独处理，且最后结果的符号位仍然有效。

四、计算机中实数的浮点表⽰①实数X的浮点形式（科学表⽰法）若采⽤⼆进制表⽰为：X=±M×2±E，M为X的尾数，采⽤⼆进制纯⼩数形式（0.xxxxx），代表X的全部有效数字，其位数反映了数据的精度。

E为X的阶码，表⽰2的⼏次⽅，通常采⽤⼆进制整数形式，决定了数的范围。

M和E都可以是正数或者负数，即阶码和尾数都是带符号的数，可以采⽤不同的码制表⽰法，例如尾数可以⽤原码或补码表⽰，阶码⽤补码表⽰。

计算机内的信息表示

计算机内的信息表示

计算机内的信息表示计算机内的信息表示数据时信息的载体,是信息的具体表示形式。

数据⎩⎩⎩数值型数据:主要用来表示数量,可比较大小非数值型数据:人工处理过的。

常用数据:字符型数据(表示文字信息。

)、图象、声音、活动图象等。

信息表示是采用二进制计数。

(0或1)采用二进制的原因:因数载计算机中是由电子器件的物理状态来表示的,而物理状态中的高、低状态较稳定且易于实现。

数制:用一组固定的数字和一套统一的规则来表示数目的方法。

数制特点:①采用进位计数方式;②有固定的数码;③使用位权表示法;④使用基数。

位权法:同样的数所处位置不同其代表的值不同,这与该数位的权值有关。

各种数制中,数的权值恰好是基数的某次幂。

八进制:有8个数码0~7,八进制基数是8,逢八进一。

十六进制:有16个数码,分别是0~9以及A ~F ,A ~F 分别表示十进制的10~15。

十六进制基数是16,逢十六进一。

二进制的算术运算和逻辑运算。

(1)二进制算术运算(算术运算会发生进位和借位处理)⎩⎩⎩加法:0+0=0;0+1=1;1+0=1;1+1=10(向高位进一)减法:0-0=0;1-0=1;1-1=0;0-1=1(向高位借一) ⎩⎩⎩乘法:0×0=0;0×1=0;1×0=0;1×1=1除法:0÷0=0;0÷1=0;(1÷0无意义);1÷1=1 (2)二进制逻辑运算(逻辑运算是按位独立进行的,位与位之间不发生进位关系。

)⎩⎩⎩⎩⎩逻辑加(“或”运算):0+0=0 0+1=1 1+0=1 1+1=1(取大)逻辑乘(“与”运算):0×0=0 0×1=0 1×0=0 1×1=1(取小)逻辑非(“取反”运算):0取反是1 1取反是0(取反)0表示假; 1表示真。

不同数制之间相互转化: 原理:用位权法表示。

例1:十进制整数转化成二进制整数。

第3章-计算机中信息的表示与存储

第3章-计算机中信息的表示与存储

2. 非十进制数转换为十进制数
非十进制数转换为十进制数采用“按权展开法”，即先把各位 非十进制数按权展开，写成多项式,然后计算十进制结果。
例如:写出(1101.01)2， (237)8，(10D)16的十进制数。
3. 二进制与八、十六进制数的转换
二进制数与八进制数，以及十六进制数存在着倍数的关系，例如
位权的表示法是指，数字的总个数为基数，每个数字都要乘以基 数的幂次，而该幂次由每个数所在的位置决定。排列方式是以小 数点为界，整数部分自右向左分别为0次幂、1次幂、2次幂、……， 小数部分自左向右分别为负1次幂、负2次幂、负3次幂、……。
2. 常用的进位记数制
（1）十进制 所使用的数码有10个，即0、1、2、…、9，基数为10 ，各位的位
2. 浮点数
小数点位置浮动变化的数称为浮点数。对十进制来说，浮点数是以10 的n次方表示的数。例如，十进制数245.78， 使用浮点表示法为 0.24578×103。其中0.24578为一个定点数，3表示小数点向右移动3位。 当浮点数采用指数形式表示时，指数部分称为“阶码”，小数部分称 为“尾数”。尾数和阶码有正负之分，例如，二进制数“-0.00111”， 浮点表示为“-0.111×2-2”，这里尾数（-0.111）和阶码（-2）都是 负数。尾数的符号表示数的正负，阶码的符号则表明小数点的实际位 置。
例如，求十进制数“+5”与“-5”的反码。 若用一个字节表示，将十进制数5转化为二进制数为00000101。 因为“+5”是正数，转化为二进制数的原码为00000101，所以
反码与原码相同，( +5 )反＝00000101；
正数 +0 +1 +2 +3 +4 +5 +6 +7

信息在计算机中的表示

信息在计算机中的表示

注意：十进制小数不一定能转换成完全等值的其他进制
小数。遇到这种情况时，根据精度要求，取近似值。
11
例：
(100.345)10(1100100.01011)2 2 2 2 2 2 2 2 100 50 25 12 6 3 1 0 0.345 2 0.690 2 1.380 2 0.760 2 1.520 2 1.040 (100)10=(144)8=(64)16 8 100 8 12 8 1 0 16 100 16 6 0
3
1、进位记计数制的概念
• 十进制（D） 十种状态，逢十进一， (0,1,2,3,4,5,6,7,8,9) • 二进制（B） 两种状态，逢二进一，（0,1） • 八进制（Q） 八种状态，逢八进一，（0,1,2,3,4,5,6,7） • 十六进制（H） 十六种状态，逢十六进一 （0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F）
逻辑性强
二进制的两种状态正好与逻辑代数中的真和假相对 应，可以方便地进行逻辑运算。
2
1、进位记计数制的概念
进位计数制（简称数制）就是按进位的方法计数。 在不同的数制中，把某一进位计数制中涉及的数字符号
的个数称为基数，用R表示，一个具体的数用(S)R的形式
表示。计算机中经常用到的数制有十进制、二进制、十 六进制和八进制。
汉字的机内表示：机内码 汉字的输出：字形码（字库
输入码
Font）
字形 检索 程序
字形码
键盘
键盘 处理 程序
代码 转换 程序
机内码
储存、加工
输出设备
码表
字模库
25
汉字输入编码
汉字输入编码的实质就是用字母、数字和一些符号代码 的组合来描述汉字。目前，汉字编码的方案有很多种，主要 可分为四种：数字编码、字音编码、字形编码、音形编码。 数字码 （利用一串数字代表一个汉字） 如：电报码、区位码、纵横码 字音码 （用汉语拼音代表一个汉字） 如：全拼、双拼、微软拼音 字形码 （根据汉字结构或笔画用字母或数字表示汉字） 如：五笔字型 音形码 （根据汉语拼音和字形结构规定汉字编码） 如：声形码、王林快码

1.2计算机中的信息表示

1.2计算机中的信息表示

数据与信息 的关系???
信息编码的意义
人类可识别理解的信息形态 编码 计算机能识别和理解的信息形态 基本符 号的种类 符号组 合规则
采用有限的基本符号,通过一个确定的原则 采用有限的基本符号 通过一个确定的原则 对这些符号加以组合,用来描述大量多变的信息 对这些符号加以组合 用来描述大量多变的信息
数据的编码
An • K n + An−1 • K n−1 + L+ A0• B1 • K −1 + B2 • K −2 + L＋Bm • K −m
例 例 （ 1110112 = 1× 25 + 1× 24 + 1× 23 + 0 × 22 + 1× 21 + 1× 20 = 59 10 ） （ ） （ F 2 A） = 1×163 + 15×162 + 2 ×161 + 10 ×160 = 7978 10 1 （ ） 16
1.2.1 数字化信息编码的概念
数据与信息
数据是人类能够识别或计算机能处理的符号 是对客观事物的具体表 数据是人类能够识别或计算机能处理的符号,是对客观事物的具体表 是人类能够识别或计算机能处理的符号 示. 信息是经过加工处理后用于人们决策或具体应用的数据 信息是经过加工处理后用于人们决策或具体应用的数据 数据是信息的具体表现形式,是各种各样的物理符号及其组合 它 数据是信息的具体表现形式 是各种各样的物理符号及其组合,它 是各种各样的物理符号及其组合 反映了信息的内容,数据的形式随物理设备的改变而变 数据的形式随物理设备的改变而变,数据是信 反映了信息的内容 数据的形式随物理设备的改变而变 数据是信 息在计算机内部的表现形式. 息在计算机内部的表现形式 信息是人们对客观世界的直接描述,可以在人们之间进行传递的 信息是人们对客观世界的直接描述 可以在人们之间进行传递的 一些知识或事实,它与承载信息的物理布局设备无关 它与承载信息的物理布局设备无关. 一些知识或事实 它与承载信息的物理布局设备无关
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

换一个角度： 162
161
1
6
160
16－1 16－2
11(B) 6
8
1
·推广：任意一个十六进制数可以表示为： (H)16 = hn×16n-1 ＋ hn-1×16n-2 ＋… h2×161 ＋ h1×160 ＋ h-1×16-1 ＋ h-2×16-2 ＋… h-m×16-m
n
m
= ∑ hi×16i-1 ＋ ∑ hj×16-j
换一个角度： 23
22
21
20
1
1
0
1
2－1 2－2
0
1
·推广：任意一个二进制数可以表示为： (B)2 = bn×2n-1 ＋ bn-1×2n-2 ＋… b2×21 ＋ b1×20 ＋ b-1×2-1 ＋ b-2×2-2 ＋… b-m×2-m
n
m
= ∑ bi×2i-1 ＋ ∑ bj×2-j
i=1
j=1
其中： bi和 bj 为0或1；n为整数部分位数；m为小数部分位数； 2i-1 和2-j分别为整数部分和小数部分位权。
济南大学信息学院公共教学部
2.1.3、八进制数（E ）
·特点： (1)、有0－7八个数 (2)、逢八进一，进位基数为8。
·举例： 八进制数2533.42可以表示为： 2533.42 =2×83 ＋ 5×82 ＋ 3×81 ＋ 3×80 ＋ 4×8-1＋ 2×8－2
= 8+4+0+1+0+0.25 = (13.25) 10 【注】括号外的下标用来表示不同的数制
问：八进制数和十六进制数如何转换成十进制数？
【注】方法同二进制数转换成十进制数
济南大学信息学院公共教学部
2.2.2、十进制数转换成二进制数(1)
A、十进制整数转换成二进制整数
【方法】除以2取余数倒排
【例】将十进制数253转换成二进制数
i=1
j=1
其中： hi和 hj 为0、1－9、A、B、C、D、E、F中一个；n为整数 部分位数；m为小数部分位数； 16i-1 和16-j分别为整数部分和小数部分
位权济。 南大学信息学院公共教学部
2、常用数制之间的相互转换
2.2.1、二进制数转换成十进制数
【例】将1101.01转换成十进制数 (1101.01)2 = 1×23 ＋ 1×22 ＋ 0×21 ＋ 1×20 ＋ 0×2－1 ＋ 1×2－2
【方法】乘2取整数法
【例】将十进制数0.45转换成二进制小数（取4位）
十进制数(D)
乘2
取整数部分
0.45
×2＝0.9
0
转换结果的最高位
0.9
×2＝1.8
1
0.8
×2＝1.6
1
0.6
×2＝1.2
1
转换结果的最低位
转换结果： (0.45)10=(0.0111)2 为取4位的近似值
问：十进制数如何转换成八进制数或十六进制数？
其中： ei和 ej 为0－7中一个；n为整数部分位数；m为小数部分位 数； 8i-1 和8-j分别为整数部分和小数部分位权。
济南大学信息学院公共教学部
2.1.4、十六进制数（H）
·特点： (1)、有0－9、A、B、C、D、E、F十六个数码 (2)、逢十六进一，进位基数为16。
·举例： 十六进制数16B.68可以表示为： 16B.68 =1×162 ＋ 6×161 ＋ B×160 ＋ 6×16-1＋ 8×16－2 =1×162 ＋ 6×161 ＋ 11×160 ＋ 6×16-1＋ 8×16－2
5
6
100 10－1 10－2
9
2
8
·推广：任意一个十进制数可以表示为： (D)10 = dn×10n-1 ＋ dn-1×10n-2 ＋… d2×101 ＋ d1×100 ＋ d-1×10-1 ＋ d-2×10-2 ＋… d-m×10-m
n
m
= ∑ di×10i-1 ＋ ∑ dj×10-j
i=1
j=1
其中： di和 dj 为0－9中任一个数字；n为整数部分位数；m为小数 部分位数； 10i-1 和10-j分别为整数部分和小数部分位权。
济南大学信息学院公共教学部
2.1.2、二进制数（B）
·特点： (1)、有0、1二个数字 (2)、逢二进一，进位基数为2。
·举例： 二进制数1101.01可以表示为： 1101.01=1×23 ＋ 1×22 ＋ 0×21 ＋ 1×20 ＋ 0×2－1 ＋ 1×2－2
二、计算机中的信息表示
1、进位计数制 2、常用数制之间的相互转换 3、计算机中数的表示 4、原码、反码、补码 5、字符编码
济南大学信息学院公共教学部
1、进位计数制
·计算机中常用的计数制
基数 位权 数字符号
十进制 10 101
0～9
二进制 2 21
0，1
八进制 8 81
0～7
十六进制 16 161
0～9，A~F
【注济】方南法同大十学进制信数转息换成学二进院制公数 共教学部
2.2.3、二进制数转换成十六进制数
【方法】将给定的二进制数以小数点为界，分别向左、向右每4位分成 一组，若不足4位，要分别前补0（整数部分）或后补0（小数部分）。 然后将每4位一组的数分别用对应的十六进制数来书写。 【例】将二进制数101101011.01101转换成十六进制数
十进制数(D)
余数
2 253
└2 126 └2 63 └2 31 └2 15 └2 7 └2 3 └2 1 └0
1
转换结果的最低位
0
1
1
1
1
1
1
转换结果的最高位
转济换结南果：大(25学3)10信=(11息1111学01)2院公共教学部
2.2.2、十进制数转换成二进制数(2)
B、十进制小数转换成二进制小数
二进制数：0001 0110 1011 . 0110 1000 十六进制数： 1 6 B . 6 8
2.2.4、十六进制数转换成二进制数
【方法】将每一位十六进制数用对应的4位二进制数来表示，其最左侧 和最右侧的0可以省去。 十六进制数： 1 6 B . 6 8
换一个角度： 8382ຫໍສະໝຸດ 81808－1 8－2
2
5
3
3
4
2
·推广：任意一个八进制数可以表示为： (E)8 = en×8n-1 ＋ en-1×8n-2 ＋… e2×81 ＋ e1×80 ＋ e-1×8-1 ＋ e-2×8-2 ＋… e-m×8-m
n
m
= ∑ ei×8i-1 ＋ ∑ ej×8-j
i=1
j=1
济南大学信息学院公共教学部
2.1.1、十进制数（D）
·特点： (1)、有0、1、2、…、9十个数字 (2)、逢十进一，进位基数为10，位的权数是十的幂。
·举例： 十进制数569.28可以表示为： 569.28=5×102 ＋ 6×101 ＋ 9×100 ＋ 2×10－1 ＋ 8×10－2
换一个角度： 102 101