集输知识点

第3节集合的基本运算集合的基本运算并集定义性质交集定义性质补集定义性质数学浪子版权所有禁止用于任何商业用途1．并集的定义由所有属于集合A 或属于集合B 的元素组成的集合，称为A 与B 的并集．即A 与B 的所有部分，记作AB （读作“A 并B ”），即{|}A B x x A x B =∈∈或．2．性质并集的常用结论：（1）A B B A =；（2）AA A =；（3）A A ∅=； （4）AB B A B =⇔⊆．1．交集的定义由属于集合A 且属于集合B 的所有元素组成的集合，叫做A 与B 的交集．即A 与B 的公共部分，记作AB （读作“A 交B ”），即{|}A B x x A x B =∈∈且．A BA B ABA B ABA B例1 {1,3,5}A =，{2,3,4}B =，求A B ．解析：并集是把两个集合中的元素放到同一个集合中，并满足互异性．{1,2,3,4,5}A B =．例2 已知集合{|14}A x x =-<<，集合{|25}B x x =<<，求A B ．解析：由数轴可知，{|15}AB x x =-<<．一、并集二、交集2．性质交集的常用结论：（1）A B B A =；（2）AA A =；（3）A ∅=∅； （4）AB A A B =⇔⊆．1．补集的定义如果一个集合含有我们所要研究问题中所涉及的全部元素，那么就称这个集合为全集，记作U ．A 是U 的一个子集（即A U ⊆），由U 中不属于A 的所有元素组成的集合，叫做U 中集合A 的补集，记作UA ，即{|}UA x x U x A =∈∉且．例3 {3,4,5,6,7}A = ，{1,2,3,4,5}B =求A B解析：A B 所得为两集合中的公共元素，故{3,4,5}A B =．例4 {|14}A x x =<≤{|25}B x x =<< 求A B解析：AB 为两集合中的公共区域，故{|24}A B x x =<≤例5 {1,2,3,4,5,6,7,8}U =，{1,3,5,6,8}A =，求U A ．解析：全集U 中除去A 的元素，即为A 在U 中的补集，所以{2,4,7}UA =三、补集2．性质补集的常用结论： （1）UA A =∅； （2）UAA U =；（3）U U =∅； （4）UU ∅=；（5）()UU A A =；（6）()()()U U UA B A B =；（7）()()()U U UA UB A B =．练习题：题号考点：并集1已知集合{1,0,1}M =-，{0,1,2}N =，则MN =（ ）A ．{0,1}B ．{1,0,1,2}-C ．{1,0,2}-D ．{1,0,1}- 解析：M N 是把两个集合元素放到一个集合中，根据互异性只保留一个相同元素，则{1,0,1,2}M N =-．答案：B2设集合{,}A a b =，{,,}B b c d =，则AB =（ ）A ．{}bB ．{,,}b c dC ．{,,}a c dD ．{,,,}a b c d例6 已知{|12}A x x =-<≤，{|3}B x x =<，求B A ．解析：根据题意，画出数轴，可知{|123}BA x x x =≤-<<或．A B 是把两个集合元素放到一个集合中，相同元素根据互异性只保留一{,,A B a b ={1,2,4}A =B =_______A B 是把两个集合元素放到一个集合中，相同元素根据互异性只保留一{1,2,4,6}AB =1,2,4,6} 1{|2x x =<B =（ 12}x ≤< 21}{x x ≤={|A B x =-答案：A已知{0,1,2}M =N =（ ．{0} D 解析：{N ={0,1,2}，则{0,1,2,4}M N ={1,2,3}B =的个数是（ ）D ．8 {1,2,3}AB =，则A 中共有2个元素，则满足条件的{1,2,3,4,5}B =1,2}{1,2,3,4,5}B=子集个数的问题，N={1,2,3,4}C．4N=，则N{1,2,3,4}子集个数的问题，M中共有2个元素，则满足条件的B=_________A B=．{3,5,13}，则A B=（）C．{1,2}A B=．{1,2},2,3}，则A B=________A B=-．，3，则{1,3}，则A B=（{0,2}DA B=．{0,2}B=（D．{2}-A B=．公共元素为2，则{2}B=（DA B=，1，则{0,1}A=（）U{2,4,7}剩下的部分，{2,4,7}A=UA=（）UC．{1,2,3,4,5}剩下的部分，{3,4,5}A=UM=（）UC．{1,2,4}剩下的部分，{2,4,6}M=UA=（U，则{2}UA =．UM =（ ）,0)(2,)-∞+∞ D [2,)+∞02}a >或，则{|02}UM a =．，那么UP =（ ）1,1] D ．(,(1,)-∞+∞，则{|}UP x x =<．{2}UA =，则集合A 的真子集共有（）个 5个 由{2}UA =可知{0,1}A =，中共有2个元素，{0,1,2,3}=，{2}UM ={0,1,3} B ．{1,3} 解析：UM 是把全集U 中元素，去掉，则{0,1,3}M =． A已知全集{0,1,2,3}U ={0,2}UA =4个 1,3}，共有两个元素，则真子集个数为⎝题型一：二次不等式的交集例 集合{|04}A x x =<<，2{|230}B x x x =--<，求A B ．解析：{|(3)(1)0}{|13}B x x x x x =-+<=-<<，由题意画出数轴，{|03}AB x x =<<．总结：主要考察二次不等式解集的求法，结合集合的知识点出题，比较基础．练习1 集合{|04}A x x =<<，1{|0}3x B x x +=<-，求A B ．解析：{|(3)(1)0}{|13}B x x x x x =-+<=-<<，由题意画出数轴，{|03}A B x x =<<．练习2 已知集合{|(1)(2)0}A x x x =+-≤，集合B 为整数集，则A B =（ ）A ．{1,0}-B ．{0,1}C ．{2,1,0,1}--D ．{1,0,1,2}- 解析：{|12}A x x =-≤≤，B 为整数集，则{1,0,1,2}A B =-．答案：D练习3 已知集合2{|20}A x x x =--≤，集合B 为整数集，则A B =（ ）A ．{1,0,1,2}-B ．{2,1,0,1}--C ．{0,1}D ．{1,0}- 解析：{|12}A x x =-≤≤，B 为整数集，则{1,0,1,2}A B =-．答案：A练习4 设集合{0,1,2}M =，2{|320}N x x x =-+≤，则MN =（ ）重要考试题型题型二：已知交并补集结果求参数值例1 已知{0,2,}A a =，2{1,2,}B a =，{0,1,2,3,9}A B =，求实数a ．当中的两个，很明显变式 已知{1,2}A a a =++，{2,1}B b b =-+，{3,2,0}A B =，求a b +的值．，比对并集中的数字，可知{1,3,5}A =例2 ，{1,5,}B a =-，{3,5}A B =，求a 的取值．，则3a =．2{1,3,31}A a a =-+变式 ，{1,5,}B a =-，{5}A B =，求a 的取值．是两个集合的公共元素，所以23a a -+，违反了集合元素的互异性，舍去；例3 设{1,2,3,4}U =，2{|50}M x U x x p =∈-+=，若{1,4}U M =，那p=________．2x ，令1x =变式 不等式31ax <解集为Q ，{|0}P x x =≤，若R1{|0}6QP x x =<<，那a=________． 解析：R{|P x x =恒成立，此时R Q =，不符合条件舍去，{1,2}M N =1{|}3Q x x a=<，根据题意画出数轴，可得1136a =，解得2a =．练习1 已知集合2{|20}A x x mx =-+=，2{|60}B x x x n =-+=，且{2,1,4}A B =，求m ，n 的值． {2,1,4}AB =中方程2x mx -+，设B 中方程，根据对应关系，2421262x ==⨯+==练习2 已知集合{1,2,}A k =，{2,5}B =，若{1,2,3,5}A B =，则k=______．练习3 已知集合{1,3,}A m =，{3,4}B =，{1,2,3,4}A B =，则m=_______．练习4 已知集合{1,2,3}A =，{2,}B a =，{0,1,2,3}A B =，则a 的值为_______．2{1,3,35}A a a =-+练习5 ，{1,5,}B a =-，{5}A B =，求a 的取值．235a -+={5}A B =，符合题意；{3,5}AB =，不符合条件，舍去；练习6 设集合{1,1,3}A =-，2{2,4}B a a =++，{3}A B =，则实数a=_______．{3}A B =，∴23a +=或21a ==-或1练习7 已知集合{1,2,3}A =，{2,,4}B m =，{2,3}A B =，则m=_______．{2,3}A B =，则3．练习8 若集合{|2}A x x =≤，{|}B x x a =≥满足{2}A B =，则实数a=________．{2}A B =，2=．练习9 设集合{1,0,3}A =-，{3,1}B a a =+-，若{3}A B =，则实数a=_______．{3}AB =，则04a =或；时，{3,B =-{1,3}A B =-不符合题意，舍去； 时，{7,3}B ={3}AB =符合题意；． 练习10 已知集合2{,1,3}A m m =+-，2{1,3,21}B m m m =+--，若{3}A B =-，实数m=______．{3}AB =-3-时，2m 3时，m ={3,1AB =-3-时，m =，{3}A B =-练习11 设集合{1,2,3}A =-，2{2,2}B a a =++，{3}A B =，则实数a=_______．{3}AB =知，时，1a =，此时，不满足元素的互异性，舍去；3时，1(a ={3}A B =符合条件；．练习12 设{0,1,2,3}U =，2{|0}A x U x mx =∈+=，若{1,2}U A =，则实数m=_______．的两个根，∴练习13 若全集{0,1,2}U =，{|10}A x ax =+=且{0,1}U A =，则a=_______．的根，带入可解得练习14 设{1,2,3,4}U =，且2{|50}M x U x x p =∈-+=，若{2,3}U M =，则实数p 的值为（ ）A ．-4B ．4C ．-6D ．6的两个根，带入解得例1 已知集合{|2}A x x =>，{|}B x x m =<，且R A B =，求m 的取值范围．解析：根据条件画出数轴，可知m 需在2的右侧，即2m >．变式1 已知集合{|2}A x x a =-<<，{|26}B x x =<<，{|26}A B x x =-<<，求a 的取值范围．解析：由题目条件，画出数轴，可知a 应在2和6中间，研究端点处的取值，如果2a =，则A 与B 集合均取不到2，不符合题意，∴2a >，如果6a =，则符合题意，综上26a <≤．变式2 已知集合{|33}A x a x a =-<≤+，2{|230}B x x x =-->，若R A B =，求a 的取值范围．解析：{|31}B x x x =><-或，根据题意画出数轴，欲使R A B =，则A 集合需把B 集合取不到的中间区域覆盖，则3a -在1-左侧，3a +在3右侧；再讨论端点处，31a -=-时，两集合都取不到1-，∴31a -<-严格，即2a <，33a +=时，A 集合可取到3，符合条件，∴33a +≥，即0a ≥； 综上02a ≤<．例2 已知集合{|7}A x x =≤，{|}B x x a =≥，若A B =∅，求a 的取值范围．解析：由条件，画出数轴，可知a 在7的右侧，则7a >．变式1 已知集合{|27}A x x =<<，{|21}B x a x a =<<+，若{|47}A B x x =<<，求a 的取值范围．解析：由题意，画出数轴，可知要满足{|47}AB x x =<<，4a =即可．变式2 已知集合{|27}A x x =<<，{|21}B x a x a =<<+，若A B =∅，求a 的取值范围．解析由题意知，两个集合没有交集，可分两种情况讨论： ①B =∅，令21a a ≥+，解得1a ≤-，满足条件； ②B ≠∅，此时1a >-，要使A B =∅，画出数轴，可知B 整体在A 的左侧或者右侧； 在左侧时，212a +≤，解得12a ≤，又1a >-，得112a -<≤； 在右侧时，7a ≥，又1a >-，得7a ≥； 综上12a ≤或7a ≥．练习1 设常数R a ∈，集合{|(1)()0}A x x x a =--≥，{|1}B x x a =≥-，若R A B =，则a的取值范围为（ ）A ．(,2)-∞B ．(,2]-∞C ．(2,)+∞D ．[2,)+∞ R A B =，∴成立，； R AB =，则1≤，即a ≤③1a <时，{|1}A x x a x =≤≥或,要满足R A B =，则应满足1a a -≤，1a a -≤是恒成立的，所以可得1a <符合条件．综上2a ≤． 答案：B练习2 已知集合{|1}A x x =≤，{|}B x x a =≥，且R A B =，则实数a 的取值范围是（ ）A ．1a ≤B ．13a ≤≤C ．1a ≥D ．3a ≥ 解析：{|1}A x x =≤，{|}B x x a =≥，要使R AB =，结合数轴可知满足1a ≤时命题成立．答案：A练习3 设集合{||2|3}S x x =->，{|8}T x a x a =<<+，R S T =，则a 的取值范围是（ ）A ．31a -<<-B ．31a -≤≤-C ．31a a ≤-≥或D ．31a a <->-或 解析：{||2|3}{|51}S x x x x x =->=><-或，又R ST =，根据数轴可知应满足13185a a a <-⎧⇒-<<-⎨+>⎩． 答案：A练习4 已知{|23}A x a x a =<<+，{|15}B x x x =<->或，若A B =∅，则a 的取值范围是（ ）A ．1322a a <-≤≤或B ．1322a a >≤≤或22解析：分两种情况讨论：①A =∅，即23a a >+时，3a >，此时A B =∅符合题意；②A ≠∅，此时3a ≤，要AB =∅，通过数轴可知需满足2135a a ≥-+≤且，解得122a -≤≤，综上3a >或122a -≤≤．答案：D练习5 集合{|121}A x a x a =-<<+，{|01}B x x =<<，若A B =∅，实数a 的取值范围是（ ）A ．(,3][2,)-∞-+∞B ．(,1][2,)-∞-+∞C ．1(,][2,)2-∞-+∞ D ．1(,][2,)2-∞+∞解析：分两种情况讨论：①A =∅，即121a a -≥+时，2a ≤-，此时A B =∅符合题意；②A ≠∅，此时2a >-，要AB =∅，通过数轴可知需满足21011a a +≤-≥或，解得1222a a -<≤-≥或．综上122a a ≤-≥或．答案：D练习6 已知集合{|}M x x a =≤，{|20}N x x =-<<，若MN =∅，则a 的取值范围是（ ） A ．0a > B ．0a ≥ C ．2a ≤- D ．2a <- M N =∅，画个数轴可以得知练习7 设集合{|2}M x x a =-≤≤非空，{|||,}N y y x x M ==∈，若MN N =，则实数aN N =可知时，{N =时，{N y =练习8 已知2{|1}2xA x x =<+，{|||1}B x x a =-<，且A B ≠∅，则a 的取值范围为（ ）A ．(3,3)-B ．(3,3]-C ．(2,3)-D ．(2,3]- 202<，即AB =∅时，； AB ≠∅时，答案：A练习9 全集R U =，集合{|0}M x x a =+≥，{|21}N x x =-<，若(){|3}U MN x x =≥，则（ ）A ．1a =-B ．1a =-C ．1a =D ．3a ≥- }{|UN x x =(){|3}U MN x =≥说明UN 是M 的子练习10 设集合2{|2240}A x x x m =-++=，{|0}B x x =<，若A B ≠∅，实数m 的取值集合是（ ）A ．(,1)-∞-B ．(,1]-∞-C ．(,2]-∞-D ．(,2)-∞-AB ≠∅的对立面AB =∅时的44(20∆=-，解得m 时，前提为m ≤，要使AB =∅，则在y 轴右侧，两个零点大于等于0，只需A B =∅时2m ≥-，则A B ≠∅时练习11 已知集合2*{|(2)10,R}R x x k x x +++=∈=∅，则实数k 的取值范围是（ ）A ．40k -<<B ．4k >-C ．2k >-D ．0k ≥没有正根，或是空集；题型四：集合的混合运算{1,2,3,4,5,6,7}U =例1 ，{2,4,6}A =，{1,4,5}B =，求()U A B ．解析：{1,35UA =，(){1,5}U A B ={1,2,3,4,5,6,7}U =变式 ，{2,4,6}A =，{1,4,5}B =，求()()U U A B ．解法一：={1,3,5,7}UA ，={2,3,6,7}UB ，则()(){3,7}U U A B =． 解法二：{1,2,4,5,6}AB =，()()(){3,7}U U UA B AB ==．例2 已知集合2{|540}A x x x =-+=，集合2{|40}B x x ax =++=，其中A B A B =，求a 的值．AB A B A B =⇒=变式 1 已知集合2{|540}A x x x =-+=，集合2{|40}B x x ax =++=，其中A B =∅且AB A =，求a 的值．解析：{|(1)(4)A x x x =--=A B =∅⇒A B A =，∴令B 中方程2160a =-<，解得4a -<变式2 已知集合2{|540}A x x x =-+≤，集合{|2}B x a x a =≤≤+，其中()U B A =∅，求a 的值．解析：{|(1)(4)0}{|14}A x x x x x =--≤=<<，()U BA B A =∅⇒⊆，根据题意画出数轴，可得124a a ≥⎧⎨+≤⎩，解得12a ≤≤．总结：关于集合的混合运算，只需要按部就班的求交并补集即可，对于能用快速公式简化计算的，可以用一下()()()U U UA B A B =和()()()U U UA UB A B =这两个公式．由混合运算的结果分析，可以得到原始两个集合的关系，例如：A B A B A B =⇒=① A B A B A A B =∅=⇒=②且()U BA B A =∅⇒⊆③练习1 若全集R U =，{|4}A x x =>，{|2}B x x =>，求()U A B ．解析：{|4}UA x x =≤，画出数轴可知(){|24}U A B x x =<≤．练习 2 设全集{N |110}U n n =∈≤≤，{1,2,3,5,8}A =，{1,3,5,7,9}B =，则()U A B=________．解析：由题意{4,6,7,9,10}UA =(){7,9}U A B =练习3 已知全集{1,2,3,4}U =，集合{1,2}A =，{2,3}B =，则()U A B =（ ）A ．{1,3,4}B ．{3,4}C ．{3}D ．{4} {1,2,3}A B =，则(){4}UA B =．练习4 已知集合{2,3,6,8}U =，{2,3}A =，{2,6,8}B =，则()U A B =________．解析：{6,8}UA =，则(){6,8}U A B =．{6,8}练习5 已知集合A 、B ，全集{1,2,3,4}U =，且(){4}U A B =，{1,2}B =，则UAB =（ ）A ．{3}B ．{4}C ．{3,4}D ．∅ 解析：由(){4}UA B =，{1,2,3}AB =，{3}=或{1,3}{1,2,3}，{3,4}UB ={3}UAB =．练习6 设集合{4,5,7,9}A =，{3,4,7,8,9}B =，全集U A B =，则集合()U A B 中的元素共有（ ）A ．3个B ．4个C ．5个D ．6个 {4,7,9}A B =，则(){3,5,8}UA B =，共有个元素．练习7 设全集为R ，集合2{|90}A x x =-<，{|15}B x x =-<≤，则RAB =（ ）A ．(3,0)-B ．(3,1)--C ．(3,1]--D ．(3,3)- ，R{|B x x =RAB =练习8 设全集为U ，集合A U B U ⊆⊆、，则下列关系中与A B ⊆等价的事（ ）．（1）AB A =（2）A B B =（3）UAB =∅（4）UBA =∅A ．（1）（2）B ．（1）（3）（4）C ．（1）（2）（3）D ．（2）（3）（4） 1）（2）（3A B ⊆是等价关系，（4）与B 等价． C练习9 已知2{|320}A x x x =++≥，2{|410}B x mx x m =-+->，若A B =∅，且AB A =，则m 的取值范围是（ ）A ．117{|}2m m -≤B ．115{|}2m m -≤C ．13{|}2m m -≥D ．17{|}2m m -≥ 解析：{A x =A B A =⇒AB =∅，B 中但它们的交集为空集，只有所以当B =∅0≤，解得． 练习10 已知集合{|21}A x x x =≤-≥-或，{|21}B x m x m =<<-，若A B =∅，且AB A =，则m 的取值范围是（ ）A ．1m ≥-B ．2m ≥C ．2m <D ．5m <- 解析：A B A =⇒A B =∅，B =∅这一种情况；B =∅时，应满足，即1m ≥-题型五：集合之间的关系例1 已知集合{0,2,}A x =，2{2,}B x =，A B A =，求x ．AB A =⇒，分两种情况讨论：{1,2,3,4}M =例2 ，{2,4}N =，则M 和N 的关系是（ ）A ．M N ⊆B ．N M ∈C ．MN N = D ．M N N =N M ⊆，C 选项符合条件． 2{|320}M x x x =-+>例3 ，{|33}N x x =-<<，{|12}M x x x =<>或A ．M N ⊆B ．N M ⊆C ．MN =∅ D ．R M N =解析：{|(1)(2)0}{|21}M x x x x x x =-->=><或，画出数轴看一下关系，可知D 正确．答案：D2{|2,N }A x x a a +==+∈例4 ，2{|23,N }B y y b b b +==-+∈，A 、B 的关系？AB ．总结：通过集合的相关性质，把题目中的条件转化为集合的包含关系，属于简单题型．列举主要通过观察元素来确定尽量两个式子变成同样的构造．练习1 已知集合{1,1}A =-，{|1}B x mx ==且A B A =，则m 的值为（ ）A ．1B ．-1C ．1或-1D ．1或-1或0 AB A =可知的子集，B 中方程至多有时，0m =；练习2 若集合2{|230}A x x x =--=，{|20}B x ax =-=，满足A B B =，则实数a 组成的集合为_______． AB B =可知解，∴{1,3}B ≠-时，0a =；时，a =-时，23a =；的取值为22,0,-练习3 若2{|60}A x x x =+-=，1{|10}B x x m=+=，且A B A =，则实数m=_______．AB A =可知解，∴B ≠时，解得时，解得m 23m -=或23或练习4 已知集合{1,2,3,4}M =，{2,2}N =-，则下列结论成立的是（ ）A ．N M ⊆B ．MN M = C ．M N N = D ．{2}M N =，所以N M ⊄错误；{2,1,2,3,4}M N M =-≠，B 错误；{2}N =≠错误；正确． 答案：D练习5 若{|1}P x x =<，{|1}Q x x =>，则（ ）A ．P Q ⊆B ．Q P ⊆C ．RP Q ⊆ D ．RQ P ⊆解析：R{|P x x =，由集合关系知RQ P ⊆正确，故选D ．D练习6 已知集合{1,2,3}M =，{2,3,4}N =，则（ ）A ．M N ⊆B ．N M ⊆C ．{2,3}M N =D ．{1,4}M N ={2,3}M N =正确，故选练习7 已知集合2{|20}A x x x =->，{|55}B x x =-<<，则（ ）A ．AB =∅ B ．R A B =C ．B A ⊆D ．A B ⊆解析：2{|0}{|A x x x x ==>R A B =，故答案：B练习8 已知集合2{|20}A x x x =--<，{|11}B x x =-<<，则（ ）A ．AB B ．BA C ．AB = D ．A B =∅解析：2{|20}A x x =-<=，由集合关系知B A 成立，故答案：B练习9 设{|4}P x x =<，2{|4}Q x x =<，则（ ）A ．P Q ⊆B ．Q P ⊆C ．RP Q ⊆D ．RQ P ⊆2}，由集合关系可知Q P ⊆正确，故选{(,)|1}A x y x y =-=例1 ，{(,)|3}B x y x y =+=，求A B ．解析：两个集合中的元素均为对应函数上的点，所以两个集合的交集变为两个函数的交点问题，解方程组可得{(2,1)}AB ={(,)|1}A x y y x ==+例2 ，{(,)|1}1yB x y x ==+，求A B ． 解析：A 集合是函数1y x =+上所有点的集合，B 集合是11yx =+上所有点的集合，B 集合可变形为1(1)y x x =+≠-，即B 中取不到点(1,0)-，其余与A 一样，则{(1,0)}A B =-．{(2,1)}AB =尤其是分式存在的情况，练习1 设集合{(,)|0}A x y x y =-=，{(,)|40}B x y x y =++=，则A B =______．{(,AB x y =2,2)}--练习2 已知2{(,)|}A x y y x ==，{(,)|}B x y y x ==，则A B =（ ）A ．RB ．[0,)+∞C ．(1,1)D ．{(0,0),(1,1)}{(,A B x y =练习3 已知集合{(,)|31}M x y y x ==+和集合2{(,)|1}N x y y x x ==++，则MN =（ ）A ．{0,2}B ．∅C ．[1,)+∞D ．{(0,1),(2,7)} {(,A B x y =练习4 设2{(,)|1(2)0}A x y x y =++-=，{1,0,1,2}B =-，则A 、B 两个集合的关系是（ ）A ．AB ⊇ B ．A B ⊆C ．A B ∈D ．以上都不对练习5 设集合2{|}P x y x ==，2{(,)|}Q x y y x ==，则P 与Q 的关系是（ ）A ．P Q ⊆B ．P Q ⊇C ．P Q =D ．以上都不对练习6 若{(,)|1}A x y y ax ==+，{(,)|}B x y y x b ==+，{(2,5)}A B =，则a b +_______．{(2,5)}AB =中的方程，把点(2,5)3b =，则a 练习7 若集合{(,)|6}A x y y ax ==+，集合{(,)|53}B x y y x ==-，若点(1,)()b A B ∈，则a b -=_______．By ：数学浪子 )AB ，可知6a b -=-．{(,)|1}A x y y x ==+练习8 ，32{(,)|}x xC x y y x x-==-，求A C ．解析：A 集合是函数1y x =+上所有点的集合，C 集合是32x xy x x-=-上所有点的集合，C 中分母不为0，即20x x -≠，解得01x x ≠≠且，C 集合可变形为1(01)y x x x =+≠≠且，即C 中取不到点(0,1)(1,2)和，其余与A 一样，则{(0,1),(1,2)}A C =．{(,)|1}1yB x y x ==+练习9 ，{(,)|1}M x y y kx ==-，B M =∅，求k ．解析：B 集合是11yx =+上所有点的集合，B 集合可变形为1(1)y x x =+≠-，即B 是取不到点(1,0)-的函数，要使BM =∅说明两直线没有交点，可分两种情况：①两直线平行时，满足斜率相等，即1k =时，成立； ②直线1y kx =-过(1,0)-，带入可得1k =-，成立； 综上：1k =±．练习10 已知集合3{(,)|1}2y A x y a x -==+-，2{(,)|(1)(1)15}B x y a x a y =-+-=，若AB =∅，则a 的所有取值是________．解析：{(A =集，要使AB =∅，则1a =时，B =∅，满足AB =∅；A B =∅；(1)x a y +-A B =∅；练习11 已知集合{(,)|210}A x y x y =+-=，{(,)|20}B x y x ay a =--=，若A B =∅，则a 的值是_______．12a=的直线，AB =∅，所以答案：1-练习12 设集合3{(,)|2}1y A x y x -==-，{(,)|4160}B x y x ay =+-=，若A B =∅，则a 的值为（ ）A ．4B ．2-C ．42-或D ．24-或 A B =∅，则中两直线没有交点，2-，验证成立； 题型七：用Venn 图计算集合例1 某次考试，数学及格28人，物理及格30人，数学物理都不及格12人，学生总数50人，问数学和物理都及格的多少人？{|7,N}U x x x =≤∈例2 ，(){2,3}U A B =，(){0,6}U B A =，()(){1,7}U U A B =，求A 、B 集合．解析：{0,1,2,3,4,5,6,7}U =，画出Venn 图，可知{2,3,4,5}A ={4,5,0,6}B =．总结：对于比较复杂的数字问题，可以画出Venn 图来辅助解题，通常需要设一个未知数x ，根据条件精确的标出交并补集中各个部分的数据，最后解出x 的值． 注意Venn 图和公式()()()U U UA B A B =以及()()()U U UA UB A B =的综合运用，对于有大量交并补集条件的题目，首先画Venn 图，然后考虑有没有可以用公式的地方，最后把条件标在相应的位置，问题迎刃而解．()()()U U UA B A B ⇔先补后交等于先并后补，反之亦然．练习1 某次考试，数学及格28人，物理及格30人，化学及格25人，数学物理都及格20人，数学化学都及格15人，物理化学都及格18人，数理化都不及格10人，学生总数50人，问数理化都及格多少人？By ：数学浪子练习2 50名学生参加甲、乙两项体育活动，每人至少参加了一项，参加甲项的学生有30名，参加乙项的学生有25名，则仅参加了一项活动的学生人数为（ ）A ．50B ．45C ．40D ．35解析：设两项都参加的人数为x ，则只参加甲的人数为30x -，只参加乙的人数为25x -，总人数为(30+(25)50x x x -+-=），解得5x =，所以仅参加了一项活动的人数为50545-=人．答案：B练习3 某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为_______．解析：设两项运动都喜爱的人数为x ，画出Venn 图，则总人数30(15)(10)8x x x =-++-+，解得3x =，所以喜爱篮球但不喜爱乒乓球人数为1512x -=人．答案：12练习4 某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26,15,13，同时参加数学和物理小组的人有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有_______人．36(20)(9)15x x x =-++-+，解得8x =．答案：8{|7,N}U x x x =≤∈练习5 ，(){2,3}U A B =，(){0,6}U B A =，()(){1,7}U U A B =，求A 、B 集合．解析：{0,1,2,3,4,5,6,7}U =，画出Venn 图，可知{2,3,4,5}A ={4,5,0,6}B =．练习6 设全集{1,2,3,4,5}U M N ==，{2,4}U M N =，则N=（ ）A ．{1,2,3}B ．{1,3,5}C ．{1,4,5}D ．{2,3,4}解析：画出Venn 图，可知U M N 为左侧阴影部分，则N 为剩余空白部分，除去{2,4}后所剩为{1,3,5}．答案：B练习7 设全集{1,2,3,4,5}U M N ==，{2,5}U M N =，则N=________． 图，可知U M N 为左侧阴影部分，则N 为剩余空白部分，除去答案：{1,3,4}练习8 已知A 、B 均为集合{1,3,5,7,9}U =的子集，且{3}A B =，(){9}U B A =，则A 等于（ ）A ．{1,3}B ．{3,7,9}C ．{3,5,9}D ．{3,9}解析：画出Venn 图，根据题意，A 中只有3和9两个元素．答案：D练习9 已知全集R U =，集合{1,2,3,4,5}A =，{|3}B x x =≥，途中阴影部分所表示的集合为（ ）A ．{1}B ．{1,2}C ．{1,2,3}D ．{0,1,2}解析：根据条件，把Venn 图中的数据补全，可知阴影部分表示的集合为{1,2}．答案：B练习10 已知全集{1,2,3,4,5}U =，集合{1,2,3}A =，{3,4,5}B =，图中阴影部分所表示的集合为（ ）A ．{3}B ．{1,2}C ．{4,5}D ．{1,2,3,4,5}答案：B练习11 已知M 、N 为集合I 的非空真子集，且M 、N 不相等，若()I N M =∅，则M N =（ ）A ．MB ．NC ．ID ．∅解析：由()I N M =∅，可知N 为M 的子集，所以M N M =．答案：A练习7 已知全集U A B =中有m 个元素，()()U U A B 中有n 个元素，若A B 非空，则A B 的元素个数为（ ）A ．mnB ．m+nC ．n-mD ．m-n解析：()()()U U U A B A B =，由Venn 图可知()U A B 为图中阴影部分，有n 个元素，总数有m 个元素，则中间白色部分A B 的个数即为m-n 个．答案：D练习8 若集合A 、B 、C 为三个集合，A B B C =，则一定有（ ）A ．A C ⊆B ．C A ⊆ C ．A C ≠D ．A =∅解析：AB BC =可分开看作为AB B =和B BC =，即A B ⊆且B C ⊆，所以A C ⊆． 答案：A 练习9 设全集{,,,}U a b c d =，集合{,}A a b =，{,,}B b c d =，则()()U U A B =_______． 解析：()()()U U U A B A B =，{}A B b =，则(){,,}U A B a c d =． 答案：{,,}a c d练习10 已知全集{0,1,2,3,4,5,6,7,8,9}U =，集合{0,1,3,5,8}A =，集合{2,4,5,6,8}B =，则()()U U A B =（ ）A ．{5,8}B ．{7,9}C ．{0,1,3}D ．{2,4,6}解析：()()()U U U A B A B =，{0,1,2,3,4,5,6,8}A B =，则(){7,9}U A B =．答案：B 练习11 设全集{1,2,3,4,5,6}U =，{2,3}M =，{1,4}N =，则集合{5,6}等于（ ）A ．M NB ．M NC ．()()U U M ND ．()()U U M N解析：观察知，{5,6}为U 中除去M 和N 剩下的元素集合，即{5,6}()U M N =，根据公式()()()U U U M N M N =可知D 正确．答案：D数学浪子版权所有，禁止用于任何商业用途。

第二章 传热学知识第一节 传热基础知识传热学是一门研究热量传递规律的科学，它在管道集输领域得到广泛的运用。

热能由物体的一端传向物体的另一端或者由一个物体传向另一物体的过程叫传热过程。

而这两个传热物体，叫热载体。

在油气集输过程中，每个环节都是与热能的传递分不开的，在加热炉给原油加热的过程中，我们总是希望得到较好的传热效果。

而在原油的输送过程中，我们又力求希望减少热量的传递损失，因此，我们必须掌握热传播的一般规律来指导生产。

热能通常都是由比较热的载体传向较冷的载体，这是传热过程的另一个规律。

热载体有气体、固体和液体。

在传热过程中，温度较高放出热量的物体叫热载热体。

而温度较低吸收热量的物体叫冷载热体。

例如加热炉管对原油来说，是热载热体，而炉管内的原油则是冷载热体。

传热过程中的两种热载体可以直接接触或通过中间介质来进行热量传递，如热传导、对流。

也可以不借任何介质进行热量传递，如辐射传热。

因此，热传递有三种基本方式，即热传导、热对流和热辐射。

第二节 热传导热传导是依靠物体的分子运动进行的，温度较高物体的分子具有较大的动能，温度较低的物体分子具有的动能也较低，热量在固体中的传播实际上是动能较大的分子将其动能的一部分传给邻近的动能较小的分子。

两个相互接触的物体或同一物体的各部分之间，由于温度不同而引起的热传递现象，称为热传导，简称导热。

热传导仅依靠分子、原子及自由电子等微观粒子的热运动传递热量。

在热传导过程中，物体分子只是振动，其相对位置并不变动。

稳定情况下的热传导，可按下式计算：式中：Q 一 传热量，W 或KW ；λ 一 导热系数，W/cm ·℃；F 一 传热面积，m2；t 1-t 2 一 温差，℃；△X 一 传热厚度，m 。

将等式的两边都用面积F 去除，便得： 式中：q 一 热流，w/m 2或kw/m 2。

导热系数λ，表示温差为1℃时，在单位时间内，通过单位长度所传导的热量。

不同物质有不同的导热系数，导热系数很大的物质，如金属类称为热的良导体。

高三数学集合知识点框架在高三数学中，集合是一个重要且常见的概念。

掌握集合的相关知识点对于理解和解决数学问题至关重要。

下面将给出高三数学集合知识点的框架。

一、集合的定义和表示方法1. 集合的定义：集合是由一些确定的对象组成的整体。

2. 集合的表示方法：列举法和描述法。

二、集合的运算与关系1. 交集：集合A和集合B的交集，记作A∩B，表示同时属于A和B的元素组成的集合。

2. 并集：集合A和集合B的并集，记作A∪B，表示属于A或B的元素组成的集合。

3. 差集：集合A和集合B的差集，记作A-B或A\B，表示属于A但不属于B的元素组成的集合。

4. 补集：集合A相对于全集U的补集，记作A'，表示全集U 中不属于A的元素组成的集合。

5. 相等关系：若两个集合A和B的元素完全相同，则称集合A 和集合B相等，记作A=B。

三、集合的性质1. 子集关系：若集合A中的每个元素都是集合B的元素，则称A是B的子集，记作A⊆B。

2. 空集和全集：空集是不包含任何元素的集合，全集是所讨论的集合中的所有元素的总和。

3. 互斥集：若两个集合A和B没有公共元素，则称A和B互斥。

4. 互补集：若两个集合A和B的并集是全集U，且A和B互斥，则称A和B互为互补集。

四、集合的应用1. 隶属关系：根据给定条件，将对象分成两个集合，其中一个满足条件，另一个不满足条件。

2. 数学推理：利用集合的运算与关系，对数学问题进行推理和解决。

3. 概率统计：利用集合的概念，进行概率统计的相关计算和分析。

总结：通过掌握上述高三数学集合知识点，我们可以清晰地理解集合的定义、表示方法、运算与关系，以及集合的性质和应用。

在解决数学问题和进行数学推理时，能够灵活运用集合知识，提高解题能力和推理能力。

集合知识在数学学习中起到了桥梁和纽带的作用，帮助我们更好地理解和应用其他数学概念。

因此，在高三数学学习中，我们应该注重集合知识的学习和掌握，提高数学素养和解题能力。

集合运算公式知识点总结
一、并集运算
集合A和集合B的并集表示为A∪B，定义为包含所有属于A或属于B或同时属于A和B
的元素的集合。

即A∪B={x|x∈A或x∈B}。

并集运算的公式：
A∪B=B∪A（交换律）
(A∪B)∪C=A∪(B∪C)（结合律）
A∪A=A（幂等律）
A∪∅=A（零元律）
二、交集运算
集合A和集合B的交集表示为A∩B，定义为包含所有既属于A又属于B的元素的集合。

即A∩B={x|x∈A且x∈B}。

交集运算的公式：
A∩B=B∩A（交换律）
(A∩B)∩C=A∩(B∩C)（结合律）
A∩A=A（幂等律）
A∩U=A（单位元律）
三、补集运算
集合A相对于集合U的补集表示为A'，定义为所有属于集合U但不属于A的元素的集合。

即A'={x|x∈U且x∉A}。

补集运算的公式：
(A')'=A（双重补律）
四、差集运算
集合A相对于集合B的差集表示为A-B，定义为包含所有属于A但不属于B的元素的集合。

即A-B={x|x∈A且x∉B}。

差集运算的公式：
A-B≠B-A（非交换律）
(A-B)∪B=A（分解律）
A-(A∩B)=A-B
(A∪B)-B=A-(A∩B)
以上是集合运算的基本知识点和相应的公式。

在集合运算中，需要注意各种运算的性质和互相之间的关系，以便正确进行集合运算。

同时，在实际问题中，集合运算也常常用于解决各种数学问题，例如概率统计、逻辑推理等方面的问题。

因此，掌握好集合运算的知识点和公式是十分重要的。

集合运算集合运算集合论是数学中最基础的部分之一，而集合运算就是我们对集合之间关系的描述和运算规律的探讨。

在实际生活和学术研究中，集合运算起着极为重要的作用，无论从数学上还是其他领域的应用来看，集合运算都是不可或缺的工具。

在此，我们将重点介绍集合运算的基础知识，按照不同的类别进行分类介绍。

一、集合的基本运算集合基本运算有三个：并集、交集和差集。

并集：当A和B是两个集合时，集合A和集合B的并集（记作A∪B）是由属于集合A或属于集合B的元素构成的新集合。

交集：当A和B是两个集合时，集合A和集合B的交集（记作A∩B）是由属于集合A且属于集合B的元素构成的新集合。

差集：当A和B是两个集合时，集合A和集合B的差集（记作A-B）是由属于集合A但不属于集合B的元素构成的新集合。

二、补集运算补集是指一个集合与它的全集的差集，即一个集合中所有不属于自己的元素的集合。

与其他运算不同，这是只需要一个集合即可完成运算的一种特殊运算方式。

补集常用符号为C(A)，表示集合A的补集，C(A)=U-A 。

其中， U 表示构成某一集合的所有元素的全部可能的“全集”。

三、笛卡尔积当A和B是两个集合时，笛卡尔积（记作A×B）是由所有形如(a,b)的有序对构成的集合，其中a∈A，b∈B。

四、集合运算除了以上几种基本运算，还有一些其它的常规运算，这里简单介绍两种：并集和交集的笛卡尔积：集合A和B的并集与交集的笛卡尔积分别是(A×B)∪(A×B) 和(A×B)∩(A×B) 。

幂集：集合A的所有子集构成的集合称为 A 的幂集。

极其重要的一点是将幂集定义为集合 A 的所有子集，不包括空集，因此 A 的幂集元素个数是 2^n，n 为集合 A 中元素的个数。

总结：集合运算是集合论中重要的一个部分，集合之间的基本运算包括并集、交集、差集以及补集等。

此外，还有笛卡尔积和幂集等其他重要概念。

在实际生活和学术研究中，集合运算帮助我们更好地描述和计算不同集合之间的关系，并提供了大量的重要工具和方法。

1.1 集合1.1.1 集合的含义与表示一集合与元素1.集合是由元素组成的集合通常用大写字母A、B、C，…表示，元素常用小写字母a、b、c，…表示。

2.集合中元素的属性（1）确定性：一个元素要么属于这个集合，要么不属于这个集合，绝无模棱两可的情况。

（2）互异性：集合中的元素是互不相同的个体，相同的元素只能出现一次。

（3）无序性：集合中的元素在描述时没有固定的先后顺序。

3.元素与集合的关系（1）元素a是集合A中的元素，记做a∈A，读作“a属于集合A”；（2）元素a不是集合A中的元素，记做a∉A，读作“a不属于集合A”。

4.集合相等如果构成两个集合的元素一样，就称这两个集合相等，与元素的排列顺序无关。

二集合的分类1.有限集：集合中元素的个数是可数的，只含有一个元素的集合叫单元素集合；2.无限集：集合中元素的个数是不可数的；3.空集：不含有任何元素的集合，记做∅.三集合的表示方法1.常用数集（1）自然数集：又称为非负整数集，记做N；（2）正整数集：自然数集内排除0的集合，记做N+或N※；（3）整数集：全体整数的集合，记做Z（4）有理数集：全体有理数的集合，记做Q（5）实数集：全体实数的集合，记做R3.集合的表示方法（1）自然语言法：用文字叙述的形式描述集合。

如大于等于2且小于等于8的偶数构成的集合。

（2）列举法：把集合的元素一一列举出来，并用花括号“｛｝”括起来表示集合的方法，一般适用于元素个数不多的有限集，简单、明了，能够一目了然地知道集合中的元素是什么。

注意事项：①元素间用逗号隔开；②元素不能重复；③元素之间不用考虑先后顺序；④元素较多且有规律的集合的表示：｛0,1,2,3，…，100｝表示不大于100的自然数构成的集合。

（3）描述法：用集合所含元素的共同特征表示集合的方法，一般形式是｛x∈I | p(x)｝.注意事项：①写清楚该集合中元素的代号；②说明该集合中元素的性质；③不能出现未被说明的字母；④多层描述时，应当准确使用“且”、“或”；⑤所有描述的内容都要写在集合符号内；⑥语句力求简明、准确。

集合运算知识点总结一、集合的基本概念集合是数学中的一个基本概念，它是由一些确定的、互不相同的对象组成的。

这些对象称为集合的元素。

如果一个集合里有限个元素，称这个集合为有限集合；如果集合的元素可以用无穷个数来表达，称这个集合为无限集合。

集合用字母表示，大写字母A、B、C表示集合，小写字母a、b、c表示集合的元素。

当元素x属于集合A时，就记作x∈A，读作x属于A。

二、集合的表示方式1. 列举法：将集合中的元素用大括号{}括起来，用逗号隔开，写出来。

例如：集合A={1,2,3,4,5}，表示A是由元素1,2,3,4,5组成的集合。

2. 描述法：用一个符合逻辑条件的语句来描述该集合。

例如：集合A={x|x是自然数，0<x<6}，表示A是由大于0且小于6的自然数组成的集合。

三、集合之间的关系1. 相等关系：当两个集合具有完全相同的元素时，它们就是相等的。

例如：A={1,2,3,4,5}，B={5,4,3,2,1}，A和B是相等的集合。

2. 包含关系：当一个集合的所有元素都是另一个集合的元素时，称前一个集合包含于后一个集合。

例如：A={1,2,3,4}，B={1,2,3,4,5}，则A⊆B，表示A包含于B。

3. 交集：两个集合A和B的交集，是由所有既属于A又属于B的元素组成的集合。

例如：A={1,2,3,4}，B={3,4,5,6}，则A∩B={3,4}。

4. 并集：两个集合A和B的并集，是由所有属于A或属于B的元素组成的集合。

例如：A={1,2,3,4}，B={3,4,5,6}，则A∪B={1,2,3,4,5,6}。

5. 补集：若全集为U，集合A是U的一个子集，那么A对于U的补集是由A不在U中的元素组成的集合。

一般记作A'。

例如：U={1,2,3,4,5,6}，A={1,2,3,4}，则A'={5,6}。

四、集合的运算1. 交集运算：设A和B是两个集合，A∩B={x|x∈A且x∈B}，即A与B的交集是由既属于A又属于B的元素组成的集合。

集合的基础知识点梳理大全集一、重点知识归纳及讲解1．集合的有关概念一组对象的全体形成一个集合，集合里的各个对象叫做集合的元素⑴集合中的元素具有以下的特性①确定性：任给一元素可确定其归属．即给定一个集合,任何一个对象是不是这个集合的元素也就确定了.例如，给出集合{1，2，3，4}，它只有1、2、3、4四个元素，其他对象都不是它的元素；而“所有的好人”、“视力比较差的全体学生”、“我国的所有小河流”就不能视为集合，因为组成它们的对象是不能确定的.②互异性：集合中的任何两个元素都是不同的对象，也就是说，集合中的元素必须是互不相同的（即没有重复现象），相同的元素在集合中只能算作一个.例如，不能有{1，1，2}，而必须写成{1，2}.③无序性：集合中的元素间是无次序关系的.例如，{1，2，3}与{3，2，1}表示同一个集合.（2）集合的元素某些指定的对象集在一起就成为一个集合，集合中的每个对象叫做这个集合的元素.若a 是集合A的元素，就说a属于集合A，记作a∈A.不含任何元素的集合叫做空集，记作φ.（3）集合的分类：有限集与无限集.（4）集合的表示法：列举法、描述法和图示法.列举法：将所给集合中的元素一一列举出来，写在大括号里，元素与元素之间用逗号分开，常用于表示有限集.描述法：将所给集合中全部元素的共同特性和性质用文字或符号语言描述出来．常用于表示无限集.使用描述法时，应注意六点：①写清集合中元素的代号；②说明该集合中元素的性质；③不能出现未被说明的字母；④多层描述时，应当准确使用“且”，“或”；⑤所有描述的内容都要写在大括号内；⑥用于描述的语句力求简明、确切.图示法：画一条封闭的曲线，用它的内部来表示一个集合，常用于表示又需给具体元素的抽象集合，对已给出了具体元素的集合当然也可用图示法来表示.如：A={1，2，3，4}例1、设集合A={a，a+b, a+2b},B={a,ac,ac2} ,且A=B，求实数c值．分析：欲求c值，可列关于c的方程或方程组，根据两集合相等的意义及集合元素的互异性，有下面两种情况：（1）a+b=ac且a+2b= ac2，（2）a+b= ac2且a+2b=ac两种情况．解析：（1）a+b=ac且a+2b= ac2，消去b得：a+ ac2-2ac=0．∵a=0时，集B中三元素均为零，根据集合元素互异性舍去a=0．∴c2-2c+1=0，即c=1，但c=1时，B中的三个元素也相同，舍去c=1，此时无解．（2）a+b= ac2且a+2b=ac，消去b得：2ac2-ac-a=0．∵a=0时，集B中三元素均为零，根据集合元素互异性舍去a=0．∴2c2-c-1=0，即c=1或，但c=1时，B中的三个元素也相同，舍去c=1，∴．点评：两集合相等的意义是两集合中的元素都相同，在求集合中元素字母的值时，可能产生与互异性相矛盾的增解，这需要解题后进行检验，去伪存真．（5）常用数集及专用记号（1）非负整数集（或自然数集）N={0，1，2，……}（2）正整数集N*（或N＋）={1，2，3，……}（3）整数集Z={0，¡1，¡2，……}（4）有理数集Q={整数与分数}（5）实数集R={数轴上的点所对应的数}.强调：实数集不可记为{R}或{实数集}，0≠≠{} ，≠{0}，≠{空集}.强调：排除0和负数的数集也可表示为R*、Z*、Q*或R＋、Z＋、Q＋．2．基本运算1. 交集（1）定义：由所有属于集合A且属于集合B的元素所组合的集合叫A与B的交集．记作，即{，且}（2）交集的图示上图阴影部分表示集合A与B的交集．（3）交集的运算律，，，2. 并集（1）定义：由所有属于集合A或属于集合B的元素所组成的集合，记作，即{，或}（2）并集的图示以上阴影部分表示集合A与B的并集．（3）并集的运算律，，，3、补集（1）定义：设S是一个集合，A是S的一个子集，由S中所有不属于A的元素组成的集合，叫做S中子集A的补集（或余集）.记作，即C S A=（2）补集的图示4、常用性质A A=A，AΦ=Φ，A B=B A，A B A，A B B．A A=A，AΦ=A，A B=B A，A B A，A B B．，，例2、集合{，且}，A U，B U，且{4，5}，{1，2，3}，{6，7，8}，求集合A和B．分析：利用集合图示较为直观．解：由{4，5}，则将4，5写在中，由{1，2，3}，则将1，2，3写在集A中，由{6，7，8}，则将6，7，8写在A、B之外，由与中均无9，10，则9，10在B中，故A={1，2，3，4，5}，B={4，5，9，10}．5、容斥原理：有限集A的元素个数记作card(A).对于两个有限集A，B，有card(A∪B)= card(A)+card(B)- card(A∩B)．二、难点知识剖析1、要注意区分一些容易混淆的符号（1）与的区别：表示元素与集合之间的关系，例如1N，-1N等；表示集合与集合之间的关系，例如N R，等．（2）a与{a}的区别：一般在，a表示一个元素，{a}而表示只有一个元素a的集合．例如，0{0},{1}{1,2,3}等，不能写成0={0}，{1}{1,2,3}，1{1,2,3}．（3）{0}与Φ的区别：是含有一个元素0的集合，Φ是不含任何元素的集合，因此Φ{0}但不能写成Φ={0}，Φ{0}．例3、已知集合M={x|x≤3}，集合P={x|x<2}，设，则下列关系式中正确的一个是（）A、P∈MB、a∈MC、P MD、{a－3}P解析：集合M、P都是部分实数组成的集合，而a是一个具体的实数，故M、P间的关系应用“包含”，“不包含”来确定，而对a与集合M、P的关系只能用“属于”，“不属于”来确定，比较实数的大小，易判断C正确.小结：正确使用集合的符号是正确分析、解答问题的关键．2．理解集合所表示的意义（1）对由条件给出的集合，要明白它所表示的意义，即元素指什么，是什么范围．如{y R|y=}表示的为函数y=中y的取值范围，故{y R|y=}={y R|y};而{x R|y=}表示y=的x的取值范围，故{x R|y=}=R．（2）用集合表示不等式（组）的解集时，要注意分辨是交集还是并集，结合数轴或韦恩图的直观性帮助思维判断．空集是任何集合的子集，但因为不好用韦恩图表示，容易被忽视，如在关系式B A中，易漏掉B=Φ的情况．例4、设A=，B=（1）若A B=B，求的值；（2）若A B=B，求的值．分析：明确A B=B和A B=B的含义，根据问题的需要，将A B=B和A B=B转化为等价的关系式：和，是解决本题的关键．解析：首先化简集合A，得A={-4，0}（1）由于A B=B，则有可知集合B或为空集Φ，或只含有根0或-4．①若B=Φ，由得②若，代入得：，当时，B=，合题意．当时，B=，也符合题意．③若，代入得：，当时，②中已讨论，合题意当时，B=不合题意．由①、②、③得，．（2）因为A B=B，所以，又A={-4，0}，而B至多只有两个根，因此应有A=B．由（1）知，【点评】：一般对于A B=B和A B=B这种类型的问题，都要注意转化为等价的关系式：和，且在包含关系中，注意不要漏掉B=的情况．并且当A、B中的元素的个数相同时，还存在或的情况时，只有A=B这一种情况．子集（1）子集定义：一般地，对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A。

集合练习题知识点一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合(简称集)．1.集合中元素具的有几个特征⑴确定性－因集合是由一些元素组成的总体，当然，我们所说的“一些元素”是确定的．⑵互异性－即集合中的元素是互不相同的，如果出现了两个(或几个)相同的元素就只能算一个，即集合中的元素是不重复出现的．⑶无序性－即集合中的元素没有次序之分．2.常用的数集及其记法我们通常用大写拉丁字母Ａ，Ｂ，Ｃ，…表示集合，用小写拉丁字母a，b，c，…表示集合中的元素．常用数集及其记法非负整数集（或自然数集），记作N正整数集，记作N*或N+；整数集，记作Z有理数集，记作Q实数集，记作R3．元素与集合之间的关系4.反馈演练1.填空题2．选择题⑴以下说法正确的( )(A) “实数集”可记为{R}或{实数集}(B){a,b,c,d}与{c,d,b,a}是两个不同的集合(C)“我校高一年级全体数学学得好的同学”不能组成一个集合,因为其元素不确定⑵已知2是集合M={ }中的元素，则实数为( )(A) 2 (B)0或3 (C) 3 (D)0,2,3均可二、集合的几种表示方法1、列举法－将所给集合中的元素一一列举出来，写在大括号里，元素与元素之间用逗号分开．*有限集与无限集*⑴有限集-------含有有限个元素的集合叫有限集例如: A={1~20以内所有质数}⑵无限集--------含有无限个元素的集合叫无限集例如: B={不大于3的所有实数}2、描述法－用集合所含元素的共同特征表示集合的方法.具体方法:在花括号内先写上表示这个集合元素的一般符号及以取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.3、图示法 -- 画一条封闭曲线,用它的内部来表示一个集合.常用于表示不需给具体元素的抽象集合.对已给出了具体元素的集合也当然可以用图示法来表示如: 集合{1,2,3,4,5}用图示法表示为:三、集合间的基本关系观察下面几组集合，集合A与集合B具有什么关系？(1) A={1，2，3}，B={1，2，3，4，5}.(2) A={x|x>3},B={x|3x-6>0}.(3) A={正方形}，B={四边形}.(4) A=∅，B={0}.1.子集定义：一般地，对于两个集合A与B，如果集合A中的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A，记作A⊆B（或B⊇A）,即若任意x∈A,有x∈B，则A⊆B(或A⊂B)。

声明：均为个人整理，仅供参考，大家努力复习，正道沧桑。

PS ：祝考研同学金榜题名一班肖帅绪论一、油气集输系统的功能：将分散在油田各处的油井产物加以收集；分离成原有、伴生天然气和采出水；进行必要的净化、加工处理使之成为油田商品（原油、天然气、液化石油气、天然汽油）以及这些商品的储存和运输。

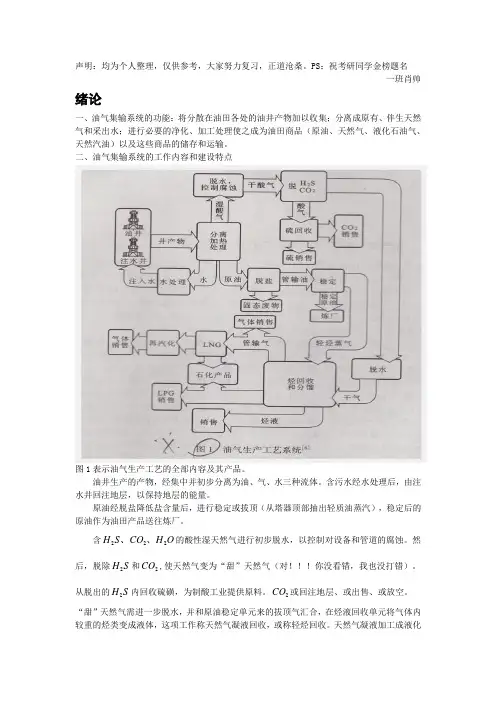
二、油气集输系统的工作内容和建设特点图1表示油气生产工艺的全部内容及其产品。

油井生产的产物，经集中并初步分离为油、气、水三种流体。

含污水经水处理后，由注水井回注地层，以保持地层的能量。

原油经脱盐降低盐含量后，进行稳定或拔顶（从塔器顶部抽出轻质油蒸汽），稳定后的原油作为油田产品送往炼厂。

含222H S CO H O 、、的酸性湿天然气进行初步脱水，以控制对设备和管道的腐蚀。

然后，脱除2H S 和2CO ,使天然气变为“甜”天然气（对！！！你没看错，我也没打错）。

从脱出的2H S 内回收硫磺，为制酸工业提供原料。

2CO 或回注地层、或出售、或放空。

“甜”天然气需进一步脱水，并和原油稳定单元来的拔顶气汇合，在烃液回收单元将气体内较重的烃类变成液体，这项工作称天然气凝液回收，或称轻烃回收。

天然气凝液加工成液化石油气（34C C 、烷烃）和稳定的轻烃5C （也称天然气汽油或轻质石脑油）。

液化石油气作为油田产品外销，或供石油化工厂做原料，或再气化为用户提供调峰天然气。

三、油气集输系统工作内容主要内容包括：1、油井计量 测出每口油井产物内的原油、天然气、采出水的产量，作为分析油藏开发动态的依据。

2、集油 将计量后的油井产物（油、气、水）或油水混合物集中，通过管线输送至有关站场经行处理。

3、集气 将油田内部一级油气分离器分离出的天然气通过管线输送至气体处理厂进行净化和加工。

4、油气水分离 将井流分离成原油、天然气、采出水。

必要时，还需要分离出井流中所含的固体杂质。

5、原油处理（脱水） 含水原油经破乳、沉降、分离，脱除游离水、乳化水和悬浮固体杂质，使商品原油含水率小于规定的质量标准。

油气集输知识点《聊聊油气集输那些事儿》嘿，朋友们！今天咱来唠唠油气集输知识点。

这可不是啥生僻玩意儿，它呀，就跟咱日常生活息息相关呢！油气集输，简单来说，就是把油啊气啊从各个地方收集起来，再输送到该去的地儿。

这可不像我们收快递那么简单哦！你想想，那石油和天然气可是从深深的地下冒出来的，它们散落在各处，就像一群调皮的小孩子到处乱跑。

这时候，油气集输就充当了“班主任”的角色，把它们一个个都集合起来，安排得明明白白。

首先呢，得有各种设备和管道来收集这些“小调皮”。

这些设备就像是一个个超级英雄，各显神通。

有的负责把油从地下抽上来，有的负责分离油和气，还有的负责把它们输送到远方。

说到这分离啊，可真是个技术活。

就像我们分豆子和沙子一样，得把它们分得清清楚楚。

油和气也得这样分离开来，可不能马虎。

要不然，混在一起可就麻烦啦！然后呢，这些油气还得经过长长的管道进行输送。

这管道就像是高速公路，让油气能快速地到达目的地。

不过这“高速公路”也得好好维护，不然哪天漏了个洞，那可就糟糕啦！就好像高速公路上突然出现个大坑，后果不堪设想。

在油气集输的过程中，还得注意安全问题。

毕竟这石油和天然气可都是“火爆脾气”，一不小心就会发脾气。

所以啊，各种安全措施都得做到位，什么防火啊、防爆啊，一个都不能少。

就像我们出门都得带好钥匙、手机一样，这都是必备的。

而且啊，这油气集输可不是一成不变的。

随着技术的发展，它也在不断进步。

就像我们的手机一样，越来越好，越来越智能。

现在的油气集输技术可比以前先进多了，效率也高了不少。

总之呢，油气集输知识点可不少，它关系到我们每天用到的石油和天然气。

没有它，我们的生活可就没那么方便啦！虽然它听起来有点复杂，但其实也挺有趣的。

就像一个神秘的世界，等待着我们去探索。

怎么样，朋友们，对油气集输有没有多一点了解呢？哈哈！。

高三集合运算知识点高三学生在学习数学时，集合运算是一个重要的知识点。

本文将向您介绍高三集合运算的相关概念、符号以及运算规则。

一、集合运算的基本概念集合是由一组确定元素所组成的整体。

常用的符号表示集合，例如大写字母A、B、C等。

集合中的元素可以是数字、字母、词语等。

在集合运算中，常用的术语及符号包括：1.1 并集：由两个或多个集合的所有元素组成的集合，用符号“∪”表示。

1.2 交集：包含两个或多个集合共有元素的集合，用符号“∩”表示。

1.3 差集：从一个集合中去除另一个集合的元素，用符号“-”表示。

1.4 互斥：两个集合没有共同的元素，用来表示两个集合之间没有交集。

1.5 子集：一个集合中的所有元素都是另一个集合的元素，则称该集合为另一个集合的子集。

二、集合运算的规则在进行集合运算时，需要根据不同的情况选择合适的运算规则。

下面是常用的集合运算规则：2.1 并集的运算规则：- 若A∪B=B∪A，表示并集满足交换律；- 若(A∪B)∪C=A∪(B∪C)，表示并集满足结合律；- 若A∪(B∩C)=(A∪B)∩(A∪C)，表示并集与交集满足分配律。

2.2 交集的运算规则：- 若A∩B=B∩A，表示交集满足交换律；- 若(A∩B)∩C=A∩(B∩C)，表示交集满足结合律；- 若A∩(B∪C)=(A∩B)∪(A∩C)，表示交集与并集满足分配律。

2.3 差集的运算规则：- A-B表示从集合A中去掉集合B的元素，即A-B={x|x∈A，x∉B}；- 若A-B≠B-A，则两个集合的差集不满足交换律。

三、集合运算的应用高三学生在解决实际问题时，可以运用集合运算的知识点，例如：3.1 判断元素是否属于某个集合：可以通过判断元素是否在集合中进行。

3.2 求多个集合的并集或交集：将多个集合合并在一起，或者找到多个集合中共有的元素。

3.3 解决排列组合问题：在计算排列组合问题中，可以将所有可能的元素组合放入集合中，利用集合运算来计算结果。

集合知识复习要点梳理1．以集合为中心的知识网络概述集合是不定义的概念，在理解集合概念的同时，必须掌握集合中元素的确定性、互异性及无序性的性质，并能运用这些性质来解题．注意元素与集合之间是属于或不属于的关系，而集合与集合之间是包含或不包含的关系，两者不能混淆．要熟练地进行集合的交、并、补的运算，在运算时，应首先将集合化简，当集合中含字母时，必须对字母的取值进行讨论．作为一种数学工具，集合与数学的其他各个分支有着密切的联系，复习时要加深对它的理解．集合是高中数学的基础，也是高考中常考的内容之一．集合思想及集合语言可以渗透到高中数学的各个分支，它可与函数、方程和不等式等许多知识综合起来进行考查．在解题时首先需要我们能读懂集合语言，将集合语言转换为数学语言，再用相关的知识解决问题．2．对集合中元素三大性质的理解高.考-资.源-网（1）确定性集合中的元素，必须是确定的．对于集合A和元素a，要么a A∈，要么a A∉，二者必居其一．比如：“所有大于100的数”组成一个集合，集合中的元素是确定的．而“较大的整数”就不能构成一个集合，因为它的对象是不确定的．再如，“较大的树”、“较高的人”等都不能构成集合．（2）互异性对于一个给定的集合，集合中的元素一定是不同的．任何两个相同的对象在同一集合中时，只能算作这个集合中的一个元素．如：由a，2a组成一个集合，则a的取值不能是0或1．（3）无序性集合中的元素的次序无先后之分．如：由123，，组成一个集合，也可以写成132，，组成一个集合，它们都表示同一个集合．3．学习集合表示方法时应注意的问题（1）注意a与{}a的区别．a是集合{}a的一个元素，而{}a是含有一个元素a的集合，二者的关系是{}a a∈．（2）注意∅与{}0的区别．∅是不含任何元素的集合，而{}0是含有元素0的集合．（3）在用列举法表示集合时，一定不能犯用｛实数集｝或{}R来表示实数集R这一类错误，因为这里“大括号”已包含了“所有”的意思．用特征性质描述法表示集合时，要特别注意这个集合中的元素是什么，它应具备哪些特征性质，从而准确地理解集合的意义．例如：集合{()x y y=，中的元素是()，，这个集合表示二元方程x yy=的解集，或者理解为曲线y=上的点组成的点集；集合{x y=中的元素是x，这个集合表示函数y=中自变量x的取值范围；集合{y y=中的元素是y，这个集合表示函数y中函数值y的取值范围；集合{y=中的元素只有一个（方程y），它是用列举法表示的单元素集合．4．集合间的关系及集合运算问题点评（1）要注意∈与⊆间的区别：“∈”表示元素与集合间的关系，如2∈N ．“⊆”表示集合与集合间的关系，如⊆N Z ．（2）理解A B ⊆与A B Ü的含义：“A B ⊆”包含“A B =”，“A B Ü”两种情况，其中必有一种且只有一种情况成立；而“A B Ü”等价于“A B ⊆且A B ≠”．（3）尝试用Venn 图表示两个集合间的关系，并逐步形成用集合的观点去认识问题、思考问题的思维方式．学会分类写出给定集合的所有子集的解题技巧，并通过对教材“探索与研究”中习题的探究，找出集合中元素的个数与它的所有子集个数的关系规律．（4）交集、并集、全集、补集的定义及其运算是本部分的重点，可以结合Venn 图去理解并且应当重视Venn 图的直观作用．（5）应重视利用空集的特性．空集是一个特殊的集合，它是任何集合的子集，利用空集的这一特性，可使一些题设中隐含有空集条件的问题得以正确解决．（6）补集思想在集合运算中的作用也是不可忽视的．对于一个问题，如果正面去求解比较困难，则可以从这个问题的反面入手，也就是采用补集的思想．例 已知集合{}312100x n n x A x x n x ≠∈∈=≠N N 或，，，≤≤，试求出集合A 的元素之和．解：设{}1234100U =，，，，，，则{}{}3100261100U x n n x A x x n x x n n x =∈1====∈N N 且，，，，，ð≤≤≤≤ 于是集合A 的元素之和(123100)(6121896)50508164234=++++-+++=-=． 高.考-资.源-网。

数学集合知识点总结_会计基础知识点总结数学集合知识点总结:1. 集合的概念集合是由一些个体组成的整体，可以是数字、物体、或者是其他对象的集合。

集合用大写字母表示，集合中的个体用小写字母表示。

2. 集合的表示方法集合可以用列举法表示，也可以用描述法表示。

列举法就是将集合中的个体逐个列举出来，描述法则是利用特定的条件描述出集合中的个体的特点。

3. 集合的运算集合有并集、交集、补集和差集四种运算。

并集就是将两个集合中的所有元素取在一起，交集是指两个集合中共有的元素，补集指一个集合中不属于另一个集合的元素，差集则是一个集合中属于另一个集合之外的元素。

4. 集合的关系集合之间可以有包含关系和相等关系。

如果一个集合的所有元素都属于另一个集合，则称前者为后者的子集。

如果两集合的元素相同，那么它们就是相等的。

5. 集合的性质集合有互补律、结合律、分配律等性质。

A∩(B∪C) = (A∩B)∪(A∩C)，这就是分配律。

会计基础知识点总结:1. 会计的概念会计是一门记账和核算的学科，通过对企业的经济活动进行记录、分析和汇总，以便提供决策支持和履行法律义务。

2. 会计的职能会计的主要职能是记录和核算企业的经济活动，包括资产、负债、收入和费用的变动情况，并提供财务信息和报表以供管理者和外部利益相关方参考。

3. 会计的基本假设会计有货币计量、持续经营、会计实体和会计分期等基本假设。

货币计量假设是指会计记录和报告的单位是货币，持续经营假设是指企业将会长期经营下去，会计实体假设是指企业和业主之间应有清晰的界限，会计分期假设是指企业应将其经济活动划分为若干会计期间。

4. 会计的基本原则会计有计量原则、实体原则、收益实现原则和费用匹配原则等基本原则。

计量原则是指会计信息应以稳定的货币单位计量，实体原则是指企业和业主应有清晰的分界线，收益实现原则是指收益应在其实现时被确认，费用匹配原则是指费用应当与相应的收益相匹配。

5. 会计的资产负债表和利润表资产负债表是记录企业在一个特定日期的财务状况，包括资产、负债和所有者权益三个部分。