矩形的判定方法

矩形的判定方法矩形是平面几何中最基本的图形之一，具有四条边和四个直角。

在日常生活和数学领域中，我们经常需要判定一个图形是否为矩形。

下面将介绍几种常见的矩形判定方法。

1. 边长判定法。

矩形的特点是四条边两两相等且相邻的两条边平行。

因此，我们可以通过测量图形的四条边长来判定其是否为矩形。

如果四条边两两相等且相邻的两条边平行，则可以确定这个图形是矩形。

2. 对角线判定法。

矩形的对角线相等且互相平分。

因此，我们可以通过测量图形的对角线来判定其是否为矩形。

如果两条对角线相等且互相平分，则可以确定这个图形是矩形。

3. 角度判定法。

矩形的内角都是直角，即90度。

因此，我们可以通过测量图形的内角来判定其是否为矩形。

如果图形的四个内角都是90度，则可以确定这个图形是矩形。

4. 边长和角度结合判定法。

除了单独测量边长、对角线和角度外，我们还可以将这些方法结合起来进行判定。

例如，可以先测量边长，如果边长符合矩形的特点，再测量角度，如果角度也符合矩形的特点，就可以确定这个图形是矩形。

5. 利用数学定理判定法。

在数学领域中，有一些定理可以用来判定一个图形是否为矩形。

例如，如果一个四边形的对角线互相垂直且相等，那么这个四边形就是矩形。

利用这些数学定理，可以更快速地判定一个图形是否为矩形。

总结。

通过上述几种方法，我们可以准确地判定一个图形是否为矩形。

在实际应用中，可以根据具体情况选择合适的方法进行判定，以提高工作效率。

希望本文介绍的方法能够帮助大家更好地理解矩形的判定方法，提高几何图形的识别能力。

《矩形的判定》教案及反思本节课注重能力和素质的培养，以最新的课程标准和考纲为依据，以方法为主线，以思维为重点，以能力为核心，将基础知识、考试内容和能力提高融为一体。

一、教学目标：1.理解并掌握矩形的判定方法.2.使学生能应用矩形定义、判定等知识，解决简单的证明题和计算题，进一步培养学生的分析能力.二、重点、难点1.重点：矩形的判定.2.难点：矩形的判定及性质的综合应用.3.难点的突破方法：矩形是有一个角是直角的平行四边形，在判定一个四边形是不是矩形时，首先看这个四边形是不是平行四边形，再看它两边的夹角是不是直角，这种用"定义"判定是最重要和最基本的判定方法(这体现了定义作用的双重性、性质和判定).而其它判定都是以"定义"为基础推导出来的.因此本节课要从复习矩形定义下手，并指出由平行四边形得到矩形只需要添加一个独立条件，然后让学生思考讨论，如果小华做出的是一个平行四边形，再加一个什么条件可以说明它是一个矩形呢?从而导出矩形判定方法.对于判定方法1，要着重说明这个性质包括两个条件：(1)是平行四边形；(2)两条对角线相等.对于判定2，只要求是四边形即可，因为由有三个角是直角，可以推出四边形是平行四边形，而由对角线相等却推不出四边形是平行四边形.为了加深印象，我安排了例1，在教学中可以适当地再增加一些判断的题目.要让学生知道(1)矩形的判定方法有以下三种：①一个角是直角的平行四边形；②对角线相等的平行四边形；③有三个角是直角的四边形.(2)而由矩形和平行四边形及四边形的从属关系将矩形的判定方法又可分为两类：①从四边形出发必须增加三个特定的独立条件；②从平行四边形出发只需再增加一个特定的独立条件.(3)特别地：①如果所给四边形添加的条件不满足三个的肯定不是矩形；②所给四边形添加的条件是三个独立条件，但若与判定方法不同，则需要利用定义和判定方法证明或举反例，才能下结论.教学过程一、复习引入：问题1：如何判定一个四边形是矩形问题2：还能有其他方法说明一个四边形是矩形吗？启发学生通过矩形的性质想到，并让学生分组证明二、新课讲解：思考:若已知四边形是平行四边形，应添加什么条件可以判定是矩形？1．猜想矩形的判定，然后加以证明。

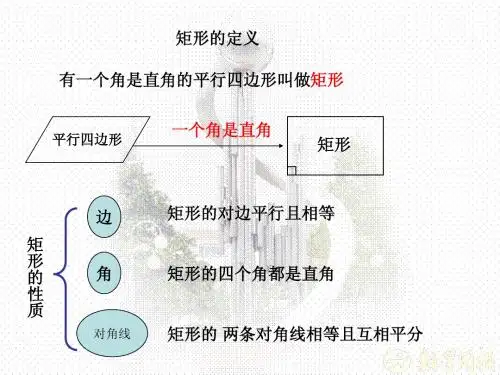
四边形的分类与判定方法四边形是几何学中一种常见的图形，它由四条边和四个角组成。

在不同的边长和角度的组合下，四边形可以被划分为多个不同的类型。

本文将介绍四边形的分类以及判定方法，以帮助读者更好地理解和应用几何学知识。

一、四边形的分类四边形的分类主要根据其边长和角度来进行划分，常见的四边形类型包括正方形、矩形、菱形、平行四边形、梯形和不规则四边形。

1. 正方形正方形是一种特殊的矩形，它的四条边相等且四个角均为直角。

可以通过边长或对角线长相等来判定一个四边形是否为正方形。

2. 矩形矩形也是一种边长相等的四边形，但它的四个角并不一定都为直角。

判定一个四边形是否是矩形的方法是检查它的对角线是否相等。

3. 菱形菱形是一种具有边长相等但角度不一定相等的四边形。

一个四边形若两对相邻边相等，则可以被判定为菱形。

4. 平行四边形平行四边形具有两对相对平行的边，它的对边长度相等。

要判断一个四边形是否为平行四边形，可以检查它的对边是否平行。

5. 梯形梯形是只有一对对边平行的四边形，其余两条边不平行。

通过检查四边形的边是否满足其中两条边平行的条件，即可判定它是否为梯形。

6. 不规则四边形不规则四边形是指不属于上述任何一种特殊类型的四边形。

它的边和角都没有特殊的限制条件，因此可以被视为一般性的四边形。

二、四边形的判定方法判定一个四边形的类型有多种方法，下面将介绍针对常见四边形类型的判定方法。

1. 正方形的判定方法（描述正方形判定方法）2. 矩形的判定方法（描述矩形判定方法）3. 菱形的判定方法（描述菱形判定方法）4. 平行四边形的判定方法（描述平行四边形判定方法）5. 梯形的判定方法（描述梯形判定方法）6. 不规则四边形的判定方法（描述不规则四边形判定方法）三、四边形的应用四边形在几何学中具有广泛的应用。

它们的性质和特点可以用于解决各种几何问题，例如计算面积、判断形状等。

1. 面积计算根据不同类型的四边形，可以通过不同的公式计算其面积。

矩形的判定方法矩形是几何学中常见的形状，具有四条边和四个角的特点。

在日常生活和数学问题中，我们经常需要判定一个图形是否为矩形。

下面将介绍几种判定矩形的方法。

1. 边长判定法。

矩形的特点是对角线相等且相互平分。

因此，我们可以通过判断四条边的长度是否符合这一特点来判定一个图形是否为矩形。

如果一个图形的对角线长度相等且相互平分，那么这个图形就是矩形。

2. 角度判定法。

矩形的特点是四个角都是直角。

因此，我们可以通过判断一个图形的四个角是否都是直角来判定这个图形是否为矩形。

如果一个图形的四个角都是直角，那么这个图形就是矩形。

3. 对角线判定法。

矩形的特点是对角线相等且相互平分。

因此，我们可以通过判断一个图形的对角线是否相等且相互平分来判定这个图形是否为矩形。

如果一个图形的对角线长度相等且相互平分，那么这个图形就是矩形。

4. 对边平行判定法。

矩形的特点是相对边两两平行且相等。

因此，我们可以通过判断一个图形的相对边是否都是平行且相等来判定这个图形是否为矩形。

如果一个图形的相对边都是平行且相等，那么这个图形就是矩形。

5. 综合判定法。

除了以上几种方法外，我们还可以综合运用边长、角度、对角线和对边平行等多种特征来判定一个图形是否为矩形。

通过综合判定法，我们可以更加准确地判断一个图形是否为矩形。

总结。

矩形是一种常见的几何图形，判定一个图形是否为矩形可以通过边长、角度、对角线和对边平行等多种方法来进行。

在实际问题中，我们可以根据具体情况选择合适的判定方法来判断一个图形是否为矩形，从而更好地解决问题。

通过以上介绍，相信大家对矩形的判定方法有了更深入的了解。

希望这些方法能够帮助大家更好地理解和应用矩形的相关知识。

矩形和菱形的判定
矩形和菱形是我们在几何学中常见的两种四边形。

它们各自具有独特的性质和判定方法。

矩形的判定主要基于以下几个条件：
有一个角是直角的平行四边形是矩形。

这是因为在平行四边形中，如果一个角是直角，那么它的相邻角也必然是直角，从而满足矩形的所有内角都是直角的性质。

对角线相等的平行四边形是矩形。

在平行四边形中，如果对角线相等，那么它的四个内角也必然都是直角，因此它是一个矩形。

有三个角是直角的四边形是矩形。

这个条件很直观，因为矩形的定义就是所有内角都是直角的四边形。

菱形的判定则基于以下几个条件：
四条边相等的四边形是菱形。

这是菱形最直接的定义，也是最容易理解的判定条件。

对角线互相垂直的平行四边形是菱形。

在平行四边形中，如果对角线互相垂直，那么它的四条边也必然相等，因此它是一个菱形。

一组邻边相等的平行四边形是菱形。

这个条件是基于平行四边形的性质，如果一组邻边相等，那么另一组邻边也必然相等，因此它是一个菱形。

对角线平分一组对角的平行四边形是菱形。

这个条件也是基于平行四边形的性质，如果对角线能平分一组对角，那么它的四条边也必然相等，因此它是一个菱形。

总的来说，矩形和菱形的判定都是基于它们的定义和性质。

在实际应用中，我们可以根据题目给出的条件，选择合适的判定方法来证明一个四边形是矩形还是菱形。