高三数学复习专题课件:8.1椭圆
- 格式:ppt
- 大小:2.38 MB
- 文档页数:1

§2.10 椭圆定义、标准方程以及几何性质的应用一、教学目标(一)知识教学点使学生进一步理解椭圆的定义,掌握椭圆的标准方程和几何性质.(二)能力训练点通过椭圆定义、标准方程和几何性质的进一步研究,培养学生综合运用椭圆的各方面知识的能力和解决一些解析几何实际问题的能力.(三)学科渗透点椭圆定义、标准方程以及几何性质是来源于实践的理论,同时服务于实践,通过本次课可进行辩证唯物主义思想教育.二、教材分析1.重点:椭圆定义、标准方程以及几何性质的应用.(解决办法:多加强这方面的题型训练,使学生掌握它们的规律.)2.难点:椭圆的焦半径和弦长问题.(解决办法:先证明焦半径公式,再用它解决一些问题.)3.疑点:用椭圆的定义判断一些椭圆的轨迹问题.(解决办法:通过例16分析两个定义的综合运用.)三、活动设计提问、讲授、回答、演板、练习、小结.四、教学过程(一)复习引入1.定义(请两名学生回答,教师板书)第一定义:平面内到两定点F1、F2的距离之和等于常数2a(2a>|F1F2|=2c)的动点M的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做焦距,即|MF1|+|MF2|=2a(2a>|F1F2|=2c).第二定义:平面内点M与一个定点F的距离和它到一定直线的距离椭圆的焦点,定直线叫做椭圆的准线,常数e是椭圆的离心率.2.标准方程、图象及几何性质:(教师事先准备一块小黑板,设计如下表格,请两名学生填写,其他同学纠错,教师巡视.)(二)应用举例例1 (1)已知一定圆C及圆内部的一个定点A,试判断过点A且与OC相切的圆的圆心轨迹(图2-20).的椭圆有多少个?(3)椭圆9x2+25y2=225上有一点P到左准线的距离是2.5,求P到右焦点的距离.分析:本例是关于椭圆的两个定义的题型,要求学生深入理解椭圆两个定义.解:(1)设圆心为M,且设动点M的半径为r,定圆C半径为R(定值),则有|MC|+|MA|=(R-r)+r=R为定值,且R>|AC|.由椭圆的定义可知,点M的轨迹是以A、C为焦点的椭圆.(2)由学生口答.由椭圆的第二定义,因为离心率不定,所以满足条件的椭圆有无穷多个.设椭圆左、右两焦点分别为F1、F2,且设P到左准线的距离为|PQ|,由椭圆的第二定义可知:又由椭圆的第一定义可知:|PF1|+|PF2|=10.∴|PF2|=10-2=8.故P到右焦点的距离为8.1)两点,求椭圆方程.分析:由题设条件焦点在哪个轴上不明确,椭圆的标准方程有两种情形,为了计算简便起见,可设其方程为mx2+ny2=1(m>0,n>0)且不必去考虑焦点的位置,直接可求出方程.由一学生演板完成.解答为:设所求椭圆方程为mx2+ny2=1(m<0,n>0).则椭圆上任一点P(x0,y0)到焦点的距离(称为焦半径)|PF1|=a+ex0,上任一点P(x0,y0)的焦半径|PF1|=a+ey0,|PF2|=a-ey0.角,求此直角三角形PF1F2的面积.解(1):椭圆的焦半径是一个经常见到的问题,可以作为椭圆的性质,结论要求大家记忆.证明由椭圆第二定义易得.下面仅证明其中一种情况,其他情况可类似证明.如图(2-21)作PQ垂直于左准线,垂足为Q.由椭圆的第二定义知:解(2):由学生演板完成,教师巡视、解答:∵a2=49,b2=24.设P(x0,y0)则有|PF1|=a+ex0,|PF2|=a-ex0.∵|PF1|2+|PF2|2=4c2,例4 已知长轴为12,短轴为6的椭圆,过它的左焦点作倾斜角为由直线方程与椭圆方程联立方程得:设x1,x2为方程两根解法二:利用椭圆的定义及余弦定理=12-m,|BF′|=12-n.在△AFF′中:|AF′|2=|AF|2+|FF′|2-2|AF|·|FF′|cos60°.这时,要求学生思考:如何利用焦半径求|AB|?(三)巩固练习1.(1)已知B(-2,0)、C(2,0)且△ABC的周长为10,求顶点A的轨迹方程.(2)点M到一定点F(0,2)的距离和它到定直线y=8的距离之比是1∶2,求M点的轨迹方程.2.(1)若m<n<0,求mx2+ny2+mn=0所表示的曲线的焦点坐标.(2)已知M是椭圆上的一点,F1、F2是椭圆的两个焦点,∠MF1F2=90°,∠MF2F1=30°,求椭圆的离心率.由学生演板.∵m<n<0,∴-m>-n>0.故椭圆焦点在y轴上,∴c2=a2-b2=-m-(-n)=n-m.(四)小结本课对椭圆的两个定义、标准方程以及几何性质的应用进行了研究,同时对焦半径、直线与椭圆的相交问题进行了分析.这些方法具有一般性,要求学生注意掌握.五、布置作业求点M的轨迹方程,并画出图形.2.求证两椭圆b2x2+a2y2=a2b2和a2x2+b2y2=a2b2的交点在以原点为中心的圆周上,并求这个圆的方程.作业答案:x2+y2+2bx+25=0(图略)六、板书设计。

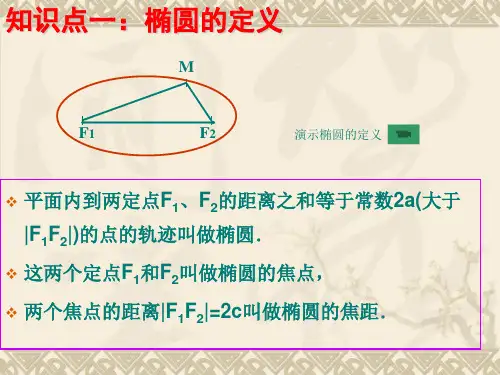





高三椭圆知识点课件1. 椭圆的定义与特点椭圆是平面上一点到两个定点的距离之和等于常数值的轨迹。
对于椭圆,其中心就是两个定点的中点,称为焦点,两个定点距离的一半是椭圆的半长轴,两焦点连线的垂直平分线称为椭圆的直径,直径的一半是椭圆的半短轴。
2. 椭圆的方程椭圆的标准方程为(x-h)²/a² + (y-k)²/b² = 1,其中(h,k)是椭圆的中心坐标,a和b分别是椭圆的半长轴和半短轴的长度。
当a=b时,椭圆退化为圆。
3. 椭圆的焦点与准线椭圆的焦点是平面上到椭圆上任意一点距离之和等于半长轴长度的两个点,焦点与椭圆的半长轴的交点称为准线。
4. 椭圆的离心率椭圆的离心率表示椭圆形状的圆度程度,计算公式为e = c/a,其中c为焦点到中心的距离,a为半长轴的长度。
离心率是0到1之间的实数,当离心率接近于0时,椭圆趋向于圆形,当离心率接近于1时,椭圆则趋向于长条形。
5. 椭圆的参数方程椭圆的参数方程x = h + a*cosθ,y = k + b*sinθ,其中θ为角度,(h,k)为椭圆的中心坐标。
6. 椭圆的性质与应用椭圆有许多重要的性质和应用。
例如,焦点到椭圆上任意一点的距离和等于定点到该点的距离差的绝对值;椭圆的周长可以通过椭圆的参数方程以及积分的方法求得;椭圆还被广泛应用于天体力学、通讯技术等领域。
7. 椭圆与其他几何图形的关系椭圆与其他几何图形有一些重要的关系。
与椭圆相似的图形有椭球体和椭圆锥,它们都具有类似的性质;椭圆还可以通过割椭圆法生成抛物线;直角坐标系中的椭圆可以通过仿射变换转化为标准方程,使得其焦点在坐标轴上。
8. 高三椭圆知识点总结高三阶段学习椭圆的知识是为了准备应对高考数学考试中相关的考点。
在椭圆的学习中,需要掌握椭圆的定义与特点、方程的推导与应用、焦点与准线的概念、离心率的计算等基础知识。
此外,还需要能够灵活运用参数方程、掌握椭圆与其他几何图形的关系。