2018年云南中考《第26讲图形的平移、对称、旋转》知识梳理
- 格式:pdf
- 大小:739.39 KB
- 文档页数:7
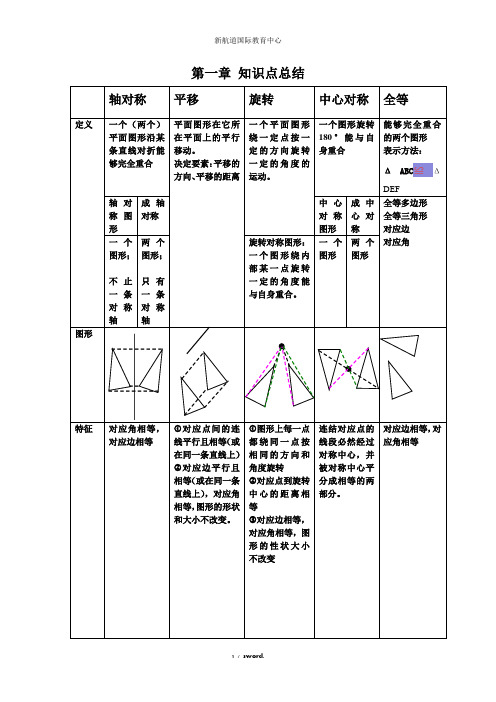
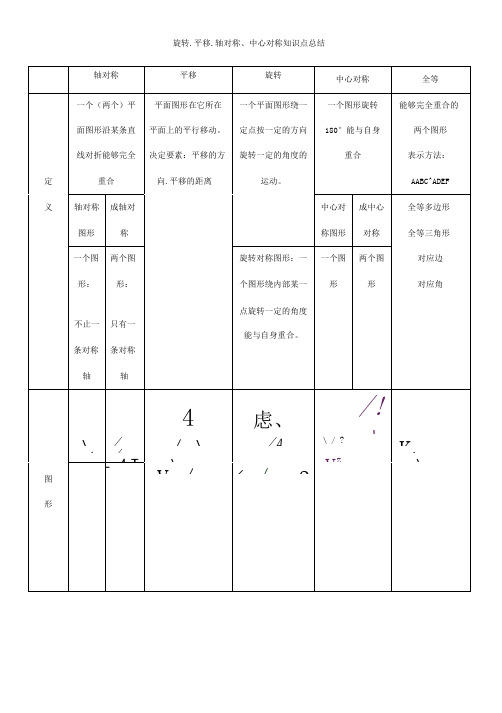

旋转、平移、轴对称、中心对称知识点总结轴对称平移旋转中心对称全等定义一个(两个)平面图形沿某条直线对折能够完全重合平面图形在它所在平面上的平行移动。
决定要素:平移的方向、平移的距离一个平面图形绕一定点按一定的方向旋转一定的角度的运动。
一个图形旋转180°能与自身重合能够完全重合的两个图形表示方法:ΔABC≌△DEF 轴对称图形成轴对称中心对称图形成中心对称全等多边形全等三角形对应边对应角一个图形;不止一条对称轴两个图形;只有一条对称轴旋转对称图形:一个图形绕内部某一点旋转一定的角度能与自身重合。
一个图形两个图形图形特征对应角相等,对应边相等①对应点间的连线平行且相等(或在同一条直线上)②对应边平行且相等(或在同一条直线上),对应角相等,图形的形状和大小不改变。
①图形上每一点都绕同一点按相同的方向和角度旋转②对应点到旋转中心的距离相等③对应边相等,对应角相等,图形的性状大小不改变连结对应点的线段必然经过对称中心,并被对称中心平分成相等的两部分。
对应边相等,对应角相等判断方法沿着某条直线对折看是否重合。
找平移的方向和距离:找一组对应点,连线即是他平移的方向和距离找旋转的方向和角度:找一组对应点,与旋转中心连线的夹角①旋转180°能否与自身重合②对应点间的连线是否经过同一点,并被这一点平分各边对应相等各角对应相等找对称轴:①找一组对应点连线,做其垂直平分线。
②找两组对应点连线,过两条中点的直线找对称中心:①找一组对应点连线找其中点②两组对应点连线的交点画法①找关键点②过每个关键点做对称轴的垂线截取与之相等的距离,标出对应点③连接对应点。
①找关键点②过每个关键点做平移方向的平行线截取与之相等的距离,标出对应点③连接对应点。
①找关键点②连接关键点与旋转中心,将这条线段按方向和角度旋转,标出对应点③连接对应点。
①找关键点②连接关键点与对称中心,延长并截取相等的长度,标出对应点③连接对应点。
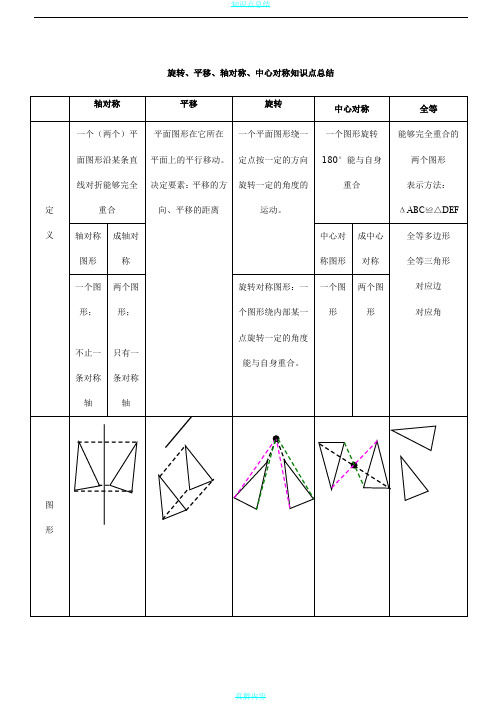
旋转、平移、轴对称、中心对称知识点总结对应点间的连线平行且相等(或在同一条直线上)对应边平行且相等(或在同一条直线上),对应角相等,图形的形状和大小不改变。
图形上每一点都绕同一点按相同的方向和角度旋转对应点到旋转中心的距离相等对应边相等,对应角相等,图形的性状大小不改变旋转180°能否与自身重合对应点间的连线是否经过同一点,并被这一点平分找对称轴:找一组对应点连线,做其垂直平分线。
找两组对应点连线,过两条中点的直线找对称中心:找一组对应点连线找其中点两组对应点连线的交点找关键点过每个关键点做对称轴的垂线截取与之相等的距离,标出对应找关键点过每个关键点做平移方向的平行线截取与之相等的距离,标出对应点找关键点连接关键点与旋转中心,将这条线段按方向和角度旋转,标出对应点找关键点连接关键点与对称中心,延长并截取相等的长度,标出对应点点连接对应点。
连接对应点。
连接对应点。
连接对应点。
线段是轴对称图形,对称轴是它的垂直平分线。
角是轴对称图形,对称轴是它的角平分线。
垂直平分线的性质:垂直平分线上任意一点到线段两端的距离相等。
④角平分线的性质:角平分线上任意一点到叫两边的距离相等。
⑤对称轴垂直平分对称点间的连线。
多次平移相当于一次平移两条对称轴平行时,两次轴对称相当于一次平移线段旋转90°后与原来的位置垂直两条对称轴相交时,两次轴对称相当于一次旋转。
中心对称一定是旋转对称,旋转对称不一定是中心对称。
任何通过中心对称图形的对称中心的直线都将这个图形分成面积相等的两部分。
两条对称轴互相垂直时,两次轴对称相当于一次中心对称一个图形经过轴对称、平移或选转等变换得到的新图形一定与原图形全等两个全等的图形总能经过轴对称、平移或旋转等变换后重合。

平移旋转轴对称的总结归纳平移、旋转、轴对称是几何学中常见的变换操作,它们在图形的变换中起着重要的作用。
本文将对平移、旋转和轴对称进行总结归纳,以便加深对这些概念的理解。
一、平移平移是指沿着固定的方向和距离,将一个点或者图形在平面内移动。
平移不改变图形的大小、形状和方向,只是改变了图形的位置。
1. 平移的特点- 平移是一种向量运算,其运算结果仍然是一个向量。
- 平移过程中,所有点的位移矢量都相等。
- 平移可以用向量表示,平移向量的起点为原图形上的一个点,终点为其平移后的位置。
2. 平移的表示方法平移可以使用向量运算的方式进行表示,如设平移向量为AB,其中A为原图形上的一个点,B为其平移后的位置。
3. 平移的性质平移具有以下性质:- 平移不改变图形的大小、形状和方向。
- 平移保持图形之间的相对位置关系不变。
二、旋转旋转是指将一个点或者图形按照一定的角度围绕某一点旋转。
旋转可以改变图形的方向,但保持其大小和形状不变。
1. 旋转的特点- 旋转是一种变换运算,将一个点或者图形按照一定的角度绕固定点旋转。
- 旋转可以用角度来描述,旋转角度可以是正数或负数,正数表示逆时针旋转,负数表示顺时针旋转。
- 旋转中心可以是任意点,也可以是图形的某个顶点。
2. 旋转的表示方法旋转可以使用坐标变换的方式进行表示,如设旋转中心为O,旋转角度为θ,则旋转过程中,点P(x, y)绕点O旋转后的新坐标为P'(x', y')。
3. 旋转的性质旋转具有以下性质:- 旋转不改变图形的大小和形状。
- 旋转改变图形的方向。
- 旋转保持图形上的点与中心点之间的距离不变。
三、轴对称轴对称是指图形相对于某条直线对称。
对称轴可以是任意直线,轴对称的图形可以通过对称轴翻转得到自身。
1. 轴对称的特点- 轴对称是一种空间变换,将图形相对于某条直线进行翻转。
- 轴对称的图形具有镜像对称性,即沿对称轴折叠后,两侧图形完全一致。
2. 轴对称的表示方法轴对称可以使用对称关系进行表示,如设对称轴为l,点P关于l的对称点为P',则P'与P关于l对称。

旋转、平移、轴对称、中心对称知识点总结轴对称平移旋转中心对称全等定义一个(两个)平面图形沿某条直线对折能够完全重合平面图形在它所在平面上的平行移动。
决定要素:平移的方向、平移的距离一个平面图形绕一定点按一定的方向旋转一定的角度的运动。
一个图形旋转180°能与自身重合能够完全重合的两个图形表示方法:ΔABC≌△DEF 轴对称图形成轴对称中心对称图形成中心对称全等多边形全等三角形对应边对应角一个图形;不止一条对称轴两个图形;只有一条对称轴旋转对称图形:一个图形绕内部某一点旋转一定的角度能与自身重合。
一个图形两个图形图形特征对应角相等,对应边相等✍对应点间的连线平行且相等(或在同一条直线上)✍对应边平行且相等(或在同一条直线上),对应角相等,图形的形状和大小不改变。
✍图形上每一点都绕同一点按相同的方向和角度旋转✍对应点到旋转中心的距离相等✍对应边相等,对应角相等,图形的性状大小不改变连结对应点的线段必然经过对称中心,并被对称中心平分成相等的两部分。
对应边相等,对应角相等判断方法沿着某条直线对折看是否重合。
找平移的方向和距离:找一组对应点,连线即是他平移的方向和距离找旋转的方向和角度:找一组对应点,与旋转中心连线的夹角✍旋转180°能否与自身重合✍对应点间的连线是否经过同一点,并被这一点平分各边对应相等各角对应相等找对称轴:✍找一组对应点连线,做其垂直平分线。
✍找两组对应点连线,过两条中点的直线找对称中心:✍找一组对应点连线找其中点✍两组对应点连线的交点画法✍找关键点✍过每个关键点做对称轴的垂线截取与之相等的距离,标出对应点✍连接对应点。
✍找关键点✍过每个关键点做平移方向的平行线截取与之相等的距离,标出对应点✍连接对应点。
✍找关键点✍连接关键点与旋转中心,将这条线段按方向和角度旋转,标出对应点✍连接对应点。
✍找关键点✍连接关键点与对称中心,延长并截取相等的长度,标出对应点✍连接对应点。
旋转、平移、轴对称、中心对称知识点总结对应点间的连线平行且相等(或在同一条直线上)对应边平行且相等(或在同一条直线上),对应角相等,图形的形状和大小不改变。
图形上每一点都绕同一点按相同的方向和角度旋转对应点到旋转中心的距离相等对应边相等,对应角相等,图形的性状大小不改变旋转180°能否与自身重合对应点间的连线是否经过同一点,并被这一点平分找对称轴:找一组对应点连线,做其垂直平分线。
找两组对应点连线,过两条中点的直线找对称中心:找一组对应点连线找其中点两组对应点连线的交点找关键点过每个关键点做对称轴的垂线截取与之相等的距离,标出对应找关键点过每个关键点做平移方向的平行线截取与之相等的距离,标出对应点找关键点连接关键点与旋转中心,将这条线段按方向和角度旋转,标出对应点找关键点连接关键点与对称中心,延长并截取相等的长度,标出对应点点连接对应点。
连接对应点。
连接对应点。
连接对应点。
线段是轴对称图形,对称轴是它的垂直平分线。
角是轴对称图形,对称轴是它的角平分线。
垂直平分线的性质:垂直平分线上任意一点到线段两端的距离相等。
④角平分线的性质:角平分线上任意一点到叫两边的距离相等。
⑤对称轴垂直平分对称点间的连线。
多次平移相当于一次平移两条对称轴平行时,两次轴对称相当于一次平移线段旋转90°后与原来的位置垂直两条对称轴相交时,两次轴对称相当于一次旋转。
中心对称一定是旋转对称,旋转对称不一定是中心对称。
任何通过中心对称图形的对称中心的直线都将这个图形分成面积相等的两部分。
两条对称轴互相垂直时,两次轴对称相当于一次中心对称一个图形经过轴对称、平移或选转等变换得到的新图形一定与原图形全等两个全等的图形总能经过轴对称、平移或旋转等变换后重合。
第26讲图形的平移、对称、旋转与位似1.(2017成都中考)下列图标中,既是轴对称图形,又是中心对称图形的是(D)2.(2017郴州中考)下列图形既是轴对称图形又是中心对称图形的是(B)3.(2017内江中考)下列图形:平行四边形、矩形、菱形、圆、等腰三角形,这些图形中只是轴对称图形的有(A)A.1个B.2个C.3个D.4个4.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是(B)5.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为(A) A.2 B.3 C.4 D.56.(2017宜宾中考)如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为(A)A.10 B.2 2C.3 D.2 57.(2017临沂中考)如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是(D)A.0 B.1 C.2 D.38.如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是(A)A.7 B.2 2 C.3 D.2 39.如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,S△PB1C=3,则BB1=__1__.10.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3),B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.(1)画出△A 1B 1C ,直接写出点A 1,B 1的坐标; (2)求在旋转过程中,△ABC 所扫过的面积. 解:(1)所求作△A 1B 1C 如图所示:由A(4,3),B(4,1)可建立如图所示坐标系,则点A 1的坐标为(-1,4),点B 1的坐标为(1,4);(2)∵AC =AB 2+BC 2=22+32=13,∠ACA 1=90°,∴在旋转过程中,△ABC 所扫过的面积为:S 扇形CAA 1+S △ABC =90π·(13)2360+12×3×2=13π4+3.11.如图,在平面直角坐标系中,直角△ABC 的三个顶点分别是A(-3,1),B(0,3),C(0,1).(1)将△ABC 以点C 为旋转中心旋转180°,画出旋转后对应的△A 1B 1C 1; (2)分别连接AB 1,BA 1后,求四边形AB 1A 1B 的面积. 解:(1)如图,△A 1B 1C 1为所求作图形;(2)S 四边形AB 1A 1B =12×6×4=12.12.如图,在平面直角坐标系中,△ABC 的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.(1)画出△ABC 关于x 轴的对称图形△A 1B 1C 1;(2)将△A 1B 1C 1沿x 轴方向向左平移3个单位长度后得到△A 2B 2C 2,写出顶点A 2,B 2,C 2的坐标.解:(1)如图所示,△A 1B 1C 1即为所求;(2)如图所示,△A 2B 2C 2即为所求,A 2(-3,-1),B 2(0,-2),C 2(-2,-4).13.如图,在平面直角坐标系中,O 是坐标原点,点A ,B 的坐标分别为A(0,4)和B(-2,0),连接AB.(1)现将△AOB 绕点A 按逆时针方向旋转90°得到△AO 1B 1,请画出△AO 1B 1,并直接写出点B 1,O 1的坐标;(注:不要求证明)(2)求经过B ,A ,O 1三点的抛物线对应的函数关系式,并画出抛物线的略图.解:(1)如图,△AO 1B 1即为所求;B 1(4,2),O 1(4,4); (2)设所求抛物线对应的函数关系式为y =ax 2+bx +c , ∵抛物线经过点A(0,4),B(-2,0),O(4,4),∴⎩⎨⎧c =4,4a -2b +c =0,16a +4b +c =4,解得⎩⎨⎧a =-13,b =43,c =4,∴所求抛物线对应的函数关系式为y =-13x 2+43x+4.所画抛物线图象如图所示.14.在如图所示的直角坐标系中,解答下列问题:(1)分别写出A ,B 两点的坐标;(2)将△ABC 绕点A 顺时针旋转90°,画出旋转后的△AB 1C 1;(3)求出线段B 1A 所在直线l 的函数解析式,并写出在直线l 上从B 1到A 的自变量x 的取值范围.解:(1)A(2,0),B(-1,-4);(2)如图;(3)设线段B 1A 所在直线 l 的解析式为:y =kx +b(k ≠0),∵B 1(-2,3),A(2,0),∴⎩⎨⎧-2k +b =3,2k +b =0,解得⎩⎨⎧k =-34,b =32.∴线段B 1A 所在直线 l 的解析式为:y =-34x +32,线段B 1A 的自变量 x 的取值范围是:-2≤x ≤2.。
2018年云南中考《第26讲图形的平移、对称、旋转》知识梳理
第26讲图形的平移、对称、旋转与位似
1.(2017成都中考)下列图标中,既是轴对称图形,又是中心对称图形的是(D)
2.(2017郴州中考)下列图形既是轴对称图形又是中心对称图形的是(B)
3.(2017内江中考)下列图形:平行四边形、矩形、菱形、圆、等腰三角形,这些图形
中只是轴对称图形的有(A)
A.1个B.2个C.3个D.4个
4.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是(B)
5.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为(A)
A.2B.3C.4D.5
6.(2017宜宾中考)如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点
A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为(A)
A.10B.22
C.3D.25
7.(2017临沂中考)如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接
AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是(D)
A.0B.1C.2D.3
8.如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是(A)
A.7B.22C.3D.23
9.如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,S△PB1C=3,则BB1=__1__.
10.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3),B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A 1B 1C ,直接写出点A 1,B 1的坐标;
(2)求在旋转过程中,△ABC 所扫过的面积.
解:(1)所求作△A 1B 1C 如图所示:
由A(4,3),B(4,1)可建立如图所示坐标系,则点A 1的坐标为(-1,4),点B 1的坐标为(1,4);
(2)∵AC =AB 2+BC 2=22+32=13,∠ACA 1=90°,
∴在旋转过程中,△ABC 所扫过的面积为:S 扇形CAA 1+S △ABC =90π·(13)2360
+12×3×2
=13π4
+3.11.如图,在平面直角坐标系中,直角△ABC 的三个顶点分别是A(-3,1),B(0,3),C(0,1).
(1)将△ABC 以点C 为旋转中心旋转180°,画出旋转后对应的△A 1B 1C 1;
(2)分别连接AB 1,BA 1后,求四边形AB 1A 1B 的面积.
解:(1)如图,△A 1B 1C 1为所求作图形;
(2)S 四边形AB 1A 1B =12
×6×4=12.12.如图,在平面直角坐标系中,△ABC 的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位长度后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求,A2(-3,-1),B2(0,-2),C2(-2,-4).
13.如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别为A(0,4)和B(-2,0),连接AB.
(1)现将△AOB绕点A按逆时针方向旋转90°得到△AO1B1,请画出△AO1B1,并直接写出点B1,O1的坐标;(注:不要求证明)
(2)求经过B,A,O1三点的抛物线对应的函数关系式,并画出抛物线的略图.
解:(1)如图,△AO1B1即为所求;B1(4,2),O1(4,4);
(2)设所求抛物线对应的函数关系式为y=ax2+bx+c,∵抛物线经过点A(0,4),B(-2,0),O(4,4),
=4,
-2b+c=0,
+4b+c=4,
=-1
3,
=4
3,
=4,
∴所求抛物线对应的函数关系式为y=-
1
3
x2+4
3
x+4.
所画抛物线图象如图所示.
14.在如图所示的直角坐标系中,解答下列问题:
(1)分别写出A ,B 两点的坐标;
(2)将△ABC 绕点A 顺时针旋转90°,画出旋转后的△AB 1C 1;
(3)求出线段B 1A 所在直线l 的函数解析式,并写出在直线l 上从B 1到A 的自变量x 的取值范围.
解:(1)A(2,0),B(-1,-4);
(2)如图;
(3)设线段B 1A 所在直线l 的解析式为:y =kx +b(k ≠0),∵B 1(-2,3),A(2,0),
2k +b =3,
+b =0,
=-34,=32.∴线段B 1A 所在直线l 的解析式为:y =-34x +32
,线段B 1A 的自变量x 的取值范围是:-2≤x ≤2.。