经典物理学实验--卡文迪许扭秤实验
- 格式:pdf
- 大小:174.85 KB
- 文档页数:4

库仑扭秤实验和卡文迪许扭秤实验原理和注意事项库仑扭秤实验和卡文迪许扭秤实验,这两个名字听起来就很高级,好像是什么科学家发明的高科技仪器。
其实,它们就是两个简单的实验,用来测量物体之间的相互作用力。
今天,我们就来聊聊这两个实验的原理和注意事项,让你也能轻松掌握这个知识点。
我们来说说库仑扭秤实验。
这个实验的名字听起来有点像是个大家伙,其实它就是一个小小的装置。
它的原理很简单,就是通过测量两个小球之间的相互作用力来计算出它们的质量。
听起来好像很难懂,其实很简单。
比如说,你有两个小球,一个重一点,一个轻一点。
当你把这两个小球放在一起时,它们会互相吸引。
这时候,你就可以用库仑扭秤实验来测量它们之间的相互作用力。
只要知道了相互作用力的大小,就可以根据万有引力定律算出它们的质量了。
接下来,我们来说说卡文迪许扭秤实验。
这个实验的名字也很高级,但是它的原理比库仑扭秤实验简单多了。
卡文迪许扭秤实验的原理是利用杠杆原理来测量物体之间的相互作用力。
具体来说,就是通过测量物体在不同方向上的扭转程度来计算出它们之间的相互作用力。
听起来好像很难懂,其实也很简单。
比如说,你有一个很重的物体和一个很轻的物体。
当你把这两个物体放在一条绳子的两端时,让它们沿着这条绳子滑动。
这时候,你就可以用卡文迪许扭秤实验来测量它们之间的相互作用力了。
只要知道了相互作用力的大小和方向,就可以根据牛顿第二定律算出它们的加速度了。
好了,现在我们已经知道了库仑扭秤实验和卡文迪许扭秤实验的原理,下面我们来说说它们的注意事项。
要注意安全。
这两个实验都是用重力和摩擦力来产生作用力的,所以一定要小心操作,避免受伤。
要注意精度。
这两个实验都需要非常精确地测量物体之间的相互作用力,所以要保证测量工具的质量和精度。
要注意环境条件。
这两个实验都受到环境因素的影响,比如温度、湿度等,所以要在合适的环境下进行实验。
库仑扭秤实验和卡文迪许扭秤实验虽然看起来很高级,但是原理和注意事项都很简单易懂。

卡文迪许扭秤实验原理
卡文迪许扭秤是一种用来测量物体的扭转力的仪器,常用于物理学、材料科学等领域的研究。
其工作原理基于胡克定律,即扭转力与扭转角度成正比。
卡文迪许扭秤由一根圆柱形的金属杆和两个固定的转轴组成。
当一个物体被夹在两个转轴之间时,它会受到扭转力,并沿着轴线发生扭转。
仪器的扭转力与物体受到的扭转角度成正比。
这个比例常称为扭曲系数,用G表示。
如果物体的长度为L,直径为D,且扭曲系数为G,那么在一个角度为θ的扭转力下,它所受到的扭转力可以由以下公式计算得出:
T = (G ×θ× L × D^4) / (32)
其中,T表示扭转力,G表示扭曲系数,θ表示扭转角度,L表示物体的长度,D表示物体的直径。
卡文迪许扭秤可以用来测量物体的刚度和弹性模量等物理性质。
在实验中,先将物体夹在两个转轴之间,然后通过旋转一个转轴来施加扭转力。
通过测量扭转角度和扭转力,可以计算出物体的扭曲系数,从而得出物体的刚度和弹性模量等物理性质。
总之,卡文迪许扭秤是一种常用的测量物体扭转力的仪器,其工作原理基于胡克定律,通过测量扭转角度和扭转力可以计算出物体的扭曲系数,从而得出物理性质。
- 1 -。

经典物理学实验——库仑扭秤实验在物理学发展的前期,人们对微弱作用的测量感到困难,因为这些微弱的作用人们通常都感觉不到。
后来,物理学家们想到了悬丝,要把一根丝拉断需要较大的力,而要使一根悬丝扭转,有一个很小的力就可以做到了。
根据这个设想,法国物理学家库仑和英国的科学家卡文迪许于1785年和1789年分别独立地发定角度的扭转;另一方面在悬丝上固定一平面镜,它可以把入射光线反射到距离平面镜较远的刻度尺上,从反射光线射到刻度尺上的光点的移动,就可以把悬丝的微小扭转显现出来。
一、库仑与库仑定律查利·奥古斯丁·库仑(1736 --1806),法国工程师、物理学家。
1736年6月14日生于法国昂古莱姆。
1806年8月23日在巴黎逝世。
主要贡献有扭秤实验、库仑定律、库伦土压力理论等。
同时也被称为“土力学之始祖”。
电荷的单位库仑就是以他的姓氏命名的,简称库,符号C。
若导线中载有1安培的稳定电流,则在1秒内通过导线横截面积的电量为1库仑。
库仑曾就学于巴黎马扎兰学院和法兰西学院,服过兵役。
1774年当选为法国科学院院士。
1784年任供水委员会监督官,后任地图委员会监督官。
1802年,拿破仑任命他为教育委员会委员,1805年升任教育监督主任。
1773年发表有关材料强度的论文,所提出的计算物体上应力和应变分布情况的方法沿用至今(2018),是结构工程的理论基础。
1777年开始研究静电和磁力问题。
当时法国科学院悬赏征求改良航海指南针中的磁针问题。
库仑认为磁针支架在轴上,必然会带来摩擦,提出用细头发丝或丝线悬挂磁针。
研究中发现线扭转时的扭力和针转过的角度成比例关系,从而可利用这种装置测出静电力和磁力的大小,这导致他发明扭秤。
他还根据丝线或金属细丝扭转时扭力和指针转过的角度成正比,因而确立了弹性扭转定律。
他根据1779年对摩擦力进行分析,提出有关润滑剂的科学理论,于1781年发现了摩擦力与压力的关系,表述出摩擦定律、滚动定律和滑动定律。
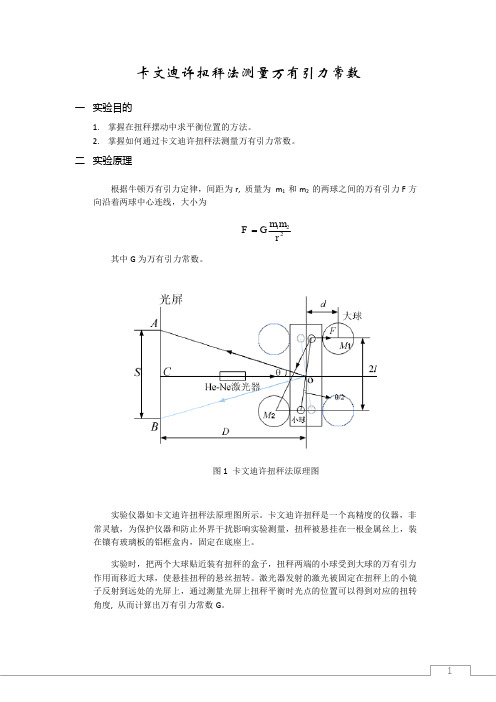
卡文迪许扭秤法测量万有引力常数一 实验目的1. 掌握在扭秤摆动中求平衡位置的方法。
2. 掌握如何通过卡文迪许扭秤法测量万有引力常数。
二 实验原理根据牛顿万有引力定律,间距为r, 质量为 m 1 和m 2 的两球之间的万有引力F 方向沿着两球中心连线,大小为221rm m GF 其中G 为万有引力常数。
图1 卡文迪许扭秤法原理图实验仪器如卡文迪许扭秤法原理图所示。
卡文迪许扭秤是一个高精度的仪器,非常灵敏,为保护仪器和防止外界干扰影响实验测量,扭秤被悬挂在一根金属丝上,装在镶有玻璃板的铝框盒内,固定在底座上。
实验时,把两个大球贴近装有扭秤的盒子,扭秤两端的小球受到大球的万有引力作用而移近大球,使悬挂扭秤的悬丝扭转。
激光器发射的激光被固定在扭秤上的小镜子反射到远处的光屏上,通过测量光屏上扭秤平衡时光点的位置可以得到对应的扭转角度, 从而计算出万有引力常数G 。
假设开始时扭秤扭转角度00=θ,把大球移动贴近盒子放置,大小球之间的万有引力为F ,小球受到力偶矩N =2 Fl 而扭转,悬挂扭秤的金属丝因扭转产生与力偶矩N 相平衡的反向转矩N ’= K(θ/2),扭秤最终平衡在扭角θ的位置:2/F GMm d =2(/2)Fl K θ=l dGMm K 24=θ 其中 K 是金属悬丝的扭转常数,M 是大球的质量,m 是小球的质量,d 是大球小球的中心的连线距离,l 是小球中心到扭秤中心的距离。
由转动方程可求得悬丝的扭转常数:通过转动惯量I 和测量扭秤扭转周期T 就可以得到金属丝的扭转系数K224TI K π= 假设小球相对大球是足够轻,那么转动惯量22ml I = 因此扭转角ld GMT 2222πθ= 当大球转动到相反的对称位置后,新平衡位置是θ-,因此平衡时的总扭转角为ld GMT 2222πθ= 通过反射光点在光屏上的位移S 可以得到悬丝扭转角度。
由于万有引力作用很弱,使得扭秤平衡时扭转角很小,此时可以认为:DS =θ2 其中D 是光屏到扭秤的距离。

引力常量的测定——卡文迪许扭秤实验牛顿认为公式中的引力常数G是普适常数,不受物体的形状、大小、地点和温度等因素影响,引力常数的准确测定对验证万有引力定律将提供直接的证据。
英国物理学家卡文迪许(H.Cavendish 1731-1810)根据牛顿提出的直接测量两个物体间的引力的想法,采用扭秤法第一个准确地测定了引力常数。
卡文迪许实验所用的扭秤是英国皇家学会的米歇尔神父制作的。
米歇尔制作扭秤的目的是为了测定地球的密度,并与卡文迪许讨论过这一问题。
但是,米歇尔还未用它来进行测定,便去世了。
米歇尔去世后,这架仪器几经辗转传到了剑桥大学杰可逊讲座教授沃莱斯顿神父手里,他又慷慨地赠送给了卡文迪许,这时卡文迪许已是年近古稀的老人了。
卡文迪许首先根据自己实验的需要对米歇尔制作的扭秤进行的分析,他认为有些部件没有达到他所希望的方便程度,为此,卡文迪许重新制作了绝大部分部件,并对原装置进行了一些改动。
卡文迪许认为大铅球对小铅球的引力是极其微小的,任何一个极小的干扰力就会是实验失败。
他发现最难以防止的干扰力来自冷热变化和空气的流动,为了排除误差来源,卡文迪许把整个仪器安置在一个关闭房间里,通过望远镜从室外观察扭秤臂杆的移动。
扭秤的主要部分是一个轻而坚固的T形架,倒挂在一根金属丝的下端。
T形架水平部分的的两端各装一个质量是m的小球,T形架的竖直部分装一面小平面镜M,它能把射来的光线反射到刻度尺上,这样就能比较精确地测量金属丝地扭转。
实验时,把两个质量都是m'地大球放在如图所示的位置,它们跟小球的距离相等。
由于m受到m'的吸引,T形架受到力矩作用而转动,使金属丝发生扭转,产生相反的扭转力矩,阻碍T形架转动。
当这两个力矩平衡时,T形架停下来不动。
这时金属丝扭转的角度可以从小镜M反射的光点在刻度尺上移动的距离求出,再根据金属丝的扭转力矩跟扭转角度的关系,就可以算出这时的扭转力矩,进而求得m与m'的引力F。

卡文迪许扭秤法测量万有引力常数班级核工程82学号 08182022姓名刘勇卡文迪许扭秤法测量万有引力常数一、实验目的1. 掌握在扭秤摆动中求平衡位置的方法。
2. 掌握如何通过卡文迪许扭秤法测量万有引力常数。
二、实验仪器卡文迪许扭秤,激光发射器, 光屏,米尺,秒表,电源三、实验原理根据牛顿万有引力定律,间距为r, 质量为 m1 和m2 的两球之间的万有引力F 方向沿着两球中心连线,大小为其中G 为万有引力常数。
实验仪器卡文迪许扭秤法原理图所示。
卡文迪许扭秤是一个高精度的仪器,非常灵敏,为保护仪器和防止外界干扰影响实验测量,扭秤被悬挂在一根金属丝上,装在镶有玻璃板的铝框盒内,固定在底座上。
实验时,把两个大球贴近装有扭秤的盒子,扭秤两端的小球受到大球的万有引力作用而移近大球,使悬挂扭秤的悬丝扭转。
激光器发射的激光被固定在扭秤rm m G F 221上的小镜子反射到远处的光屏上,通过测量光屏上扭秤平衡时光点的位置可以得到对应的扭转角度, 从而计算出万有引力常数 G 。
假设开始时扭秤扭转角度θ0=0,把大球移动贴近盒子放置,大小球之间的万有引力为F ,小球受到力偶矩N =2 Fl 而扭转,悬挂扭秤的金属丝因扭转产生与力偶矩N 相平衡的反向转矩N ’= K(θ/2),扭秤最终平衡在扭角θ的位置:F=G M m /d 22Fl= K(θ/2)其中 K 是金属悬丝的扭转常数,M 是大球的质量,m 是小球的质量,d 是大球小球的中心的连线距离,l 是小球中心到扭秤中心的距离。
由转动方程可求得悬丝的扭转常数:通过转动惯量I 和测量扭秤扭转周期T 就可以得到金属丝的扭转系数K :假设小球相对大球是足够轻,那么转动惯量lm I22=因此由上述几式得,扭转角ld222πT2GM θ=。
当大球转动到相反的对称位置后,新平衡位置是-θ, 因此平衡时的总扭转角为ld222πTGM 2θ=通过反射光点在光屏上的位移S 可以得到悬丝扭转角度。
卡文迪许扭秤实验原理
实验原理:
实验装置:
实验步骤:
1.将试样夹持在扭转秤上,使其能够自由扭转。
2.首先,给试样施加一个较小的扭转力矩,使其产生弹性扭转变形,此时记录变形角度和扭转力矩。
3.逐渐增加扭转力矩,重复步骤2,记录不同扭转力矩下的变形角度和扭转力矩。
4.根据变形角度和扭转力矩的变化关系,得出扭转角和扭转力矩的线性关系。
5.利用胡克定律的公式,根据扭转角度、试样尺寸和材料几何形状计算出材料的扭转模量。
工作原理:
其中,τ表示扭转力矩,G表示扭转模量,θ表示单位长度处的扭转角,L为试样长度,Φ为试样横截面的惯性矩。
实验中扭转力矩和扭转角都可以测量得到,通过测量得到的扭转角和扭转力矩,利用上述公式可以计算出材料的扭转模量。
此外,还可以通过变形角度和扭转力矩的线性关系计算出试样材料的切应力、切应变和极限剪应力等参数。
总结:
卡文迪许扭秤实验是一种测定材料扭转模量的常用方法,它通过施加扭转力矩使材料发生扭转变形,并根据变形角度和扭转力矩的关系计算出扭转模量。
这个实验具有简单、直观和准确的特点,被广泛应用于材料力学和工程实验中。
卡文迪许扭秤实验原理
实验中,金属丝一端固定,另一端连接一个可扭转的圆环或者片状物体,被试样。
当对被试样施加一个扭转力矩时,金属丝会扭转一定的角度。
实验测量的基本量是扭转角度和扭转力矩。
通过实验测量金属丝在不同扭转力矩下的扭转角度,可以得到其扭转
力矩与扭转角度之间的关系曲线。
常见的曲线为线性关系,即弹性区域,
斜率代表了材料的刚度。
而在超过一定扭转力矩之后,曲线会变得非线性,金属丝开始发生塑性变形。
该点称为屈服点,屈服点之后的区域称为塑性
区域。
T=Gθ/L
其中,T是扭转力矩,G是材料的剪切模量,θ是扭转角度,L是金
属丝的长度。
通过测量扭转角度和与之对应的扭转力矩,可以计算得到剪
切模量。
1.确保金属丝具有足够的长度,以便在实验中能够产生足够的变形。
2.确保金属丝在弹性区域内进行扭转,避免超过屈服点产生塑性变形。
3.使用精确的测量仪器来测量扭转角度和扭转力矩,以获得准确的结果。
4.进行多次实验来验证结果的可靠性,并计算平均值以减小误差。
库仑扭秤实验和卡文迪许扭秤实验原理和注意事项库仑扭秤实验和卡文迪许扭秤实验原理及注意事项嘿,朋友们!今天咱们来聊聊科学界的两大“重量级”实验——库仑扭秤实验和卡文迪许扭秤实验。
这两个实验可是物理学的瑰宝,不仅让我们对物质间的作用力有了更深刻的认识,还为我们揭示了万有引力的秘密呢!咱们说说那个大名鼎鼎的库仑扭秤实验。
想象一下,你手里有个大扭秤,两边各绑着一个带电的小球。
你轻轻一扭,小球就动起来了。
这可不是简单的物理现象哦,它告诉我们电荷之间也有“磁力”。
这个实验的原理就是电磁感应,简单来说就是磁场能影响电荷的运动。
不过,操作起来可得小心,一不小心就可能“电”到自己或者别人哦!再来说说卡文迪许扭秤实验。
想象一下,你站在一个巨大的天平上,两边各挂着一个质量差不多的砝码。
你轻轻一转,砝码就稳稳地平衡了。
这个实验告诉我们什么呢?它告诉我们地球对物体有引力,而且这个引力跟物体的质量成正比。
这可是牛顿爷爷的一大发现啊!不过,做这个实验的时候,你得特别细心,因为一不小心,砝码可能会掉下来砸到你头上哦!那么,这两个实验到底有什么不一样的地方呢?其实呀,它们都是通过测量物体之间的相互作用来探索引力的奥秘。
但是,卡文迪许扭秤实验更侧重于研究引力与质量的关系,而库仑扭秤实验则更注重研究电荷之间的相互作用。
在操作这些实验时,可得注意好多事。
比如,库仑扭秤实验中,你得确保两个小球都带电,这样才能产生足够的磁场。
而在卡文迪许扭秤实验里,你得保证砝码的质量足够大,这样地球的引力才能把它拉得稳稳当当。
还有啊,别忘了安全第一,别让自己或别人受伤哦!无论是库仑扭秤实验还是卡文迪许扭秤实验,都是我们探索世界、揭示自然规律的重要工具。
它们不仅让我们了解到了电荷和质量之间的关系,还让我们对宇宙有了更深的认识。
所以,下次当你看到这些实验时,不妨多了解一下它们的工作原理和注意事项,说不定还能发现一些有趣的知识点呢!。
经典物理学实验--卡文迪许扭秤实验
一、卡文迪许简介
卡文迪许(Henry Cavendish,1731 ~ 1810 年)
英国化学家、物理学家。
1731 年10 月10 日生于
法国尼斯。
1742—1748 年他在伦敦附近的海克纳
学校读书。
1749— 1753 年期间在剑桥彼得豪斯学
院求学。
在伦敦定居后,卡文迪许在他父亲的实验
室中当助手,做了大量的电学、化学研究工作。
他
的实验研究持续达50 年之久。
1760 年卡文迪许被
选为伦敦皇家学会成员,1803 年又被选为法国研
究院的18名外籍会员之一。
1810年3 月10 日,卡文迪许在伦敦逝世,终身未婚。
与伽利略和开普勒等科学家不同,卡文迪许非常富有,从不为自己的生存而担心。
伽利略玩笑的说:“他是一切有学问的人当中最富有的,一切富有的人当中最有学问的”。
与众多科学家一样,卡文迪许具有很多怪癖的性格。
据说卡文迪许很有素养,但是没有当时英国的那种绅士派头。
他不修边幅,几乎没有一件衣服是不掉扣子的;他不好交际,不善言谈,终生未婚,过着奇特的隐居生活。
卡文迪许为了搞科学研究,把客厅改作实验室,在卧室的床边放着许多观察仪器,以便随时观察天象。
他从祖上接受了大笔遗产,成为百万富翁。
不过他一点也不吝啬。
有一次,他的一个仆人因病生活发生困难,向他借钱,他毫不犹豫地开了一张一万英镑的支票,还问够不够用。
卡文迪许酷爱图书,他把自己收藏的大量图书,分门别类地编上号,管理得井井有序,无论是借阅,甚至是自己阅读,也都毫无例外地履行登记手续。
卡文迪许可算是一位活到老、干到老的学者,直到79 岁高龄、逝世前夜还在做实验。
卡文迪许一生获得过不少外号,有“科学怪人”,“科学巨擘”,“最富有的学者,最博学的富豪”等。
卡文迪许虽然爱好孤独的生活,但对于别人所作的研究工作却是很感兴趣,例如,他曾将一些钱送给青年科学家戴维作实验之用,有时还亲自跑到皇家学会去参加戴维的分解碱类的实验。
卡文迪许于1773 年底前就完成了一系列的静电实验,可是他没有发表那些重要的成果。
当时发表的两篇论文,只包括了一些
次要的部分。
100 年之后,剑桥大学物理学教授的麦克斯韦发现和整理了卡文迪许在1771 年至1781 年间的实验论文,才以《尊敬的卡文迪许的电学研究》为题于1879 年出版。
麦克斯韦指出“这些论文证明卡文迪许几乎预料到电学上所有的伟大事实,这些伟大事实后来通过库仑和法国哲学家们的著作而闻名于科学界”;卡文迪许还深入地研究了电容器的电容量。
他用“电时”表示相同电容器的球体的电容。
卡文迪许曾把49 个莱顿瓶组成电容器组,发现它含有321000“电时”的电容(约1/2 微法);他曾测了几种物质的电容率,例如,他得出石蜡的电容率为1.81 到2.47,而现在对石蜡的电容率为2.1;卡文迪许用实验揭示了静电荷分布在导体表面的性质,还用实验精确地验证了点电荷之间的静电力跟距离的平方成反比的规律,并确认至少不会与这个比率相差1/50 以上; 1781 年,他进行了相当于预测欧姆定律的探讨。
二、实验背景
我们生活在地球上,可是,你知道地球有多重吗?你知道如何去称量地球吗?对一般人来说,这可真是个难以回答的问题。
我们知道,要称量一个物体,我们需要用天平或者杆秤。
可是,地球那么重,到哪里才能找到这么大的一杆秤呢?就算找到了,我们又怎么能够把地球放到秤上去呢?第一个回答称量地球这个问题的人,是英国科学家卡文迪许。
牛顿虽然发现了万有引力定律,却没能给出准确的引力常量。
这是因为一般物体间的引力非常小,由于当时实验条件和技术的限制,很难用实验的方法将它显示出来,直到1798 年,即在牛顿发现万有引力定律,一百多年以后,英国物理学家卡文迪许(1731 —1810) 才巧妙地利用扭秤装置,第一次在实验室里比较准确地测出了引力常量。
三、实验装置及原理
这是一个卡文迪许扭秤的模型。
简单来讲:这个扭秤的主要部分是一个T字形轻而结实的框架,把这个T形架倒挂在一根石英丝下。
若在T形架的两端施加两个大小相等、方向相反的力,石英丝就会扭转一个角度。
力越大,扭转的角度也越大。
反过来,如果测出T形架转过的角度,也就可以测出T形架两端所受力的大小。
现在在T形架的两端各固定一个小球,再在每个小球的附近各放一个大球,大小两个球间的距离是可以较容易测定的。
根据万有引力定律,大球会对小球产生引力,T形架会随之扭转,只要测出其扭转的角度,就可以测出引力的大小。
由于引力很小,这个扭转的角度会很小。
为了把这个角度测出来,卡文迪许在T形架上装了一面小镜子,用一束光射向镜子,经镜子反射后的光射向远处的刻度尺,当镜子与T形架一起发生一个很小的转动时,刻度尺上的光斑会发生较大的移动。
这样,就起到一个化小为大的效果,通过测定光斑的移动,测定了T形架在放置大球前后扭转的角度,从而测定了此时大球对小球的引力。
卡文迪许用此扭秤验证了牛顿万有引力定律,并测定出引力常量G 的数值。
这个数值与近代用更加科学的方法测定的数值是非常接近的。
具体来说,卡文迪许扭秤装置的部分是一个轻而坚固的T型架,倒挂在一根石英丝的下端,T 型架水平部分的两端各装一个质量为m的小球,T型架的竖直部分装一面水平面镜M,能把光源射来的光线反射至圆弧形刻度尺上,从而比较准确地测出金属丝扭转的角度,用两个质量均为m′的大铅球接近两个小球m( 它们与所接近小球的距离
均为r),由于对称性,可以认为每个小球只受到所接近大铅球的万有引力F,从而使T型架受到一个扭转力矩:M
l
=F×L而转动,使金属丝发生扭转,产生反方向的
扭转力矩( k 为金属丝的扭转系数,事先可以测, M
l =M
2
时,T形架处于静止平
衡状态,则:FL= kθ,依据万有引力定律,测出容易测的量,即可求得G。
四、扭秤实验的原理两次放大及等效的思想
1、图中固定两个小球m的T型架,可以使m 、m′之间微小的万有引力产生较大的力矩,使石英丝产生一定角度的扭转,这是一次“放大”效应。
2、装置中发出的光线射到平面镜M时上,当平面镜偏转θ角时,反射光线偏转2θ角,光点在刻度尺上移动的弧长s=2θR ,因此增大小平面镜到刻度尺的距离R,光点在刻度尺上移动的弧长s就会相应增大,这样就可以使石英丝的扭转形变加以“放大”,这是二次“放大”效应。
3、要体会多次巧妙“放大”从而显示并测量微小量的精巧的设计思想和独特方法。
物理上观察实验效果的方法,还包括“转化”法、“对比法”等。
五、卡文迪许实验的意义
1、证明了万有引力的存在的普遍性正确性。
卡文迪许通过改变质量和距离,证实了万有引力的存在及万有引力定律的正确性。
2、测出了引力常量使得万有引力定律有了真正的实用价值,可测定远离地球的天体的质量、密度等。
引力常量的测出,使万有引力定律能够应用于定量计算,可以用测定地球表面物体重力加速度的方法,测定地球质量,也正因为如此,卡文迪许被人们称为第一个“能称出地球质量的人”。
3、卡文迪许扭秤实验巧妙地利用等效法合理地将微小量进行放大,实验的构思、设计与操作巧妙和精致,英国物理学家坡印廷曾对这个实验下过这样的评语:“开创了弱力测量的新时代。
”。