ansys分析结果评价

《ANSYS屈曲分析总结》很多现有的ANSYS资料都对特征值屈曲分析进行了较为详细的解释，特征值屈曲分析属于线性分析，它对结构临界失稳力的预测往往要高于结构实际的临界失稳力，因此在实际的工程结构分析时一般不用特征值屈曲分析。

但特征值屈曲分析作为非线性屈曲分析的初步评估作用是非常有用的。

1. 非线性屈曲分析的第一步最好进行特征值屈曲分析，特征值屈曲分析能够预测临界失稳力的大致所在，因此在做非线性屈曲分析时所加力的大小便有了依据。

特征值屈曲分析想必大家都熟练的不行了，所以小弟不再罗嗦。

小弟只说明一点，特征值屈曲分析所预测的结果我们只取最小的第一阶，所以你所得出的特征值临界失稳力的大小应为F＝实际施加力*第一价频率。

2. 由于非线性屈曲分析要求结构是不“完善”的，比如一个细长杆，一端固定，一端施加轴向压力。

若次细长杆在初始时没有发生轻微的侧向弯曲，或者侧向施加一微小力使其发生轻微的侧向挠动。

那么非线性屈曲分析是没有办法完成的，为了使结构变得不完善，你可以在侧向施加一微小力。

这里由于前面做了特征值屈曲分析，所以你可以取第一阶振型的变形结果，并作一下变形缩放，不使初始变形过于严重，这步可以在Main Menu> Preprocessor> Modeling> Update Geom中完成。

3. 上步完成后，加载计算所得的临界失稳力，打开大变形选项开关，采用弧长法计算，设置好子步数，计算。

4. 后处理，主要是看节点位移和节点反作用力（力矩）的变化关系，找出节点位移突变时反作用力的大小，然后进行必要的分析处理。

特载值分析得到的是第一类稳定问题的解，只能得到屈曲荷载和相应的失稳模态，它的优点就是分析简单，计算速度快。

事实上在实际工程中应用还是比较多的，比如分析大型结果的温度荷载，而且钢结构设计手册中的很多结果都是基于特征值分析的结果，例如钢梁稳定计算的稳定系数，框架柱的计算长度等。

它的缺点主要是：不能得到屈曲后路径，不能思忖初始缺陷如初始的变形和应力状态，不能思忖材料的非线性。

有限元法分析结果的误差影响2009年12月23日安世亚太一、引言有限元法分析起源于50年代初杆系结构矩阵的分析。

随后，Clough于1960年第一次提出了“有限元法”的概念。

其基本思想是利用结构离散化的概念，将连续介质体或复杂结构体划分成许多有限大小的子区域的集合体，每一个子区域称为单元（或元素），单元的集合称为网格，实际的连续介质体（或结构体）可以看成是这些单元在它们的节点上相互连接而组成的等效集合体；通过对每个单元力学特性的分析，再将各个单元的特性矩阵组集成可以建立整体结构的力学方程式，即力学计算模型；按照所选用计算程序的要求，输入所需的数据和信息，运用计算机进行求解。

当前，有限元方法/理论已经发展的相当成熟和完善，而计算机技术的不断革新，又在很大程度上推进了有限元法分析在工程技术领域的应用。

然而，如此快速地推广和应用使得人们很容易忽视一个前提，即有限元分析软件提供的计算结果是否可靠、满足使用精度的前提，是合理地使用软件和专业的工程分析。

只有这两者很好地结合，我们才能得到工程上切实可信的计算结果，否则只会在工程上造成极大的浪费，甚至带来严重的工程事故。

二、误差分析有限元法分析一般包括四个步骤：物理模型的简化、数学模型的程序化、计算模型的数值化和计算结果的分析。

每一个步骤在操作过程中都或多或少地引入了误差，这些误差的累积最终可能会对计算结果造成灾难性的影响，进而蒙蔽我们的认识和判断。

第一步，物理模型的简化，主要有几何实体、连接/装配关系、环境边界条件和材料特性的简化，进而构建数学模型。

这些简化或者说假设，是必要的，也是必须的，但是也由此在模型中引入了理想化误差（idealization error）。

有些理想化误差是非良性奇异的，比如几何实体简化时细节部位上忽略小的圆/倒角，连接/装配关系简化时忽略焊缝和螺栓连接等，往往导致模型发生结构方面（诸如L形截面的角点）的奇异，即结构奇异（奇异的数学定义是在某一点处导数无穷）；有些理想化误差是良性奇异的，比如边界条件简化时添加集中载荷和孤立点约束，导致模型发生边界条件的奇异，即边界奇异；其它理想化误差，比如几何实体简化时三维壳/面体简化为二维壳/面、三维梁简化为一维梁，边界条件简化时非均匀温度场和压力场简化为均匀温度场和压力场等，只会影响计算结果的准确度，不会引发计算结果方面的数值奇异，即应力奇异和位移奇异等。

ANSYS分析报告引言：1.问题描述：在这个分析中，我们将研究一个承重结构的稳定性。

该结构由一根钢杆和两个支撑点组成，其中一端支撑固定，另一端加有外部力。

我们的目标是确定结构在受力情况下的位移和应力分布，并评估结构的稳定性。

2.建模与加载条件：我们使用ANSYS软件对该结构进行三维建模，并为其设置了适当的边界条件和加载条件。

钢杆的材料参数和几何尺寸通过实验测定获得。

加载条件设为一端受到垂直向下的力，同时另一端固定。

我们采用静态结构分析模块进行分析。

3.结果与分析：经过ANSYS分析，我们获得了结构的位移和应力分布情况。

在受力情况下，钢杆的位移主要集中在受力一侧，而另一侧的位移较小。

应力分布也呈现相似的趋势，受力一侧的应力较大，而另一侧的应力较小。

这是由于外部力对结构的影响导致结构发生变形。

4.结构稳定性评估：在评估结构的稳定性时，我们对结构进行了稳定性分析。

通过计算结构的临界载荷，我们可以确定结构在受力情况下的稳定性。

根据计算结果，结构的临界载荷大于所施加的外部力，说明结构是稳定的，不会发生失稳现象。

5.敏感性分析：为了进一步评估结构的性能，我们进行了敏感性分析。

通过改变结构的材料参数和几何尺寸，我们得到了不同条件下结构的位移和应力分布。

根据敏感性分析结果，我们发现结构的位移和应力对材料的弹性模量和截面尺寸非常敏感。

较高的弹性模量和更大的截面尺寸会使结构更加稳定。

结论：通过ANSYS软件进行的分析，我们得到了结构在受力情况下的位移和应力分布，并评估了结构的稳定性。

我们发现外部力对结构的位移和应力分布有明显的影响，但结构仍然保持稳定。

此外，结构的性能对材料参数和几何尺寸非常敏感。

综合分析结果，我们可以优化结构设计，以提高结构的稳定性和性能。

以上是对ANSYS分析报告的一个简单写作示例，可以根据实际情况进行适当调整和修改。

试验分析目录试验分析 (1)1.试验荷载的取值 (2)1.1重力荷载（取29.8/g m s） (2)1.2施工荷载 (2)1.3水平风荷载的计算：（10年一遇大风时） (2)2.ANSYS建模分析结果 (5)2.1工况一：（1.0恒载，重力荷载） (6)2.1.1支座反力 (6)2.1.2位移变形图 (6)2.1.3X向位移云图 (7)2.1.4Z向位移云图 (7)2.1.5Y向弯矩图 (8)2.2工况二：施工荷载位于最高台阶处（1.0恒载+1.4工作荷载） (8)2.2.1支座反力 (9)2.2.2位移变形图 (9)2.2.3X向位移云图 (10)2.2.4Z向位移云图 (10)2.2.5Y向弯矩图 (11)2.3工况三：施工荷载位于最低台阶处（1.0恒载+1.4工作荷载） (11)2.3.1支座反力 (12)2.3.2位移变形图 (12)2.3.3X向位移云图 (13)2.3.4Z向位移云图 (13)2.3.5Y向弯矩图 (14)2.4工况四：1.0恒载+风荷载等效水平荷载设计值 (14)2.4.1支座反力 (15)2.4.2位移变形图 (15)2.4.3X向位移云图 (16)2.4.4Z向位移云图 (16)2.4.5Y向弯矩图 (17)2.5 与工况四加载位置相同的水平力下左侧约束压力为零时，对应的基本风压1w 的计算值： (17)1.试验荷载的取值1.1重力荷载（取29.8/g m s =）1.2施工荷载当施工荷载位于最高台阶处时，抗倾覆最不利。

此时，施工荷载所产生力矩对于倾覆转动点H 来说，是属于倾覆力矩（如施工荷载位于另外两个台阶，则其作用属于抗倾覆力矩）。

故以此为工作时验算工况。

假定施工荷载位于最高台阶时，共有作业人员4人，每人重75Kg ，每人持有30Kg 施工材料。

此时荷载设计值4(0.750.30) 1.4 5.88N Q F k =⨯+⨯=。

1.3水平风荷载的计算：（10年一遇大风时）图1 平台风荷载体型系数图2 风荷载计算简图1)平台所受风荷载标准值，按下式确定：0w w z s z k μμβ=式中：k w —风荷载标准值（2/m kN ）；z β—高度Z 处的风振系数，取1.0；s μ—风荷载体型系数，按图1平台风荷载体型系数取值；z μ—风压高度变化系数，按荷载规范（GB50009-2012），按离地面高度60m 取1.56；0w —基本风压（2N /k m ），取重现期10=n 对应的风压值，金华地区为20.25N /k m 。

ANSYS 实验分析报告1. 引言在工程设计和科学研究中，计算机仿真技术的应用越来越广泛。

ANSYS是一种常用的工程仿真软件，它可以帮助工程师和科学家分析和解决各种复杂的问题。

本文将介绍我对ANSYS进行实验分析的过程和结果。

2. 实验目标本次实验的主要目标是使用ANSYS软件对一个特定的工程问题进行仿真分析。

通过这个实验，我希望能够了解ANSYS的基本操作和功能，并在解决工程问题方面获得一定的经验。

3. 实验步骤步骤一：导入模型首先，我需要将要分析的模型导入到ANSYS软件中。

通过ANSYS提供的导入功能，我可以将CAD模型或者其他文件格式的模型导入到软件中进行后续操作。

步骤二：设置边界条件在进行仿真分析之前，我需要设置边界条件。

这些边界条件可以包括约束条件、初始条件和加载条件等。

通过设置边界条件，我可以模拟出真实工程问题中的各种情况。

步骤三：选择分析类型ANSYS提供了多种不同的分析类型，包括结构分析、流体力学分析、热传导分析等。

根据实际情况，我需要选择适合的分析类型来解决我的工程问题。

步骤四：运行仿真设置好边界条件和选择好分析类型后，我可以开始运行仿真了。

ANSYS会根据我所设置的条件，在计算机中进行仿真计算，并生成相应的结果。

步骤五：分析结果仿真计算完成后，我可以对生成的结果进行分析。

通过对结果的分析，我可以得出一些关键的工程参数，如应力分布、温度分布等。

这些参数可以帮助我评估设计的合理性和性能。

4. 实验结果在本次实验中，我成功地使用ANSYS对一个特定的工程问题进行了仿真分析。

通过分析结果，我得出了一些有价值的结论和数据。

这些数据对于进一步改进设计和解决工程问题非常有帮助。

5. 总结与展望通过本次实验，我对ANSYS软件的使用有了更深入的了解，并且积累了一定的实践经验。

在未来的工程设计和科学研究中，我将更加灵活地应用ANSYS软件，以解决更加复杂和挑战性的问题。

同时，我也会继续学习和探索其他相关的仿真软件和工具，以提高自己的技术水平。

ansys分析报告ANSYS分析报告ANSYS是一个广泛应用于工程领域的数值模拟软件，可以进行结构分析、流体分析、电磁场分析等多种模拟计算。

本文将对ANSYS分析报告进行700字的简要介绍。

ANSYS分析报告是针对特定问题进行计算和模拟分析后所得到的结果的总结和展示，通常包括以下几个部分：问题描述、模型建立、计算设置、结果分析和结论等。

首先，问题描述部分需要详细描述需要分析的问题的背景和目标，例如一个结构材料的强度分析，可以描述该材料的工作环境和所需的强度。

对问题的准确描述有助于确定分析的内容和方向。

其次，模型建立部分是将实际问题转化为计算模型的过程，包括几何建模、材料属性和加载条件等的设置。

在ANSYS中，可以通过绘制几何图形或导入CAD模型来创建计算模型，然后定义材料的性质和加载的边界条件。

接下来，计算设置部分是对分析过程中的各种数值计算参数进行设置和调整，例如网格密度、收敛准则等。

在ANSYS中，通过选择适当的求解器和控制参数，可以在保证计算精度的前提下尽可能提高计算效率。

然后，结果分析部分是对计算结果进行全面和详细的分析和解释。

ANSYS提供了丰富的结果输出和可视化工具，可以直观地展示计算结果，如应力云图、变形云图等。

通过对计算结果的分析，可以评估结构的安全性、性能和优化方案等。

最后，结论部分是对分析结果的总结和归纳，给出解决问题的建议或改进方案。

结论应该简明扼要地回答分析问题中所关心的核心问题，以便让读者迅速了解分析的结果和含义。

总之，ANSYS分析报告是基于ANSYS软件进行模拟计算和分析的结果总结和展示。

通过问题描述、模型建立、计算设置、结果分析和结论等环节的详细分析，可以准确评估分析目标的实现程度，为工程决策提供科学依据。

四大强度理论1、最大拉应力理论（第一强度理论）(材料脆性断裂的强度理论)：这一理论认为引起材料脆性断裂破坏的因素是最大拉应力，无论什么应力状态，只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb，材料就要发生脆性断裂。

于是危险点处于复杂应力状态的构件发生脆性断裂破坏的条件是：σ1=σb。

σb/s=[σ]所以按第一强度理论建立的强度条件为：σ1≤[σ]。

2、最大伸长线应变理论（第二强度理论）（材料塑性屈服的强度理论）：这一理论认为最大伸长线应变是引起断裂的主要因素，无论什么应力状态，只要最大伸长线应变ε1达到单向应力状态下的极限值εu，材料就要发生脆性断裂破坏。

εu=σb/E；ε1=σb/E。

由广义虎克定律得：ε1=[σ1-u(σ2+σ3)]/E所以σ1-u(σ2+σ3)=σb。

按第二强度理论建立的强度条件为：σ1-u(σ2+σ3)≤[σ]。

3、最大切应力理论（第三强度理论）：这一理论认为最大切应力是引起屈服的主要因素，无论什么应力状态，只要最大切应力τmax达到单向应力状态下的极限切应力τ0，材料就要发生屈服破坏。

τmax=τ0。

轴向拉伸斜截面上的应力公式可知τ0=σs/2（σs——横截面上的正应力）由公式得：τmax=τ1s=（σ1-σ3）/2。

所以破坏条件改写为σ1-σ3=σs。

按第三强度理论的强度条件为：σ1-σ3≤[σ]。

4、形状改变比能理论（第四强度理论）（最大歪形能理论）：这一理论认为形状改变比能是引起材料屈服破坏的主要因素，无论什么应力状态，只要构件内一点处的形状改变比能达到单向应力状态下的极限值，材料就要发生屈服破坏。

发生塑性破坏的条件为：所以按第四强度理论的强度条件为：sqrt(σ1^2+σ2^2+σ3^2-σ1σ2-σ2σ3-σ3σ1)<[σ]Von mise应力Von Mises 应力是基于剪切应变能的一种等效应力其值为(((a1-a2)^2+(a2-a3)^2+(a3-a1)^2)/2)^0.5 其中a1,a2,a3分别指第一、二、三主应力，^2表示平方，^0.5表示开方。

有限元与CAE分析报告专业：班级：学号：姓名：指导教师：2016年 1 月 2 日简支梁的静力分析一、问题提出长3m的工字型梁两端铰接中间1.5m位置处受到6KN的载荷作用，材料弹性模量E=200e9，泊松比0.28，密度7850kg/㎡二、建立模型1.定义单元类型依次单击Main Menu→Preprocessor→Elementtype→Add/Edit/Delete，出现对话框如图，单击“Add”，出现一个“Library of Element Type”对话框，在“Library of Element Type”左面的列表栏中选择“Structural Beam”，在右面的列表栏中选择3 node 189,单击“OK”。

2设置材料属性依次单击Main Menu→Preprocessor→MaterialProps>Material Modes，出现“Define Material ModelBehavior”对话框，在“Material Model Available”下面的对话框中，双击打开“Structural→Linear→Elastic→Isotropic”,出现对话框，输入弹性模量EX=2E+011,PRXY=0.28，单击“OK”。

依次单击Main Menu→Preprocessor→MaterialProps>Material Modes，出现“Define Material ModelBehavior”对话框，在“Material Model Available”下面的对话框中，双击打开“Structural→Density”弹出对话框，输入DENS为78503.创建几何模型1)设定梁的截面尺寸选择菜单Main Menu→preprocessor→Beam→Common Sections弹出Beam tool设置菜单，在Sub-Type截面形状选择工字钢，依次按下图输入W1，W2，W3，T1，T2，T3截面尺寸。

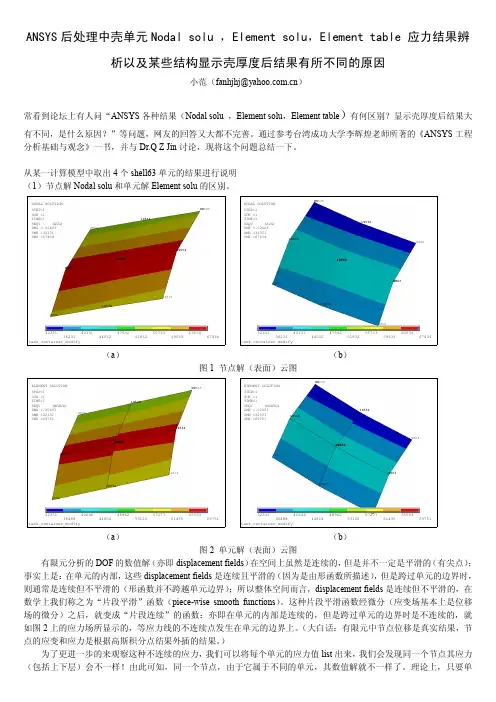
ANSYS 后处理中壳单元Nodal solu ，Element solu ，Element table 应力结果辨析以及某些结构显示壳厚度后结果有所不同的原因小范（fanhjhj@ ）常看到论坛上有人问“ANSYS 各种结果（Nodal solu ，Element solu ，Element table ）有何区别？显示壳厚度后结果大有不同，是什么原因？”等问题，网友的回答又大都不完善。

通过参考台湾成功大学李辉煌老师所著的《ANSYS 工程分析基础与观念》一书，并与Dr.Q Z Jin 讨论，现将这个问题总结一下。

从某一计算模型中取出4个shell63单元的结果进行说明 19535 195731955419536980419574195559803 9802MNMXtank_container_modify323313623140131440324793251832557335963363534SEQV (AVG)DMX =.00403SMN =32331SMX =6743419535 19573195549804195361957498029803 19555MNMXtank_container_modify3623140131440324793251832557335963363534NODAL SOLUTION SEQV (AVG)（a ） （b ）图1 节点解（表面）云图19535 19573195541953698041957419555 98039802MNMXtank_container_modify323313648840646448044896253120572776143565593ELEMENT SOLUTION SEQV (NOAVG)DMX =.00403SMN =32331SMX =6975119535 1957319554980419536195749802980319555 MNMXtank_container_modify323313648840646448044896253120572776143565593ELEMENT SOLUTION SEQV (NOAVG)（a ） （b ）图2 单元解（表面）云图有限元分析的DOF 的数值解（亦即displacement fields ）在空间上虽然是连续的，但是并不一定是平滑的（有尖点）；事实上是：在单元的内部，这些displacement fields 是连续且平滑的（因为是由形函数所描述），但是跨过单元的边界时，则通常是连续但不平滑的（形函数并不跨越单元边界）；所以整体空间而言，displacement fields 是连续但不平滑的，在数学上我们称之为“片段平滑”函数（piece-wise smooth functions ）。

ansys分析报告ANSYS分析报告。

一、引言。

本报告旨在对ANSYS进行全面的分析和评估，以便更好地了解其性能和应用范围。

ANSYS是一种广泛应用于工程领域的有限元分析软件，通过对其进行深入研究和分析，可以帮助工程师们更好地应用该软件进行工程设计和分析。

二、软件概述。

ANSYS是一种基于有限元分析理论的工程仿真软件，其功能涵盖了结构分析、流体动力学分析、热传导分析等多个领域。

通过ANSYS软件，工程师可以对各种工程结构和系统进行仿真分析，以评估其性能和稳定性。

三、功能特点。

1. 结构分析，ANSYS可以对各种结构进行静力学和动力学分析，包括线性和非线性分析，以及疲劳和断裂分析。

这使得工程师可以更加全面地评估结构的强度和稳定性。

2. 流体动力学分析，ANSYS可以模拟流体在复杂几何形状中的流动情况，包括湍流、层流等各种流动状态。

这对于设计液体管道、风力发电机等工程系统具有重要意义。

3. 热传导分析，ANSYS可以模拟材料的热传导性能，包括传热、热对流、热辐射等多种热传导方式。

这对于设计散热器、热交换器等热工系统至关重要。

四、应用案例。

1. 结构分析，使用ANSYS对一座桥梁进行有限元分析，评估其在不同荷载条件下的变形和应力分布，为桥梁设计提供重要参考。

2. 流体动力学分析，使用ANSYS对一台风力发电机进行气流仿真，评估其叶片在不同风速下的受力情况，为风力发电机的设计提供优化方案。

3. 热传导分析，使用ANSYS对一台电子设备进行热仿真，评估其在长时间工作状态下的散热效果，为电子设备的散热设计提供技术支持。

五、结论。

通过对ANSYS软件的分析和评估，我们可以得出结论，ANSYS具有强大的功能和广泛的应用范围，可以帮助工程师们进行结构、流体和热传导等多个领域的仿真分析。

在工程设计和优化过程中，ANSYS将发挥重要作用，为工程师们提供更多的技术支持和优化方案。

希望本报告对大家对ANSYS软件有更深入的了解和认识，并能够更好地应用于工程实践中。

ansys分析报告
ANSYS分析报告是通过使用ANSYS软件对工程问题进行模拟和分析后生成的文档。

该报告通常包括以下几个部分：
1. 问题描述：对分析目标和背景进行描述，包括需要解决的工程问题、分析的对象以及相关的边界条件和假设。

2. 模型建立：描述了建立模型的过程，包括对几何模型进行建模、材料属性定义、加载条件设置等。

3. 网格生成：描述了如何生成合适的有限元网格，确保模型的准确性和计算效率。

4. 边界条件和加载：详细描述了施加在模型上的约束和加载条件，以及相应的数值设置。

5. 计算设置：描述了计算过程中使用的求解器、网格控制策略、收敛准则和其他相关设置。

6. 结果分析：给出了模拟结果的定量和定性分析，包括应力分布、位移变化、温度变化等。

7. 结论和讨论：根据模拟结果对问题进行评价和总结，提出可能的改进和优化方案。

在ANSYS分析报告中，通常还会包括模型验证和验证结果的详细说明，以及对模型和方法的限制和局限性进行讨论。

此外，报告还可能包括图表、表格、图片和动画等可视化内容，以更好地展示分析结果和解释分析过程。

ansys 有限元分析结果与理论公式计算结果对比1、有限元是近似求解一般连续场问题的数值方法2、有限元法将连续的求解域离散为若干个子域,得到有限个单元,单元和单元之间用节点连接3、直梁在外力的作用下,横截面的内力有剪力和弯矩两个.解： （1）梁的最大弯矩m N m •=⨯==K 45.023.0102ql M 22ax（2抗弯截面模量 3333m m 1028.6324032d ⨯=⨯==ππz W（3）梁的最大弯曲应力Mpa 7.711028.61045.036m ax m a =⨯⨯==M W z x σ ANSYS 计算结果与分析一、 有限元原理:有限元的解题思路可简述为:从结构的位移出发,通过寻找位移和应变, 应变与应力,应力与内力,内力与外力的关系,建立相应的方程组,从而由已知的外力求出结构的内应力和位移。

有限元分析过程由其基本代数方程组成:[K] {V}={Q},[K]为整个结构的刚变矩阵,{V}为未知位移量,{Q}为载荷向量。

这些量是不确定的,依靠所需解决的问题进行定量描述。

上述结构方程是通过应用边界条件,将结构离散化成小单元,从综合平衡方程中获得。

有限元是通过单元划分, 在某种程度上模拟真实结构,并由数字对结构诸方面进行描述。

其描述的准确性依赖于单元细划的程度,载荷的真实性,材料力学参数的可信度,边界条件处理的正确程度。

本算例采用三角形六结点来划分单元。

二、 有限元解题步骤:有限元的解题步骤为: ①连续体的离散化;②选择单元位移函数;③建立单元刚度矩阵;④求解代数方程组,得到所有节点位移分量;⑤由节点位移求出内力或应力。

本例子中，梁的受力模型如图所示网格划分如图边界条件：根据受力情况，使用右手定则，判断横梁受弯曲m N m •=K 45.0M ax时施加在X 轴正方向。

计算结果及结果分析：如图示，最大弯曲应力值为71.849Mpa 。

通过与手动计算比较，准确率达99.8%以上。

ANSYS有限元分析报告1. 引言有限元分析（Finite Element Analysis, FEA）是一种常用的工程分析方法，可以用于预测材料和结构在各种工况下的行为和性能。

本报告旨在通过使用ANSYS软件进行有限元分析，对某一具体的工程问题进行模拟和分析，并得出相应的结论和建议。

2. 问题描述本次有限元分析的问题是研究某结构在受载情况下的应力分布和变形情况。

具体而言，我们关注的结构是一个柱形零件，其材料为XXX，尺寸为XXX。

该结构在受到垂直向下的均布载荷时，会发生弯曲变形和应力集中现象。

我们的目标是通过有限元方法对该结构进行分析，预测其应力分布情况，并评估其承载能力。

3. 模型建立我们使用ANSYS软件来建立和分析该结构的有限元模型。

首先，我们将导入该零件的几何数据，然后通过ANSYS的建模工具创建相应的有限元模型。

在建立模型的过程中，我们需要注意几何尺寸、材料特性、约束条件和加载方式等参数的设定，以确保模型的准确性和可靠性。

4. 材料属性和加载条件在进行有限元分析之前，我们需要确定材料的特性和加载条件。

根据提供的信息，我们将采用XXX材料的力学特性进行模拟。

同时，我们假设该结构受到均布载荷的作用，其大小为XXX。

这些参数将在后续的分析中使用。

5. 模型网格划分在进行有限元分析之前，我们需要对模型进行网格划分。

网格的密度和质量将直接影响分析结果的准确性和计算效率。

在本次分析中，我们将采用适当的网格划分策略，以满足准确性和计算效率的要求。

6. 模型分析和结果通过ANSYS软件进行有限元分析后，我们得到了该结构在受载情况下的应力分布和变形情况。

根据分析结果，我们可以观察到应力集中区域和变形程度，并根据材料的特性进行评估。

同时，我们可以通过对加载条件的变化进行分析，预测该结构的承载能力和安全系数。

7. 结论和建议根据有限元分析的结果，我们得出以下结论和建议：•该结构在受均布载荷作用下发生应力集中现象，需要对其进行加强和优化设计。

分析报告实例一和实例二建模过程遵从ansys的基本建模步骤：（1）建立有限元模型在ANSYS中建立有限元模型的过程大致可分为以下3个主要步骤：①建立或导入几何模型②定义材料属性③划分网格建立有限元模型（2）施加载荷并求解在ANSYS中施加载荷及求解的过程大致可以分为以下3个主要步骤：①定义约束②施加载荷③设置分析选项并求解（3）查看分析结果在ANSYS中查看分析结果的过程大致可以分为以下2个主要步骤：①查看分析结果②检验分析结果（验证结果是否正确）实例分析一：例一所要分析的问题是平面带孔平板在均布载荷作用下板内的应力情况分布。

实例类型为ANSYS结构分析，分析类型为线性静力分析。

通过在ansys中基本的实体建模操作，布尔运算和网格细化，施加均布载荷，到最后的求解，方可得到显示变形后形状和应力等值线图、单元信息列表等等结果。

下面查看分析结果，对于静力分析主要是模型位移及等效应力等值线图或者节点结果数据列表。

模型变形图如下所示：最大变形量图如下所示：等效应力等值线图如下所示：列表显示位移结果数据如下所示：列表显示节点应力值如下所示：实例分析二：例二所要分析的问题是大坝在约束和载荷作用下的应力，应变情况。

实例类型为ANSYS结构分析，分析类型为线性静力分析。

通过在ansys中基本的实体建模操作，网格划分，施加载荷，到最后的求解，方可得到显示变形后形状和应力等值线图等结果。

下面查看分析结果，对于静力分析主要是模型位移及等效应力等值线图或者节点结果数据列表。

模型变形图如下所示：最大变形量图如下所示：等效应力等值线图如下所示：列表显示位移结果数据如下所示：列表显示节点应力值如下所示：以下是两个结构的*.log文件：Plane：/BATCH/COM,ANSYS RELEASE 12.0.1UP20090415 17:04:30 03/24/2011 /CWD,'E:\Ansys.work\3-24-plane'/TITLE,plane/REPLOT!*/NOPR/PMETH,OFF,0KEYW,PR_SET,1KEYW,PR_STRUC,1KEYW,PR_FLUID,0KEYW,PR_MULTI,0/GO!*/COM,/COM,Preferences for GUI filteringhave been set to display:/COM, Structural!*/PREP7!*ET,1,PLANE82!*KEYOPT,1,3,3KEYOPT,1,5,0KEYOPT,1,6,0!*!*MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,EX,1,,2e5MPDATA,PRXY,1,,0.3!*R,1,20,!*SAVEFINISH/SOLFINISH/PREP7 BLC4,0,0,200,100CYL4,100,50,20 ASBA, 1, 2 SAVEAESIZE,ALL,20, TYPE, 1MAT, 1REAL, 1 ESYS, 0 SECNUM,!*MSHAPE,0,2DMSHKEY,0!*CM,_Y,AREAASEL, , , , 3 CM,_Y1,AREACHKMSH,'AREA' CMSEL,S,_Y!*AMESH,_Y1!*CMDELE,_YCMDELE,_Y1CMDELE,_Y2!*SAVEFINISH/SOL!*ANTYPE,0FLST,2,1,4,ORDE,1 FITEM,2,4!*/GODL,P51X, ,ALL,0FLST,2,1,4,ORDE,1 FITEM,2,2/GO!*SFL,P51X,PRES,-1,/STATUS,SOLUSOLVEFINISH/POST1PLDISP,0!*/EFACET,1PLNSOL, U,SUM, 0,1.0/RGB,INDEX,100,100,100, 0 /RGB,INDEX, 80, 80, 80,13 /RGB,INDEX, 60, 60, 60,14 /RGB,INDEX, 0, 0, 0,15/REPLOTFINISH! /EXIT,ALLDam：/BATCH/COM,ANSYS RELEASE 12.0.1UP20090415 20:54:59 03/24/2011 /TITLE,dam_fenxi!*/NOPR/PMETH,OFF,0KEYW,PR_SET,1KEYW,PR_STRUC,1KEYW,PR_FLUID,0KEYW,PR_MULTI,0/GO!*/COM,/COM,Preferences for GUI filteringhave been set to display:/COM, Structural!*/PREP7!*ET,1,PLANE42!*KEYOPT,1,1,0KEYOPT,1,2,0KEYOPT,1,3,2KEYOPT,1,5,0KEYOPT,1,6,0!*!* MPTEMP,,,,,,,,MPTEMP,1,0MPDATA,EX,1,,2.1e11 MPDATA,PRXY,1,,0.3SAVEK,1,0,0,,K,2,1,0,,K,3,1,5,,K,4,0.45,5,,FLST,2,4,3FITEM,2,1FITEM,2,2FITEM,2,3FITEM,2,4A,P51XFLST,5,2,4,ORDE,2 FITEM,5,1FITEM,5,3CM,_Y,LINELSEL, , , ,P51XCM,_Y1,LINECMSEL,,_Y!*LESIZE,_Y1, , ,15, , , , ,1 !*FLST,5,2,4,ORDE,2 FITEM,5,2FITEM,5,4CM,_Y,LINELSEL, , , ,P51XCM,_Y1,LINECMSEL,,_Y!*LESIZE,_Y1, , ,20, , , , ,1!*TYPE, 1MAT, 1REAL,ESYS, 0SECNUM,!*MSHAPE,0,2DMSHKEY,1!*CM,_Y,AREAASEL, , , , 1CM,_Y1,AREACHKMSH,'AREA'CMSEL,S,_Y!*AMESH,_Y1!*CMDELE,_YCMDELE,_Y1CMDELE,_Y2!*SAVE*DEL,_FNCNAME*DEL,_FNCMTID*DEL,_FNCCSYS*SET,_FNCNAME,'dam'*SET,_FNCCSYS,0! /INPUT,dam.func,,,1*DIM,%_FNCNAME%,TABLE,6,3,1,,,,%_FNCCSYS% !! Begin of equation: 1000*{X}*SET,%_FNCNAME%(0,0,1), 0.0, -999*SET,%_FNCNAME%(2,0,1), 0.0*SET,%_FNCNAME%(3,0,1), 0.0*SET,%_FNCNAME%(4,0,1), 0.0*SET,%_FNCNAME%(5,0,1), 0.0*SET,%_FNCNAME%(6,0,1), 0.0*SET,%_FNCNAME%(0,1,1), 1.0, -1, 0, 1000, 0, 0, 2*SET,%_FNCNAME%(0,2,1), 0.0, -2, 0, 1, -1, 3, 2 *SET,%_FNCNAME%(0,3,1), 0, 99, 0, 1, -2, 0, 0! End of equation: 1000*{X}!-->FINISH/SOLFLST,2,1,4,ORDE,1FITEM,2,4/GO!*!*SFL,P51X,PRES, %DAM%FLST,2,1,4,ORDE,1FITEM,2,1!*/GODL,P51X, ,ALL,0FLST,2,1,4,ORDE,1FITEM,2,2!*/GODL,P51X, ,ALL,0/STATUS,SOLUSOLVEFINISH/POST1PLDISP,1!*/EFACET,1PLNSOL, U,SUM, 0,1.0!*/EFACET,1PLNSOL, S,EQV, 0,1.0PLNSOL,S,EQV!*ANCNTR,10,0.5PLNSOL,U,SUM!*ANCNTR,10,0.5!*PRNSOL,U,COMPPRRSOL,FINISH! /EXIT,ALL。

ANSYS计算结果与分析一、有限元原理：有限元的解题思路可简述为：从结构的位移出发，通过寻找位移和应变，应变与应力，应力与内力，内力与外力的关系，建立相应的方程组，从而由已知的外力求出结构的内应力和位移。

有限元分析过程由其基本代数方程组成：[K]{V}={Q}，[K]为整个结构的刚变矩阵，{V}为未知位移量，{Q}为载荷向量。

这些量是不确定的，依靠所需解决的问题进行定量描述。

上述结构方程是通过应用边界条件，将结构离散化成小单元，从综合平衡方程中获得。

有限元是通过单元划分，在某种程度上模拟真实结构，并由数字对结构诸方面进行描述。

其描述的准确性依赖于单元细划的程度，载荷的真实性，材料力学参数的可信度，边界条件处理的正确程度。

本算例采用三角形六结点来划分单元。

二、有限元解题步骤：有限元的解题步骤为：①连续体的离散化；②选择单元位移函数；③建立单元刚度矩阵；④求解代数方程组，得到所有节点位移分量；⑤由节点位移求出内力或应力。

三、工程实例分析现已知一混凝土截面梁，长为L=2.4m，梁高为h=0.3m，梁宽设为单位宽度。

混凝土材料的各项属性为：容重γ=25KN/m3，E=2.4E10Pa，λ=0.2。

若该混凝土梁分别受到以下两种不同约束和不同受力的作用：（1）两端受固定约束作用，中间作用一个集中荷载P=10KN作用，如图A所示。

（2）一端受固定约束作用悬臂梁，梁上作用一均布荷载q=5KN/m作用，如图B 所示。

现要求使用有限元中的三角形六节点单元来计算两种情况下梁的位移与应力，并与力学计算结果进行比较和分析ANSYS分析过程（1）两端固定有限元模型Y方向位移图X方向应力图具体节点位移如下表：x应力表（单位：pa）NODE SX SY SZ SXY SYZ SXZ 1 -0.47117E+06 -94234. 0.0000 -71939. 0.00000.0000 2 -0.44824E+06 -43524. 0.0000 36804. 0.0000 0.0000 4 -0.26659E+06 24017.0.0000 11756. 0.0000 0.0000 6 -0.11092E+06 -1675.1 0.0000 -1416.0 0.0000 0.0000 8 26454. -287.29 0.0000 -529.21 0.0000 0.0000 10 0.14396E+06 -296.19 0.0000 -428.64 0.0000 0.0000 12 0.24665E+06 -154.80 0.0000 -931.20 0.0000 0.0000 14 0.31294E+06 -651.06 0.0000 1868.1 0.0000 0.0000 16 0.25514E+06 777.86 0.0000 2607.3 0.0000 0.0000 18 0.15259E+06 421.23 0.0000 955.79 0.0000 0.0000 20 36815. 350.40 0.0000 1367.3 0.0000 0.0000 22 -99169. 406.51 0.0000 1539.1 0.0000 0.0000 24 -0.25029E+06 709.47 0.0000 469.07 0.0000 0.0000 26 0.47021E+06 94043. 0.0000 71822. 0.0000 0.0000 28 -0.26849E+06 -41899. 0.0000 46711. 0.0000 0.0000 30 -0.12480E+06 -20589. 0.0000 44463. 0.0000 0.0000 32 2346.1 1441.3 0.0000 44301. 0.0000 0.0000 34 0.13084E+06 23544. 0.0000 46007. 0.0000 0.0000 36 0.27890E+06 44622. 0.0000 49721. 0.0000 0.0000 38 0.44740E+06 43435. 0.0000 -36738. 0.0000 0.000040 0.26576E+06 -23958. 0.0000 -11724. 0.0000 0.0000 42 0.11006E+06 1672.9 0.0000 1413.1 0.0000 0.0000 44 -27364. 285.26 0.0000 538.86 0.0000 0.0000 46 -0.14505E+06 297.97 0.0000 455.70 0.0000 0.0000 48 -0.23089E+06 828.18 0.0000 -2277.4 0.0000 0.0000 50 -0.35045E+06 -94932. 0.0000 4506.0 0.0000 0.0000 52 -0.23867E+06 40010. 0.0000 13774. 0.0000 0.0000 54 -0.15354E+06 -1579.2 0.0000 -2170.7 0.0000 0.0000 56 -37694. -287.51 0.0000 -1318.8 0.0000 0.0000 58 98366. -412.70 0.0000 -1539.9 0.0000 0.0000 60 0.24952E+06 -708.11 0.0000 -474.61 0.0000 0.0000 63 0.26768E+06 41770. 0.0000 -46653. 0.0000 0.0000 65 0.12400E+06 20454.0.0000 -44435. 0.0000 0.0000 67 -3155.0 -1579.4 0.0000 -44304. 0.0000 0.0000 69 -0.13167E+06 -23682. 0.0000 -46041. 0.0000 0.0000 71 -0.27977E+06 -44758. 0.0000 -49784. 0.0000 0.0000 151 0.18243E+06 -5692.4 0.0000 37694. 0.0000 0.0000 153 93763. -895.44 0.0000 60650. 0.0000 0.0000 155 2906.0 1964.2 0.0000 67290. 0.0000 0.0000 157 -87037. 5292.4 0.0000 58490. 0.0000 0.0000 159 -0.17211E+06 11178. 0.0000 31663. 0.0000 0.0000 167 73372. -851.10 0.0000 31158. 0.0000 0.0000 169 39292. -840.75 0.0000 49441. 0.0000 0.0000 171 3787.8 -337.99 0.0000 55813. 0.0000 0.0000 173 -32101. 100.68 0.0000 50074. 0.0000 0.0000 175 -67944. 717.92 0.0000 32029. 0.0000 0.0000 183 -17938. -922.76 0.0000 27092. 0.0000 0.0000 185 -6795.5 -612.85 0.0000 42946. 0.0000 0.0000 187 3071.2 18.206 0.0000 48306. 0.0000 0.0000 189 12803. 565.23 0.0000 43126. 0.0000 0.0000 191 22747. 538.90 0.0000 27571.0.0000 0.0000 199 -96298. -717.39 0.0000 22710. 0.0000 0.0000 201 -46228. -1019.6 0.0000 36320. 0.0000 0.0000 203 2626.4 121.91 0.0000 40665. 0.0000 0.0000 205 51239. 880.36 0.0000 36356. 0.0000 0.0000 207 0.10012E+06 736.28 0.0000 23263.0.0000 0.0000 215 -0.15923E+06 18494. 0.0000 11061. 0.0000 0.0000 217 -83947. 9075.8 0.0000 29103. 0.0000 0.0000 219 -2385.6 4224.8 0.0000 35294. 0.0000 0.0000 221 80991. 2496.3 0.0000 32516. 0.0000 0.0000 223 0.16576E+06 1612.2 0.0000 21754. 0.0000 0.0000 231 -0.20646E+06 -75438. 0.0000 -1738.1 0.0000 0.0000 233 -93006. -51133. 0.0000 -1579.6 0.0000 0.0000 235 6530.2 -30687. 0.0000 -666.930.0000 0.0000237 0.10345E+06 -14749. 0.0000 125.67 0.0000 0.0000 239 0.20441E+06 -4119.40.0000 970.85 0.0000 0.0000 247 -0.16755E+06 9862.5 0.0000 -17509. 0.0000 0.0000 249 -87809. 3440.9 0.0000 -31319. 0.0000 0.0000 251 -5584.0 978.66 0.0000 -35737.0.0000 0.0000 253 77562. 806.61 0.0000 -31968. 0.0000 0.0000 255 0.16243E+06 1086.9 0.0000 -20148. 0.0000 0.0000 263 -0.10061E+06 -689.88 0.0000 -23108.0.0000 0.0000 265 -51874. -100.28 0.0000 -35992. 0.0000 0.0000 267 -3478.2 629.38 0.0000 -40521. 0.0000 0.0000 269 45225. 1049.3 0.0000 -36167. 0.0000 0.0000 271 95246. 1060.4 0.0000 -22892. 0.0000 0.0000 279 -23597. -576.87 0.0000 -27627.0.0000 0.0000 281 -13606. -652.21 0.0000 -43170. 0.0000 0.0000 283 -3857.7 -89.957 0.0000 -48308. 0.0000 0.0000 285 5980.8 542.38 0.0000 -42912. 0.0000 0.0000 287 17073. 893.21 0.0000 -27066. 0.0000 0.0000 295 67130. -714.95 0.0000 -32028.0.0000 0.0000 297 31274. -97.707 0.0000 -50075. 0.0000 0.0000 299 -4624.8 340.23 0.0000 -55817. 0.0000 0.0000 301 -40137. 841.32 0.0000 -49444. 0.0000 0.0000 303 -74225. 850.89 0.0000 -31160. 0.0000 0.0000 311 0.17131E+06 -11152. 0.0000 -31681.0.0000 0.0000 313 86204. -5274.6 0.0000 -58500. 0.0000 0.0000 315 -3755.8 -1950.0 0.0000 -67295. 0.0000 0.0000 317 -94623. 911.23 0.0000 -60649. 0.0000 0.0000 319 -0.18330E+06 5714.3 0.0000 -37686. 0.0000 0.0000由以上分析结果可以得出：跨中最大挠度为：2.95E-05m 梁端上截面应力为：-0.35Mpa 跨中上截面应力: 0.47Mpa 跨中下截面应力为：-0.471Mpa 用材料力学进行校核：Wz=bh6222，左右杆端弯矩为：=ql12ql2，跨中弯矩为：2ql24 左右杆端截面正应力为：σ跨中截面正应力为：σ=ql2bh6ql=22ql222bh=0.32MPa 242bh6=4bh=0.47MPa由图乘法求跨中截面的挠度，具体的计算公式如下：W===1EI11EI(412⨯1112-ql2⨯l2⨯1l2⨯)23-12⨯124ql2⨯l2⨯l2⨯13-23⨯l2⨯132ql2⨯l2⨯12)ql(ql41576144-384374EI=2.95E-05m（2）一端固定一端自由Y方向位移图X方向应力图具体节点位移如下表：x应力表（单位：pa）NODE SX SY SZ SXY SYZ SXZ 1 -0.25013E+07-0.50026E+06 0.0000 -0.23536E+06 0.0000 0.0000 2 2344.3 55.551 0.0000 1381.4 0.0000 0.0000 4 -0.20145E+070.13137E+06 0.0000 42962. 0.0000 0.0000 6 -0.16765E+07 -5697.0 0.0000 -4238.2 0.0000 0.0000 8 -0.13587E+07 -602.67 0.0000 -1529.1 0.0000 0.0000 10 -0.10740E+07 -762.28 0.0000 -1374.8 0.0000 0.0000 12 -0.82262E+06 -655.05 0.0000 -1117.5 0.0000 0.0000 14 -0.60460E+06 -562.14 0.0000 -863.89 0.0000 0.0000 16 -0.41991E+06 -468.62 0.0000 -610.04 0.0000 0.0000 18 -0.26856E+06 -375.13 0.0000 -356.22 0.0000 0.0000 20 -0.15053E+06 -281.65 0.0000 -102.36 0.0000 0.0000 22 -65843. -187.66 0.0000 150.44 0.0000 0.0000 24 -14504. -102.05 0.0000 417.31 0.0000 0.0000 26 -3100.4 -5193.8 0.0000 775.10 0.0000 0.0000 28 742.77 684.07 0.0000 633.96 0.0000 0.0000 30 -17.938 -317.56 0.0000 -285.27 0.0000 0.0000 32 -477.64 -2424.3 0.0000 -770.67 0.0000 0.000034 -781.28 -4602.3 0.0000 -570.42 0.0000 0.0000 36 -1125.5 -5696.4 0.0000 -174.96 0.0000 0.0000 38 0.24391E+07 0.24437E+06 0.0000 -0.11805E+06 0.0000 0.0000 40 11812. -4996.7 0.0000 -1071.1 0.0000 0.0000 42 60425. -5175.6 0.0000 -1154.9 0.0000 0.0000 44 0.14240E+06 -5280.4 0.0000 -1421.3 0.0000 0.0000 46 0.25771E+06 -5372.8 0.0000 -1674.3 0.0000 0.0000 48 0.40636E+06 -5466.3 0.0000 -1928.2 0.0000 0.0000 50 0.58834E+06 -5559.8 0.0000 -2182.0 0.0000 0.0000 52 0.80365E+06 -5653.3 0.0000 -2435.9 0.0000 0.0000 54 0.10523E+07 -5746.8 0.0000 -2689.9 0.0000 0.0000 56 0.13342E+07 -5842.7 0.0000 -2932.1 0.0000 0.0000 58 0.16503E+07 -5879.4 0.0000 -3376.0 0.0000 0.0000 60 0.19778E+07 -7803.0 0.0000 2914.3 0.0000 0.0000 63 0.15354E+07 0.22889E+06 0.0000 -0.10713E+06 0.0000 0.0000 650.73975E+06 0.11355E+06 0.0000 -70967. 0.0000 0.0000 67 -7600.7 -6004.9 0.0000 -61499. 0.0000 0.0000 69 -0.75765E+06-0.12447E+06 0.0000 -78773. 0.0000 0.0000 71 -0.15608E+07-0.23582E+06 0.0000 -0.12284E+06 0.0000 0.0000 151 9798.9 -5221.2 0.0000 -7608.6 0.0000 0.0000 153 4996.1 -4256.1 0.0000 -11467. 0.0000 0.0000 155 -911.85 -2609.3 0.0000 -12699. 0.0000 0.0000 157 -6764.9 -887.12 0.0000 -11142.0.0000 0.0000 159 -11230. 312.08 0.0000 -6755.7 0.0000 0.0000 167 42347. -5311.7 0.0000 -14833. 0.0000 0.0000 169 20742. -4334.3 0.0000 -22836. 0.0000 0.0000 171 -1834.5 -2501.8 0.0000 -25426. 0.0000 0.0000 173 -24341. -653.58 0.0000 -22464.0.0000 0.0000 175 -45318. 505.18 0.0000 -13939. 0.0000 0.0000 183 97163. -5261.6 0.0000 -22022. 0.0000 0.0000 185 47621. -4327.6 0.0000 -34159. 0.0000 0.0000 187 -2750.4 -2507.1 0.0000 -38140. 0.0000 0.0000 189 -53018. -662.65 0.0000 -33786.0.0000 0.0000 191 -0.10162E+06 539.25 0.0000 -21132. 0.0000 0.0000 1990.17420E+06 -5215.6 0.0000 -29214. 0.0000 0.0000 201 85610. -4326.4 0.0000 -45483.0.0000 0.0000 203 -3667.2 -2509.3 0.0000 -50853. 0.0000 0.0000 205 -92806. -660.75 0.0000 -45110. 0.0000 0.0000 207 -0.18014E+06 586.11 0.0000 -28324. 0.0000 0.0000 215 0.27346E+06 -5169.3 0.0000 -36406. 0.0000 0.0000 217 0.13471E+06 -4324.80.0000 -56807. 0.0000 0.0000 219 -4584.1 -2511.7 0.0000 -63566. 0.0000 0.0000 221 -0.14371E+06 -659.14 0.0000 -56434. 0.0000 0.0000 223 -0.28088E+06 632.39 0.0000 -35517. 0.0000 0.0000231 0.39494E+06 -5123.0 0.0000 -43599. 0.0000 0.0000 233 0.19492E+06 -4323.20.0000 -68131. 0.0000 0.0000 235 -5500.9 -2514.0 0.0000 -76279. 0.0000 0.0000 237 -0.20572E+06 -657.53 0.0000 -67758. 0.0000 0.0000 239 -0.40384E+06 678.71 0.0000 -42709. 0.0000 0.0000 247 0.53864E+06 -5076.5 0.0000 -50791. 0.0000 0.0000 249 0.26624E+06 -4321.2 0.0000 -79456. 0.0000 0.0000 251 -6417.7 -2516.1 0.0000 -88993. 0.0000 0.0000 253 -0.27884E+06 -655.95 0.0000 -79083. 0.0000 0.0000 255 -0.54903E+06 724.90 0.0000 -49901. 0.0000 0.0000 263 0.70456E+06 -5031.3 0.0000 -57983. 0.0000 0.0000 265 0.34868E+06 -4322.8 0.0000 -90782. 0.0000 0.0000 267 -7336.1 -2519.0 0.0000 -0.10171E+06 0.0000 0.0000 269 -0.36307E+06 -649.67 0.0000 -90406. 0.0000 0.0000 271 -0.71644E+06 772.81 0.0000 -57090. 0.0000 0.0000 279 0.89269E+06 -5018.3 0.0000 -65150. 0.0000 0.0000 281 0.44225E+06 -4346.5 0.0000 -0.10206E+06 0.0000 0.0000 283 -8193.7 -2657.9 0.0000 -0.11441E+06 0.0000 0.0000 285 -0.45838E+06 -751.50 0.0000 -0.10180E+06 0.0000 0.0000 287 -0.90611E+06 819.40 0.0000 -64358. 0.0000 0.0000 295 0.11033E+07 -4700.3 0.0000 -72715. 0.0000 0.0000 297 0.54631E+06 -1332.2 0.0000 -0.11431E+06 0.0000 0.0000 299 -10032. -610.15 0.0000 -0.12657E+06 0.0000 0.0000 301 -0.56488E+06 156.41 0.0000 -0.11184E+06 0.0000 0.0000由以上分析结果可一得出：梁端最大挠度为：9.72E-04m 梁端截面最大应力为：-2.5Mpa 用材料力学进行校核：Wz=bh62，杆端弯矩为：FL =ql22左右杆端截面正应力为：σ固端截面正应力为：σ=6bh==ql222bh=0.32MPa FLbh26FL2bh2226=2.4MPa 左右杆端截面正应力为：σ=ql6bh=ql222bh=0.32MPa由图乘法可知自由端的挠度为：W=1EI(12⨯FL⨯L⨯23L)=1FL3EI3=9.60E-04m结论在对本工程进行ANSYS有限元数值分析过程中，作者采用的单元形式为三角形六节点单元PLANE2单元，因其为平面单元，ANSYS计算过程中没有输入梁的宽度，其计算默认的梁宽为一个单位。

ANSYS实验分析报告本次实验是利用ANSYS软件对一个弯曲结构进行有限元分析。

主要目的是研究在不同载荷下，该结构的应力和变形情况。

以下是本次实验的过程与结果分析。

一、建立模型首先，我们在ANSYS中建立出该结构的三维模型。

我们通过几何体建模的方法，将其仿真为一个由四个梁柱组成的简单框架结构。

具体的建模操作如下：1. 在“DesignModeler”中选择几何体建模，先建立底部两个支撑，分别为长方体和正方体，通过旋转复制成两组，组成左右两侧的支撑。

2. 手动建立横向梁和纵向柱，将其分别连接在底部的支撑之间，形成框架的主体。

3. 将上部吊挂点也建立为长方体，通过旋转复制成两组，分别连接在左右两侧的支撑之上。

4. 最后，将整个模型导出为STEP文件，方便之后进行后续的有限元分析。

二、设定边界条件在进行有限元分析之前，我们需要确定边界条件。

在本次实验中，我们将底部的两个支撑固定不动，作为模型的固支部分。

三、设置载荷接下来，我们将模型的上部吊挂点承载了一个垂直向下的载荷，模拟在实际使用中被吊载的情况。

我们对载荷大小和方向进行了多次调整，使得其尽可能满足实际情况，并且能够顺利完成有限元分析。

四、进行有限元分析有了模型和边界条件的设定，我们开始进行有限元分析。

在ANSYS中，我们选择了静力学模块，并且设置了相应的分析参数（包括材料属性、单元类型等）。

分析过程中，我们关注了应力和变形两个方面的计算，通过查看各个节点的数值以及色彩分布图，能够更清晰地了解结构的状态。

五、结果分析通过分析，我们获得了如下两个方面的结果：1. 应力分布我们观察到，该结构的应力主要集中在上部吊挂点以及梁柱连接处，尤其是梁柱连接处的应力相对较大且分布比较均匀。

而在其余区域，则几乎没有应力产生或仅产生了很小的应力。

2. 变形情况在载荷作用下，该结构的变形情况较为明显，上部吊挂点相对底部固支发生了垂直方向的变形，同时某些连接处也出现了微小的变形。

ANSYS屈曲分析报告1. 引言本报告旨在使用ANSYS软件进行屈曲分析，并对结果进行解释和分析。

屈曲分析是一种重要的工程分析方法，用于确定结构在受力作用下的稳定性能。

在本次分析中，我们将针对特定的结构进行屈曲分析，以评估其在实际应用中的可靠性和稳定性。

2. 分析模型本次分析使用的模型是一个具有特定几何形状和材料属性的结构。

具体的几何形状和材料属性将在下文中详细介绍。

3. 材料属性为了进行准确的屈曲分析，我们需要了解材料的力学性质。

在本次分析中，我们假设材料为均匀各向同性的弹性材料。

材料的力学性质如下：•弹性模量：E = XXX GPa•泊松比：ν = XXX•密度：ρ = XXX kg/m^34. 几何模型本次分析使用的结构模型的几何形状如下所示：（此处以文字描述结构模型的几何形状）5. 约束条件和加载在进行屈曲分析时，我们需要为结构模型设置适当的约束条件和加载。

在本次分析中，我们假设结构的底部固定，并在顶部施加垂直向下的集中力。

施加的加载大小为XXX N。

6. 分析步骤屈曲分析可以通过逐步增加加载的方法进行。

在本次分析中，我们将使用以下步骤进行屈曲分析：1.施加约束条件和加载；2.进行线性静力分析，确定结构的初始状态；3.逐步增加加载，进行非线性分析，直到发生屈曲现象；4.记录并分析屈曲点。

7. 分析结果与讨论经过屈曲分析后，我们得到了以下结果：•屈曲载荷：XXX N•屈曲模态：X 模态•屈曲形状：（此处以文字描述屈曲形状的特征）根据分析结果，我们可以得出以下结论和讨论：•结构在受到XXX N的载荷时，发生了屈曲现象；•屈曲模态X是结构的主要屈曲模态，表示了结构在该模态下的变形形态；•屈曲形状的特征表明结构在屈曲时出现了X类型的失稳现象。

8. 结论本次屈曲分析报告对特定结构进行了屈曲分析，并得出了结构的屈曲载荷、屈曲模态和屈曲形状的结果。

根据分析结果，我们可以评估结构在实际应用中的可靠性和稳定性，并采取相应的措施来改进和优化结构设计。