示波管原理图

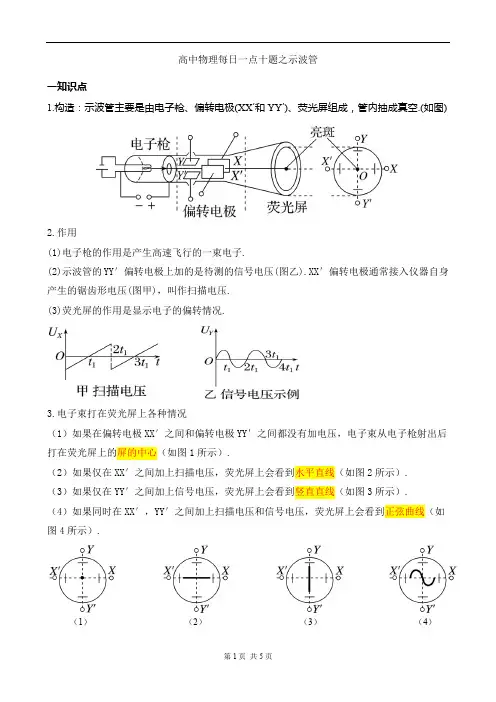
高中物理每日一点十题之示波管一知识点1.构造：示波管主要是由电子枪、偏转电极(XX′和YY′)、荧光屏组成，管内抽成真空.(如图)2.作用(1)电子枪的作用是产生高速飞行的一束电子.(2)示波管的YY′偏转电极上加的是待测的信号电压(图乙).XX′偏转电极通常接入仪器自身产生的锯齿形电压(图甲)，叫作扫描电压.(3)荧光屏的作用是显示电子的偏转情况.3.电子束打在荧光屏上各种情况（1）如果在偏转电极XX′之间和偏转电极YY′之间都没有加电压，电子束从电子枪射出后打在荧光屏上的屏的中心（如图1所示）.（2）如果仅在XX′之间加上扫描电压，荧光屏上会看到水平直线（如图2所示）.（3）如果仅在YY′之间加上信号电压，荧光屏上会看到竖直直线（如图3所示）.（4）如果同时在XX′，YY′之间加上扫描电压和信号电压，荧光屏上会看到正弦曲线（如图4所示）.（1）（2）（3）（4）十道练习题（含答案）一、单选题（共7小题）1. 如图所示的示波管，当两偏转电极XX′、YY′电压为零时，电子枪发射的电子经加速电场加速后会打在荧光屏上的正中间(图示坐标系的O点，其中x轴与XX′电场的场强方向重合，x轴正方向垂直于纸面向里，y轴与YY′电场的场强方向重合，y轴正方向竖直向上)．若要电子打在图示坐标系的第Ⅲ象限，则( )A.X、Y极接电源的正极，X′、Y′接电源的负极B.X、Y′极接电源的正极，X′、Y接电源的负极C.X′、Y极接电源的正极，X、Y′接电源的负极D.X′、Y′极接电源的正极，X、Y接电源的负极2. 关于带电粒子(不计重力)在匀强电场中的运动情况，下列说法正确的是( )A. 一定是匀变速运动B. 不可能做匀减速运动C. 一定做曲线运动D. 可能做匀变速直线运动，不可能做匀变速曲线运动3. 图甲为示波管的原理图．如果在电极YY′之间所加的电压按图乙所示的规律变化，在电极XX′之间所加的电压按图丙所示的规律变化，则在荧光屏上会看到的图形是( )A. B. C. D.4. 如图所示，在匀强电场E中，一带电粒子(不计重力)－q的初速度v0恰与电场线方向相同，则带电粒子－q在开始运动后，将( )A. 沿电场线方向做匀加速直线运动B. 沿电场线方向做变加速直线运动C. 沿电场线方向做匀减速直线运动D. 偏离电场线方向做曲线运动5. 一带电粒子在电场中只受到电场力作用时，它不可能出现的运动状态是( )A. 匀速直线运动B. 匀加速直线运动C. 匀变速曲线运动D. 匀速圆周运动6. 如图所示，在匀强电场E中，一带电粒子－q的初速度v0恰与电场线方向相同，则带电粒子－q在开始运动后，将( )A. 沿电场线方向做匀加速直线运动B. 沿电场线方向做变加速直线运动C. 沿电场线方向做匀减速直线运动D. 偏离电场线方向做曲线运动7. 如图所示，是一个示波器工作原理图，电子经过加速后以速度v0垂直进入偏转电场，离开电场时偏转量是h，两平行板间距离为d，电势差为U，板长为l，每单位电压引起的偏移量(h/U)叫示波器的灵敏度．若要提高其灵敏度，可采用下列办法中的( )A. 增大两极板间的电压B. 尽可能使板长l做得短些C. 尽可能使板间距离d减小些D. 使电子入射速度v0大些二、多选题（共3小题）8. 如图是示波管的原理图．它由电子枪、偏转电极(XX′和YY′)、荧光屏组成，管内抽成真空．给电子枪通电后，如果在偏转电极XX′和YY′上都没有加电压，电子束将打在荧光屏的中心O点，在那里产生一个亮斑．下列说法正确的是( )A. 要想让亮斑沿OY向上移动，需在偏转电极YY′上加电压，且Y′比Y电势高B. 要想让亮斑移到荧光屏的右上方，需在偏转电极XX′、YY′上加电压，且X比X′电势高、Y比Y′电势高C. 要想在荧光屏上出现一条水平亮线，需在偏转电极XX′上加特定的周期性变化的电压(扫描电压)D. 要想在荧光屏上出现一条正弦曲线，需在偏转电极XX′上加适当频率的扫描电压、在偏转电极YY′上加按正弦规律变化的电压9. 一台正常工作的示波管，突然发现荧光屏上画面的高度缩小，则产生故障的原因可能是( )A. 加速电压突然变大B. 加速电压突然变小C. 偏转电压突然变大D. 偏转电压突然变小10. 示波管的构造如图所示．如果在荧光屏上P点出现亮斑，那么示波管中的( )A.极板X应带正电B. 极板X′应带正电C. 极板Y应带正电D. 极板Y′应带正电1. 【答案】D【解析】若要使电子打在题图所示坐标系的第Ⅲ象限，电子在x轴上向负方向偏转，则应使X′接正极，X接负极；电子在y轴上也向负方向偏转，则应使Y′接正极，Y接负极，所以选项D正确2. 【答案】A【解析】带电粒子在匀强电场中受恒定合外力(电场力)作用，一定做匀变速运动，初速度与合外力共线时，做直线运动，不共线时做曲线运动，选项A正确，选项B、C、D错误3. 【答案】B【解析】由于电极XX′之间所加的是扫描电压，电极YY′之间所加的电压为信号电压，所以荧光屏上会看到B选项所示的图形4. 【答案】C【解析】在匀强电场E中，带电粒子所受静电力为恒力．带电粒子受到与运动方向相反的恒定的电场力作用，产生与运动方向相反的恒定的加速度，因此，带电粒子－q在开始运动后，将沿电场线做匀减速直线运动5. 【答案】A【解析】在电场力的作用下，说明电荷受到的合外力的大小为电场力，不为零，所以选项A不可能；当电荷在匀强电场中由静止释放后，电荷做匀加速直线运动，选项B可能；当电荷垂直进入匀强电场后，电荷做类平抛运动，选项C可能；正电荷周围的负电荷只在电场力作用下且电场力恰好充当向心力时，可以做匀速圆周运动，选项D可能6. 【答案】C【解析】在匀强电场E中，带电粒子所受电场力为恒力．带电粒子受到与运动方向相反的恒定的电场力作用，产生与运动方向相反的恒定的加速度，因此，带电粒子－q在开始运动后，将沿电场线做匀减速直线运动7. 【答案】C【解析】题是一个通过计算进行选择的问题．因为h＝at2＝(a＝，t＝)，所以，＝.要使灵敏度大些，选项中合乎要求的只有C8. 【答案】BCD【解析】要想让亮斑沿OY向上移动，电子受力向Y方向，即电场方向为YY′，即Y电势高，A项错误；要想让亮斑移到荧光屏的右上方，同理Y为高电势，X为高电势才可，B项正确；要想在荧光屏上出现一条水平亮线，说明电子只在XX′方向偏转，当然要在这个方向加扫描电压，C项正确；要想在荧光屏上出现一条正弦曲线，就是水平与竖直方向都要有偏转电压，所以D项正确．综述本题选项为B、C、D.9. 【答案】AD【解析】若加速电压为U1，偏转电压为U2，则在加速电场中qU1＝mv，在偏转电场中a＝，L ＝v0t，y＝at2，所以y＝，画面高度缩小，说明粒子的最大偏转位移减小，由上式分析可得，可能是加速电压U1增大，也可能是偏转电压U2减小，选项A、D正确10. 【答案】AC【解析】根据亮斑的位置，电子偏向XY区间，说明电子受到电场力作用发生了偏转，因此极板X、极板Y均应带正电．。

§1.9(3)示波管的原理【自主学习】1．示波管构造（参看教材35页下）示波管是示波器的核心部件，如图所示，外部是一个抽成真空的玻璃壳，内部主要由电子枪（由发射电子的灯丝、加速电极组成）、偏转电极（由偏转电极XX′和偏转电极YY'组成)和荧光屏组成.注意：示波器可用来观察电信号随时间变化的情况.2．示波管的工作原理电子枪通电后发射电子，电子在加速电场中加速，然后进入偏转电场，偏转电极一般有相互垂直的两组，一组控制水平偏转，一组控制竖直偏转，电子经过偏转电场后到达荧光屏上使荧光粉发光.(1)偏转电极不加电压：从电子枪射出的电子将沿直线运动，射到荧光屏的中心点形成一个亮斑．(2)在XX′(或YY′)加电压：若所加电压稳定，则电子被加速，偏转后射到XX′(或YY′)所在直线上某一点，形成一个亮斑(不在中心)，如下图所示．（3）示波管实际工作时，竖直偏转板和水平偏转板都加上电压，一般地，加在竖直偏转板上的电压是要研究的信号电压，加在水平偏转板上的电压是扫描电压，若两者周期相同，在荧光屏上就会显示出信号电压随时间变化的波形图．（教材36页下）【典例探究】1、如果仅在YY'之间加不变的电压，使Y板电势比Y' 高(有时说Y正，Y'负)，电子束将受到指向__________板的电场力，在荧光屏的__________轴上将出现____________________。

2、如果仅在X X '之间加不变的电压，使X板的电势比X' 高（X正，X'负），电子束将受到指向__________板的电场力，在荧光屏的_________轴上将出现____________________ 。

3、如果仅在YY'之间加如图2甲所示的电压，在荧光屏上的__________ 轴上将出现____________________ 。

4、如果在YY'之间加图2甲所示的电压，而在XX'之间加不变的电压(X正、X'负)，在荧光屏上将会出现____________________ 。

实验八 示波器的原理和使用示波器是一种用途广泛的基本电子测量仪器，用它能观察电信号的波形、幅度和频率等电参数。

用双踪示波器还可以测量两个信号之间的时间差，一些性能较好的示波器甚至可以将输入的电信号存储起来以备分析和比较。

在实际应用中凡是能转化为电压信号的电学量和非电学量都可以用示波器来观测。

实 验 原 理示波器都包括了如图1所示的几个基本组成部分：示波器、垂直放大电路（Y 放大）、水平放大电路（X 放大）、扫描信号发生电路（锯齿波发生器）、自检标准信号发生电路（自检信号）、触发同步电路、电源等。

1. 示波管的基本结构 示波管的基本结构如图2所示。

主要由电子枪、偏转系统和荧光屏三部分组成，全都密封在玻璃壳体内，里面抽成高真空。

（1）电子枪由灯丝、阴极、控制栅极、第一阳极和第二阳极五部分组成。

灯丝通电后加热阴极。

阴极是一个表面涂有氧化物的金属圆筒，被加热后发射电子。

控制栅极是一个顶端有小孔的圆筒，套在阴极外面。

它的电位比阴极低，对阴极发射出来的电子起控制作用，只有初速度较大的电子才能穿过栅极顶端的小孔然后在阳极加速下奔向荧光屏。

示波器面板上的“辉度”调整就是通过调节电位以控制射向荧光屏的电子流密度，从而改变了荧光屏上的光斑亮度。

阳极电位比阴极电位高很多，电子被它们之间的电场加速形成射线。

当控制栅极、第一阳极与第二阳极电位之间电位调节合适时，电子枪内的电场对电子射线有聚焦作用，所以，第一阳极也称聚焦阳极。

第二阳极电位更高，又称加速阳极。

面板上的“聚焦”调节，就是调第一阳极电位，使荧光屏上的光斑成为明亮、清晰的小圆点。

有的示波器还有“辅助聚焦”，实际是调节第二阳极电位。

Y 图2 示波管结构图H -灯丝 K -阴极 G 1，G 2- 控制栅极 A 1-第一阳极A 2-第二阳极 Y -竖直偏转板 X -水平偏转板（2）偏转系统：它由两对互相垂直的偏转板组成 ，一对竖直偏转板，一对水平偏转板。

在偏转板上加以适当电压，电子束通过时，其运动方向发生偏转，从而使电子束在荧光屏上产生的光斑位置也发生改变。

《静电场》专题12 示波管的工作原理带电粒子在交变电场中的运动一、知识清单（一）示波管1．构造及功能(如图1所示)图1(1)电子枪：发射并加速电子．(2)偏转电极YY′：使电子束竖直偏转(加信号电压)；偏转电极XX′：使电子束水平偏转(加扫描电压)．2．工作原理偏转电极XX′和YY′不加电压，电子打到屏幕中心；若只在XX′之间加电压，只在X方向偏转；若只在YY′之间加电压，只在Y方向偏转；若XX′加扫描电压，YY′加信号电压，屏上会出现随信号而变化的图象．（二）带电粒子在交变电场中的运动1．常见的交变电场常见的产生交变电场的电压波形有方形波、锯齿波、正弦波等．2．常见的题目类型(1)粒子做单向直线运动(一般用牛顿运动定律求解)．(2)粒子做往返运动(一般分段研究)．(3)粒子做偏转运动(一般根据交变电场特点分段研究)．3．思维方法(1)注重全面分析(分析受力特点和运动规律)，抓住粒子的运动具有周期性和在空间上具有对称性的特征，求解粒子运动过程中的速度、位移、做功或确定与物理过程相关的边界条件．(2)分析时从两条思路出发：一是力和运动的关系，根据牛顿第二定律及运动学规律分析；二是功能关系．(3)注意对称性和周期性变化关系的应用．（4）充分利用V-T图像结合运动过程示意图分析问题二、典型题型（一）示波管的工作原理例题1、如图2所示为一真空示波管的示意图，电子从灯丝K发出(初速度可忽略不计)，经灯丝与A板间的电压U1加速，从A板中心孔沿中心线KO射出，然后进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场)，电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点．已知M、N两板间的电压为U2，两板间的距离为d，板长为L，电子的质量为m，电荷量为e，不计电子受到的重力及它们之间的相互作用力．图2(1)求电子穿过A 板时速度的大小； (2)求电子从偏转电场射出时的侧移量；(3)若要使电子打在荧光屏上P 点的上方，可采取哪些措施？ 答案 (1)2eU 1m (2)U 2L 24U 1d(3)减小U 1或增大U 2 解析 (1)设电子经电压U 1加速后的速度为v 0，由动能定理得eU 1＝12m v 20－0解得v 0＝2eU 1m(2)电子以速度v 0进入偏转电场后，垂直于电场方向做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动．设偏转电场的电场强度为E ，电子在偏转电场中运动的时间为t ，加速度为a ，电子离开偏转电场时的侧移量为y .由牛顿第二定律和运动学公式得t ＝L v 0，F ＝ma ，F ＝eE ，E ＝U 2d ，y ＝12at 2解得y ＝U 2L 24U 1d .(3)减小加速电压U 1；增大偏转电压U 2.例题2、(2011·安徽·18)图2为示波管的原理图，如果在电极YY ′之间所加的电压按图3甲所示的规律变化，在电极XX ′之间所加的电压按图乙所示的规律变化，则在荧光屏上会看到的图形是 ( B )甲 乙图3解析 由图甲及图乙知，当U Y 为正时，Y 板电势高，电子向Y 偏，而此时U X 为负，即X ′板电势高，电子向X ′板偏，所以选B.练习1-1：(多选)示波管是示波器的核心部件，它由电子枪、偏转电极和荧光屏组成，如图1所示．如果在荧光屏上P 点出现亮斑，那么示波管中的( ) A ．极板X 应带正电 B ．极板X ′应带正电 C ．极板Y 应带正电 D ．极板Y ′应带正电答案 AC解析根据亮斑的位置，电子水平方向偏向X，竖直方向偏向Y，电子受到电场力作用发生偏转，因此极板X、极板Y均应带正电．练习1-2：某示波器在XX′、YY′不加偏转电压时光斑位于屏幕中心，现给其加如图1所示偏转电压，则在光屏上将会看到下列哪个图形(圆为荧光屏，虚线为光屏坐标)( D)图1练习1-3：示波管是示波器的核心部件，它由电子枪、偏转电极和荧光屏组成，如图4所示．如果在荧光屏上P点出现亮斑，那么示波管中的(AC)图4A．极板X应带正电B．极板X′应带正电C．极板Y应带正电D．极板Y′应带正电解析根据亮斑的位置，电子偏向XY区间，说明电子受到电场力作用发生了偏转，因此极板X、极板Y均应带正电．练习1-4：(多选)示波管的内部结构如图1甲所示．如果偏转电极XX′、YY′之间都没有加电压，电子束将打在荧光屏中心．如果在偏转电极XX′之间和YY′之间加上图丙所示的几种电压，荧光屏上可能会出现图乙中(a)、(b)所示的两种波形．则()甲A．若XX′和YY′分别加电压(3)和(1)，荧光屏上可以出现图乙中(a)所示波形B．若XX′和YY′分别加电压(4)和(1)，荧光屏上可以出现图乙中(a)所示波形C．若XX′和YY′分别加电压(3)和(2)，荧光屏上可以出现图乙中(b)所示波形D．若XX′和YY′分别加电压(4)和(2)，荧光屏上可以出现图乙中(b)所示波形答案AC解析要使荧光屏上出现图乙中(a)所示波形，XX′加扫描电压(3)，YY′加正弦电压(1)，则A正确；要使荧光屏上出现图乙中(b)所示波形，XX′加扫描电压(3)，YY′加方波电压(2)，则C正确．练习1-5：如图2是示波管的原理图．它由电子枪、偏转电极(XX′和YY′)、荧光屏组成，管内抽成真空．给电子枪通电后，如果在偏转电极XX′和YY′上都没有加电压，电子束将打在荧光屏的中心O点．图2(1)带电粒子在________区域是加速的，在________区域是偏转的．(2)若U YY′＞0，U XX′＝0，则粒子向________板偏移，若U YY′＝0，U XX′＞0，则粒子向________板偏移．答案(1)ⅠⅡ(2)Y X（二）带电粒子在交变电场中的运动例题3、如图所示，AB两平行金属板，A板接地，B板的电势做如图的周期性变化，在两板间形成交变电场。

第四部分示波管一、示波管的构造1．电子枪：通电加热后在热阴极产生电子，经过电场的加速而发射出去。

2．偏转电极（1）YY′：使电子束在竖直方向发生偏转，一般加信号电压。

（2）XX′：使电子束在水平方向发生偏转，一般加扫描电压（锯齿电压，如图）。

3．荧光屏：承接电子产生亮斑，当所加电压的周期很小时，由于视觉暂留，会在屏上看到亮线。

二、示波管的图像1．亮斑：偏转电极YY′、XX′上不加电压时，荧光屏中心形成一个亮斑。

2．亮斑：偏转电极YY′、XX′上加恒定电压时，荧光屏形成一个亮斑。

YY′上电压为零时，亮斑在XX′上；XX′上电压为零时，亮斑在YY′上。

3．亮线：（1）偏转电极YY′上加恒定电压，XX′上加周期变化的电压时，荧光屏上形成平行YY′的线段；（2）偏转电极XX′上加恒定电压，YY′上加周期变化的电压时，荧光屏上形成平行XX′的线段。

4．偏转电极XX′上加扫描电压，YY′上加信号电压（如正弦波、锯齿波、方波等），且扫描电压的周期是信号电压周期T的N倍（N为整数）时，荧光屏上形成N个周期的信号图像。

三、电子在示波管中的运动1．电子在示波管中的运动，一般忽略电子从阴极逸出的速度、电子受到的重力、电子间的相互作用。

2．运动过程：（1）电子（m，e）在加速电压U1作用下加速，由动能定理有eU1=12mv2（2）在偏转电压U2作用下做类平抛运动，极板长L、板间距d运动时间t=Lv=12mLeU，加速度a=2eUmd，射出电场时的偏转距离y=12at2=2214U LU d偏转距离只与示波管的结构和所加电压有关，与带电粒子的质量、电荷量无关（3）电子在偏转电极与荧光屏间（距离为s）做匀速直线运动，电子在荧光屏上的总偏转距离为Y=/2/2L syL+=21(2)4U L L sU d+【典例精析1】示波管的内部结构如图甲所示。

如果在偏转电极XX'、YY'上都没有加电压，电子束将打在荧光屏中心。

课时2示波管原理带电粒子在电场中的加速和偏转[学习目标] 1.知道示波管的主要构造和工作原理.2.了解带电粒子在电场中只受电场力作用时的两种典型运动．一、示波管原理1．示波管(阴极射线管)的构造(如图1所示)．图12．电子在阴极射线管中运动的三个阶段(1)加速：电子在阴极和阳极之间形成的电场中受电场力，电场力做正功，其动能增大，阳极和阴极间电压越高，电子穿过阳极小孔时获得的速度越大．(2)偏转：电子在水平平行金属板间的匀强电场中所受电场力方向与水平初速度垂直，因此电子在水平方向做匀速直线运动，在竖直方向做初速度为零的匀加速运动．偏转电极所加电压越大，电子飞出电场时的偏转角度就越大．(3)匀速直线运动：电子射出电场后，不再受电场力作用，保持偏转角度不变，做匀速直线运动，直到打在荧光屏上，显示出荧光亮点．二、实验观察：带电粒子在电场中的偏转1．实验室里的示波管的构造如图2所示，示波管中有水平和竖直两个方向上的两对偏转电极．图22．工作原理(1)若在两对偏转电极上所加电压为零，则电子束将打在O点产生亮斑．(2)若只在偏转电极Y1、Y2上加一稳定电压，则电子束将沿y方向发生偏转．(3)若只在偏转电极X1、X2上加一稳定电压，则电子束将沿x方向发生偏转．(4)若在偏转电极X 1、X 2和Y 1、Y 2上均加了一定的电压，则亮斑既偏离y 轴又偏离x 轴． (5)若加在X 1、X 2上的电压随时间按图3甲所示的规律周期性地变化，在Y 1、Y 2上的电压随时间以正弦函数变化，则示波器显示的图形如图乙所示．图31．判断下列说法的正误．(1)带电粒子(不计重力)在电场中由静止释放时，一定做匀加速直线运动．( × ) (2)对带电粒子在电场中的运动，从受力的角度来看，遵循牛顿运动定律；从做功的角度来看，遵循能量守恒定律．( √ )(3)动能定理能分析匀强电场中的直线运动问题，不能分析非匀强电场中的直线运动问题．( × )(4)带电粒子在匀强电场中偏转时，加速度不变，粒子的运动是匀变速曲线运动．( √ ) (5)示波管电子枪的作用是产生高速飞行的电子束，偏转电极的作用是使电子束偏转，打在荧光屏不同位置．( √ )(6)若只在示波管Y 1、Y 2上加电压，且UY 1Y 2>0，则电子向Y 2方向偏转．( × )2.如图4所示，M 和N 是匀强电场中的两个等势面，相距为d ，电势差为U ，一质量为m (不计重力)、电荷量为－q 的粒子，以速度v 0通过等势面M 射入两等势面之间，则该粒子穿过等势面N 的速度应是________．图4答案v 02＋2qU m解析 由动能定理有：qU ＝12m v 2－12m v 02，解得v ＝v 02＋2qUm.一、示波管的原理1．示波管主要由电子枪(由发射电子的灯丝、加速电极组成)、偏转电极(由一对X偏转电极和一对Y偏转电极组成)和荧光屏组成．2．扫描电压：XX′偏转电极接入的是由仪器自身产生的锯齿形电压．3．示波管工作原理：被加热的灯丝发射出热电子，电子经加速电场加速后，以很大的速度进入偏转电场，如果在Y偏转电极上加一个信号电压，在X偏转电极上加一扫描电压，在荧光屏上就会出现按Y偏转电压规律变化的可视图像．例1(多选)示波管的构造如图5所示．如果在荧光屏上P点出现亮斑，那么示波管中的()图5A．极板X应带正电B．极板X′应带正电C．极板Y应带正电D．极板Y′应带正电答案AC解析根据亮斑的位置，电子偏向XY区间，说明电子受到电场力作用发生了偏转，因此极板X、极板Y均应带正电．二、带电粒子的加速如图6所示，平行金属板间的距离为d，电势差为U.一质量为m、带电荷量为q的α粒子，在电场力的作用下由静止开始从正极板A向负极板B运动．图6(1)比较α粒子所受电场力和重力的大小，说明重力能否忽略不计(α粒子质量是质子质量的4倍，即m＝4×1.67×10－27 kg，电荷量是质子的2倍)．(2)α粒子的加速度是多大(结果用字母表示)？在电场中做何种运动？(3)计算粒子到达负极板时的速度大小．(结果用字母表示，尝试用不同的方法求解)(4)若上述电场是非匀强电场，粒子经过电压为U的电场加速，(3)中方法与结果是否成立？为什么？答案 (1)α粒子所受电场力大、重力小；因重力远小于电场力，故可以忽略重力． (2)α粒子的加速度为a ＝qUmd .在电场中做初速度为零的匀加速直线运动．(3)方法1 利用动能定理求解． 由动能定理可知qU ＝12m v 2v ＝2qUm. 方法2 利用牛顿运动定律结合运动学公式求解． 设粒子到达负极板时所用时间为t ，则 d ＝12at 2 v ＝at a ＝qU md 联立解得v ＝2qUm. (4)方法1成立．因为动能定理对任意电场都适用； 方法2不成立．因为粒子的运动不是匀变速直线运动．1．带电粒子的分类及受力特点(1)电子、质子、α粒子、离子等基本粒子，一般都不考虑重力．(2)质量较大的微粒：带电小球、带电油滴、带电颗粒等，除有说明或有明确的暗示外，处理问题时一般都不能忽略重力．2．分析带电粒子在电场力作用下做匀变速运动的两种方法 (1)利用牛顿第二定律F ＝ma 和运动学公式，只适用于匀强电场． (2)利用动能定理：qU ＝12m v 2－12m v 02，适用于任意电场．例2 (2019·盐城市第三中学期中)如图7所示，在A 板附近有一电子由静止开始向B 板运动，则关于电子到达B 板时的速率，下列解释正确的是( )图7A ．两板间距离越大，加速的时间越长，则获得的速率越大B ．两板间距离越小，加速的时间就越长，则获得的速率越大C ．获得的速率大小与两板间的距离无关，仅与加速电压U 有关D ．两板间距离越小，加速的时间越短，则获得的速率越小 答案 C解析 根据动能定理有，qU ＝12m v 2，解得v ＝2qUm，可知获得的速率与加速电压有关，与板间距离d 无关，由于板间电压U 不变，故获得的速率不变，C 正确；由牛顿第二定律可知，qE ＝ma ，而E ＝U d ，故a ＝qE m ＝qU md ，电子在两板间做匀加速直线运动，故有d ＝12at 2＝qUt 22md ，可得t ＝d 2mqU，可知两板间距离越小，加速时间越短，综合以上分析可知，A 、B 、D 错误．三、带电粒子的偏转如图8所示，带电粒子以初速度v 0垂直于电场线方向射入两平行板间的匀强电场中．图8设带电粒子的电荷量为－q 、质量为m (不计重力)，平行板长为L ，两板间距离为d ，电势差为U .(1)①你认为带电粒子的运动同哪种运动类似，这种运动的研究方法是什么？ ②带电粒子在电场中的运动可以分解为哪两种运动？ (2)如图9所示，求射出电场的带电粒子在电场中运动的时间t .图9(3)求粒子运动的加速度．(4)求粒子射出电场时在电场力方向上的偏转距离y . (5)求粒子离开电场时速度的偏转角θ(用正切值表示)．答案 (1)①带电粒子以初速度v 0垂直于电场线方向射入匀强电场时，受到恒定的与初速度方向垂直的电场力作用而做匀变速曲线运动，类似于力学中的平抛运动，平抛运动的研究方法是运动的合成和分解．②a.带电粒子在垂直于电场线方向上不受力，做匀速直线运动．b ．在平行于电场线方向上，受到电场力的作用做初速度为零的匀加速直线运动． (2)粒子在电场中的运动时间t ＝L v 0.(3)匀强电场的场强E ＝U d ，带电粒子所受电场力F ＝qE ，则加速度a ＝F m ＝qUmd .(4)电场力方向上的偏转距离： y ＝12at 2＝12×qU md ×⎝⎛⎭⎫L v 02＝qUL 22md v 02. (5)沿电场方向v y ＝at ，tan θ＝v y v 0＝at v 0＝qUL md v 02.1．运动分析及规律应用粒子在板间做类平抛运动，应用运动分解的知识进行分析处理． (1)在v 0方向：做匀速直线运动；(2)在电场力方向：做初速度为零的匀加速直线运动． 2．过程分析如图10所示，设粒子不与平行板相撞图10初速度方向：粒子通过电场的时间t ＝lv 0电场力方向：加速度a ＝qE m ＝qUmd离开电场时垂直于板方向的分速度 v y ＝at ＝qUlmd v 0速度与初速度方向夹角的正切值 tan θ＝v y v 0＝qUl md v 02离开电场时沿电场力方向的偏移量y ＝12at 2＝qUl 22md v 02. 3．两个重要推论(1)粒子从偏转电场中射出时，其速度方向的反向延长线与初速度方向的延长线交于一点，此点为粒子沿初速度方向位移的中点．(2)位移方向与初速度方向间夹角α的正切值为速度偏转角θ正切值的12，即tan α＝12tan θ.4．分析粒子的偏转问题也可以利用动能定理，即qEy ＝ΔE k ，其中y 为粒子在偏转电场中沿电场力方向的偏移量．例3 如图11所示为示波管中偏转电极的示意图，两板间距离为d ，长度为l 的平行板A 、B 加上电压后，可在A 、B 之间的空间中(设为真空)产生电场(设为匀强电场)．在距A 、B 等距离处的O 点，有一电荷量为＋q 、质量为m 的粒子以初速度v 0沿水平方向(与A 、B 板平行)射入电场(图中已标出)，不计粒子重力，要使此粒子能从C 处射出电场，则A 、B 间的电压应为( )图11A.m v 02d 2ql 2B.m v 02l 2qd 2 C.lm v 0qd D.q v 0dl答案 A解析 带电粒子只受电场力作用，在平行板间做类平抛运动．设粒子由O 到C 的运动时间为t ，则有l ＝v 0t ；设A 、B 间的电压为U ，则偏转电极间匀强电场的场强E ＝Ud ，粒子所受电场力F ＝qE ＝qU d ；根据牛顿第二定律可得粒子沿电场方向的加速度a ＝F m ＝qUmd ，粒子在沿电场方向做匀加速直线运动，位移为12d ，由匀加速直线运动的规律得d 2＝12at 2，联立解得U＝m v 02d 2ql 2，选项A 正确．例4 一束电子流经U 1＝5 000 V 的加速电压加速后，在距两极板等距离处垂直进入平行板间的匀强电场，如图12所示，两极板间电压U 2＝400 V ，两极板间距离d ＝2.0 cm ，板长L 1＝5.0 cm.图12(1)求电子在两极板间穿过时的偏移量y ；(2)若平行板的右边缘与屏的距离L 2＝5 cm ，求电子打在屏上的位置与中心O 的距离Y (O 点位于平行板水平中线的延长线上)；(3)若另一个质量为m (不计重力)的二价负离子经同一电压U 1加速，再经同一偏转电场射出，则其射出偏转电场的偏移量y ′和打在屏上的偏移量Y ′各是多大？ 答案 (1)0.25 cm (2)0.75 cm (3)0.25 cm 0.75 cm 解析 (1)电子加速过程，由动能定理得eU 1＝12m v 02①进入偏转电场，电子在平行于极板的方向上做匀速直线运动， L 1＝v 0t ②在垂直于极板的方向上做匀加速直线运动，加速度为 a ＝F m ＝eU 2dm ③ 偏移距离y ＝12at 2④由①②③④得：y ＝U 2L 124dU 1，代入数据得：y ＝0.25 cm.(2)如图，由几何关系知：yY ＝L 12L 12＋L 2得：Y ＝L 1＋2L 2L 1y 代入数据得：Y ＝0.75 cm.(3)因y ＝U 2L 124dU 1，Y ＝L 1＋2L 2L 1y ，偏移量与粒子的质量m 和电荷量q 无关，故二价负离子经同样装置后，y ′＝y ＝0.25 cm ，Y ′＝Y ＝0.75 cm.电性相同的不同粒子经相同电场加速再经同一偏转电场，射出偏转电场时，不会分开. 例5 如图13所示，两个板长均为L 的平板电极，平行正对放置，两极板间距离为d ，极板之间的电势差为U ，板间电场可以认为是匀强电场．一个带电粒子(质量为m ，电荷量为＋q ，可视为质点)从正极板边缘以某一初速度垂直于电场方向射入两极板之间，到达负极板时恰好落在极板边缘．忽略重力和空气阻力的影响．求：图13(1)两极板间的电场强度大小E . (2)该粒子的初速度大小v 0.(3)该粒子落到负极板时的末动能E k . 答案 (1)U d (2)LdUq 2m(3)Uq ⎝⎛⎭⎫1＋L 24d 2解析 (1)两极板间的电压为U ，两极板间的距离为d ，所以电场强度大小为E ＝Ud .(2)带电粒子在极板间做类平抛运动，在平行于极板方向上有L ＝v 0t 在垂直于极板方向上有d ＝12at 2根据牛顿第二定律可得：a ＝Fm ，而F ＝Eq所以a ＝Uqdm解得：v 0＝LdUq 2m. (3)根据动能定理可得Uq ＝E k －12m v 02解得E k ＝Uq ⎝⎛⎭⎫1＋L 24d 2.1．(示波管的原理)如图14是示波管的原理图．它由电子枪、偏转电极(XX ′和YY ′)、荧光屏组成，管内抽成真空．给电子枪通电后，如果在偏转电极XX ′和YY ′上都没有加电压，电子束将打在荧光屏的中心O 点．图14(1)带电粒子在________区域是加速的，在________区域是偏转的．(2)若U YY ′＞0，U XX ′＝0，则粒子向________极板偏移，若U YY ′＝0，U XX ′＞0，则粒子向________极板偏移． 答案 (1)Ⅰ Ⅱ (2)Y X2．(带电粒子的直线运动)两平行金属板间距离为d ，电势差为U ，一电子质量为m ，电荷量为e ，从O 点沿垂直于极板的方向射入，最远到达A 点，然后返回，如图15所示，OA ＝L ，则此电子具有的初动能是( )图15A.edL U B ．edUL C.eU dL D.eULd答案 D解析 电子从O 点运动到A 点，因受电场力作用，速度逐渐减小．根据能量守恒定律得12m v 02＝eU OA ，U OA ＝EL ＝UL d ，故12m v 02＝eULd，所以D 正确．3．(带电粒子的偏转)(2019·荆州市车胤中学高二上月考)如图16所示，电子在电势差为U 1的加速电场中由静止开始运动，然后射入电势差为U 2的两块平行极板间的电场中，射入方向跟极板平行，整个装置处在真空中，电子的重力可忽略．在满足电子能射出平行极板的条件下，下述四种情况，一定能使电子的偏转角θ变大的是( )图16A ．U 1变大、U 2变大B ．U 1变小、U 2变大C ．U 1变大、U 2变小D ．U 1变小、U 2变小答案 B解析 设电子被加速后获得的速度为v 0，由动能定理得qU 1＝12m v 02，设极板长为l ，则电子在极板间偏转的时间t ＝lv 0，设电子在平行极板间运动的加速度为a ，由牛顿第二定律得a＝qE m ＝qU 2dm ，电子射出平行极板时，竖直分速度v y ＝at ，联立可得：v y ＝qU 2ldm v 0，tan θ＝v y v 0＝U 2l 2dU 1，故U 2变大、U 1变小时，一定能使偏转角θ变大，选项B 正确，选项A 、C 、D 错误．4．(带电粒子的偏转)如图17所示，电子从静止开始被U ＝180 V 的电场加速，沿直线垂直进入另一个场强为E ＝6 000 V/m 的匀强偏转电场，而后电子从极板右侧离开偏转电场．已知电子比荷为e m ≈169×1011 C/kg ，不计电子的重力，偏转极板长为L ＝6.0×10－2 m ．求：图17(1)电子经过电压U 加速后的速度大小v x ； (2)电子在偏转电场中运动的加速度大小a ；(3)电子离开偏转电场时的速度方向与进入该电场时的速度方向之间的夹角θ. 答案 (1)8×106 m /s (2)1.1×1015 m/s 2 (3)45° 解析 (1)根据动能定理有eU ＝12m v x 2，解得v x ＝8×106 m/s.(2)电子在偏转电场中受到竖直向下的电场力， 根据牛顿第二定律有a ＝eEm ，解得a ≈1.1×1015 m/s 2.(3)电子在水平方向上做匀速直线运动，故t ＝Lv x ，在竖直方向上做初速度为零的匀加速直线运动， 故v y ＝at ，又tan θ＝v yv x ，联立解得θ＝45°.考点一 带电粒子的直线运动1．质子(11H)、α粒子(42He)、钠离子(Na ＋)三个粒子分别从静止状态经过电压为U 的同一电场加速后，获得动能最大的是( ) A ．质子(11H) B ．α粒子(42He) C ．钠离子(Na ＋)D ．都相同答案 B解析 qU ＝12m v 2－0，U 相同，α粒子带的正电荷多，电荷量最大，所以α粒子获得的动能最大，故选项B 正确．2.(多选)一质量为m 、电荷量为q 的带正电粒子(重力不计)以速度v 0逆着电场线方向射入有左边界的匀强电场，场强为E (如图1所示)，则( )图1A ．粒子射入的最大深度为m v 02qEB ．粒子射入的最大深度为m v 022qEC ．粒子在电场中运动的最长时间为m v 0qED ．粒子在电场中运动的最长时间为2m v 0qE答案 BD解析 粒子射入到最右端，由动能定理得－Eqx max ＝－12m v 02，最大深度x max ＝m v 022qE ；由v 0＝at ，a ＝Eqm ，可得t ＝m v 0Eq ，则粒子在电场中运动的最长时间为2m v 0qE ，选项B 、D 正确．考点二 带电粒子的偏转3．一电子以初速度v 0沿垂直场强方向射入两平行金属板间的匀强电场中，现减小两板间的电压，则电子穿过两平行板所需的时间( ) A ．随电压的减小而减小 B ．随电压的减小而增大 C ．与电压减小与否无关 D ．随两板间距离的增大而减小 答案 C解析 电子垂直于场强方向射入两平行金属板间的匀强电场中，在平行于金属板的方向电子不受力而做匀速直线运动，由L ＝v 0t 得，电子穿过平行板所需要的时间为t ＝Lv 0，与金属板的长度成正比，与电子的初速度大小成反比，与其他因素无关，即与电压及两板间距离均无关，故C 正确．4.(2019·人大附中高二期中)如图2所示，有一带电粒子贴着A 板沿水平方向射入匀强电场，当偏转电压为U 1时，带电粒子沿①轨迹从两板正中间飞出；当偏转电压为U 2时，带电粒子沿②轨迹落到B 板中间；设粒子两次射入电场的水平速度相同，则两次偏转电压之比为( )图2A ．U 1∶U 2＝1∶8B ．U 1∶U 2＝1∶4C ．U 1∶U 2＝1∶2D ．U 1∶U 2＝1∶1答案 A解析 带电粒子在匀强电场中做类平抛运动，水平位移为x ＝v 0t ，两次运动的水平位移大小之比为2∶1；两次运动的水平速度相同，故运动时间之比为t 1∶t 2＝2∶1；由于竖直方向上的位移为h ＝12at 2，h 1∶h 2＝1∶2，故加速度大小之比为a 1∶a 2＝1∶8，又a ＝Uq md AB ，故两次偏转电压之比为U 1∶U 2＝1∶8，故A 正确．5.(多选)如图3所示，矩形区域ABCD 内存在竖直向下的匀强电场，两个带正电的粒子a 和b 以相同的水平速度射入电场，粒子a 由顶点A 射入，从BC 的中点P 射出，粒子b 由AB 的中点O 射入，从顶点C 射出，若不计重力，则( )图3A ．a 和b 在电场中运动的时间之比为1∶2B ．a 和b 在电场中运动的时间之比为2∶1C ．a 和b 的比荷之比为1∶8D ．a 和b 的比荷之比为8∶1 答案 AD解析 两个粒子在水平方向上做匀速直线运动，a 、b 两粒子的水平位移大小之比为1∶2，根据x ＝v 0t 可知运动时间之比为1∶2；粒子在竖直方向上做初速度为零的匀加速直线运动，根据y ＝12at 2，两粒子在竖直方向上的位移大小之比为2∶1，则a 、b 的加速度大小之比为8∶1，根据牛顿第二定律知加速度大小a ＝qEm，则加速度之比等于两粒子的比荷之比，故两粒子的比荷之比为8∶1，A 、D 正确，B 、C 错误． 考点三 带电粒子的加速与偏转6.(多选)(2019·扬州市高一期末)如图4所示是某示波管的示意图，电子先由电子枪加速后进入偏转电场，如果在偏转电极上加一个电压，则电子束将会偏转，并飞出偏转电场．下列措施中能使电子偏转距离变大的是( )图4A ．尽可能把偏转极板L 做得长一点B ．尽可能把偏转极板L 做得短一点C ．尽可能把偏转极板间的距离d 做得小一点D ．将电子枪的加速电压提高 答案 AC解析 设加速电压为U 1， 则qU 1＝12m v 02①设偏转电压为U 2，则由L ＝v 0t ，a ＝Eq m ，y ＝12at 2可得y ＝qU 2L 22md v 02② 联立①②解得，y ＝U 2L 24dU 1，故选A 、C.7．有一种电荷控制式喷墨打印机的打印头的结构简图如图5所示，其中墨盒可以喷出极小的墨汁微粒，此微粒经过带电室后以一定的初速度垂直射入偏转电场，再经偏转电场后打到纸上，显示出字符．现为了使打在纸上的字迹扩大，下列措施可行的是( )图5A ．增大墨汁微粒所带的电荷量B ．增大墨汁微粒的质量C ．减小极板的长度D ．减小偏转板间的电压答案 A解析 使打在纸上的字迹扩大，实质是指速度偏向角θ增大，tan θ＝v y v 0＝Uqldm v 02增大，微粒所带的电荷量q 增大时，tan θ增大，字迹扩大，选项A 正确；增大墨汁微粒的质量或减小偏转板间的电压或减小极板的长度时，tan θ减小，字迹缩小，选项B 、C 、D 错误．8.(多选)(2019·广州二中期中)如图6所示，氕、氘、氚的原子核自初速度为零经同一电场加速后，又经同一匀强电场偏转，最后打在荧光屏上，那么( )图6A ．经过加速电场的过程中，电场力对氚核做的功最多B ．经过偏转电场的过程中，电场力对三种核做的功一样多C ．三种原子核打在屏上的速度一样大D ．三种原子核都打在屏的同一位置上 答案 BD解析 设偏转极板的长度为L ，板间距离为d ，在加速电场中电场力做的功W ＝qU 1＝12m v 02，由于加速电压相同，电荷量相等，所以电场力做的功相等，故选项A 错误；在偏转电场中的偏转位移y ＝12at 2＝12·qU 2md ·(L v 0)2，解得y ＝U 2L 24U 1d ，同理可得到偏转角度的正切值tan θ＝U 2L2U 1d ，可见y 和tan θ与电荷的电荷量和质量无关，所以q U 2yd 为定值，出射点的位置相同，出射速度的方向也相同，故三种原子核打在屏上同一点，故选项B 、D 正确；整个过程运用动能定理得12m v 2＝qU 1＋q U 2yd ，由于三种原子核的电荷量相同，质量不同，则v 不同，故选项C 错误．9.如图7所示，有一电子(电荷量为e )经电压U 0由静止加速后，进入两块间距为d 、电压为U 的平行金属板间．若电子从两板正中间垂直电场方向射入，且正好能穿过电场，求：图7(1)金属板AB 的长度； (2)电子穿出电场时的动能． 答案 (1)d2U 0U(2)e ⎝⎛⎭⎫U 0＋U 2 解析 (1)设电子离开加速电场时速度为v 0，由动能定理得eU 0＝12m v 02①设金属板AB 的长度为l ，则电子偏转时间t ＝lv 0②偏转加速度a ＝eUmd ③偏转位移y ＝12d ＝12at 2④由①②③④得l ＝d2U 0U. (2)设电子穿出电场时的动能为E k ，根据动能定理得 E k ＝eU 0＋e ·U2＝e ⎝⎛⎭⎫U 0＋U 2. 10．长为L 的平行金属板水平放置，两极板带等量的异种电荷，板间形成匀强电场，一个带电荷量为＋q 、质量为m 的带电粒子，以初速度v 0紧贴上极板垂直于电场线方向进入该电场，刚好从下极板边缘射出，射出时速度恰与水平方向成30°角，如图8所示，不计粒子重力，求：图8(1)粒子离开电场时速度的大小； (2)匀强电场的场强大小； (3)两板间的距离．答案 (1)23v 03 (2)3m v 023qL (3)36L解析 (1)粒子离开电场时，速度与水平方向夹角为30°，由几何关系得：v ＝v 0cos 30°＝23v 03.(2)粒子在匀强电场中做类平抛运动，在水平方向上：L ＝v 0t ，在竖直方向上：v y ＝atv y ＝v 0tan 30°＝3v 03由牛顿第二定律有：qE ＝ma 联立解得：E ＝3m v 023qL.(3)粒子在匀强电场中做类平抛运动，在竖直方向上： d ＝12at 2，解得：d ＝36L .11．如图9所示为真空示波管的示意图，电子从灯丝K 发出(初速度不计)，经灯丝与A 板间的加速电压U 1加速，从A 板中心孔沿中心线KO 射出，然后进入两块平行金属板M 、N 间的偏转电场中(偏转电场可视为匀强电场)，电子进入偏转电场时的速度与电场方向垂直，电子经过偏转电场后打在荧光屏上的P 点．已知M 、N 两板间的电压为U 2，两板间的距离为d ，板长为L 1，板右端到荧光屏的距离为L 2，电子质量为m ，电荷量为e .求：图9(1)电子穿过A 板时的速度大小； (2)电子从偏转电场射出时的侧移量； (3)P 点到O 点的距离． 答案 (1)2eU 1m (2)U 2L 124U 1d (3)(2L 2＋L 1)U 2L 14U 1d解析 (1)设电子经电压U 1加速后的速度为v 0，根据动能定理得eU 1＝12m v 02，解得v 0＝2eU 1m. (2)电子以速度v 0进入偏转电场后，垂直于电场方向做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动，设偏转电场的电场强度为E ，电子在偏转电场中运动的时间为t 1，电子的加速度为a ，离开偏转电场时的侧移量为y 1，根据牛顿第二定律和运动学公式得F ＝eE ，E ＝U 2d ，F ＝ma ，t 1＝L 1v 0，y 1＝12at 12，解得y 1＝U 2L 124U 1d.(3)设电子离开偏转电场时沿电场方向的速度为v y ，根据运动学公式得v y ＝at 1，电子离开偏转电场后做匀速直线运动，设电子离开偏转电场后打在荧光屏上所用的时间为t 2，电子从离开偏转电场到打到荧光屏上的侧移量为y 2，如图所示．有t 2＝L 2v 0，y 2＝v y t 2，解得y 2＝U 2L 1L 22dU 1P 点到O 点的距离为y ＝y 1＋y 2＝(2L 2＋L 1)U 2L 14U 1d.。