交流电有效值的求法

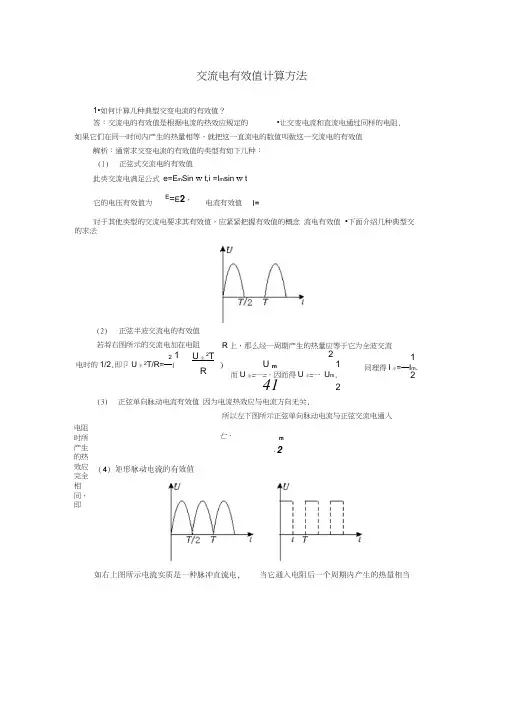
交流电有效值计算方法1•如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的•让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值解析：通常求交变电流的有效值的类型有如下几种：(1)正弦式交流电的有效值此类交流电满足公式e=E m Sin w t,i =I m sin w t对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念流电有效值的求法(2)正弦半波交流电的有效值若将右图所示的交流电加在电阻2 1电时的1/2,即卩U半2T/R=—(2U m 1而U全=—=，因而得U半=一U m,412(3)正弦单向脉动电流有效值因为电流热效应与电流方向无关,电阻时所产生的热效应完全相同，即它的电压有效值为E=E2，电流有效值•下面介绍几种典型交R上，那么经一周期产生的热量应等于它为全波交流U全2TR1同理得I半=—I m.2所以左下图所示正弦单向脉动电流与正弦交流电通入七，m、222 于直流电产生热量的—，这里t是一个周期内脉动时间.由I矩2RT= ( — ) I m2RT或()T T RT=T(牛)「得1矩=：T Im，U矩=4.当T=1/2时，1：2im，U矩、2Um.(5)非对称性交流电有效值假设让一直流电压U和如图所示的交流电压分别加在冋一电阻上，交变电流在一个周期内产生的热量为Q1=2 2U1 T U2 T ..................... . .............. ..，直流电在相等时间内产生的热量R 2 R 22•—电压U o=1O V的直流电通过电阻R在时间t内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t时间内直流电压U o在电阻R上产生的热量与同一时间内交流电压的有效值U在电阻R/2上产生的热量相同，则3•在图示电路中，已知交流电源电压u=200si n10n t V,电阻R=10 Q ,则电流表和电压表读数分别为A.14.1 A,200 VC.2 A,200 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为200V=141 V,电流值i=U= ：00R 衬2汉10 A=14.1 A.U2T,根据它们的热量相等有+U 2 )，同理有I = £(I 1I22).2 2知=胡「所以U哼=5 2 VB.14.1 A,141 VD.2 A,141 V答案：B2。

求交流电有效值的方法
交流电的有效值是根据电流的热效应规定的。

在求交流电的有效值时，通常采用以下几种方法：
直接计算法：对于已知波形的交流电，如正弦波、方波、三角波等，可以根据其波形特点直接计算出有效值。

例如，对于正弦波交流电，其有效值等于峰值除以根号2。

积分法：对于任意波形的交流电，可以通过积分的方式计算其有效值。

具体步骤是，将交流电在一个周期内的瞬时值进行平方，然后对时间进行积分，最后取平方根即可得到有效值。

这种方法需要知道交流电的瞬时值表达式或者采样数据。

仪表测量法：在实际应用中，通常使用电表来测量交流电的有效值。

电表内部采用了专门的电路和算法来计算有效值，可以直接显示出测量结果。

需要注意的是，不同类型的电表可能采用不同的计算方法，因此测量结果可能存在一定的误差。

需要注意的是，在求交流电的有效值时，需要明确所求的是电压有效值还是电流有效值，并且要注意单位的一致性。

此外，对于非正弦波形的交流电，其有效值并不能简单地用峰值除以根号2来计算，而需要根据其波形特点进行具体分析。

总之，求交流电的有效值需要根据具体情况选择合适的方法，并且要注意测量误差和单位的一致性。

在实际应用中，还需要考虑交流电的频率、波形等因素对有效值的影响。

余弦式交流电有效值公式交流电有效值公式是余弦式交流电有效值（简称 TP)公式的简称，是指用一个数表示两个数之间相等或相反关系的一种常用数学式。

其计算过程为:(a+ b):其中 a= b+ c表示一个被测量事物与一个被测量物体之间、被测量事物与电源线之间、电源线与电流源之间是等价关系。

当用 TP来表示时，余弦式交流电有效值公式为：下面我们来看看 TP公式到底有什么不同？一、TP的意义对于实际交流电，其电流与电压的相等或相反关系就是实际的有效量，如直流电流与交流电压的相等、交流电压与交流电流的相等等等。

所以，交流电有效值(TP)是反映直流电和交流电有效值的一个重要指标。

用直流电流的有效值(TP)表示交流电的有效量，可表示为：交流电有效值(TP)=交流电流有效值(tP)/两个交流电流有效值(tP)= TP÷2+ TP,其中 TP/2= tP/2,且 tP为整数。

当交流电有效值表示 TP时可选用电压有效值(tP)或电流有效值(tP)作为测量手段。

TP中 TP可表示为: TP/2=50-50; TP/2=1-1; TP/2=0.5-1; TP/2=0.5-1; TP/2=1-1, TP/2=0.5-1。

二、TP是电的参数通过上面的计算可以知道，余弦式有效值公式在计算电流时所采用的参数基本相同，而且在计算电压时也基本相同。

对于电压为(Vd, Vr, Ve)的交流电来说, TP实际上就是在电路中所产生的一种电压和电流。

也就是说 TP就是电(Vd和 Vr)的参数，它反映了一种客观存在的电流和电压的关系。

电压如果不是非常大，也不是非常小，则很难通过计算求出其 TP值。

而电流往往是在电路中一次通过导体产生的能量多于一次通过导体产生的能量的总和。

三、TP和电流源之间的关系如果要求额定电流的电压 A,可以采用额定电流 A=额定电压，这也是理论上可以理解的一种近似方法。

因此在实际工作中，要用电流 A与电流源 B的乘积来表示。

交流电有效值的计算交流电有效值的计算是电力工程中非常重要的一个概念。

有效值是指交流电信号的大小，用来衡量交流电的功率和能量。

在电力系统中，有效值是计算电流、电压以及功率等重要参数的基础。

下面将详细介绍交流电有效值的计算方法。

首先，我们需要了解什么是交流电。

交流电是指电流和电压在正负方向之间周期性地变化的电信号。

交流电的波形通常为正弦波，在一个周期内，电流和电压的大小是不断变化的，有正向峰值和负向峰值。

要计算交流电的有效值，我们首先需要了解什么是有效值。

有效值是指在交流电信号变化周期内的等效直流电量的大小，也可以理解为交流电信号的均方根值。

有效值与交流电信号的振幅有关，但并不等于峰值或均值。

对于正弦波信号来说，有效值可以通过峰值的大小来计算。

峰值是指正弦波信号的最大幅值，即电流或电压的最大值。

通过峰值可以计算有效值的大小。

具体的计算公式为：U_eff = U_peak / √2其中，U_eff 代表电压的有效值，U_peak 代表电压的峰值。

对于其他波形的信号，有效值的计算可能比较复杂。

但是在实际工程中，我们通常会将非正弦波信号近似为正弦波信号进行计算，因为正弦波信号的计算方式较为简单，而且与真实波形相差并不大。

在实际应用中，我们通常会用示波器来测量交流电信号的波形，然后通过示波器读数来计算有效值。

示波器可以将交流信号的波形显示在屏幕上，并且可以读取波形的峰值。

通过读取峰值，我们可以应用上述公式计算出有效值。

除了示波器的方法，还可以使用多种仪器来测量交流电信号的有效值。

例如，数字多用表、电子万用表等仪器都有专门用来测量交流电信号有效值的功能。

这些仪器可以直接给出交流电信号的有效值，而无需进行计算。

除了测量，我们还可以通过数学方法来计算交流电信号的有效值。

这种方法适用于已知交流电信号的数学函数表达式的情况。

根据电流或电压的数学表达式，我们可以利用积分等方法求得交流电信号在一个周期内的均方根值，从而得到有效值。

有效值的计算公式在我们学习电学知识的时候，有一个非常重要的概念——有效值。

有效值的计算公式可是解决很多电学问题的关键哟！先来说说什么是有效值。

想象一下，我们家里用的交流电，它的电压和电流可不是一直保持不变的，而是像个调皮的孩子，一会儿高一会儿低，不断地变化。

那怎么衡量这种变化的电流或电压对电器的实际作用效果呢？这就引出了有效值的概念。

有效值指的是，让交流电和直流电通过相同的电阻，如果在相同的时间内它们产生的热量相等，那么这个直流电的数值就是交流电的有效值。

那有效值的计算公式是怎么来的呢？这就得从热效应说起啦。

假设一个交流电的表达式是 i = Iₘsin(ωt) ，其中 Iₘ 是交流电的峰值。

在一个周期 T 内，交流电产生的热量可以通过积分来计算。

经过一番复杂但有趣的数学推导（这里就不详细展开啦，不然会把大家绕晕的），最终得出有效值 I = Iₘ / √2 。

给大家举个我曾经遇到的例子。

有一次，我去一个朋友家，他正在为家里的电器故障发愁。

他说新买的灯泡没用多久就坏了，怀疑是电压出了问题。

我就用有效值的知识帮他分析，发现他们小区的电压波动较大，超过了灯泡所能承受的有效值范围。

经过和物业沟通，调整了电压，问题就解决啦。

再来说说在实际生活中的应用。

比如我们常见的电器，像电视、冰箱、空调等等，它们标注的电压和电流值通常都是有效值。

因为有效值能够更准确地反映出交流电对电器的实际作用效果，让我们知道电器在正常工作时所需要的稳定电压和电流。

在高中物理的学习中，掌握有效值的计算公式对于解决电路相关的题目至关重要。

比如说，当给出一个交流电的峰值，要计算通过电阻的电功率时，就得先求出有效值，再用公式 P = I²R 来计算。

总之，有效值的计算公式虽然看起来有点复杂，但只要我们理解了它的原理和应用，就能轻松应对各种电学问题，让我们在电学的世界里畅游无阻！就像我们在生活中解决一个又一个的小难题一样，只要找对方法，一切都会变得简单起来。

交流电有效值的计算交流电有效值的计算是指通过测量或计算得出交流电信号在一定时间内的平均能量大小。

在交流电中，电流和电压都是随时间变化的，因此不能直接使用最大值或峰值来表示电流或电压的大小。

有效值的概念旨在提供一个与直流电相同功率的参考值。

要计算交流电的有效值，可以使用以下三种方法：平均值法、功率法和积分法。

1. 平均值法：交流电的有效值可通过将电流或电压的平方信号取平均并开方来计算。

假设电流的波形为I(t)，则交流电的有效值表示为Irms，可用以下公式计算：Irms = √(1/T ∫[0 to T] I(t)²dt)其中，T表示一个完整的周期。

例如，如果电流的波形是正弦波，那么该方法可以简化为使用最大峰值电流的70.71%：Irms = Imax/√22.功率法：根据交流电功率的定义，可以使用功率计来测量电流和电压之间的功率输出。

根据功率的平方等于电流和电压乘积的平均值，可以将交流电的有效值表示为：Irms = √(Pavg/Vrms)其中，Pavg表示平均功率输出，Vrms表示电压的有效值。

这种方法适用于通过功率计间接测量交流电的有效值。

3.积分法：通过将电流或电压信号与一个参考信号进行积分，并将结果除以积分时间来计算有效值。

该方法需要使用一些数学和信号处理技术，通常在数字信号处理领域使用。

这些方法可以适用于各种交流电信号的有效值计算。

但需要注意的是，对于非线性或非周期性的波形，这些方法可能不适用。

在这种情况下，可以借助计算机和数值计算技术进行数值模拟和数据处理。

除了计算交流电的有效值，也可以使用示波器等检测设备来显示电流和电压的波形，并通过与标准波形进行比较来估计有效值。

交流电有效值计算在电力系统分析、电路设计和实际应用中具有重要意义。

它能够描述交流电信号的实际能量，为电力传输、电能计量和电气设备的设计和使用提供准确的参考值。

有效值计算也是交流电工程中一项基本的测量和分析技术。

交流电有效值的求解1．交变电流有效值的规定：交变电流、恒定电流I 直分别通过同一电阻R ，在相等时间内产生焦耳热分别为Q 交、Q 直，若Q 交＝Q 直，则交变电流的有效值I ＝I 直(直流有效值也可以这样算)．2．对有效值的理解：(1)交流电流表、交流电压表的示数是指有效值；(2)用电器铭牌上标的值(如额定电压、额定功率等)指的均是有效值；(3)计算热量、电功率及保险丝的熔断电流指的是有效值；(4)没有特别加以说明的，是指有效值；(5)“交流的最大值是有效值的2倍”仅用于正弦式电流．3．交流电通过电阻产生的焦耳热的计算只能用交变电流的有效值(不能用平均值)求解，求解电荷量时只能用交变电流的平均值(不能用有效值)计算．图10例2 一个匝数为100匝，电阻为0.5 Ω的闭合线圈处于某一磁场中，磁场方向垂直于线圈平面，从某时刻起穿过线圈的磁通量按图10所示规律变化．则线圈中产生交变电流的有效值为( )A ．5 2 AB ．2 5 AC ．6 AD ．5 A答案 B解析 0～1 s 内线圈中产生的感应电动势E 1＝n ΔΦΔt＝100×0.01 V ＝1 V ,1～1.2 s 内线圈中产生的感应电动势E 2＝n ΔΦΔt ＝100×0.010.2 V ＝5 V ，在一个周期内产生的热量Q ＝Q 1＋Q 2＝E 21Rt 1＋E 22R t 2＝12 J ，根据交变电流有效值的定义Q ＝I 2Rt ＝12 J 得I ＝2 5 A ，故B 正确，A 、C 、D 错误．例3 如图11所示电路，电阻R 1与电阻R 2串联接在交变电源上，且R 1＝R 2＝10 Ω，正弦交流电的表达式为u ＝202sin 100πt (V)，R 1和理想二极管D (正向电阻可看做零，反向电阻可看做无穷大)并联，则R 2上的电功率为( )图11A ．10 WB ．15 WC ．25 WD ．30 W二级管正向电阻可看做零，反向电阻可看做无穷大．答案 C解析 由图可知，当A 端输出电流为正时，R 1被短路，则此时R 2上电压有效值为：U 2＝U m 2＝20 V ，当B 端输出电流为正时，R 1、R 2串联，则R 2两端电压有效值为U 2′＝U 22＝10 V ，则在一个周期内的电压有效值为：U 2′2R 2×T 2＋U 22R 2×T 2＝U 2R 2×T 解得：U ＝510 V 则有：P 2＝U 2R 2＝25010 W ＝25 W.。

交流电有效值推导公式
交流电有效值指的是一个变化周而复始的电流或电压定义该信号的均值。

它在一种规律交流电路中比平均值大一倍，它是交流电路中最重要的参数之一。

对电流而言，有效值是指在钟形电流谱图的钟的半径，而电压的有效值则是指在正弦波电压谱图的正弦曲线的半峰值。

由此可见，有效值是很重要的概念，有效值推导公式旨在揭示这一概念使得其在实际应用中更加可视化和实现。

有效值推导公式的一般形式如下：对于任何有形式为f(t)的波形，其有效值可以写为：
f_eff=\frac{1}{T}\int^T_0 (f(t))^2dt
其中，T是波形的周期。

另一种经典形式则是：
f_eff=\sqrt{\frac{2}{pi}P_o}
其中，po是波形的功率。

不论是上述的哪种形式推导出的有效值，其准确性都要求波形信号完全遵从数学形状，不能存在任何外部干扰和异常断裂现象。

交流电的有效值推导公式可以应用到实际的日常生活中，例如汽车电子设备检测时需要测量电压和电流的有效值。

有效值推导公式能够更准确地表征出其实际特性，从而让维修工程师对电子设备进行更加科学的维护。

有效值推导公式对我们熟知的交流电有着重要的影响，已经运用到许多实际应用场景中去了，它能够更加有效地处理多种交流电相关的应用场景，提高维修效率以及增加研究发展的潜力。

交流电压有效值推导公式交流电压有效值是指在交流电压波形中，与该电压产生相同功率的直流电压。

它是交流电压的一种重要参数，也是电气工程中常用的参考值。

有效值的大小与交流电压的波形有关，不同波形的交流电压有效值不同。

下面将从基本概念、计算方法和应用等方面介绍交流电压有效值的推导公式。

一、基本概念交流电压是指电压随时间变化的信号，其波形一般为正弦波。

在正弦波中，电压的大小随时间按照正弦函数的规律变化，通过对其进行积分求平均值，得到交流电压的有效值。

有效值代表了交流电压的大小，并且与直流电压相当。

二、计算方法以正弦波为例，设交流电压的峰值为Vp，则其有效值记为Vrms。

根据正弦函数的性质可知，正弦波的峰值与有效值之间存在着一定的关系。

具体推导公式如下：1. 正弦波的峰值与有效值的关系正弦波的峰值是指波形中的最大值，通常用Vp表示。

有效值是指交流电压在一个周期内的平均值，通常用Vrms表示。

根据正弦波的性质可知，正弦波的峰值与有效值之间的关系为：Vp = Vrms * √2。

2. 交流电压有效值的推导公式由于正弦波的周期为2π，所以一个周期内的平均值可以通过对正弦函数进行积分求解。

对正弦函数积分得到的结果除以周期长度，即可得到交流电压的平均值。

为了方便计算，我们可以选择一个周期内的正半个周期进行计算。

具体推导过程如下：设正弦波的周期T，正半个周期长度为T/2，电压随时间的函数为V(t) = Vp * sin(ωt)，其中ω为角频率。

对V(t)在一个正半个周期内进行积分，得到的结果除以T/2，即可得到交流电压的平均值。

具体计算过程如下：∫[0, T/2] V(t) dt = ∫[0, T/2] Vp * sin(ωt) dt= -Vp/ω * cos(ωt) |[0, T/2]= -Vp/ω * (cos(ωT/2) - cos(0))= -Vp/ω * (cos(ωT/2) - 1)由于正弦函数的周期为2π，即ωT = 2π，所以cos(ωT/2) = cos(π) = -1。

1.如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻，如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值.解析：通常求交变电流的有效值的类型有如下几种：（1）正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2mE ，电流有效值I =2mI对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.（2）正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（R T U 2全），而U 全=2m U ，因而得U 半=21U m ，同理得I 半=21I m . （3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同，即U =2mU ，I =2mI .（4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ，这里t 是一个周期内脉动时间.由I 矩2R T =（T t ）I m 2RT 或（R U 2矩）T =T t （R u 2m ）T ,得I 矩=T t I m ，U 矩=T t U m .当Tt =1/2时，I 矩=21I m ，U 矩=21U m . （5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=RU 2T ，根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同，则3.在图示电路中，已知交流电源电压u=200s in 10πt V ，电阻R=10 Ω，则电流表和电压表读数分别为A,200 V A,141 VA,200 V A,141 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为 u =2200V=141 V ，电流值i =R U =102200 A= A. 答案：B。

交流电有效值计算方法交流电一般可以表示为一个周期性变化的正弦函数，即I(t) = I_m * sin(ωt+θ)其中，I(t)表示交流电流随时间变化的函数，I_m表示电流的峰值，ω表示角频率，t表示时间，θ表示相位。

有效值的计算方法有两种：平方平均法和积分法。

一、平方平均法：平方平均法是最常用的计算方法，它的基本思想是对交流电流或电压进行平方运算，并求取其平均值的平方根。

1.对交流电流或电压进行平方运算：I^2(t) = I_m^2 * sin^2(ωt+θ)或U^2(t) = U_m^2 * sin^2(ωt+θ)2.求取平均值并开根号：I_rms = sqrt(1/T * ∫[0, T] (I^2(t)) dt)或U_rms = sqrt(1/T * ∫[0, T] (U^2(t)) dt)其中，T是一个周期的时间长度。

二、积分法：积分法是直接对交流电流或电压进行积分运算，并求取积分结果与周期长度的比值的平方根。

1.对交流电流或电压进行积分运算：∫[0, T] (I(t)) dt或∫[0, T] (U(t)) dt2.求取积分结果与周期长度的比值的平方根：I_rms = sqrt(1/T * (∫[0, T] (I(t)) dt)^2)或U_rms = sqrt(1/T * (∫[0, T] (U(t)) dt)^2)其中，T是一个周期的时间长度。

无论是平方平均法还是积分法，求取有效值的步骤是类似的，只是具体的计算过程有所差别。

需要注意的是，对于其他波形，如方波、三角波等，求取有效值的方法可能会稍有不同，但基本思想是一致的。

在实际应用中，计算交流电有效值非常重要，因为有效值是描述交流电大小的一个重要指标，也是进行电路设计、电能计量和电能消耗分析等的基础。

总结起来，交流电有效值的计算方法可以通过平方平均法或积分法来实现，根据具体情况选择合适的方法进行计算。

交流电的有效值公式
关于交流电的有效值公式，我们首先需要了解的是什么是交流电的有效值。

交流电的有效值是其瞬时值的简单算术平均值，并不能真实反映出交流电能量的大小，因此我们采用一个能够真实反映交流电能量大小的数值——有效值。

有效值也叫
均方根值，它的定义是这样的一个常数，其在单位时间内的热效应等于同样时间内直流电流的热效应。

交流电的有效值公式表示为：I=I0/√2。

在这个公式中，I表示交流电的有效值，I0表示交流电的峰值。

这个公式简单明了，易于理解。

对于正弦交流电流，其有效值I=I0/√2约等于0.707I0。

意思是交流电流有效值
是峰值的0.707倍。

对于其他非正弦的交流电流，其有效值的计算会相对复杂，通
常需通过积分计算得出，这超出了我们这里的讨论范围。

综上，交流电的有效值公式为 I=I0/√2，其中I是交流电的有效值，也叫均方根值，I0是交流电的峰值。

这个公式直观地给出了交流电的有效值和峰值之间的关系，对于理解和计算交流电的有效值有重要的参考意义。

电流有效值计算公式对于正弦交流电流，其有效值等于其峰值电流的0.707倍。

换句话说，如果交流电流的峰值电流是I0，则其有效值为Irms = I0 × 0.707、这个公式适用于正弦交流电流的情况。

然而，在实际应用中，很多交流电流并不是正弦波形的，且频率也不一定一致。

为了计算这种非正弦波形交流电流的有效值，需要用到实际信号的波形特征。

为了计算非正弦波形交流电流的有效值，可以利用均方根法。

均方根法将交流电流信号平方后取均值，然后再开平方根。

这样可以保留原始信号的幅值信息，并且忽略它的相位信息。

设交流电流信号为I(t)，其平方为I2(t)。

令周期为T，则有：I2(t) = I1²sin²(ωt + φ1) + I2²cos²(ωt + φ2) +I3²sin²(ωt + φ3) + ...其中，I1, I2, I3...为不同频率的分量幅值，φ1, φ2, φ3...为不同频率的分量相位差。

根据均方根法，交流电流的有效值Irms可以通过以下公式计算：Irms = √[ (1/T)∫T[I2(t)dt] ]展开计算可得：Irms = √[1/T ∫T(I1²sin²(ωt + φ1) +I2²cos²(ωt + φ2) +I3²sin²(ωt + φ3) + ... )dt]将其中的正弦函数和余弦函数用它们的关系式转换为三角函数形式：sin²(ωt + φ) = (1 - cos(2ωt + 2φ))/2cos²(ωt + φ) = (1 + cos(2ωt + 2φ))/2代入原公式得：Irms = √[1/(2T) ∫T(I1²(1 - cos(2ωt + 2φ1)) + I2²(1 + cos(2ωt + 2φ2)) + I3²(1 - cos(2ωt + 2φ3)) + ... )dt]由于整个信号周期的积分值是一样的，所以可以将积分项化简为：Irms = √[1/2(I1² + I2² + I3² + ...) ]从上述公式可以看出，计算交流电流的有效值需要对不同频率的分量幅值进行平方求和，然后再开平方根。

正弦式交流电的有效值是指在相同的电阻上，如果通过一个直流电压能够产生与该交流电在一个周期内产生的平均功率相等的热量，则这个直流电压就称为该交流电的有效值。

对于正弦交流电而言，其数学表达式通常写作：\[ u(t) = A \cdot \sin(\omega t + \phi) \]其中：- \( A \) 是最大（峰值）电压或电流幅度，- \( \omega \) 是角频率，\( \omega = 2\pi f \)，其中\( f \) 是频率，- \( t \) 是时间，- \( \phi \) 是初相位。

有效值定义为：使交流电在电阻负载上产生的热量在相同时间内与恒定直流电在相同电阻上产生的热量相等的等效直流值。

推导过程可以基于功率计算来实现。

交流电的瞬时功率是电压和电流的乘积，对于阻性负载，电压和电流呈正比关系且同相位：\[ P(t) = u(t) \cdot i(t) \]而对于正弦交流电，电流\( i(t) \) 也具有类似的形式，即\( i(t) = I_m \cdot \sin(\omega t + \phi) \)，其中\( I_m \) 是电流的峰值。

平均功率在一个完整周期内的积分应当等于直流功率，即：\[ P_{avg} = \frac{1}{T} \int_{0}^{T} u(t) \cdot i(t) dt \]将正弦波形代入并利用三角函数的性质进行积分后，可以得到平均功率只与振幅的平方成比例：\[ P_{avg} = \frac{U_{rms}^2}{R} \]其中\( R \) 是负载电阻，\( U_{rms} \) 是电压的有效值。

解这个方程求得\( U_{rms} \)：\[ U_{rms} = \sqrt{\frac{1}{T} \int_{0}^{T} u^2(t) dt} \]对正弦波形\( u(t) = A \cdot \sin(\omega t) \) 进行平方并积分后，得到：\[ U_{rms} = \frac{A}{\sqrt{2}} \]因此，正弦交流电的有效值与其峰值之间的关系就是：\[ U_{rms} = \frac{A}{\sqrt{2}} \]这就是正弦交流电有效值的具体推导方法。

交流电有效值计算方法1.如何计算几种典型交变电流的有效值?答：交流电的有效值是根据电流的热效应规定的。

让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值. 解析：通常求交变电流的有效值的类型有如下几种：（1)正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2m E ，电流有效值I =2m I对于其他类型的交流电要求其有效值,应紧紧把握有效值的概念。

下面介绍几种典型交流电有效值的求法。

(2）正弦半波交流电的有效值 若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（R T U 2全）,而U 全=2m U ，因而得U 半=21U m ，同理得I 半=21I m 。

（3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同,即U =2m U ，I =2m I 。

（4)矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ，这里t 是一个周期内脉动时间.由I 矩2R T =(T t ）I m 2RT 或（R U 2矩）T =T t (R u 2m ）T ，得I 矩=T t I m ，U 矩=T t U m .当T t =1/2时，I 矩=21I m ，U 矩=21U m 。

（5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=R U 2T ，根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +。

交流电有效值计算公式推导交流电的有效值计算公式推导主要基于电流或电压的热效应。

有效值是指在一个周期内，交流电流或电压产生的热量与相同电阻的直流电流产生的热量相等的那个值。

为了推导交流电的有效值计算公式，我们以正弦交流电为例进行说明。

假设交流电压u(t) = Umsin(ωt)，其中Um为峰值，ω为角频率。

设电阻为R，交流电在一个周期T内通过电阻产生的热量为Q1，直流电在同样时间T内通过电阻产生的热量为Q2。

根据热效应原理，这两个热量相等，即Q1 = Q2。

首先计算交流电在一个周期内通过电阻产生的热量Q1。

由于交流电的电压是变化的，各瞬间功率不同，我们可以将一个周期内的热量计算分为无数个极短时间dt的累加。

在dt时间内，交流电的功率为i^2R，其中i为交流电流。

因此，在dt时间内产生的热量为i^2Rdt。

将一个周期T分为N个极短时间dt，那么交流电在一个周期内产生的热量Q1为：Q1 = ∫(0, T) i^2Rdt = R * [i^2(t)]_0^T接下来计算直流电在同样时间T内通过电阻产生的热量Q2。

由于直流电的电压和电流是恒定的，所以直流电在T时间内的功率为I^2R，其中I为直流电流。

因此，直流电在T时间内产生的热量Q2为：Q2 = I^2RT根据热效应原理，交流电和直流电产生的热量相等，即Q1 = Q2。

将上面两个公式相等，得到：R * [i^2(t)]_0^T = I^2RT由于交流电的有效值I与峰值Um和电阻R有关，我们需要求解上述公式中的I。

经过推导和化简，可以得到正弦交流电的有效值计算公式为：I = Um / √2这个公式表明，正弦交流电的有效值等于其峰值除以根号2。

类似地，对于正弦交流电流，其有效值计算公式为：I = Im / √2其中Im为交流电流的峰值。

对于其他类型的交流电，如矩形波、锯齿波等，有效值的计算方法与正弦交流电类似，需要根据有效值的定义进行求解。

交流电有效值的计算江苏省新海高级中学 崔晓霞 222006交变电流的大小和方向随时间作周期性变化。

为方便研究交变电流的特性，根据电流的热效应引入了有效值这一物理量。

一、 正弦交流电有效值表达式的推导：交流电的有效值是用它的热效应规定的，因此设法求出正弦交流电的热效应，才能求出其有效值，正弦交流电电压的瞬时值u =U m ·sinωt ，如果把这加在负载电阻R 上，它的瞬时电功率22cos 1sin 2222t R U t R U R u P mm ⋅-⋅=⋅==ωω 其图像如图1所示．由微元法可知，P-t 图线和t 轴之间所包围的面积就是功（图中打斜条的部分）．不难看出，图中有斜条打△的部分和无斜条打△的部分面积是相同的，因此打斜条部分的面积就是P =U 2m /2R 线和t 轴之间的面积．设正弦交流电电压的有效值是U ，根据有效值的定义：RU R U m 222= 可得：2/m U U = 同理可得：2/m I I =；2/m E E =此关系式仅适用于正弦交流电，那么非正弦交流电的有效值又该如何求解呢？二、非正弦交流电有效值的计算例1. 如图2甲乙所示分别表示交变电流随时间变化的图象，则这两个交流电的有效值分别是 V 和 A 。

解析：对于图甲，该交变电流在每个周期T 内都可看作两个阶段的直流电流：前T /3中，U 1=100V ，后2T /3中，U 2=50V 。

在一个周期中，该交变电流在电阻R 上产生的热量为：32503100323222221T R T R T R U T R U Q ⋅+⋅=+⋅= ① 设该交流电电压的有效值为U ，则上述热量T Q ⋅=RU 2②联立①、②两式，可得有效值为V 250=U 对于图乙，从t ＝0开始的任意一个周期内，前半周期是大小不变的直流电，为I A 15=，图1图2 甲 乙后半周期是有效值为I A 252=的交变电流。

设所求交变电流的有效值为I ，根据有效值的定义，选择一个周期的时间，利用在相同时间内通过相同的电阻所产生的热量相等，由焦耳定律得 I RT I R T I R T 2122222=+ 即I 2225125212=⨯+⨯() 解得I A =532 点评：对于非正弦交流电，要从有效值从定义出发，根据热效应求解。