应变si材料

strain的标准单位一、概述strain，也被称为应变，是材料科学、生物医学工程、机械工程等领域中的一个重要参数。

它描述了物体在受到应力作用后产生伸长或缩短的程度。

在国际单位制（SI）中，strain的标准单位是“百分之一”。

但是，这个单位并不是真正的“百分之一”，而是指物体长度相对于原始长度的变化量，即ε。

二、定义和公式在材料科学中，应变定义为物体伸长或缩短的长度与原始长度的百分比，即：ε = (L1 - L0) / L0其中，L1 是应变后的长度，L0 是原始长度。

需要注意的是，这个公式中的百分号并不是真正的百分之一，而是指ε这个参数的量级在百分之一左右。

三、单位换算在国际单位制（SI）中，strain的标准单位是“百分之一”，但实际上，它也可以用其他单位来表示，例如“微米”或“米”。

1% strain等于1微米，1米长的物体产生1%的应变等于1纳米。

需要注意的是，虽然可以用其他单位来表示strain，但是在科学和工程领域中，通常还是使用百分之一作为strain的标准单位。

四、应用场景strain是一个非常重要的参数，广泛应用于材料科学、生物医学工程、机械工程等领域。

在材料科学中，了解材料的应变性质可以帮助我们更好地了解材料的力学性能，例如强度、韧性等。

在生物医学工程中，了解组织的应变性质可以帮助我们更好地了解组织的生理功能和病理变化。

在机械工程中，了解机器部件的应变性质可以帮助我们更好地设计和维护这些部件。

五、结论总的来说，strain是一个非常重要的参数，它描述了物体在受到应力作用后产生伸长或缩短的程度。

在国际单位制（SI）中，它的标准单位是“百分之一”，但也可以用其他单位来表示。

了解和应用strain 的性质和单位，对于科学和工程领域的实践具有重要的意义。

同时，随着科技的发展，我们期待 strain 在未来会有更多的应用和探索。

六、参考文献1. 材料力学（张三著，李四出版社，2023年）2. 生物力学（王五主编，赵六出版社，2022年）3. 机械工程基础（孙七等著，刘八出版社，2021年）以上就是关于《strain的标准单位》的详细介绍，如想了解更多相关信息，请参考相关学术文献和网络资源。

国际单位制(si)泊松比
在国际单位制（SI）中，泊松比（Poisson's ratio）是一个无量纲的量，用于描述材料在受到外力作用时，垂直于外力方向的应变与外力方向上的应变的比值。

这个比值通常是横向应变与轴向应变的负值。

对于许多典型的固体材料，泊松比的值通常在0.2到0.3的范围内。

请注意，泊松比的值取决于材料的类型。

例如，对于体积模量远高于剪切模量的橡胶等软材料，泊松比接近0.5。

而对于开孔聚合物泡沫等材料，泊松比接近于零，因为在压缩时孔往往会塌陷。

在国际单位制（SI）中，泊松比并没有特定的单位，因为它是一个比值，没有具体的物理量纲。

在描述材料性质时，泊松比是一个重要的参数，因为它有助于理解材料在受力时的变形行为。

RPCVD生长应变Si-应变SiGe薄膜的研究摘要：本研究采用反应物化学气相沉积（RPCVD）技术，探究了应变Si和应变SiGe薄膜在不同生长条件下的微观结构和物理性质。

利用X射线衍射（XRD）、扫描电子显微镜（SEM）和透射电子显微镜（TEM）等手段，研究了不同温度、气压和气体混合比例对Si/SiGe界面形貌和晶体结构的影响。

结果表明，在合适的生长条件下，RPCVD可以生长出具有优异应变性和结晶质量的Si/SiGe多层薄膜。

同时，研究还探讨了生长过程中的应变行为和物理机制，为进一步优化RPCVD生长工艺提供了理论基础。

关键词：RPCVD；应变Si；应变SiGe；生长条件；微观结构；物理性质正文：引言在半导体电子学中，应变Si和应变SiGe材料的研究一直是热门领域之一。

应变技术可以有效提高传统Si材料的电学和光学性能，是实现高速电子器件和集成光电器件的有效手段。

RPCVD生长技术作为一种无污染、低成本、大面积制备应变材料的方法，具有广泛的应用前景。

本研究利用RPCVD技术生长应变Si和应变SiGe材料，并系统地探究了外延生长条件对Si/SiGe界面形貌和晶体结构的影响，旨在为研究应变材料的应用提供理论基础。

实验本实验采用RPCVD技术，在p-Si（001）衬底上生长Si和SiGe异质结构（SiGe厚度为20nm），并探究了不同生长条件对微观结构和物理性质的影响。

生长过程中，使用SiH4、GeH4和H2作为反应气体，生长温度和反应气压均在0.1~0.35Torr范围内，具体参数见表1。

表1. RPCVD生长条件参数值生长温度650~800℃反应气压 0.1~0.35TorrSiH4流量 20~40sccmGeH4流量 0~10sccmH2流量剩余结果与讨论样品生长后，用XRD对其结构进行了表征。

图1展示了不同生长温度下的XRD谱图。

可以看出，无论在哪种生长条件下，所有样品都表现为具有强烈的Si（004）和SiGe（004）峰的多层异质结构。

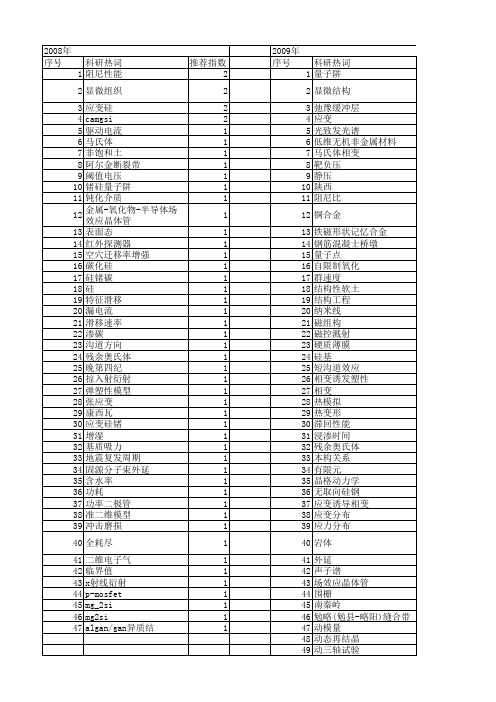
１０固体电子学研究与进展２８卷护№妇踹泡，应变＆ｈ＆。

譬竺薹慧兰表示搿副：∽，其中‘７潮：５是应变能，ＦＴ可表示为‘副：卧卅ｅｘｎｐ［＋－菩二赢Ｔ鼬）３∥。

Ｈ㈣，‘ｅ—Ｔ：带１则◆㈣，（△ｌ＇一△Ｉ）肛Ｂ｝（２３）一＋ｙ＾ｏ．ｊ。

ｕ叫＾…．２ｎ。

，。

ｎ低温时，晶格失配率可表示为‘６’１０］：△ＩＩ＝５２号ＤｕＰＴ（２４）１瓯瀛叫埔Ｂ怡大阢早ｗ衣小爿，一口璺生！苎２１［；：兰二三！±！：５ｘ一］一（ｔ一３００）×１０＿６｝一ａｓｉｅｘｐｌ－２．４４（ｔ一３００）×１０叫］，ｏ¨Ｊ２—————————ａ—ｓ＃—ｘｐ［匿．２—４４（≯ｔ１３—００）万可１０而汀——————＿皑＂一×叫）］…’Ｓｉ。

二，Ｇｅ。

合金和Ｓｉ轻空穴带的能量差△ｌ可表示押｝一搿７御；，Ⅳｃ№ｘｐ（一学ＩＨ些喾塑１１厶Ｉ‘虿１［一万５＋（９５２＋小一２ｓＡ）１脂－１（ｅＶ）（３３）（２８）价带劈裂能４可表示为［７’８］：Ａ２虿１［一云一（９ｓ２＋Ａｚ一２ｓＡ）１７２］（ｅＶ）（２９）其中Ａ＝０．０４４１＋０．２５３ｘ（ｅＶ）对于杂质电离能，采用线性内插法：Ｅ＾＝４３．８（１一ｚ）＋１０．４ｚ一△Ｅ。

，辩。

（ｍｅＶ）（３０）对于电子，若载流子浓度咒≤０．１Ⅳｃ，经典统计与费米统计的结果是一致的，若咒～Ⅳｃ，费米能级ＥＦ已经进人带内，属于简并的情况，必须用费米分布函数来计算ｍ］。

由于电子和空穴服从相同的统计分布，所以可以认为：若户≤０．１Ｍ，价带空穴浓度可用波尔兹曼统计计算；若Ｐ＞Ｐ，～Ｎｖ，价带空穴浓度可用费米分布函数来计算。

在０．１Ⅳｖ＜户＜夕。

，空穴浓度符合的统计规律由波尔兹曼统计向费米统计过渡。

为此，可以进行对空穴浓度作如下修正：没有进入简并时的空穴浓度ＰＡ用符号ＰＡ－表示，进入简并后的空穴浓度户一用符号户Ａｚ表示。

夕＾＝ａｐＡｌｅｘｐ（一７）＋少子的计算可采用如下公式：以＾－＝丢㈨，通过计算，可得到任意温度下的少子浓度。