高等数学A1试卷

高等数学试卷A1 一、一选择题1.函数的定义域为．A.正确B.不正确答案：A2.函数在点处可导．A.正确B.不正确答案：B3.极限．A.正确B.不正确答案：B4.定积分．A.正确B.不正确答案：A二、二选择题5.是偶函数．A.正确B.不正确答案：A6.设，则．A.正确B.不正确答案：A7.极限．A.正确B.不正确答案：B8.设，则微分．B.不正确答案：B9.不定积分．A.正确B.不正确答案：B10.是微分方程．A.正确B.不正确答案：A三、三选择题11.极限（）．A.B.C.D.答案：B12.设函数，则（）．A.B.C.D.答案：B13.设函数，则（）．A.B.C.D.14.不定积分（）．A.B.C.D.答案：C15.函数的图形如图示，则是函数的( ).A.最大值点B.最小值点C.极大值点D.极小值点答案：C16.下列表达式成立的是（）．A.B.C.D.答案：A四、四选择题17.不定积分（）．A.B.C.D.答案：B18.设则（）．A.B.C.D.答案：D19.函数, 则（）．A.是的驻点，但不是极值点B.是的驻点且为极小值点C.是的驻点且为极大值点D.不是的驻点答案：C20.微分方程的通解为( )．A.B.C.D.答案：A。

2015-2016年第二学期《高等数学AII 》期末考试试卷一、单项选择题（从4个备选答案中选择最适合的一项，每小题2分共20分） 1、三重积分⎰⎰⎰Ω=dV z y x f I ),,(，其中Ω由平面1=++z y x ，1=+y x ，0=x ，0=y ，1=z 所围，化为三次积分是（ B ） A 、 ⎰⎰⎰---=211010),,(y x x dz z y x f dy dx I ； B 、 ⎰⎰⎰---=111010),,(y x x dz z y x f dy dx I ；C 、 ⎰⎰⎰--=11110),,(yx dz z y x f dy dx I ； D 、 ⎰⎰⎰--=11010),,(yx x dz z y x f dy dx I .2、设y e x u 2=，则=du （ A ）A. dy e x dx xe y y 22+；B. dy e xdx y +2；C. dy xe dx e x y y 22+；D. dy e x dx e x y y 22+. 3、微分方程y dxdyx= 的通解为（ C ）. A. C x y +-=； B. C x y +=； C. Cx y =； D. x y =.4、设1∑是222y x R z --=上侧，2∑是222y x R z ---=下侧，3∑是xoy 平面上圆222R y x ≤+的上侧，R Q P ,,在3R 空间上有一阶连续偏导数，且0=∂∂+∂∂+∂∂zR y Q x P ，则与曲面积分⎰⎰∑++1Rdxdy Qdzdx Pdydz 相等的积分是（ B ）(A) ⎰⎰∑++2Rdxdy Qdzdx Pdydz ；(B) ⎰⎰∑++3Rdxdy Qdzdx Pdydz ；(C)Rdxdy Qdzdx pdydz ++⎰⎰∑∑21 ；(D)Rdxdy Qdzdx pdydz ++⎰⎰∑∑31 .5、微分方程x xe y y y 396-=+'-''的特解形式为（ B ）A 、x axe 3-；B 、x e b ax 3)(-+；C 、x e b ax x 3)(-+；D 、x e b ax x 32)(-+ 解：特征方程0)3(9622=-=+-r r r ，321==r r ，特解形式为x e b ax y 3)(-*+=.选（B ）. 6、当)0,0(),(→y x 时， 22yx xyu +=的极限为（ A ） A 、不存在； B 、1； C 、2； D 、0. 7、下列级数收敛的是（ B ） A 、∑+∞=+121n n ； B 、∑+∞=131sin n n ； C 、∑+∞=+1441n n n ； D 、∑+∞=-121)1(n n n . 8、微分方程02=-'+''y y y 的通解为（ C ）A. x x e C e C y --=21；B. 221x xe C e C y --=； C. 221x xe C eC y -=-； D. x x e C e C y 221+=-.解：特征方程0)1)(12(122=+-=-+r r r r ，11-=r ，212=r ，通解为221xx e C e C y -=-.选（C ）.9、设⎰⎰+=Ddxdy y x I 21)(，⎰⎰+=Ddxdy y x I 32)(，D 由直线1=x ，1=y 与1=+y x 围成，则1I 与2I 的大小关系是（ A ）A 、21I I <；B 、21I I =；C 、21I I >；D 、21I I ≥. 10、积分 0 0adx ⎰⎰的极坐标形式的二次积分为（ B ）A 、⎰⎰40csc 02πθθa dr r d ；B 、⎰⎰40sec 02πθθa dr r d ；C 、⎰⎰20tan 02πθθa dr r d ；D 、⎰⎰40sec 0πθθa rdr d .二、填空题（每空3分，共30分）1、微分方程0))(,,(4='''y x y y x F 的通解含有(独立的)任意常数的个数是 2 个.2、设)(x f 是周期为π2的周期函数，且⎩⎨⎧<≤<≤--=ππx x x x f 000)(，它的傅立叶级数的和函数为)(x S ，则=)5(πS 2π. 3、已知函数)ln(22y x z +=，则=∂∂-∂∂xzy y z x0 . 4、设平面曲线L 为1||||=+y x ，则曲线积分=⎰+ds e Ly x ||||e 24.5、若曲线积分⎰---=Ldy y ax xy dx y xy I )(3)6(2232与路径无关,则=a 2 。

高等数学a1
高等数学a1是一门基础性的数学课程，旨在为学生们打下良好的
数学基础。

它涵盖了基本代数，几何，微积分，矩阵理论等一系列重
要的数学课程。

主要目的是教授现代数学的基础概念及其应用，使学
生能掌握数学的基本技能，建立科学的思维模式，为学习各种问题解
决方法打下坚实的基础。

完成这门课程，学生需要掌握一系列关于二次、三次和高次方程
的基本问题，以及如何解决这类方程的问题。

包括如何解方程组，进
行元素替换，求解偏微分方程，求解杨辉三角，内积及外积的计算，
极限的求解，复数的概念，多项式的分析等等。

学生还应该掌握基本
的圆锥曲面重心，圆的各种参数及椭圆的定义，扩展的数论方程和相
关的数学分析等方面的知识。

此外，学生还需要理解和运用凸优化，概率论，拟合函数拟合，
矩阵理论，线性及非线性回归分析，不等式，推理，条件概率，复杂
性理论，离散数学及对对称性等概念及其应用。

完成这门课程，学生们需要掌握数学解题的重要策略，更广泛地
理解数学概念及其应用，不断地提高解决科学问题的能力，提高数学
思维的能力。

同时，学生也可以通过这门课程扩展你的抽象思维能力，更加有效地分析复杂的问题。

高等数学a1不仅可以为学生打下扎实的数学基础，而且可以提高学生的抽象思维能力，增强对复杂数学概念及其应用的认识，并发展学科问题解决能力。

因此，它不仅可以提高学生未来学习科学素质，而且可以提高学生未来从事科学应用领域的创新能力。

2006-2007学年第一学期 高等数学（A1）试题(A 卷)一、填空(本题共5小题,每小题3分,满分15分) 1.已知=++=⎪⎭⎫ ⎝⎛+)(,31122x f xx x x f 则 ____________. 2.设)(0x f '存在,则()()=--+→hh x f h x f h 000lim ____________.3.设)(x f 的原函数为xx ln ,则()='⎰dx x f ____________.4.向量{}4,3,4-=a在向量{}1,2,2=b上的投影是____________. 5. )1(1)(+=x xx f 按的幂展开到n 阶的泰勒公式是_________ .二、选择题(本题共5小题,每小题3分,满分15分) 1.设()x f 可导且()210='x f ，当0→∆x 时，()x f 在0x 处的微分dy与x ∆比较是（ ）无穷小.(A ) 等价 (B ) 同阶 (C ) 低阶 (D ) 高阶2．已知c bx ax x y +++=3323,在1-=x 处取得极大值,点(0,3)是拐点, 则（ ）.3,0,1)(3,1,0)(==-==-==c b a B c b a A 均错以上)( 0,1,3)(D c b a C =-==3．设)(x f 在[-5，5]上连续，则下列积分正确的是（ ）.[][]0)()()(0)()()(5555=--=-+⎰⎰--dx x f x f B dx x f x f A[][]0)()()(0)()()(550=--=-+⎰⎰dx x f x f D dx x f x f C4. 设直线L 为12241z y x =-+=-,平面0224:=-+-z y x π 则( ).上；在；平行于ππL L A )B ()(.(D);)(斜交与垂直于ππL L C5. 若0532<-b a ,则方程043235=++-c bx ax x ( ) (A ) 无实根; (B ) 有五个不同的实根. (C ) 有三个不同的实根; (D ) 有惟一实根;三、计算下列各题(本题共4小题,每小题7分,共28分) 1. .,1ln2sec 22dxdy ee y xxx求+-=2．设)(x y y =是由方程)ln()(2y x y x x y --=-确定的隐函数，求d y .3．求32)21ln(limxdtt x x ⎰+→.4. 求由参数方程()⎩⎨⎧=+=ty t x arctan 1ln 2所确定的函数的二阶导数.22dx yd四、求下列积分(本题共3小题,每小题7分,满分21分) 1.dx xx ⎰-21ln .2.⎰-dxxx42.3.().ln 11 12dx x x e ⎰-五、(7分)设,ln 1)(,1x xx f b a +=<<求证：)(41)()(0a b a f b f -≤-<.六、(7分)已知直线L 在平面01:=-++z y x π上,并且与直线⎪⎩⎪⎨⎧=+-=+=t z t y t x L 11:1垂直相交,求L 的方程.七、(7分)过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D .(1) 求D 的面积A .(2) 求D 绕直线x=e 旋转一周所成的旋转体的体积V .2006-2007学年第一学期 高等数学（A1）试题(A 卷)答案一、填空(本题共5小题,每小题3分,满分15分) 1．1)(2+=x x f ； 2. )(20x f '; 3.C xx +-2ln 1; 4. 2;5.[]之间与介于1,)1()1()1()1()1(111212-+-++++++++-=+++x x x x x xn n n nξξ二、选择题(本题共5小题,每小题3分,满分15分) 1. B 2. A 3. B 4. C 5. D三、计算下列各题(本题共4小题,每小题7分,共28分) 1. 解：()'⎪⎪⎭⎫ ⎝⎛+-'='1ln 2sec 22x xxe e y 2分⎪⎪⎭⎫ ⎝⎛+--=122212tan 2sec 2ln 222x xxxx e e6分112tan 2sec 2ln 22+-=xxx x e7分2. 解：[]1)ln()(2+--=-y x dy dx dx dy 5分 ()()dxy x y x dy -+-+=ln 3ln 2 7分3. 解：220323)21l n (l i m )21l n (l i mxx xdtt x x x +=+→→⎰4分 ⎪⎪⎪⎪⎭⎫⎝⎛+==→→xx x x x x x 6214l i m32l i m 2022032= 7分4. 解：ttt t dxdy21121122=++= 4分3222224112121tt tt tdxy d +-=+⋅-= 7分四、求下列积分(本题共3小题,每小题7分,满分21分) 1. 解：⎪⎭⎫⎝⎛--=-⎰⎰x d x dx x x 1112)ln (ln 2分⎰+--=dxxxx 211ln 4分C xx C xxx +-=+---=ln 11ln 7分2. 解：⎰⎰=∈=-tdtdxxx tx t 2220224tansec ),(π3分C t t dt t +-=-=⎰2tan 2)1(sec 22 6分Cxx+--=2242arccos7分3. 解：()()x d x dx x x e e ln ln 11lim ln 11 1212⎰⎰-→-=-+εε 4分()[]2ln arcsin lim 1πεε==-→+e x 7分五、(7分)设,ln 1)(,1x xx f b a +=<<求证：)(41)()(0a b a f b f -≤-<.证明：由拉格朗日中值定理()01)()(2>--=-a b a f b f ξξ 3分记)1(1)(2>-=x xx x g 4分⎪⎩⎪⎨⎧><==<<>-='20,2 ,021 ,02)(3x x x x x x g 5分 因此2=x 是)(x g 在),1(+∞内的最大值点，且41)2()(=≤g x g ，于是)(41)()(0a b a f b f -≤-< 7分六、(7分)已知直线L 在平面01:=-++z y x π上,并且与直线⎪⎩⎪⎨⎧=+-=+=t z t y t x L 11:1垂直相交,求L 的方程.解：直线L 的方向向量为k i kj is22111111-=-= 3分 将L 1代入平面方程得：1-=t ，π与1L 的交点坐标为（0，2，-1） 5分 直线L 的方程为：11021-+=-=z y x 或⎩⎨⎧==++201y z x 7分七、(7分)过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D .(1) 求D 的面积A .(2) 求D 绕直线x=e 旋转一周所成的旋转体的体积V .解：设切点坐标为：()00x x ln ,切线方程为：)(ln 0001x x x x y -=- 1分由于切线过原点，得切点坐标为：()1,e 2分 切线方程为：ex y =3分（1）()12ln 2ln 21 1-=--=-=⎰e x x x e xdx e D ee 5分（2）()22 65 312122πππππ+-=--=⎰e e dy e e e V y7分。

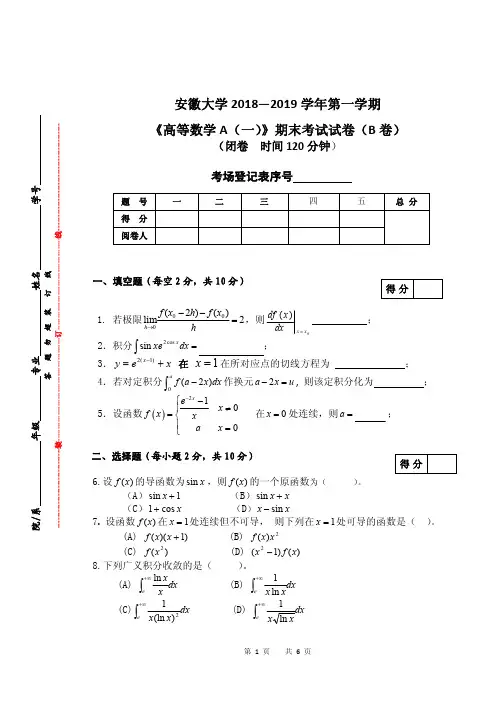
安徽大学2018—2019学年第一学期《高等数学A （一）》期末考试试卷（B 卷）（闭卷时间120分钟）考场登记表序号一、填空题（每空2分，共10分）1.若极限2)()2(lim000=--→h x f h x f h ，则0)(x x dxx df =；2．积分=⎰dx xe x cos 2sin ；3．x e y x +=-)1(2在1x =在所对应点的切线方程为；4．若对定积分0(2)a f a x dx -⎰作换元2a x u -=,则该定积分化为；5．设函数()2100x e x f x xa x -⎧-≠⎪=⎨⎪=⎩在0x =处连续，则a =；二、选择题（每小题2分，共10分）6.设)(x f 的导函数为x sin ，则)(x f 的一个原函数为（）。

（A）1sin +x （B）x x +sin （C）x cos 1+（D ）xx sin -7.设函数)(x f 在1=x 处连续但不可导，则下列在1=x 处可导的函数是（）。

(A))1)((+x x f (B)2)(x x f (C))(2x f (D))()1(2x f x -8.下列广义积分收敛的是（）。

(A)dx x x e ⎰+∞ln (B)dx x x e ⎰+∞ln 1(C)dx x x e ⎰+∞2)(ln 1(D)dx x x e ⎰+∞ln 1题号一二三四五总分得分阅卷人得分得分院/系年级专业姓名学号答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------9..设)(x f 为),(+∞-∞内连续的偶函数,)()(x f dxx dF =,则原函数)(x F （）。

南京工业大学 高等数学A-2 试题（A ）卷（闭）2013---2014 学年 第2学期 使用班级 江浦大一学生 班级 学号 姓名一、单项选择题(本大题共5小题, 每小题3分, 总计15分)1、直线12:201x y z l --==与平面:2+60x y z π--=之间的夹角为（ ） )(A 0 )(B 6π )(C 4π )(D 2π2、设函数(,)f x y 在点(,)a b 的偏导数存在，则0(,)(,)limx f a x b f a x b x→+--=（ ） )(A 0 )(B (2,)x f a b )(C (,)x f a b )(D 2(,)x f a b3、二次积分40(,)xdx f x y dy ⎰⎰交换积分次序后为（ ）)(A 40(,)y dy f x y dx ⎰⎰)(B 2404(,)yy dy f x y dx ⎰⎰)(C 2440(,)yydy f x y dx ⎰⎰)(D 44(,)dy f x y dx ⎰⎰4、设椭圆L ：13422=+y x 的周长为l ，则⎰=+L ds y x 2)23(（ ） )(A l )(B l 3 )(C l 4 )(D l 125、极限lim 0n n u →∞=是级数1nn u∞=∑收敛的（ ）)(A 充要条件 )(B 充分条件 )(C 必要条件 )(D 既非充分也非必要条件二、填空题（本大题共5小题, 每小题3分，总计15分)1、已知曲面224z x y =--在点M 处的切平面与平面2210x y z ++-=平行，则点M 的坐标 为__________________。

2、设函数2x y xe =是某二阶常系数线性齐次微分方程的解，则该微分方程为_________________。

3、设∑为曲面2222x y z R ++=，则曲面积分2221dS x y z ∑++⎰⎰＝ _______ 。

4、函数1()f x x=展开成2x -的幂级数为____________________________。

高等数学a1 压弯
【原创实用版】
目录
1.压弯简介
2.压弯的原理及公式
3.压弯的应用
4.压弯的优缺点
5.总结
正文
一、简介
压弯是一种将材料弯曲成特定形状的工艺。

它可以将材料的长度缩短，同时增加材料的截面积，从而提高材料的强度和承受力。

压弯广泛应用于建筑、汽车制造、航空航天等领域。

二、原理及公式
压弯的原理是基于材料的力学性质。

通过施加压力，将材料弯曲成所需形状，并使其内部产生应力。

应力可以通过以下公式计算：σ=F/A，其中σ为应力（单位为Pa），F为施加的压力（单位为N），A为截面积（单
位为m）。

三、应用
1.建筑：建筑结构中经常使用压弯工艺来制作梁、柱等支撑结构。

通过压弯工艺，可以制作出形状复杂的结构，从而提高建筑物的承载能力和稳定性。

2.汽车制造：汽车车身和底盘部件通常采用压弯工艺制造。

通过压弯工艺，可以生产出轻量化的车身结构，从而提高汽车的燃油效率。

3.航空航天：压弯工艺在航空航天领域也有广泛应用。

例如，飞机机翼、发动机壳体等结构都采用压弯工艺制造。

四、优缺点
1.优点：压弯工艺可以生产出形状复杂、轻量化的结构，从而提高材料的强度和承受力。

此外，压弯工艺还可以提高生产效率，降低制造成本。

2.缺点：压弯工艺需要高精度的设备和工艺技术，因此制造成本较高。

此外，压弯工艺需要使用大量的材料，因此不适合生产小型零件。

五、总结
压弯是一种重要的金属加工工艺，广泛应用于建筑、汽车制造、航空航天等领域。

高等数学a1 谐振腔
谐振腔是指一个封闭空间中的电磁波或机械波在特定频率下产生共振现象的现象。

在高等数学中，谐振腔可以通过偏微分方程来描述，其中最常见的一种是亥姆霍兹方程。

亥姆霍兹方程可以写为：
∇²u + k²u = 0
其中∇²表示Laplace算子，u是波函数，k是波数，与波长和频率有关。

谐振腔的边界条件也是方程求解的重要部分，它们决定了波函数在腔体边界处的行为。

常见的边界条件有：
1. 无边界条件：波函数在腔体外部为零，也即自由空间边界条件。

2. 零边界条件：波函数在腔体边界上为零。

3. 非零边界条件：波函数在腔体边界上满足特定的非零函数关系。

通过求解亥姆霍兹方程和边界条件，可以得到谐振腔中的波函数及其对应的能量分布。

谐振腔通常具有离散的能量级，即只有特定频率下的波能够在腔体中共振。

谐振腔在物理学、电磁学和量子力学等领域中有重要应用，比如光学中的光谱分
析、微波炉中的微波共振加热等。

在实际工程中，设计合适的谐振腔可以实现对特定频率的波进行增强或滤波的功能。

1《高等数学A1》测试题1一、填空、选择题（24%）1. 21lim __________;1xx x x →∞-⎛⎫= ⎪+⎝⎭2.若0(),0x f x a x ⎧≠==⎩在0x =处连续，则______;a =3. 设函数()f x 可导，且(1)2f '=，则0(1)(1)lim()2x f x f x∆→-∆-=∆(A) 1； (B) 1-； (C) 2； (D) 2-。

4. 223_______________;310x dx x x +=++⎰5.22(cos )__________;2x xe ex dx ππ---+=⎰6. 设21()txF x te dt =⎰，则()_______________;dF x = 7. 若12lim (),lim (),x ax af x k f x k +-→→==其中12,k k 是确定的常数，则x a =不可能是()f x 的( )(A) 连续点； (B) 可去间断点； (C) 跳跃间断点； (D) 无穷间断点。

8.设曲线()y f x =上任一点切线斜率为这点横坐标的3次方，并且曲线经过点(1,1)，则该曲线方程为( ) (A) 41344y x =+(B) 41344y x =-(C) 443y x =+ (D) 443y x =-二、解答下列各题（30%） 1. 3tan sin lim;1xx x x e→--2. 0limxx →3. 21sinxy e=，求y ';4. 3();(1).tx f t y f e π=-⎧⎨=-⎩其中f 可导，且(0)0f '≠，求0t dydx =;5. y e xy e +=，求(0)y ''.三、解答下列题（30%） 1. 22322x dxx x +++⎰; 2. 1arctan x xdx ⎰;3. 设(0)(3)(3)3f f f '===，()f x 二阶导数连续，求3()xf x dx ''⎰;4.求微分方程2321xy y x x '+=++的通解;5.求微分方程32x y y y xe '''-+=的通解. 四、解答下列各题（16%）1.已知函数32()f x x ax bx =++在1x =处有极小值2-，(1).求a 与b 的值； (2). 求()f x 的极大值点与极大值。

四川大学《高等数学I-1》2019-2020学年第一学期高等数学试题（A ）一、填空题（共5小题，每题4分，共20分）1. 判断级数21sin ln n n n π∞=⎛⎫+ ⎪⎝⎭∑的敛散性 。

2. 设23,y u x e z =，其中(),z z x y =由方程33330x y z xyz ++-=所确定，则1,0x y du=-== 。

3. 已知两直线的方程是1212321:,:101211x y z x y zL L ---+-====-，则过1L 且平行于2L 的平面方程是 。

4. 设L 为从点()1,0A -到点()3,0B 的上半个圆周()22212,0x y y -+=≥，则()()22Lx y dx x y dyx y-+++⎰= 。

5. 设曲面S 是()2212z x y =+的被平面2z =所截下的有限部分外侧面，则曲面积分SzdS ⎰⎰= 。

二、选择题（共5小题，每题4分，共20分） 6．若级数21nn a∞=∑收敛，则下列结论不成立的是 。

(A)31nn a∞=∑必收敛， (B)1nn a n∞=∑必收敛，(C)()11nn n a ∞=-∑必收敛， (D)11n n n a a∞+=∑必收敛。

7．已知直线L 过点()01,0,4M -，且与直线120:2240x y z L x y z +-=⎧⎨+++=⎩垂直，又与平面:34100x y z π-+-=平行，则L 的方程为 。

(A)14125x y z +-==； (B) 14125x y z +-==--； (C)14125x y z +-==-； (D) 14125x y z +-==--8．()()()()(),0,0,0,,0,0x y f x y x y ≠==⎩，则(),f x y 在点()0,0O 处 。

(A) 极限不存在； (B) 极限存在但不连续； (C)连续但不可微； (D) 可微 9．设Ω是由曲面221,1,0x y z z +===所围成的闭区域，则()323tan 3z e x y dV Ω⎡⎤+=⎣⎦⎰⎰⎰ 。

高等数学期末试卷(带答案)
一、高等数学选择题
1．由曲线，直线，轴及所围成的平面图形的面积为．
A、正确
B、不正确
【答案】A
2．（）．
A、
B、
C、
D、
【答案】B
3．设函数，则（）．
A、
B、
C、
D、
【答案】A
4．设函数，则．
A、正确
B、不正确
【答案】A
5．不定积分，其中为任意常数．
A、正确
B、不正确
【答案】B
6．设函数，，则函数．
A、正确
B、不正确
【答案】A
7．．
A、正确
B、不正确
【答案】A
8．函数的图形如图示，则函数的单调减少区间为
( )．
A、
B、
C、
D、
【答案】D
9．不定积分（）．
A、
B、
C、
D、
【答案】D
10．函数的图形如图示，则是函数的
( )．
A、最大值点
B、极大值点
C、极小值点也是最小值点
D、极小值点但非最小值点
【答案】C
11．（）．
A、
B、
C、
D、
【答案】B
12．设，则．
A、正确
B、不正确
【答案】B
13．不定积分.
A、正确
B、不正确
【答案】A
二、二选择题
14．函数在点处连续．
A、正确
B、不正确
【答案】A
15．．
A、正确
B、不正确
【答案】B。

2011-2012学年第一学期期末高等数学A1考试试卷一．选择题(每小题3分，共18分)1. 微分方程xy y ′=+是( )。

(A) 可分离变量方程； (B) 齐次方程；(C) 一阶线性方程； (D) 伯努利方程。

2．若()f x 的导函数为sin x ，则()f x 的一个原函数( )。

(A ) 1sin x +； (B ) 1sin x −； (C ) 1cos x +； (D ) 1cos x −。

3．已知()0411cos 2xf t dt x ⎡⎤−=−⎣⎦∫，则()0f ′=( )。

(A) 2； (B)21e −； (C) 1； (D) 1e −。

4．阿基米德螺线()0a a ρθ=>相应于θ从0变到π2的一段弧与极轴所围成图形的面积为( )。

(A)2212a d ππθθ−∫； (B)220122a d πθθ∫； (C)222012a d πθθ∫； (D)22012a d πθθ∫。

5．通解为212x x x y C e C e xe −=++的微分方程是 ( )。

(A) 23x y y y xe ′′′−−=； (B) +23x y y y e ′′′−=；(C) +23x y y y xe ′′′−= ； (D) 23x y y y e ′′′−−=。

6．设()y f x =是方程240y y y ′′′−+=的一个解，若()00f x >，且0()0f x ′=，则()f x 在0x 处 ( )。

(A) 取得极大值； (B) 取得极小值；(C) 某邻域内单调增加； (D) 某邻域内单调减少。

二．填空题(每小题3分，共18分)1．函数(y C x C =−为任意常数）是微分方程1xy y ′′′−= ，（在“通解、特解、解”中选择一个答案）。

2．抛物线2y ax bx c =++在处，曲率最大。

3．=∫。

4．设()f x 的一个原函数是ln xx，则()d x f x x ′∫=。

高等数学a1 裂纹
（最新版）
目录
1.高等数学的概念与意义
2.高等数学中的裂纹问题
3.裂纹问题的解决方法与应用
正文
高等数学，作为一门重要的学科，是研究多元函数微分方程、线性代数、概率论与数理统计等知识的学科，对于现代科学研究和工程技术有着广泛的应用。

高等数学在很多领域中都有着重要的作用，如物理学、力学、计算机科学、经济学等。

在高等数学中，裂纹问题是一个重要的研究内容。

裂纹，通常是指物体在受到外力或者内部应力作用下，出现的断裂现象。

裂纹问题在工程领域中具有很大的实际意义，如建筑物的裂缝、机械设备的磨损、材料的疲劳等，都与裂纹问题有关。

对于裂纹问题的解决，通常需要运用高等数学中的知识，如微分方程、线性代数等。

通过建立数学模型，可以对裂纹的扩展进行预测和控制，从而有效地防止裂纹的进一步发展，保证工程结构的安全和稳定。

例如，对于建筑物的裂缝问题，可以通过对建筑物的应力分布进行分析，建立相应的微分方程模型，预测裂缝的扩展情况，从而及时采取措施，防止裂缝的扩大，保证建筑物的安全。

第1页共1页。