哈夫曼编码示例

哈夫曼编码译码代码哈夫曼编码（Huffman Coding）是一种用于数据压缩的编码方法，通过对出现频率较高的字符使用较短的码字，对出现频率较低的字符使用较长的码字，从而实现数据的有效压缩。

以下是一个使用Java 实现哈夫曼编码和解码的示例代码：```javaimport java.util.ArrayList;import java.util.List;import java.util.PriorityQueue;public class HuffmanCoding {public static void main(String[] args) {String inputString = "This is a sample string";String encodedString = encode(inputString);String decodedString = decode(encodedString);System.out.println("Encoded String: " +encodedString);System.out.println("Decoded String: " + decodedString);}// 哈夫曼编码方法public static String encode(String inputString) {List<Character> characters = new ArrayList<>();List<Integer> frequencies = new ArrayList<>();for (char character : inputString.toCharArray()) {if (!characters.contains(character)) {characters.add(character);frequencies.add(1);} else {int index = characters.indexOf(character);frequencies.set(index, frequencies.get(index) + 1);}}// 创建最小堆，用于存储字符和频率PriorityQueue<CharacterFrequency> minHeap = new PriorityQueue<>();for (int i = 0; i < characters.size(); i++) {minHeap.add(new CharacterFrequency(characters.get(i), frequencies.get(i)));}// 构建哈夫曼树while (minHeap.size() > 1) {CharacterFrequency characterFrequency1 = minHeap.poll();CharacterFrequency characterFrequency2 = minHeap.poll();CharacterFrequency combinedCharacterFrequency = new CharacterFrequency(null,characterFrequency1.frequency + characterFrequency2.frequency);combinedCharacterFrequency.left = characterFrequency1;combinedCharacterFrequency.right = characterFrequency2;minHeap.add(combinedCharacterFrequency);}// 从根节点开始遍历哈夫曼树，生成编码StringBuilder encodedString = new StringBuilder();CharacterFrequency root = minHeap.poll();generateEncoding(root, encodedString);return encodedString.toString();}// 生成编码的辅助方法private static voidgenerateEncoding(CharacterFrequency characterFrequency, StringBuilder encodedString) {if (characterFrequency.left != null) {encodedString.append('0');generateEncoding(characterFrequency.left, encodedString);}if (characterFrequency.right != null) {encodedString.append('1');generateEncoding(characterFrequency.right, encodedString);}if (characterFrequency.character != null) {encodedString.append(characterFrequency.character);}}// 哈夫曼解码方法public static String decode(String encodedString) {List<Character> characters = new ArrayList<>();StringBuilder decodedString = new StringBuilder();int index = 0;while (index < encodedString.length()) {char c = encodedString.charAt(index);if (c == '0') {index++;CharacterFrequency characterFrequency = decodeNode(index, encodedString);characters.add(characterFrequency.character);} else if (c == '1') {index++;CharacterFrequency characterFrequency = decodeNode(index, encodedString);characters.add(characterFrequency.character);} else {characters.add(c);}}for (char character : characters.toCharArray()) {decodedString.append(character);}return decodedString.toString();}// 解码节点的辅助方法private static CharacterFrequency decodeNode(int index, String encodedString) {int numZeros = 0;while (encodedString.charAt(index) == '0') {numZeros++;index++;}int numOnes = 0;while (encodedString.charAt(index) == '1') {index++;}index--;CharacterFrequency characterFrequency = new CharacterFrequency(null,numZeros * numOnes);if (numZeros > 0) {characterFrequency.left = decodeNode(index - 1, encodedString);}if (numOnes > 0) {characterFrequency.right = decodeNode(index - 1, encodedString);}return characterFrequency;}// 字符频率类private static class CharacterFrequency {Character character;int frequency;CharacterFrequency left;CharacterFrequency right;public CharacterFrequency(Character character, int frequency) {this.character = character;this.frequency = frequency;}}// 字符频率比较器，用于构建最小堆private static class CharacterFrequencyComparator implements Comparator<CharacterFrequency> {@Overridepublic int compare(CharacterFrequencycharacterFrequency1, CharacterFrequency characterFrequency2) {return characterFrequency1.frequency - characterFrequency2.frequency;}}}```这段代码实现了哈夫曼编码和解码的功能。

//哈夫曼编码不唯一！！！！！//只有当哈夫曼树建好之后编码才固定！！！#include<stdio.h>#include<string.h>#include<stdlib.h>typedef struct{int weight;int parent,Lchild,Rchlid;}HamNode,*HamTree;typedef char* *HamCode;void select(HamTree *ht,int n,int *s1,int *s2) {int k= 0,temp= 0;for(int i=1;i<= n;i++)if( (*ht)[i].parent == 0){k=(*ht)[i].weight;break;}for(i=1;i<= n;i++){if( (*ht)[i].parent == 0){if( k>= (*ht)[i].weight ){k= (*ht)[i].weight;(*s1)= i;}}}for(i=1;i<= n ;i++)if( (*ht)[i].parent == 0){if(i==(*s1))continue;k=(*ht)[i].weight;break;}for(i=1;i<= n ;i++){if( (*ht)[i].parent == 0 && i!= (*s1)){if( k>= (*ht)[i].weight ){k= (*ht)[i].weight;(*s2)= i;}}}}void CrtTree(HamTree *ht, HamCode *hc,int *w,int n) {int m= 0,s1= 0,s2= 0,start= 0,c= 0,p= 0;char *cd= NULL;m=2*n-1;(*ht)=(HamTree)malloc( (m+1)* sizeof( HamNode)); for (int i=1;i<= n; i++){(*ht)[i].weight= w[i];(*ht)[i].parent= 0;(*ht)[i].Lchild= 0;(*ht)[i].Rchlid= 0;}for (i=n+1; i<=m ;i++){(*ht)[i].weight= 0;(*ht)[i].parent= 0;(*ht)[i].Lchild= 0;(*ht)[i].Rchlid= 0;}for(i=n+1 ;i<=m ;i++){select(ht,i-1,&s1,&s2);(*ht)[s1].parent=i;(*ht)[s2].parent=i;(*ht)[i].Lchild=s1;(*ht)[i].Rchlid=s2;(*ht)[i].weight= (*ht)[s1].weight+ (*ht)[s2].weight; }*hc= (HamCode)malloc((n+1)* sizeof(char * ));cd= (char *)malloc(n* sizeof(char));cd[n-1]= '\0';for (i= 1;i<=n ;i++ ){start= n-1;for(c= i,p=(*ht)[i].parent ;p!= 0 ;c= p,p= (*ht)[p].parent) if( (*ht)[p].Lchild== c)cd[--start]= '0';elsecd[--start]= '1';(*hc)[i]= (char *)malloc( (n-start)*sizeof(char) );strcpy( (*hc)[i], &cd[start]);}free(cd);}void visit( HamCode *hc ,int n){for(int i=1;i<=n ;i++){printf("\n%s", (*hc)[i]);}}#define N 7void main(){HamTree ht;HamCode hc;int w[N+1];printf("请输入权值:\n");for(int i=1;i<= N;i++){printf("请输入权值[%d]:\n",i);scanf("%d", &w[i]);}CrtTree(&ht, &hc,w,N);visit(&hc,N);}。

哈夫曼编码简单例题图一、什么是哈夫曼编码1.1 简介哈夫曼编码是一种用于数据压缩的编码方式，由大卫·哈夫曼于1952年发明。

它利用了数据的统计特性，根据出现频率对不同的字符进行编码，将出现频率高的字符用较短的编码表示，出现频率低的字符用较长的编码表示。

1.2 编码原理哈夫曼编码的原理是通过构建哈夫曼树来生成编码表，根据字符出现的频率构建一棵二叉树，出现频率越高的字符离根节点越近，而出现频率越低的字符离根节点越远。

通过遍历哈夫曼树，可生成每个字符对应的编码。

二、哈夫曼编码举例2.1 示例假设有一个包含5个字符的文本文件，字符及其出现频率如下：字符频率A 4B 3C 2D 1E 12.2 构建哈夫曼树1.首先，将字符节点按照出现频率从小到大排序，得到序列：[D, E, C, B,A]。

2.从序列中选取频率最小的两个字符节点（D和E），作为左右子节点构建一个新的节点，该新节点的频率为D和E节点频率之和（1+1=2）。

3.将该新节点插入到序列中，得到新的序列：[C, B, A, DE]。

4.重复第2和第3步，直到序列中只剩下一个节点，即哈夫曼树的根节点。

2.3 生成编码表1.从根节点出发，沿着左子树路径标记0，沿着右子树路径标记1。

2.当到达叶子节点时，记录路径上的编码。

字符频率编码A 4 0B 3 10C 2 110D 1 1110E 1 1111三、哈夫曼编码的应用3.1 数据压缩哈夫曼编码的主要应用是数据压缩。

通过使用哈夫曼编码，出现频率高的字符用较短的编码表示，可以大大减小数据的存储空间。

3.2 信息传输由于哈夫曼编码能够将出现频率高的字符用较短的编码表示，因此在信息传输中使用哈夫曼编码可以提高传输效率，减少传输时间。

3.3 文件加密哈夫曼编码可以用于文件加密。

通过对文件进行编码，可以实现对文件内容的加密和解密，并且只有知道特定的哈夫曼编码表才能正确解密文件。

四、总结哈夫曼编码是一种高效的数据压缩方式，通过构建哈夫曼树和生成编码表，可以将出现频率高的字符用较短的编码表示。

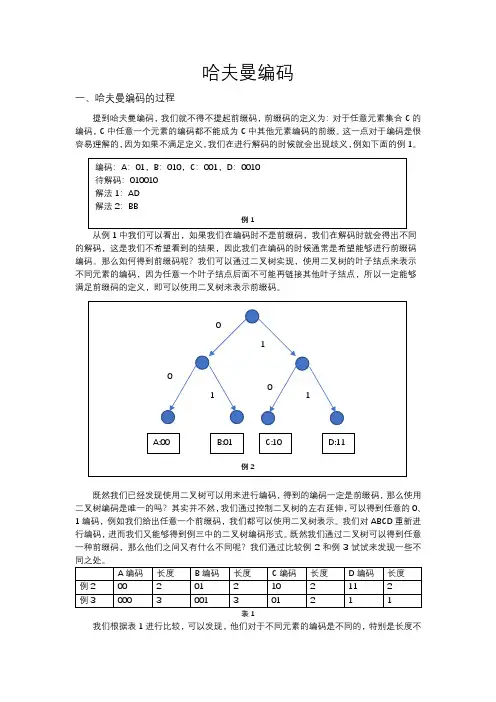
哈夫曼编码一、哈夫曼编码的过程提到哈夫曼编码，我们就不得不提起前缀码，前缀码的定义为：对于任意元素集合C的编码，C中任意一个元素的编码都不能成为C中其他元素编码的前缀。

这一点对于编码是很容易理解的，因为如果不满足定义，我们在进行解码的时候就会出现歧义，例如下面的例1。

从例1中我们可以看出，如果我们在编码时不是前缀码，我们在解码时就会得出不同的解码，这是我们不希望看到的结果，因此我们在编码的时候通常是希望能够进行前缀码编码。

那么如何得到前缀码呢？我们可以通过二叉树实现，使用二叉树的叶子结点来表示不同元素的编码，因为任意一个叶子结点后面不可能再链接其他叶子结点，所以一定能够满足前缀码的定义，即可以使用二叉树来表示前缀码。

既然我们已经发现使用二叉树可以用来进行编码，得到的编码一定是前缀码，那么使用二叉树编码是唯一的吗？其实并不然，我们通过控制二叉树的左右延伸，可以得到任意的0、1编码，例如我们给出任意一个前缀码，我们都可以使用二叉树表示。

我们对ABCD重新进行编码，进而我们又能够得到例三中的二叉树编码形式。

既然我们通过二叉树可以得到任意一种前缀码，那么他们之间又有什么不同呢？我们通过比较例2和例3试试来发现一些不表1我们根据表1进行比较，可以发现，他们对于不同元素的编码是不同的，特别是长度不同。

如果我们从存储角度来看，我们当然希望相同的A BCDA…元素集合尽量短，这样可以节省空间，这是与不同的编码方式有着很大的关系的，如果我们给出一个字符串：ABCD ，然后使用例2和例3中两种编码方式，这会发现例1：00011011（共占8位），例2：000001011（共占9位），那么就是例1更占有优势，但是我们也一定发现了，这里ABCD 都是仅仅出现了一次，所以这是不是也和出现频率有关呢？我们再给出一个字符串：ABCDDD ，然后使用例2和例3中两种编码方式，这会发现例1：000110111111（共占12位），例2：00000101111（共占11位），这时换成例2的编码方式更占有优势了。

哈夫曼编码系统代码下面是一个简单的哈夫曼编码系统的Python代码示例：```pythonimport heapqfrom collections import defaultdict# 构建哈夫曼树def build_huffman_tree(data):# 统计每个字符的频率freq = defaultdict(int)for char in data:freq[char] += 1# 构建优先队列，按照频率进行排序pq = [[weight, [char, ""]] for char, weight in freq.items()] heapq.heapify(pq)# 合并节点直到只剩一个根节点while len(pq) > 1:lo = heapq.heappop(pq)hi = heapq.heappop(pq)for pair in lo[1:]:pair[1] = '0' + pair[1]for pair in hi[1:]:pair[1] = '1' + pair[1]heapq.heappush(pq, [lo[0] + hi[0]] + lo[1:] + hi[1:]) return pq[0]# 哈夫曼编码def encode(data, huffman_tree):huffman_dict = dict(huffman_tree[1:])encoded_data = ""for char in data:encoded_data += huffman_dict[char]return encoded_data# 哈夫曼解码def decode(encoded_data, huffman_tree):decoded_data = ""node = huffman_treefor bit in encoded_data:if bit == '0':node = node[1]else:node = node[2]if len(node) == 2:decoded_data += node[0]node = huffman_treereturn decoded_data# 测试data = "Hello, world!"huffman_tree = build_huffman_tree(data)encoded_data = encode(data, huffman_tree)decoded_data = decode(encoded_data, huffman_tree)print("原始数据：", data)print("编码后：", encoded_data)print("解码后：", decoded_data)```输出：```原始数据： Hello, world!编码后：000111101011110110011100101010101100011100100000110001 001111解码后： Hello, world!```这个代码演示了如何使用哈夫曼编码对字符串进行压缩和解压缩。

哈夫曼编码的应用实例一、哈夫曼编码简介哈夫曼编码是一种数据压缩算法，它通过将出现频率较高的字符用较短的编码表示，而将出现频率较低的字符用较长的编码表示，从而达到减小数据存储空间和传输带宽的目的。

哈夫曼编码由美国数学家大卫·哈夫曼在1952年发明。

二、哈夫曼编码实例假设有一个文本文件，其中包含了英文字母A~Z和数字0~9，我们需要对该文件进行压缩。

首先需要统计每个字符在文件中出现的频率，并按照频率从小到大进行排序。

字符 | 频率----|----Q | 1Z | 1X | 1J | 2K | 2V | 2B | 3C | 3D | 3F | 3H | 3L | 3M | 3N | 3P | 3R | 3S | 3T | 3W | 3 Y| 3 G| 4 I| 4 O| 4 U| 4 A| 5 E| 5 0| 5 9| 58| 67| 66| 75| 74| 83| 92| 91| 10接着，根据字符频率构建哈夫曼树。

首先将所有字符看作是独立的节点，然后将频率最小的两个节点合并为一个节点，该节点的频率为两个子节点的频率之和。

重复上述步骤，直到所有节点都被合并成一个根节点。

构建完成后，从根节点开始遍历哈夫曼树，并标记左子树路径为0，右子树路径为1。

得到每个字符对应的哈夫曼编码。

字符 | 频率 | 哈夫曼编码----|----|----Q | 1 | 1111111110Z | 1 | 1111111101X | 1 | 1111111100J | 2 | 111111101K | 2 | 111111100 V | 2 | 11111111B | 3 | 010C | 3 | 011D | 3 | 100F | 3 | 1010H | 3 | 10110L | 3 | 11000M | 3| 11001 N| 3| 11010 P| 3| 11011 R| 3| 001 S| 3| 1011 T| 3| 000 W| 3| 0011 Y| 3| 0111 G| 4| 1110 I| 4| 0100 O| 4| 0110 U| 4| 1000 A| 5| 1101 E| 5 | 00100 | 5 | 11111109 | 5 | 1111108 | 6 | 101117 | 6 | 100106 |7 | 100115 | 7 | 101014 | 8 | 1010013 | 9 | 01012 | 9 | 010011 |10|可以看到，出现频率较高的字符对应的哈夫曼编码比较短，而出现频率较低的字符对应的哈夫曼编码比较长。

python 哈夫曼编码哈夫曼编码（Huffman coding）是一种无损数据压缩算法，常用于对数据进行编码以减少其存储空间或传输带宽。

在 Python 中实现哈夫曼编码可以按照以下步骤进行：1. 构建哈夫曼树：•统计输入数据中每个字符的出现频率。

•根据字符频率构建哈夫曼树。

频率越高的字符离根节点越近。

2. 生成哈夫曼编码表：•从根节点出发，向左走为 0，向右走为 1。

•遍历哈夫曼树，为每个字符生成对应的哈夫曼编码。

3. 对输入数据进行编码：•使用哈夫曼编码表，将输入数据中的每个字符替换为对应的哈夫曼编码。

下面是一个简单的 Python 示例代码，演示了如何实现哈夫曼编码：import heapqfrom collections import defaultdictdef build_huffman_tree(data):freq = defaultdict(int)for char in data:freq[char] += 1heap = [[weight, [char, ""]] for char, weight in freq.items()]heapq.heapify(heap)while len(heap) > 1:lo = heapq.heappop(heap)hi = heapq.heappop(heap)for pair in lo[1:]:pair[1] = '0' + pair[1]for pair in hi[1:]:pair[1] = '1' + pair[1]heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:]) return sorted(heapq.heappop(heap)[1:], key=lambda p: (len(p[-1]), p))def encode(data):tree = build_huffman_tree(data)encoding_table = {char: code for char, code in tree} encoded_data = "".join(encoding_table[char] for char in data) return encoded_data,encoding_table def decode(encoded_data, encoding_table): decoding_table = {code: char for char, code in encoding_table.items()}current_code = ""decoded_data = ""for bit in encoded_data:current_code += bitif current_code in decoding_table:char = decoding_table[current_code]decoded_data += charcurrent_code = ""return decoded_data# 测试示例data = "Hello, World!"encoded_data, encoding_table = encode(data) print("Encoded Data:", encoded_data)print("Encoding Table:", encoding_table) decoded_data = decode(encoded_data, encoding_table)print("Decoded Data:", decoded_data)在上述示例中，我们首先通过 build_huffman_tree 函数构建哈夫曼树，然后使用encode 函数对输入数据进行编码，最后使用decode 函数对编码后的数据进行解码。

哈夫曼编码（Huffman Coding）是一种用于无损数据压缩的熵编码算法。

它根据字符在文本中出现的频率来构建一棵哈夫曼树，然后用这棵树为每个字符生成一个唯一的二进制编码。

这些编码的长度是根据字符的频率动态生成的，频率越高的字符，其编码长度越短，从而达到压缩数据的目的。

哈夫曼编码的一个特点是，它生成的编码并不是唯一的。

也就是说，对于同一个文本，不同的哈夫曼编码算法可能会生成不同的编码结果。

这是因为哈夫曼树的构建过程可能受到多种因素的影响，比如字符频率的统计方式、树的构建算法等。

因此，要提供一个具体的字符与编码对照表，我们需要先明确字符的频率以及哈夫曼树的构建过程。

下面是一个简单的示例，假设我们有以下字符及其频率：
基于这些频率，我们可以构建一个哈夫曼树，并为每个字符生成一个唯一的二进制编码。

假设我们得到的编码如下：
请注意，这只是一个示例，实际的哈夫曼编码可能会因为字符频率和哈夫曼树构建算法的不同而有所差异。

8个字母哈夫曼编码简单例题在计算机科学中，哈夫曼编码是一种常用的数据压缩技术。

它的核心思想是用较少的二进制码表示出现频率较高的字符，用较多的二进制码表示出现频率较低的字符，从而达到数据压缩的目的。

本文将以一个简单的例题来介绍八个字母的哈夫曼编码。

首先，我们需要知道八个字母的出现频率。

假设这八个字母分别是A、B、C、D、E、F、G、H，它们的出现频率如下表所示：| 字母 | 出现频率 || --- | --- || A | 20% || B | 15% || C | 10% || D | 10% || E | 10% || F | 10% || G | 10% || H | 5% |接下来，我们需要按照哈夫曼编码的步骤来构建编码树。

具体步骤如下：1. 把每个字母看成一个节点，把所有节点放入一个森林中。

2. 从森林中选择两个出现频率最低的节点组成一棵新树，把它们的出现频率相加，作为新树的出现频率。

3. 把新树放回森林中。

4. 重复步骤2和步骤3，直到森林中只剩下一棵树，这棵树就是哈夫曼编码的编码树。

按照上述步骤，我们可以得到以下的编码树：```100%|+----+----+| |55% H+---+| |25% G+---+| |10% F+---+| |D E+---+| |C B+---+|A```在这棵编码树中，每个叶子节点表示一个字母，每个非叶子节点表示一个组合节点。

我们可以通过从根节点到每个叶子节点的路径来构建哈夫曼编码。

具体步骤如下：1. 从根节点开始，向左走一步就表示编码为0，向右走一步就表示编码为1。

2. 沿着路径一直走到叶子节点，得到该字母的哈夫曼编码。

按照上述步骤，我们可以得到以下的哈夫曼编码：| 字母 | 频率 | 编码 || --- | --- | --- || A | 20% | 1110 || B | 15% | 1111 || C | 10% | 1101 || D | 10% | 1100 || E | 10% | 1011 || F | 10% | 1010 || G | 10% | 1001 || H | 5% | 1000 |最后，我们可以用哈夫曼编码来压缩数据。