上海初二暑假班 八年级数学试题 新王牌-王老师

初中八年级数学（沪科版）多媒体暑假作业（二十一）一. 相信自己。

1． 等腰三角形一底角为30°，底边上的高为9cm ，则这个等腰三角形的腰长为18cm2． 某楼梯如图所示，欲在楼梯上铺设红色地毯，已知这种地毯每平方米售价为30元，楼梯宽为2m ，则购买这种地毯至少需要420元3． 若代数式x +11在实数范围内有意义，则x 取值范围是≥x 04． 一元二次方程0)1()12(2=-+++m x m x 的根的情况是有两个不相等的实数根5． 已知方程02)21(2=--+x x 的两个根x 1和x 2，则2221x x +=36． 直角三角形中，自锐角顶点所引的两条中线长为5和40，那么这个直角三角形的斜边长为1327． 一个多边形的外角和是内角和的72，则这个多边形的边数为_9_ 8． 把容量是64的样本分成8组，从第1组到第4组的频数分别是5，7，11，13，第5组到第7组的频率是0.125，那么第8组的频数20二.择优录用。

1．下列说法中不正确的是（ A ）A ．三个角度之比为3：4：5的三角形是直角三角形B ．三边之比为3：4：5的三角形是直角三角形C ．三个角度之比为1：2：3的三角形是直角三角形D ．三边之比为1：2：3的三角形是直角三角形2．等边三角形边长为a ，则该三角形的面积为（ C ）A ．23aB ．223aC ．243aD ．233a 3．对于任意实数a ．b ，下列等式总能成立的是（ C ）A ．b a b a +=+2)(B ．b a b a +=+22C ．22222)(b a b a +=+D ．b a b a +=+2)(4．若103-=a ，则代数式262--a a 的值是（ C ）A ．0B ．1C ．－1D ．105．如果04)2(3)2(2=-+++y x y x ，那么y x 2+的值为（ C ）A ．1B ．－4C ．1 或－4D ．－1或36．把方程01422=--x x 化为n m x =+2)(的形式，则m ．n 的值是（ B ）A ．23,2==n mB ．23,1=-=n m C ．4,1==n m D ．2==n m 7．在给定的条件中，能画出平行四边形的是（ C ）A ．以60cm 为一条对角线，20cm ．34cm 为两条邻边B ．以6cm ．10cm 为两条对角线，8cm 为一边C ．以20cm ．36cm 为两条对角线，22cm 为一边D ．以6cm 为一条对角线，3cm ．10cm 为两条邻边8．正方形具有而菱形不一定具有性质的是（ B ）A．对角线互相平分B．对角线相等C．对角线平分一组对角D．对角线互相垂直9．用两个完全相同的直角三角板，不能．．拼成如下图形的是（ D ）A．平行四边形B．矩形C．等腰三角形D．梯形10．为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐次数，并给制成如图所示的频数分布直方图，请根据图中信息，计算仰卧起坐次数在25~30次的频率是（ A ）A．0.4 B．0.3 C．0.2 D．0.1三.挑战奥数。

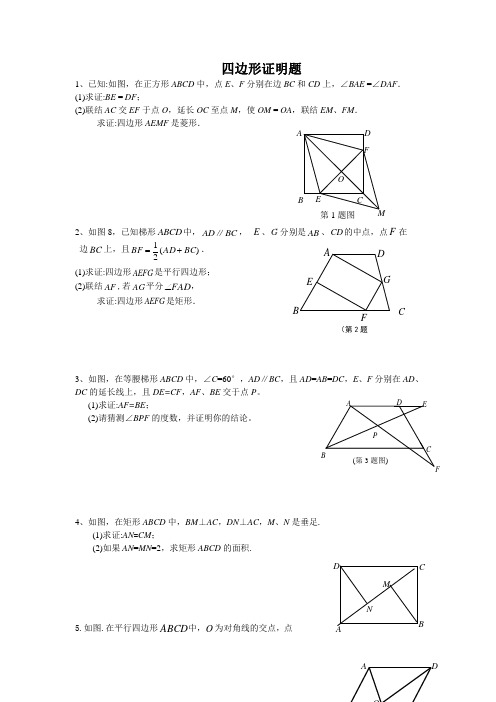
四边形证明题1、已知:如图，在正方形ABCD 中，点E 、F 分别在边BC 和CD 上，∠BAE =∠DAF ． (1)求证:BE = DF ；(2)联结AC 交EF 于点O ，延长OC 至点M ，使OM = OA ，联结EM 、FM ．求证:四边形AEMF 是菱形．2、如图8，已知梯形ABCD 中，AD BC ∥， E 、G 分别是AB 、CD 的中点，点F 在边BC 上，且)(21BC AD BF +=． (1)求证:四边形AEFG 是平行四边形； (2)联结AF ,若AG 平分FAD ∠，求证:四边形AEFG 是矩形．3、如图，在等腰梯形ABCD 中，∠C =60°，AD ∥BC ，且AD =AB =DC ，E 、F 分别在AD 、DC 的延长线上，且DE=CF ，AF 、BE 交于点P 。

(1)求证:AF=BE ；(2)请猜测∠BPF 的度数，并证明你的结论。

4、如图，在矩形ABCD 中，BM ⊥AC ，DN ⊥AC ，M 、N 是垂足.(1)求证:AN =CM ；(2)如果AN =MN =2，求矩形ABCD 的面积.5.如图.在平行四边形ABCD 中，O 为对角线的交点，点A DBEF O CM第1题图B EA D GC F（第2题图） AE 为线段BC 延长线上的一点，且BC CE 21=.过点E 作EF ∥CA ，交CD 于点F ，联结OF . (1)求证:OF ∥BC ；(2)如果梯形OBEF 是等腰梯形，判断四边形ABCD 的形状， 并给出证明.6、如图，在正方形ABCD 中，点E 、F 分别是边AB 、AD 的中点，DE 与CF 相交于G ，DE 、CB 的延长线相交于点H ，点M 是CG 的中点． 求证:(1)BM//GH ； (2)BM ⊥CF ．7．已知:如图，AE ∥BF ，AC 平分∠BAD ，交BF 于点C ，BD 平分∠ABC ，交AE 于点D ，联结CD .求证:四边形ABCD 是菱形．8．如图，在正方形ABCD 中，点E 、F 分别是边AB 、AD 的中点，DE 与CF 相交于G ，DE 、CB 的延长线相交于点H ，点M 是CG 的中点.求证:(1)//BM GH (2)BM CF ⊥（第6题）FO EDC BA第21题图9．已知:如图，在梯形ABCD 中，AD //BC ，AB =CD ，点E 、F 在边BC 上，BE =CF ，EF =AD ．求证:四边形AEFD 是矩形．10．如图，在□ABCD 中，E 、F 分别为边ABCD 的中点，BD 是对角线，过A 点作AG //DB 交CB 的延长线于点G ．(1)求证:DE ∥BF ；(2)若∠G ＝90 ，求证:四边形DEBF 是菱形．11．已知:如图，在梯形ABCD 中，AD //BC ，BC =2AD ，AC ⊥AB ，点E 是AC 的中点，DE的延长线与边BC 相交于点F ．求证:四边形AFCD 是菱形．12．(本题共2小题，每小题6分，满分12分)已知:如图，在梯形ABCD 中，AD // BC ，点E 、F 在边BC 上，DE // AB ，A F // CD ，且四边形AEFD 是平行四边形．(1)试判断线段AD 与BC 的长度之间有怎样的数量关系？并证明你的结论；(2)现有三个论断:①AD = AB ；②∠B +∠C = 90°；③∠B = 2∠C ．请从上述三个论断中选择一个论断作为条件，证明四边形AEFD 是菱形．A B E F C D (第9题) ABD GEF （第11题图）ABFCD E ABDCEF（第12题图）四边形证明题答案1．证明:(1)∵正方形ABCD ，∴AB=AD ，∠B =∠D =90°…………………………(2分)∵∠BAE = ∠DAF∴△ABE ≌△ADF ……………………………………………………………(1分) ∴BE = DF ……………………………………………………………………(2分) (2)∵正方形ABCD ，∴∠BAC =∠DAC ………………………………………(1分) ∵∠BAE =∠DAF ∴∠EAO =∠FAO ……………………………………(1分)∵△ABE ≌△ADF ∴AE = AF …………………………………………(1分) ∴EO=FO ，AO ⊥EF …………………………………………………………(2分) ∵OM = OA ∴ 四边形AEMF 是平行四边形……………………………(1分) ∵AO ⊥EF ∴四边形AEMF 是菱形……………………………………(1分) 2．(1)证明:联结EG ，∵ 梯形ABCD 中，AD BC ∥，且E 、G 分别是AB 、CD 的中点， ∴ EG //B C ，且)(21BC AD EG +=，…………………………(2分) 又∵)(21BC AD BF +=∴ EG =BF ．……………………………………………………(1分) ∴ 四边形AEFG 是平行四边形．…………………(2分)(2)证明:设AF 与EG 交于点O ， ∵ EG //AD ，∴∠DAG =∠AGE∵AG 平分FAD ∠，∴∠DAG =∠GAO ∴∠GAO =∠AGE∴ AO=GO ．………………………………(2分)∵四边形AEFG 是平行四边形，∴ AF =EG ，四边形AEFG 是矩形…………………………(2分)3．证明:(1)∵梯形ABCD 是等腰梯形，AD ∥BC∴ ∠BAE=∠ADF ………………………………………………(1分)∵AD = DC ∴ AE=DF …………………………………………(1分)∵BA=AD ∴△BAE ≌△ADF ， …………………………………(1分) ∴BE=AF ． …………………………………………………………(1分) (2)猜想∠BPF=120°．……………………………………………………(1分)∵由(1)知△BAE ≌△ADF ，∴∠ABE=∠DAF ．…………………(1分) ∴∠BPF=∠ABE+∠BAP=∠BAE ．……………………………………(1分) 而AD ∥BC ，∠C=∠ABC=60°，∴=120°．∴∠BPF=∠BAE =120°．………………………………………………(1分)4、证:(1)∵四边形ABCD 是矩形，∴AD ∥BC ，AD =BC . ∴∠DAC =∠BCA .又∵DN ⊥AC ，BM ⊥AC ，∴∠DNA =∠BMC .∴⊿DAN ≌⊿BCM , ---------------------------------------------------(3分)∴AN =CM . ---------------------------------------------------------------(1分) (2)联结BD 交AC 于点O ， ∵AN = NM =2,∴AC = BD =6,又∵四边形ABCD 是矩形， ∴AO =DO =3，在⊿ODN 中，OD =3，ON =1，∠OND =︒90,∴DN =2222=-ON OD ,--------------------------------------(2分) ∴矩形ABCD 的面积=212=⨯DN AC .-----------------------(1分)5.解:(1)方法1:延长EF 交AD 于G (如图1).……………1分 在平行四边形ABCD 中，AD ∥BC ，BC AD =. ∵EF ∥CA ，EG ∥CA ， ∴四边形ACEG 是平行四边形. ∴ CE AG =.……………1分又∵BC CE 21=，BC AD =，∴ GD AD BC CE AG ====2121.……………1分∵AD ∥BC ，∴ECF ADC ∠=∠. 在CEF △和DGF △中，∵DFG CFE ∠=∠，ECF ADC ∠=∠，DG CE =，∴CEF △≌DGF △(A.A.S). ∴DF CE =.…………………1分 ∵四边形ABCD 是平行四边形，∴OD OB =.∴OF ∥BE . ………………1分 方法2:将线段BC 的中点记为G ，联结OG (如图2). ………………1分∵四边形ABCD 是平行四边形，∴OD OB =.∴OG ∥CD . …………1分 ∴FCE OGC ∠=∠.∵EF ∥CA ，∴FEC OCG ∠=∠.∵BC GC 21=，BC CE 21=，∴CE GC =.AB（第5题图1）DCOEFGAB（第5题图2）DC OEFG在OGC △和FCE △中，∵FEC OCG ∠=∠，CE GC =，FCE OGC ∠=∠， ∴OGC △≌FCE △(A.S.A). …………………1分 ∴FC OG =. 又∵OG ∥CF ，∴四边形OGCF 是平行四边形. …………………1分∴OF ∥GC . …………………1分 其他方法，请参照上述标准酌情评分.(2)如果梯形OBEF 是等腰梯形，那么四边形ABCD 是矩形. ……………1分 ∵OF ∥CE ，EF ∥CO ，∴四边形OCEF 是平行四边形. ∴OC EF =.……………1分又∵梯形OBEF 是等腰梯形，∴EF BO =. ∴OC OB =.(备注:使用方法2的同学也可能由OGC △≌FCE △找到解题方法；使用方法1的同学也可能由四边形ACEG 是平行四边形找到解题方法).∵四边形ABCD 是平行四边形，∴OC AC 2=，BO BD 2=. ∴BD AC =.……………1分∴平行四边形ABCD 是矩形. ……………1分6．证明:(1)∵在正方形ABCD 中，AD //BC ，∴∠A =∠HBE ，∠ADE =∠H ，…(1分)∵AE =BE ，∴△ADE ≌△BHE ．………………………………………(1分) ∴BH =AD =BC ．…………………………………………………………(1分) ∵CM =GM ，∴BM //GH ．………………………………………………(1分)(2)∵在正方形ABCD 中，AB =AD =CD ，∠A =∠ADC =90º，又∵DF =21AD ，AE =21AB ，∴AE =DF ．∴△AED ≌△DFC ．………(1分) ∴∠ADE =∠DCF ．………………………………………………………(1分) ∵∠ADE +∠GDC =90º，∴∠DCF +∠GDC =90º．∴∠DGC =90º．…(1分) ∵BM //GH ，∴∠BMG =∠DGC =90º，即BM ⊥CF ．…………………(1分)7、证明:∵AC 平分∠BAD ， ∴∠BAC=∠CAD .又 ∵AE ∥BF ， ∴∠BCA=∠CAD . --------------------------1分∴∠BAC=∠BCA .∴ AB=BC . --------------------1分 同理可证AB=AD .∴ AD=BC . ----------------------1分 又 AD ∥BC ，∴ 四边形ABCD 是平行四边形. -----1分 又AB=BC ，∴□ABCD 是菱形. -----1分 8. 证明:(1)∵正方形ABCD ∴90A EBH ∠=∠=︒AD BC =…………1′∵E 是AB 的中点 ∴ AB BE =…………1′ ∵AED BEH ∠=∠∴AED BEH ≅…………1′∴AD BH = ∴BC BH =…………1′ ∵M 是CG 的中点 ∴//BM GH …………1′(2)证AED CDF ≅ …………1′ ∴ADE DCF ∠=∠ ∵90DCF CDE ∠+∠=︒ ∴90CGH ∠=︒ ………1′ ∵//BM GH ∴90CMB CGH ∠=∠=︒ ∴BM CF ⊥ …………1′9．证法一: ∵在梯形ABCD 中，AD //BC ，又∵EF =AD∴四边形AEFD 是平行四边形．………………………………………(1分) ∴AD //DF ，∴∠AEF =∠DFC ．………………………………………(1分)∵AB =CD ，∴∠B =∠C ．………………………………………………(1分) 又∵BE =CF ，∴△ABE ≌△DCF ．……………………………………(1分) ∴∠AEB =∠DFC ，……………………………………………………(1分) ∴∠AEB =∠AEF ．………………………………………………………(1分) ∵∠AEB +∠AEF =180º，∴∠AEF =90º．……………………………(1分) ∴四边形AEFD 是矩形．………………………………………………(1分)证法二: 联结AF 、DE ．…………………………………………………………(1分)∵在梯形ABCD 中，AD //BC ，又∵EF =AD ，∴四边形AEFD 是平行四边形．………………………………………(1分)∵AB =CD ，∴∠B =∠C ．......................................................(1分) ∵BE =CF ，∴BE +EF =CF +EF ，即BF =CE ， (1))∴△ABF ≌△DCE ．……………………………………………………(1分) ∴AF =DE ，………………………………………………………………(2分) ∴四边形AEFD 是矩形．………………………………………………(1分)10、证明:(1)∵□ABCD ，∴A B ∥CD ，AB ＝CD -----------------------------------1分 ∵E 、F 分别为AB 、CD 的中点，∴DF ＝12DC ，BE ＝12AB∴DF ∥BE ，DF ＝BE ---------------------------------------------------------------------1分 ∴四边形DEBF 为平行四边形∴DE ∥BF -----------------------------------------------------------------------------------1分 (2)证明:∵AG ∥BD ，∴∠G ＝∠DBC ＝90°，∴∆DBC 为直角三角形---1分 又∵F 为边CD 的中点．∴BF ＝12DC ＝DF ------------------------------------------1分又∵四边形DEBF 为平行四边形，∴四边形DEBF 是菱形----------------------1分 11．证明:∵在梯形ABCD 中，AD //BC ，∴∠DAE =∠FAE ，∠ADE =∠CFE ．……(1分)又∵AE =EC ，∴△ADE ≌△CFE ．…………………………………………(1分) ∴AD =FC ，…………………………………………………………………(1分) ∴四边形AFCD 是平行四边形．……………………………………………(1分)∵BC =2AD ，∴FC =AD =21BC ．……………………………………………(1分) ∵AC ⊥AB ，∴AF =21BC ．…………………………………………………(1分) ∴AF =FC ，……………………………………………………………………(1分) ∴四边形AFCD 是菱形．……………………………………………………(1分)12．(1)解:线段AD 与BC 的长度之间的数量为:3BC AD =．…………………(1分)证明:∵ AD // BC ，DE // AB ，∴ 四边形ABED 是平行四边形．∴ AD = B E ．………………………………………………………(2分) 同理可证，四边形AFCD 是平行四边形．即得 AD = FC ．……(1分) 又∵ 四边形AEFD 是平行四边形，∴ AD = EF ．……………(1分) ∴ AD = BE = EF = FC ．∴ 3BC AD =．……………………………………………………(1分)(2)解:选择论断②作为条件．…………………………………………………(1分)证明:∵ DE // AB ，∴ ∠B =∠DEC ．…………………………………(1分)∵ ∠B +∠C = 90°，∴ ∠DEC +∠C = 90°． 即得 ∠EDC = 90°．………………………………………………(2分) 又∵ EF = FC ，∴ DF = EF ．……………………………………(1分) ∵ 四边形AEFD 是平行四边形，∴ 四边形AEFD 是菱形．…………………………………………(1分)。

初中八年级数学（沪科版）多媒体暑假作业（三）一.择优录用。

1.下列长度的各组线段中，能组成三角形的是（ C ）A．1，1，2 B．3，7，11 C．6，8，9 D．3，3，62.下列语句中，不是A．两点之间线段最短 B．对顶角相等C．不是对顶角不相等 D．过直线AB外一点P作直线AB的垂线3.下列A．如果|a|=a，则a≥0 B ．如果，那么a=b或a=-bC．如果ab>0，则a>0，b>0 D ．若，则a是一个负数4.若△ABC的三个内角满足关系式∠B＋∠C=3∠A，则这个三角形（ A ）A．一定有一个内角为45° B．一定有一个内角为60°C．一定是直角三角形 D．一定是钝角三角形5.三角形的一个外角大于相邻的一个内角，则它是（ D ）A.直角三角形B.锐角三角形C.钝角三角形D.不能确定6.下列A．三角形可分为斜三角形.直角三角形和锐角三角形B．等腰三角形任一个内角都有可能是钝角或直角C．三角形外角一定是钝角D．△ABC中，如果∠A>∠B>∠C，那么∠A>60°，∠C<60°7.若一个三角形的三个内角的度数之比为1：2：3，那么相对应的三个外角的度数之比为（ B ）A．3：2：1 B．5：4：3 C．3：4：5 D．1：2：38.设三角形三边之长分别为3，8，1－2a，则a的取值范围为（ B ）A．－6<a<－3 B．－5<a<－2 C．－2<a<5 D．a<－5或a>29.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点, 且S △ABC=4cm2,则S阴影等于（ B ）A.2cm2B.1cm2C.12cm2 D.14cm2FED CBA10.已知：如图，在△ABC中，∠C=∠ABC=2∠A，BD是AC边的高，则∠DBC=（ B ）A．10° B．18° C．20° D．30°二. 相信自己。

沪版初二数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是方程2x + 3 = 9的解？A. x = 1B. x = 2C. x = 3D. x = 4答案：C2. 如果一个角的补角是其本身，那么这个角是：A. 45°B. 90°C. 180°D. 360°答案：B3. 一个数的平方是其本身，这个数可以是：A. 0B. 1C. -1D. 以上都是答案：D4. 一个三角形的两边长分别为3和4，第三边长可能是：A. 1B. 2C. 5D. 7答案：C5. 一个数的绝对值是其本身，这个数可以是：A. 正数B. 负数C. 零D. 正数和零答案：D6. 一个数的立方是其本身，这个数可以是：A. 0B. 1C. -1D. 以上都是答案：D7. 一个圆的直径增加一倍，其面积将：A. 增加一倍B. 增加两倍C. 增加四倍D. 增加八倍答案：C8. 一个等腰三角形的底角是45°，那么顶角是：A. 45°B. 90°C. 135°D. 180°答案：B9. 如果一个数的相反数是其本身，那么这个数是：A. 0B. 1C. -1D. 以上都不是答案：A10. 一个数的倒数是其本身，这个数可以是：A. 0B. 1C. -1D. 以上都是答案：B二、填空题（每题4分，共20分）11. 一个数的平方根是其本身，这个数是______。

答案：0或112. 一个数的立方根是其本身，这个数是______。

答案：0，1，-113. 一个数的绝对值是5，这个数可以是______。

答案：5或-514. 一个三角形的两边长分别为5和12，第三边长x满足的条件是______。

答案：7 < x < 1715. 一个数的相反数是-3，这个数是______。

答案：3三、解答题（每题10分，共50分）16. 解方程：3x - 5 = 10。

沪教版八年级下册数学考试真题及答案全文共2篇示例，供读者参考沪教版八年级下册数学考试真题及答案1第一章勾股定理1.勾股定理：直角三角形两直角边的平方和等于斜边的平方;即。

2.勾股定理的证明：用三个正方形的面积关系进行证明(两种方法)。

3.勾股定理逆定理：如果三角形的三边长，，满足，那么这个三角形是直角三角形。

满足的三个正整数称为勾股数。

第二章实数1.平方根和算术平方根的概念及其性质：(1)概念：如果，那么是的平方根，记作：;其中叫做的算术平方根。

(2)性质：①当≥0时，≥0;当<0时，无意义;② = ;③ 。

2.立方根的概念及其性质：(1)概念：若，那么是的立方根，记作：;(2)性质：① ;② ;③ =3.实数的概念及其分类：(1)概念：实数是有理数和无理数的统称;(2)分类：按定义分为有理数可分为整数的分数;按性质分为正数、负数和零。

无理数就是无限不循环小数;小数可分为有限小数、无限循环小数和无限不循环小数;其中有限小数和无限循环小数称为分数。

4.与实数有关的概念：在实数范围内，相反数，倒数，绝对值的意义与有理数范围内的意义完全一致;在实数范围内，有理数的运算法则和运算律同样成立。

每一个实数都可以用数轴上的`一个点来表示;反过来，数轴上的每一个点都表示一个实数，即实数和数轴上的点是一一对应的。

因此，数轴正好可以被实数填满。

5.算术平方根的运算律：( ≥0，≥0); ( ≥0，>0)。

第三章图形的平移与旋转1.平移：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

平移不改变图形大小和形状，改变了图形的位置;经过平移，对应点所连的线段平行且相等;对应线段平行且相等，对应角相等。

2.旋转：在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转。

这点定点称为旋转中心，转动的角称为旋转角。

旋转不改变图形大小和形状，改变了图形的位置;经过旋转，图形点的每一个点都绕旋转中心沿相同方向转动了相同和角度;任意一对对应点与旋转中心的连线所成的角都是旋转角;对应点到旋转中心的距离相等。

初二数学练习题沪教版一、选择题1. 下列哪个数是无理数？A. -4B. 0C. √5D. 2/32. 若 a + b = 5，且 a - b = 3，那么 a 的值是多少？A. 1B. 2C. 3D. 43. 下列哪个数是质数？A. 1B. 13C. 25D. 504. 若 2x - 5 = 13，那么 x 的值是多少？A. 8B. 9C. 10D. 115. 若正方体的表面积为 54 平方厘米，那么它的体积是多少？A. 27 平方厘米B. 54 平方厘米C. 81 平方厘米D. 108 平方厘米二、填空题1. 三个相同大小的正方体一共有多少个面？答：54 个面2. 若 a = 5，那么 a² = ？答：253. 若一个角的补角是 60°，那么该角的度数是多少？答：30°4. 若一辆汽车以每小时 60 公里的速度行驶，那么它 5 小时行驶的距离是多少？答：300 公里5. 若从 1 到 100，所有奇数的和是多少？答：2500三、解答题1. 甲、乙两人同时从相距 120 千米的地点出发，乙以每小时 50 千米的速度向甲追赶，若甲以每小时 40 千米的速度行驶，则多少小时后乙能追上甲？答：设乙追上甲时的时间为 t 小时，则甲行进的距离为 40t 千米，乙行进的距离为120 - 50t 千米。

当两者相遇时，两者行进的距离相等，所以有方程 40t = 120 - 50t。

解方程可得 t = 6。

所以乙能在 6 小时后追上甲。

2. 已知一正方形 ABCD，点 E、F、G 分别是边 BC、CD、DA 的中点，连接 AF 和 GD。

若 AF 的长度为 x，求 GD 的长度。

答：由题意可知，正方形 ABCD 的边长为 2x。

在三角形 AFB 和GDC 中，根据中位线定理可知 AF = GD。

所以 GD 的长度为 x。

3. 若一个整数的个位数字比十位数字大 7，且个位数字和百位数字的和为 10，求这个整数。

初中八年级数学（沪科版）多媒体暑假作业（十四）一. 相信自己。

1．比较大小：2-> —3（填“>，<或=”符号）2．分解因式：2218x -=2（x+3）（x-3）．3．若代数式13x 2x -+有意义，则x 的取值范围是X ≥-2且X ≠31 4．数轴上与原点的距离等于2个单位长度的点表示的数是±25．计算()0331622007603π⎛⎫-+÷-+- ⎪⎝⎭ = -1 6．把0.090876保留三个有效数字后得 0.0909，此时的精确度是万分位。

7．《达.芬奇密码》中的一个故事出现一列数：1，1，2，3，5，8，…，按此规律排列下去，这列数中的第8个数是 218．根据如图所示的程序计算，若输入x 的值为1，则输出y 的值为 4二.择优录用。

1．3-的倒数的绝对值是（ A ）A ．13B ．13-C ．3D ．3-2．温家宝总理有句名言：多么小的问题乘以13亿，都会变得很大；多么大的经济总量，除以13亿都会变得很小．将13亿用科学记数法表示为（ B ）A.1.3×108 B1.3×109 C.1.3×1010 D.1.3×10113．下列计算中，正确的是（ D ）A ．325a b ab +=B ．44a a a =∙C ．623a a a ÷=D ．3262()a b a b =4．下列因式分解正确的是（ C ）A ．x x x x x 3)2)(2(342++-=+-；B ．)1)(4(432-+-=++-x x x x ；C ．22)21(41x x x -=+-；D ．)(232y x y xy x y x xy y x +-=+-。

5．2008年8月第29届奥运会将在北京开幕，5个城市的国标标准时间（单位：时）在数轴上表示如图所示，那么北京时间2008年8月8日20时应是（ B ）Ａ．伦敦时间2008年8月8日11时 Ｂ．巴黎时间2008年8月8日13时Ｃ．纽约时间2008年8月8日5时 Ｄ．汉城时间2008年8月8日19时6．实数a ．b ．c ．d 在数轴上的位置如图，下列关系式不正确的是（ B ）A ．b a >B ．ac ac =C ．b ＜dD ．c+d ＞07．已知31a b a b a y x 32y 0.5x --+-与是同类项，则（ D ） A ．{2b 1a =-= B ．{2b 1a -== C ．{1b 1a =-= D ．{-1b 2a == 8．代数式3x 2-4x+6的值是9，则x 2-43x +6的值是 ( A ) A ．7 B ．18 C ．12 D ．99C ）A ．在9.1和9.2之间B ．在9，2和9.3之间C ．在9.3和9.4之间D ．在9.4和9.5之间10．某种细胞开始有2个，1小时后分裂成4个并死去1个，2小时分裂成6个并死去1个，3小时后分裂成10个并死去1个，按此规律，5小时后细胞存活的个数是（ B ）A. 31B. 33C. 35D. 37北京 汉城 巴黎 伦敦 纽约 5-089三.挑战奥数。

Word 文档仅限参照初中八年级数学（沪科版）多媒体暑期作业（三）一. 择优录取。

1.以下长度的各组线段中，能构成三角形的是（C）A. ．1，1，2B．3，7，11C．6，8，9D．3，3， 62.以下语句中，不是命题的是（ D ）A. ．两点之间线段最短B．对顶角相等C．不是对顶角不相等D．过直线 A.B 外一点 P 作直线 A.B 的垂线3.以下命题中，假命题是（ C ）A. ．假如 |A.|=A.，则 A.≥0B．假如，那么 A.=b 或 A.=-bC．假如 A.b>0 ，则 A.>0 ，b>0D．若，则 A. 是一个负数4.若△ A.BC 的三个内角知足关系式∠B＋∠ C=3∠A. ，则这个三角形（ A.）A. ．必定有一个内角为45°B．必定有一个内角为60°C．必定是直角三角形D．必定是钝角三角形5.三角形的一个外角大于相邻的一个内角，则它是（D）A.. 直角三角形B.锐角三角形C.钝角三角形D.不可以确立6.以下命题中正确的选项是（D）A. ．三角形可分为斜三角形. 直角三角形和锐角三角形B．等腰三角形任一个内角都有可能是钝角或直角C．三角形外角必定是钝角D．△ A.BC 中，假如∠ A.>∠ B>∠ C，那么∠ A.>60 °，∠ C<60°7.若一个三角形的三个内角的度数之比为 1：2：3，那么相对应的三个外角的度数之比为（ B ）A. ．3：2：1 B．5：4：3 C．3：4：5 D ．1：2：38. 设三角形三边之长分别为3， 8， 1－ 2A. ，则 A. 的取值范围为（ B ）A. ．－ 6<A.<－ 3 B ．－ 5<A.< －2C．－ 2<A.<5 D．A.<－5 或 A.>29. 如图 , 在△ A.BC 中 , 已知点 D,E,F 分别为边 BC,A.D,CE 的中点 ,2则 S阴且 S △ A.BC=4cm,影等于（ B）A..2cm2B.1cm212 D.12 C.cm4cm2AEFB D CWord 文档仅限参照Word 文档仅限参照A. ．10°B．18°C．20°D．30°二. 相信自己。

DCBA 沪教版初二数学暑假作业函数几何计算题有答案1、如图7，平面直角坐标系中，已知一个一次函数的图像通过点A （0，4）、B （2，0）． （1）求那个一次函数的解析式；（2）把直线AB 向左平移，若平移后的直线与x 轴交于点C且AC ＝BC ．求点C2.如图9，已知矩形ABCD ，把矩形ABCD 沿直线BD 翻折，点C 落在点E 处，联结AE ．（1）若AB=3，BC=6，试求四边形ABDE 的面积； （2）记AD 与BE 的交点为P ，若AB=a ，BC ＝b ，试求PD 的长（用a 、b 表示）．3．上周六，小明一家共7人从南桥动身去参观世博会。

小明提议：让爸爸载着爷爷、奶奶、外公、外婆去，自己和妈妈坐世博41路车去，最后在地铁8号线航天博物馆站邻近汇合。

图中 l 1，l 2分别表示世博41路车与小轿车在行驶中的路程（千米） 与时刻（分钟）的关系，试观看图像并回答下列问题：（1）世博41路车在途中行驶的平均速度为_______千米/分钟； 此次行驶的路程是____ ___千米．（2分） （2）写出小轿车在行驶过程中s 与t 的函数关系式：________________，定义域为___________．（3分）（3）小明和妈妈乘坐的世博41路车动身 分钟后被爸爸的小轿车追上了．（3分） 4、（本题7分）如图，在梯形ABCD 中，AB ∥CD .（1）假如∠A =︒50，∠B =︒80，求证：AB CD BC =+.（2）假如AB CD BC =+，设∠A =︒x ，∠B =︒y ，那么y 关于x 的函数关系式是_______.5． 如图，一次函数b x y +=31的图像与x 轴相交于点A （6，0）、与y 轴相交于点B ，（图1）（图2）CD(第3题图)(分钟)点C 在y 轴的正半轴上，BC =5．（1）求一次函数的解析式和点B 、C 的坐标；（2）假如四边形ABCD 是等腰梯形，求点D 的坐标．6．如图，在等腰梯形ABCD知//AD BC ,AB CD =,AE BC ⊥于E ，60B ∠=︒,45DAC ∠=︒,AC =求梯形ABCD 的周长。