七年级数学上册第六章图形的初步知识6.9直线的相交6.9.1对顶角同步练习(新版)浙教版

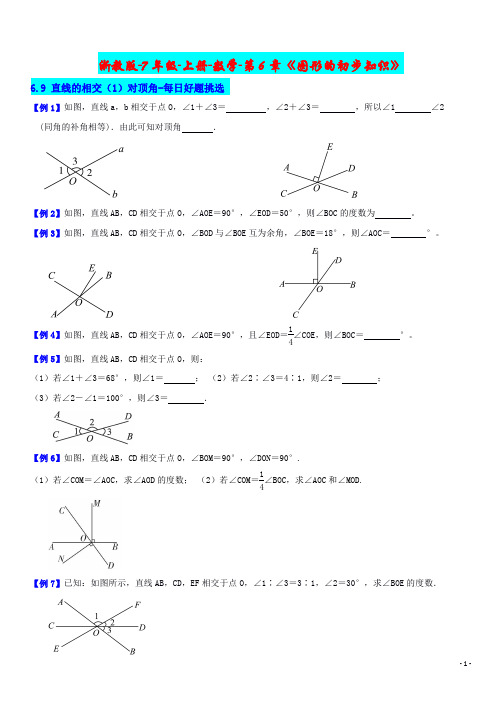
浙教版-7年级-上册-数学-第6章《图形的初步知识》6.9直线的相交（1）对顶角-每日好题挑选【例1】如图，直线a，b 相交于点O，∠1＋∠3＝，∠2＋∠3＝，所以∠1∠2(同角的补角相等)．由此可知对顶角．【例2】如图，直线AB，CD 相交于点O，∠AOE＝90°，∠EOD＝50°，则∠BOC 的度数为。

【例3】如图，直线AB，CD 相交于点O，∠BOD 与∠BOE 互为余角，∠BOE＝18°，则∠AOC＝°。

【例4】如图，直线AB，CD 相交于点O，∠AOE＝90°，且∠EOD＝14∠COE，则∠BOC＝°。

【例5】如图，直线AB，CD 相交于点O，则：（1）若∠1＋∠3＝68°，则∠1＝；（2）若∠2∶∠3＝4∶1，则∠2＝；（3）若∠2－∠1＝100°，则∠3＝．【例6】如图，直线AB，CD 相交于点O，∠BOM＝90°，∠DON＝90°.（1）若∠COM＝∠AOC，求∠AOD 的度数；（2）若∠COM＝14∠BOC，求∠AOC 和∠MOD.【例7】已知：如图所示，直线AB，CD，EF 相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE 的度数．【例8】如图，直线AE与CD相交于点B，射线BF平分∠ABC，射线BG在∠ABD内，（1）若∠DBE的补角是它的余角的3倍，求∠FBC的度数；（2）在（1）的件下，若∠DBG＝∠ABG－33°，求∠ABG的度数；（3）若∠FBG＝100°，求∠ABG和∠DBG的度数的差．【例9】如图，已知直线AB与直线CD相交于点O，∠BOE＝90°，OF平分∠BOD，∠BOC∶∠AOC＝1∶3.（1）求∠DOE，∠COF的度数；（2）若射线OF，OE同时绕O点分别以2°/s，4°/s的速度，顺时针匀速旋转，当射线OE，OF的夹角为90°时，两射线同时停止旋转．设旋转时间为t，试求t的值．【例9】观察图，回答下列各题．（1）图①中，共有对对顶角，可以看做＝×；（2）图②中，共有对对顶角，可以看做＝×；（3）图③中，共有对对顶角，可以看做＝×；（4）通过（1）～（3）题中直线条数与对顶角对数之间的关系，说明n(n≥2)条直线相交于一点，可以形成几对对顶角。

6.9 直线的相交第1课时对顶角知识点1 对顶角的意义1．下列图形中，∠1与∠2是对顶角的是( )图6－9－12．如图6－9－2所示，BE，CF相交于点O，OA，OD是射线，其中构成对顶角的角是____________．图6－9－2知识点2 对顶角的性质3．如图6－9－3，直线a，b相交于点O，∠1＋∠3＝________，∠2＋∠3＝________(邻补角的定义)，所以∠1________∠2(同角的补角相等)．由此可知对顶角________．图6－9－34．已知∠α和∠β是对顶角，∠α＝30°，则∠β的度数为( )A．30°B．60°C．70°D．150°5．如图6－9－4，图中是对顶角量角器，用它测量角的原理是______________.图6－9－46．如图6－9－5，直线AB，CD，EF交于一点O.图6－9－5(1)∠EOB的对顶角是________；(2)________是∠AOE的对顶角；(3)若∠AOC＝76°，则∠BOD的度数为________．7．如图6－9－6所示，直线AB与CD相交于点O，若∠AOC＋∠BOD＝90°，则∠BOC ＝________°.图6－9－68．如图6－9－7所示，∠1＝120°，∠2＋∠3＝180°，则∠4＝________°.图6－9－79. 如图6－9－8，直线AB，CD相交于点O，∠1＝40°，求∠2，∠3，∠4的度数．图6－9－810．如图6－9－9所示，直线AB，CD相交于点O，OE平分∠AOC，∠EOC＝35°，求∠BOD的度数．图6－9－911．如图6－9－10，直线AB，CD，EF相交于点O，∠AOD＝150°，∠EOD＝80°，求∠AOF的度数．图6－9－1012．如图6－9－11，直线AB，CD相交于点O，OE平分∠AOC，OF平分∠DOB，则点E，O，F在同一直线上，请说明理由．(补全解答过程)图6－9－11解：∵直线AB，CD相交于点O，∴∠AOC＝________(对顶角相等)．∵OE平分∠AOC，OF平分∠DOB，∴∠AOE＝______∠AOC，∠BOF＝______∠DOB，∴∠AOE＝________．∵∠AOF＋∠BOF＝∠AOB＝180°，∴∠AOF＋∠AOE＝∠EOF＝180°，∴点E，O，F在同一直线上．13．如图6－9－12，直线AB与CD相交于点O，∠BOE＝∠COF＝90°，且∠BOF＝32°，求∠AOC与∠EOD的度数．图6－9－1214．已知：如图6－9－13所示，直线AB，CD，EF相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE的度数．图6－9－1315．观察图6－9－14，回答下列各题．(1)图①中，共有________对对顶角，可以看作________＝________×________；(2)图②中，共有________对对顶角，可以看作________＝________×________；(3)图③中，共有________对对顶角，可以看作________＝________×________；(4)通过(1)～(3)各题中直线条数与对顶角对数之间的关系，若有n(n≥2)条直线相交于一点，则可形成几对对顶角？图6－9－141．C 2.∠EOF和∠BOC，∠COE和∠BOF 3．180°180°＝相等4．A 5.对顶角相等6．(1)∠AOF(2)∠BOF(3)76°7．135 8.609．解：∵∠1＝40°，∠1＝∠2，∴∠2＝40°.∵∠1＝40°，∠1＋∠3＝180°，∴∠3＝140°.又∵∠3＝∠4，∴∠4＝140°.10. 解：∵OE平分∠AOC，∠EOC＝35°，∴∠AOC＝2∠EOC＝35°×2＝70°.由对顶角相等可知：∠BOD＝∠AOC＝70°. 11．解：∵∠AOD＝150°，∠AOD＋∠BOD＝180°，∴∠BOD＝30°.又∵∠EOD＝80°，∴∠EOB＝80°－30°＝50°，∴∠AOF＝∠EOB＝50°.12．∠DOB 1212∠BOF13．解：∵∠COF＝90°，∠BOF＝32°，∴∠COB＝90°－32°＝58°＝∠AOD.∵∠BOE＝90°，∴∠EOA＝180°－90°＝90°，∠EOC＝90°－∠COB＝32°，∴∠AOC＝∠EOA＋∠EOC＝122°，∠EOD＝∠EOA＋∠AOD＝148°.14．解：∵∠1＋∠2＋∠3＝180°，且∠1∶∠3＝3∶1，∠2＝30°，∴∠1＝112.5°，∠3＝37.5°，∴∠BOE＝∠1＝112.5°.15．解：(1)共有2对对顶角，可以看作2＝2×1.(2)单个角是对顶角的有3对，两个角组成复合角的对顶角有3对，共有6对，可以看作6＝3×2.(3)单个角是对顶角的有4对，两个角组成复合角的对顶角有4对，三个角组成复合角的对顶角有4对，共有12对，可以看作12＝4×3.(4)n(n≥2)条直线相交于一点，可形成n(n－1)对对顶角．。

第2课时垂直知识点一垂直的概念当两条直线相交所构成的四个角中有一个是________时，我们就说这两条直线互相垂直，其中的一条直线叫做另一直线的垂线，它们的交点叫做垂足．两条线段垂直是指这两条线段所在的______垂直．1．以下两条直线互相垂直的是( )①两条直线相交所成的四个角中有一个是直角；②两条直线相交所成的四个角相等；③两条直线相交，有一组邻补角相等；④两条直线相交，对顶角互补．A．①③B．①②③C．②③④D．①②③④知识点二点到直线的距离从直线外一点到这条直线的________的长度，叫做点到直线的距离．2．如图6－9－5，点A到直线CD的距离是指哪一条线段的长( )图6－9－5A．AC B．CDC．AB D．BD类型一过一点画已知直线的垂线例1 教材补充例题在图6－9－6中，分别过点P作AB的垂线．图6－9－6【归纳总结】用三角尺作垂线的步骤：“一落”，即三角尺的一条直角边落在已知直线上；“二过”，即三角尺的另一条直角边经过已知点；“三画线”，即沿着经过已知点的直角边画垂线．类型二与垂直有关的角度计算例2 教材例3针对训练如图6－9－7，直线AB，CD相交于点O，OE⊥AB，垂足为O.如果∠EOD＝42°，求∠AOC的度数．图6－9－7类型三垂线的性质例3 教材补充例题如图6－9－8所示，下列各种说法：(1)把图甲中弯曲的河道BCA改成直道BA，可以缩短航程；(2)把图乙中的渠水引到水池C中，可在渠岸AB边上找到一点D，使CD⊥AB，沿CD挖水渠，水渠最短；(3)如图丙所示，甲、乙两辆汽车分别从A，B处沿道路AC，BC同时出发开往C城，若两车速度相同，则甲车先到达C城．其中运用“垂线段最短”这个性质的是( )图6－9－8A．(1)(2) B．(1)(3)C．(2)(3) D．(1)(2)(3)【归纳总结】垂线的性质：(1)在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线．(2)连结直线外一点与直线上各点的所有线段中，垂线段最短．(3)从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．小结◆◆◆)反思◆◆◆)互相垂直的两条直线是相交线吗？它们是一种怎样的特殊情况？详解详析【学知识】知识点一直角直线1．[答案]D知识点二垂线段2．[答案]C【筑方法】例1解：如图所示：例2解：∵OE⊥AB，∴∠EOB＝90°.又∵∠EOD＝42°，∴∠BOD＝90°－42°＝48°，∴∠AOC＝∠BOD＝48°.例3[答案]C【勤反思】[反思] 是相交线，它们相交所成的角是90°.。

6.9 直线的相交一、选择题（共15小题；共75分）1. 下列图形中，线段PQ的长表示点P到直线MN的距离的是 ( )A. B.C. D.2. 下列图形中，∠1与∠2是对顶角的是 ( )A. B.C. D.3. 如图，A是直线l外一点，点B、C、E、D在直线l上，且AD⊥l，D为垂足，如果量得AC=8 cm，AD=6 cm，AE=7 cm，AB=13 cm，那么，点A到直线l的距离是 ( )A. 13 cmB. 8 cmC. 7 cmD. 6 cm4. 如图，直线AB，CD相交于点O．OE平分∠AOD，若∠BOC=80∘，则∠AOE的度数是 ( )A. 40∘B. 50∘C. 80∘D. 100∘5. 下列说法：①两点确定一条直线；②射线AB和射线BA是同一条射线；③相等的角是对顶角；④三角形任意两边和大于第三边的理由是两点之间线段最短．正确的是 ( )A. ①③④B. ①②④C. ①④D. ②③④6. 下列说法中错误的是 ( )A. 一个锐角的补角一定是钝角；B. 同角或等角的余角相等；C. 两点间的距离是连接这两点的线段的长度；D. 过直线l上的一点有且只有一条直线垂直于l．7. 下列说法正确的个数有 ( )①若AB=BC，则点B是线段AC的中点；②从直线外一点到这条直线的垂线段，叫做点到直线的距离；③若AB=MA+MB，AB<NA+NB，则点M在线段AB上，点N在线段AB外；④在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线．A. 0B. 1C. 2D. 38. 挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，⋯，则第6次应拿走 ( )A. ②号棒B. ⑦号棒C. ⑧号棒D. ⑩号棒9. 如图，直线AB，CD，EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=28∘，则∠AOG为 ( )A. 56∘B. 59∘C. 60∘D. 62∘10. 已知如图，直线AB、CD相交于点O，∠AOC=70∘，OE把∠BOD分成两部分，且∠BOE:∠EOD=2:3，则∠AOE= ( )A. 162∘B. 152∘C. 142∘D. 132∘11. 如图所示，已知AB⊥BD，BC⊥CD，AD=6 cm，BC=4 cm，则线段BD的范围是 ( )A. 大于4 cmB. 小于4 cmC. 大于4 cm且小于6 cmD. 小于6 cm或大于4 cm12. 用3根火柴棒最多能拼出 ( )A. 4个直角B. 8个直角C. 12个直角D. 16个直角13. 三条直线两两相交于同一点时，对顶角有m对，交于不同三点时，对顶角有n对，则m与n的关系 ( )A. m=nB. m>nC. m<nD. m+n=1014. 观察下列图形，并阅读图形下面的相关文字：两条直线相交，三条直线相交，四条直线相交，⋯⋯最多有1个交点；最多有3个交点；最多有6个交点⋯⋯像这样，十条直线相交，最多交点的个数是 ( )．A. 40个B. 45个C. 50个D. 55个15. 如图，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15∘30’，则下列结论中不正确的是 ( )．A. ∠2=45∘B. ∠1=∠3C. ∠AOD与∠1互为补角D. ∠1的余角等于75∘30ʹ二、填空题（共15小题；共75分）16. A是直线l外的一点，A到l的距离为10 cm，P是l上任意一点，则PA的最小值是cm．17. 如图所示，直线a、b相交于点O，∠1=50∘，则∠2=度．18. 如图，直线AB，CD相交于点O．若∠BOD=40∘，OA平分∠COE，则∠AOE=．∠B，那么∠B=．19. 若∠A与∠B互为邻补角，且∠A=1320. 如图，直线AB和CD相交于点O，OE平分∠DOB，∠AOC=40∘，则∠DOE=度．21. 如图所示，点P是∠AOB的边OB上的一点．①过点P作OB的垂线，交OA于点C．②过点P作OA的垂线，垂足为H．③线段PH的长度是点P到的距离，线段的长度是点C到直线OB的距离．④因为直线外一点与直线上各点所连的所有线中，垂线段最短，所以PC，PH，OC这三条线段的大小关系是（用“ <”连接）．22. 在同一平面内，三条直线两两相交，最多有3个交点，那么4条直线两两相交，最多有个交点，8条直线两两相交，最多有个交点．23. 下列说法正确的是．（写出正确的序号）① 三条直线两两相交有三个交点；② 两条直线相交不可能有两个交点；③在同一平面内的三条直线的交点个数可能为0，1，2，3；n(n−1)个交点；④同一平面内的n条直线两两相交，其中无三线共点，则可得12⑤ 同一平面内的n条直线经过同一点可得2n(n−1)个角（平角除外）．24. O为平面上一点，过O在这个平面上引2005条不同的直线l1，l2，l3，⋯，l2005，则可形成对以O为顶点的对顶角．25. 如图，AB与CD相交于点O，若∠DOE=90∘，∠BOE=52∘，则∠AOC=．26. 如图，AB、CD、EF相交于O点，EF⊥AB，OG为∠COF的平分线，OH为∠DOG的平分线．若∠AOC:∠COG=4:7，则∠DOH=度.27. 如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=35∘，则∠COB= .28. 如图，直线AB，CD相交于点O，已知∠AOC=70∘，OE把∠BOD分成两部分，且∠BOE:∠EOD=3:2．则∠EOD=．29. 已知OA⊥OB，∠AOC：∠AOB=2：3，则∠BOC=．30. 如图所示，两条直线相交，有对对顶角，三条直线相交于同一点，有对顶角；四条直线相交于同一点，有对对顶角，⋯，n条直线相交于同一点有对对顶角．三、解答题（共5小题；共65分）31. 如图，建筑工人经常要测量两堵围墙所成的∠AOB，但人不能进入围墙，聪明的你帮助工人师傅想想办法吧．要求：画出两种不同测量方案示意图，直接给出求∠AOB的表达式．32. 如图：点C是∠AOB的边OB上的一点，按下列要求画图并回答问题．Ⅰ过C点画OB的垂线，交OA于点D；Ⅱ过C点画OA的垂线，垂足为E；Ⅲ比较线段CE，OD，CD的大小（请直接写出结论）；Ⅳ请写出第（3）小题图中与∠AOB互余的角（不增添其它字母）．33. 如图，直线AB，CD相交于点O，OE⊥CD，OF平分∠BOD，若∠AOE=26∘，求∠COF的度数．34. 根据下列条件画图如图示点A、B、C分别代表三个村庄Ⅰ画射线ACⅡ画线段ABⅢ若线段AB是连接A村和B村的一条公路，现C村庄也要修一条公路与A、B两村庄之间的公路连通，为了减少修路开支，C村庄应该如何修路?请在同一图上用三角板画出示意图，并说明画图理由．35. 两条直线相交，四个交角中的一个锐角或一个直角称为这两条直线的“夹角”（如图）．如果在平面上画L条直线，要求它们两两相交，并且“夹角”只能是15∘，30∘，45∘，60∘，75∘，90∘之一，问：ⅠL的最大值是多少?Ⅱ当L取最大值时，问所有的“夹角”的和是多少?答案第一部分1. A2. C3. D4. A5. C6. D7. C8. D9. B 10. B11. C 12. C 13. A 14. B 15. D第二部分16. 1017. 5018. 40∘19. 135∘20. 2021. ①②如图所示．③ OA，PC．④ PH<PC<OC．22. 6；2823. ② ③ ④ ⑤24. 401802025. 38∘26. 72.5∘27. 125∘28. 28∘．29. 150∘或30∘30. 两；六；十二；n(n−1)第三部分31. 方案1图：∠AOB=∠DOC．方案2图：∠AOB=180∘−∠BOC．32. （1）如图：（2）如图：（3）CE<CD<OD．（4）∵CE⊥OA，∴∠AOB+∠OCE=90∘．∵CD⊥OB，∴∠AOB+∠ODC=90∘．∴与∠AOB互余的角是∠OCE与∠ODC．33. ∵OE⊥CD，∴∠EOD=90∘．∵∠AOE=26∘，∴∠DOB=180∘−∠AOE−∠EOD=64∘．∵OF平分∠BOD，∠DOB=32∘．∴∠DOF=12∴∠COF=180∘−∠DOF=148∘．34. （1）（2）（3）如图所示，过点C作CD⊥AB，垂足为D．理由：连接直线外一点与直线上各点的所有线段中，垂线段最短．35. （1）固定平面上一条直线，其它直线与此条固定直线的交角自这条固定直线起逆时针计算，只能是15∘，30∘，45∘，60∘，75∘，90∘，105∘，120∘，135∘，150∘，165∘十一种角度之一，所以，平面上最多有12条直线．否则，必有两条直线平行．（2）如图，将所有直线做平行移动，使它们交于同一个点，这样的平行移动显然不改变两条直线的“夹角”．无妨设其中一条直线水平，从水平直线开始，逆时针将12条直线分别记为第一条、第二条、⋯和第十二条直线．（1）如图：第二条至第十二条直线与第一条直线的“夹角”和是：15+30+45+60+75+90+75+60+45+30+15=540（度）；（2）第三条至第十二条直线与第二条直线相交的“夹角”和是：15+30+45+60+75+90+75+60+45+30=(540−15)（度）；（3）第四条至第十二条直线与第三条直线相交的“夹角”和是：15+30+45+60+75+90+75+60+45=(540−15−30)（度）；⋯；（10）第十一条和第十二条直线与第十条直线相交的“夹角”和是(30+15)（度），（11）第十二条直线与第十一条直线相交的“夹角”和是15（度）；将（2）和（11）、（3）和（10）、（4）和（9）、（5）和（8）、（6）和（7）配对，得到所有的“夹角”之和是6×540=3240（度）．。

6．9 直线的相交第1课时对顶角知识点一对顶角的概念对顶角的定义有两种叙述：一是两条直线相交成四个角，其中不相邻的两个角是对顶角；二是一个角的两边分别是另一个角的两边的反向延长线，这两个角叫做对顶角．1．下列图形中，∠1与∠2是对顶角的是( )图6－9－1知识点二对顶角的性质对顶角的性质：对顶角______．2．如图6－9－2，直线AB与CD相交于点O，OE平分∠AOC，若∠EOC＝25°，则∠BOD 的度数为________．图6－9－2类型有关对顶角的计算例1 教材补充例题已知：如图6－9－3所示，直线AB，CD，EF相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE的度数．图6－9－3例2 教材例2拓展题如图6－9－4所示，已知直线AB，CD，EF相交于点O，OG是∠AOF 的平分线，∠BOD＝35°，∠COE＝18°.求∠COG的度数．图6－9－4【归纳总结】在相交直线中，利用对顶角进行角的转换是常用的方法，这体现了转化思想的运用．小结◆◆◆)反思◆◆◆)我们已经知道“对顶角相等”，而相等的角一定是对顶角吗？详解详析【学知识】知识点一1．[答案]C知识点二 相等2．[答案] 50°【筑方法】例1 解：∵∠1＋∠2＋∠3＝180°，且∠1∶∠3＝3∶1，∠2＝30°，∴∠1＝112.5°，∴∠BOE ＝∠1＝112.5°.例2 [解析] 根据图形易知，∠COG ＝∠AOC ＋∠AOG ＝∠BOD＋12∠AOF ，因此只需求出∠AOF 即可．解：∵∠DOF＝∠COE＝18°，∴∠BOF ＝∠BOD＋∠DOF＝35°＋18°＝53°.又∵∠AOF＋∠BOF＝180°，∴∠AOF ＝180°－∠BOF＝127°.∵OG 是∠AOF 的平分线，∴∠AOG ＝12∠AOF ＝12×127°＝63.5°. 因此∠COG＝∠AOC＋∠AOG＝∠BOD＋∠AOG＝35°＋63.5°＝98.5°.【勤反思】[小结] 对顶角相等[反思] 相等的角不一定是对顶角．。

6.9 直线的相交(第1课时)1．如果两条直线____________，就说这两条直线相交，该公共点叫做这两条直线的____________．2．顶点____________，角的两边____________所组成的角叫对顶角．3．对顶角____________．A组基础训练1．以下四种说法：①对顶角相等；②相等的角是对顶角；③不是对顶角的两个角不相等；④不相等的两个角不是对顶角．其中正确的是( )A．1个 B．2个C．3个 D．4个2．∠1的对顶角是∠2，∠2与∠3互补，若∠3＝45°，则∠1的度数为( )A．45° B．135°C．45°或135° D．90°3．平面内三条直线两两相交构成的对顶角共有( )A．3对 B．6对C．12对 D．不能确定4．(宁波中考)如图，直线AB与直线CD相交于点O，E是∠AOD内一点，已知∠AOE＝90°，∠BOD＝45°，则∠COE的度数是( )第4题图A．125° B．135°C．145° D．155°5．(1)如图1，用图中这种测量工具，可以量出图中零件上AB与CD两条轮廓线的延长线所成的角．其中的道理是____________．图1图2第5题图(2)如图2，当剪刀口∠AOB增大15°时，∠COD增大____________．6．如图，三条直线交于同一点，若∠1＋∠2＝80°，则∠3＝____________.第6题图7．如图，已知直线AB，BC，CA两两相交于A，B，C三点，已知∠1与∠3互补，若∠2＝51°，则∠4＝____________.第7题图8．如图，直线EF分别交∠AOB的两边于C，D两点，写出图中所有的对顶角．第8题图9．如图，直线AB与CD相交于点O，∠AOD＋∠BOC＝260°，求∠AO C的度数．第9题图10．如图，直线AB，CD交于点O，OE平分∠AOD.(1)若∠AOC＝46°，求∠DOE的度数；(2)若∠AOC＝x，求∠COE的度数．第10题图11．如图，直线AB，CD相交于点O，∠AOE比∠DOE大30°，∠BOD比∠DOE小30°，求∠AOE和∠A OC的度数．第11题图12．如图所示，直线AB，CD相交于点O，OE平分∠AOD，∠FOC＝90°，∠1＝40°，求∠2和∠3的度数．第12题图B组自主提高13．同一平面内的三条直线的交点个数为____________．14．如图，已知直线AB与CD交于点O，OE平分∠BOD，OF平分∠AOB.(1)若∠BOE＝40°，求∠AOF与∠COF的度数；(2)若∠BOE＝x(x＜45°)，请用含x的代数式表示∠COF的度数．第14题图C组综合运用15．观察下图，回答下列问题．第15题图(1)图1中共有____________对对顶角；(2)图2中共有____________对对顶角；(3)图3中共有____________对对顶角；(4)当n(n≥2，且n为整数)条直线相交于一点时，会形成____________对对顶角．参考答案6．9 直线的相交(第1课时)【课堂笔记】1．只有一个公共点 交点 2.相同 互为反向延长线 3.相等 【分层训练】 1．B 2.B 3.B 4.B 5．(1)对顶角相等 (2)15° 6．100° 7.51°8．∠ECO 与∠ACD，∠ACE 与∠OCD，∠CDO 与∠BDF，∠CDB 与∠ODF. 9．∠AOC＝50°10．(1)∵∠AOC＋∠AOD＝180°，∠AOC ＝46°，∴∠AOD ＝180°－46°＝134°.∵OE 平分∠AOD，∴∠DOE ＝12∠AOD ＝67°.(2)∠COE＝∠AOC＋∠AOE＝x ＋12(180°－x)＝90°＋12x.11．∠AOE＝90°，∠AOC ＝30°.12．∠3＝180°－∠COF－∠1＝50°，∴∠AOD ＝180°－∠3＝130°.∵OE 平分∠AOD，∴∠2＝12∠AOD ＝65°.13．0个或1个或2个或3个14．(1)∵OE 平分∠BOD，∴∠BOE ＝12∠BOD.∵∠BOE ＝40°，∴∠BOD ＝80°，∴∠BOC＝100°.∵OF 平分∠AOB，∴∠AOF ＝∠BOF＝90°，∴∠COF ＝100°－90°＝10°. (2)∠COF ＝180°－2x －90°＝90°－2x.15．(1)2 (2)6 (3)12 (4)n(n －1)。

浙教版七年级数学上册第6章图形的初步知识 6.9 直线的相交6.9.1 对顶角同步练习1．如图，直线a，b相交于点O，若∠1等于50°，则∠2等于( )A．50° B．40° C．140° D．130°2. 如图，直线AB，CD相交于点O，OE，OF是过点O的两条射线，其中构成对顶角的是( )A．∠AOF与∠DOE B．∠EOF与∠BOEC．∠BOC与∠AOD D．∠COF与∠BOD3. 如图，直线AB，CD相交于点O.若∠1＋∠3＝60°，则∠2，∠3的度数分别为( )A．120°，60° B．130°，50°C．140°，40° D．150°，30°4. 如图，直线l1，l2，l3相交于点O，则∠1，∠2，∠3的度数和为( )A．90° B．120° C．180° D．30°5. ∠1的对顶角是∠2，∠2的补角是∠3.若∠3＝45°，则∠1的度数是( ) A．45° B．135° C．45°或135° D．90°6. 如图，直线MN和∠AOB的两边分别相交于点C，D.已知∠1＋∠2＝180°，则图中与∠1相等的角(不含∠1)有( )A．1个 B．2个 C．3个 D．4个7. 如图是一个对顶角量角器，用它测量角的原理是____________．8. 如图，直线AB与CD相交于点O，ON平分∠DOB，若∠BOC＝110°，则∠AON 的度数为________°.9. 如图，直线AB和CD相交于点O，∠EOB＝90°，∠AOD＝128°，则∠COE 的度数是_______度．10. 如图，直线AB，CD相交于点O，OE平分∠COD，∠BOE＝68°，则∠AOC＝_________．11. 如图，直线a，b，c相交于点O，若∠1＝2∠2，∠3－∠1＝30°，则∠4的度数是_______．12. 如图，直线AB，CD，EF相交于点O，OG是∠AOF的平分线，∠BOD＝35°，∠COE＝18°，则∠COG的度数是________．13. 如图，直线AB，CD，EF相交于点O，∠BOD＝45°，∠COF＝80°.(1)图中有多少对对顶角(不含平角)?(2)每一对对顶角中，各角的度数是多少？14. 如图，直线AB，CD，EF相交于点O，∠1与∠2互余，∠2与∠3互余．若∠DOF＝32°，求∠1，∠2，∠3的度数．15. 如图，直线AB，CD，EF相交于点O，∠AOF＝3∠FOB，∠AOC＝90°，求∠EOC的度数．16. 如图，直线a，b相交于点O，∠1＝∠2.(1)指出∠3的对顶角；(2)指出∠5的补角；(3)若∠1与∠4的度数之比为1∶4，求∠3的度数．17. 如图，两条笔直的街道AB，CD相交于点O，街道OE，OF分别平分∠AOC，∠BOD，比较∠1与∠2的关系，并说明街道EOF是笔直的．18. 观察下列图形，寻找对顶角(不含平角)．(1)如图①，图中共有______对对顶角；(2)如图②，图中共有______对对顶角；(3)如图③，图中共有______对对顶角；(4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成__________对对顶角；(5)若20条直线相交于一点，则可形成对顶角多少对？参考答案：1---6 ACDCB C7. 对顶角相等8. 1459. 3810. 22°11. 30°12. 98.5°13. 解：(1)6对(2)∠AOC＝∠BOD＝45°，∠AOE＝∠BOF＝55°，∠EOD＝∠COF＝80°，∠AOD ＝∠BOC＝135°，∠BOE＝∠AOF＝125°，∠EOC＝∠DOF＝100°14. 解：因为直线CD与EF相交于点O，所以∠1＝∠DOF＝32°.因为∠1与∠2互余，所以∠1＋∠2＝90°，所以∠2＝90°－∠1＝90°－32°＝58°.因为∠1与∠2互余，∠2与∠3互余，所以∠1＝∠3，所以∠3＝32°15. 解：因为∠FOB＋∠AOF＝180°，∠AOF＝3∠FOB，所以∠FOB＋3∠FOB ＝180°，所以∠FOB＝45°，所以∠AOE＝∠FOB＝45°，所以∠EOC＝∠AOC －∠AOE＝90°－45°＝45°16. 解：(1)∠2(2)∠2，∠3，∠1(3)因为∠1∶∠4＝1∶4，所以∠4＝4∠1，因为∠1＝∠2，∠1＋∠2＋∠4＝180°，所以∠2＋∠2＋4∠2＝180°，解得∠2＝30°，因为∠2与∠3是对顶角，所以∠3＝∠2＝30°17. 解：因为∠AOC 与∠BOD 是对顶角，所以∠AOC＝∠BOD，又因为∠1＝12∠AOC，∠2＝12∠BOD，所以∠1＝∠2，因为∠2＋∠AOF＝180°，所以∠1＋∠AOF＝180°，所以∠EOF＝180°，所以EOF 是一条直线，即街道EOF 是笔直的 18. (1) 2 (2) 6 (3) 12 (4) n(n －1)(5)当n ＝20时，n(n －1)＝20×19＝380(对)。

第1课时对顶角一、选择题1．已知∠α和∠β是对顶角，∠α＝30°，则∠β的度数为( )A．30° B．60° C．70° D．150°2．如图1所示，直线AB，CD相交于点O，∠EOB＝90°，图中∠EOD与∠AOC的关系是( )图1A．对顶角 B．相等C．互补 D．互余3．以下四种说法：①对顶角相等；②相等的角是对顶角；③不是对顶角的两个角不相等；④不相等的两个角不是对顶角．其中正确的有( )A．1个 B．2个 C．3个 D．4个4．如图2，三条直线l1，l2，l3相交于点O，则∠1＋∠2＋∠3等于( )A．90° B．120° C．180° D．360°图25．2017·海淀期末如图3，直线AB，CD相交于点O，OE平分∠BOD.若∠COE＝160°，则∠AOC等于( )图3A．20° B．40°C．60° D．80°二、填空题6．图4是对顶角量角器，用它测量角的原理是______________．图47．如图5所示，BE，CF相交于点O，OA，OD是射线，其中构成对顶角的角是________．图58．三条直线两两相交，其中对顶角共有________对．9．如图6所示，已知直线AB，CD，EF交于一点O，则(1)∠EOB的对顶角是________；(2)________是∠AOE的对顶角；(3)若∠AOC＝76°，则∠BOD的度数为________．图610．如图7所示，直线AB与CD相交于点O，若∠AOC＋∠BOD＝90°，则∠BOC＝________°.图711．如图8所示，直线c与直线a，b分别交于点D，E，若∠1＝120°，∠2＋∠3＝180°，则∠4的度数为________．。

6.9 直线的相交第1课时对顶角知识点1 对顶角的意义1．下列图形中，∠1与∠2是对顶角的是( )图6－9－12．如图6－9－2所示，BE，CF相交于点O，OA，OD是射线，其中构成对顶角的角是____________．图6－9－2知识点2 对顶角的性质3．如图6－9－3，直线a，b相交于点O，∠1＋∠3＝________，∠2＋∠3＝________(邻补角的定义)，所以∠1________∠2(同角的补角相等)．由此可知对顶角________．图6－9－34．已知∠α和∠β是对顶角，∠α＝30°，则∠β的度数为( )A．30° B．60° C．70° D．150°5．如图6－9－4，图中是对顶角量角器，用它测量角的原理是______________.图6－9－46．如图6－9－5，直线AB，CD，EF交于一点O.图6－9－5(1)∠EOB的对顶角是________；(2)________是∠AOE的对顶角；(3)若∠AOC＝76°，则∠BOD的度数为________．7．如图6－9－6所示，直线AB与CD相交于点O，若∠AOC＋∠BOD＝90°，则∠BOC＝________°.图6－9－68．如图6－9－7所示，∠1＝120°，∠2＋∠3＝180°，则∠4＝________°.图6－9－79. 如图6－9－8，直线AB，CD相交于点O，∠1＝40°，求∠2，∠3，∠4的度数．图6－9－810．如图6－9－9所示，直线AB，CD相交于点O，OE平分∠AOC，∠EOC＝35°，求∠BOD 的度数．图6－9－911．如图6－9－10，直线AB，CD，EF相交于点O，∠AOD＝150°，∠EOD＝80°，求∠AOF 的度数．图6－9－1012．如图6－9－11，直线AB，CD相交于点O，OE平分∠AOC，OF平分∠DOB，则点E，O，F在同一直线上，请说明理由．(补全解答过程)图6－9－11解：∵直线AB，CD相交于点O，∴∠AOC＝________(对顶角相等)．∵OE平分∠AOC，OF平分∠DOB，∴∠AOE＝______∠AOC，∠BOF＝______∠DOB，∴∠AOE＝________．∵∠AOF＋∠BOF＝∠AOB＝180°，∴∠AOF＋∠AOE＝∠EOF＝180°，∴点E，O，F在同一直线上．13．如图6－9－12，直线AB与CD相交于点O，∠BOE＝∠COF＝90°，且∠BOF＝32°，求∠AOC与∠EOD的度数．图6－9－1214．已知：如图6－9－13所示，直线AB，CD，EF相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE的度数．图6－9－1315．观察图6－9－14，回答下列各题．(1)图①中，共有________对对顶角，可以看作________＝________×________；(2)图②中，共有________对对顶角，可以看作________＝________×________；(3)图③中，共有________对对顶角，可以看作________＝________×________；(4)通过(1)～(3)各题中直线条数与对顶角对数之间的关系，若有n(n≥2)条直线相交于一点，则可形成几对对顶角？图6－9－141．C 2.∠EOF和∠BOC，∠COE和∠BOF3．180°180°＝相等4．A 5.对顶角相等6．(1)∠AOF(2)∠BOF(3)76°7．135 8.609．解：∵∠1＝40°，∠1＝∠2，∴∠2＝40°. ∵∠1＝40°，∠1＋∠3＝180°，∴∠3＝140°. 又∵∠3＝∠4，∴∠4＝140°.10. 解：∵OE平分∠AOC，∠EOC＝35°，∴∠AOC＝2∠EOC＝35°×2＝70°.由对顶角相等可知：∠BOD＝∠AOC＝70°. 11．解：∵∠AOD＝150°，∠AOD＋∠BOD＝180°，∴∠BOD＝30°.又∵∠EOD＝80°，∴∠EOB＝80°－30°＝50°，∴∠AOF＝∠EOB＝50°.12．∠DOB 1212∠BOF13．解：∵∠COF＝90°，∠BOF＝32°，∴∠COB＝90°－32°＝58°＝∠AOD.∵∠BOE＝90°，∴∠EOA＝180°－90°＝90°，∠EOC＝90°－∠COB＝32°，∴∠AOC＝∠EOA＋∠EOC＝122°，∠EOD＝∠EOA＋∠AOD＝148°.14．解：∵∠1＋∠2＋∠3＝180°，且∠1∶∠3＝3∶1，∠2＝30°，∴∠1＝112.5°，∠3＝37.5°，∴∠BOE＝∠1＝112.5°.15．解：(1)共有2对对顶角，可以看作2＝2×1.(2)单个角是对顶角的有3对，两个角组成复合角的对顶角有3对，共有6对，可以看作6＝3×2.(3)单个角是对顶角的有4对，两个角组成复合角的对顶角有4对，三个角组成复合角的对顶角有4对，共有12对，可以看作12＝4×3.(4)n(n≥2)条直线相交于一点，可形成n(n－1)对对顶角．2.2 有理数的减法第2课时 有理数的加减混合运算知识点1 有理数加减混合运算1．计算：(＋5)－(＋2)－(－3)＋(－9)＝(＋5)＋(________)＋(________)＋(－9)＝________．2．计算：(1)(－5)－(＋1)－(－6)＝________； (2)－7＋13－6＋20＝________．3．2017·绍兴计算6－(＋3)－(－7)＋(－5)所得的结果是( ) A ．－7 B ．－9 C ．5 D ．－34．下列交换加数位置的变形，正确的是( ) A ．－5＋34－2＝34－5－2B ．5－3＋9＝3－5＋9C ．3－4＋6－7＝4－3＋7－6D ．－8＋12－16－23＝－8－16＋23－12 5．计算：(1)(－14)＋56＋23－12；(2)4.7－(－8.9)－7.5＋(－6)；(3)0－(－6)＋2－(－13)－(＋8)；(4)13－(＋0.25)＋(－34)－(－23)．知识点2 有理数加减混合运算的简单应用6．一架飞机在空中做特技表演，起飞后的高度变化情况如下：上升4.5 km ，下降3.2 km ，上升1.1 km ，下降1.4 km.此时飞机比起飞点高________．7．列式计算：(1)－25与－35的和减去－415的差是多少？(2)－3.6与234的和减去一个数的差为－2，求这个数．8．小明家某月的收支情况如下：爸爸、妈妈的工资分别为8000元和6500元，水电费190元，买菜、米等花去1000元，煤气费110元，更换冰箱3000元．只看这个月，小明家是收入还是支出？如果是收入，收入多少钱？如果是支出，支出多少钱？9. 下列各式中，与3－19＋5的值相等的是( )A ．3＋(－19)－(－5)B ．－3＋(－19)＋(－5)C ．－3＋(－19)＋5D ．3－(＋19)－(＋5)10．若x wy z 表示运算x ＋z －(y ＋w )，则3 －5－2 －1的结果是() A ．5 B ．7 C ．9 D ．1111．计算：1－2＋3－4＋5－6＋…＋99－100＝________.12．计算：(1)(＋1.75)＋⎝ ⎛⎭⎪⎫－13＋⎝ ⎛⎭⎪⎫＋45＋(＋1.05)＋⎝ ⎛⎭⎪⎫－23＋(＋2.2)；(2)－2－⎝ ⎛⎭⎪⎫＋712＋⎝ ⎛⎭⎪⎫－715－⎝ ⎛⎭⎪⎫－14－⎝ ⎛⎭⎪⎫－13＋715.13．兴华粮食中转站仓库在9月1日至9月10日的时间内运进、运出粮食情况如下(运进记做“＋”，运出记做“－”)：＋1050吨，－500吨，＋2300吨，－80吨，－150吨，－320吨，＋600吨，－360吨，＋500吨，－210吨．在9月1日前仓库内没有粮食．(1)求9月3日仓库内共有粮食多少吨；(2)哪一天仓库内的粮食最多？最多是多少？(3)若每吨粮食的运费(包括运进、运出)是10元，从9月1日到9月10日仓库共需付运费多少元？14．小明在电脑中设置了一个有理数的运算程序：输入数a ，加*键，再输入数b ，就可以得到运算：a *b ＝(a －b )－|b －a |.(1)求(－3)*2的值；(2)求(3*4)*(－5)的值．1．－2 ＋3 －3 2.(1)0 (2)203．C 4.A5．解：(1)(－14)＋56＋23－12＝－14－12＋56＋23＝－14－12＋(56＋23) ＝－34＋32＝34. (2)4.7－(－8.9)－7.5＋(－6)＝4.7＋8.9－7.5－6＝4.7＋8.9＋[－7.5＋(－6)]＝13.6＋(－13.5)＝0.1.(3)0－(－6)＋2－(－13)－(＋8)＝6＋2－(－13)－(＋8)＝8＋13－8＝13.(4)13－(＋0.25)＋(－34)－(－23)＝13＋(－14)＋(－34)＋23＝13＋23＋[－14＋⎝ ⎛⎭⎪⎫－34] ＝1＋(－1)＝0.6．1 km7．解：(1)[(－25)＋(－35)]－(－415)＝(－1)－(－415)＝－1115. (2)这个数为⎝⎛⎭⎪⎫－3.6＋234－(－2)＝1.15. 8．解：∵爸爸、妈妈的工资分别为8000元和6500元，水电费190元，买菜、米等花去1000元，煤气费110元，更换冰箱3000元，∴8000＋6500－190－1000－110－3000＝10200(元)，∴只看这个月，小明家是收入，收入10200元．9．A.10．C11．－5012． 解：(1)原式＝(1.75＋1.05)＋(0.8＋2.2)－⎝ ⎛⎭⎪⎫13＋23 ＝2.8＋3－1＝4.8.(2)原式＝－2＋⎝ ⎛⎭⎪⎫－712＋⎝ ⎛⎭⎪⎫－715＋⎝ ⎛⎭⎪⎫＋14＋⎝ ⎛⎭⎪⎫＋13＋⎝ ⎛⎭⎪⎫＋715 ＝－2＋⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫－712＋⎝ ⎛⎭⎪⎫＋14＋⎝ ⎛⎭⎪⎫＋13＋ ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫－715＋⎝ ⎛⎭⎪⎫＋715 ＝－2＋0＋0＝－2.13．解：(1)1050－500＋2300＝2850(吨)．答：9月3日仓库内共有粮食2850吨．(2)9月9日仓库内的粮食最多，最多是2850－80－150－320＋600－360＋500＝3040(吨)．(3)运进1050＋2300＋600＋500＝4450(吨)，运出|－500－80－150－320－360－210|＝1620(吨)．10×(4450＋1620) ＝10×6070＝60700(元)．答：从9月1日到9月10日仓库共需付运费60700元．14．解：(1)(－3)*2＝(－3－2)－|2－(－3)|＝－5－5＝－10.(2)∵3*4＝(3－4)－|4－3|＝－2，(－2)*(－5)＝[(－2)－(－5)]－|－5－(－2)|＝0，∴(3*4)*(－5)＝0.。