概率论与数理统计exc32stu2017519

【最新整理，下载后即可编辑】《概率论与数理统计》第一章 概率论的基本概念 §2．样本空间、随机事件1．事件间的关系 B A ⊂则称事件B 包含事件A ，指事件A 发生必然导致事件B 发生B }x x x { ∈∈=⋃或A B A 称为事件A 与事件B 的和事件，指当且仅当A ，B 中至少有一个发生时，事件B A ⋃发生 B }x x x { ∈∈=⋂且A B A 称为事件A 与事件B 的积事件，指当A ，B 同时发生时，事件B A ⋂发生B }x x x { ∉∈=且—A B A 称为事件A 与事件B 的差事件，指当且仅当A 发生、B 不发生时，事件B A —发生φ=⋂B A ，则称事件A 与B 是互不相容的，或互斥的，指事件A 与事件B 不能同时发生，基本事件是两两互不相容的且S =⋃B A φ=⋂B A ，则称事件A 与事件B 互为逆事件，又称事件A 与事件B 互为对立事件 2．运算规则 交换律A B B A A B B A ⋂=⋂⋃=⋃结合律)()( )()(C B A C B A C B A C B A ⋂=⋂⋃⋃=⋃⋃ 分配律 )()B (C A A C B A ⋃⋂⋃=⋂⋃）（))(()( C A B A C B A ⋂⋂=⋃⋂徳摩根律B A B A A B A ⋃=⋂⋂=⋃ B —§3．频率与概率定义 在相同的条件下，进行了n 次试验，在这n 次试验中，事件A 发生的次数A n 称为事件A 发生的频数，比值n n A 称为事件A 发生的频率概率：设E 是随机试验，S 是它的样本空间，对于E 的每一事件A 赋予一个实数，记为P （A ），称为事件的概率 1．概率)(A P 满足下列条件：（1）非负性：对于每一个事件A 1)(0≤≤A P （2）规范性：对于必然事件S 1)S (=P（3）可列可加性：设n A A A ,,,21 是两两互不相容的事件，有∑===nk k nk k A P A P 11)()( （n 可以取∞）2．概率的一些重要性质： （i ） 0)(=φP（ii ）若n A A A ,,,21 是两两互不相容的事件，则有∑===nk k nk k A P A P 11)()( （n 可以取∞）（iii ）设A ，B 是两个事件若B A ⊂，则)()()(A P B P A B P -=-，)A ()B (P P ≥（iv ）对于任意事件A ，1)(≤A P（v ）)(1)(A P A P -= （逆事件的概率）（vi ）对于任意事件A ，B 有)()()()(AB P B P A P B A P -+=⋃ §4等可能概型（古典概型）等可能概型：试验的样本空间只包含有限个元素，试验中每个事件发生的可能性相同若事件A 包含k 个基本事件，即}{}{}{2]1ki i i e e e A =，里个不同的数，则有中某，是，，k k n 2,1i i i ,21 ()中基本事件的总数包含的基本事件数S }{)(1j A n k e P A P kj i ===∑=§5．条件概率（1） 定义：设A,B 是两个事件，且0)(>A P ，称)()()|(A P AB P A B P =为事件A 发生的条件下事件B 发生的条件概率 （2） 条件概率符合概率定义中的三个条件1。

概率论与数理统计知识点概率论与数理统计是一门研究随机现象及其规律的学科，它在众多领域都有着广泛的应用，如自然科学、工程技术、社会科学、经济金融等。

下面就让我们一起来了解一下这门学科的一些重要知识点。

一、随机事件与概率随机事件是指在一定条件下，可能出现也可能不出现的事件。

比如掷骰子出现的点数，明天是否下雨等。

而概率则是用来衡量随机事件发生可能性大小的数值。

概率的计算方法有多种。

古典概型是一种常见的情形，假设某个试验有 n 个等可能的结果，而事件 A 包含其中的 m 个结果，那么事件 A 发生的概率 P(A) ＝ m ／ n 。

还有几何概型，比如在一个区间内随机取一个点，计算这个点落在某个特定子区间的概率。

条件概率也是一个重要概念。

如果已知事件 B 发生的条件下，事件A 发生的概率，称为条件概率，记作 P(A|B)。

二、随机变量及其分布随机变量是用来表示随机现象结果的变量。

它可以是离散型的，比如掷骰子的点数；也可以是连续型的，比如某地区一天的气温。

常见的离散型随机变量分布有二项分布和泊松分布。

二项分布适用于 n 次独立重复试验中成功的次数，比如抛硬币正面朝上的次数。

泊松分布则常用于描述在一定时间或空间内稀有事件发生的次数。

连续型随机变量的分布通常用概率密度函数来描述，常见的有正态分布。

正态分布在自然界和社会现象中非常常见，很多测量数据都近似服从正态分布。

三、多维随机变量及其分布当考虑多个随机变量时，就有了多维随机变量。

比如同时考虑一个学生的数学和语文成绩。

联合分布函数可以描述多维随机变量的概率分布情况。

边缘分布则是从多维随机变量中单独取出某个变量的分布。

条件分布是在已知某个变量取值的条件下，另一个变量的分布。

四、随机变量的数字特征期望是随机变量取值的平均值，它反映了随机变量取值的平均水平。

方差则衡量了随机变量取值相对于期望的分散程度。

协方差和相关系数用于描述两个随机变量之间的线性关系程度。

五、大数定律和中心极限定理大数定律表明，在大量重复试验中，随机事件发生的频率接近于其概率。

《概率论与数理统计》.doc《概率论与数理统计》是数学专业中非常重要的一门基础课程，通常在大一或大二就会开设，也是很多其他学科中的必修课程。

本文将介绍一下《概率论与数理统计》这门课程的涉及内容。

概率论是从某些可重复实验中得到一些变量的值或者某些事件的发生情况，从而得到不确定性的描述。

因此，概率论主要研究的是随机变量和随机事件的性质。

数学上，概率论主要涉及的内容包括随机变量的定义、分布和密度函数、期望、方差等。

在此基础上，就可以进一步研究随机变量之间的相关性以及一些随机过程的性质，如随机游走、马尔可夫过程等。

概率论是很多其他学科的重要基础，如统计学、金融学、生物学等。

数理统计是从已知的数据出发推断出总体的性质和规律，从而得到预测和决策的依据。

因此，数理统计主要研究的是如何从样本中推断总体的性质和规律。

数学上，数理统计主要涉及的内容包括概率分布的参数估计、假设检验、方差分析、回归分析等。

在此基础上，统计学家可以进一步研究一些更加细致和复杂的问题，如非参数统计、贝叶斯统计等。

《概率论与数理统计》课程的主要目的就是让学生系统地学习概率论和数理统计这两门基础课程的主要内容。

在掌握这些基础知识之后，学生可以更加深入地学习其他相关学科，并且在实际工作中可以进行数据分析、预测和决策。

这些都是现代社会中非常重要的能力，所以学生们在学习《概率论与数理统计》的时候一定要认真对待，努力去掌握这些基础知识。

总的来说，《概率论与数理统计》是数学专业中非常重要的一门基础课程，它的内容非常广泛，包括概率论和数理统计的基础知识以及一些高级概念和工具。

只有通过深入的学习和理解，我们才能真正将这些知识应用到实际生活和工作中。

概率论与数理统计知识点总结免费超详细版概率论与数理统计是一门研究随机现象数量规律的学科，它在众多领域都有着广泛的应用，如统计学、物理学、工程学、经济学等。

以下是对概率论与数理统计知识点的超详细总结。

一、随机事件与概率（一）随机事件随机事件是指在一定条件下，可能出现也可能不出现的事件。

随机事件通常用大写字母 A、B、C 等来表示。

（二）样本空间样本空间是指随机试验的所有可能结果组成的集合，通常用Ω表示。

（三）事件的关系与运算1、包含关系：若事件 A 发生必然导致事件 B 发生，则称事件 B 包含事件 A，记作 A⊂B。

2、相等关系：若 A⊂B 且 B⊂A，则称事件 A 与事件 B 相等，记作A ＝ B。

3、并事件：事件 A 与事件 B 至少有一个发生的事件称为 A 与 B的并事件，记作 A∪B。

4、交事件：事件 A 与事件 B 同时发生的事件称为 A 与 B 的交事件，记作A∩B 或 AB。

5、互斥事件：若事件 A 与事件 B 不能同时发生，则称 A 与 B 为互斥事件，即 AB ＝∅。

6、对立事件：若事件 A 与事件 B 满足 A∪B ＝Ω 且 AB ＝∅，则称 A 与 B 为对立事件，记作 B ＝A。

（四）概率的定义与性质1、概率的古典定义：若随机试验的样本空间Ω只包含有限个基本事件，且每个基本事件发生的可能性相等，则事件 A 的概率为 P(A) ＝n(A) ／n(Ω) ，其中 n(A) 为事件 A 包含的基本事件个数，n(Ω) 为样本空间Ω包含的基本事件个数。

2、概率的统计定义：在大量重复试验中，事件 A 发生的频率稳定在某个常数 p 附近，则称 p 为事件 A 的概率，即 P(A) ＝ p 。

3、概率的公理化定义：设随机试验的样本空间为Ω，对于Ω中的每一个事件 A，都赋予一个实数 P(A)，如果满足以下三个条件：（1）非负性：0 ≤ P(A) ≤ 1 ；（2）规范性：P(Ω) ＝ 1 ；（3）可列可加性：对于两两互斥的事件 A1，A2，，有P(A1∪A2∪）＝ P(A1) ＋ P(A2) ＋，则称 P(A) 为事件 A 的概率。

数理统计与概率分析教材32课时1. 课程目标本教材旨在为学生提供数理统计与概率分析方面的基础知识和技能。

通过32个课时的研究，学生将掌握以下内容：- 数理统计的基本概念和原理- 概率分析的基本方法和技巧- 统计推断的基本理论和应用- 概率分布的性质和应用- 随机变量和随机过程的概念和性质- 统计模型的建立和推断2. 课程安排本教材共分为32个课时，每个课时的内容安排如下：第一课时：数理统计的概念和应用- 数理统计的定义和重要性- 数据的收集、整理和描述性统计- 简单随机抽样和抽样分布的基本原理第二课时：概率分析的基本原理- 概率的定义和性质- 随机事件和概率空间的概念- 条件概率和独立性的概念及其应用...第三十二课时：统计模型的建立和推断- 统计模型的概念和基本假设- 参数估计和假设检验的基本方法- 统计推断在实际问题中的应用3. 教学方法本教材采用多种教学方法，包括理论授课、案例分析和实践操作。

在理论授课中，重点讲解数理统计和概率分析的基本原理和方法；案例分析将通过实际问题的解决，帮助学生理解和应用所学知识；实践操作将通过统计软件和数据分析工具的使用，加强学生对数理统计和概率分析的实际操作能力。

4. 考核方式本教材的考核方式包括课堂测验、实验报告和期末考试。

课堂测验将检验学生对每个课时内容的掌握程度；实验报告将要求学生运用所学知识解决实际问题，并进行实证分析；期末考试将综合考察学生对数理统计和概率分析知识的综合运用能力。

5. 参考书目- Casella, G., & Berger, R. L. (2002). Statistical inference. Cengage Learning.- Montgomery, D. C., & Runger, G. C. (2018). Applied statistics and probability for engineers. John Wiley & Sons.。

概率论与数理统计1. 前言概率论与数理统计是数学的一个重要分支，它是研究随机现象规律性的数学学科。

概率论是研究随机现象的规律性和数量关系的学科，而数理统计则是利用数学方法研究大量数据中的规律性和趋势的学科。

本文将介绍概率论与数理统计的基本概念、方法和应用。

2. 概率论概率论是研究随机现象的规律性和数量关系的数学学科。

随机现象是指在一定条件下，每次实验的结果无法预知，但在一系列相同实验中，某些现象出现的频率具有稳定的规律性。

概率论通过概率分布、概率密度函数、条件概率等概念来描述随机现象，并提供了一系列计算概率的方法。

2.1 基本概念•样本空间：样本空间是随机现象所有可能结果的集合，常用符号为S。

例如，抛一枚硬币的样本空间为$\\{H, T\\}$，其中H表示正面，T表示反面。

•事件：事件是样本空间的一个子集，表示随机现象的一个可能结果或一组可能结果组成的集合。

如果随机事件A中包含了样本空间S中的某些结果，则称事件A发生。

•概率：概率是描述随机事件发生可能性大小的数值，通常用P(A)表示，表示事件A发生的可能性大小。

概率的取值范围在[0,1]之间。

•概率分布：概率分布是随机变量所有可能取值及其发生的概率的描述。

常见的概率分布包括二项分布、泊松分布、正态分布等。

2.2 概率计算概率计算是概率论的核心内容之一，常用的计算方法包括加法法则、乘法法则、全概率公式和贝叶斯定理等。

这些方法可以帮助我们计算复杂事件的概率，进行概率分布的推导和分析。

3. 数理统计数理统计是利用数学方法研究大量数据中的规律性和趋势的学科。

在现代社会中，大量的数据被广泛应用于科学研究、经济分析、医学诊断等领域，而数理统计提供了一系列工具和方法来处理和分析这些数据。

3.1 基本概念•总体与样本：总体是指研究对象的全部个体或事物的集合，样本是从总体中选取的一部分个体或事物。

数理统计的目标通常是通过对样本的统计量进行分析来进行对总体的推断。

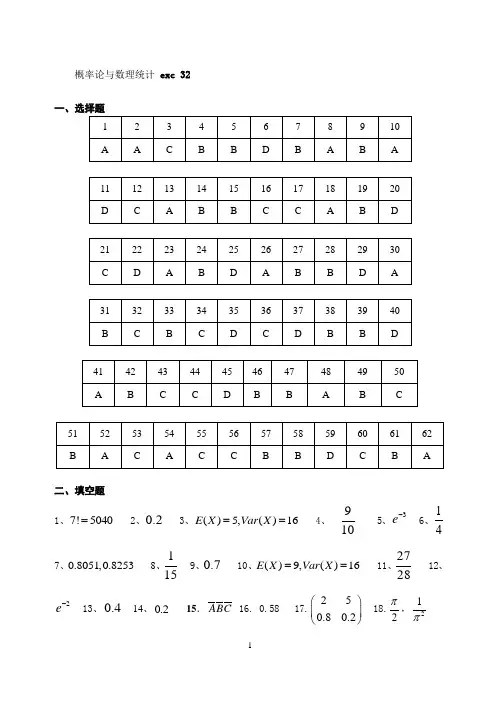
概率论与数理统计 exc 32二、填空题1、7!5040=2、0.23、()5,()16E X Var X ==4、9105、3e - 6、147、0.8051,0.8253 8、115 9、0.7 10、()9,()16E X Var X == 11、272812、2e - 13、0.4 14、0.2 15．ABC 16. 0.58 17.250.80.2⎛⎫⎪⎝⎭18.2π，21π19.38， 20. (2)P 21．ABC 22. 1 23. 150.40.6⎛⎫ ⎪⎝⎭24. 41(1)p -- 25. 115264， 26. (1.4)P 27. 89 28. 1631 29. 2,(,)(,)0,x y D f x y ∈⎧=⎨ ⎩其它 30. 8 31. 0.6 32. 0.25 33. 0.3264 34.0.7 35.0.3456 36. 0.75 37. 038.-0.5 39. 1,(,)(,)40,x y Df x y ⎧∈⎪=⎨⎪ ⎩其它 40. 0.2734 41、(,)F y +∞ 42、710 43、59 44、0.9772 45、21();()().F b F y F y -46、3847、1536 48、1()()()n i i i P B P A P B A ==∑ 49、350.80.2⎛⎫ ⎪⎝⎭50、()()b a μμσσ--Φ-Φ 51、 ()(,)()X f x f x y dy x +∞-∞=-∞<<+∞⎰,()(,)()Y f y f x y dx y +∞-∞=-∞<<+∞⎰52、 存在常数,a b ，使得()1P Y aX b =+=53、0.2 54、0.2 55、91056、()()()F x P X x x =≤-∞<<+∞,1221()()()P x X x F x F x <≤=- 57、x e -三、计算题1、解：设A 表示取到的都是合格品，则24262()5C P A C ==设B 表示取到的一个合格品一个次品，则 1142262!8()15C C P B C == 设C 表示至少有是一个合格品，则 2814()()()51515P C P A P B =+=+=2、解： 设A ，B ，C 表示产品来自甲乙丙三个工厂，D 表示抽到次品，则有以下概率()0.2,()0.3,()0.5P A P B P C ===(|)0.05,(|)0.04,(|)0.02P D A P D B P D C ===由全概率公式，得 ()0.20.050.30.040.50.020.032P D =⨯+⨯+⨯= 由贝叶斯公式，得0.20.0550.30.046(|)(|)0.032160.03216P A D P B D ⨯⨯== == 0.50.035(|)0.03216P C D ⨯==3、解：（1） 0()()0 0x xe x f x F x x -⎧>'==⎨≤⎩（2） 2(1)1(1)1(1)P X P X F e≥=-<=-=， （3） 221(2)(2)1(12)13P X F e e-<==-+=- 4、解：由已知可得联合分布律为：5、解：设A 表示恰好有一位精通英语，则 1223353()5C C P A C == 设B 表示恰好有2位精通英语，则 1232353()10C C P B C ==设C 表示有人精通英语，则 339()()()51010P C P A P B =+=+= 6、解： 设A 表示服用违禁药，B 表示检查呈阳性，则有以下概率51()0.1,(|)0.9,(|)900180P A P B A P B A ==== 由全概率公式，得 119()0.10.90.9180200P B =⨯+⨯= 由贝叶斯公式，得0.10.918(|)1919200P A B ⨯== 7、解：（1） 01()2xx f x dx Ae dx Ae dx A +∞+∞--∞-∞==+=⎰⎰⎰12A ∴=（2） 10111(01)(1)22x P X e dx e-<<==-⎰ 8、解：由已知可得X由已知可得X+Y 的分布律为9. 解：(1) ()1()10.360.64P A P A =-=-=， .(2) ()()0P A B P -=∅=，()()()0.43P B A P B P A -=-=。

概率论与数理统计课程概述概率论与数理统计是一门重要的数学课程，它主要研究随机现象的规律性及其应用。

在现代科学、工程技术、经济管理等领域中，概率论和数理统计都有着广泛的应用，因此掌握这门课程对于学生来说非常重要。

一、概率论1.1 概率的基本概念概率是指一个事件发生的可能性大小，通常用一个介于0和1之间的数来表示。

在概率论中，我们通常将样本空间、事件和概率三者联系起来。

样本空间是指所有可能出现的结果组成的集合，事件是指样本空间中某些结果组成的子集，而概率则是指事件发生的可能性大小。

1.2 随机变量与分布随机变量是指取值不确定、由随机试验产生的变量。

在概率论中，我们通常将随机变量分为离散型随机变量和连续型随机变量。

离散型随机变量取值有限或可数无限个，而连续型随机变量则可以取任意实数值。

对于离散型随机变量，我们可以通过定义它的分布函数来描述它的概率分布。

而对于连续型随机变量，则需要使用概率密度函数来描述其概率分布。

1.3 期望与方差期望是指随机变量的平均值，通常用E(X)表示。

方差是指随机变量的取值偏离其期望的程度，通常用Var(X)表示。

在概率论中，我们通常使用期望和方差来描述随机变量的性质。

二、数理统计2.1 统计学基础统计学是一门研究如何收集、处理和分析数据的学科。

在数理统计中，我们通常将数据分为总体和样本两类。

总体是指所有可能出现的结果组成的集合，而样本则是从总体中抽取出来的一部分数据。

2.2 参数估计与假设检验参数估计是指根据样本数据推断总体参数值的过程。

在参数估计中，我们通常使用点估计和区间估计两种方法来推断总体参数值。

假设检验是指根据样本数据对总体参数进行推断并进行决策的过程。

在假设检验中，我们通常将原假设和备择假设进行比较，并通过显著性水平来判断是否拒绝原假设。

2.3 方差分析与回归分析方差分析是一种用于比较多个总体均值是否相等的方法。

在方差分析中，我们通常使用F检验来判断多个总体均值是否相等。

概率论和数理统计简介概率论与数理统计是对随机现象的统计规律进行演绎和归纳的科学，从数量侧面研究随机现象的统计规律性的基础数学学科，概率论与数理统计又可分为概率论和数理统计两个分支。

概率是用来刻画随机事件发生的可能性大小的量。

概率论的主要内容包括古典概型的计算、随机变量的分布及特征数字和极限定理等等。

数理统计乃数学中联系实际最直接最广泛的分支之一，它介绍了点估计(矩法估计、极大似然估计)、参数假设检验、非参数假设检验、方差分析和多元回归分析、、可靠性分析等基本知识和原理，使学生对统计学原理的作用有一深刻的了解。

通过本课程的学习，使学生能全面理解、掌握概率论与数理统计的思想与方法，掌握基本而常用的分析和计算方法，并能运用概率论与数理统计的观点和方法来研究解决经济与管理中的实践问题。

随机现象从随机现象说起，在自然界和现实生活中，一些事物都是相互联系和不断发展的。

在它们彼此间的联系和发展中，根据它们是否有必然的因果联系，可以分成截然不同的两大类：一类是确定性的现象。

这类现象是在一定条件下，必定会导致某种确定的结果。

举例来说，在标准大气压下，水加热到100摄氏度，就必然会沸腾。

事物间的这种联系是属于必然性的。

通常的自然科学各学科就是专门研究和认识这种必然性的，寻求这类必然现象的因果关系，把握它们之间的数量规律。

另一类是不确定性的现象。

这类现象是在一定条件下，它的结果是不确定的。

举例来说，同一个工人在同一台机床上加工同一种零件若干个，它们的尺寸总会有一点差异。

又如，在同样条件下，进行小麦品种的人工催芽试验，各棵种子的发芽情况也不尽相同，有强弱和早晚的分别等等。

为什么在相同的情况下，会出现这种不确定的结果呢？这是因为，我们说的“相同条件”是指一些主要条件来说的，除了这些主要条件外，还会有许多次要条件和偶然因素又是人们无法事先一一能够掌握的。

正因为这样，我们在这一类现象中，就无法用必然性的因果关系，对个别现象的结果事先做出确定的答案。

概率论与数理统计 exc 32一、 单项选择题1．设A 与B 互为对立事件，且P （A ）>0，P （B ）>0，则下列各式中错误．．的是（A ） A ．(|)0P A B = 1 B ．P （B |A ）=0 √ C ．P （AB ）=0 √ D ．P （A ∪B ）=1√2．() f x 任何一个连续型随机变量的密度函数一定满足（）A+- () () 1 ()() 0() 1 () ()0A f x dx B C f x D f x ∞∞=≤≤>⎰在定义域内单调不减3.设二维随机变量(X ，Y)的分布律为且X 与Y 相互独立，则下列结论正确的是（ C ）0.4,0.6A a b ==． 0.1,0.9B a b =-=． 0.2,0.3C a b ==． 0.6,0.D a b ==． 4．设随机变量X 服从参数为0.5的泊松分布，则E (X )=（ B ）11. . . 2 . 442A B C D 泊松分布的期望和方差都是λ5．设(X ，Y )为二维随机变量,且D (X )>0，D (Y )>0，则下列等式成立的是（ ） A ．)()()(Y E X E XY E ⋅= B ．)()(Cov Y D X D (X,Y)XY ⋅⋅=ρ C ．)()()(Y D X D Y X D +=+D ．),(Cov 2)2,2(Cov Y X Y X =6.设A ，B 为两个随机事件，且P （AB ）>0，则P （B |AB ）=（ ） A ．P （A ） B ．P （AB ） C ．P （A |B ） D ．17.设离散型随机变量X 的分布律为10120.20.10.30.4XP⎛-⎫⎪⎝⎭，则1{}1P X -<≤=（ ）。

A ．0.3B ．0.4C ．0.6D ．0.78. 设随机变量X ～B （8，21），Y ～N （2，9），又E （XY ）=12，则X 与Y 的协方差(,)Cov X Y =（ ）A ．4B ．6C ．-4D ． -69. 设随机变量X 的概率密度为5,0;()0,0,x ce x f x x -⎧⎪≥=⎨⎪<⎩ 则常数c 等于（ ）A ．-51 B ．51 C ．1 D ．510. 袋中有12球，8个红球，4个白球，从中任抽一球无放回地连抽两次，事件A 表示第二次抽出的是红球，则()P A =（ ）。