2020高考数学(理科)一轮总复习练(新课标) 第四章 三角函数 作业28Word版含解析

第四章 三角函数、解三角形第一节任意角和弧度制及任意角的三角函数1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形． (2)分类：①按旋转方向不同分为正角、负角、零角；②按终边位置不同分为象限角和轴线角．(3)终边相同的角❶：所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋2kπ，k ∈Z}．2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad. (2)公式：(1)定义：设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么sin α＝y ，cos α＝x ，tan α＝yx (x ≠0)．(2)几何表示：三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x 轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP ，OM ，AT 分别叫做角α的正弦线、余弦线和正切线❷.(3)三角函数值在各象限内的符号,(1)终边相同的角不一定相等．(2)“锐角”不等同于“第一象限的角”，锐角的集合为{α|0°＜α＜90°}，第一象限的角的集合为{α|k ·360°＜α＜k ·360°＋90°，k ∈Z}，小于90°的角包括锐角、负角、零角．(3)角的集合的表示形式不是唯一的，如⎩⎨⎧⎭⎬⎫α|α＝2k π＋π3，k ∈Z ＝⎩⎨⎧⎭⎬⎫β|β＝2k π＋7π3，k ∈Z . 当角α的终边与x 轴重合时，正弦线、正切线都变成一个点，此时角α的正弦值和正切值都为0；当角α的终边与y 轴重合时，余弦线变成一个点，正切线不存在，此时角α的余弦值为0，正切值不存在．[熟记常用结论]1．象限角2．轴线角3．若α∈⎝⎛⎭⎫0，π2，则tan α＞α＞sin α. [小题查验基础]一、判断题(对的打“√”，错的打“×”) (1)小于90°的角是锐角．( )(2)锐角是第一象限角，反之亦然．( )(3)相等的角终边一定相同，终边相同的角也一定相等．( ) (4)三角形的内角必是第一、二象限角．( ) 答案：(1)× (2)× (3)× (4)× 二、选填题1．下列与9π4的终边相同的角的表达式中正确的是( )A ．2k π＋45°(k ∈Z)B ．k ·360°＋94π(k ∈Z)C ．k ·360°－315°(k ∈Z)D ．k π＋5π4(k ∈Z) 解析：选C 由定义知终边相同的角中不能同时出现角度和弧度，应为π4＋2k π(k ∈Z)或k ·360°＋45°(k ∈Z)，结合选项知C 正确．2.若角α＝2 rad(rad 为弧度制单位)，则下列说法错误的是( ) A ．角α为第二象限角 B ．α＝⎝⎛⎭⎫360π°C ．sin α＞0D ．sin α＜cos α解析：选D 对于A ，∵π2＜α＜π，∴角α为第二象限角，故A 正确；对于B ，α＝2×⎝⎛⎭⎫180π°＝2 rad ，故B 正确；对于C ，sin α＞0，故C 正确；对于D ，sin α＞0，cos α＜0，故D 错误．选D.3．已知角α的终边与单位圆的交点P ⎝⎛⎭⎫x ，32，则tan α＝( ) A. 3 B ．±3 C.33D ．±33解析：选B 由|OP |2＝x 2＋34＝1，得x ＝±12.所以tan α＝yx＝±3.故选B.4．已知扇形的圆心角为60°，其弧长为2π，则此扇形的面积为________． 解析：设此扇形的半径为r ，由题意得π3r ＝2π，所以r ＝6，所以此扇形的面积为12×2π×6＝6π.答案：6π5．在0到2π范围内，与角－4π3终边相同的角是________． 解析：与角－4π3终边相同的角是2k π＋⎝⎛⎭⎫－4π3，k ∈Z ，令k ＝1，可得在0到2π范围内与角－4π3终边相同的角是2π3.答案：2π3考点一象限角及终边相同的角[基础自学过关][题组练透]1．设集合M ＝⎩⎨⎧⎭⎬⎫x |x ＝k 2·180°＋45°，k ∈Z ，N ＝⎩⎨⎧⎭⎬⎫x |x ＝k 4·180°＋45°，k ∈Z ，那么( )A ．M ＝NB ．M ⊆NC ．N ⊆MD ．M ∩N ＝∅解析：选B 由于M 中，x ＝k2·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；而N中，x ＝k4·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N .2．若角α是第二象限角，则α2是( )A ．第一象限角B ．第二象限角C ．第一或第三象限角D ．第二或第四象限角解析：选C ∵α是第二象限角， ∴π2＋2k π＜α＜π＋2k π，k ∈Z ， ∴π4＋k π＜α2＜π2＋k π，k ∈Z. 当k 为偶数时，α2是第一象限角；当k 为奇数时，α2是第三象限角．∴α2是第一或第三象限角． 3．集合⎩⎨⎧⎭⎬⎫α⎪⎪k π＋π4≤α≤k π＋π2，k ∈Z 中的角所表示的范围(阴影部分)是( )解析：选C 当k ＝2n (n ∈Z)时，2n π＋π4≤α≤2n π＋π2(n ∈Z)，此时α的终边和π4≤α≤π2的终边一样；当k ＝2n ＋1(n ∈Z)时，2n π＋π＋π4≤α≤2n π＋π＋π2(n ∈Z)，此时α的终边和π＋π4≤α≤π＋π2的终边一样，结合选项知选C.4．与－2 010°终边相同的最小正角是________．解析：因为－2 010°＝(－6)×360°＋150°，所以150°与－2 010°终边相同，又终边相同的两个角相差360°的整数倍，所以在0°～360°中只有150°与－2 010°终边相同，故与－2 010°终边相同的最小正角是150°.答案：150°5．终边在直线y ＝3x 上，且在[－2π，2π)内的角α的集合为______________________． 解析：如图，在平面直角坐标系中画出直线y ＝3x ，可以发现它与x轴的夹角是π3，在[0,2π)内，终边在直线y ＝3x 上的角有两个：π3，4π3；在[－2π，0)内满足条件的角有两个：－2π3，－5π3，故满足条件的角α构成的集合为⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3.答案：⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3[名师微点]1．判断象限角的2种方法 2.确定kα，αk (k ∈N *)的终边位置3步骤 (1)用终边相同角的形式表示出角α的范围； (2)再写出kα或αk 的范围；(3)然后根据k 的可能取值讨论确定kα或αk 的终边所在的位置．3．求终边在某直线上角的4个步骤(1)数形结合，在平面直角坐标系中画出该直线； (2)按逆时针方向写出[0,2π]内的角；(3)再由终边相同角的表示方法写出满足条件角的集合； (4)求并集化简集合．考点二扇形的弧长及面积公式的应用[师生共研过关][典例精析]已知扇形的圆心角是α，半径是r ，弧长为l . (1)若α＝100°，r ＝2，求扇形的面积；(2)若扇形的周长为20，求扇形面积的最大值，并求此时扇形圆心角的弧度数． [解] (1)因为α＝100°＝100×π180＝5π9， 所以S 扇形＝12lr ＝12αr 2＝12×5π9×4＝10π9.(2)由题意知，l ＋2r ＝20，即l ＝20－2r ， 故S 扇形＝12l ·r ＝12(20－2r )·r ＝－(r －5)2＋25，当r ＝5时，S 的最大值为25，此时l ＝10，则α＝lr＝2.[解题技法]有关弧长及扇形面积问题的注意点(1)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度．(2)求扇形面积最大值的问题时，常转化为二次函数的最值问题，利用配方法使问题得到解决．(3)在解决弧长问题和扇形面积问题时，要合理地利用圆心角所在的三角形．[过关训练]1．已知2弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长是( ) A ．2 B ．sin 2 C.2sin 1D ．2sin 1解析：选C 如图，∠AOB ＝2弧度，过O 点作OC ⊥AB 于C ，并延长OC 交AB 于D .则∠AOD ＝∠BOD ＝1弧度， 且AC ＝12AB ＝1，在Rt △AOC 中，AO ＝AC sin ∠AOC ＝1sin 1，即r ＝1sin 1，从而AB 的长l ＝α·r ＝2sin 1. 2．若圆弧长度等于圆内接正三角形的边长，则其圆心角的弧度数为( ) A.π6 B.π3 C ．3D. 3解析：选D 如图，等边三角形ABC 是半径为r 的圆O 的内接三角形，则线段AB 所对的圆心角∠AOB ＝2π3，作OM ⊥AB ，垂足为M ，在Rt △AOM 中，AO ＝r ，∠AOM ＝π3，∴AM ＝32r ，AB ＝3r ， ∴l ＝3r ，由弧长公式得α＝l r ＝3rr ＝ 3.3．已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为( ) A ．2 B ．4 C ．6D ．8解析：选C 设扇形的半径为r (r ＞0)，弧长为l ，则由扇形面积公式可得2＝12lr ＝12|α|r 2＝12×4×r 2，解得r ＝1，l ＝|α|r ＝4，所以所求扇形的周长为2r ＋l ＝6. 考点三三角函数的定义及应用[师生共研过关][典例精析](1)若sin αtan α＜0，且cos αtan α＜0，则角α是( )A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角(2)(2019·广州模拟)在平面直角坐标系中，以x 轴的非负半轴为角的始边，角α，β的终边分别与单位圆交于点⎝⎛⎭⎫1213，513和⎝⎛⎭⎫－35，45，则sin(α＋β)＝( )A ．－3665 B.4865 C ．－313D.3365(3)已知角α的终边经过点P (－x ，－6)，且cos α＝－513，则1sin α＋1tan α＝________. [解析] (1)由sin αtan α＜0可知sin α，tan α异号， 则α为第二象限角或第三象限角． 由cos αtan α＜0可知cos α，tan α异号， 则α为第三象限角或第四象限角． 综上可知，α为第三象限角．(2)因为角α，β的终边分别与单位圆交于点⎝⎛⎭⎫1213，513和⎝⎛⎭⎫－35，45，所以sin α＝513，cos α＝1213，sin β＝45，cos β＝－35，所以sin(α＋β)＝sin αcos β＋cos αsin β＝513×⎝⎛⎭⎫－35＋1213×45＝3365. (3)因为角α的终边经过点P (－x ，－6)，且cos α＝－513， 所以cos α＝－xx 2＋36＝－513，解得x ＝52或x ＝－52(舍去)，所以P ⎝⎛⎭⎫－52，－6，所以sin α＝－1213， 所以tan α＝sin αcos α＝125，则1sin α＋1tan α＝－1312＋512＝－23. [答案] (1)C (2)D (3)－23[解题技法]利用三角函数定义解题的常见类型及方法(1)已知角α终边上一点P 的坐标求三角函数值．先求出点P 到原点的距离r ，然后利用三角函数定义求解．(2)已知角α的终边与单位圆的交点坐标求三角函数值．可直接根据三角函数线求解． (3)已知角α的终边所在的直线方程求三角函数值．先设出终边上一点的坐标，求出此点到原点的距离，然后利用三角函数定义求解相关问题，同时注意分类讨论．(4)判断三角函数值的符号问题．先判断角所在的象限，再根据各象限的符号规律判断．[过关训练]1．下列各选项中正确的是( ) A ．sin 300°＞0 B ．cos(－305°)＜0 C ．tan ⎝⎛⎭⎫－223π＞0 D ．sin 10＜0解析：选D 300°＝360°－60°，则300°是第四象限角，故sin 300°＜0；－305°＝－360°＋55°，则－305°是第一象限角，故cos(－305°)＞0；而－223π＝－8π＋2π3，所以－223π是第二象限角，故tan ⎝⎛⎭⎫－22π3＜0；因为3π＜10＜7π2，所以10是第三象限角，故sin 10＜0. 2．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( )A ．－45B ．－35C.35D.45解析：选B 设P (t,2t )(t ≠0)为角θ终边上任意一点，则cos θ＝t 5|t |.当t ＞0时，cos θ＝55；当t ＜0时，cos θ＝－55.因此cos 2θ＝2cos 2θ－1＝25－1＝－35. 3．已知角α的终边上一点P (－3，m )(m ≠0)，且sin α＝2m4，求cos α，tan α的值． 解：设P (x ，y )．由题设知x ＝－3，y ＝m ，所以r 2＝|OP |2＝(－3)2＋m 2(O 为原点)，r ＝3＋m 2， 所以sin α＝m r ＝2m 4＝m22，所以r ＝3＋m 2＝22，即3＋m 2＝8， 解得m ＝±5.当m ＝5时，r ＝22，x ＝－3，y ＝5， 所以cos α＝－322＝－64，tan α＝－153；当m ＝－5时，r ＝22，x ＝－3，y ＝－5， 所以cos α＝－322＝－64，tan α＝153.综上，cos α＝－64，tan α＝－153或cos α＝－64，tan α＝153.。

教学资料范本2020高考数学一轮复习第4章三角函数与解三角形章末总结分层演练文-精装版编辑：__________________时间：__________________【精选】20xx最新高考数学一轮复习第4章三角函数与解三角形章末总结分层演练文章末总结知识点考纲展示任意角的概念与弧度制、任意角的三角函数❶了解任意角的概念．❷了解弧度制的概念，能进行弧度与角度的互化．❸理解任意角三角函数(正弦、余弦、正切)的定义.同角三角函数的基本关系式与诱导公式❶理解同角三角函数的基本关系式：sin2x＋cos2x＝1，sin xcos x＝tan x.❷能利用单位圆中的三角函数线推导出π2±α，π±α的正弦、余弦、正切的诱导公式.和与差的三角函数公式❶会用向量的数量积推导出两角差的余弦公式．❷能利用两角差的余弦公式导出两角差的正弦、正切公式．❸能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式，导出二倍角的正弦、余弦、正切公式，了解它们的内在联系.简单的三角恒等变换能运用公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式，但对这三组公式不要求记忆).三角函数的图象与性质❶能画出y＝sin x，y＝cos x，y＝tan x的图象，了解三角函数的周期性．❷理解正弦函数、余弦函数在区间[0，2π]上的性质(如单调性、最大值和最小值以及与x轴的交点等)，理解正切函数在区间⎝⎛⎭⎪⎫－π2，π2内的单调性.函数y＝A sin(ωx ＋φ)的图象及三角函数模型的简单应用❶了解函数y＝A sin(ωx＋φ)的物理意义；能画出函数y＝A sin(ωx＋φ)的图象，了解参数A，ω，φ对函数图象变化的影响．❷了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题.正弦定理和余弦定理掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.解三角形应用举例能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.一、点在纲上，源在本里考点考题考源三角函数的基本关系(20xx·高考全国卷Ⅲ，T4，5分)已知sin α－cos α＝43，则sin 2α＝( )A.－79B．－29C.29D.79必修4 P146A组T6(2)三角函数的周期(20xx·高考全国卷Ⅱ，T3，5分)函数f(x)＝sin⎝⎛⎭⎪⎫2x＋π3的最小正周期为( )A.4π B．2π C．π D.π2必修4 P35例2(2)三角函数值域(20xx·高考全国卷Ⅲ，T6，5分)函数f(x)＝15sin(x＋π3)＋cos(x－π6)的最大值为( )A.65B．1 C.35D.15必修4 P143A组T5三角函数图象(20xx·高考全国卷Ⅰ，T9，5分)已知曲线C1：y＝cosx，C2：y＝sin⎝⎛⎭⎪⎫2x＋2π3，则下面结论正确的是( )A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2必修4 P55练习T2(2)正余弦定理 与面积公式 的应用(20xx·高考全国卷Ⅱ，T 16，5分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若2b cos B ＝a cos C ＋c cos A ，则B ＝________.必修5 P 18练习T 3 (20xx·高考全国卷Ⅲ，T 15，5分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知C ＝60°，b ＝6，c ＝3，则A ＝________.必修5 P 10A 组T 2(1)(20xx·高考全国卷Ⅰ，T 17，12分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知△ABC 的面积为a23sin A. (1)求sin B sin C ；(2)若6cos B cos C ＝1，a ＝3，求△ABC 的周长. 必修5 P 20B 组T 1二、根置教材，考在变中一、选择题1．(必修4 P146A 组T6(3)改编)已知sin 2θ＝，则sin4θ＋cos4θ的值为( )A ． B.59 C ．D.79解析：选D.因为sin 2θ＝，所以sin4θ＋cos4θ＝(sin2θ＋cos2θ)2－2sin2θcos2θ＝1－sin22θ＝1－×＝.故选D.2．(必修4 P147A 组T12改编)已知函数f(x)＝sin ＋sin ＋cos x ＋a 的最大值为1，则a 的值为( )A ．－1B ．0C ．1D ．2解析：选A.f(x)＝sin xcos ＋cos xsin ＋sin xcos －cos xsin ＋cos x ＋a ＝sin x ＋cos x ＋a ＝2sin(x ＋)＋a ，所以f(x)max ＝2＋a ＝1.所以a ＝－1.选A.3．(必修4 P69A 组T8改编)已知tan α＝3，则sin 的值为( )A ．B ．－210 C ．D ．－7210解析：选B.因为tan α＝3，所以sin 2α＝＝＝＝，cos 2α＝＝＝＝－，所以sin ＝(sin 2α＋cos 2α)＝＝－.选B.4．(必修4 P58A 组T2(3)改编)如图是y ＝Asin(ωx ＋φ)的部分图象，则其解析式为( )A ．y ＝2sinB ．y ＝2sin ⎝ ⎛⎭⎪⎫2x －π6C ．y ＝2sinD ．y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6解析：选D.由题图知＝－＝.所以T ＝π，所以ω＝＝2.当x ＝－时，y ＝0，当x ＝0时，y ＝1.所以，所以φ＝，A ＝2.所以y ＝2sin.故选D.5．(必修5 P18练习T1(1)改编)在锐角△ABC 中，a ＝2，b ＝3，S△ABC＝2，则c ＝( )A ．2B ．3C ．4 D.17解析：选B.由已知得×2×3×sin C＝2，所以sin C ＝.由于C ＜90°，所以cos C ＝＝.由余弦定理得c2＝a2＋b2－2abcos C ＝22＋32－2×2×3×＝9，所以c ＝3，故选B.6．(必修5 P18练习T3改编)已知△ABC 三内角A 、B 、C 的对边分别为a ，b ，c ，3acos A ＝bcos C ＋ccos B ，b ＝2，则asin B ＝( )A ．B.232 C ．D ．62解析：选C.因为3acos A ＝bcos C ＋ccos B ， 即3acos A ＝b·＋c·＝a ，所以cos A ＝，又0＜A ＜π.所以sin A ＝.又b ＝2，所以asin B ＝bsin A ＝2×＝.故选C. 二、填空题7．(必修4 P146A 组T5(1)改编)－＝______．解析：－＝3cos 80°－sin 80°si n 80°cos 80°＝＝4sin （60°－80°）sin 160°＝＝－4. 答案：－48．(必修5 P20A 组T11(3)改编)△ABC 的三内角A ，B ，C 的对边分别为a ，b ，c.A ＝120°，a ＝7，S △ABC ＝，则b ＋c ＝________．解析：由题意得，即，所以b2＋c2＋2bc ＝64.所以b ＋c ＝8. 答案：89．(必修4 P56练习T3改编)关于函数f(x)＝sin(x －)的下列结论：①f(x)的一个周期是－8π； ②f(x)的图象关于x ＝对称；③f(x)的图象关于点对称； ④f(x)在上单调递增；⑤f(x)的图象可由g(x)＝cosx 向右平移个单位得到．其中正确的结论有____________(填上全部正确结论的序号)． 解析：f(x)的最小正周期T ＝＝4π.所以f(x)的一个周期为－8π.①正确．f ＝0，故②错误．③正确．由2kπ－＜x －＜2kπ＋，k∈Z，得 4k π－＜x ＜4k π＋π.令k ＝0得，－＜x ＜π.⊆.故④正确．g(x)＝cosx ＝sin ⎝ ⎛⎭⎪⎫12x ＋π2＝sin ，f(x)＝sin ＝sin ，所以g(x)的图象向右平移－(－π)＝π即可得到f(x)的图象．故⑤错误，即①③④正确．答案：①③④ 三、解答题10．(必修 4 P147A 组T10改编)已知函数f(x)＝4sin(ωx －)·cos ωx 在x ＝处取得最值，其中ω∈(0，2)．(1)求函数f(x)的最小正周期；(2)将函数f(x)的图象向左平移个单位，再将所得图象上各点的横坐标伸长为原来的3倍，纵坐标不变，得到函数y ＝g(x)的图象，若α为锐角，g(α)＝－，求cos α.解：(1)f(x)＝4sin·cos ωx＝2sin ωx·cos ωx－2cos2ωx ＝(sin 2ωx－cos 2ωx)－＝2sin －，由于f(x)在x ＝处取得最值，因此2ω·－＝kπ＋，k∈Z，所以ω＝2k ＋，因为ω∈(0，2)，所以ω＝， 因此，f(x)＝2sin －，所以T ＝.(2)将函数f(x)的图象向左平移个单位，得到h(x)＝2sin －＝2sin －的图象，再将h(x)图象上各点的横坐标伸长为原来的3倍，纵坐标不变，得到g(x)＝2sin －的图象，故g(α)＝2sin －＝－， 可得sin ＝，因为α为锐角，所以－＜α－＜， 因此cos ＝＝，故cos α＝cos ＝coscos －sinsin ＝×－×＝.11．(必修5 P20A 组T13改编)D 为△ABC 的边BC 的中点．AB ＝2AC ＝2AD ＝2.(1)求BC 的长；(2)若∠ACB 的平分线交AB 于E ，求S△ACE. 解：(1)由题意知AB ＝2，AC ＝AD ＝1. 设BD ＝DC ＝m.在△ADB 与△ADC 中， 由余弦定理得AB2＝AD2＋BD2－2AD ·BDcos ∠ADB ， AC2＝AD2＋DC2－2AD ·DCcos ∠ADC.即1＋m2－2mcos∠ADB＝4，① 1＋m2＋2mcos ∠ADB ＝1.② ①＋②得m2＝， 所以m ＝，即BC ＝.(2)在△ACE 与△BCE 中，由正弦定理得AEsin∠ACE＝，＝，由于∠ACE＝∠BCE， 且＝，所以＝＝.所以BE ＝AE ，所以AE ＝(－1)． 又cos ∠BAC＝＝22＋12－（6）22×2×1＝－，所以sin ∠BAC＝，所以S△ACE＝AC·AE·sin ∠BAC ＝×1×(－1)×＝.。

第5讲三角函数的图象与性质[基础达标］1．最小正周期为π且图象关于直线x＝错误!对称的函数是（) A．y＝2sin错误!B．y＝2sin错误!C．y＝2sin错误!D．y＝2sin错误!解析：选B。

由函数的最小正周期为π，可排除C.由函数图象关于直线x＝错误!对称知，该直线过函数图象的最高点或最低点，对于A，因为sin错误!＝sin π＝0，所以选项A不正确．对于D，sin错误!＝sin错误!＝错误!,所以D不正确，对于B，sin错误!＝sin错误!＝1，所以选项B正确,故选B。

2．(2019·合肥市第一次教学质量检测)函数y＝sin(ωx＋错误!)在x ＝2处取得最大值,则正数ω的最小值为（）A．错误!B．错误!C．错误!D．错误!解析:选D。

由题意得,2ω＋错误!＝错误!＋2kπ（k∈Z)，解得ω＝错误!＋kπ（k∈Z），因为ω〉0，所以当k＝0时，ωmin＝错误!,故选D.3．(2019·浙江省名校协作体高三联考)下列四个函数：y＝sin｜x｜，y＝cos｜x｜，y＝｜tan x|，y＝－ln｜sin x｜，以π为周期,在错误!上单调递减且为偶函数的是（）A．y＝sin｜x｜B．y＝cos｜x|C．y＝｜tan x| D．y＝－ln｜sin x｜解析：选D。

A。

y＝sin｜x|在错误!上单调递增,故A错误；B。

y＝cos|x｜＝cos x周期为T＝2π，故B错误；C。

y＝|tan x｜在错误!上单调递增,故C错误；D。

f(x＋π)＝－ln|sin(x＋π）｜＝－ln|sin x|，周期为π，当x∈错误!时，y＝－ln(sin x）是在错误!上单调递减的偶函数，故D正确，故选D。

4．（2017·高考全国卷Ⅲ)设函数f(x)＝cos（x＋错误!），则下列结论错误的是( )A．f(x)的一个周期为－2πB．y＝f(x)的图象关于直线x＝错误!对称C．f(x＋π)的一个零点为x＝错误!D．f(x）在(错误!，π）单调递减解析:选D.根据函数解析式可知函数f(x）的最小正周期为2π,所以函数的一个周期为－2π，A正确；当x＝错误!时,x＋错误!＝3π，所以cos错误!＝－1,所以B正确；f(x＋π）＝cos错误!＝cos错误!，当x＝错误!时，x＋错误!＝错误!，所以f（x＋π)＝0,所以C正确；函数f(x）＝cos错误!在错误!上单调递减，在错误!上单调递增,故D不正确．所以选D.5．若函数f（x）＝sin错误!（ω〉0)在区间(π,2π）内没有最值，则ω的取值范围是（）A．错误!∪错误!B．错误!∪错误!C．错误!D．错误!解析:选B。

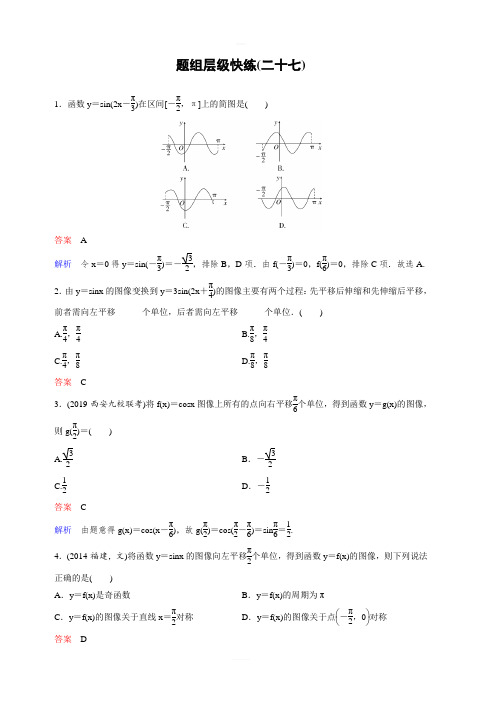
题组层级快练(二十七)1．函数y ＝sin(2x －π3)在区间[－π2，π]上的简图是( )答案 A解析 令x ＝0得y ＝sin(－π3)＝－32，排除B ，D 项．由f(－π3)＝0，f(π6)＝0，排除C 项．故选A.2．由y ＝sinx 的图像变换到y ＝3sin(2x ＋π4)的图像主要有两个过程：先平移后伸缩和先伸缩后平移，前者需向左平移______个单位，后者需向左平移______个单位．( ) A.π4，π4 B.π8，π4 C.π4，π8 D.π8，π8答案 C3．(2019·西安九校联考)将f(x)＝cosx 图像上所有的点向右平移π6个单位，得到函数y ＝g(x)的图像，则g(π2)＝( )A.32B ．－32 C.12 D ．－12答案 C解析 由题意得g(x)＝cos(x －π6)，故g(π2)＝cos(π2－π6)＝sin π6＝12.4．(2014·福建，文)将函数y ＝sinx 的图像向左平移π2个单位，得到函数y ＝f(x)的图像，则下列说法正确的是( ) A ．y ＝f(x)是奇函数B ．y ＝f(x)的周期为πC ．y ＝f(x)的图像关于直线x ＝π2对称D ．y ＝f(x)的图像关于点⎝⎛⎭⎫－π2，0对称 答案 D解析 由题意知，f(x)＝cosx ，所以它是偶函数，A 错；它的周期为2π，B 错；它的对称轴是直线x ＝kπ，k ∈Z ，C 错；它的对称中心是点⎝⎛⎭⎫kπ＋π2，0，k ∈Z ，D 对． 5．函数y ＝sinx －cosx 的图像可由y ＝sinx ＋cosx 的图像向右平移( ) A.3π2个单位 B ．π个单位 C.π4个单位 D.π2个单位 答案 D解析 y ＝sinx ＋cosx ＝2sin ⎝⎛⎭⎫x ＋π4，y ＝sinx －cosx ＝2sin ⎝⎛⎭⎫x －π4＝2sin ⎣⎡⎦⎤⎝⎛⎭⎫x －π2＋π4. 6．(2017·课标全国Ⅰ，理)已知曲线C 1：y ＝cosx ，C 2：y ＝sin(2x ＋2π3)，则下面结论正确的是( )A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2 答案 D解析 本题考查三角函数图像的变换、诱导公式．C 1：y ＝cosx 可化为y ＝sin(x ＋π2)，所以C 1上的各点的横坐标缩短到原来的12倍，得函数y ＝sin(2x ＋π2)的图像，再将得到的曲线向左平移π12个单位长度得y ＝sin[2(x ＋π12)＋π2]，即y ＝sin(2x ＋2π3)的图像，故选D. 7．将函数y ＝sin(2x ＋π4)的图像上各点的纵坐标不变，横坐标伸长到原来的2倍，再向右平移π4个单位，所得到的图像解析式是( ) A ．f(x)＝sinx B ．f(x)＝cosx C ．f(x)＝sin4x D ．f(x)＝cos4x答案 A解析 y ＝sin(2x ＋π4)→y ＝sin(x ＋π4)→y ＝sin(x －π4＋π4)＝sinx.8．(2013·山东理)将函数y ＝sin(2x ＋φ)的图像沿x 轴向左平移π8个单位后，得到一个偶函数的图像，则φ的一个可能取值为( ) A.3π4 B.π4 C ．0 D ．－π4答案 B解析 把函数y ＝sin(2x ＋φ)的图像向左平移π8个单位后，得到的图像的解析式是y ＝sin(2x ＋π4＋φ)，该函数是偶函数的充要条件是π4＋φ＝kπ＋π2，k ∈Z ，根据选项检验可知φ的一个可能取值为π4.9.电流强度I(安)随时间t(秒)变化的函数I ＝Asin(ωt ＋φ)(A>0，ω>0，0<φ<π2)的图像如右图所示，则当t ＝1100秒时，电流强度是( )A ．－5 AB ．5 AC ．5 3 AD ．10 A答案 A解析 由图像知A ＝10，T 2＝4300－1300＝1100.∴ω＝2πT ＝100π.∴T ＝10sin(100πt ＋φ)．∵(1300，10)为五点中的第二个点，∴100π×1300＋φ＝π2. ∴φ＝π6.∴I ＝10sin(100πt ＋π6)，当t ＝1100秒时，I ＝－5 A ，故选A.10．(2019·沧州七校联考)将函数f(x)＝sin(2x ＋θ)(－π2<θ<π2)的图像向右平移φ(φ>0)个单位长度后得到函数g(x)的图像，若f(x)，g(x)的图像都经过点P(0，32)，则φ的值可以是( ) A.5π3 B.5π6 C.π2 D.π6答案 B解析 因为函数f(x)的图像过点P ，所以θ＝π3，所以f(x)＝sin(2x ＋π3)．又函数f(x)的图像向右平移φ个单位长度后，得到函数g(x)＝sin[2(x －φ)＋π3]的图像，所以sin(π3－2φ)＝32，所以φ可以为5π6，故选B.11．(2019·福建宁德一模)将函数y ＝3sin(2x ＋π6)的图像上各点沿x 轴向右平移π6个单位长度，所得函数图像的一个对称中心为( ) A ．(7π12，0)B ．(π6，0)C ．(5π8，0)D ．(2π3，－3)答案 A解析 将函数y ＝3sin(2x ＋π6)的图像上各点沿x 轴向右平移π6个单位长度，可得函数y ＝3sin[2(x －π6)＋π6]＝3sin(2x －π6)的图像．由2x －π6＝kπ，k ∈Z ，可得x ＝kπ2＋π12，k ∈Z .故所得函数图像的对称中心为(kπ2＋π12，0)，k ∈Z .令k ＝1可得一个对称中心为(7π12，0)．故选A.12．(高考真题·湖北卷)将函数y ＝3cosx ＋sinx(x ∈R )的图像向左平移m(m>0)个单位长度后，所得到的图像关于y 轴对称，则m 的最小值是( ) A.π12 B.π6 C.π3 D.5π6 答案 B解析 y ＝3cosx ＋sinx ＝2(32cosx ＋12sinx)＝2sin(x ＋π3)的图像向左平移m 个单位后，得到y ＝2sin(x ＋m ＋π3)的图像，此图像关于y 轴对称，则x ＝0时，y ＝±2，即2sin(m ＋π3)＝±2，所以m ＋π3＝π2＋kπ，k ∈Z ，由于m>0，所以m min ＝π6，故选B.13．(2019·辽宁沈阳一模)将函数f(x)＝2sin(ωx ＋π4)(ω>0)的图像向右平移π4ω个单位长度，得到函数y＝g(x)的图像．若y ＝g(x)在[－π6，π3]上为增函数，则ω的最大值为( )A ．3B ．2 C.32 D.54答案 C解析 函数f(x)＝2sin(ωx ＋π4)(ω>0)的图像向右平移π4ω个单位长度，可得g(x)＝2sin[ω(x －π4ω)＋π4]＝2sinωx 的图像．若g(x)在[－π6，π3]上为增函数，则－π2＋2kπ≤－πω6且πω3≤π2＋2kπ，k ∈Z ，解得ω≤3－12k 且ω≤32＋6k ，k ∈Z .∵ω>0，∴当k ＝0时，ω取得最大值为32.故选C.14．(2019·湖南长沙联考)把函数y ＝sin2x 的图像向左平移π4个单位长度，再把所得图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得函数图像的解析式为________． 答案 y ＝cosx解析 把函数y ＝sin2x 的图像向左平移π4个单位长度，得函数y ＝sin2(x ＋π4)＝sin(2x ＋π2)＝cos2x 的图像，再把y ＝cos2x 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y ＝cosx 的图像．15．已知函数y ＝sinωx(ω>0)在一个周期内的图像如图所示，要得到函数y ＝sin(12x ＋π12)的图像，则需将函数y ＝sinωx 的图像向________平移________个单位长度．答案 左，π6解析 由图像知函数y ＝sinωx 的周期为T ＝3π－(－π)＝4π， ∴ω＝2πT ＝12，故y ＝sin 12x.又y ＝sin(x 2＋π12)＝sin 12(x ＋π6)，∴将函数y ＝sin 12x 的图像向左平移π6个单位长度，即可得到函数y ＝sin(x 2＋π12)的图像．16．若函数y ＝sin2x 的图像向右平移φ(φ>0)个单位，得到的图像恰好关于直线x ＝π6对称，则φ的最小值是________． 答案5π12解析 y ＝sin2x 的图像向右平移φ(φ>0)个单位，得y ＝sin2(x －φ)＝sin(2x －2φ)．因其中一条对称轴方程为x ＝π6，则2·π6－2φ＝kπ＋π2(k ∈Z )．因为φ>0，所以φ的最小值为5π12.17．(2019·上饶地区联考)已知函数f(x)＝4cosxsin(x ＋π6)＋a 的最大值为2.(1)求实数a 的值及f(x)的最小正周期； (2)在坐标纸上作出f(x)在[0，π]上的图像． 答案 (1)a ＝－1，T ＝π (2)略解析 (1)f(x)＝4cosx(sinxcos π6＋cosxsin π6)＋a ＝3sin2x ＋cos2x ＋1＋a ＝2sin(2x ＋π6)＋a ＋1，最大值为3＋a ＝2，∴a ＝－1.T ＝2π2＝π.(2)列表如下：2x ＋π6π6 π2 π 3π2 2π 13π6 x 0 π6 5π12 2π3 11π12 π f(x)12－2118.(2019·湖北七校联考)已知函数f(x)＝Asin(ωx ＋φ)(A>0，ω>0，0<φ<π2)的部分图像如图所示，其中点P(1，2)为函数f(x)图像的一个最高点，Q(4，0)为函数f(x)的图像与x 轴的一个交点，O 为坐标原点．(1)求函数f(x)的解析式；(2)将函数y ＝f(x)的图像向右平移2个单位长度得到y ＝g(x)的图像，求函数h(x)＝f(x)·g(x)的图像的对称中心．答案 (1)f(x)＝2sin(π6x ＋π3) (2)(3k ＋12，1)(k ∈Z )解析 (1)由题意得A ＝2，周期T ＝4×(4－1)＝12. 又∵2πω＝12，∴ω＝π6.将点P(1，2)代入f(x)＝2sin(π6x ＋φ)，得sin(π6＋φ)＝1.∵0<φ<π2，∴φ＝π3，∴f(x)＝2sin(π6x ＋π3)．(2)由题意，得g(x)＝2sin[π6(x －2)＋π3]＝2sin π6x.∴h(x)＝f(x)·g(x)＝4sin(π6x ＋π3)·sin π6x ＝2sin 2π6x ＋23·sin π6x ·cos π6x ＝1－cos π3x ＋3sin π3x ＝1＋2sin(π3x －π6)． 由π3x －π6＝kπ(k ∈Z )，得x ＝3k ＋12(k ∈Z )．1∴函数y＝h(x)图像的对称中心为(3k＋2，1)(k∈Z)．。

题组层级快练(二十九)1．(2019·沧州七校联考)已知△ABC，a ＝5，b ＝15，∠A ＝30°，那么c ＝( ) A ．2 5 B.5C ．25或5D ．均不正确答案 C解析 ∵asinA ＝bsinB ，∴sinB ＝bsinAa ＝155·sin30°＝32.∵b>a ，∴B ＝60°或120°. 假设B ＝60°，C ＝90°，∴c ＝a 2＋b 2＝25.假设B ＝120°，C ＝30°，∴a ＝c ＝ 5.2．(2019·安徽马鞍山一模)△ABC 的内角A ，B ，C 的对边别离为a ，b ，c.已知a ＝3，b ＝2，A ＝60°，那么c ＝( ) A.12 B ．1 C.3 D ．2答案 B解析 ∵a ＝3，b ＝2，A ＝60°，∴由余弦定理a 2＝b 2＋c 2－2bccosA ，得3＝4＋c 2－2×2×c ×12，整理得c 2－2c＋1＝0，解得c ＝1.应选B.3．(2019·安徽合肥模拟)在△ABC 中，A ＝60°，AB ＝2，且△ABC 的面积为32，那么BC 的长为( ) A.32B. 3 C ．2 3 D ．2答案 B解析 因为S ＝12AB ·ACsinA ＝12×2×32AC ＝32，因此AC ＝1，因此BC 2＝AB 2＋AC 2－2AB·ACcos60°＝3. 因此BC ＝ 3.4．(2016·山东)△ABC 中，角A ，B ，C 的对边别离是a ，b ，c.已知b ＝c ，a 2＝2b 2(1－sinA)，那么A ＝( ) A.3π4B.π3C.π4D.π6答案 C解析 由余弦定理得a 2＝b 2＋c 2－2bccosA ＝2b 2－2b 2cosA ，因此2b 2(1－sinA)＝2b 2(1－cosA)，因此sinA ＝cosA ，即tanA ＝1，又0<A<π，因此A ＝π4.5．(2019·陕西西安一中期中)在△ABC 中，sin 2A ≤sin 2B ＋sin 2C －sinBsinC ，那么A 的取值范围是( ) A ．(0，π6]B ．[π6，π)C ．(0，π3]D ．[π3，π)答案 C解析 ∵sin 2A ≤sin 2B ＋sin 2C －sinBsinC ，由正弦定理，得a 2≤b 2＋c 2－bc ，∴bc ≤b 2＋c 2－a 2.∴cosA ＝b 2＋c 2－a 22bc ≥12，∴A ≤π3.∵A>0，∴A 的取值范围是(0，π3]．应选C. 6．(2019·广东惠州三调)在△ABC 中，角A ，B ，C 的对边别离是a ，b ，c ，已知b ＝2，c ＝22，且C ＝π4，则△ABC的面积为( ) A.3＋1 B.3－1 C ．4 D ．2 答案 A解析 由正弦定理b sinB ＝c sinC ，得sinB ＝bsinC c ＝12.又c>b ，且B ∈(0，π)，因此B ＝π6，因此A ＝7π12，因此S ＝12bcsinA＝12×2×22sin 7π12＝12×2×22×6＋24＝3＋1.应选A. 7．(2019·江西七校一联)在△ABC 中，假设sin(A －B)＝1＋2cos(B ＋C)sin(A ＋C)，则△ABC 的形状必然是( ) A ．等边三角形 B ．不含60°的等腰三角形 C ．钝角三角形 D ．直角三角形 答案 D解析 sin(A －B)＝1＋2cos(B ＋C)sin(A ＋C)＝1－2cosAsinB ，∴sinAcosB －cosAsinB ＝1－2cosAsinB ，∴sinAcosB ＋cosAsinB ＝1，即sin(A ＋B)＝1，那么有A ＋B ＝π2，故三角形为直角三角形．8．(2021·江西，理)在△ABC 中，内角A ，B ，C 所对的边别离是a ，b ，c ，假设c 2＝(a －b)2＋6，C ＝π3，则△ABC的面积是( ) A ．3 B.932C.332D ．3 3答案 C解析 利用所给条件和余弦定理整体求解ab 的值，再利用三角形面积公式求解． ∵c 2＝(a －b)2＋6，∴c 2＝a 2＋b 2－2ab ＋6.① ∵C ＝π3，∴c 2＝a 2＋b 2－2abcos π3＝a 2＋b 2－ab.②由①②得－ab ＋6＝0，即ab ＝6. ∴S △ABC ＝12absinC ＝12×6×32＝332.9．(2021·新课标全国Ⅱ，理)已知钝角三角形ABC 的面积是12，AB ＝1，BC ＝2，那么AC ＝( )A ．5 B. 5 C ．2 D ．1答案 B解析 由题意可得12AB ·BC ·sinB ＝12，又AB ＝1，BC ＝2，因此sinB ＝22，因此B ＝45°或B ＝135°.当B ＝45°时，由余弦定理可得AC ＝AB 2＋BC 2－2AB·BC·cosB ＝1，现在AC ＝AB ＝1，BC ＝2，易患A ＝90°，与“钝角三角形”条件矛盾，舍去．因此B ＝135°.由余弦定理可得AC ＝AB 2＋BC 2－2AB·BC·cosB ＝ 5.应选B.10．(2021·安徽，文)在△ABC 中，AB ＝6，∠A ＝75°，∠B ＝45°，那么AC ＝________． 答案 2解析 因为∠A ＝75°，∠B ＝45°，因此∠C ＝60°，由正弦定理可得AC sin45°＝6sin60°，解得AC ＝2. 11．(2021·重庆，文)设△ABC 的内角A ，B ，C 的对边别离为a ，b ，c ，且a ＝2，cosC ＝－14，3sinA ＝2sinB ，那么c ＝________． 答案 4解析 由3sinA ＝2sinB 及正弦定理，得3a ＝2b ，因此b ＝32a ＝3.由余弦定理cosC ＝a 2＋b 2－c 22ab ，得－14＝22＋32－c22×2×3，解得c ＝4.12．(2019·河北唐山一模)在△ABC 中，角A ，B ，C 的对边a ，b ，c 成等差数列，且A －C ＝90°，那么cosB ＝________． 答案 34解析 ∵a ，b ，c 成等差数列，∴2b ＝a ＋c. ∴2sinB ＝sinA ＋sinC.∵A －C ＝90°，∴2sinB ＝sin(90°＋C)＋sinC. ∴2sinB ＝cosC ＋sinC. ∴2sinB ＝2sin(C ＋45°)．①∵A ＋B ＋C ＝180°且A －C ＝90°，∴C ＝45°－B 2，代入①式中，2sinB ＝2sin(90°－B2)．∴2sinB ＝2cos B2.∴4sin B 2cos B 2＝2cos B 2.∴sin B 2＝24.∴cosB ＝1－2sin 2B 2＝1－14＝34.13．(2018·北京，文)若△ABC 的面积为34(a 2＋c 2－b 2)，且∠C 为钝角，则∠B ＝________；ca的取值范围是________． 答案 60° (2，＋∞)解析 △ABC 的面积S ＝12acsinB ＝34(a 2＋c 2－b 2)＝34×2accosB ，因此tanB ＝3，因为0°<∠B<180°，因此∠B＝60°.因为∠C 为钝角，因此0°<∠A<30°，因此0<tanA<33，因此c a ＝sinCsinA ＝sin （2π3－A ）sinA ＝sin 2π3cosA －cos 2π3sinAsinA ＝32tanA ＋12>2，故ca的取值范围为(2，＋∞)． 14．(2017·北京，理)在△ABC 中，∠A ＝60°，c ＝37a.(1)求sinC 的值；(2)假设a ＝7，求△ABC 的面积． 答案 (1)3314(2)6 3解析 (1)依照正弦定理：a sinA ＝c sinC ⇒sinC ＝csinA a ＝37×sin60°＝37×32＝3314.(2)当a ＝7时，c ＝37a ＝3<a ，又sinC ＝3314，∴cosC ＝1－sin 2C ＝1314.在△ABC 中，sinB ＝sin[π－(A ＋C)]＝sin(A ＋C)＝sinAcosC ＋cosAsinC ＝32×1314＋12×3314＝437，∴S △ABC ＝12ac ×sinB ＝12×7×3×437＝6 3.15．(2019·福建高中毕业班质检)在△ABC 中，角A ，B ，C 的对边别离为a ，b ，c ，2bcosC －c ＝2a. (1)求B 的大小；(2)假设a ＝3，且AC 边上的中线长为192，求c 的值． 答案 (1)2π3(2)5解析 (1)∵2bcosC －c ＝2a ，∴由余弦定理得2b·a 2＋b 2－c 22ab－c ＝2a ，化简得a 2＋c 2－b 2＝－ac ，∴cosB ＝a 2＋c 2－b 22ac ＝－12.∵B ∈(0，π)，∴B ＝2π3.(2)由(1)可得b 2＝a 2＋c 2＋ac ＝c 2＋3c ＋9.① 又cosC ＝a 2＋b 2－c 22ab，②取AC 的中点D ，连接BD ，在△CBD 中，cosC ＝BC 2＋CD 2－BD 22BC ·CD ＝a 2＋b 24－194ab，③ 由②③得2c 2－b 2＝1.④由①④得c 2－3c －10＝0，解得c ＝5或c ＝－2(舍去)，∴c ＝5.16．(2019·衡水中学调研卷)设△ABC 的内角A ，B ，C 所对边的长别离为a ，b ，c ，且有2sinBcosA ＝sinAcosC ＋cosAsinC. (1)求角A 的大小；(2)假设b ＝2，c ＝1，D 为BC 的中点，求AD 的长． 答案 (1)π3 (2)72解析 (1)方式一：由题设知，2sinBcosA ＝sin(A ＋C)＝sinB ，因为sinB ≠0，因此cosA ＝12.由于0<A<π，故A ＝π3.方式二：由题设可知，2b ·b 2＋c 2－a 22bc ＝a·a 2＋b 2－c 22ab ＋c ·b 2＋c 2－a 22bc ，于是b 2＋c 2－a 2＝bc ，因此cosA ＝b 2＋c 2－a 22bc ＝12. 由于0<A<π，故A ＝π3.(2)方式一：因为AD →2＝(AB →＋AC →2)2＝14(AB →2＋AC →2＋2AB →·AC →)＝14(1＋4＋2×1×2×cos π3)＝74，因此|AD →|＝72，从而AD ＝72. 方式二：因为a 2＝b 2＋c 2－2bccosA ＝4＋1－2×2×1×12＝3，因此a 2＋c 2＝b 2，B ＝π2.因为BD ＝32，AB ＝1，因此AD ＝1＋34＝72. 17．(2018·天津)在△ABC 中，内角A ，B ，C 所对的边别离为a ，b ，c.已知bsinA ＝acos(B －π6)．(1)求角B 的大小；(2)设a ＝2，c ＝3，求b 和sin(2A －B)的值． 答案 (1)π3 (2)7 3314解析 (1)在△ABC 中，由正弦定理a sinA ＝b sinB ，可得bsinA ＝asinB ，又由bsinA ＝acos(B －π6)，得asinB ＝acos(B－π6)，即sinB ＝cos(B －π6)，可得tanB ＝ 3.又因为B ∈(0，π)，可得B ＝π3. (2)在△ABC 中，由余弦定理及a ＝2，c ＝3，B ＝π3，有b 2＝a 2＋c 2－2accosB ＝7，故b ＝7.由bsinA ＝acos(B －π6)，可得sinA ＝37.因为a<c ，故cosA ＝27.因此sin2A ＝2sinAcosA ＝437，cos2A ＝2cos 2A －1＝17， 因此sin(2A －B)＝sin2AcosB －cos2AsinB ＝437×12－17×32＝3314.。

专题层级快练(二十八)1．函数y ＝cos(x ＋π6)，x ∈[0，π2]的值域是( ) A ．(－32，12] B ．[－12，32] C ．[12，32] D ．[－32，－12] 答案 B解析 x∈[0，π2]，x ＋π6∈[π6，23π]，∴y ∈[－12，32]． 2．若是|x|≤π4，那么函数f(x)＝cos 2x ＋sinx 的最小值是( ) A.2－12 B ．－2＋12 C ．－1 D.1－22 答案 D解析 f(x)＝－sin 2x ＋sinx ＋1＝－(sinx －12)2＋54，当sinx ＝－22时，有最小值，y min ＝24－22＝1－22. 3．(2017·课标全国Ⅲ，文)函数f(x)＝15sin(x ＋π3)＋cos(x －π6)的最大值为( ) A.65B ．1 C.35D.15答案 A 解析 因为cos(x －π6)＝cos[(x ＋π3)－π2] ＝sin(x ＋π3)，因此f(x)＝65sin(x ＋π3)，因此f(x)的最大值为65，应选A. 4．(2019·沧州七校联考)函数y ＝2sin(πx 6－π3)(0≤x ≤9)的最大值与最小值之和为( ) A ．2－ 3B ．0C ．－1D ．－1－ 3 答案 A解析 当0≤x ≤9时，－π3≤πx 6－π3≤7π6，－32≤sin(πx 6－π3)≤1，因此函数的最大值为2，最小值为－3，其和为2－ 3.5．(2019·湖南衡阳月考)概念运算：a*b ＝⎩⎪⎨⎪⎧a ，a ≤b ，b ，a>b.例如1*2＝1，那么函数f(x)＝sinx*cosx 的值域为( )A ．[－22，22] B ．[－1，1] C ．[22，1] D ．[－1，22] 答案 D解析 依照三角函数的周期性，咱们只看在一个最小正周期内的情形即可．设x ∈[0，2π]，当π4≤x ≤5π4时，sinx ≥cosx ，f(x)＝cosx ，f(x)∈[－1，22]，当0≤x<π4或5π4<x ≤2π时，cosx>sinx ，f(x)＝sinx ，f(x)∈[0，22)∪[－1，0]．综上知f(x)的值域为[－1，22]． 6．当0＜x ＜π4时，函数f(x)＝cos 2x cosxsinx －sin 2x的最小值是( ) A.14B.12 C ．2D ．4答案 D解析 f(x)＝1－tan 2x ＋tanx ＝1－（tanx －12）2＋14，当tanx ＝12时，f(x)的最小值为4，应选D. 7．已知f(x)＝sinx ＋1sinx，x ∈(0，π)．以下结论正确的选项是( ) A ．有最大值无最小值B ．有最小值无最大值C ．有最大值且有最小值D ．既无最大值又无最小值 答案 B解析 令t ＝sinx ，t ∈(0，1]，那么y ＝1＋1t，t ∈(0，1]是一个减函数，则f(x)只有最小值而无最大值．另外还可通过y ＝1＋1sinx ，得出sinx ＝1y －1，由sinx ∈(0，1]也可求出，应选B. 8．(2019·河北石家庄一检)假设函数f(x)＝3sin(2x ＋θ)＋cos(2x ＋θ)(0<θ<π)的图像关于点(π2，0)对称，那么函数f(x)在[－π4，π6]上的最小值是( ) A ．－1 B ．－ 3 C ．－12D ．－32 答案 B解析 因为f(x)＝3sin(2x ＋θ)＋cos(2x ＋θ)＝2sin(2x ＋θ＋π6)，那么由题意，知f(π2)＝2sin(π＋θ＋π6)＝0.又0<θ<π，因此θ＝5π6，因此f(x)＝－2sin2x ，那么f(x)在[－π4，π6]上是减函数，因此函数f(x)在[－π4，π6]上的最小值为f(π6)＝－2sin π3＝－ 3.应选B.9．当函数y ＝sinx －3cosx(0≤x<2π)取得最大值时，x ＝________．答案 56π 解析 y ＝sinx －3cosx ＝2sin(x －π3)，∵x ∈[0，2π)，∴x －π3∈[－π3，5π3)，∴当x －π3＝π2，即x ＝56π时，函数取得最大值2.10．(2018·北京西城模拟)已知函数f(x)＝sin(2x ＋π6)，其中x ∈[－π6，α]．当α＝π3时，f(x)的值域是________；假设f(x)的值域是[－12，1]，那么α的取值范围是________． 答案 [－12，1] [π6，π2] 解析 假设－π6≤x ≤π3，那么－π3≤2x ≤2π3，－π6≤2x ＋π6≤5π6，现在－12≤sin(2x ＋π6)≤1，即f(x)的值域是[－12，1]． 假设－π6≤x ≤α，那么－π3≤2x ≤2α，－π6≤2x ＋π6≤2α＋π6. ∵当2x ＋π6＝－π6或2x ＋π6＝7π6时，sin(2x ＋π6)＝－12，∴要使f(x)的值域是[－12，1]，那么有π2≤2α＋π6≤7π6，即π3≤2α≤π，∴π6≤α≤π2，即α的取值范围是[π6，π2]． 11．(2021·课标全国Ⅱ，理)函数f(x)＝sin(x ＋2φ)－2sinφcos(x ＋φ)的最大值为________．答案 1解析 f(x)＝sin[(x ＋φ)＋φ]－2sinφcos (x ＋φ)＝sin(x ＋φ)cosφ－cos(x ＋φ)sinφ＝sin(x ＋φ－φ)＝sinx ，因为x ∈R ，因此f(x)的最大值为1.12．(2019·湖北武汉调研)已知函数f(x)＝3sin2x ＋2cos 2x ＋m 在区间[0，π2]上的最大值为3，那么： (1)m ＝________；(2)对任意a ∈R ，f(x)在[a ，a ＋20π]上的零点个数为________．答案 (1)0 (2)40或41解析 (1)f(x)＝3sin2x ＋2cos 2x ＋m ＝3sin2x ＋1＋cos2x ＋m ＝2sin(2x ＋π6)＋m ＋1， 因为0≤x ≤π2，因此π6≤2x ＋π6≤7π6. 因此－12≤sin(2x ＋π6)≤1，f(x)max ＝2＋m ＋1＝3＋m ＝3，因此m ＝0. (2)由(1)f(x)＝2sin(2x ＋π6)＋1，T ＝2π2＝π， 在区间[a ，a ＋20π]上有20个周期，故零点个数为40或41.13．函数y ＝1sin 2x ＋2cos 2x的最小值是________．答案 3＋2 2解析 y ＝1sin 2x ＋2cos 2x ＝sin 2x ＋cos 2x sin 2x ＋2sin 2x ＋2cos 2x cos 2x ＝3＋cos 2x sin 2x ＋2sin 2x cos 2x≥3＋22， ∴y min ＝3＋2 2.14．(2021·天津)已知函数f(x)＝sin 2x －sin 2(x －π6)，x ∈R . (1)求f(x)的最小正周期；(2)求f(x)在区间[－π3，π4]上的最大值和最小值． 答案 (1)T ＝π (2)34，－12解析 (1)由已知，有f(x)＝1－cos2x 2－1－cos （2x －π3）2＝12(12cos2x ＋32sin2x)－12cos2x ＝34sin2x －14cos2x ＝12sin(2x －π6)． 因此，f(x)的最小正周期T ＝2π2＝π. (2)方式一：因为f(x)在区间[－π3，－π6]上是减函数，在区间[－π6，π4]上是增函数，f(－π3)＝－14，f(－π6)＝－12，f(π4)＝34.因此，f(x)在区间[－π3，π4]上的最大值为34，最小值为－12. 方式二：∵x ∈[π3，π4]，∴2x －π6∈[－56π，π3] ∴sin(2x －π6)∈[－1，32] ∴12sin(2x －π6)∈[－12，34]， ∴f(x)在区间[－π3，π4]内的最大值和最小值别离为34，－12. 15．(2019·吉林长春朝阳实验中学二模)设函数f(x)＝3sinxcosx ＋cos 2x ＋a.(1)写出函数f(x)的最小正周期及单调递减区间；(2)当x ∈[－π6，π3]时，函数f(x)的最大值与最小值的和为32，求实数a 的值． 答案 (1)T ＝π [π6＋kπ，2π3＋kπ](k ∈Z ) (2)a ＝0解析 (1)f(x)＝32sin2x ＋1＋cos2x 2＋a ＝sin(2x ＋π6)＋a ＋12，∴T ＝π.由π2＋2kπ≤2x ＋π6≤3π2＋2kπ(k ∈Z )，得π6＋kπ≤x ≤2π3＋kπ(k ∈Z )．故函数f(x)的单调递减区间是[π6＋kπ，2π3＋kπ](k ∈Z )． (2)∵－π6≤x ≤π3，∴－π6≤2x ＋π6≤5π6，∴－12≤sin(2x ＋π6)≤1. 当x ∈[－π6，π3]时，函数f(x)的最大值与最小值的和为(1＋a ＋12)＋(－12＋a ＋12)＝32，解得a ＝0. 16．(2019·沧州一中月考)设f(x)＝4cos(ωx －π6)sinωx －cos(2ωx ＋π)，其中ω>0. (1)求函数y ＝f(x)的值域；(2)假设f(x)在区间[－3π2，π2]上为增函数，求ω的最大值． 答案 (1)[1－3，1＋3] (2)16解析 (1)f(x)＝4(32cos ωx ＋12sinωx )sinωx ＋cos2ωx ＝23sin ωxcos ωx ＋2sin 2ωx ＋cos 2ωx －sin 2ωx ＝3sin2ωx ＋1，因为－1≤sin2ωx ≤1，因此函数y ＝f(x)的值域为[1－3，1＋3]．(2)因y ＝sinx 在每一个闭区间[2kπ－π2，2k π＋π2](k ∈Z )上为增函数，故f(x)＝3sin2ωx ＋1(ω>0)在每一个闭区间[kπω－π4ω，kπω＋π4ω](k ∈Z )上为增函数． 依题意知[－3π2，π2]⊆[kπω－π4ω，kπω＋π4ω]对某个k ∈Z 成立，现在必有k ＝0， 于是⎩⎪⎨⎪⎧－3π2≥－π4ω，π2≤π4ω，解得ω≤16，故ω的最大值为16.。

任意角的三角函数1．(2018·龙岩期中)已知角α的顶点为坐标原点，始边为x 轴的非负半轴，若点P (6，y )是角α的终边上一点，且sin α＝－45，则y 的值为(D)A ．4B ．－4C ．8D ．－8由题意知P 的坐标为(6，y )，由三角函数定义知，sin α＝y36＋y2＝－45，得m ＝－8.2．点P 从(－1,0)出发，沿单位圆顺时针方向运动7π3弧长到达点Q ，则点Q 的坐标为(A)A ．(－12，32)B ．(－32，－12)C ．(－12，－32)D ．(－32，12)设Q 的坐标为(x ，y )，则x ＝cos(π－7π3)＝cos(π－2π－π3)＝cos(π－π3)＝－12.y ＝sin(π－7π3)＝sin(π－2π－π3)＝sin(π－π3)＝32. 3．若tan α>0，则(C) A ．sin α>0 B ．cos α>0 C ．sin 2α>0 D ．cos 2α>0由tan α>0得α在第一、三象限．若α在第三象限，则A ，B 都错．由sin 2α＝2sin αcos α知sin 2α>0，C 正确． α取π3，cos 2α＝cos 2π3＝－12<0，D 错．4．(2018·湖北5月冲刺试题)《九章算术》是中国古代第一部数学专著，成于公元一世纪左右，系统总结了战国、秦、汉时期的数学成就．其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式：弧田面积＝12(弦×矢＋矢×矢)，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．按照上述经验公式计算所得弧田面积与其实际面积之间存在误差．现有圆心角为2π3，弦长为40 3m 的弧田．其实际面积与按照上述经验公式计算出弧田的面积之间的误差为(B)(其中π≈3，3≈1.73) A ．15 m 2B ．16 m 2C ．17 m 2D ．18 m 2因为圆心角为2π3，弦长为40 3 m ，设半径为R ，则203R ＝sin π3＝32，所以R ＝40， 圆心到弦的距离d ＝R cos π3＝40×12＝20.所以弦＝403，矢＝R －d ＝20. 弧田实际面积＝13πR 2－12×弦长×d＝16003π－4003＝908， 由经验公式得：弧田面积＝12(弦×矢＋矢×矢)＝12(403×20＋20×20) ＝4003＋200＝892. 其误差为908－892＝16(m 2)．5. α的终边与π6的终边关于直线y ＝x 对称，则α＝ 2k π＋π3(k ∈Z ) .因为π3的终边与π6的终边关于y ＝x 对称，所以α＝2k π＋π3(k ∈Z )．6．已知角α终边过点(3，－1)，则2sin α＋3cos α的值为 12 .因为sin α＝y r ＝－12，cos α＝x r ＝32；所以2sin α＋3cos α＝2×(－12)＋3×32＝12.7. 如果角α的终边在直线y ＝3x 上，求cos α与tan α的值．因为角α的终边在直线y ＝3x 上，所以角α的终边在第一、三象限．当α的终边在第一象限时，因为直线过点(1,3)， 因为r ＝1＋32＝10，所以cos α＝1010，tan α＝3. 当α的终边在第三象限时，同理可得 cos α＝－1010，tan α＝3.8．(2018·北京卷)在平面直角坐标系中，AB ，CD ，EF ，GH 是圆x 2＋y 2＝1上的四段弧(如图)，点P 在其中一段上，角α以Ox 为始边，OP 为终边．若tan α＜cos α＜sin α，则P 所在的圆弧是 (C)A.ABB.CDC.EFD.GH由题知四段弧是单位圆上的第Ⅰ、Ⅱ、Ⅲ象限的弧，在AB 上，tan α＞sin α，不满足； 在CD 上，tan α＞sin α，不满足；在EF 上，sin α＞0，cos α＜0，tan α＜0，且cos α＞tan α，满足； 在GH 上，tan α＞0，sin α＜0，cos α＜0，不满足．9．在直角坐标系xOy 中，已知任意角θ以坐标原点O 为顶点，以x 轴的非负半轴为始边，若其终边经过点P (x 0，y 0)，且|OP |＝r (r >0)，定义：sicos θ＝y 0－x 0r，称sicos θ为“θ的正余弦函数”．若sicos θ＝0，则sin(2θ－π3)＝ 12.因为sicos θ＝0，所以y 0＝x 0，所以θ的终边在直线y ＝x 上．所以θ＝2k π＋π4，或θ＝2k π＋5π4，k ∈Z .当θ＝2k π＋π4，k ∈Z 时，sin(2θ－π3)＝sin(4k π＋π2－π3)＝cos π3＝12；当θ＝2k π＋5π4，k ∈Z 时，sin(2θ－π3)＝sin(4k π＋5π2－π3)＝cos π3＝12.综上得sin(2θ－π3)＝12.10．要建一个扇环形花园，外圆半径是内圆半径的2倍，周长为定值2l ，问当圆心角α(0<α<π)为多少时，扇环面积最大？最大面积是多少？设内圆半径为r ，则外圆半径为2r ，扇环面积为S ，因为αr ＋α·2r ＋2r ＝2l ，所以3α＝2l －2rr，所以S ＝12α·(2r )2－12α·r 2＝32α·r 2＝12·2l －2r r ·r 2＝(l －r )·r ＝－r 2＋lr ＝－(r －12l )2＋14l 2，所以当r ＝12l 时，S 取得最大值，此时3α＝2l －2r r ＝2，α＝23.当α＝23时，S 取得最大值14l 2.同角三角函数的基本关系与诱导公式1．tan 300°＋－sin 765°的值是(B)A ．1＋ 3B ．1－ 3C ．－1－ 3D ．－1＋ 3原式＝tan(360°－60°)＋＋＋＝－tan 60°＋1tan 45°＝1－ 3.2．(2018·广州一模)已知sin(x －π4)＝35，则cos(x ＋π4)＝(D)A.45B.35 C ．－45 D ．－35(方法一)进行角的配凑cos(x ＋π4)＝cos[π2＋(x －π4)]＝－sin(x －π4)＝－35.(方法二)换元法设x －π4＝θ，则cos θ＝35，且x ＝θ＋π4，所以cos(x ＋π4)＝cos(θ＋π4＋π4)＝cos(π2＋θ)＝－sin θ＝－35.3．(2018·华南师大附中模拟)已知sin α＋3cos α3cos α－sin α＝5，则cos 2α＋12sin 2α的值是(A)A.35 B ．－35 C ．－3 D ．3由sin α＋3cos α3cos α－sin α＝5得tan α＋33－tan α＝5，所以tan α＝2. 所以cos 2α＋12sin 2α＝cos 2α＋12sin 2αsin 2α＋cos 2α＝cos 2α＋sin αcos αsin 2α＋cos 2α ＝1＋tan α1＋tan 2α＝1＋21＋4＝35. 4．(2018·湖北宜昌模拟)已知sin θ＋cos θ＝43，θ∈(0，π4)，则sin θ－cos θ的值为(B)A.23 B ．－23C.13 D ．－13由已知sin θ＋cos θ＝43，平方得2sin θ·cos θ＝79，而(sin θ－cos θ)2＝1－2sin θcos θ＝1－79＝29，又θ∈(0，π4)，所以cos θ>sin θ>0，所以sin θ－cos θ<0，故sin θ－cos θ＝－23. 5．已知cos α＝15，－π2<α<0，则π2＋αα＋π－αα的值为612.π2＋αα＋π－αan α＝－sin αtan αsin α＝－cos αsin α，因为cos α＝15，－π2<α<0，所以sin α＝－265.所以原式＝－cos αsin α＝－15－265＝612. 6．若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为 1－ 5 .由题意⎩⎪⎨⎪⎧sin θ＋cos θ＝－m2，sin θ·cos θ＝m4，且Δ＝4m 2－16m ≥0，(sin θ＋cos θ)2＝1＋2sin θcos θ＝m 24，所以m 24＝1＋m2，所以m ＝1± 5.由Δ＝4m 2－16m ≥0，得m ≤0，或m ≥4，所以m ＝1－ 5. 7．已知tan α＝2. (1)求tan(α＋π4)的值；(2)求sin 2αsin 2α＋sinαcos α－cos 2α－1的值．(1)tan(α＋π4)＝tan α＋tanπ41－tan αtanπ4＝2＋11－2×1＝－3.(2)sin 2αsin 2α＋sin αcos α－cos 2α－1 ＝2sin αcos αsin 2α＋sin αcos α－2cos 2α＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1.8．如图所示，A ，B 是单位圆O 上的点，且B 在第二象限，C 是单位圆与x 轴正半轴的交点，点A 的坐标为(513，1213)，∠AOB ＝90°，则tan ∠COB ＝(B)A.512 B ．－512 C.125 D ．－125因为cos ∠COB ＝cos(∠COA ＋90°)＝－sin ∠COA＝－1213.又因为点B 在第二象限， 所以sin ∠COB ＝1－cos 2∠COB ＝513， 所以tan ∠COB ＝sin ∠COB cos ∠COB ＝－512.9．已知x ∈R ，则函数y ＝(1＋sin x )(1＋cos x )的值域为 [0，32＋2] .因为y ＝(1＋sin x )(1＋cos x )＝1＋sin x ＋cos x ＋sin x cos x ，令t ＝sin x ＋cos x ，则t ∈[－2，2]，sin x cos x ＝t 2－12，所以y ＝12t 2＋t ＋12＝12(t ＋1)2，t ∈[－2，2]．所以所求函数的值域为[0，32＋2]．10．已知0<α<π2，若cos α－sin α＝－55.(1)求tan α的值；(2)把11－sin αcos α用tan α表示出来，并求出其值．(1)因为cos α－sin α＝－55， 所以(cos α－sin α)2＝15.所以1－2sin αcos α＝15，即sin αcos α＝25，所以(sin α＋cos α)2＝1＋2sin αcos α＝95，因为0<α<π2，所以sin α＋cos α＝355.与cos α－sin α＝－55联立解得： sin α＝255，cos α＝55，所以tan α＝2.(2)11－sin αcos α＝sin 2α＋cos 2αsin 2α＋cos 2α－sin αcos α＝tan 2α＋1tan 2α－tan α＋1， 因为tan α＝2，所以11－sin αcos α＝22＋122－2＋1＝53.两角和与差的三角函数1．sin 15°cos 75°＋cos 15°sin 105°等于(D) A ．0 B.12C.32D ．1原式＝sin 15°cos 75°＋cos 15°sin 75°＝sin 90°＝1.2．(2018·临沂期中)已知f (x )＝sin(x ＋π6)，若sin α＝35(π2<α<π)，则f (α＋π12)＝(B)A ．－7210B ．－210C.210D.7210由sin α＝35(π2<α<π)，得cos α＝－45.所以f (α＋π12)＝sin(α＋π12＋π6)＝sin(α＋π4)＝22(sin α＋cos α)＝22×(35－45)＝－210. 3．(2018·淄博模拟)已知cos(α＋π6)＋sin α＝235，则sin(α＋4π3)的值是(A)A ．－235 B.235C ．－45 D.45因为cos(α＋π6)＋sin α＝32cos α＋12sin α＝sin(α＋π3)＝235，所以sin(α＋π3)＝235.所以sin(α＋4π3)＝sin(α＋π3＋π)＝－235.4．若tan α＝2tan π5，则α－3π10α－π5＝(C)A ．1B ．2 C ．3 D ．4因为cos(α－310π)＝cos(α＋π5－π2)＝sin(α＋π5)，所以原式＝α＋π5α－π5＝sin αcos π5＋cos αsinπ5sin αcos π5－cos αsinπ5＝tan α＋tanπ5tan α－tanπ5.又因为tan α＝2tan π5，所以原式＝2tan π5＋tanπ52tan π5－tanπ5＝3.5．(2017·全国卷Ⅰ)已知α∈(0，π2)，tan α＝2，则cos(α－π4)＝ 31010 .cos(α－π4)＝cos αcos π4＋sin αsin π4＝22(cos α＋sin α)． 又由α∈(0，π2)，tan α＝2，知sin α＝255，cos α＝55，所以cos(α－π4)＝22×(55＋255)＝31010.6．(2017·江苏卷)若tan(α－π4)＝16，则tan α＝ 75.(方法一)因为tan(α－π4)＝tan α－tanπ41＋tan αtanπ4＝tan α－11＋tan α＝16，所以6tan α－6＝1＋tan α(tan α≠－1)，所以tan α＝75.(方法二)tan α＝tan[(α－π4)＋π4] ＝α－π4＋tan π41－α－π4π4＝16＋11－16×1＝75.7．已知α是第二象限角，sin α＝35，β为第三象限角，tan β＝43.(1)求tan(α＋β)的值； (2)求cos(2α－β)的值．(1)因为α是第二象限角，sin α＝35，所以cos α＝－1－sin 2α＝－45，tan α＝sin αcos α＝－34，又tan β＝43，所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝724.(2)因为β为第三象限角，tan β＝43，所以sin β＝－45，cos β＝－35.又sin 2α＝2sin αcos α＝－2425，cos 2α＝1－2sin 2α＝725，所以cos(2α－β)＝cos 2αcos β＋sin 2αsin β＝35.8．(2018·华大新高考联盟教学质量测评)某房间的室温T (单位：摄氏度)与时间t (单位：小时)的函数关系是：T ＝a sin t ＋b cos t ，t ∈(0，＋∞)，其中a ，b 是正实数，如果该房间的最大温差为10摄氏度，则a ＋b 的最大值是(A)A ．5 2B ．10C ．10 2D ．20由辅助角公式：T ＝a sin t ＋b cos t ＝a 2＋b 2sin(t ＋φ)，其中φ满足条件：sin φ＝b a 2＋b2，cos φ＝a a 2＋b 2.则函数T 的值域为[－a 2＋b 2，a 2＋b 2]， 由室内最大温差为2a 2＋b 2＝10， 得a 2＋b 2＝5，a 2＋b 2＝25， 设a ＝5cos θ，b ＝5sin θ，则a ＋b ＝5cos θ＋5sin θ＝52sin(θ＋π4)，故a ＋b ≤52，当且仅当a ＝b ＝522时等号成立．9．(2018·全国卷Ⅱ)已知sin α＋cos β＝1，cos α＋sin β＝0，则sin(α＋β)＝ －12.因为sin α＋cos β＝1，①cos α＋sin β＝0，②所以①2＋②2得1＋2(sin αcos β＋cos αsin β)＋1＝1， 所以sin αcos β＋cos αsin β＝－12，所以sin(α＋β)＝－12.10．如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A ，B 两点，已知A ，B 的横坐标分别为210，255. (1)求tan(α＋β)的值； (2)求α＋2β的值．由条件得cos α＝210，cos β＝255. 因为α，β为锐角，所以sin α＝1－cos 2α＝7210， 同理可得sin β＝55.所以tan α＝7，tan β＝12. (1)tan(α＋β)＝tan α＋tan β1－tan αtan β＝－3.(2)因为tan(α＋2β)＝tan[(α＋β)＋β]＝α＋β＋tan β1－α＋ββ＝－3＋121－－12＝－1. 因为α，β为锐角，所以0<α＋2β<3π2，所以α＋2β＝3π4.倍角公式及简单的三角恒等变换1．若tan α＝3，则sin 2αcos 2α的值等于(D) A ．2 B ．3 C ．4 D ．6因为sin 2αcos 2α＝2sin αcos αcos 2α＝2tan α＝6. 2．已知sin 2α＝23，则cos 2(α＋π4)＝(A)A.16B.13 C.12 D.23因为sin 2α＝23，所以cos 2(α＋π4)＝1＋α＋π22＝1－sin 2α2＝1－232＝16.3．(2018·佛山一模)已知tan θ＋1tan θ＝4，则cos 2(θ＋π4)＝(C)A.12B.13 C.14 D.15由tan θ＋1tan θ＝4，得sin θcos θ＋cos θsin θ＝4， 即sin 2θ＋cos 2θsin θcos θ＝4，所以sin θcos θ＝14，所以cos 2(θ＋π4)＝1＋θ＋π22＝1－sin 2θ2＝1－2sin θcos θ2＝1－2×142＝14.4．(2018·全国卷Ⅰ)已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (1，a )，B (2，b )，且cos 2α＝23，则|a －b |＝(B)A.15B.55C.255D ．1由cos 2α＝23，得cos 2α－sin 2α＝23，所以cos 2α－sin 2αcos 2α＋sin 2α＝23，即1－tan 2α1＋tan 2α＝23， 所以tan α＝±55，即b －a 2－1＝±55，所以|a －b |＝55. 5．(2016·浙江卷)已知2cos 2x ＋sin 2x ＝A sin(ωx ＋φ)＋b (A >0)，则A ＝ 2 ，b＝ 1 .因为2cos 2x ＋sin 2x ＝1＋cos 2x ＋sin 2x ＝2sin(2x ＋π4)＋1＝A sin(ωx ＋φ)＋b ，所以A ＝2，b ＝1.6．已知tan(π4＋θ)＝3，则sin 2θ－2cos 2θ＝ －45 .因为tan(π4＋θ)＝3，所以1＋tan θ1－tan θ＝3，所以tan θ＝12.sin 2θ－2cos 2θ＝2sin θcos θ－2cos 2θsin 2θ＋cos 2θ＝2tan θ－2tan 2θ＋1＝－45. 7．已知cos α＝35，cos(α－β)＝1213，且0<β<α<π2，求cos β的值．因为cos α＝35，0<α<π2，所以sin α＝1－cos 2α＝45，因为0<β<α<π2，所以0<α－β<π2，又cos(α－β)＝1213，所以sin(α－β)＝1－cos2α－β＝513， 所以cos β＝cos[α－(α－β)]＝cos αcos(α－β)＋sin αsin(α－β)＝35×1213＋45×513＝5665.8.sin 47°－sin 17°cos 30°cos 17°的值为(C)A ．－32 B ．－12C.12D.32原式＝＋－sin 17°cos 30°cos 17°＝sin 30°cos 17°＋cos 30°sin 17°－sin 17°cos 30°cos 17°＝sin 30°cos 17°cos 17°＝sin 30°＝12.9.3tan 12°－3212°－＝ －4 3 .原式＝2312sin 12°－32212°－＝－23－sin 24°cos 24°＝－43sin 48°2sin 24°cos 24°＝－4 3.10．(2018·江苏卷)已知α，β为锐角，tan α＝43，cos(α＋β)＝－55.(1)求cos 2α的值； (2)求tan(α－β)的值．(1)因为tan α＝43，tan α＝sin αcos α，所以sin α＝43cos α.因为sin 2α＋cos 2α＝1，所以cos 2α＝925，因此，cos 2α＝2cos 2α－1＝－725.(2)因为α，β为锐角，所以α＋β∈(0，π)． 又因为cos(α＋β)＝－55， 所以sin(α＋β)＝1－cos 2α＋β＝255，因此tan(α＋β)＝－2.因为tan α＝43，所以tan 2α＝2tan α1－tan 2α＝－247. 因此，tan(α－β)＝tan[2α－(α＋β)] ＝tan 2α－tan α＋β1＋tan 2αtan α＋β＝－211.三角函数的图象与性质（一）1．若动直线x ＝a 与函数f (x )＝sin x 和g (x )＝cos x 的图象分别交于M ，N 两点，则|MN |的最大值为(B)A ．1 B. 2 C. 3 D ．2|MN |＝|sin a －cos a |＝2|sin(a －π4)|≤ 2.2．函数f (x )＝3sin x ＋cos(π3＋x )的最大值为(C)A ．2 B. 3 C ．1 D.12因为f (x )＝3sin x ＋12cos x －32sin x＝32sin x ＋12cos x ＝sin x cos π6＋cos x sin π6＝sin(x ＋π6)．所以f (x )的最大值为1.3．(2016·全国卷Ⅱ)函数f (x )＝cos 2x ＋6cos(π2－x )的最大值为(B)A ．4B ．5C ．6D ．7因为f (x )＝cos 2x ＋6cos(π2－x )＝cos 2x ＋6sin x ＝1－2sin 2x ＋6sin x ＝－2(sin x －32)2＋112，又sin x ∈[－1,1]，所以当sin x ＝1时，f (x )取得最大值5.故选B. 4．(2017·全国卷Ⅲ)函数f (x )＝15sin(x ＋π3)＋cos(x －π6)的最大值为(A)A.65 B ．1 C.35 D.15(方法一)因为f (x )＝15sin(x ＋π3)＋cos(x －π6)＝15(12sin x ＋32cos x )＋32cos x ＋12sin x ＝110sin x ＋310cos x ＋32cos x ＋12sin x ＝35sin x ＋335cos x ＝65sin(x ＋π3)， 所以当x ＝π6＋2k π(k ∈Z )时，f (x )取得最大值65.(方法二)因为(x ＋π3)＋(π6－x )＝π2，所以f (x )＝15sin(x ＋π3)＋cos(x －π6)＝15sin(x ＋π3)＋cos(π6－x ) ＝15sin(x ＋π3)＋sin(x ＋π3) ＝65sin(x ＋π3)≤65.所以f (x )max ＝65. 5．函数f (x )＝cos 2x ＋sin x 在区间[－π4，π4]上的最小值为 1－22 .f (x )＝1－sin 2x ＋sin x ＝－(sin x －12)2＋54，因为x ∈[－π4，π4]，所以－22≤sin x ≤22，所以当x ＝－π4，即sin x ＝－22时，f (x )min ＝1－12－22＝1－22.6．如图，半径为R 的圆的内接矩形周长的最大值为 42R .设∠BAC ＝θ，周长为p ，则p ＝2AB ＋2BC ＝2(2R cos θ＋2R sin θ) ＝42R sin(θ＋π4)≤42R ，当且仅当θ＝π4时取等号．所以周长的最大值为42R .7．已知函数f (x )＝sin 2x －sin 2(x －π6)，x ∈R .(1)求f (x )的最小正周期；(2)求f (x )在区间[－π3，π4]上的最大值和最小值．(1)由已知，有f (x )＝1－cos 2x 2－1－x －π32＝12(12cos 2x ＋32sin 2x )－12cos 2x ＝34sin 2x －14cos 2x ＝12sin(2x －π6)． 所以f (x )的最小正周期T ＝2π2＝π. (2)因为f (x )在区间[－π3，－π6]上是减函数，在区间[－π6，π4]上是增函数，且f (－π3)＝－14，f (－π6)＝－12，f (π4)＝34，所以f (x )在区间[－π3，π4]上的最大值为34，最小值为－12.8．(2018·天津市和平区月考)若f (x )＝2cos(2x ＋φ)(φ>0)的图象关于直线x ＝π3对称，且当φ取最小值时，x 0∈(0，π2)，使得f (x 0)＝a ，则a 的取值范围是(D)A ．(－1,2]B ．[－2，－1)C ．(－1,1)D ．[－2,1)因为f (x )的图象关于直线x ＝π3对称，所以2π3＋φ＝k π(k ∈Z )，即φ＝k π－2π3(k ∈Z )，因为φ>0，所以φmin＝π3，此时f (x )＝2cos(2x ＋π3)． 因为x 0∈(0，π2)，所以2x 0＋π3∈(π3，4π3)，所以－1≤cos(2x 0＋π3)<12，所以－2≤2cos(2x 0＋π3)<1，即－2≤f (x 0)<1，因为f (x 0)＝a ，所以－2≤a <1，故选D.9．(2018·北京卷)设函数f (x )＝cos(ωx －π6)(ω>0)．若f (x )≤f (π4)对任意的实数x 都成立，则ω的最小值为 23.因为f (x )≤f (π4)对任意的实数x 都成立，所以当x ＝π4时，f (x )取得最大值，即f (π4)＝cos(π4ω－π6)＝1，所以π4ω－π6＝2k π，k ∈Z ，所以ω＝8k ＋23，k ∈Z .因为ω>0，所以当k ＝0时，ω取得最小值23.10．已知函数f (x )＝sin 2ωx ＋3sin ωx sin(ωx ＋π2)(ω>0)的最小正周期为π.(1)求ω的值；(2)求函数f (x )在区间[0，2π3]上的取值范围．(1)f (x )＝1－cos 2ωx 2＋32sin 2ωx＝32sin 2ωx －12cos 2ωx ＋12＝sin(2ωx －π6)＋12.因为函数f (x )的最小正周期为π，且ω＞0， 所以2π2ω＝π，解得ω＝1.(2)由(1)得f (x )＝sin(2x －π6)＋12. 因为0≤x ≤2π3，所以－π6≤2x －π6≤7π6，所以－12≤sin(2x －π6)≤1，因此0≤sin(2x －π6)＋12≤32.即f (x )在区间[0，2π3]上的取值范围为[0，32]．三角函数的图象与性质（二）1．(2018·全国卷Ⅲ)函数f (x )＝tan x1＋tan 2x的最小正周期为(C) A.π4 B.π2C ．πD ．2π(方法一：直接法)由已知得f (x )的定义域为{x |x ≠k π＋π2，k ∈Z }，又f (x )＝tan x1＋tan 2x ＝sin x cos x 1＋sin xcos x 2＝sin x cos x cos 2x ＋sin 2x cos 2x＝sin x cos x ＝12sin 2x ，所以f (x )的最小正周期为T ＝2π2＝π.(方法二：验证法)因为f (x ＋π)＝f (x )，所以π是f (x )的周期；f (x ＋π2)＝x ＋π21＋tan2x ＋π2＝－tan x 1＋tan 2x≠f (x )，所以π2不是f (x )的周期．故选C.2．在函数①y ＝cos |2x |，②y ＝|cos x |，③y ＝cos(2x ＋π6)，④y ＝tan(2x －π4)中，最小正周期为π的所有函数为(A)A ．①②③B ．①③④C ．②③D ．①③①y ＝cos |2x |＝cos 2x ，最小正周期为π；②由图象知y ＝|cos x |的最小正周期为π； ③y ＝cos(2x ＋π6)的最小正周期T ＝2π2＝π；④y ＝tan(2x －π4)的最小正周期T ＝π2.因此最小正周期为π的函数为①②③.3．已知函数y ＝tan ωx 在(－π2，π2)内是减函数，则(B)A ．0＜ω≤1 B．－1≤ω＜0 C ．ω≥1 D．ω≤－1(方法一：直接法)由y ＝tan x 在(－π2，π2)内是增函数知ω<0，且T ＝π|ω|≥π，即－1≤ω<0，选B.(方法二：特值法)取ω＝－1满足题意，排除A ，C ；又取ω＝－2，不满足题意，排除D ，故选B.4．使函数f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ)为奇函数，且在[0，π4]上是减函数的θ的一个值可以是(D)A ．－π3 B.π3C.π6D.2π3f (x )＝2sin(2x ＋θ＋π3)，因为f (x )是奇函数，所以θ＋π3＝k π，即θ＝k π－π3，k ∈Z ，排除B ，C.若θ＝－π3，则f (x )＝2sin 2x 在[0，π4]上递增，排除A.故选D.5．函数f (x )＝tan(x ＋π4)的单调递增区间是 (k π－3π4，k π＋π4)(k ∈Z ) .由k π－π2<x ＋π4<k π＋π2(k ∈Z )，解得k π－3π4<x <k π＋π4(k ∈Z )．6．函数f (x )＝sin 2x ＋sin x cos x ＋1的最小正周期是 π ，单调递减区间是 [k π＋38π，k π＋78π](k ∈Z ) .因为f (x )＝sin 2x ＋sin x cos x ＋1 ＝1－cos 2x 2＋12sin 2x ＋1 ＝12sin 2x －12cos 2x ＋32 ＝22sin(2x －π4)＋32， 所以函数f (x )的最小正周期T ＝π. 令π2＋2k π≤2x －π4≤3π2＋2k π，k ∈Z ， 所以f (x )的递减区间为[k π＋38π，k π＋78π](k ∈Z )．7．(2017·浙江卷)已知函数f (x )＝sin 2x －cos 2x －23sin x cos x (x ∈R )． (1)求f (2π3)的值；(2)求f (x )的最小正周期及单调递增区间．(1)由sin 2π3＝32，cos 2π3＝－12，得f (2π3)＝(32)2－(－12)2－23×32×(－12)，所以f (2π3)＝2.(2)由cos 2x ＝cos 2x －sin 2x 与sin 2x ＝2sin x cos x 得f (x )＝－cos 2x －3sin 2x ＝－2sin(2x ＋π6)，所以f (x )的最小正周期是π.由正弦函数的性质得π2＋2k π≤2x ＋π6≤3π2＋2k π，k ∈Z ，解得π6＋k π≤x ≤2π3＋k π，k ∈Z ，所以f (x )的单调递增区间是[π6＋k π，2π3＋k π]，k ∈Z .8．(2018·天津卷)将函数y ＝sin(2x ＋π5)的图象向右平移π10个单位长度，所得图象对应的函数(A)A ．在区间[3π4，5π4]上单调递增B ．在区间[3π4，π]上单调递减C ．在区间[5π4，3π2]上单调递增D ．在区间[3π2，2π]上单调递减函数y ＝sin(2x ＋π5)的图象向右平移π10个单位长度后的解析式为y ＝sin[2(x －π10)＋π5]＝sin 2x ，则函数y ＝sin 2x 的一个单调增区间为[3π4，5π4]，一个单调减区间为[5π4，7π4]．由此可判断选项A 正确．9．函数f (x )＝sin(x －π3)的图象为C ，有如下结论：①图象C 关于直线x ＝5π6对称；②图象C 关于点(4π3，0)对称；③函数f (x )在区间[π3，5π6]内是增函数．其中正确的结论的序号是 ①②③ .(写出所有正确结论的序号)①把x ＝5π6代入f (x )＝sin(x －π3)得f (5π6)＝sin(5π6－π3)＝sin π2＝1， 所以图象C 关于直线x ＝5π6对称．②把x ＝4π3代入f (x )＝sin(x －π3)得f (4π3)＝sin(4π3－π3)＝sin π＝0， 所以图象C 关于点(4π3，0)对称．③由2k π－π2≤x －π3≤2k π＋π2(k ∈Z )，所以2k π－π6≤x ≤2k π＋5π6，k ∈Z .取k ＝0，得到一个增区间为[－π6，5π6]，而[π3，5π6－π6，5π6]， 所以函数f (x )在区间[π3，5π6]内是增函数．10．已知函数f (x )＝sin(ωx ＋φ)，其中ω>0，|φ|<π2.(1)若cos π4cos φ－sin 3π4sin φ＝0，求φ的值；(2)在(1)的条件下，若函数f (x )的图象的相邻两条对称轴之间的距离等于π3，求函数f (x )的解析式；并求最小正实数m ，使得函数f (x )的图象向左平移m 个单位后所对应的函数是偶函数．(1)由cos π4cos φ－sin 3π4sin φ＝0，得cos π4cos φ－sin π4sin φ＝0，即cos(π4＋φ)＝0.又|φ|<π2，所以φ＝π4.(2)由(1)得f (x )＝sin(ωx ＋π4)．依题意T 2＝π3，又T ＝2πω，故ω＝3，所以f (x )＝sin(3x ＋π4)．函数f (x )的图象向左平移m 个单位后所对应的函数为g (x )＝sin[3(x ＋m )＋π4]．g (x )是偶函数当且仅当3m ＋π4＝k π＋π2(k ∈Z )，即m ＝k π3＋π12(k ∈Z )． 从而，最小正实数m ＝π12.函数y ＝A sin(ωx ＋φ)的图象与性质1．(2018·雁峰区校级期末)将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的取值不可能为(B)A ．－3π4B ．－π4C.π4D.5π4y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后变为函数y ＝sin[2(x ＋π8)＋φ]＝sin(2x ＋π4＋φ)的图象，又y ＝sin(2x ＋π4＋φ)为偶函数，所以π4＋φ＝π2＋k π(k ∈Z )，所以φ＝π4＋k π(k ∈Z )．若k ＝0，则φ＝π4；若k ＝－1时，φ＝－3π4；若k ＝1时，φ＝5π4，故选B.2．为了得到 y ＝sin(x ＋π3)的图象，可将函数y ＝sin x 的图象向左平移m 个单位长度或向右平移n 个单位长度(m ，n 为正数)，则|m －n |的最小值为(A)A.23πB.34πC.45πD.56πy ＝sin x 向左平移m 个单位长度，得到y ＝sin(x ＋π3), 所以m ＝π3＋2k 1π(k 1∈Z )，y ＝sin x 向右平移n 个单位长度，得到y ＝sin(x ＋π3)，所以n ＝53π＋2k 2π(k 2∈Z )，所以|m －n |最小值即|π3＋2k 1π－53π－2k 2π|＝|－43π＋2(k 1－k 2)π| 的最小值．当k 1－k 2＝1时， |m －n |的最小值为|2π－43π|＝23π，所以所求的最小值是23π.3．(2018·佛山一模)把曲线C 1：y ＝2sin(x －π6)上所有点向右平移π6个单位长度，再把得到的曲线上所有点的横坐标缩短为原来的12，得到曲线C 2，则C 2(B)A ．关于直线x ＝π4对称B ．关于直线x ＝5π12对称C ．关于点(π12，0)对称 D ．关于点(π，0)对称y ＝2sin(x －π6)――→向右平移π6个单位y ＝2sin(x －π3)――→横坐标缩短为原来的12y ＝2sin(2x －π3)． 对于曲线C 2：y ＝2sin(2x －π3)． 令x ＝π4，得y ＝1，不是最值，所以它的图象不关于直线x ＝π4对称，A 错误；令x ＝5π12，得y ＝2为最值，所以它的图象关于直线x ＝5π12对称，B 正确；令x ＝π12，得y ＝－1，所以它的图象不关于点(π12，0)对称，C 错误；令x ＝π，得y ＝－3，故它的图象不关于点(π，0)对称，D 错误．4．(2018·石家庄市一模)函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0)的部分图象如下图所示，则f (11π24)的值为(D)A ．－62B ．－32C ．－22D ．－1显然A ＝2，T 4＝7π12－π3＝π4，所以T ＝π，所以ω＝2，则f (x )＝2sin(2x ＋φ)， 因为f (x )的图象经过点(π3，0)，结合正弦函数的图象特征知，2×π3＋φ＝2k π＋π，k ∈Z ，所以φ＝2k π＋π3，k ∈Z .所以f (x )＝2sin(2x ＋2k π＋π3)，k ∈Z ，所以f (11π24)＝2sin(11π12＋2k π＋π3)＝2sin(2k π＋π＋π4)＝－2sin π4＝－1，k ∈Z .故选D.5．直线y ＝a (a 为常数)与函数y ＝tan ωx (ω为常数且ω>0)的图象相交的相邻两点间的距离是πω.直线y ＝a 与曲线y ＝tan ωx 相邻两点间的距离就是此曲线的一个最小正周期，为πω. 6．(2018·江苏卷)已知函数y ＝sin(2x ＋φ)(－π2<φ<π2)的图象关于直线x ＝π3对称，则φ的值为 －π6.由题意得f (π3)＝sin(23π＋φ)＝±1，所以23π＋φ＝k π＋π2，所以φ＝k π－π6，k ∈Z .因为φ∈(－π2，π2)，所以取k ＝0得φ＝－π6.7．已知函数f (x )＝3sin(x 2＋π6)＋3.(1)指出f (x )的周期、振幅、初相、对称轴； (2)用五点法画出它在一个周期内的闭区间上的图象；(3)说明此函数图象可由y ＝sin x 的图象经过怎样的变换得到．(1)周期T ＝4π，振幅A ＝3，初相φ＝π6，由x 2＋π6＝k π＋π2(k ∈Z )，得x ＝2k π＋2π3(k ∈Z )即为对称轴． (2)列表：描点，连线，得到f (x )在一个周期内的图象．(3)①由y ＝sin x 的图象上各点向左平移π6个长度单位，得y ＝sin(x ＋π6)的图象．②由y ＝sin(x ＋π6)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得y ＝sin(x 2＋π6)的图象．③由y ＝sin(x 2＋π6)的图象上各点的纵坐标伸长为原来的3倍(横坐标不变)，得y ＝3sin(x 2＋π6)的图象．④由y ＝3sin(x 2＋π6)的图象上各点向上平移3个长度单位，得y ＝3sin(x 2＋π6)＋3的图象．8．(2017·天津卷)设函数f (x )＝2sin(ωx ＋φ)，x ∈R ，其中ω>0，|φ|<π.若f (5π8)＝2，f (11π8)＝0，且f (x )的最小正周期大于2π，则(A)A ．ω＝23，φ＝π12B ．ω＝23，φ＝－11π12C ．ω＝13，φ＝－11π24D ．ω＝13，φ＝7π24因为f (5π8)＝2，f (11π8)＝0，且f (x )的最小正周期大于2π，所以f (x )的最小正周期为4(118π－58π)＝3π， 所以ω＝2π3π＝23，所以f (x )＝2sin(23x ＋φ)．因为f (5π8)＝2，所以2sin(23×58π＋φ)＝2，得φ＝2k π＋π12，k ∈Z .又|φ|＜π，所以取k ＝0，得φ＝π12.9．函数y ＝cos(2x ＋φ)(－π≤φ<π)的图象向右平移π2个单位后，与函数y ＝sin(2x＋π3)的图象重合，则φ＝ 5π6.将y ＝cos(2x ＋φ)的图象向右平移π2个单位后，得到y ＝cos[2(x －π2)＋φ]＝cos(2x －π＋φ)＝sin(2x －π＋φ＋π2)＝sin(2x ＋φ－π2)，而它与函数y ＝sin(2x ＋π3)的图象重合，令2x ＋φ－π2＝2x ＋π3＋2k π(k ∈Z )，得φ＝5π6＋2k π(k ∈Z )．又－π≤φ<π，故φ＝5π6.10．设f (x )＝23sin(π－x )sin x －(sin x －cos x )2. (1)求f (x )的单调递增区间；(2)把y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再把得到的图象向左平移π3个单位，得到函数y ＝g (x )的图象，求g (π6)的值．(1)f (x )＝23sin(π－x )sin x －(sin x －cos x )2＝23sin 2x －(1－2sin x cos x ) ＝3(1－cos 2x )＋sin 2x －1 ＝sin 2x －3cos 2x ＋3－1 ＝2sin(2x －π3)＋3－1，由2k π－π2≤2x －π3≤2k π＋π2(k ∈Z )，得k π－π12≤x ≤k π＋5π12(k ∈Z )，所以f (x )的单调递增区间是[k π－π12，k π＋5π12](k ∈Z )(或(k π－π12，k π＋5π12)(k ∈Z ))．(2)由(1)知f (x )＝2sin(2x －π3)＋3－1，把y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y ＝2sin(x －π3)＋3－1的图象， 再把得到的图象向左平移π3个单位，得到y ＝2sin x ＋3－1的图象，即g (x )＝2sin x ＋3－1， 所以g (π6)＝2sin π6＋3－1＝ 3.正弦定理与余弦定理1．在△ABC 中，a 2＝b 2＋c 2＋bc ，则角A 等于(C) A ．60° B．45° C ．120° D．30°因为cos A ＝b 2＋c 2－a 22bc ＝－12，又因为0°<A <180°，所以A ＝120°.2．如图所示，正方形ABCD 的边长为1，延长BA 至E ，使AE ＝1，连接EC ，ED ，则sin ∠CED ＝(B)A.31010B.1010 C.510 D.515EB ＝EA ＋AB ＝2，EC ＝EB 2＋BC 2＝4＋1＝5，∠EDC ＝∠EDA ＋∠ADC ＝π4＋π2＝3π4.由正弦定理，得sin ∠CED sin ∠EDC ＝DC CE ＝15＝55，所以sin ∠CED ＝55sin ∠EDC ＝55sin 3π4＝1010. 3．(2018·全国卷Ⅱ)在△ABC 中，cos C 2＝55，BC ＝1，AC ＝5，则AB ＝(A)A ．4 2 B.30 C.29 D ．2 5因为cos C 2＝55，所以cos C ＝2cos 2C 2－1＝2×(55)2－1＝－35.在△ABC 中，由余弦定理，得AB 2＝AC 2＋BC 2－2AC ·BC ·cos C＝52＋12－2×5×1×(－35)＝32，所以AB ＝32＝4 2.4．(2016·全国卷Ⅲ)在△ABC 中，B ＝π4，BC 边上的高等于13BC ，则sin A ＝(D)A.310B.1010 C.55 D.31010如图，AD 为△ABC 中BC 边上的高．设BC ＝a ，由题意知AD ＝13BC ＝13a ，B ＝π4，易知BD ＝AD ＝13a ，DC ＝23a .在Rt △ABD 中，由勾股定理得，AB ＝13a 2＋13a 2＝23a . 同理，在Rt △ACD 中，AC ＝13a 2＋23a 2＝53a . 因为S △ABC ＝12AB ·AC ·sin∠BAC ＝12BC ·AD ，所以12×23a ×53a ·sin∠BAC ＝12a ·13a ，所以sin ∠BAC ＝310＝31010. 5．(2016·北京卷)在△ABC 中，∠A ＝2π3，a ＝3c ，则bc ＝ 1 .在△ABC 中，∠A ＝2π3，所以a 2＝b 2＋c 2－2bc cos 2π3，即a 2＝b 2＋c 2＋bc .因为a ＝3c ，所以3c 2＝b 2＋c 2＋bc ，所以b 2＋bc －2c 2＝0， 所以(b ＋2c )(b －c )＝0，所以b －c ＝0，所以b ＝c ，所以b c＝1.6．在△ABC 中，B ＝120°，AB ＝2，A 的角平分线AD ＝3，则AC ＝6 .如图，在△ABD 中，由正弦定理，得ADsin B＝ABsin ∠ADB，所以sin ∠ADB ＝22. 所以∠ADB ＝45°，所以∠BAD ＝180°－45°－120°＝15°. 所以∠BAC ＝30°，∠C ＝30°，所以BC ＝AB ＝2， 所以AC ＝ 6.7．在△ABC 中，∠A ＝3π4，AB ＝6，AC ＝32，点D 在BC 边上，AD ＝BD ，求AD 的长．设△ABC 的内角A ，B ，C 所对边的长分别是a ，b ，c ，由余弦定理得a 2＝b 2＋c 2－2bc cos A＝(32)2＋62－2×32×6×cos 3π4＝18＋36－(－36)＝90. 所以a ＝310. 又由正弦定理得sin B ＝b sin A a ＝3310＝1010， 由题设知0＜B ＜π4，所以cos B ＝1－sin 2B ＝1－110＝31010. 在△ABD 中，因为AD ＝BD ，所以∠ABD ＝∠BAD ， 所以∠ADB ＝π－2B ，故由正弦定理得AD ＝AB ·sin B π－2B ＝6sin B 2sin B cos B ＝3cos B＝10.8. △ABC 中，AB ＝1，BC ＝2，则角C 的范围是(A)A ．0<C ≤π6B ．0<C <π2C.π4<C <π2D.π6<C <π3设AC ＝x ，则1<x <3，cos C ＝4＋x 2－14x ＝3＋x 24x ＝34x ＋x 4≥234x ·x 4＝32，当且仅当x ＝3时，取“＝”． 故0<C ≤π6.9．设在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos A ＝35，cos B ＝513，b ＝3，则c ＝145.因为cos A ＝35，cos B ＝513，所以sin A ＝45，sin B ＝1213，所以sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝45×513＋35×1213＝5665. 因为b sin B ＝c sin C ，又b ＝3，所以c ＝b sin C sin B ＝145.10．(2018·天津卷)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知b sin A ＝a cos(B －π6)．(1)求角B 的大小；(2)设a ＝2，c ＝3，求b 和sin(2A －B )的值．(1)在△ABC 中，由正弦定理a sin A ＝bsin B ，可得b sin A ＝a sin B .又由b sin A ＝a cos(B －π6)，得a sin B ＝a cos(B －π6)，即sin B ＝cos(B －π6)，可得tan B ＝ 3.又因为B ∈(0，π)，所以B ＝π3.(2)在△ABC 中，由余弦定理及a ＝2，c ＝3，B ＝π3，得b 2＝a 2＋c 2－2ac cos B ＝7，故b ＝7.由b sin A ＝a cos(B －π6)，可得sin A ＝37.因为a ＜c ，所以cos A ＝27.因此sin 2A ＝2sin A cos A ＝437，cos 2A ＝2cos 2A －1＝17.所以sin(2A －B )＝sin 2A cos B －cos 2A sin B ＝437×12－17×32＝3314.正弦定理、余弦定理的综合应用1．在△ABC 中，若sin 2A ＋sin 2B <sin 2C ，则△ABC 一定是(A) A ．钝角三角形 B ．锐角三角形 C ．直角三角形D ．不确定2．在△ABC 中，两边的差为2，两边夹角的余弦值为35，且三角形面积为14，则这两边的长分别是(D)A ．3,5B ．4,6C ．6,8D ．5,7不妨设两边为b ，c (b >c )，则b －c ＝2，cos A ＝35，则sin A ＝45，所以S △ABC ＝12bc sin A ＝25bc ＝14，所以bc ＝35.所以b ＝7，c ＝5.3．如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75°，30°，此时气球的高是60 m ，则河流的宽度BC 等于(C)A ．240(3－1)mB ．180(2－1)mC ．120(3－1)mD ．30(3＋1)m如图，∠ACD ＝30°，∠ABD ＝75°，AD ＝60 m ，在Rt △ACD 中，CD ＝AD tan ∠ACD ＝60tan 30°＝60 3 m ，在Rt △ABD 中，BD ＝ADtan ∠ABD ＝60tan 75°＝602＋3＝60(2－3)m ，所以BC ＝CD －BD ＝603－60(2－3)＝120(3－1)m.4．(2016·山东卷)△ABC 中，角A ，B ，C 的对边分别是a ，b ，c .已知b ＝c ，a 2＝2b 2(1－sin A )，则A ＝(C)A.3π4B.π3C.π4D.π6因为b ＝c ，所以B ＝C .又由A ＋B ＋C ＝π得B ＝π2－A2.由正弦定理及a 2＝2b 2(1－sin A )得 sin 2A ＝2sin 2B (1－sin A )，即sin 2A ＝2sin 2(π2－A 2)(1－sin A )，即sin 2A ＝2cos 2A2(1－sin A )，即4sin 2A2cos 2A2＝2cos 2A2(1－sin A )，整理得cos 2A2(1－sin A －2sin 2A2)＝0，即cos 2A2(cos A －sin A )＝0.因为0<A <π，所以0<A 2<π2，所以cos A2≠0，所以cos A ＝sin A ．又0<A <π，所以A ＝π4.5．在相距2千米的A ，B 两点处测量目标C ，若∠CAB ＝75°，∠CBA ＝60°，则A ，C 两点间的距离是6 千米．在△ABC 中，∠ACB ＝180°－60°－75°＝45°.由正弦定理得AC sin 60°＝2sin 45°，解得AC ＝ 6.6．(2017·浙江卷)已知△ABC ，AB ＝AC ＝4，BC ＝2.点D 为AB 延长线上一点，BD ＝2，连接CD ，则△BDC 的面积是152，cos ∠BDC ＝ 104.依题意作出图形，如图所示， 则sin ∠DBC ＝sin ∠ABC .由题意知AB ＝AC ＝4，BC ＝BD ＝2， 则cos ∠ABC ＝14，sin ∠ABC ＝154.所以S △BDC ＝12BC ·BD ·sin∠DBC＝12×2×2×154＝152. 因为cos ∠DBC ＝－cos ∠ABC ＝－14，所以CD ＝BD 2＋BC 2－2BD ·BC ·cos ∠DBC ＝10. 由余弦定理，得cos ∠BDC ＝4＋10－42×2×10＝104.7.(2017·山东卷)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .已知b ＝3，AB →·AC →＝－6，S △ABC ＝3，求A 和a .因为AB →·AC →＝－6，所以bc cos A ＝－6.又S △ABC ＝3，所以bc sin A ＝6.。

第四章 三角函数、解三角形第一节 任意角和弧度制及任意角的三角函数一、基础知识1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)分类⎩⎪⎨⎪⎧按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋2k π，k ∈Z }． 终边相同的角不一定相等，但相等的角其终边一定相同．2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad. (2)公式：有关角度与弧度的两个注意点(1)角度与弧度的换算的关键是π＝180°，在同一个式子中，采用的度量制度必须一致，不可混用． (2)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度． 3．任意角的三角函数(1)定义：设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么sin α＝y ，cos α＝x ，tan α＝yx (x ≠0)． (2)几何表示：三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x 轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP ，OM ，AT 分别叫做角α的正弦线、余弦线和正切线．二、常用结论汇总——规律多一点(1)一个口诀三角函数值在各象限的符号：一全正、二正弦、三正切、四余弦． (2)三角函数定义的推广设点P (x ，y )是角α终边上任意一点且不与原点重合，r ＝|OP |，则sin α＝y r ，cos α＝x r ，tan α＝yx (x ≠0)．(3)象限角(4)轴线角考点一 象限角及终边相同的角[典例] (1)若角α是第二象限角，则α2是( )A ．第一象限角B ．第二象限角C ．第一或第三象限角D ．第二或第四象限角(2)终边在直线y ＝3x 上，且在[－2π，2π)内的角α的集合为________． [解析] (1)∵α是第二象限角， ∴π2＋2k π<α<π＋2k π，k ∈Z ， ∴π4＋k π<α2<π2＋k π，k ∈Z. 当k 为偶数时，α2是第一象限角；当k 为奇数时，α2是第三象限角．故选C.(2)如图，在坐标系中画出直线y ＝3x ，可以发现它与x 轴的夹角是π3，在[0,2π)内，终边在直线y ＝3x 上的角有两个：π3，4π3；在[－2π，0)内满足条件的角有两个：－2π3，－5π3，故满足条件的角α构成的集合为⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3. [答案] (1)C (2)⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3[题组训练]1．集合⎩⎨⎧⎭⎬⎫α⎪⎪k π≤α≤k π＋π4，k ∈Z 中的角所表示的范围(阴影部分)是( )解析：选B 当k ＝2n (n ∈Z )时，2n π≤α≤2n π＋π4(n ∈Z )，此时α的终边和0≤α≤π4的终边一样，当k ＝2n＋1(n ∈Z )时，2n π＋π≤α≤2n π＋π＋π4(n ∈Z )，此时α的终边和π≤α≤π＋π4的终边一样． 2．在－720°～0°范围内所有与45°终边相同的角为________． 解析：所有与45°终边相同的角可表示为： β＝45°＋k ×360°(k ∈Z )，则令－720°≤45°＋k ×360°<0°(k ∈Z )， 得－765°≤k ×360°<－45°(k ∈Z )， 解得－765360≤k <－45360(k ∈Z )，从而k ＝－2或k ＝－1， 代入得β＝－675°或β＝－315°. 答案：－675°或－315°考点二 三角函数的定义[典例] 已知角α的终边经过点P (－x ，－6)，且cos α＝－513，则1sin α＋1tan α＝________.[解析] ∵角α的终边经过点P (－x ，－6)，且cos α＝－513，∴cos α＝－xx 2＋36＝－513，解得x ＝52或x ＝－52(舍去)，∴P ⎝⎛⎭⎫－52，－6，∴sin α＝－1213， ∴tan α＝sin αcos α＝125，则1sin α＋1tan α＝－1312＋512＝－23.[答案] －23[解题技法]用定义法求三角函数值的2种类型及解题方法(1)已知角α终边上一点P 的坐标，则可先求出点P 到原点的距离r ，然后用三角函数的定义求解． (2)已知角α的终边所在的直线方程，则可先设出终边上一点的坐标，求出此点到原点的距离，然后用三角函数的定义来求解．[题组训练]1．已知角α的终边经过点(3，－4)，则sin α＋1cos α＝( )A ．－15B.3715C.3720D.1315解析：选D ∵角α的终边经过点(3，－4)，∴sin α＝－45，cos α＝35，∴sin α＋1cos α＝－45＋53＝1315.2．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( ) A ．－45B ．－35C ．35D ．45解析：选B 设P (t,2t )(t ≠0)为角θ终边上任意一点，则cos θ＝t 5|t |.当t >0时，cos θ＝55；当t <0时，cosθ＝－55.因此cos 2θ＝2cos 2θ－1＝25－1＝－35. 考点三 三角函数值符号的判定[典例] 若sin αtan α<0，且cos αtan α<0，则角α是( ) A ．第一象限角 B ．第二象限角 C ．第三象限角D ．第四象限角[解析] 由sin αtan α<0可知sin α，tan α异号， 则α为第二象限角或第三象限角．由cos αtan α<0可知cos α，tan α异号， 则α为第三象限角或第四象限角． 综上可知，α为第三象限角． [答案] C[解题技法] 三角函数值符号及角所在象限的判断三角函数在各个象限的符号与角的终边上的点的坐标密切相关．sin θ在一、二象限为正，cos θ在一、四象限为正，tan θ在一、三象限为正.学习时首先把取正值的象限记清楚，其余的象限就是负的，如sin θ在一、二象限为正，那么在三、四象限就是负的．值得一提的是：三角函数的正负有时还要考虑坐标轴上的角，如sin π2＝1>0，cos π＝－1<0.[题组训练]1．下列各选项中正确的是( ) A ．sin 300°>0 B ．cos(－305°)<0 C ．tan ⎝⎛⎭⎫－22π3>0 D ．sin 10<0解析：选D 300°＝360°－60°，则300°是第四象限角，故sin 300°<0；－305°＝－360°＋55°，则－305°是第一象限角，故cos(－305°)>0；－22π3＝－8π＋2π3，则－22π3是第二象限角，故tan ⎝⎛⎭⎫－22π3<0；3π<10<7π2，则10是第三象限角，故sin 10<0，故选D.2．已知点P (cos α，tan α)在第三象限，则角α的终边在( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限解析：选B 由题意得⎩⎪⎨⎪⎧ cos α<0，tan α<0⇒⎩⎪⎨⎪⎧cos α<0，sin α>0，所以角α的终边在第二象限．[课时跟踪检测]A 级1．已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为( ) A ．2 B ．4 C ．6D ．8解析：选C 设扇形的半径为r (r >0)，弧长为l ，则由扇形面积公式可得2＝12lr ＝12|α|r 2＝12×4×r 2，解得r＝1，l ＝|α|r ＝4，所以所求扇形的周长为2r ＋l ＝6.2．(2019·石家庄模拟)已知角α(0°≤α<360°)终边上一点的坐标为(sin 150°，cos 150°)，则α＝( ) A ．150°B ．135°C ．300°D ．60°解析：选C 由sin 150°＝12>0，cos 150°＝－32<0，可知角α终边上一点的坐标为⎝⎛⎭⎫12，－32，故该点在第四象限，由三角函数的定义得sin α＝－32，因为0°≤α<360°，所以角α为300°. 3．(2018·长春检测)若角α的顶点为坐标原点，始边在x 轴的非负半轴上，终边在直线y ＝－3x 上，则角α的取值集合是( )A.⎩⎨⎧⎭⎬⎫α⎪⎪α＝2k π－π3，k ∈Z B.⎩⎨⎧⎭⎬⎫α⎪⎪α＝2k π＋2π3，k ∈Z C.⎩⎨⎧⎭⎬⎫α⎪⎪ α＝k π－2π3，k ∈Z D.⎩⎨⎧⎭⎬⎫α⎪⎪α＝k π－π3，k ∈Z 解析：选D 当α的终边在射线y ＝－3x (x ≤0)上时，对应的角为2π3＋2k π，k ∈Z ，当α的终边在射线y＝－3x (x ≥0)上时，对应的角为－π3＋2k π，k ∈Z ，所以角α的取值集合是⎩⎨⎧⎭⎬⎫α⎪⎪α＝k π－π3，k ∈Z . 4．已知角α的终边经过点(3a －9，a ＋2)，且cos α≤0，sin α＞0，则实数a 的取值范围是( ) A ．(－2,3] B ．(－2,3) C ．[－2,3)D ．[－2,3]解析：选A 由cos α≤0，sin α＞0可知，角α的终边落在第二象限或y 轴的正半轴上，所以有⎩⎪⎨⎪⎧3a －9≤0，a ＋2＞0，解得－2＜a ≤3.5．在平面直角坐标系xOy 中，α为第二象限角，P (－3，y )为其终边上一点，且sin α＝2y4，则y 的值为( )A. 3 B ．－ 5 C. 5 D.3或5解析：选C 由题意知|OP |＝3＋y 2，则sin α＝y 3＋y 2＝2y4，解得y ＝0(舍去)或y ＝±5，因为α为第二象限角，所以y >0，则y ＝ 5.6．已知角α＝2k π－π5(k ∈Z )，若角θ与角α的终边相同，则y ＝sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|的值为( )A ．1B ．－1C ．3D ．－3解析：选B 由α＝2k π－π5(k ∈Z )及终边相同的概念知，角α的终边在第四象限，因为角θ与角α的终边相同，所以角θ是第四象限角，所以sin θ＜0，cos θ＞0，tan θ＜0.所以y ＝－1＋1－1＝－1.7．已知一个扇形的圆心角为3π4，面积为3π2，则此扇形的半径为________． 解析：设此扇形的半径为r (r >0)，由3π2＝12×3π4×r 2，得r ＝2.答案：28．(2019·江苏高邮模拟)在平面直角坐标系xOy 中，60°角终边上一点P 的坐标为(1，m )，则实数m 的值为________．解析：∵60°角终边上一点P 的坐标为(1，m )，∴tan 60°＝m1，∵tan 60°＝3，∴m ＝ 3.答案： 39．若α＝1 560°，角θ与α终边相同，且－360°＜θ＜360°，则θ＝________. 解析：因为α＝1 560°＝4×360°＋120°， 所以与α终边相同的角为360°×k ＋120°，k ∈Z ， 令k ＝－1或k ＝0，可得θ＝－240°或θ＝120°. 答案：120°或－240°10．在直角坐标系xOy 中，O 为坐标原点，A (3，1)，将点A 绕O 逆时针旋转90°到B 点，则B 点坐标为__________．解析：依题意知OA ＝OB ＝2，∠AOx ＝30°，∠BOx ＝120°， 设点B 坐标为(x ，y )，则x ＝2cos 120°＝－1，y ＝2sin 120°＝3，即B (－1，3)． 答案：(－1，3)11．已知1|sin α|＝－1sin α，且lg(cos α)有意义．(1)试判断角α所在的象限；(2)若角α的终边上一点M ⎝⎛⎭⎫35，m ，且|OM |＝1(O 为坐标原点)，求m 的值及sin α的值． 解：(1)由1|sin α|＝－1sin α，得sin α<0， 由lg(cos α)有意义，可知cos α>0， 所以α是第四象限角．(2)因为|OM |＝1，所以⎝⎛⎭⎫352＋m 2＝1，解得m ＝±45. 又因为α是第四象限角，所以m <0， 从而m ＝－45，sin α＝y r ＝m |OM |＝－451＝－45.12．已知α为第三象限角．(1)求角α2终边所在的象限；(2)试判断 tan α2sin α2cos α2的符号．解：(1)由2k π＋π＜α＜2k π＋3π2，k ∈Z ， 得k π＋π2＜α2＜k π＋3π4，k ∈Z ，当k 为偶数时，角α2终边在第二象限；当k 为奇数时，角α2终边在第四象限．故角α2终边在第二或第四象限．(2)当角α2在第二象限时，tan α2＜0，sin α2＞0, cos α2＜0，所以tan α2sin α2cos α2取正号；当角α2在第四象限时，tan α2＜0，sin α2＜0, cos α2＞0， 所以 tan α2sin α2cos α2也取正号．因此tan α2sin α2cos α2取正号．B 级1．若－3π4<α<－π2，从单位圆中的三角函数线观察sin α，cos α，tan α的大小是( )A ．sin α<tan α<cos αB ．cos α<sin α<tan αC ．sin α<cos α<tan αD ．tan α<sin α<cos αAT ，因为－3π4解析：选C 如图所示，作出角α的正弦线MP ，余弦线OM ，正切线<α<－π2，所以α终边位置在图中的阴影部分，观察可得AT >OM >MP ，故有sin α<cosα<tan α.2．已知点P (sin α－cos α，tan α)在第一象限，且α∈[0,2π]，则角α的取值范围是( ) A.⎝⎛⎭⎫π2，3π4∪⎝⎛⎭⎫π，5π4 B.⎝⎛⎭⎫π4，π2∪⎝⎛⎭⎫π，5π4 C.⎝⎛⎭⎫π2，3π4∪⎝⎛⎭⎫5π4，3π2D.⎝⎛⎭⎫π4，π2∪⎝⎛⎭⎫3π4，π解析：选B 因为点P 在第一象限，所以⎩⎪⎨⎪⎧ sin α－cos α>0，tan α>0，即⎩⎪⎨⎪⎧sin α>cos α，tan α>0.由tan α>0可知角α为第一或第三象限角，画出单位圆如图．又sin α>cos α，用正弦线、余弦线得满足条件的角α的终边在如图所示的阴影部分(不包括边界)，即角α的取值范围是⎝⎛⎭⎫π4，π2∪⎝⎛⎭⎫π，5π4.3．已知角θ的终边过点P (－4a,3a )(a ≠0)． (1)求sin θ＋cos θ的值；(2)试判断cos(sin θ)·sin(cos θ)的符号．解：(1)因为角θ的终边过点P (－4a,3a )(a ≠0)， 所以x ＝－4a ，y ＝3a ，r ＝5|a |，当a ＞0时，r ＝5a ，sin θ＋cos θ＝35－45＝－15；当a ＜0时，r ＝－5a ，sin θ＋cos θ＝－35＋45＝15.(2)当a ＞0时，sin θ＝35∈⎝⎛⎭⎫0，π2， cos θ＝－45∈⎝⎛⎭⎫－π2，0， 则cos(sin θ)·sin(cos θ)＝cos 35·sin ⎝⎛⎭⎫－45＜0；当a ＜0时，sin θ＝－35∈⎝⎛⎭⎫－π2，0， cos θ＝45∈⎝⎛⎭⎫0，π2， 则cos(sin θ)·sin(cos θ)＝cos ⎝⎛⎭⎫－35·sin 45＞0. 综上，当a ＞0时，cos(sin θ)·sin(cos θ)的符号为负； 当a ＜0时，cos(sin θ)·sin(cos θ)的符号为正．第二节 同角三角函数的基本关系与诱导公式一、基础知识1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1； (2)商数关系：tan α＝sin αcos α.平方关系对任意角都成立，而商数关系中α≠k π＋π2(k ∈Z)．2．诱导公式诱导公式可简记为：奇变偶不变，符号看象限.“奇”“偶”指的是“k ·π2＋α(k ∈Z )”中的k 是奇数还是偶数.“变”与“不变”是指函数的名称的变化，若k 是奇数，则正、余弦互变；若k 为偶数，则函数名称不变.“符号看象限”指的是在“k ·π2＋α(k ∈Z )”中，将α看成锐角时，“k ·π2＋α(k ∈Z )”的终边所在的象限.二、常用结论同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)； cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝⎛⎭⎫α≠π2＋k π，k ∈Z .考点一 三角函数的诱导公式[典例] (1)已知f (α)＝cos ⎝⎛⎭⎫π2＋αsin ⎝⎛⎭⎫3π2－αcos (－π－α)tan (π－α)，则f ⎝⎛⎭⎫－25π3的值为________． (2)已知cos ⎝⎛⎭⎫π6－α＝23，则sin ⎝⎛⎭⎫α－2π3＝________. [解析] (1)因为f (α)＝cos ⎝⎛⎭⎫π2＋αsin ⎝⎛⎭⎫3π2－αcos (－π－α)tan (π－α)＝－sin α(－cos α)(－cos α)⎝⎛⎭⎫－sin αcos α＝cos α， 所以f ⎝⎛⎭⎫－25π3＝cos ⎝⎛⎭⎫－25π3＝cos π3＝12. (2)sin ⎝⎛⎭⎫α－2π3＝－sin ⎝⎛⎭⎫2π3－α＝－sin ⎣⎡⎦⎤π－⎝⎛⎭⎫π3＋α＝－sin ⎝⎛⎭⎫π3＋α＝－sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π6－α＝－cos ⎝⎛⎭⎫π6－α＝－23. [答案] (1)12 (2)－23[题组训练]1.已知tan α＝12，且α∈⎝⎛⎭⎫π，3π2，则cos ⎝⎛⎭⎫α－π2＝________. 解析：法一：cos ⎝⎛⎭⎫α－π2＝sin α，由α∈⎝⎛⎭⎫π，3π2知α为第三象限角， 联立⎩⎪⎨⎪⎧tan α＝sin αcos α＝12，sin 2α＋cos 2α＝1，解得5sin 2α＝1，故sin α＝－55.法二：cos ⎝⎛⎭⎫α－π2＝sin α，由α∈⎝⎛⎭⎫π，3π2知α为第三象限角，由tan α＝12，可知点(－2，－1)为α终边上一点，由任意角的三角函数公式可得sin α＝－55. 答案：－552. sin(－1 200°)·cos 1 290°＋cos(－1 020°)·sin(－1 050°)＋tan 945°＝________.解析：原式＝sin(－3×360°－120°)cos(3×360°＋180°＋30°)＋cos(－3×360°＋60°) sin(－3×360°＋30°)＋tan(2×360°＋180°＋45°)＝sin 120°cos 30°＋cos 60°sin 30°＋tan 45°＝34＋14＋1＝2.答案：23.已知tan ⎝⎛⎭⎫π6－α＝33，则tan ⎝⎛⎭⎫5π6＋α＝________. 解析：tan ⎝⎛⎭⎫5π6＋α＝tan ⎝⎛⎭⎫π－π6＋α＝tan ⎣⎡⎦⎤π－⎝⎛⎭⎫π6－α＝－tan ⎝⎛⎭⎫π6－α＝－33. 答案：－33考点二 同角三角函数的基本关系及应用[典例] (1)若tan α＝2，则sin α＋cos αsin α－cos α＋cos 2α＝( )A.165 B ．－165C.85D ．－85(2)已知sin αcos α＝38，且π4<α<π2，则cos α－sin α的值为( )A.12 B ．±12C ．－14D ．－12[解析] (1)sin α＋cos αsin α－cos α＋cos 2α＝sin α＋cos αsin α－cos α＋cos 2αsin 2α＋cos 2α ＝tan α＋1tan α－1＋1tan 2α＋1，将tan α＝2代入上式，则原式＝165.(2)因为sin αcos α＝38，所以(cos α－sin α)2＝cos 2α－2sin αcos α＋sin 2α＝1－2sin αcos α＝1－2×38＝14，因为π4<α<π2，所以cos α<sin α，即cos α－sin α<0， 所以cos α－sin α＝－12.[答案] (1)A (2)D[题组训练]1．(2018·甘肃诊断)已知tan φ＝43，且角φ的终边落在第三象限，则cos φ＝( )A.45 B ．－45C.35D ．－35解析：选D 因为角φ的终边落在第三象限，所以cos φ<0，因为tan φ＝43，所以⎩⎪⎨⎪⎧sin 2φ＋cos 2φ＝1，sin φcos φ＝43，cos φ<0，解得cos φ＝－35.2．已知tan θ＝3，则sin 2θ＋sin θcos θ＝________. 解析：sin 2θ＋sin θcos θ＝sin 2θ＋sin θcos θsin 2θ＋cos 2θ＝tan 2θ＋tan θtan 2θ＋1＝32＋332＋1＝65.答案：653．已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α＝________.解析：由已知可得sin α＋3cos α＝5(3cos α－sin α)， 即sin α＝2cos α，所以tan α＝sin αcos α＝2， 从而sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝22－222＋1＝25.答案：254．已知－π<α<0，sin(π＋α)－cos α＝－15，则cos α－sin α的值为________．解析：由已知，得sin α＋cos α＝15，sin 2α＋2sin αcos α＋cos 2α＝125， 整理得2sin αcos α＝－2425.因为(cos α－sin α)2＝1－2sin αcos α＝4925，且－π<α<0，所以sin α<0，cos α>0， 所以cos α－sin α>0，故cos α－sin α＝75.答案：75[课时跟踪检测]A 级1．已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan x 的值为( ) A.34B ．－34C.43 D ．－43解析：选B 因为x ∈⎝⎛⎭⎫－π2，0，所以sin x ＝－1－cos 2x ＝－35，所以tan x ＝sin x cos x ＝－34. 2．(2019·淮南十校联考)已知sin ⎝⎛⎭⎫α－π3＝13，则cos ⎝⎛⎭⎫α＋π6的值为( ) A ．－13B.13C.223D ．－223解析：选A ∵sin ⎝⎛⎭⎫α－π3＝13，∴cos ⎝⎛⎭⎫α＋π6＝cos ⎣⎡⎦⎤π2＋⎝⎛⎭⎫α－π3＝－sin ⎝⎛⎭⎫α－π3＝－13. 3．计算：sin 11π6＋cos 10π3的值为( ) A ．－1 B ．1 C ．0D.12－32解析：选A 原式＝sin ⎝⎛⎭⎫2π－π6＋cos ⎝⎛⎭⎫3π＋π3 ＝－sin π6－cos π3＝－12－12＝－1.4．若sin (π－θ)＋cos (θ－2π)sin θ＋cos (π＋θ)＝12，则tan θ的值为( )A ．1B ．－1C ．3D ．－3解析：选D 因为sin (π－θ)＋cos (θ－2π)sin θ＋cos (π＋θ)＝sin θ＋cos θsin θ－cos θ＝12，所以2(sin θ＋cos θ)＝sin θ－cos θ， 所以sin θ＝－3cos θ，所以tan θ＝－3.5．(2018·大庆四地六校调研)若α是三角形的一个内角，且sin ⎝⎛⎭⎫π2＋α＋cos ⎝⎛⎭⎫3π2＋α＝15，则tan α的值为( ) A ．－43B ．－34C ．－43或－34D ．不存在解析：选A 由sin ⎝⎛⎭⎫π2＋α＋cos ⎝⎛⎭⎫3π2＋α＝15， 得cos α＋sin α＝15，∴2sin αcos α＝－2425<0.∵α∈(0，π)，∴sin α>0，cos α<0， ∴sin α－cos α＝1－2sin αcos α＝75，∴sin α＝45，cos α＝－35，∴tan α＝－43.6．在△ABC 中，3sin ⎝⎛⎭⎫π2－A ＝3sin(π－A )，且cos A ＝－3cos(π－B )，则△ABC 为( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等边三角形解析：选B 将3sin ⎝⎛⎭⎫π2－A ＝3sin(π－A )化为3cos A ＝3sin A ，则tan A ＝33，则A ＝π6，将cos A ＝－3cos(π－B )化为 cos π6＝3cos B ，则cos B ＝12，则B ＝π3，故△ABC 为直角三角形．7．化简：1－cos 22θcos 2θtan 2θ＝________.解析：1－cos 22θcos 2θtan 2θ＝sin 22θcos 2θ·sin 2θcos 2θ＝sin 2θ.答案：sin 2θ8．化简：cos ⎝⎛⎭⎫α－π2sin ⎝⎛⎭⎫5π2＋α·sin(α－π)·cos(2π－α)＝________. 解析：原式＝cos ⎝⎛⎭⎫π2－αsin ⎝⎛⎭⎫2π＋π2＋α·(－sin α)·cos α＝sin αsin ⎝⎛⎭⎫π2＋α·(－sin α)·cos α ＝sin αcos α·(－sin α)·cos α＝－sin 2α. 答案：－sin 2α9．sin 4π3·cos 5π6·tan ⎝⎛⎭⎫－4π3的值为________． 解析：原式＝sin ⎝⎛⎭⎫π＋π3·cos ⎝⎛⎭⎫π－π6·tan ⎝⎛⎭⎫－π－π3 ＝⎝⎛⎭⎫－sin π3·⎝⎛⎭⎫－cos π6·⎝⎛⎭⎫－tan π3 ＝⎝⎛⎭⎫－32×⎝⎛⎭⎫－32×(－3)＝－334.答案：－33410．(2019·武昌调研)若tan α＝cos α，则1sin α＋cos 4α＝________.解析：tan α＝cos α⇒sin αcos α＝cos α⇒sin α＝cos 2α，故1sin α＋cos 4α＝sin 2α＋cos 2αsin α＋cos 4α＝sin α＋cos 2αsin α＋cos 4α＝sin α＋sin αsin α＋sin 2α＝sin 2α＋sin α＋1＝sin 2α＋cos 2α＋1＝1＋1＝2.答案：211．已知α为第三象限角，f (α)＝sin ⎝⎛⎭⎫α－π2·cos ⎝⎛⎭⎫3π2＋α·tan (π－α)tan (－α－π)·sin (－α－π).(1)化简f (α)；(2)若cos ⎝⎛⎭⎫α－3π2＝15，求f (α)的值． 解：(1)f (α)＝sin ⎝⎛⎭⎫α－π2·cos ⎝⎛⎭⎫3π2＋α·tan (π－α)tan (－α－π)·sin (－α－π)＝(－cos α)·sin α·(－tan α)(－tan α)·sin α＝－cos α.(2)∵cos ⎝⎛⎭⎫α－3π2＝15， ∴－sin α＝15，从而sin α＝－15.又∵α为第三象限角，∴cos α＝－1－sin 2α＝－265，∴f (α)＝－cos α＝265.12．已知sin α＝255，求tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α的值．解：因为sin α＝255>0，所以α为第一或第二象限角．tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α＝tan α＋cos αsin α＝sin αcos α＋cos αsin α＝1sin αcos α.①当α为第一象限角时，cos α＝1－sin 2α＝55，原式＝1sin αcos α＝52.②当α为第二象限角时，cos α＝－1－sin 2α＝－55， 原式＝1sin αcos α＝－52.综合①②知，原式＝52或－52.B 级1．已知sin α＋cos α＝12，α∈(0，π)，则1－tan α1＋tan α＝( )A ．－7 B.7 C. 3D ．－ 3解析：选A 因为sin α＋cos α＝12，所以(sin α＋cos α)2＝1＋2sin αcos α＝14，所以sin αcos α＝－38，又因为α∈(0，π)，所以sin α>0，cos α<0，所以cos α－sin α<0，因为(cos α－sin α)2＝1－2sin αcos α＝1－2×⎝⎛⎭⎫－38＝74， 所以cos α－sin α＝－72， 所以1－tan α1＋tan α＝1－sin αcos α1＋sin αcos α＝cos α－sin αcos α＋sin α＝－7212＝－7.2．已知θ是第一象限角，若sin θ－2cos θ＝－25，则sin θ＋cos θ＝________.解析：∵sin θ－2cos θ＝－25，∴sin θ＝2cos θ－25，∴⎝⎛⎭⎫2cos θ－252＋cos 2θ＝1， ∴5cos 2θ－85cos θ－2125＝0，即⎝⎛⎭⎫cos θ－35⎝⎛⎭⎫5cos θ＋75＝0. 又∵θ为第一象限角，∴cos θ＝35，∴sin θ＝45，∴sin θ＋cos θ＝75.答案：753．已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根分别是sin θ和cos θ，θ∈(0,2π)，求： (1)sin 2θsin θ－cos θ＋cos θ1－tan θ的值； (2)m 的值；(3)方程的两根及此时θ的值． 解：(1)原式＝sin 2θsin θ－cos θ＋cos θ1－sin θcos θ＝sin 2θsin θ－cos θ＋cos 2θcos θ－sin θ ＝sin 2θ－cos 2θsin θ－cos θ＝sin θ＋cos θ. 由条件知sin θ＋cos θ＝3＋12， 故sin 2θsin θ－cos θ＋cos θ1－tan θ＝3＋12.(2)由已知，得sin θ＋cos θ＝3＋12，sin θcos θ＝m2， 因为1＋2sin θcos θ＝(sin θ＋cos θ)2， 所以1＋2×m 2＝⎝ ⎛⎭⎪⎫3＋122，解得m ＝32. (3)由⎩⎪⎨⎪⎧sin θ＋cos θ＝3＋12，sin θcos θ＝34，得⎩⎨⎧sin θ＝32，cos θ＝12或⎩⎨⎧sin θ＝12，cos θ＝32.又θ∈(0,2π)，故θ＝π3或θ＝π6.故当sin θ＝32，cos θ＝12时，θ＝π3； 当sin θ＝12，cos θ＝32时，θ＝π6.第三节 三角函数的图象与性质一、基础知识1．用五点法作正弦函数和余弦函数的简图 (1)“五点法”作图原理：在正弦函数y ＝sin x ，x ∈[0,2π]的图象上，五个关键点是：(0,0)，⎝⎛⎭⎫π2，1，(π，0)，⎝⎛⎭⎫3π2，－1，(2π，0)． 在余弦函数y ＝cos x ，x ∈[0,2π]的图象上，五个关键点是：(0,1)，⎝⎛⎭⎫π2，0，(π，－1)，⎝⎛⎭⎫3π2，0，(2π，1). 函数y ＝sin x ，x ∈[0，2π]，y ＝cos x ，x ∈[0，2π]的五个关键点的横坐标是零点和极值点(最值点). (2)五点法作图的三步骤：列表、描点、连线(注意光滑)． 2．正弦、余弦、正切函数的图象与性质三角函数性质的注意点(1)正、余弦函数一个完整的单调区间的长度是半个周期；y ＝tan x 无单调递减区间；y ＝tan x 在整个定义域内不单调．(2)要注意求函数y ＝A sin(ωx ＋φ)的单调区间时A 和ω的符号，尽量化成ω>0的形式，避免出现增减区间的混淆.二、常用结论1．对称与周期的关系正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻两个对称中心之间的距离是半个周期．2．与三角函数的奇偶性相关的结论(1)若y ＝A sin(ωx ＋φ)为偶函数，则有φ＝k π＋π2(k ∈Z )；若为奇函数，则有φ＝k π (k ∈Z )．(2)若y ＝A cos(ωx ＋φ)为偶函数，则有φ＝k π(k ∈Z )；若为奇函数，则有φ＝k π＋π2 (k ∈Z )．(3)若y ＝A tan(ωx ＋φ)为奇函数，则有φ＝k π(k ∈Z )．第一课时 三角函数的单调性 考点一 求三角函数的单调区间[典例] (2017·浙江高考)已知函数f (x )＝sin 2x －cos 2x －23sin x cos x (x ∈R )． (1)求f ⎝⎛⎭⎫2π3的值；(2)求f (x )的最小正周期及单调递增区间．[解] (1)由题意，f (x )＝－cos 2x －3sin 2x ＝－2⎝⎛⎭⎫32sin 2x ＋12cos 2x ＝－2sin ⎝⎛⎭⎫2x ＋π6， 故f ⎝⎛⎭⎫2π3＝－2sin ⎝⎛⎭⎫4π3＋π6＝－2sin 3π2＝2. (2)由(1)知f (x )＝－2sin ⎝⎛⎭⎫2x ＋π6. 则f (x )的最小正周期是π. 由正弦函数的性质，令π2＋2k π≤2x ＋π6≤3π2＋2k π(k ∈Z)， 解得π6＋k π≤x ≤2π3＋k π(k ∈Z)，所以f (x )的单调递增区间是⎣⎡⎦⎤π6＋k π，2π3＋k π(k ∈Z)．[题组训练]1．函数y ＝|tan x |在⎝⎛⎭⎫－π2，3π2上的单调递减区间为________． 解析：作出y ＝|tan x |的示意图如图，观察图象可知，y ＝|tan x |在⎝⎛⎭⎫－π2，3π2上的单调递减区间为⎝⎛⎦⎤－π2，0和⎝⎛⎦⎤π2，π. 答案：⎝⎛⎦⎤－π2，0，⎝⎛⎦⎤π2，π 2．函数g (x )＝－cos ⎝⎛⎭⎫－2x ＋π3⎝⎛⎭⎫x ∈⎣⎡⎦⎤－π2，π2的单调递增区间为________． 解析：g (x )＝－cos ⎝⎛⎭⎫－2x ＋π3＝－cos ⎝⎛⎭⎫2x －π3， 欲求函数g (x )的单调递增区间，只需求函数y ＝cos ⎝⎛⎭⎫2x －π3的单调递减区间．由2k π≤2x －π3≤2k π＋π(k ∈Z)，得k π＋π6≤x ≤k π＋2π3(k ∈Z)．故函数g (x )的单调递增区间为⎣⎡⎦⎤k π＋π6，k π＋2π3(k ∈Z)． 因为x ∈⎣⎡⎦⎤－π2，π2， 所以函数g (x )的单调递增区间为⎣⎡⎦⎤－π2，－π3，⎣⎡⎦⎤π6，π2. 答案：⎣⎡⎦⎤－π2，－π3，⎣⎡⎦⎤π6，π2 3．(2019·金华适应性考试)已知函数f (x )＝3cos 2x －2sin 2(x －α)，其中0<α<π2，且f ⎝⎛⎭⎫π2＝－3－1. (1)求α的值；(2)求f (x )的最小正周期和单调递减区间．解：(1)由已知得f ⎝⎛⎭⎫π2＝－3－2sin 2⎝⎛⎭⎫π2－α＝－3－2cos 2α＝－3－1，整理得cos 2α＝12. 因为0<α<π2，所以cos α＝22，α＝π4.(2)由(1)知，f (x )＝3cos 2x －2sin 2⎝⎛⎭⎫x －π4 ＝3cos 2x －1＋cos ⎝⎛⎭⎫2x －π2 ＝3cos 2x ＋sin 2x －1 ＝2sin ⎝⎛⎭⎫2x ＋π3－1. 易知函数f (x )的最小正周期T ＝π. 令t ＝2x ＋π3，则函数f (x )可转化为y ＝2sin t －1.显然函数y ＝2sin t －1与y ＝sin t 的单调性相同， 当函数y ＝sin t 单调递减时， 2k π＋π2≤t ≤2k π＋3π2(k ∈Z)，即2k π＋π2≤2x ＋π3≤2k π＋3π2(k ∈Z)，解得k π＋π12≤x ≤k π＋7π12(k ∈Z)．所以函数f (x )的单调递减区间为⎣⎡⎦⎤k π＋π12，k π＋7π12(k ∈Z)．考点二 求三角函数的值域(最值)[典例] (1)函数f (x )＝3sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤0，π2上的值域为( ) A.⎣⎡⎦⎤－32，32 B.⎣⎡⎦⎤－32，3 C.⎣⎡⎦⎤－332，332 D.⎣⎡⎦⎤－332，3(2)(2017·全国卷Ⅱ)函数f (x )＝sin 2x ＋3cos x －34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2的最大值是________． [解析] (1)当x ∈⎣⎡⎦⎤0，π2时， 2x －π6∈⎣⎡⎦⎤－π6，5π6，sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－12，1， 故3sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－32，3， 所以函数f (x )的值域为⎣⎡⎦⎤－32，3. (2)依题意，f (x )＝sin 2x ＋3cos x －34＝－cos 2x ＋3cos x ＋14＝－⎝⎛⎭⎫cos x －322＋1，因为x ∈⎣⎡⎦⎤0，π2，所以cos x ∈[0,1]， 因此当cos x ＝32时，f (x )max ＝1. [答案] (1)B (2)1[变透练清]1.(变条件)若本例(1)中函数f (x )的解析式变为：f (x )＝3cos ⎝⎛⎭⎫2x －π6，则f (x )在区间⎣⎡⎦⎤0，π2上的值域为________．解析：当x ∈⎣⎡⎦⎤0，π2时，2x －π6∈⎣⎡⎦⎤－π6，5π6， cos ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－32，1， 故f (x )＝3cos ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－332，3. 答案：⎣⎡⎦⎤－332，32.(变条件)若本例(2)中函数f (x )的解析式变为：函数f (x )＝sin x ＋cos x ＋sin x cos x ，则f (x )的最大值为________．解析：设t ＝sin x ＋cos x (－2≤t ≤2)，则sin x cos x ＝t 2－12，y ＝t ＋12t 2－12＝12(t ＋1)2－1，当t ＝2时，y ＝t ＋12t 2－12取最大值为2＋12.故f (x )的最大值为22＋12.答案：22＋123．已知函数f (x )＝sin ⎝⎛⎭⎫x ＋π6，其中x ∈⎣⎡⎦⎤－π3，a ，若f (x )的值域是⎣⎡⎦⎤－12，1，则实数a 的取值范围是________． 解析：由x ∈⎣⎡⎦⎤－π3，a ，知x ＋π6∈⎣⎡⎦⎤－π6，a ＋π6. ∵x ＋π6∈⎣⎡⎦⎤－π6，π2时，f (x )的值域是⎣⎡⎦⎤－12，1， ∴由函数的图象知π2≤a ＋π6≤7π6，∴π3≤a ≤π. 答案：⎣⎡⎦⎤π3，π考点三 根据三角函数单调性确定参数[典例] (1)(2018·全国卷Ⅱ)若f (x )＝cos x －sin x 在[－a ，a ]是减函数，则a 的最大值是( ) A.π4 B.π2C.3π4D ．π(2)若f (x )＝2sin ωx (ω>0)在区间⎣⎡⎦⎤－π2，2π3上是增函数，则ω的取值范围是________． [解析] (1)f (x )＝cos x －sin x ＝－2sin ⎝⎛⎭⎫x －π4， 当x ∈⎣⎡⎦⎤－π4，3π4，即x －π4∈⎣⎡⎦⎤－π2，π2时， y ＝sin ⎝⎛⎭⎫x －π4单调递增， 则f (x )＝－2sin ⎝⎛⎭⎫x －π4单调递减． ∵函数f (x )在[－a ，a ]是减函数， ∴[－a ，a ]⊆⎣⎡⎦⎤－π4，3π4，∴0<a ≤π4，∴a 的最大值是π4.(2)法一：因为x ∈⎣⎡⎦⎤－π2，2π3(ω>0)， 所以ωx ∈⎣⎡⎦⎤－πω2，2πω3， 因为f (x )＝2sin ωx 在⎣⎡⎦⎤－π2，2π3上是增函数， 所以⎩⎪⎨⎪⎧－πω2≥－π2，2πω3≤π2，ω>0，故0<ω≤34.法二：画出函数f (x )＝2sin ωx (ω>0)的图象如图所示．要使f (x )在⎣⎡⎦⎤－π2，2π3上是增函数， 需⎩⎨⎧－π2ω≤－π2，2π3≤π2ω，ω>0，即0<ω≤34.[答案] (1)A (2)⎝⎛⎦⎤0，34[解题技法]已知三角函数的单调区间求参数范围的3种方法(1)求出原函数的相应单调区间，由所给区间是所求某区间的子集，列不等式(组)求解．(2)由所给区间求出整体角的范围，由该范围是某相应正、余弦函数的某个单调区间的子集，列不等式(组)求解．(3)由所给区间的两个端点到其相应对称中心的距离不超过14周期列不等式(组)求解．[题组训练]1．若函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，且|φ|<π2在区间⎣⎡⎦⎤π6，2π3上是单调递减函数，且函数值从1减少到－1，则f ⎝⎛⎭⎫π4＝________.解析：由题意知T 2＝2π3－π6＝π2，故T ＝π，所以ω＝2πT＝2，又因为f ⎝⎛⎭⎫π6＝1，所以sin ⎝⎛⎭⎫π3＋φ＝1. 因为|φ|<π2，所以φ＝π6，即f (x )＝sin ⎝⎛⎭⎫2x ＋π6. 故f ⎝⎛⎭⎫π4＝sin ⎝⎛⎭⎫π2＋π6＝cos π6＝32. 答案：322．（2019·贵阳检测）已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4(ω>0)在⎝⎛⎭⎫π2，π上单调递减，则ω的取值范围是________． 解析：由π2<x <π，得π2ω＋π4<ωx ＋π4<πω＋π4，由题意知⎝⎛⎭⎫π2ω＋π4，πω＋π4⊆⎣⎡⎦⎤π2，3π2， 所以⎩⎨⎧π2ω＋π4≥π2，πω＋π4≤3π2，解得12≤ω≤54.答案：⎣⎡⎦⎤12，54[课时跟踪检测]A 级1．函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2－π12，k π2＋5π12(k ∈Z )B.⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z )C.⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z ) D.⎝⎛⎭⎫k π＋π6，k π＋2π3(k ∈Z ) 解析：选B 由k π－π2＜2x －π3＜k π＋π2(k ∈Z)，得k π2－π12＜x ＜k π2＋5π12(k ∈Z)，所以函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z)．2．y ＝|cos x |的一个单调递增区间是( ) A.⎣⎡⎦⎤－π2，π2 B ．[0，π] C.⎣⎡⎦⎤π，3π2 D.⎣⎡⎦⎤3π2，2π解析：选D 将y ＝cos x 的图象位于x 轴下方的部分关于x 轴对称向上翻折，x 轴上方(或x 轴上)的部分不变，即得y ＝|cos x |的图象(如图)．故选D.3．已知函数y ＝2cos x 的定义域为⎣⎡⎦⎤π3，π，值域为[a ，b ]，则b －a 的值是( ) A ．2 B ．3 C.3＋2D ．2－ 3解析：选B 因为x ∈⎣⎡⎦⎤π3，π，所以cos x ∈⎣⎡⎦⎤－1，12，故y ＝2cos x 的值域为[－2,1]，所以b －a ＝3. 4．(2019·西安八校联考)已知函数f (x )＝cos(x ＋θ)(0<θ<π)在x ＝π3时取得最小值，则f (x )在[0，π]上的单调递增区间是( )A.⎣⎡⎦⎤π3，πB.⎣⎡⎦⎤π3，2π3C.⎣⎡⎦⎤0，2π3D.⎣⎡⎦⎤2π3，π解析：选A 因为0<θ<π，所以π3<π3＋θ<4π3，又因为f (x )＝cos(x ＋θ)在x ＝π3时取得最小值，所以π3＋θ＝π，θ＝2π3，所以f (x )＝cos ⎝⎛⎭⎫x ＋2π3.由0≤x ≤π，得2π3≤x ＋2π3≤5π3.由π≤x ＋2π3≤5π3，得π3≤x ≤π，所以f (x )在[0，π]上的单调递增区间是⎣⎡⎦⎤π3，π.5．(2018·北京东城质检)函数f (x )＝sin 2x ＋3sin x cos x 在区间⎣⎡⎦⎤π4，π2上的最小值为( ) A ．1 B.1－32C.32D ．1－ 3解析：选A 函数f (x )＝sin 2x ＋3sin x cos x ＝12－12cos 2x ＋32sin 2x ＝sin ⎝⎛⎭⎫2x －π6＋12. ∵x ∈⎣⎡⎦⎤π4，π2，∴2x －π6∈⎣⎡⎦⎤π3，5π6. 当2x －π6＝5π6时，函数f (x )取得最小值为1.6．(2019·广西五市联考)若函数f (x )＝2sin ωx (0<ω<1)在区间⎣⎡⎦⎤0，π3上的最大值为1，则ω＝( ) A.14 B.13C.12D.32解析：选C 因为0<ω<1,0≤x ≤π3，所以0≤ωx <π3，所以f (x )在区间⎣⎡⎦⎤0，π3上单调递增，则f (x )max ＝f ⎝⎛⎭⎫π3＝2sinωπ3＝1，即sin ωπ3＝12.又因为0≤ωx <π3，所以ωπ3＝π6，解得ω＝12. 7．函数y ＝sin x －cos x 的定义域为________．解析：要使函数有意义，需sin x －cos x ≥0，即sin x ≥cos x ， 由函数的图象得2k π＋π4≤x ≤2k π＋5π4(k ∈Z)，故原函数的定义域为⎣⎡⎦⎤2k π＋π4，2k π＋5π4(k ∈Z)． 答案：⎣⎡⎦⎤2k π＋π4，2k π＋5π4(k ∈Z ) 8．函数f (x )＝cos 2x ＋6cos ⎝⎛⎭⎫π2－x 的最大值为________．解析：因为f (x )＝cos 2x ＋6cos ⎝⎛⎭⎫π2－x ＝1－2sin 2x ＋6sin x ＝－2⎝⎛⎭⎫sin x －322＋112，而sin x ∈[－1,1]，所以当sin x ＝1时，f (x )取最大值5.答案：59．函数f (x )＝2sin ⎝⎛⎭⎫π6x －π3(0≤x ≤9)的最大值与最小值之和为________． 解析：因为0≤x ≤9，所以0≤π6x ≤3π2，即－π3≤π6x －π3≤7π6，所以－32≤sin ⎝⎛⎭⎫π6x －π3≤1， 故f (x )的最大值为2，最小值为－3，它们之和为2－ 3. 答案：2－ 310．若函数f (x )＝sin ωx (ω>0)在区间⎣⎡⎦⎤0，π3上单调递增，在区间⎣⎡⎦⎤π3，π2上单调递减，则ω＝________. 解析：法一：由于函数f (x )＝sin ωx (ω>0)的图象经过坐标原点，由已知并结合正弦函数 的图象可知，π3为函数f (x )的14周期，故2πω＝4π3，解得ω＝32.法二：由题意，得f (x )max ＝f ⎝⎛⎭⎫π3＝sin π3ω＝1. 由已知并结合正弦函数图象可知，π3ω＝π2，解得ω＝32.答案：3211．已知函数f (x )＝2sin ⎝⎛⎭⎫2x ＋π4. (1)求函数f (x )的单调递增区间；(2)当x ∈⎣⎡⎦⎤π4，3π4时，求函数f (x )的最大值和最小值． 解：(1)令2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，则k π－3π8≤x ≤k π＋π8，k ∈Z.故函数f (x )的单调递增区间为⎣⎡⎦⎤k π－3π8，k π＋π8，k ∈Z. (2)因为当x ∈⎣⎡⎦⎤π4，3π4时，3π4≤2x ＋π4≤7π4， 所以－1≤sin ⎝⎛⎭⎫2x ＋π4≤22，所以－2≤f (x )≤1， 所以当x ∈⎣⎡⎦⎤π4，3π4时，函数f (x )的最大值为1，最小值为－ 2. 12．已知函数f (x )＝12sin 2x －32cos 2x －32.(1)求函数f (x )的最小正周期和最大值；(2)讨论函数f (x )在⎣⎡⎦⎤π6，2π3上的单调性．解：(1)因为函数f (x )＝12sin 2x －32cos 2x －32＝sin ⎝⎛⎭⎫2x －π3－32， 所以函数f (x )的最小正周期为π，最大值为2－32.(2)当x ∈⎣⎡⎦⎤π6，2π3时，0≤2x －π3≤π， 从而当0≤2x －π3≤π2，即π6≤x ≤5π12时，f (x )单调递增；当π2≤2x －π3≤π，即5π12≤x ≤2π3时，f (x )单调递减． 综上可知，f (x )在⎣⎡⎦⎤π6，5π12上单调递增，在⎣⎡⎦⎤5π12，2π3上单调递减．B 级1．已知函数f (x )＝2sin ⎝⎛⎭⎫x ＋7π3，设a ＝f ⎝⎛⎭⎫π7，b ＝f ⎝⎛⎭⎫π6，c ＝f ⎝⎛⎭⎫π3，则a ，b ，c 的大小关系是________(用“<”表示)．解析：函数f (x )＝2sin ⎝⎛⎭⎫x ＋π3＋2π＝2sin ⎝⎛⎭⎫x ＋π3， a ＝f ⎝⎛⎭⎫π7＝2sin 10π21， b ＝f ⎝⎛⎭⎫π6＝2sin π2， c ＝f ⎝⎛⎭⎫π3＝2sin 2π3＝2sin π3， 因为y ＝sin x 在⎣⎡⎦⎤0，π2上单调递增，且π3<10π21<π2， 所以sin π3<sin 10π21<sin π2，即c <a <b . 答案：c <a <b2．(2018·四川双流中学模拟)已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4(ω>0)，f ⎝⎛⎭⎫π6＝f ⎝⎛⎭⎫π3，且f (x )在⎝⎛⎭⎫π2，π上单调递减，则ω＝________.解析：由f ⎝⎛⎭⎫π6＝f ⎝⎛⎭⎫π3，可知函数f (x ) 的图象关于直线x ＝π4对称， ∴π4ω＋π4＝π2＋k π，k ∈Z ， ∴ω＝1＋4k ，k ∈Z ，又∵f (x )在⎝⎛⎭⎫π2，π上单调递减， ∴T 2≥π－π2＝π2，T ≥π， ∴2πω≥π，∴ω≤2， 又∵ω＝1＋4k ，k ∈Z ，∴当k ＝0时，ω＝1. 答案：13．已知函数f (x )＝2a sin ⎝⎛⎭⎫x ＋π4＋a ＋b . (1)若a ＝－1，求函数f (x )的单调递增区间；(2)若x ∈[0，π]，函数f (x )的值域是[5,8]，求a ，b 的值． 解：(1)当a ＝－1时，f (x )＝－2sin ⎝⎛⎭⎫x ＋π4＋b －1， 由2k π＋π2≤x ＋π4≤2k π＋3π2(k ∈Z)，得2k π＋π4≤x ≤2k π＋5π4(k ∈Z)，所以f (x )的单调递增区间为⎣⎡⎦⎤2k π＋π4，2k π＋5π4(k ∈Z)． (2)因为0≤x ≤π，所以π4≤x ＋π4≤5π4，所以－22≤sin ⎝⎛⎭⎫x ＋π4≤1，依题意知a ≠0. ①当a >0时，有{ 2a ＋a ＋b ＝8，b ＝5， 所以a ＝32－3，b ＝5. ②当a <0时，有{ b ＝8，2a ＋a ＋b ＝5，所以a ＝3－32，b ＝8.综上所述，a ＝32－3，b ＝5或a ＝3－32，b ＝8.第二课时 三角函数的周期性、奇偶性及对称性考点一 三角函数的周期性[典例] (1)(2018·全国卷Ⅲ)函数f (x )＝tan x1＋tan 2x的最小正周期为( )A.π4 B.π2C ．πD ．2π(2)若函数f (x )＝2tan ⎝⎛⎭⎫kx ＋π3的最小正周期T 满足1<T <2，则正整数k 的值为________． [解析] (1)由已知得f (x )＝tan x 1＋tan 2x ＝sin x cos x 1＋⎝⎛⎭⎫sin x cos x 2＝sin xcos x cos 2x ＋sin 2x cos 2x ＝sin x cos x ＝12sin 2x ，所以f (x )的最小正周期为T ＝2π2＝π.(2)由题意知1<πk <2，即π2<k <π.又因为k ∈N *，所以k ＝2或k ＝3. [答案] (1)C (2)2或3[解题技法]1．三角函数最小正周期的求解方法 (1)定义法；(2)公式法：函数y ＝A sin(ωx ＋φ)(y ＝A cos(ωx ＋φ))的最小正周期T ＝2π|ω|，函数y ＝A tan(ωx ＋φ)的最小正周期T ＝π|ω|；(3)图象法：求含有绝对值符号的三角函数的周期时可画出函数的图象，通过观察图象得出周期． 2．有关周期的2个结论(1)函数y ＝|A sin(ωx ＋φ)|，y ＝|A cos(ωx ＋φ)|，y ＝|A tan(ωx ＋φ)|的周期均为T ＝π|ω|.(2)函数y ＝|A sin(ωx ＋φ)＋b |(b ≠0)，y ＝|A cos(ωx ＋φ)＋b |(b ≠0)的周期均为T ＝2π|ω|.[题组训练]1．在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝⎛⎭⎫2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③解析：选A 因为y ＝cos|2x |＝cos 2x ， 所以该函数的周期为2π2＝π；由函数y ＝|cos x |的图象易知其周期为π；函数y ＝cos ⎝⎛⎭⎫2x ＋π6的周期为2π2＝π； 函数y ＝tan ⎝⎛⎭⎫2x －π4的周期为π2，故最小正周期为π的函数是①②③. 2．若x ＝π8是函数f (x )＝2sin ⎝⎛⎭⎫ωx －π4，x ∈R 的一个零点，且0<ω<10，则函数f (x )的最小正周期为________． 解析：依题意知，f ⎝⎛⎭⎫π8＝2sin ⎝⎛⎭⎫ωπ8－π4＝0， 即ωπ8－π4＝k π，k ∈Z ，整理得ω＝8k ＋2，k ∈Z. 又因为0<ω<10，所以0<8k ＋2<10，得－14<k <1，而k ∈Z ，所以k ＝0，ω＝2，所以f (x )＝2sin ⎝⎛⎭⎫2x －π4，f (x )的最小正周期为π. 答案：π考点二 三角函数的奇偶性[典例] 函数f (x )＝3sin ⎝⎛⎭⎫2x －π3＋φ，φ∈(0，π)满足f (|x |)＝f (x )，则φ的值为( ) A.π6 B.π3C.5π6D.2π3[解析] 因为f (|x |)＝f (x )，所以函数f (x )＝3sin ⎝⎛⎭⎫2x －π3＋φ是偶函数， 所以－π3＋φ＝k π＋π2，k ∈Z ，所以φ＝k π＋5π6，k ∈Z ，又因为φ∈(0，π)，所以φ＝5π6. [答案] C[解题技法] 判断三角函数奇偶性的方法三角函数中奇函数一般可化为y ＝A sin ωx 或y ＝A tan ωx 的形式，而偶函数一般可化为y ＝A cos ωx ＋b 的形式．[题组训练]1．(2018·日照一中模拟)下列函数中，周期为π，且在⎣⎡⎦⎤π4，π2上单调递增的奇函数是( ) A ．y ＝sin ⎝⎛⎭⎫2x ＋3π2 B ．y ＝cos ⎝⎛⎭⎫2x －π2 C ．y ＝cos ⎝⎛⎭⎫2x ＋π2 D ．y ＝sin ⎝⎛⎭⎫π2－x解析：选C y ＝sin ⎝⎛⎭⎫2x ＋3π2＝－cos 2x 为偶函数，排除A ；y ＝cos ⎝⎛⎭⎫2x －π2＝sin 2x 在⎣⎡⎦⎤π4，π2上为减函数，排除B ；y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x 为奇函数，在⎣⎡⎦⎤π4，π2上单调递增，且周期为π，符合题意；y ＝sin ⎝⎛⎭⎫π2－x ＝cos x 为偶函数，排除D.故选C.2．若函数f (x )＝3cos(3x －θ)－sin(3x －θ)是奇函数，则tan θ等于________． 解析：f (x )＝3cos(3x －θ)－sin(3x －θ) ＝2sin ⎝⎛⎭⎫π3－3x ＋θ ＝－2sin ⎝⎛⎭⎫3x －π3－θ， 因为函数f (x )为奇函数， 所以－π3－θ＝k π，k ∈Z ，即θ＝－k π－π3，k ∈Z ，故tan θ＝tan ⎝⎛⎭⎫－k π－π3＝－ 3. 答案：－ 3考点三 三角函数的对称性[典例] (1)已知函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋π6(ω>0)的最小正周期为4π，则该函数的图象( ) A ．关于点⎝⎛⎭⎫π3，0对称 B ．关于点⎝⎛⎭⎫5π3，0对称 C ．关于直线x ＝π3对称D ．关于直线x ＝5π3对称(2)(2018·江苏高考)已知函数y ＝sin(2x ＋φ)⎝⎛⎭⎫－π2<φ<π2的图象关于直线x ＝π3对称，则φ的值为________．。

第四章 三角函数、解三角形 第一节 弧度制及任意角的三角函数1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)分类⎩⎪⎨⎪⎧按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋k ·360°，k ∈Z}．2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad. (2)公式3.任意角的三角函数[小题体验]1．(教材习题改编)将－11π4表示成θ＋2k π(k ∈Z)的形式，则使|θ|最小的θ值为________．解析：∵－11π4＝－3π4＋(－2π)，∴θ＝－3π4.答案：－3π42．(教材习题改编)如图，用弧度表示顶点在原点，始边重合于x 轴的非负半轴，终边落在阴影部分内的角的集合(不包括边界)为________． 解析：因为75°＝5π12，330°＝11π6，故集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪11π6＋2k π<α<5π12＋2π＋2k π，k ∈Z ， 即⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π－π6<α<2k π＋5π12，k ∈Z. 答案：⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π－π6<α<2k π＋5π12，k ∈Z 3．(教材习题改编)若角θ同时满足sin θ<0且tan θ<0，则角θ的终边一定落在第________象限．解析：由sin θ<0，可知θ的终边可能位于第三或第四象限，也可能与y 轴的非正半轴重合．由tan θ<0，可知θ的终边可能位于第二象限或第四象限，所以θ的终边只能位于第四象限．答案：四4．已知半径为120 mm 的圆上，有一条弧的长是144 mm ，则该弧所对的圆心角的弧度数为________．答案：1.21．注意易混概念的区别：象限角、锐角、小于90°的角是概念不同的三类角．第一类是象限角，第二、第三类是区间角．2．角度制与弧度制可利用180°＝π rad 进行互化，在同一个式子中，采用的度量制度必须一致，不可混用．3．已知三角函数值的符号确定角的终边位置不要遗漏终边在坐标轴上的情况． 4．三角函数的定义中，当P (x ，y )是单位圆上的点时有sin α＝y ，cos α＝x ，tan α＝y x ，但若不是单位圆时，如圆的半径为r ，则sin α＝y r ，cos α ＝x r ，tan α＝y x.[小题纠偏]1．下列命题正确的是________．①小于90°的角都是锐角；②第一象限的角都是锐角；③终边相同的角一定相等；④－950°12′是第二象限的角．答案：④2．已知角θ的终边经过点P (－3，m )(m ≠0)且sin θ＝24m ，则cos θ＝________，tan θ＝________.解析：由题意，得r ＝3＋m 2，∴m3＋m2＝24m . ∵m ≠0，∴m ＝±5，故角θ是第二或第三象限角．当m ＝5时，r ＝22，点P 的坐标为(－3，5)，角θ是第二象限角，∴cos θ＝x r ＝－322＝－64，tan θ＝y x ＝5－3＝－153；当m ＝－5时，r ＝22，点P 的坐标为(－3，－5)，角θ是第三象限角，∴cos θ＝x r ＝－322＝－64，tan θ＝y x ＝－5－3＝153.答案：－64 ±1533．若α是第一象限角，则α3是第________象限角． 解析：∵α是第一象限角，∴k ·360°<α<k ·360°＋90°，k ∈Z ，∴k 3·360°<α3<k3·360°＋30°，k ∈Z. 当k ＝3n 时，有n ·360°<α3<n ·360°＋30°，k ∈Z ，∴α3为第一象限角． 当k ＝3n ＋1时，有n ·360°＋120°<α3<n ·360°＋150°，k ∈Z ，∴α3为第二象限角． 当k ＝3n ＋2时，有n ·360°＋240°<α3<n ·360°＋270°，k ∈Z ，∴α3为第三象限角． 综上可知，α3为第一、二、三象限角．答案：一、二、三考点一 角的集合表示及象限角的判定基础送分型考点——自主练透[题组练透]1．给出下列四个命题：①－3π4是第二象限角；②4π3是第三角限角；③－400°是第四象限角；④－315°是第一象限角．其中正确的命题有________(填序号)．解析：－3π4是第三象限角，故①错误；4π3＝π＋π3，从而4π3是第三象限角，故②正确；－400°＝－360°－40°，从而③正确； －315°＝－360°＋45°，从而④正确． 答案：②③④2．(易错题)若角α是第二象限角，则α2是第________象限角．解析：∵α是第二象限角， ∴π2＋2k π＜α＜π＋2k π，k ∈Z ， ∴π4＋k π＜α2＜π2＋k π，k ∈Z. 当k 为偶数时，α2是第一象限角；当k 为奇数时，α2是第三象限角．答案：一、三3．若角α与8π5终边相同，则在[0,2π]内终边与α4角终边相同的角是________．解析：由题意，得α＝8π5＋2k π(k ∈Z)，α4＝2π5＋k π2(k ∈Z)．又α4∈[0,2π]，所以k可取的所有值为0,1,2,3，故α4可取的所有值为2π5，9π10，7π5，19π10.答案：2π5，9π10，7π5，19π104．在－720°～0°范围内所有与45°终边相同的角为________． 解析：所有与45°有相同终边的角可表示为：β＝45°＋k ×360°(k ∈Z)，则令－720°≤45°＋k ×360°<0°， 得－765°≤k ×360°<－45°，解得－765360≤k <－45360，从而k ＝－2或k ＝－1，代入得β＝－675°或β＝－315°. 答案：－675°或－315°[谨记通法]1．终边在某直线上角的求法4步骤(1)数形结合，在平面直角坐标系中画出该直线； (2)按逆时针方向写出[0,2π)内的角；(3)再由终边相同角的表示方法写出满足条件角的集合； (4)求并集化简集合．2．确定k α，αk(k ∈N *)的终边位置3步骤(1)用终边相同角的形式表示出角α的范围； (2)再写出k α或αk的范围；(3)然后根据k 的可能取值讨论确定k α或αk的终边所在位置，如“题组练透”第2题易错．考点二 扇形的弧长及面积公式 基础送分型考点——自主练透[题组练透]1．已知扇形的周长是6，面积是2，则扇形的圆心角的弧度数是________． 解析：设此扇形的半径为r ，弧长为l ， 则⎩⎪⎨⎪⎧2r ＋l ＝6，12rl ＝2，解得⎩⎪⎨⎪⎧r ＝1，l ＝4或⎩⎪⎨⎪⎧r ＝2，l ＝2.从而α＝l r ＝41＝4或α＝l r ＝22＝1.答案：4或12．(易错题)若扇形的圆心角是α＝120°，弦长AB ＝12 cm ，则弧长l ＝________cm.解析：设扇形的半径为r cm ，如图． 由sin 60°＝6r，得r ＝4 3 cm ，∴l ＝|α|·r ＝2π3×43＝833π cm.答案：833π3．已知扇形周长为40，当它的半径和圆心角分别取何值时，扇形的面积最大？ 解：设圆心角是θ，半径是r ， 则2r ＋r θ＝40. 又S ＝12θr 2＝12r (40－2r )＝r (20－r )＝－(r －10)2＋100≤100. 当且仅当r ＝10时，S max ＝100， 此时2×10＋10θ＝40，θ＝2.所以当r ＝10，θ＝2时，扇形的面积最大．[谨记通法]弧度制下有关弧长、扇形面积问题的解题策略(1)明确弧度制下弧长公式l ＝αr ，扇形的面积公式是S ＝12lr ＝12αr 2(其中l 是扇形的弧长，α是扇形的圆心角)．(2)求扇形面积的关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量，如“题组练透”第2题．考点三 三角函数的定义常考常新型考点——多角探明[命题分析]任意角的三角函数(正弦、余弦、正切)的定义属于理解内容．在高考中多以填空题的形式出现．常见的命题角度有： (1)三角函数值的符号判定；(2)由角的终边上一点的P 的坐标求三角函数值； (3)由三角函数的定义求参数值．[题点全练]角度一： 三角函数值的符号判定 1．若sin αtan α＜0，且cos αtan α＜0，则角α是第________象限角． 解析：由sin αtan α＜0可知sin α，tan α异号， 则α为第二或第三象限角．由cos αtan α＜0可知cos α，tan α异号， 则α为第三或第四象限角．综上可知，α为第三象限角． 答案：三角度二：由角的终边上一点P 的坐标求三角函数值2．如图所示，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ，点A 的纵坐标为45，则cos α＝________.解析：因为A 点纵坐标y A ＝45，且A 点在第二象限，又因为圆O 为单位圆，所以A 点横坐标x A ＝－35，由三角函数的定义可得cos α＝－35.答案：－353．(2016·苏州调研)已知角α的终边上一点P (－3，m )(m ≠0)，且sin α＝2m 4，则m ＝________.解析：由题设知x ＝－3，y ＝m ，∴r 2＝|OP |2＝(－3)2＋m 2(O 为原点)，r ＝3＋m 2. ∴sin α＝m r＝2m 4＝m 22， ∴r ＝3＋m 2＝22， 即3＋m 2＝8，解得m ＝± 5. 答案：± 5角度三：由三角函数的定义求参数值4．已知角α的终边经过点P (x ，－6)，且tan α＝－35，则x 的值为________．解析：由三角函数的定义知tan α＝－6x ，于是－6x ＝－35，解得x ＝10.答案：105．已知角α的终边经过点(3a －9，a ＋2)，且cos α≤0，sin α>0，则实数a 的取值范围是________．解析：∵cos α≤0，sin α>0，∴角α的终边落在第二象限或y 轴的正半轴上．∴⎩⎪⎨⎪⎧3a －9≤0，a ＋2>0，∴－2<a ≤3.答案：(－2,3][方法归纳]应用三角函数定义的3种求法(1)已知角α终边上一点P 的坐标，可求角α的三角函数值．先求P 到原点的距离，再用三角函数的定义求解．(2)已知角α的某三角函数值，可求角α终边上一点P 的坐标中的参数值，可根据定义中的两个量列方程求参数值．(3)已知角α的终边所在的直线方程或角α的大小，根据三角函数的定义可求角α终边上某特定点的坐标.一抓基础，多练小题做到眼疾手快1．若一扇形的圆心角为72°，半径为20 cm ，则扇形的面积为________cm 2. 解析：∵72°＝2π5，∴S 扇形＝12αr 2＝12×2π5×202＝80π(cm 2)．答案：80π2．已知点P (tan α，cos α)在第三象限，则角α的终边在第________象限．解析：因为点P 在第三象限，所以⎩⎪⎨⎪⎧tan α＜0，cos α＜0，所以角α的终边在第二象限．答案：二3．在与2 010°终边相同的角中，绝对值最小的角的弧度数为________． 解析：∵2 010°＝67π6＝12π－5π6，∴与2 010°终边相同的角中绝对值最小的角的弧度数为－5π6.答案：－5π64．(2016·南京六校联考)点A (sin 2 015°，cos 2 015°)位于第________象限． 解析：因为sin 2 015°＝sin(11×180°＋35°) ＝－sin 35°＜0，cos 2 015°＝cos(11×180°＋35°) ＝－cos 35°＜0，所以点A (sin 2 015°，cos 2 015°)位于第三象限． 答案：三5．(2016·福州一模)设α是第二象限角，P (x,4)为其终边上的一点，且cos α＝15x ，则tan α＝________.解析：因为α是第二象限角，所以cos α＝15x ＜0，即x ＜0.又cos α＝15x ＝xx 2＋16.解得x ＝－3，所以tan α＝4x ＝－43.答案：－43二保高考，全练题型做到高考达标1．将表的分针拨快10分钟，则分针旋转过程中形成的角的弧度数是________． 解析：将表的分针拨快应按顺时针方向旋转，为负角．又因为拨快10分钟，故应转过的角为圆周的16.即为－16×2π＝－π3.答案：－π32．(2016·宿迁模拟)已知角α终边上一点P 的坐标是(2sin 2，－2cos 2)，则sin α等于________．解析：因为r ＝2＋－2＝2，由任意三角函数的定义，得sin α＝yr＝－cos 2. 答案：－cos 23．若一圆弧长等于其所在圆的内接正三角形的边长，则其圆心角α∈(0，π)的弧度数为________．解析：设圆半径为r ，则其内接正三角形的边长为3r ，所以3r ＝αr ， ∴α＝ 3. 答案： 34．(1)已知扇形周长为10，面积是4，则扇形的圆心角为________． (2)已知扇形周长为40，若扇形面积最大，则圆心角为________． 解析：(1)设圆心角为θ，半径为r ， 则⎩⎪⎨⎪⎧2r ＋r θ＝10，12θ·r 2＝4，解得⎩⎪⎨⎪⎧r ＝4，θ＝12或⎩⎪⎨⎪⎧r ＝1，θ＝8.(舍去)故扇形圆心角为12.(2)设圆心角为θ，半径为r ， 则2r ＋r θ＝40.S ＝12θ·r 2＝12r (40－2r )＝r (20－r )＝－(r －10)2＋100≤100， 当且仅当r ＝10时，S max ＝100. 此时圆心角θ＝2. 答案：(1)12(2)25．(2016·镇江调研)已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝________.解析：取终边上一点(a,2a )(a ≠0)，根据任意角的三角函数定义，可得cos θ＝±55，故 cos 2θ＝2cos 2θ－1＝－35.答案：－356．已知α是第二象限的角，则180°－α是第________象限的角．解析：由α是第二象限的角可得90°＋k ·360°＜α＜180°＋k ·360°(k ∈Z)，则180°－(180°＋k ·360°)＜180°－α＜180°－(90°＋k ·360°)，即－k ·360°＜180°－α＜90°－k ·360°(k ∈Z)，所以180°－α是第一象限的角．答案：一7．在直角坐标系中，O 是原点，A (3，1)，将点A 绕O 逆时针旋转90°到B 点，则B 点坐标为__________．解析：依题意知OA ＝OB ＝2，∠AOx ＝30°，∠BOx ＝120°，设点B 坐标为(x ，y )，所以x ＝2cos 120°＝－1，y ＝2sin 120°＝3，即B (－1，3)． 答案：(－1，3)8．在(0,2π)内，使sin x >cos x 成立的x 的取值范围为____________________．解析：如图所示，找出在(0,2π)内，使sin x ＝cos x 的x 值，sin π4＝cos π4＝22，sin 5π4＝cos 5π4＝－22.根据三角函数线的变化规律标出满足题中条件的角x ∈⎝ ⎛⎭⎪⎫π4，5π4.答案：⎝⎛⎭⎪⎫π4，5π4 9．已知角α的终边在直线y ＝－3x 上，求10sin α＋3cos α的值．解：设α终边上任一点为P (k ，－3k )， 则r ＝k 2＋－3k2＝10|k |.当k >0时，r ＝10k ， ∴sin α＝－3k10k＝－310，1cos α＝10 k k ＝10，∴10sin α＋3cos α＝－310＋310＝0；当k <0时，r ＝－10k ，∴sin α＝－3k －10k ＝310，1cos α＝－10kk＝－10， ∴10sin α＋3cos α＝310－310＝0.综上，10sin α＋3cos α＝0.10．已知扇形AOB 的周长为8.(1)若这个扇形的面积为3，求圆心角的大小；(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB . 解：设扇形AOB 的半径为r ，弧长为l ，圆心角为α， (1)由题意可得⎩⎪⎨⎪⎧2r ＋l ＝8，12lr ＝3，解得⎩⎪⎨⎪⎧r ＝3，l ＝2或⎩⎪⎨⎪⎧r ＝1，l ＝6，∴α＝l r ＝23或α＝lr＝6.(2)法一：∵2r ＋l ＝8，∴S 扇＝12lr ＝14l ·2r≤14⎝ ⎛⎭⎪⎫l ＋2r 22＝14×⎝ ⎛⎭⎪⎫822＝4， 当且仅当2r ＝l ，即α＝l r＝2时，扇形面积取得最大值4. ∴圆心角α＝2，弦长AB ＝2sin 1×2＝4sin 1. 法二：∵2r ＋l ＝8，∴S 扇＝12lr ＝12r (8－2r )＝r (4－r )＝－(r －2)2＋4≤4，当且仅当r ＝2，即α＝l r＝2时， 扇形面积取得最大值4. ∴弦长AB ＝2sin 1×2＝4sin 1.三上台阶，自主选做志在冲刺名校1．若A 是第三象限角，且⎪⎪⎪⎪⎪⎪sin A 2＝－sin A 2，则A2是第________象限角．解析：因为A 是第三象限角，所以2k π＋π<A <2k π＋3π2(k ∈Z)，所以k π＋π2<A 2<k π＋3π4(k ∈Z)，所以A2是第二、四象限角． 又因为⎪⎪⎪⎪⎪⎪sin A 2＝－sin A2，所以sin A2<0， 所以A2是第四象限角．答案：四2．已知角α＝2k π－π5(k ∈Z)，若角θ与角α的终边相同，则y ＝sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|的值为________．解析：由α＝2k π－π5(k ∈Z)及终边相同的概念知，角α的终边在第四象限， 又角θ与角α的终边相同， 所以角θ是第四象限角，所以sin θ＜0，cos θ＞0，tan θ＜0. 所以y ＝－1＋1－1＝－1. 答案：－13．已知sin α＜0，tan α＞0. (1)求α角的集合； (2)求α2终边所在的象限；(3)试判断 tan α2sin α2cos α2的符号．解：(1)由sin α＜0，知α在第三、四象限或y 轴的负半轴上； 由tan α＞0, 知α在第一、三象限， 故α角在第三象限，其集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π＋π＜α＜2k π＋3π2，k ∈Z .(2)由2k π＋π＜α＜2k π＋3π2，k ∈Z ，得k π＋π2＜α2＜k π＋3π4，k ∈Z ，故α2终边在第二、四象限． (3)当α2在第二象限时，tan α2＜0，sin α2＞0, cos α2＜0，所以tan α2 sin α2 cos α2取正号；当α2在第四象限时， tan α2＜0， sin α2＜0, cos α2＞0，所以 tan α2sin α2cos α2也取正号．因此，tan α2sin α2cos α2取正号．第二节 同角三角函数的基本关系与诱导公式_1．同角三角函数的基本关系式 (1)平方关系 sin 2α＋cos 2α＝1； (2)商数关系 tan α＝sin αcos α.2．诱导公式[小题体验]1．(教材习题改编)若α是第二象限角，tan α＝－815，则sin α＝________.解析：由题意得⎩⎪⎨⎪⎧sin 2α＋cos 2α＝1，sin αcos α＝－815，解得sin α＝±817.因为α为第二象限角，所以sin α>0，所以sin α＝817.答案：8172．(教材习题改编)已知tan θ＝2，则sin ⎝ ⎛⎭⎪⎫π2＋θ－π－θsin ⎝ ⎛⎭⎪⎫π2＋θ－π－θ＝________.解析：原式＝cos θ－－cos θcos θ－sin θ＝2cos θcos θ－sin θ＝21－tan θ＝－2. 答案：－23．若sin θcos θ＝12，则tan θ＋cos θsin θ的值是________．解析：tan θ＋cos θsin θ＝sin θcos θ＋cos θsin θ＝1cos θsin θ＝2.答案：24．(1)sin ⎝ ⎛⎭⎪⎫－31π4＝________；(2)tan ⎝ ⎛⎭⎪⎫－26π3＝________. 答案：(1)22(2) 31．利用诱导公式进行化简求值时，先利用公式化任意角的三角函数为锐角三角函数，其步骤：去负—脱周—化锐．特别注意函数名称和符号的确定．2．在利用同角三角函数的平方关系时，若开方，要特别注意判断符号． 3．注意求值与化简后的结果一般要尽可能有理化、整式化． [小题纠偏]1．已知α为第四象限角，且 sin(π－α)＝－13，则tan α＝________.解析：由 sin(π－α)＝－13，得 sin α＝－13.因为α在第四象限，所以 cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫－132＝223，则 tan α＝sin αcos α＝－13223＝－24.答案：－242．若sin(3π＋θ)＝13，则sin θ＝________.答案：－133．已知cos(π＋α)＝－12，且α是第四象限角，计算：(1)sin(2π－α)＝________； (2)sin[α＋n ＋π]＋sin[α－n ＋π]α＋2n πα－2n π(n ∈Z)＝______.解析：因为cos(π＋α)＝－12，所以－cos α＝－12，cos α＝12.又因为α是第四象限角， 所以sin α＝－1－cos 2α＝－32. (1)sin(2π－α)＝sin[2π＋(－α)]＝sin(－α)＝－sin α＝32. (2)sin[α＋n ＋π]＋sin[α－n ＋π]α＋2n πα－2n π＝n π＋π＋α＋－2n π－π＋αnπ＋α－2n π＋α＝π＋α＋－π＋αsin αcos α＝－sin α－π－αsin αcos α＝－2sin αsin αcos α＝－2cos α＝－4.答案：(1)32(2)－4考点一 三角函数的诱导公式基础送分型考点——自主练透[题组练透]1．sin 210°cos 120°的值为________．解析：sin 210°cos 120°＝－sin 30°(－cos 60°)＝12×12＝14.答案：142．(2016·淮安模拟)已知角α终边上一点M 的坐标为(3，1)，则cos ⎝ ⎛⎭⎪⎫α＋π3的值是________．解析：由题可知，cos α＝32，sin α＝12，所以cos ⎝⎛⎭⎪⎫α＋π3＝12cos α－32sin α＝0.答案：03．已知tan ⎝ ⎛⎭⎪⎫π6－α＝33，则tan ⎝ ⎛⎭⎪⎫5π6＋α＝________.解析：tan ⎝⎛⎭⎪⎫5π6＋α＝tan ⎝ ⎛⎭⎪⎫π－π6＋α＝tan ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫π6－α＝－tan ⎝ ⎛⎭⎪⎫π6－α＝－33.答案：－334．(易错题)设f (α)＝π＋απ－α－π＋α1＋sin 2α＋cos ⎝ ⎛⎭⎪⎫3π2＋α－sin 2⎝ ⎛⎭⎪⎫π2＋α⎝⎛⎭⎪⎫sin α≠－12，则f ⎝ ⎛⎭⎪⎫－23π6＝________.解析：∵f (α)＝－2sin α－cos α＋cos α1＋sin 2α＋sin α－cos 2α＝2sin αcos α＋cos α2sin 2α＋sin α ＝cos α＋2sinαsin α＋2sinα＝1tan α， ∴f ⎝ ⎛⎭⎪⎫－23π6＝1tan ⎝ ⎛⎭⎪⎫－23π6＝1tan ⎝ ⎛⎭⎪⎫－4π＋π6＝1tan π6＝ 3. 答案： 3[谨记通法]1．利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤也就是：“负化正，大化小，化到锐角就好了．” 2．利用诱导公式化简三角函数的要求 (1)化简过程是恒等变形；(2)结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值，如“题组练透”第4题．考点二 同角三角函数的基本关系题点多变型考点——纵引横联已知α是三角形的内角，且sin α＋cos α＝15.求tan α的值．[解] 法一： 联立方程⎩⎪⎨⎪⎧sin α＋cos α＝15， ①2α＋cos 2α＝1， ②由①得cos α＝15－sin α，将其代入②，整理得25sin 2α－5sin α－12＝0. ∵α是三角形的内角，∴⎩⎪⎨⎪⎧sin α＝45，cos α＝－35，∴tan α＝－43.法二：∵sin α＋cos α＝15，∴(sin α＋cos α)2＝⎝ ⎛⎭⎪⎫152，即1＋2sin αcos α＝125，∴2sin αcos α＝－2425，∴(sin α－cos α)2＝1－2sin αcos α＝1＋2425＝4925.∵sin αcos α＝－1225＜0且0＜α＜π，∴sin α＞0，cos α＜0，∴sin α－cos α＞0. ∴sin α－cos α＝75.由⎩⎪⎨⎪⎧sin α＋cos α＝15，sin α－cos α＝75，得⎩⎪⎨⎪⎧sin α＝45，cos α＝－35，∴tan α＝－43.[类题通法]同角三角函数基本关系式的应用技巧[越变越明][变式一] 保持母题条件不变， 求：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋2sin αcos α的值． 解：由母题可知：tan α＝－43.(1)sin α－4cos α5sin α＋2cos α＝tan α－45tan α＋2 ＝－43－45×⎝ ⎛⎭⎪⎫－43＋2＝87.(2)sin 2α＋2sin αcos α＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝tan 2α＋2tan α1＋tan 2α＝169－831＋169＝－825. [变式二] 若母题条件变为“sin α＋3cos α3cos α－sin α＝5”， 求tan α的值．解：法一：由sin α＋3cos α3cos α－sin α＝5, 得tan α＋33－tan α＝5，即tan α＝2.法二：由sin α＋3cos α3cos α－sin α＝5，得sin α＋3cos α＝15cos α－5sin α，∴6sin α＝12cos α，即tan α＝2.[变式三] 若母题中的条件和结论互换：已知α是三角形的内角，且tan α＝－13， 求sin α＋cos α的值．解：由tan α＝－13，得sin α＝ －13cos α，将其代入 sin 2α＋cos 2α＝1，得109cos 2α＝1，∴cos 2α＝910，易知cos α＜0， ∴cos α＝－31010， sin α＝1010，故 sin α＋cos α＝－105. [破译玄机]1．三角形中求值问题，首先明确角的范围，才能求出角的值或三角函数值．2．三角形中常用的角的变形有：A ＋B ＝π－C,2A ＋2B ＝2π－2C ，A 2＋B 2＋C 2＝π2等，于是可得sin(A ＋B )＝sin C ，cos ⎝⎛⎭⎪⎫A ＋B 2＝sin C 2等．一抓基础，多练小题做到眼疾手快1．若α∈⎝ ⎛⎭⎪⎫－π2，π2，sin α＝－35，则cos(－α)＝________.解析：因为α∈⎝ ⎛⎭⎪⎫－π2，π2，sin α＝－35，所以cos α＝45，即cos(－α)＝45.答案：452．已知sin(π＋θ)＝－3cos(2π－θ)，|θ|＜π2，则θ＝________.解析：∵sin(π＋θ)＝－3cos(2π－θ)，∴－sin θ＝－3cos θ，∴tan θ＝ 3.∵|θ|＜π2，∴θ＝π3.答案：π33．已知sin ⎝ ⎛⎭⎪⎫α－π4＝13，则cos ⎝ ⎛⎭⎪⎫π4＋α＝________.解析：cos ⎝ ⎛⎭⎪⎫π4＋α＝sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π4＋α＝sin ⎝ ⎛⎭⎪⎫π4－α＝－sin ⎝ ⎛⎭⎪⎫α－π4＝－13.答案：－134．已知α∈⎝ ⎛⎭⎪⎫π2，π，sin α＝45，则tan α＝________.解析：∵α∈⎝ ⎛⎭⎪⎫π2，π，∴cos α＝－1－sin 2α＝－35，∴tan α＝sin αcos α＝－43.答案：－435．如果sin(π＋A )＝12，那么cos ⎝ ⎛⎭⎪⎫3π2－A 的值是________．解析：∵sin(π＋A )＝12，∴－sin A ＝12.∴cos ⎝⎛⎭⎪⎫3π2－A ＝－sin A ＝12.答案：12二保高考，全练题型做到高考达标1．(2016·南师附中检测)角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点P (1,2)，则sin(π－α)的值是________．解析：因为角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点P (1,2)，所以sin α＝255，sin(π－α)＝sin α＝255.答案：2552．若sin(π－α)＝－2sin ⎝ ⎛⎭⎪⎫π2＋α，则sin α·cos α的值等于________．解析：由sin(π－α)＝－2sin ⎝ ⎛⎭⎪⎫π2＋α，可得sin α＝－2cos α，则tan α＝－2，sin α·cos α＝tan α1＋tan 2α＝－25. 答案：－253．(2016·苏北四市调研)cos 350°－2sin 160°－＝________.解析：原式＝－－－－＋＝cos 10°－－－－＝cos 10°－2⎝ ⎛⎭⎪⎫12cos 10°－32sin 10°sin 10°＝ 3.答案： 3 4．已知f (α)＝π－απ－α－π－αα，则f ⎝⎛⎭⎪⎫－31π3＝________. 解析：∵f (α)＝sin α·cos α－cos αtan α＝－cos α，∴f ⎝ ⎛⎭⎪⎫－31π3＝－cos ⎝ ⎛⎭⎪⎫－31π3＝－cos ⎝ ⎛⎭⎪⎫10π＋π3 ＝－cos π3＝－12.答案：－125．已知sin αcos α＝18，且5π4<α<3π2，则cos α－sin α＝__________.解析：∵5π4<α<3π2，∴cos α<0，sin α<0且|cos α|<|sin α|， ∴cos α－sin α>0.又(cos α－sin α)2＝1－2sin αcos α＝1－2×18＝34，∴cos α－sin α＝32. 答案：326．化简：sin ⎝ ⎛⎭⎪⎫π2＋α·cos ⎝ ⎛⎭⎪⎫π2－απ＋α＋π－α⎝ ⎛⎭⎪⎫π2＋απ＋α＝________.解析：原式＝cos α·sin α－cos α＋sin α－sin α－sin α＝－sin α＋sin α＝0. 答案：07．sin 4π3·cos 5π6·tan ⎝ ⎛⎭⎪⎫－4π3＝________.解析：原式＝sin ⎝ ⎛⎭⎪⎫π＋π3·cos ⎝ ⎛⎭⎪⎫π－π6·tan ⎝ ⎛⎭⎪⎫－π－π3＝⎝ ⎛⎭⎪⎫－sin π3·⎝ ⎛⎭⎪⎫－cos π6·⎝ ⎛⎭⎪⎫－tan π3＝⎝ ⎛⎭⎪⎫－32×⎝ ⎛⎭⎪⎫－32×(－3)＝－334. 答案：－3348．(2016·南通调研)已知cos ⎝ ⎛⎭⎪⎫π6－θ＝a (|a |≤1)，则cos ⎝ ⎛⎭⎪⎫5π6＋θ＋sin ⎝⎛⎭⎪⎫2π3－θ＝________.解析：由题意知，cos ⎝⎛⎭⎪⎫5π6＋θ＝cos ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫π6－θ＝－cos ⎝ ⎛⎭⎪⎫π6－θ＝－a .sin ⎝⎛⎭⎪⎫2π3－θ＝sin ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫π6－θ＝cos ⎝ ⎛⎭⎪⎫π6－θ＝a ， ∴cos ⎝⎛⎭⎪⎫5π6＋θ＋sin ⎝ ⎛⎭⎪⎫2π3－θ＝0.答案：09．已知函数f (x )＝A sin ⎝⎛⎭⎪⎫x ＋π4，x ∈R ，且f (0)＝1.(1)求A 的值；(2)若f (α)＝－15，α是第二象限角，求cos α.解：(1)由f (0)＝1，得A sin π4＝1，A ×22＝1，∴A ＝ 2.(2)由(1)得，f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π4＝sin x ＋cos x .由f (α)＝－15，得sin α＋cos α＝－15，∴sin α＝－cos α－15，即sin 2α＝⎝ ⎛⎭⎪⎫－cos α－152，∴1－cos 2α＝cos 2α＋25cos α＋125，cos 2α＋15cos α－1225＝0，解得cos α＝35或cos α＝－45.∵α是第二象限角，∴cos α<0， ∴cos α＝－45.10．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α； (2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α ＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.三上台阶，自主选做志在冲刺名校1．sin 21°＋sin 22°＋…＋sin 290°＝________.解析：sin 21°＋sin 22°＋…＋sin 290°＝sin 21°＋sin 22°＋…＋sin 244°＋sin 245°＋cos 244°＋cos 243°＋…＋cos 21°＋sin 290°＝(sin 21°＋cos 21°)＋(sin 22°＋cos 22°)＋…＋(sin 244°＋cos 244°)＋sin 245°＋sin 290°＝44＋12＋1＝912.答案：9122．若f (x )＝sin ⎝ ⎛⎭⎪⎫π2x ＋α＋1，且f (2 013)＝2，则f (2 015)＝________.解析：因为f (2 013)＝sin ⎝ ⎛⎭⎪⎫π2×2 013＋α＋1＝ sin ⎝ ⎛⎭⎪⎫1 006π＋π2＋α＋1＝sin ⎝⎛⎭⎪⎫π2＋α＋1＝cos α＋1＝2，所以cos α＝1. 所以f (2 015)＝sin ⎝⎛⎭⎪⎫π2×2 015＋α＋1＝sin ⎝ ⎛⎭⎪⎫1 007π＋π2＋α＋1＝－sin ⎝⎛⎭⎪⎫π2＋α＋1＝－cos α＋1＝0. 答案：03．已知f (x )＝cos2n π＋x2n π－xcos2n ＋π－x ](n ∈Z)．(1)化简f (x )的表达式；(2)求f ⎝ ⎛⎭⎪⎫π2 014＋f ⎝ ⎛⎭⎪⎫503π1 007的值．解：(1)当n 为偶数，即n ＝2k (k ∈Z)时， f (x )＝cos 2k π＋x2k π－xcos2k ＋π－x ]＝cos 2x ·sin 2－xcos 2π－x ＝cos 2x －sin x2－cos x2＝sin 2x ；当n 为奇数，即n ＝2k ＋1(k ∈Z)时， f (x )＝cos 2k ＋π＋x ]·sin 2k ＋π－x ]cos2k ＋＋1]π－x }＝cos 2[2k π＋π＋x 2[2k π＋π－x cos 2k ＋π＋π－x＝cos2π＋x2π－xcos 2π－x＝－cos x 2sin 2x－cos x2＝sin 2x ，综上得f (x )＝sin 2x .(2)由(1)得f ⎝ ⎛⎭⎪⎫π2 014＋f ⎝ ⎛⎭⎪⎫503π1 007＝sin2π2 014＋sin 21 006π2 014＝sin 2π2 014＋sin 2⎝ ⎛⎭⎪⎫π2－π2 014 ＝sin2π2 014＋cos 2π2 014＝1. 第三节 三角函数的图象与性质1．用五点法作正弦函数和余弦函数的简图正弦函数y ＝sin x ，x ∈[0,2π]的图象上，五个关键点是：(0,0)，⎝ ⎛⎭⎪⎫π2，1，(π，0)，⎛⎭⎪⎫3π2，－1，(2π，0)．余弦函数y ＝cos x ，x ∈[0,2π]的图象上，五个关键点是：(0,1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫3π2，0，(2π，1)．2．正弦、余弦、正切函数的图象与性质(表中k ∈Z).[小题体验]1．(教材习题改编)函数y ＝2sin x －1的定义域为______________________． 解析：由2sin x －1≥0，得sin x ≥12，则x ∈⎣⎢⎡⎦⎥⎤2k π＋π6，2k π＋5π6(k ∈Z)． 答案：⎣⎢⎡⎦⎥⎤2k π＋π6，2k π＋5π6(k ∈Z) 2．(教材习题改编)使函数y ＝3cos ⎝ ⎛⎭⎪⎫2x －2π3取最小值时x 的集合为________________．解析：要使函数取最小值，则2x －2π3＝2k π＋π(k ∈Z)，知x ＝k π＋5π6，k ∈Z.答案：⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝k π＋5π6，k ∈Z3．(教材习题改编)函数y ＝2sin x ⎝ ⎛⎭⎪⎫π6≤x ≤2π3的值域是________．解析：根据正弦函数图象，可知x ＝π6时，函数取到最小值1；x ＝π2时，函数取到最大值2.答案：[1,2]4．函数y ＝－tan ⎝⎛⎭⎪⎫x ＋π6＋2的定义域为______________．答案：⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠k π＋π3，k ∈Z1．闭区间上最值或值域问题，首先要在定义域基础上分析单调性，含参数的最值问题，要讨论参数对最值的影响．2．要注意求函数y ＝A sin(ωx ＋φ)的单调区间时ω的符号，尽量化成ω>0时的情况． 3．三角函数存在多个单调区间时易错用“∪”联结． [小题纠偏]1．函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π4在区间⎣⎢⎡⎦⎥⎤0，π2上的最小值为________． 解析：由已知x ∈⎣⎢⎡⎦⎥⎤0，π2， 得2x －π4∈⎣⎢⎡⎦⎥⎤－π4，3π4，所以sin ⎝ ⎛⎭⎪⎫2x －π4∈⎣⎢⎡⎦⎥⎤－22，1， 故函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π4在区间⎣⎢⎡⎦⎥⎤0，π4上的最小值为－22.答案：－222．函数y ＝cos ⎝⎛⎭⎪⎫π4－2x 的单调减区间为____________．解析：由y ＝cos ⎝ ⎛⎭⎪⎫π4－2x ＝cos ⎝ ⎛⎭⎪⎫2x －π4得2k π≤2x －π4≤2k π＋π(k ∈Z)，解得k π＋π8≤x ≤k π＋5π8(k ∈Z)．所以函数的单调减区间为⎣⎢⎡⎦⎥⎤k π＋π8，k π＋5π8(k ∈Z)．答案：⎣⎢⎡⎦⎥⎤k π＋π8，k π＋5π8(k ∈Z)3．函数y ＝lg sin(cos x )的定义域为________． 解析：由sin(cos x )>0⇒2k π<cos x <2k π＋π(k ∈Z)． 又－1≤cos x ≤1，∴0<cos x ≤1.故所求定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ∈⎝ ⎛⎭⎪⎫2k π－π2，2k π＋π2，k ∈Z. 答案：⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ∈⎝ ⎛⎭⎪⎫2k π－π2，2k π＋π2，k ∈Z考点一 三角函数的定义域与值域基础送分型考点——自主练透[题组练透]1．函数y ＝2sin ⎝⎛⎭⎪⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为________．解析：∵0≤x ≤9，∴－π3≤π6x －π3≤7π6，∴sin ⎝ ⎛⎭⎪⎫π6x －π3∈⎣⎢⎡⎦⎥⎤－32，1.∴y ∈[－3，2]，∴y max ＋y min ＝2－ 3答案：2－ 32．(易错题)函数y ＝1tan x －1的定义域为______________．解析：要使函数有意义，必须有⎩⎪⎨⎪⎧tan x －1≠0，x ≠π2＋kx ，k ∈Z ，即⎩⎪⎨⎪⎧x ≠π4＋k π，k ∈Z ，x ≠π2＋k π，k ∈Z.故函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠π4＋k π且x ≠π2＋k π，k ∈Z .答案：⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠π4＋k π且x ≠π2＋k π，k ∈Z3．函数y ＝lg(sin 2x )＋9－x 2的定义域为______________．解析：由⎩⎪⎨⎪⎧sin 2x >0，9－x 2≥0，得⎩⎪⎨⎪⎧k π<x <k π＋π2，k ∈Z ，－3≤x ≤3.∴－3≤x <－π2或0<x <π2.∴函数y ＝lg(sin 2x )＋9－x 2的定义域为⎣⎢⎡⎭⎪⎫－3，－π2∪⎝ ⎛⎭⎪⎫0，π2.答案：⎣⎢⎡⎭⎪⎫－3，－π2∪⎝ ⎛⎭⎪⎫0，π2 4．(易错题)求函数y ＝cos 2x ＋sin x ⎝ ⎛⎭⎪⎫|x |≤π4的最大值与最小值．解：令t ＝sin x ，∵|x |≤π4，∴t ∈⎣⎢⎡⎦⎥⎤－22，22. ∴y ＝－t 2＋t ＋1＝－⎝ ⎛⎭⎪⎫t －122＋54，∴当t ＝12时，y max ＝54，当t ＝－22时，y min ＝1－22.∴函数y ＝cos 2x ＋sin x ⎝⎛⎭⎪⎫|x |≤π4的最大值为54，最小值为1－22.[谨记通法]1．三角函数定义域的2种求法(1)应用正切函数y ＝tan x 的定义域求函数y ＝A tan(ωx ＋φ)的定义域，如“题组练透”第2题易忽视．(2)转化为求解简单的三角不等式求复杂函数的定义域． 2．三角函数最值或值域的3种求法(1)直接法：直接利用sin x 和cos x 的值域求解．(2)化一法：把所给三角函数化为y ＝A sin(ωx ＋φ)＋k 的形式，由正弦函数单调性写出函数的值域．(3)换元法：把sin x 、cos x 、sin x cos x 或sin x ±cos x 换成t ，转化为二次函数，如“题组练透”第4题．考点二 三角函数的单调性重点保分型考点——师生共研[典例引领]写出下列函数的单调区间：(1)f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π4，x ∈[0，π]；(2)f (x )＝|tan x |；(3)f (x )＝cos ⎝ ⎛⎭⎪⎫2x －π6，x ∈⎣⎢⎡⎦⎥⎤－π2，π2. 解：(1)由－π2＋2k π≤x ＋π4≤π2＋2k π，k ∈Z ，得－3π4＋2k π≤x ≤π4＋2k π，k ∈Z.又x ∈[0，π]，所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤0，π4，递减区间为⎣⎢⎡⎦⎥⎤π4，π.(2)观察图象可知，y ＝|tan x |的增区间是⎣⎢⎡⎭⎪⎫k π，k π＋π2，k ∈Z ，减区间是⎝ ⎛⎦⎥⎤k π－π2，k π，k ∈Z.(3)当2k π－π≤2x －π6≤2k π(k ∈Z)，即k π－5π12≤x ≤k π＋π12，k ∈Z ，函数f (x )是增函数．因此函数f (x )在⎣⎢⎡⎦⎥⎤－π2，π2上的单调递增区间是⎣⎢⎡⎦⎥⎤－5π12，π12，递减区间为⎣⎢⎡⎦⎥⎤－π2，－5π12，⎣⎢⎡⎦⎥⎤π12，π2.[由题悟法]求三角函数单调区间的2种方法(1)代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u (或t )，利用基本三角函数的单调性列不等式求解．(2)图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间．[提醒] 求解三角函数的单调区间时若x 的系数为负应先化为正，同时切莫漏掉考虑函数自身的定义域．[即时应用]1．(2016·宿迁调研)函数f (x )＝sin ⎝⎛⎭⎪⎫－2x ＋π3的单调减区间为______．解析：由已知函数为y ＝－sin ⎝ ⎛⎭⎪⎫2x －π3，欲求函数的单调减区间，只需求y ＝sin ⎝ ⎛⎭⎪⎫2x －π3的单调增区间即可．由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z.故所给函数的单调减区间为⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12(k ∈Z)．答案：⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12(k ∈Z)2．若函数f (x )＝sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤0，π3上单调递增，在区间⎣⎢⎡⎦⎥⎤π3，π2上单调递减，则ω＝________.解析：∵f (x )＝sin ωx (ω>0)过原点，∴当0≤ωx ≤π2，即0≤x ≤π2ω时，y ＝sin ωx 是增函数；当π2≤ωx ≤3π2，即π2ω≤x ≤3π2ω时，y ＝sin ωx 是减函数． 由f (x )＝sin ωx (ω>0)在⎣⎢⎡⎦⎥⎤0，π3上单调递增，在⎣⎢⎡⎦⎥⎤π3，π2上单调递减知，π2ω＝π3，∴ω＝32.答案：32考点三 三角函数的奇偶性、周期性及对称性常考常新型考点——多角探明[命题分析]正、余弦函数的图象既是中心对称图形，又是轴对称图形．正切函数的图象只是中心对称图形，应把三角函数的对称性与奇偶性结合，体会二者的统一．常见的命题角度有： (1)三角函数的周期；(2)求三角函数的对称轴或对称中心； (3)三角函数对称性的应用．[题点全练]角度一：三角函数的周期1．函数y ＝2sin ⎝ ⎛⎭⎪⎫π4－2x 的最小正周期为________． 解析：T ＝2π|－2|＝π.答案：π2．(2016·南京调研)若函数f (x )＝2tan ⎝ ⎛⎭⎪⎫kx ＋π3的最小正周期T 满足1＜T ＜2，则自然数k 的值为________．解析：由题意知，1＜πk＜2，即k ＜π＜2k .又k ∈N ，所以k ＝2或k ＝3. 答案：2或3角度二：求三角函数的对称轴或对称中心3．已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π4(ω>0)的最小正周期为π，则函数f (x )的对称轴为________．解析：由题意得，2πω＝π，ω＝2，所以f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π4. 令2x ＋π4＝π2＋k π(k ∈Z)，得x ＝π8＋k π2(k ∈Z)即为函数f (x )的对称轴．答案：x ＝π8＋k π2(k ∈Z)4．函数y ＝3tan ⎝ ⎛⎭⎪⎫2x ＋π3的对称中心是________．解析：2x ＋π3＝k π2，k ∈Z ，所以x ＝k π4－π6，k ∈Z.答案：⎝⎛⎭⎪⎫k π4－π6，0(k ∈Z)角度三：三角函数对称性的应用5．(2015·南京四校联考)若函数y ＝cos ⎝⎛⎭⎪⎫ωx ＋π6(ω∈N *)图象的一个对称中心是⎝ ⎛⎭⎪⎫π6，0，则ω的最小值为________．解析：πω6＋π6＝k π＋π2(k ∈Z)⇒ω＝6k ＋2(k ∈Z)⇒ωmin ＝2.答案：26.设偶函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)的部分图象如图所示，△KLM 为等腰直角三角形，∠KML ＝90°，KL ＝1，则f ⎝ ⎛⎭⎪⎫16的值为________．解析：由题意知，点M 到x 轴的距离是12，根据题意可设f (x )＝12cos ωx ，又由题图知12·2πω＝1，所以ω＝π，所以f (x )＝12cos πx ，故f ⎝ ⎛⎭⎪⎫16＝12cos π6＝34.答案：34[方法归纳]函数f (x )＝A sin(ωx ＋φ)的奇偶性、周期性和对称性(1)若f (x )＝A sin(ωx ＋φ)为偶函数，则当x ＝0时，f (x )取得最大或最小值；若f (x )＝A sin(ωx ＋φ)为奇函数，则当x ＝0时，f (x )＝0.(2)对于函数y ＝A sin(ωx ＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线x ＝x 0或点(x 0,0)是否是函数的对称轴或对称中心时，可通过检验f (x 0)的值进行判断．一抓基础，多练小题做到眼疾手快 1．函数y ＝cos x －32的定义域为________． 解析：∵cos x －32≥0，得cos x ≥32，∴2k π－π6≤x ≤2k π＋π6，k ∈Z. 答案：⎣⎢⎡⎦⎥⎤2k π－π6，2k π＋π6(k ∈Z) 2．函数y ＝2cos 2x ＋5sin x －4的值域为________． 解析：y ＝2cos 2x ＋5sin x －4 ＝2(1－sin 2x )＋5sin x －4 ＝－2sin 2x ＋5sin x －2 ＝－2⎝⎛⎭⎪⎫sin x －542＋98. 故当sin x ＝1时，y max ＝1，当sin x ＝－1时，y min ＝－9， 故y ＝2cos 2x ＋5sin x －4的值域为[－9,1]． 答案：[－9,1]3．函数f (x )＝tan ωx (ω>0)的图象相邻的两支截直线y ＝π4所得线段长为π4，则f ⎝ ⎛⎭⎪⎫π4的值是________．解析：由题意知，T ＝π4，所以πω＝π4，所以ω＝4，所以f (x )＝tan 4x ，所以f ⎝ ⎛⎭⎪⎫π4＝0.答案：04．函数f (x )＝sin(－2x )的单调增区间是____________． 解析：由f (x )＝sin(－2x )＝－sin 2x ，2k π＋π2≤2x ≤2k π＋3π2得k π＋π4≤x ≤k π＋3π4(k ∈Z)．答案：⎣⎢⎡⎦⎥⎤k π＋π4，k π＋3π4(k ∈Z)5．函数y ＝3－2cos ⎝⎛⎭⎪⎫x ＋π4的最大值为________，此时x ＝______.解析：函数y ＝3－2cos ⎝ ⎛⎭⎪⎫x ＋π4的最大值为3＋2＝5，此时x ＋π4＝π＋2k π，即x ＝3π4＋2k π(k ∈Z)．答案：53π4＋2k π(k ∈Z) 二保高考，全练题型做到高考达标1．函数y ＝tan ⎝ ⎛⎭⎪⎫2x ＋π4的图象与x 轴交点的坐标是_______________________________. 解析：由2x ＋π4＝k π(k ∈Z)得，x ＝k π2－π8(k ∈Z)．∴函数y ＝tan ⎝ ⎛⎭⎪⎫2x ＋π4的图象与x 轴交点的坐标是⎝ ⎛⎭⎪⎫k π2－π8，0，k ∈Z.答案：⎝⎛⎭⎪⎫k π2－π8，0，k ∈Z 2．(2016·苏锡常镇四市调研)设函数f (x )＝sin(ωx ＋φ)＋3cos(ωx ＋φ)⎝ ⎛⎭⎪⎫ω>0，|φ|<π2的最小正周期为π，且满足f (－x )＝－f (x )，则函数f (x )的单调增区间为________．解析：因为f (x )＝sin(ωx ＋φ)＋3cos(ωx ＋φ)＝2sin ⎝⎛⎭⎪⎫ωx ＋φ＋π3⎝⎛⎭⎪⎫ω>0，|φ|<π2的最小正周期为π，且满足f (－x )＝－f (x )，所以ω＝2，φ＝－π3，所以f (x )＝2sin 2x ，令2x ∈⎣⎢⎡⎦⎥⎤2k π－π2，2k π＋π2(k ∈Z)，解得函数f (x )的单调增区间为⎣⎢⎡⎦⎥⎤k π－π4，k π＋π4(k ∈Z)． 答案：⎣⎢⎡⎦⎥⎤k π－π4，k π＋π4(k ∈Z)3．已知函数y ＝tan ωx 在⎝ ⎛⎭⎪⎫－π2，π2内是减函数，则ω的取值范围是________．解析：因为y ＝tan ωx 在⎝ ⎛⎭⎪⎫－π2，π2内是减函数，所以ω<0且π|ω|≥π，则－1≤ω<0. 答案：[－1,0)4．若函数f (x )＝sin ⎝⎛⎭⎪⎫ωx ＋π6(ω>0)的图象的相邻两条对称轴之间的距离为π2，且该函数图象关于点(x 0,0)成中心对称，x 0∈⎣⎢⎡⎦⎥⎤0，π2，则x 0＝________.解析：由题意得T 2＝π2，T ＝π，ω＝2.又2x 0＋π6＝k π(k ∈Z)，x 0＝k π2－π12(k ∈Z)，而x 0∈⎣⎢⎡⎦⎥⎤0，π2，所以x 0＝5π12. 答案：5π125．若函数f (x )＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω＞0，且|φ|＜π2在区间⎣⎢⎡⎦⎥⎤π6，2π3上是单调减函数，且函数值从1减少到－1，则f ⎝ ⎛⎭⎪⎫π4＝________.解析：由题意得函数f (x )的周期T ＝2⎝⎛⎭⎪⎫2π3－π6＝π，所以ω＝2，此时f (x )＝sin(2x＋φ)，将点⎝ ⎛⎭⎪⎫π6，1代入上式得sin ⎝ ⎛⎭⎪⎫π3＋φ＝1⎝ ⎛⎭⎪⎫|φ|＜π2，所以φ＝π6，所以f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6，于是f ⎝ ⎛⎭⎪⎫π4＝sin ⎝ ⎛⎭⎪⎫π2＋π6＝cos π6＝32.答案：326．已知函数f (x )＝2sin(ωx ＋φ)，对于任意x 都有f ⎝ ⎛⎭⎪⎫π6＋x ＝f ⎝ ⎛⎭⎪⎫π6－x ，则f ⎝ ⎛⎭⎪⎫π6的值为________．解析：∵f ⎝ ⎛⎭⎪⎫π6＋x ＝f ⎝ ⎛⎭⎪⎫π6－x ，∴x ＝π6是函数f (x )＝2sin(ωx ＋φ)的一条对称轴．∴f ⎝ ⎛⎭⎪⎫π6＝±2. 答案：2或－27．(2015·南通调研)已知f 1(x )＝sin ⎝⎛⎭⎪⎫3π2＋x cosx ，f 2(x )＝sin x sin(π＋x )，若设f (x )＝f 1(x )－f 2(x )，则f (x )的单调增区间是________．解析：由题意知，f 1(x )＝－cos 2x ，f 2(x )＝－sin 2x ，f (x )＝sin 2x －cos 2x ＝－cos 2x ，令2x ∈[2k π，2k π＋π](k ∈Z)，即x ∈⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z)，故f (x )的单调增区间为⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z)．答案：⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z)。