整式的加减思维导图

第一章 有理数思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧<≤⨯⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧分配律乘法结合律加法结合律结合律乘法交换律加法交换律交换律运算律乘方的运算符号法则有理数的除法法则有理数的乘法法则有理数的减法法则有理数的加法法则法则运算方法叫做科学记数法是正整数），这种记数，的形式（其中把一个数表示乘——科学记数法数相同因数的个数叫做指相同的因数叫做底数，叫做幂叫做乘方，乘方的结果个相同因数的积的运算求——乘方的两个数互为倒数—乘积是—倒数的绝对值叫做数的点与原点的距离，一般地，数轴上表示数——绝对值数，叫做互为相反数—只有符号不同的两个—相反数相关概念负有理数正有理数按性质符号分分数整数按定义分分类有理数n 10a 110a n 1a a 0n第二章 整式的加减思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧合并同类项去括号步骤反的符号与原来的符号相去括号后原括号内各项——括号外因数为负同的符号与原来的符号相去括号后原括号内各项——括号外因数为正去括号作为合并后项的系数所得的结果把同类项的系数相加，——合并同类项同字母的指数也相同—所含字母相同并且相—同类项整式的加减的次数—多项式中次数最高项—次数—不含字母的项—常数项项式—组成多项式的每个单—项—几个单项式的和—定义多项式指数的和—单项式中所有字母的—次数—单项式中的数字因数—系数的式子—由数或字母的积组成—定义单项式用字母表示数减加的式整第三章 一元一次方程思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧际意义符合题意，是否符合实验：检验所求的解是否值中所要求的相关数量的出未知数的值以及题目解：解所列的方程，求一个数字列方程关系以及若干倍多或少关系、相等关系、倍数列：根据题目中的数量与所列方程有关的数量含未知数的代数式表示设：设未知数，并且用数量间的关系知量和未知量，明确各审：弄清题意，分清已解应用题一次方程列一元系数化为合并同类项移项去括号去分母解一元一次方程的步骤的数，结果仍相等，或除以同一个不为：等式两边乘同一个数性质，结果仍相等或式子同一个数或减：等式两边加性质等式的性质过程解方程：求方程的解的数的值号左右两边相等的未知方程的解：使方程中等等号两边都是整式，，未知数的次数都是元一个未知数一元一次方程：只含有式方程：含有未知数的等一元一次方程程方次一元一102)()(11)(第四章 几何图形初步思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧角的度量互补互余两角的特殊关系比较大小的方法表示方法定义角线段的和、差与画法线段的中点两点之间的距离段最短基本事实：两点之间线比较方法特点表示方法线段特点表示方法射线条直线基本事实：两点确定一特点表示方法直线线平面图形立体图形的平面展示图从上面看从左面看从正面看形从不同的方向看立体图常见的立体图形立体图形几何图形初步。

其中专业理论知识内容包括：保安理论知识、消防业务知识、职业道德、法律常识、保安礼仪、救护知识。

作技能训练内容包括：岗位操作指引、勤务技能、消防技能、军事技能。

二．培训的及要求培训目的 安全生产目标责任书 为了进一步落实安全生产责任制，做到“责、权、利”相结合，根据我公司2015年度安全生产目标的内容，现与财务部签订如下安全生产目标： 一、目标值： 1、全年人身死亡事故为零，重伤事故为零，轻伤人数为零。

2、现金安全保管，不发生盗窃事故。

3、每月足额提取安全生产费用，保障安全生产投入资金的到位。

4、安全培训合格率为100%。

二、本单位安全工作上必须做到以下内容： 1、对本单位的安全生产负直接领导责任，必须模范遵守公司的各项安全管理制度，不发布与公司安全管理制度相抵触的指令，严格履行本人的安全职责，确保安全责任制在本单位全面落实，并全力支持安全工作。

2、保证公司各项安全管理制度和管理办法在本单位内全面实施，并自觉接受公司安全部门的监督和管理。

3、在确保安全的前提下组织生产，始终把安全工作放在首位，当“安全与交货期、质量”发生矛盾时，坚持安全第一的原则。

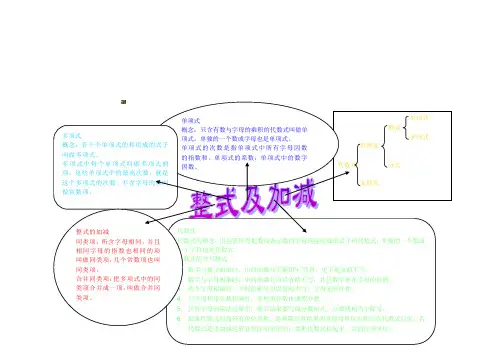
代数式 代数式的概念：用运算符号把数或表示数的字母连接而成的式子叫代数式，单独的一个数或一个字母也是代数式。

代数式的书写格式 1. 数字与数字相乘时，中间的乘号不能用“• ”代替，更不能省略不写。

2. 数字与字母相乘时，中间的乘号可以省略不写，并且数字放在字母的前面。

3. 两个字母相乘时，中间的乘号可以省略不写，字母无顺序性。

4. 当字母和带分数相乘时，要把带分数化成假分数。

5. 含有字母的除法运算中，最后结果要写成分数形式，分数线相当于除号。

6. 如果代数式后面带有单位名称，是乘除运算结果的直接将单位名称写在代数式后面，若代数式是带加减运算且须注明单位的，要把代数式括起来，后面注明单位。

单项式 整式 多项式 有理式 代数式 分式 无理式单项式概念：只含有数与字母的乘积的代数式叫做单项式，单独的一个数或字母也是单项式。

初一上册二三单元数学思维导图汇总初一上册二三单元数学：整式的加减的知识点2.1 整式1、单项式：由数字和字母乘积组成的式子。

判断代数式是否是单项式，关键要看代数式中数与字母是否是乘积关系，即分母中不含有字母，若式子中含有加、减运算关系，其也不是单项式。

2、多项式：几个单项式的和。

判断代数式是否是多项式，关键要看代数式中的每一项是否是单项式。

每个单项式称项，常数项，多项式的次数就是多项式中次数最高的次数。

3、单项式和多项式统称为整式。

2.2整式的加减1、同类项：所含字母相同，并且相同字母的指数也相同的项。

与字母前面的系数(0)无关。

2、同类项必须同时满足两个条件：(1)所含字母相同;(2)相同字母的次数相同，二者缺一不可.同类项与系数大小、字母的排列顺序无关3、合并同类项：把多项式中的同类项合并成一项。

可以运用交换律，结合律和分配律。

4、合并同类项法则：合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变;5、去括号法则：去括号，看符号：是正号，不变号;是负号，全变号。

6、整式加减的一般步骤：一去、二找、三合(1)如果遇到括号按去括号法则先去括号. (2)结合同类项. (3)合并同类项初一上册二三单元数学：一元一次方程知识点3.1 一元一次方程1、方程是含有未知数的等式。

2、方程都只含有一个未知数(元)x，未知数x的指数都是1(次)，这样的方程叫做一元一次方程。

注意：判断一个方程是否是一元一次方程要抓住三点：1)未知数所在的式子是整式(方程是整式方程);2)化简后方程中只含有一个未知数;3)经整理后方程中未知数的次数是1.3、解方程就是求出使方程中等号左右两边相等的未知数的值，这个值就是方程的解。

4、等式的性质： 1)等式两边同时加(或减)同一个数(或式子)，结果仍相等;2)等式两边同时乘同一个数，或除以同一个不为0的数，结果仍相等。

注意：运用性质时，一定要注意等号两边都要同时变;运用性质2时，一定要注意0这个数.3.2 、3.3解一元一次方程在实际解方程的过程中，以下步骤不一定完全用上，有些步骤还需重复使用. 因此在解方程时还要注意以下几点：①去分母：在方程两边都乘以各分母的最小公倍数，不要漏乘不含分母的项;分子是一个整体，去分母后应加上括号;去分母与分母化整是两个概念，不能混淆;②去括号：遵从先去小括号，再去中括号，最后去大括号;不要漏乘括号的项;不要弄错符号;③移项：把含有未知数的项移到方程的一边，其他项都移到方程的另一边(移项要变符号) 移项要变号;④合并同类项：不要丢项，解方程是同解变形，每一步都是一个方程，不能像计算或化简题那样写能连等的形式;⑤系数化为1：:字母及其指数不变系数化成1，在方程两边都除以未知数的系数a，得到方程的解。

整式的加减单元教学设计
主题单元学习目标
知识与技能
1.理解整式、单项式、多项式、同类项的概念；
2.熟练指出单项式的系数、次数和多项式的项数、次数，把一个多项式写成按某个字母的降幂或升幂排列；
3.掌握合并同类项法则；
4.能灵活应用去括号法则，进行整式加减运算.
过程与方法
1.通过回忆和交流,经历对已有知识的归纳；对本章内容的认识更全面、更系统化
2.通过应用与实践,提高分析问题、解决问题的能力;培养学生主动分
1．主要概念：
(1)关于单项式，你都知道什么?
(2)关于多项式，你又知道什么?
引导学生积极回答所提问题，通过几名同学的回答，复习单项式的定义、单项式的系数、次数的定义，多项式的定义以及多项式的项、同类项、次数、升降幂排列等定义。

(3)什么叫整式?
在学生回答的基础上，进行归纳、总结：
整式
2．主要法则：
①提问：在本章中，我们学习了哪几个重要的法则?分别如何叙述?
②在学生回答的基础上，进行归纳总结：
整式的加减
活动2：自主学习，合作交流
出示相关练习：1.计算：―2y3+(3xy2―x2y)―2(xy2―y3)
化简求值：(2x3―xyz)―2(x3―y3+xyz)+(xyz―2y3)，其中x=1，y=2，z=―3
小组之间，师生之间交流，共同总结整式的加减运算的步骤
活动3：巩固提升
布置适当的练习，巩固所学知识。

整式的加减整式的加减
同类项所含字母和字母的指数都相同
合并同类项系数相加，字母不变
去括号法则去括号，看符号，是正号不变号，是负号全变号代数式
有理式
整式
单项式
多项式
分式
无理式含有字母的根式
整式
单项式
定义
数字与字母的积的形式
单独的一个数或字母
系数数字因数
次数所有字母的指数和
写法
假分数
省略系数“1”
分母不能含字母
多项式
定义几个单项式的和叫做多项式
项每一个单项式
次数最高的项的次数
常数项不含字母的项
排列升幂或降幂。

整式的概念思维导图
整式的概念为单项式和多项式的统称，是有理式的一部分，在有理式中可以包含加，减，乘，除、乘方五种运算，但在整式中除数不能含有字母。

整式又分单项式与多项式：
1、单项式
由数与字母的积或字母与字母的积所组成的代数式叫做单项式（monomial）。

单独一个数或一个字母也是单项式，如Q，-1，a ，β等。

2、多项式
由有限个单项式的代数和组成的代数式叫做多项式（polynomial）。

扩展资料：
整式的加减：
整式的加减即单项式和多项式的加减，可利用去括号法
则和合并同类项来完成。

例题：
5xy+（-2xy）+6x+（-7x）+3y+（-8y）
=3xy+（-x）+（-5y）
=3xy-x-5y
整式为单项式和多项式的统称，是有理式的一部分，在有理式中可以包含加，减，乘，除、乘方五种运算，但在整式中除数不能含有字母。

1、单项式
由数与字母的积或字母与字母的积所组成的代数式叫做单项式（monomial）。

2、多项式
由有限个单项式的代数和组成的代数式叫做多项式(polynomial)。

扩展资料
因式分解原则——
1、分解因式是多项式的恒等变形，要求等式左边必须是多项式。

2、分解因式的结果必须是以乘积的形式表示。

3、每个因式必须是整式，且每个因式的次数都必须低于原来多项式的次数。

4、结果最后只留下小括号，分解因式必须进行到每一个多项式因式都不能再分解为止。

整式知识结构图1. 由数与字母的乘积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式。

如：等都是单项式。

2. 单项式的系数、次数，单项式中的数字因数叫做单项式的系数。

如的系数分别是5，，单项式ab的系数是“1”，单项式的系数是。

单项式中，所有字母的指数的和叫做单项式的次数，如单项式叫5次单项式，叫做三次单项式。

3. 多项式及多项式的次数。

几个单项式的和叫做多项式，在多项式中，每个单项式叫多项式的项，不含字母的项叫常数项。

多项式里，次数最高项的次数，就是这个多项式的次数。

如多项式是一个四次三项式。

多项式是一个七次二项式。

4. 多项式的升幂排列和降幂排列：把一个多项式按某一字母的指数从大到小的顺序排列起来，叫做这个多项式按这个字母降幂排列。

把一个多项式按某一字母的指数从小到大的顺序排列起来，叫做这个多项式按这个字母升幂排列。

由于多项式的项包括它前面的性质符号，因此在排列时，需带符号一起移动，在含有两个或两个以上字母的多项式，按某一字母排列时，要特别注意按哪一个字母排列。

5. 整式的概念单项式和多项式统称为整式6. 同类项的概念：所含字母相同，并且相同字母的次数也相同的项叫做同类项，几个常数项也是同类项。

判断几个单项式（或同一个多项式的项）是不是同类项有两个条件（1）所含有的字母相同（2）相同字母的指数分别相同。

只有这两个条件同时具备了才能说它们是同类项。

同类项与其系数无关，与字母的顺序无关。

7. 合并同类项合并同类项的法则：把同类项的系数相加，所得的结果作为系数，字母和字母的指数保持不变。

合并同类项的具体步骤：第一步：准确地找出同类项第二步：利用分配律，把同类项的系数加在一起（用小括号），字母和字母的指数不变。

第三步：写出合并结果。

8. 去括号和添括号去括号法则：括号前是“+”号，把括号和它前面的“+”号去掉，括号里各项都不变符号。

括号前是“－”号，把括号和它前面的“－”号去掉。

括号里各项都改变符号。

七年级数学上册《整式加减法》思维导图与考点梳理
1.都是数或字母的积的式子叫做单项式，单独的一个数或一个字母也是单项式。

2.单项式中的数字因数叫做这个单项式的系数。

3. 一个单项式中，所有字母的指数的和叫做这个单项式的次数。

4.几个单项的和叫做多项式，其中，每个单项式叫做多项式的项，不含字母的项叫做常数项。

5.多项式里次数最高项的次数，叫做这个多项式的次数。

6.把多项式中的同类项合并成一项，叫做合并同类项。

合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变。

7.如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同。

8.如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反。

9.一般地，几个整式相加减，如果有括号就先去括号，然后再合并同类项。

你现在的努力要对得起别人对你的好！
Math 实验室-1-人教版七年级数学上册章节思维导图
共4章
人教版七年级数学上册教材目录
第1章有理数的思维导图
1.1正数和负数
1.2有理数
1.3有理数的加减法
1.4有理数的乘除法
1.5有理数的乘方
第2章整式的加减的思维导图
2.1整式
2.2整式的加减
第3章一元一次方程的思维导图
3.1从算式到方程
3.2解一元一次方程(一)——合并同类项与移项
3.3解一元一次方程(二)——去括号与去分母
3.4实际问题与一元一次方程
第4章几何图形初步的思维导图
4.1几何图形
4.2直线、射线、线段
4.3角
4.4课题学习
设计制作长方体形状的包装纸盒。

第一章 有理数思维导图 ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧<≤⨯⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧分配律乘法结合律加法结合律结合律乘法交换律加法交换律交换律运算律乘方的运算符号法则有理数的除法法则有理数的乘法法则有理数的减法法则有理数的加法法则法则运算方法叫做科学记数法是正整数），这种记数，的形式（其中把一个数表示乘——科学记数法数相同因数的个数叫做指相同的因数叫做底数，叫做幂叫做乘方，乘方的结果个相同因数的积的运算求——乘方的两个数互为倒数—乘积是—倒数的绝对值叫做数的点与原点的距离，一般地，数轴上表示数——绝对值数，叫做互为相反数—只有符号不同的两个—相反数相关概念负有理数正有理数按性质符号分分数整数按定义分分类有理数n 10a 110a n 1a a 0n第二章 整式的加减思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧合并同类项去括号步骤反的符号与原来的符号相去括号后原括号内各项——括号外因数为负同的符号与原来的符号相去括号后原括号内各项——括号外因数为正去括号作为合并后项的系数所得的结果把同类项的系数相加，——合并同类项同字母的指数也相同—所含字母相同并且相—同类项整式的加减的次数—多项式中次数最高项—次数—不含字母的项—常数项项式—组成多项式的每个单—项—几个单项式的和—定义多项式指数的和—单项式中所有字母的—次数—单项式中的数字因数—系数的式子—由数或字母的积组成—定义单项式用字母表示数减加的式整第三章 一元一次方程思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧际意义符合题意，是否符合实验：检验所求的解是否值中所要求的相关数量的出未知数的值以及题目解：解所列的方程，求一个数字列方程关系以及若干倍多或少关系、相等关系、倍数列：根据题目中的数量与所列方程有关的数量含未知数的代数式表示设：设未知数，并且用数量间的关系知量和未知量，明确各审：弄清题意，分清已解应用题一次方程列一元系数化为合并同类项移项去括号去分母解一元一次方程的步骤的数，结果仍相等，或除以同一个不为：等式两边乘同一个数性质，结果仍相等或式子同一个数或减：等式两边加性质等式的性质过程解方程：求方程的解的数的值号左右两边相等的未知方程的解：使方程中等等号两边都是整式，，未知数的次数都是元一个未知数一元一次方程：只含有式方程：含有未知数的等一元一次方程程方次一元一102)()(11)(第四章 几何图形初步思维导图⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧角的度量互补互余两角的特殊关系比较大小的方法表示方法定义角线段的和、差与画法线段的中点两点之间的距离段最短基本事实：两点之间线比较方法特点表示方法线段特点表示方法射线条直线基本事实：两点确定一特点表示方法直线线平面图形立体图形的平面展示图从上面看从左面看从正面看形从不同的方向看立体图常见的立体图形立体图形几何图形初步。