克里格插值基础arcgis
- 格式:doc
- 大小:63.50 KB
- 文档页数:2

A R C G I S克里金插值法 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】1、mapgis转化arcgis打开mapgis 文件转换装入点---输出shape文件输出shape文件另存2、arcgis克里金插值a、载入文件打开arcmap载入点文件载入后右击---join and relates——join点Ok右击—data---export data另存—ok 提示是否载入点击是删除原来的shape文件,使用新保存的这个B、添加区域框()就是边界还可以直接添加一些已转换为shape的现状地物另存后点ok为所需要成区的范围线(必须保证无拓扑错误,可在mapgis 中检查,其实在mapgis 中若是有相应的区文件 可以直接转换shape成的区用于后期剪裁)分析范围——-----options上下左右要调整这个范围就是生成的光栅图的范围C、分析数据(插值到光栅)--interpolate to raster ----其中为分辨率为分析对象保存位置和名字D 、进行重新分级-----------classify-------分级后点保存路径如果需要,转化成光栅——————-----convert----分多少级分级临界值切割以上是切割光栅文件 切割为一个整体统一颜色的 如果需要彩色图 可以用双击该图---symbology---categories —unique values---value field —GRIDCDDE —修改颜色若是直接裁剪彩色文件 是在分级后对分级之后的文件直接用要切的范围框 就是那个区保存路径切完得到修饰后即可出图这是出图模式从上到下依次是标题、图例、指北针、比例尺出图横向出图,存为jepg即可。

arcgis克里金插值等值线标注摘要:1.ArcGIS克里金插值介绍2.克里金插值原理与应用3.等值线标注方法与步骤4.插值结果的可视化与分析正文:ArcGIS是一款强大的地理信息系统软件,其中克里金插值(Kriging Interpolation)是一种常用的空间数据插值方法。
本文将详细介绍ArcGIS克里金插值的原理、应用,以及如何进行等值线标注,最后对插值结果进行可视化和分析。
一、ArcGIS克里金插值介绍克里金插值是一种基于统计学的空间插值方法,它通过利用已知的样本点数据,估算未知的空间位置值。
ArcGIS中的克里金插值工具可以根据不同的数据类型和需求,生成不同类型的插值结果,如栅格数据、点数据等。
二、克里金插值原理与应用克里金插值原理主要基于变异函数理论和最小二乘法。
变异函数描述了空间数据在不同距离上的变化规律,而最小二乘法则用于求解最佳拟合参数。
在ArcGIS中,克里金插值应用于各种领域,如土壤侵蚀、矿产资源预测、气象数据重建等。
三、等值线标注方法与步骤1.准备数据:首先,需要准备好克里金插值所需的样本点数据和相应的属性值。
这些数据可以是栅格数据、点数据或线数据等。
2.创建表面:在ArcGIS中,利用克里金插值工具生成插值表面。
可以根据需求选择不同的插值类型,如普通克里金插值、简单克里金插值等。
3.提取等值线:利用ArcGIS的等值线提取工具,根据插值表面的数值范围和间隔,提取等值线。
4.标注等值线:在提取的等值线上添加标注,如数值、图例等。
可以通过ArcGIS的标注工具或Python脚本实现。
四、插值结果的可视化与分析1.插值结果可视化:利用ArcGIS的图层功能,将插值表面、等值线和标注等数据进行可视化展示。
2.插值结果分析:通过ArcGIS的属性查询、统计分析等功能,对插值结果进行进一步分析,如空间分布特征、趋势分析等。
总之,ArcGIS克里金插值是一种实用且广泛应用于地理信息系统领域的空间插值方法。

arcgis 克里金原理摘要:一、ArcGIS 简介二、克里金插值法的基本原理三、ArcGIS 中克里金插值法的应用四、克里金插值法的优缺点分析五、总结正文:ArcGIS 是一款由美国环境系统研究所(Esri)公司开发的地理信息系统软件,广泛应用于地图制作、数据分析、空间建模等领域。
在ArcGIS 中,克里金插值法是一种常用的空间数据分析工具,可以用于插值、拟合和预测等任务。
克里金插值法(Kriging Interpolation)是一种基于最小二乘法的插值方法,它的基本原理是寻找一个最佳函数来描述数据点之间的关系。
这个函数被称为克里金多项式,可以通过最小化数据点与克里金多项式之间的误差平方和来求解。
在ArcGIS 中,克里金插值法可以通过“Spatial Analyst T ools”工具箱中的“Interpolate”工具来实现。
在ArcGIS 中,克里金插值法的应用广泛,例如在土地利用、土壤侵蚀、地下水位、气象数据等方面都有涉及。
以土地利用为例,通过克里金插值法可以预测不同土地利用类型在空间上的分布,为土地资源管理和规划提供科学依据。
克里金插值法具有以下优点:1.适用于各种空间数据类型,如点、线、面等;2.可以处理缺失值和噪声数据;3.考虑了空间数据的变异性和相关性;4.生成的插值表面具有较高的精度和稳定性。
然而,克里金插值法也存在一定的局限性:1.计算复杂度较高,对计算资源需求较大;2.对于具有复杂空间特征的数据,克里金插值法的效果可能不佳;3.克里金插值法假设数据点之间的空间关系是线性的,对于非线性关系的数据,可能需要采用其他插值方法。
综上所述,ArcGIS 中的克里金插值法是一种强大的空间数据分析工具,在许多应用场景中都能发挥重要作用。

克里格插值基础来源:互联网1. 克里格方法概述克里格方法(Kriging)又称空间局部插值法,是以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法,是地统计学的主要内容之一。
南非矿产工程师D.R.Krige(1951年)在寻找金矿时首次运用这种方法,法国著名统计学家G.Matheron随后将该方法理论化、系统化,并命名为Kriging,即克里格方法。
克里格方法的适用范围为区域化变量存在空间相关性,即如果变异函数和结构分析的结果表明区域化变量存在空间相关性,则可以利用克里格方法进行内插或外推;否则,是不可行的。
其实质是利用区域化变量的原始数据和变异函数的结构特点,对未知样点进行线性无偏、最优估计。
无偏是指偏差的数学期望为0,最优是指估计值与实际值之差的平方和最小。
也就是说,克里格方法是根据未知样点有限邻域内的若干已知样本点数据,在考虑了样本点的形状、大小和空间方位,与未知样点的相互空间位置关系,以及变异函数提供的结构信息之后,对未知样点进行的一种线性无偏最优估计。
克里格方法与反距离权插值方法类似的是,两者都通过对已知样本点赋权重来求得未知样点的值,可统一表示为:式中,Z(x 0 为未知样点的值,Z(x i 为未知样点周围的已知样本点的值,为第i个已知样本点对未知样点的权重,n为已知样本点的个数。
不同的是,在赋权重时,反距离权插值方法只考虑已知样本点与未知样点的距离远近,而克里格方法不仅考虑距离,而且通过变异函数和结构分析,考虑了已知样本点的空间分布及与未知样点的空间方位关系。
2. 克里格方法的具体步骤用克里格方法进行插值的主要步骤如图1所示:图1 克里格方法的主要步骤在克里格插值过程中,需注意以下几点:(1)数据应符合前提假设(2)数据应尽量充分,样本数尽量大于80,每一种距离间隔分类中的样本对数尽量多于10对(3)在具体建模过程中,很多参数是可调的,且每个参数对结果的影响不同。

arcgis克里金插值等值线标注摘要:一、arcgis 简介1.1 arcgis 的定义1.2 arcgis 的主要功能二、克里金插值2.1 克里金插值的定义2.2 克里金插值的基本原理2.3 克里金插值的常用算法三、等值线标注3.1 等值线的定义3.2 等值线标注的意义3.3 等值线标注的方法四、arcgis 克里金插值等值线标注操作步骤4.1 准备工作4.2 克里金插值4.3 等值线标注4.4 结果分析正文:一、arcgis 简介ArcGIS 是由美国环境系统研究所(Esri)公司开发的一款地理信息系统(GIS)软件。
它具有丰富的功能,可以用于数据采集、管理、分析和可视化等方面,广泛应用于城市规划、环境保护、资源管理和国土监测等领域。
1.1 arcgis 的定义ArcGIS 是一个集成了多种功能模块的GIS 软件平台,包括了数据采集、编辑、管理、分析和可视化等功能。
它不仅可以用于处理地理空间数据,还可以用于制作地图、分析空间关系和模拟地理过程等。
1.2 arcgis 的主要功能ArcGIS 的主要功能包括:数据采集与编辑、空间分析、地图制作、可视化、数据库管理、网络分析、地理处理、三维分析等。
二、克里金插值克里金插值(Kriging Interpolation)是一种常用的插值方法,它是一种基于最小二乘原则的插值方法。
2.1 克里金插值的定义克里金插值是一种以最小二乘原则为基础的空间插值方法,它通过计算待插点周围相邻点之间的协方差,来预测待插点的值。
2.2 克里金插值的基本原理克里金插值的基本原理是通过计算待插点周围相邻点之间的协方差,来预测待插点的值。


arcgis克里金插值等值线标注(原创实用版)目录1.引言2.ArcGIS 克里金插值的概念和原理3.ArcGIS 克里金插值等值线标注的方法和步骤4.应用实例5.总结正文1.引言ArcGIS 是一款功能强大的地理信息系统软件,它可以帮助用户处理、分析和可视化地理空间数据。
在地理数据分析中,插值是一种常用的方法,它可以根据已知的数据点预测未知区域的地理特征。
克里金插值是一种基于空间变异理论的插值方法,它具有较强的适应性和精确度。
在 ArcGIS 中,可以通过插值工具创建克里金插值图,并通过等值线标注方法对插值结果进行可视化表达。
本篇文章将详细介绍 ArcGIS 克里金插值等值线标注的方法和步骤。
2.ArcGIS 克里金插值的概念和原理克里金插值(Kriging Interpolation)是一种基于空间变异理论的插值方法,它通过对空间数据的变异特征进行建模,预测未知区域的地理特征。
克里金插值的基本原理是:在空间域中,一个点的值受到其邻近点的影响,而邻近点的影响程度与其距离成反比。
因此,可以通过构建空间权重矩阵,计算每个点对预测点的影响程度,从而预测未知区域的值。
3.ArcGIS 克里金插值等值线标注的方法和步骤(1)准备数据:首先需要准备一组地理空间数据,包括需要预测的变量值和空间坐标。
(2)创建克里金插值图:在 ArcGIS 中,使用"Spatial Analyst Tools"工具箱中的"Interpolate"工具创建克里金插值图。
需要设置插值方法、插值参数和输出参数等。
(3)计算等值线:使用"Spatial Analyst Tools"工具箱中的"Calculate Distance"工具计算每个点与其邻近点的距离。
然后,根据插值图和距离信息,使用"Spatial Analyst Tools"工具箱中的"Raster Calculator"工具计算等值线。

arcgis克里金插值等值线标注ArcGIS克里金插值等值线标注等值线标注是一种常用的地图制作技术,通过将等值线与图上的数值对应,可以直观地展示地理现象的分布情况。
在GIS领域,ArcGIS软件提供了克里金插值方法来生成等值线,并且可以对等值线进行标注,使得地图更加直观和易于理解。
克里金插值是一种常用的空间插值方法,它基于地理学中的克里金原理,通过对已知点的空间关系进行分析,推断未知点的数值。
在ArcGIS中,克里金插值可以通过“插值”工具来实现。
首先,我们需要将已知点的数据导入到ArcGIS中,这些数据可以是实测的地理现象数值,比如温度、降雨量等。
然后,选择插值方法为克里金,设置插值参数,如克里金模型类型、搜索半径等。
点击运行,ArcGIS会自动进行插值计算,生成一个栅格图层。
接下来,我们可以使用“等值线”工具将栅格图层转换为等值线图层。
在生成的等值线图层中,每条等值线代表一个数值,可以根据需要进行标注。
ArcGIS提供了多种等值线标注的方法,比如标注线上数值、标注线段的起始和终止数值等。
在标注过程中,我们可以根据地图的比例尺和显示效果进行调整,使得标注文字清晰可读。
此外,ArcGIS还支持对标注进行样式设置,可以调整字体、颜色、大小等属性,以满足不同的制图需求。
等值线标注在地理信息系统中具有广泛的应用。
例如,在气象领域,通过等值线标注可以直观地展示气温、降雨量等气象要素的分布情况,帮助人们了解气候变化和天气预报。
在地质勘探中,等值线标注可以用于展示地下水位、地下资源等分布情况,为资源开发提供参考。
在城市规划中,等值线标注可以显示地形起伏、地势高低等信息,为城市规划和土地利用提供依据。
使用ArcGIS进行克里金插值等值线标注有一些注意事项。
首先,插值结果的准确性和可靠性取决于已知点的数据质量和空间分布。
因此,在进行插值之前,我们应该对已知点的数据进行质量检查和处理,确保数据的可靠性。
其次,插值参数的选择也是影响结果的重要因素,需要根据具体情况进行合理设置。

第7卷%第12期软件导刊2008年12月Software GuideVol.7No.12Dec. 2008ArcGIS 中的地统计克里格插值法及其应用王艳妮,谢金梅,郭祥(中国地质大学资源学院,湖北武汉430074)摘要:ArcGIS 软件的地统计分析扩展模块是一个功能强大、简单易用的数据分析与表面建模工具,应用领域广泛。
首先介绍了地质统计学的概念和克里格插值的各种方法,然后从地统计的角度出发,运用ArcGIS 软件中地统计分析模块,探讨了克里格插值法在土地平整工程中的应用。
关键词:GIS ;ArcGIS 地统计分析;克里格插值;土方量中图分类号:TP312文献标识码:A文章编号:1672-7800(2008)12-0036-030引言地质统计学是上个世纪60年代法国人Matheron 在前人的它是数学地质领域中一门发展迅速且有着广泛应用前景的新兴学科。
经过广大数学地质工作者、地质统计学工作者、矿山地质和采矿设计专家及其他地质统计学应用者和爱好者的不断努力,现在已经形成了一套独立的理论体系,成为数学地质中比较活跃的一个分支。
基础上总结并提出的,它又称为克里格方法(Kriging )。
地质统计学中的克里格插值方法,由于其具有插值和估计的双重特点,在许多领域中都得到了广泛应用,已成为空间统计学上的一个重要分支,同时也成为许多专业、商业软件的重要组成部分。
近几十年来,地理信息系统(Geographic Information Sys -——空间tem ,简称GIS )技术发展很快,作为其重要的组成部分—信息分析,也已经发展出一些重要的理论模型方法。
空间分析的应用领域含盖面极广,包含空间分析、空间数据分析、空间统计、地质统计学等。
在目前众多的GIS 软件中,虽有许多都涉足了空间分析领域,但其中有关地质统计学方面的内容却非常少。
ArcGIS8及以上版本软件中,将地质统计学单独作为一个分析扩展模块(即Geostatistical Analyst ,简称GA )纳入到了整个1.2克里格插值基础克里格插值(Kriging )又称空间局部插值法,是以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法,是地统计学的主要内容之一。
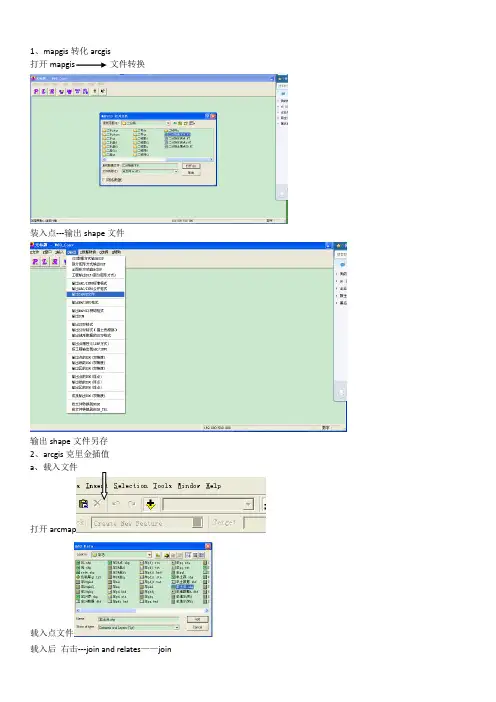
1、mapgis转化arcgis打开mapgis 文件转换装入点---输出shape文件输出shape文件另存2、arcgis克里金插值a、载入文件打开arcmap载入点文件载入后右击---join and relates——join点Ok右击—data---export data另存—ok 提示是否载入点击是删除原来的shape文件,使用新保存的这个B、添加区域框()就是边界还可以直接添加一些已转换为shape的现状地物为所需要成区的范围线(必须保证无拓扑错误,可在mapgis 中检查,其实在mapgis中若是有相应的区文件可以直接转换shape 成的区用于后期剪裁)另存后点ok分析范围——-----options上下左右要调整这个范围就是生成的光栅图的范围C、分析数据(插值到光栅)--interpolate to raster ----其中为分辨率为分析对象保存位置和名字D、进行重新分级------- ----classify-------分级后点ok 保存路径如果需要,转化成光栅——————-----convert----分多少级分级临界值切割以上是切割光栅文件 切割为一个整体统一颜色的 如果需要彩色图 可以用双击该图---symbology---categories —unique values---value field —GRIDCDDE?—修改颜色若是直接裁剪彩色文件 是在分级后对分级之后的文件直接用要切的范围框 就是那个区保存路径切完得到修饰后即可出图这是出图模式从上到下依次是标题、图例、指北针、比例尺出图横向出图,存为jepg即可。

arcgis克里金插值符号系统等值线标注
ArcGIS中的克里金插值是一种常用的地理数据分析方法,用于推断未知点的属性值。
通过基于已知点的属性值和其空间位置的统计关系,克里金插值方法可以生成表面模型,并根据这个模型生成等值线符号系统。
在ArcGIS中进行克里金插值时,可以按照以下步骤进行等值线标注:
1. 打开ArcGIS软件并加载要进行插值分析的数据。
2. 在“Geoprocessing(地理处理)”工具箱中找到“Geostatistical Analyst Tools(地质统计分析工具)”,选择“Interpolation(插值分析)”。
3. 在弹出的对话框中选择克里金插值方法,并设置合适的参数,比如输入数据、字段、输出格网大小等。
4. 点击“OK”开始进行插值分析,等待分析过程完成。
5. 完成插值后,在结果中找到生成的表面模型,并将其添加到地图中。
6. 在图层列表中右键点击表面模型图层,选择“Properties(属性)”。
7. 在属性对话框中选择“Symbology(符号系统)”,选择“Contour(等值线)”作为渲染类型。
8. 根据需要调整等值线的间隔、颜色、线型等参数。
9. 可选择对等值线进行标注,可以通过“Labels(标注)”选项进行设置,并调整标注的显示样式。
10. 完成设置后,点击“OK”应用并关闭属性对话框,等值线标注效果即可显示在地图中。
请注意,在进行克里金插值和等值线标注时,需要根据具体数据和需求调整参数以及保证数据的准确性和合法性。
ArcGIS 地统计克里金插值1.1 地统计扩ArcGIS 地统在软件中轻易地统计学的功(1)ESDA:(2)表面预(3)模型检地统计学起源的克里格方法方法是最主要1.2 表面预测ArcGIS 地统程。
一个完整的空现数据的特点Data 菜单及选择和预测模Geostatistic部分,一部分下面将按上述(注:[1]文章量样本),整本理论一般未准名称的也未我们下面的任扩展模块简介统计分析模块在易实现。
体现了功能在地统计分:探索性空间数测(模拟)和验与对比。
源于克里格。
当法。
虽然空间数要、最常用的空测主要过程统计扩展模块的空间数据分析过点,比如是否为其下级菜单完模型的选择;最cal Wizard 菜分作为训练样本述表面预测过程章示例中所使用整个过程均使用未进行解释,可未进行解释。
)任务是根据测量ArcGIS 打印20在地统计学与 G了以人为本、可分析模块的都能数据分析,即数误差建模;当时他用此法预数据分析还有其空间分析方法,的菜单非常简单过程,或者说表为正态分布、有成);然后选最后检验模型是菜单完成)。
1/ 12C本,一部分作为程进行叙述。
用的数据为 Ar用此数据;[2]文可查阅相关地统量所得到的某地地统计学习印 | 推荐 | 评007-8-1 09: GIS 之间架起了可视化发展的趋能实现,包括:数据检查;预测矿产分布,其他方法,如 I下面也以此法单,如下所示,表面预测模型,有没有趋势效应择合适的模型是否合理或几种Create Subse为检验样本。
rcGIS 扩展模文章以操作方统计理论资料;地臭氧浓度数据习指南( 一)评分 11 了一座桥梁。
使趋势。
后来经过别人IDW(反距离加法为主进行。
但由此却可以一般为。
拿到应、各向异性等进行表面预测种模型进行对比ets菜单的作块中所带的学法介绍为主,操作中所用到据进行全区的臭使得复杂的地统改进修改发展加权插值法)等完成完整的空到数据,首先要等等(此功能主,这其中包括比;(后两种功用是为把采样习数据(某地所涉及到的地的某些参数为臭氧浓度预测。
arcgis 克里金插值实验步骤克里金插值是地理信息系统(GIS)中常用的一种插值方法,用于根据已知点的空间分布和属性值来推断未知点的属性值。
在ArcGIS软件中,克里金插值是一个强大的空间分析工具,可以帮助用户更好地理解空间数据的分布规律。
在进行克里金插值实验之前,首先需要准备一些必要的数据和工具。
下面是在ArcGIS中进行克里金插值实验的具体步骤:1. 打开ArcGIS软件,并加载要进行插值的数据。
这些数据可以是点数据、线数据或面数据,其中点数据最为常用。
确保数据的属性字段中包含有用于插值的数值字段。
2. 确定插值的参数设置。
在ArcGIS中,克里金插值的参数包括插值方法、搜索半径、插值权重等。
根据实际情况,选择合适的参数值进行插值。
3. 打开“空间分析”工具箱,在“插值”工具集中选择“克里金插值”工具。
在弹出的参数设置对话框中,选择要插值的数据图层、插值字段和输出栅格数据的保存位置。
4. 设置克里金插值的参数。
根据实际情况,设置插值方法(如简单克里金、普通克里金、泛克里金等)、搜索半径、插值权重等参数值。
5. 运行插值分析。
点击“运行”按钮,ArcGIS将根据所设置的参数值进行克里金插值分析,并生成插值结果。
在插值结果中,可以看到未知点的预测值和插值的插值误差。
6. 分析插值结果。
查看插值结果的插值图和插值误差图,分析插值的精度和可靠性。
根据需要,可以对插值结果进行进一步的处理和分析。
通过以上步骤,您可以在ArcGIS中进行克里金插值实验,并得到插值结果。
克里金插值是一种常用的空间插值方法,可以帮助您更好地理解地理数据的分布规律,为地理分析和决策提供有力的支持。
希望以上步骤对您有所帮助,祝您实验顺利!。
arcgis 克里金插值实验步骤克里金插值是一种常用的空间插值方法,它通过已知点数据来推测未知点的值。
在ArcGIS中,克里金插值是一种内插法,可以用于生成表面模型。
下面是克里金插值的实验步骤及相关参考内容:1. 数据准备与导入:首先,需要准备好已知点数据,这些数据是我们用来插值的基础。
可以使用Excel或其他数据源来存储这些数据,并将其导入到ArcGIS中。
参考内容:《ArcGIS教程与实例:数据处理篇》一书第5章数据导入部分。
2. 创建插值点数据集:在ArcGIS中,需要将已知点数据转换为插值点数据集。
插值点数据集是一种特殊的GIS数据集,它包含已知点数据的几何位置和值。
可以通过选择已知点数据并使用“创建插值点数据集”工具来实现。
参考内容:《ArcGIS 中插值点数据集的创建方法》一文。
3. 设置插值环境参数:在进行插值前,可以通过设置克里金插值的环境参数来调整插值结果。
这些参数包括:插值方法、克里金参数、搜索半径等。
参考内容:《ArcGIS帮助文档:设置克里金插值环境参数》。
4. 执行克里金插值:在ArcGIS中,通过选择插值点数据集和设置好的环境参数,可以执行克里金插值操作。
插值结果将以表面模型的形式呈现。
参考内容:《ArcGIS帮助文档:执行克里金插值的方法》。
5. 分析与评估插值结果:在插值完成后,需要对插值结果进行分析与评估。
可以使用ArcGIS中的工具和技术来计算不确定性、生成错误图、绘制等高线等。
参考内容:《ArcGIS实战技巧:克里金插值结果分析与评估》一文。
6. 结果展示与输出:最后,可以将插值结果展示出来,并输出为各种格式的数据、图表或地图。
可以使用ArcGIS中的图表、符号等功能来美化结果的展示。
参考内容:《ArcGIS中结果展示与输出的方法》。
总结:通过以上实验步骤,我们可以使用ArcGIS中的克里金插值方法来生成表面模型,并进行相关分析和评估。
这些步骤可以帮助我们更好地理解和利用克里金插值的原理和应用。
arcgis中克里金插值法的步骤嘿,朋友们!今天咱来聊聊 ArcGIS 中克里金插值法那些事儿。
啥是克里金插值法呢?简单来说,就像是给数据织一张密密的网,让那些没数据的地方也能有个靠谱的估计值。
那这克里金插值法到底咋弄呢?听我慢慢道来哈。
首先,你得有一堆数据点吧,就像拼图的小块儿。
这些数据点可重要了,它们是基础呀!然后呢,要对这些数据进行分析,看看它们的分布情况,是集中呢还是分散呢?这就好比你要了解一群人的分布特点一样。
接下来,就要选择合适的模型啦。
这就跟你挑衣服似的,得选适合的款式和尺码。
不同的模型有不同的特点,要根据数据的实际情况来选哦。
选好了模型,就开始计算啦!这计算过程可有点像解方程,要一步一步来,不能着急。
在这个过程中,电脑就像个聪明的小助手,帮你算出那些关键的数据。
算完了,你就得到了一个插值结果。
哇塞,就好像变魔术一样,那些没数据的地方也有值啦!不过可别高兴得太早,还得检查检查这个结果靠不靠谱呢。
你想想,要是随随便便就弄出来个结果,那能行吗?就像你做饭,
不认真做能好吃吗?
再说说这克里金插值法的好处吧。
它能让你的数据变得更完整,更
有参考价值。
就好比给一幅画添上了缺失的色彩,让它变得更加生动。
而且哦,它在很多领域都能用得上呢!比如地理呀、环境呀等等。
就像一把万能钥匙,可以打开很多知识的大门。
总之呢,ArcGIS 中的克里金插值法是个很实用的工具,但要想用
得好,可得认真对待每一个步骤哦!别马虎,别偷懒,这样才能得到
准确又有用的结果呀!大家都学会了吗?哈哈!。
克里金插值法(Kriging Interpolation)是一种用于空间数据插值的地统计学方法,常用于地理信息系统(GIS)软件如ArcGIS中。
它基于统计学原理,根据已知点的空间分布和变量值,预测未知位置的变量值。
以下是克里金插值法的基本原理:
1. 空间自相关性:克里金插值法的核心思想是假设同一地理区域内的点之间存在空间自相关性,即相邻点之间的变量值具有一定的关联性。
这意味着离得越近的点之间的变化趋势可能更相似。
2. 半变异函数:插值过程中使用了半变异函数(Semi-Variogram Function)来描述点之间的变异性。
半变异函数展示了不同距离下变量值之间的相关性或协方差。
这个函数可以帮助确定变量值在不同方向上的变异性和相关性。
3. 权重计算:在插值过程中,为了预测未知点的变量值,需要根据已知点的位置、变量值以及它们之间的空间关系来计算权重。
与离目标点距离近且变异性较小的点会得到较大的权重,而距离远或变异性大的点则得到较小的权重。
4. 插值预测:通过计算权重,将已知点的变量值加权平均,从而预测未知点的变量值。
权重的计算基于半变异函数和点之间的距离。
5. 交叉验证:为了评估插值的精度,通常会采用交叉验证方法。
该方法将已知数据分成训练集和测试集,通过对测试集进行插值并与真实值比较,评估克里金插值法的预测能力。
总之,克里金插值法通过考虑空间自相关性和半变异函数,利用已知点之间的关系来预测未知点的变量值。
这使得它在GIS等领域中广泛用于空间数据插值和预测。
1/ 1。
克里格插值基础
来源:互联网
1. 克里格方法概述
克里格方法(Kriging)又称空间局部插值法,是以变异函数理论和结构分析为基础,
在有限区域内对区域化变量进行无偏最优估计的一种方法,是地统计学的主要内容之一。
南非矿产工程师D.R.Krige(1951年)在寻找金矿时首次运用这种方法,法国著名统计学家G.Matheron随后将该方法理论化、系统化,并命名为Kriging,即克里格方法。
克里格方法的适用范围为区域化变量存在空间相关性,即如果变异函数和结构分析的结果表明区域化变量存在空间相关性,则可以利用克里格方法进行内插或外推;否则,是不可行的。
其实质是利用区域化变量的原始数据和变异函数的结构特点,对未知样点进行线性无偏、最优估计。
无偏是指偏差的数学期望为0,最优是指估计值与实际值之差的平方和最小。
也就是说,克里格方法是根据未知样点有限邻域内的若干已知样本点数据,在考虑了样本点的形状、大小和空间方位,与未知样点的相互空间位置关系,以及变异函数提供的结构信息之后,对未知样点进行的一种线性无偏最优估计。
克里格方法与反距离权插值方法类似的是,两者都通过对已知样本点赋权重来求得未知样点的值,可统一表示为:
式中,Z(x 0 )为未知样点的值,Z(x i )为未知样点周围的已知样本点的值,为第i个已知样本点对未知样点的权重,n为已知样本点的个数。
不同的是,在赋权重时,反距离权插值方法只考虑已知样本点与未知样点的距离远近,而克里格方法不仅考虑距离,而且通过变异函数和结构分析,考虑了已知样本点的空间分布及与未知样点的空间方位关系。
2. 克里格方法的具体步骤
用克里格方法进行插值的主要步骤如图1所示:
图1 克里格方法的主要步骤
在克里格插值过程中,需注意以下几点:
(1)数据应符合前提假设
(2)数据应尽量充分,样本数尽量大于80,每一种距离间隔分类中的样本对数尽量多于10对(3)在具体建模过程中,很多参数是可调的,且每个参数对结果的影响不同。
如:块金值:误差随块金值的增大而增大;基台值:对结果影响不大;变程:存在最佳变程值;拟合函数:存在最佳拟合函数(4)当数据足够多时,各种插值方法的效果相差不大。
3. 克里格方法的分类
目前,克里格方法主要有以下几种类型:普通克里格(Ordinary Kriging);简单克里格(Simple Kriging);泛克里格(Universal Kriging);协同克里格(Co-Kriging);对数正态克里格(Logistic Normal Kriging);指示克里格(Indicator Kriging);概率克里格(Probability Kriging);析取克里格(Disjunctive Kriging)等。
下面简要介绍一下ArcGIS中常用的几种克里格方法的适用条件,其具体的算法、原理可查阅相关文献资料。
不同的方法有其适用的条件,按照以上流程图所示步骤,当数据不服从正态分布时,若服从对数正态分布,则选用对数正态克里格;若不服从简单分布时,选用析取克里格。
当数据存在主导趋势时,选用泛克里格。
当只需了解属性值是否超过某一阈值时,选用指示克里格。
当同一事物的两种属性存在相关关系,且一种属性不易获取时,可选用协同克里格方法,借助另一属性实现该属性的空间内插。
当假设属性值的期望值为某一已知常数时,选用简单克里格。
当假设属性值的期望值是未知的,选用普通克里格。