下载文档原格式
立体几何线面平行证明要证明两个线面平行，一般可以通过以下几种方法来进行证明：方法一：使用平行线的性质假设我们有线面A和线面B，要证明A和B平行，可以通过以下步骤进行证明：1.假设线面A和线面B不平行，即存在一条线a与线面A不平行，又与线面B相交于一点P。
2.假设在线面A上存在一点Q，它与直线a上相交于一点R。
3.由于线a与线面B相交于P，所以线段PR必然属于线面B。
4.由于线a与线面A相交于R，所以线段PR必然属于线面A。
5.由于线面A和线面B都包含线段PR，所以它们必然相交。
6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。
方法二：使用支撑面的性质假设我们有线面A和线面B，要证明A和B平行，可以通过以下步骤进行证明：1.假设在线面A上存在一条直线a，它与线面B相交于一点P。
2.过直线a作平行于线面B的平面，该平面与线面A相交于线段QR。
3.由于直线a与线面B相交于点P，所以线段PR必然属于线面B。
4.由于平面上的任意两点可以确定一条直线，所以线段QR也属于线面B。
5.因此，线段QR同时属于线面A和线面B，所以它们不是平行的。
6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。
方法三：使用平行四边形的性质假设我们有线面A和线面B，要证明A和B平行1.假设在线面A上存在一条直线a，它与线面B相交于一点P。
2.在线面A上选择一点Q，并通过P点作一条平行于线面A的直线b。
3.连接直线a和直线b，得到平行四边形PQRD。
4.由于平行四边形的特性，相邻两边平行且长度相等，所以线段PD也是平行于线面A的，并且它必然属于线面B。
5.因此，线段PD同时属于线面A和线面B，所以它们不是平行的。
6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。
以上三种方法是一些常用的证明线面平行的方法，根据实际问题的具体情况，可以选择适合的方法进行证明。
专题二：立体几何---线面平行、面面平行一、知识点（1）线面平行性质定理（2）线面平行判定定理（3）面面平行性质定理（2）面面平行判定定理总结：立体几何中证明线面平行或面面平行都可转化为线线平行，而证明线线平行一般有以下的一些方法：（1）通过“平移”。
（2）利用三角形中位线的性质。
（3）利用平行四边形的性质。
（4）利用对应线段成比例。
（5）利用面面平行，等等。
二、练习题(1) 通过“平移”再利用平行四边形的性质1．如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分别为棱AB 、PD 的中点。
求证：AF ∥平面PCE ；2、如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面;（第1题图）(2) 利用三角形中位线的性质3、如图，已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点，求证：AM∥平面EFG。
4、如图，ABCD是正方形，O是正方形的中心，E是PC的中点。
求证：PA ∥平面BDE5．如图，三棱柱ABC—A1B1C1中，D为AC的中点.求证：AB1//面BDC1；ABCDEFGM6、如图，平面ABEF ⊥平面ABCD ，四边形ABEF 与ABCD 都是直角梯形，090,BAD FAB BC∠=∠=//=12AD ，BE //=12AF ，,G H 分别为,FA FD 的中点 证明：四边形BCHG 是平行四边形；（3） 利用平行四边形的性质7．正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心， M 为BB 1的中点，求证： D 1O//平面A 1BC 1;8、在四棱锥P-ABCD 中，AB ∥CD ，AB=21DC ，中点为PD E . 求证：AE ∥平面PBC ；9、在如图所示的几何体中，四边形ABCD 为平行四边形，∠ ACB=90 ，ＥＡ⊥平面ＡＢＣＤ，EF ∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ.Ｍ是线段ＡＤ的中点，求证：ＧＭ∥平面ＡＢＦＥ;(4)利用对应线段成比例10、如图：S 是平行四边形ABCD 平面外一点，M 、N 分别是SA 、BD 上的点，且SM AM =NDBN， 求证：MN ∥平面SDC11、如图正方形ABCD 与ABEF 交于AB ，M ，N 分别为AC 和BF 上的点且AM=FN 。
高中立体几何证明线面平行的常见方法1.通过“平移”再利用平行四边形的性质题目1：四棱锥P-ABCD的底面是平行四边形，点E、F分别为棱AB、PD的中点。
证明AF∥平面PCE。
证明：将四棱锥P-ABCD平移，使其底面平移到平面PCE上，得到四棱锥P'-A'B'C'D'，其中A'B'C'D'与ABCD平行，且P'、E'、F'分别为A'B'、C'D'、A'D'的中点。
因为AF∥PD，所以AF'=PD'=C'F'，又因为AD'=C'D'/2=AB'/2=AF'/2，所以AD'∥B'C'。
因此，根据平行四边形的性质，AF'∥B'C'，即AF∥CE。
题目3：四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点，证明EB∥平面PAD。
证明：连接PE，因为E为PC的中点，所以PE∥AD。
又因为CD⊥AD，所以CD∥PE。
又因为CD=2AB，所以AB∥PE。
因此，根据平行四边形的性质，EB∥PA，即EB∥平面PAD。
2.利用三角形中位线的性质题目4：四面体ABCD中，E、F、G、M分别是棱AD、CD、BD、BC的中点，证明AM∥平面EFG。
证明：连接EF、EG、FG，因为E、F、G分别为三角形BCD、ACD、ABD的中点，所以EF、EG、FG分别是这三个三角形的中位线。
因此，EF∥AD，EG∥BD，FG∥AC。
又因为M为BC的中点，所以AM∥FG。
因此，AM∥平面EFG。
3.利用平行四边形的性质题目7：正方体ABCD-A' B' C' D'中O为正方形ABCD的中心，M为B'B的中点，求证D'O∥平面A'BC'。
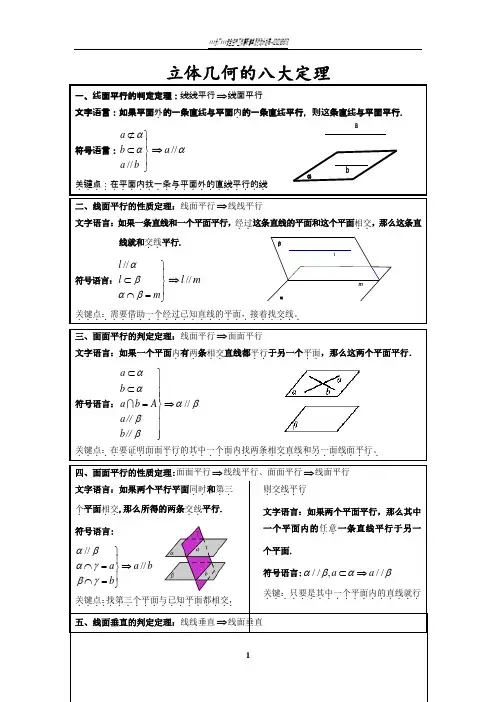
lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点．．．：．在．平面内．．．找一条与．．．．平面外．．．的．直线平行的线．．．．．． 二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要．．．．．．借助一个．．．．经过已知直线．．．．．．的．平面．．，接着找交线。
．．．．．．． 三、面面平行的判定定理：线面平行⇒面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行． 符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：．．．．在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 四、面面平行的性质定理:面面平行⇒线线平行、面面平行⇒线面平行 文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点．．．：找．．第三个平面．．．．．与已知平面都相交，．．．．．．．．．则交线平行．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．五、线面垂直的判定定理：线线垂直⇒线面垂直nmAαaBA l βαaβα文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面.符号语言：,a m a na m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．． 六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．． 七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点：在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。
DB A 1高中立体几何证明平行的专题(基本方法)立体几何中证明线面平行或面面平行都可转化为 线线平行，而证明线线平行一般有以下的一些方法： (1)通过“平移”。
(2)利用三角形中位线的性质。
(3)利用平行四边形的性质。
(4)利用对应线段成比例。
(5)利用面面平行，等等。
(1) 通过“平移”再利用平行四边形的性质1．如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分 别为棱AB 、 PD 的中点．求证：AF ∥平面PCE ；分析：取PC 的中点G ，连EG.，FG ，则易证AEGF 是平行四边形2、如图，已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝1＋3， 过A 作AE ⊥CD ，垂足为E ，G 、F 分别为AD 、CE 的中点，现将△ADE 沿AE 折叠，使得DE ⊥EC.（Ⅰ）求证：BC ⊥面CDE ； （Ⅱ）求证：FG ∥面BCD ；分析：取DB 的中点H ，连GH,HC 则易证FGHC 是平行四边形3、已知直三棱柱ABC －A 1B 1C 1中，D, E, F 分别为AA 1, CC 1, AB 的中点， M 为BE 的中点, AC ⊥BE. 求证：（Ⅰ）C 1D ⊥BC ； （Ⅱ）C 1D ∥平面B 1FM. 分析：连EA ，易证C 1EAD 是平行四边形，于是MF//EA（第1题图）4、如图所示, 四棱锥P -ABCD 底面是直角梯形,,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点,证明: //EB PAD 平面;分析:：取PD 的中点F ，连EF,AF 则易证ABEF 是平行四边形(2) 利用三角形中位线的性质5、如图，已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点，求证：AM ∥平面EFG 。
分析：连MD 交GF 于H ，易证EH 是△AMD 的中位线6、如图，ABCD 是正方形，O 是正方形的中心，E 是PC 的中点。
立体几何线面面面平行的证明线面、面面平行是立体几何中重要的概念，在几何证明中经常会遇到。
下面将分别介绍线面平行和面面平行的证明。
一、线面平行的证明：线面平行是指一条直线与其中一平面上的其他线段或射线都平行。
下面给出线面平行的证明。
设直线l与平面α相交于点A，我们要证明直线l与平面上任意一条线段或射线都平行。
设平面上有一条线段BC，先证明直线l与线段BC平行。
假设直线l与线段BC的其中一点D相交，连接线段AD和CD。
现在需要证明线段AD与线段BC平行。
根据平面几何的基本知识，在平面上，如果三个点在同一条直线上，那么该直线上的任意两点连线也位于平面上。
故点A、D、C三点在同一条直线上，那么线段AD也位于平面α上。
又因为直线l与线段BC和AD的交点分别为D和A，根据定理“若两条直线平行，则与这两条直线分别相交的两个平行线交点连线也平行”。
所以，直线l与线段AD平行。
同理，可以证明直线l与线段CD平行。
综上所述，直线l与线段BC平行。
接下来证明直线l与平面上的任意一条射线EF平行。
同样以与射线EF有相交点E的直线l为基准，连接射线BE和EF。
然后使用相同的证明方法，即证明射线BE与EF平行。
通过以上证明，我们可以得出结论：直线l与平面α上的任意一条线段或射线都平行。
即证明了线面平行。
二、面面平行的证明：面面平行是指两个平面平行，这在立体几何中也有重要应用。
下面给出面面平行的证明。
设平面α与平面β相交于一条直线l，我们要证明平面α与平面β上的任意一条线段或射线都平行。
以直线l为基准，设平面α上有一条线段AB，我们需要证明线段AB 与平面β平行。
作直线AB的平行线于平面β相交于点C。
现在需要证明直线BC与线段AB平行。
根据平面几何的基本知识，若两条直线平行，那么有一个点在一条直线上，则另一条直线上的点的连线也在同一平面上。
因此点C在平面β上，那么连接线段BC位于平面β上。
又因为平面α与平面β分别与直线AB和BC相交于A和C两点，根据定理“若两个平面分别与一条直线相交，那么它们的交线上的任意两点连线也在这两个平面的交线上”。
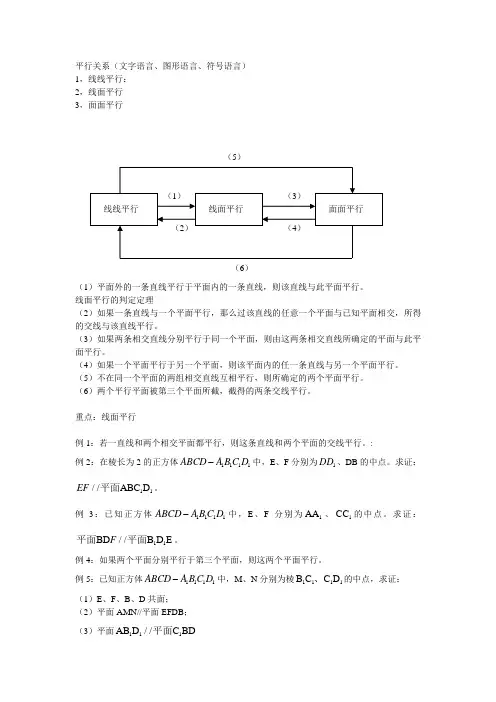
平行关系（文字语言、图形语言、符号语言） 1，线线平行： 2，线面平行 3，面面平行
（1）平面外的一条直线平行于平面内的一条直线，则该直线与此平面平行。
线面平行的判定定理
（2）如果一条直线与一个平面平行，那么过该直线的任意一个平面与已知平面相交，所得的交线与该直线平行。
（3）如果两条相交直线分别平行于同一个平面，则由这两条相交直线所确定的平面与此平面平行。
（4）如果一个平面平行于另一个平面，则该平面内的任一条直线与另一个平面平行。
（5）不在同一个平面的两组相交直线互相平行，则所确定的两个平面平行。
（6）两个平行平面被第三个平面所截，截得的两条交线平行。
重点：线面平行
例1：若一直线和两个相交平面都平行，则这条直线和两个平面的交线平行。
:
例2：在棱长为2的正方体1111ABC D A B C D -中，E 、F 分别为1DD 、DB 的中点。
求证：
11//ABC D EF 平面。
例3：已知正方体1111ABC D A B C D -中，E 、F 分别为1A A 、1C C 的中点。
求证：
11BD //B D E F 平面平面。
例4：如果两个平面分别平行于第三个平面，则这两个平面平行。
例5：已知正方体1111ABC D A B C D -中，M 、N 分别为棱1111B C C D 、的中点，求证： （1）E 、F 、B 、D 共面；
（2）平面AMN//平面EFDB ； （3）平面111AB D //C BD 平面
（5）
（6）。
直线、平面平行的判定
【要点梳理】
要点一、直线和平面平行的判定
文字语言：直线和平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线
与此平面平行.简记为：线线平行，则线面平行.
图形语言：
符号语言：a α⊄、b α⊂，//a b //a α⇒.
要点诠释：
（1）用该定理判断直线a 与平面α平行时，必须具备三个条件：
①直线a 在平面α外，即a α⊄；
②直线b 在平面α内，即b α⊂；
③直线a ，b 平行，即a ∥b ．
这三个条件缺一不可，缺少其中任何一个，结论就不一定成立．
（2）定理的作用
将直线和平面平行的判定转化为直线与直线平行的判定，也就是说，要证明一条直线和一个平面
平行，只要在平面内找一条直线与已知直线平行即可．
要点二、两平面平行的判定
文字语言：如果一个平面内有两条相交直线与另一个平面平行，则这两个平面平行.
图形语言：
符号语言：若a α⊂、b α⊂，a b A =，且//a β、//b β，则//αβ.
要点诠释：
（1）定理中平行于同一个平面的两条直线必须是相交的．
（2）定理充分体现了等价转化的思想，即把面面平行转化为线面平行，可概述为：线面平行⇒面
面平行．
要点三、判定平面与平面平行的常用方法
1．利用定义：证明两个平面没有公共点，有时直接证明非常困难，往往采用反证法．
2．利用判定定理：要证明两个平面平行，只需在其中一个平面内找两条相交直线，分别证明它们
平行于另一个平面，于是这两个平面平行，或在一个平面内找到两条相交的直线分别与另一个平面内两条相交的直线平行．
3．平面平行的传递性：即若两个平面都平行于第三个平面，则这两个平面互相平行．
【典型例题】
类型一、直线与平面平行的判定
例1．已知AB ，BC ，CD 是不在同一平面内的三条线段，E ，F ，G 分别是AB ，BC ，CD 的中点，
求证：AC//平面EFG ， BD//平面EFG ．
例2．已知有公共边AB 的两个全等的矩形ABCD 和ABEF 不在同一个平面内，P 、Q 分别为对
角线AE 、BD 上的点，且AP=DQ ，如右图．求证：PQ ∥平面CBE ．
【变式1】在正方体1111ABCD A B C D 中，1O 是正方形1111A B C D 的中心，求证：1//AO 面1BC D ．
【变式2】 已知P 是平行四边形ABCD 所在平面外一点，E 、F 分别为AB 、PD 的中点，求证：AF ∥平面PEC.
【变式3】 如右图所示，在四棱锥P —ABCD 中，底面ABCD 是矩形，PA ⊥平面ABCD ，AP=AB ，BP=BC=2，E ，F 分别是PB ，PC 的中点．
（1）证明：EF ∥平面PAD ；
（2）求三棱锥E —ABC 的体积V ．
类型二、平面与平面平行的判定
例3．如右图，已知正方体ABC D —A 1B 1C 1D 1，求证：平面AB 1D 1∥平面BDC 1．
例4．如右图，正方体ABCD —A 1B 1C 1D 1中，M 、N 、E 、F 分别是棱A 1B 1、A 1D 1、B 1C 1、C 1D 1的中点．
求证：平面AMN ∥平面EFDB ．
【变式1】点P 是△ABC 所在平面外一点，123,,G G G 分别是△PBC ，△APC ，△ABP 的重心，求
证：面123//G G G 面ABC .
【变式2】 如右图所示，在三棱柱ABC —A 1B 1C 1中，点D ，E 分别是BC 与B 1C 1的中点．
求证：平面A 1EB ∥平面ADC 1．
【变式3】 已知在正方体''''ABCD A B C D 中 ，M ，N 分别是''A D ，''A B 的中点，在该正方体中作出过顶点且与平面AMN 平行的平面，并证明你的结论．
【巩固练习】
1．下列说法中正确的是（ ）
A ．如果一个平面内有一条直线和另一个平面平行，那么这两个平面平行
B ．如果一个平面内有无数条直线和另一个平面平行，那么这两个平面平行
C ．如果一个平面内的任何一条直线都与另一个平面平行，那么这两个平面平行
D ．如果两个平面平行于同一直线，则这两个平面平行
2．已知三条互相平行的直线a 、b 、c 中，a α⊂，,b c α⊂，则平面α、β的位置关系是（ ）
A ．平行
B ．相交
C ．平行或相交
D ．重合
3．已知m ，n 是两条不重合的直线，α、β是两个不重合的平面，给出下列三个命题：
①////m m n n ββ⎧⇒⎨⊂⎩；②//m n n m ββ
⎧⇒⎨⎩与异面与相交；③//////m n m n αα⎧⇒⎨⎩。
其中正确命题的个数是（ ）
A ．0
B ．1
C ．2
D ．3
4．在下列条件中，可判断平面α与β平行的是( )
A ．α、β都平行于直线l
B ．α内存在不共线的三点到β的距离相等
C ．l 、m 是α内两条直线，且l ∥β，m ∥β
D ．l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β
5．下列四个正方体图形中，,A B 为正方体的两个顶点，M 、N 、P
分别是为其所在棱的中点，能得出//AB MNP 平面的图形的序号是
( )
A.①③
B.①④
C.②③
D.②④( )
6．已知平面α，β和直线,,a b c ，给出下列条件：
①//,//a c b c ；
②//,//,//a b αβαβ；
③,,//a b αβαβ⊂⊂。
其中可以使结论//a b 成立的条件有（ ）
A.①②
B. ②③
C. ①③
D. ①
7．过已知直线外一点与已知直线平行的直线有 条；过平面外一点与已知平面平行的直线有 条，与已知平面平行的平面有 个。
8．当//,//αβγβ，则α与γ的关系是 。
9．①若平面α内有一条直线平行于另一个平面β，则//αβ；
②若平面α内有两条直线平行于另一个平面β，则//αβ；
③若平面α内有无数条直线平行于另一个平面β，则//αβ；
④若平面α内任意一条直线平行于另一个平面β，则//αβ；
⑤若平面α内两条相交直线平行于另一个平面β，则//αβ。
以上命题正确的是________．
10．AB 、BC 、CD 是不在同一平面内的三条线段，经过它们中点的平面和AC 的位置关系是________，和BD 的位置关系是________。
三、解答题
11．如右图，P 是平行四边形ABCD 所在平面外一点，Q 是PA 的中点．
求证：PC ∥平面BDQ ．
12．如右图，P 为梯形ABCD 所在平面外一点，CD //2AB ，E 为PC 的中点。
求证：BE ∥平面PAD 。
13． 在正方体1111ABCD A B C D -中，P 为11A C 上任意一点。
（1）求证：//DP 平面1AB C ；
（2）求证：平面11AB D //平面1C BD .
14．两个全等的正方形ABCD 和ABEF 所在平面相交于AB ，M ∈AC ，N ∈FB ，且AM=FN ，过M 作MH ⊥AB 于H.
求证：MN ∥平面BCE ．。
