点线面体数学一年级上40页PPT

k●
平投影积聚成一个点，故
a
●1(2) c 交点K的水平投影也积聚在
n
该点上。
b
作图
k
m(n●2)
c
① 求交点
用面上取点法
●
a
1
② 判别可见性
点Ⅰ位于平面上，在前；
点Ⅱ位于MN上，在后。
故k2为不可见。
51
2) 两平面相交
两平面相交其交线为直线，交线是两平面 的共有线，同时交线上的点都是两平面的共 有点。
解法一：
b
解法二：
d
b
m●
n
●
c
c
a
a
m● a
b n● c
b d
a c
有多少解？
有无数解！
38
例：在平面ABC内作一条水平线，使其到 H面的距离为10mm。
a
有多少解？
m
n
c
唯一解！
b
ห้องสมุดไป่ตู้
10
b
c
n
m
a
39
2) 平面上取点
面上取点的方法：
首先面上取线
先找出过此点而又在平面上的一条直线作为辅 助线，然后再在该直线上确定点的位置。
O
Y
ay
V a
●
X ax
Z
az
A
●
O
●a W
a●
Y ay
点的投影规律:
a●
H
ay
Y
① aa⊥OX轴 aa⊥OZ轴 ② aax= aaz =y=Aa（A到V面的距离）
aay= aaz =x=Aa（A到W面的距离） aax= aay =z=Aa（A到H面的距离） 6

浙教版一年级数学 上册全套PPT课件
1
1、能正确区分立体图形，了 解你们的特征。
2、能找出生活中的立体图形。
正方体
长 方 体
圆柱体
球
蒙上眼睛，从布 袋里摸出一块积 木，然后说出它 们的名称。
找一找
你在生活中找到了什麽？
分一分：
长方体 球
正方体 圆柱
判断：在正方体下面画√
3
（2）
5
7
9
7
5
3
1
原来荷叶上有7只青蛙， 3只青蛙跳进了水里。 荷叶上还剩4只青蛙。
原来荷叶上有7只青蛙， 3只青蛙跳进了水里。 荷叶上还剩4只青蛙。
7-3=4
摆一摆、说一说。
原来有……，拿开……，还剩……，减法算式是……
-2 5 -4 5
8- 5=3
8 -4=4 8- 5=3 8 - 6= 2
6 1
2 57
3 4
10 9
8
4
5
2
3
1 6
10
87 9
10
10
（ 2） （ 4）
（ 7）
（10）
9 ＜ 10
10 ＞ 9
摆一摆 分一分
10 10 10 10 10 19 28 37 4655
10 10 10 10 91 82 73 64
一九一九好朋友， 二八二八手拉手， 三七三七真亲密， 四六四六一起走， 五五凑成一双手。
售票处
售票处
售票处
售票处
售票处
售票处
售票处
售票处
售票处
1、从左边开始按要求涂一涂
涂4个
4个
涂第4个
第4个
2.你能说说戴蓝色帽子的小猴子在第几个位置？

图中有（ 3）个 。
学以致用
1.看数圈一圈。
学以致用
2.接着画。
学以致用
3.连一连。
学以致用
4.把数量一样的连起来。
学以致用
5. 数一数，用不同的符号圈一圈。
课堂小结
你学会了哪 些知识？
数数时，一定 要有顺序。
1.数数时，要按照一定的顺序数，边数边做记号，做 到不重复、不遗漏，数到最后一个物体所对应的那 个数,就是这种物体的总个数。
人教实验版
一年级 数学 上册
第1单元 准备课
1 数一数
学习目标
1. 通过数数活动,掌握数数的方法。 2. 能正确数出图中物体的个数。
3.培养学生的观察能力和语言表达能 力。
复习导入
数一数 1.我们班有几块黑板？
2.我们班有几把笤帚？ 3.我们班有几个戳子？
复习导入
4.你的衣服上有几个纽扣？ 5.你的文具盒里有几支铅笔？ 6.你有几个手指？
2.确定前后的标准一般是面对的方向是前,背对的方向是后。
3.确定左右位置关系的方法:与右手对应的一面是右,与左手对 应的一面是左。
人教实验版
一年级 数学 上册
第3单元 1~5的认识和加减法
1 1~5的认识
学习目标
1. 认识1~5各数,知道1~5的数序。
2.会正确读、写1~5各数，会用1~5 各数表示物体的个数。
3.了解数学在生活中的运用，感受数 学与生活的密切联系。
复习导入
图中有什么？各有多少个？
情景导入
农家小院
数一数小院中各种物体的数量 分别是多少？
探索新知
1
探索新知
课件PPT
12
探索新知
课件PPT

精选ppt课件2021
14
• 直线具有明确性、简洁性、锐利性，给人以紧迫感、速度 感和力度感，富于男性性格的情感特征。
曲线具有丰满、优雅、柔软、
和谐和律动的审美意味，富有
女性性格的情感特征。几何曲
线如圆、椭圆、抛物线等，具
有节奏、比例、规整性与单纯
中的和谐感，富于现代感的审
美意味。自由曲线如开放曲线、
精选ppt课件2021
18
精选ppt课件2021
19
精选ppt课件2021
20
精选ppt课件2021
21
精选ppt课件2021
22
（三）面的表现方法
• 二次元空间构成的形都可以称之为面。二次元空间是平 面形的组织原则。不同形态的面，是由点或线密集，或线 的移动构成的。
• 面的形态，富有整体感的视觉特征。面和线一样，具有多 形态的属性。作为视觉元素的面，一般有以下一些形态：
波形线、螺旋线等，曲率不定，
富于变化，是极富个性的曲线。
追求自然的节奏感和韵律感时，
常运用自由曲线。
精选ppt课件2021
15
线的排列可以表现出虚面的特性，线与线之间相距越短虚面
的特性愈强。不同粗细、不同曲直、不同方向的线作交差排
。 列，可以表现出变化丰富的虚面
精选ppt课件2021
16
不同粗细或不同疏密的直线（曲线），作有秩序的渐变 排列，可以表现具有三次元空间的“曲面”，给人以强 烈的节奏与韵律感。
精选ppt课件2021
7
• 三个以上并相隔一定距离的点，我们的视线会来回于各点 之间，而产生“面”的感觉。点的个数越多，点与点之间 的距离越短，“面”的感觉愈强。
精选ppt课件2021

• 就带有方向性的点来说，例如在处理椭圆或短的线段 的时候，可以从事特别复杂的线化表现。
具有方向性的点之 线化构成
• 利用点的大小来从事线的表现，由于点的方向逐渐变 大，给人以强烈的方向感。
不具方向性的点之集合造成的线化表现
③ 点的面化 • 点的移动产生线，点的聚集又产生面的感觉。
点的间隔逐渐改变造成的金属表面的光辉效果
• 平面构成是研究平面组成形式和构成规律的设计基础实 践课程。
在两维的平面内创造理想的形态，或是将形态要素 按照一定的法则进行分解,排列，组合，从而构成理想形 态造型的基础训练。
三. 为什么要学习构成课？
• 从构成的角度分析理解设计作品，训练对视觉元素 的理解和表现能力；把构成的分析方法运用到生活 中，能够理解和感受寻常事物中的形式美，培养新 的审美趣味，为进入设计状态作准备。
• 点的构成可表现曲面、阴影、及其他复杂的立体感。 以点的大小造成的曲面表现
④ 叠纹 • 在印刷等情况中，由于网点的重置，会产生干涉条纹般 的花纹，如此便无法获致清晰的照相图版。这种条纹称 为叠纹。这是整齐并列的细点在重叠之际，由于少许的 错开造成的。
点间距离微秒错开的两组 网纹造成的叠纹构成
• 线是设计中最富表现力的元素
线的不同排列方式 可以产生空间感。
3. 面 1）.面的造型特征 面是线移动 的轨迹。从视觉上 看，任何点的扩大 和聚集，线的宽度 增加与围合都形成 了面。其造型特征 是视觉上的充实感。
2）.面的分类 面与“形状”
的关系密切，由 此可分为几何面 和有机面。
•点 线 面 的综合运用
摆动摄影
④ 线的面化
线如果大量的密 集使用，将会形成 面的感觉。
线的方向的改变 及疏密造成的效果 均可产生曲面感。

你能找出常见的几何体吗?
常见的立体图形
长方体
正方体
圆柱
圆锥
球
棱柱
棱锥
面 曲面
平面
曲面
平面
平面
1、“手和脑在一块干是创造教育的开始，手脑双全是创造教育的目的。” 2、一切真理要由学生自己获得，或由他们重新发现，至少由他们重建。 3、反思自我时展示了勇气，自我反思是一切思想的源泉。 4、好的教师是让学生发现真理，而不只是传授知识。 5、数学教学要“淡化形式，注重实质.
曲面
曲面
平面
曲面
练习：围成下面这些立体图形的各 个面中，哪些面是平的？哪些面是 曲的？
平面
曲面
线：直线和曲线
面与面相交的地方形成线
面与面相交的地方形成线
面与面相交的地方形成线
点
点
几何图形是由点、线、面、体组成的
探究
点动成线
点 动 成 线
点 动 成 线
线 动 成 面
线 动 成 面
线 动 成 面
三角形 绕一边 旋转成 圆锥体
长方形 绕一边 旋转成 圆柱体
点动成—— 线 线动成—— 面 面动成—— 体
体是由面组成 面与面相交成线 线与线相交成点
练习：把下面第一行的平面图形绕 线旋转一周，便能形成第二行的某个几 何体，请用虚线连一连：
12Βιβλιοθήκη 345A
B
C
D
E
6、“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”。2021年11月2021/11/72021/11/72021/11/711/7/2021 7、“教师必须懂得什么该讲，什么该留着不讲，不该讲的东西就好比是学生思维的器，马上使学生在思维中出现问题。”“观察是 思考和识记之母。”2021/11/72021/11/7November 7, 2021 8、普通的教师告诉学生做什么，称职的教师向学生解释怎么做，出色的教师示范给学生，最优秀的教师激励学生。 2021/11/72021/11/72021/11/72021/11/7

作业
作业
课本第122页 练习1.2
10
复习提问 教学过程 课堂练习 小结
作业
11
复习提问 教学过程 课堂练习 小结
作业
12
复习提问 教学过程 课堂练习 小结
作业
返回点线面体的13概念
复习提问 教学过程 课堂练习 小结
作业
几何体有:长方体、正方体、圆柱、圆锥、棱锥、球等.
返回点线面体的14概念
复习提问 教学过程 课堂练习 小结
作业
返回点线面体的24概念
复习提问 教学过程 课堂练习 小结
作业
b
25
复习提问 教学过程 课堂练习 小结
作业
焰火脚印承接历史足迹
返回点线面体的26关系
复习提问 教学过程 课堂练习 小结
作业
27
复习提问 教学过程 课堂练习 小结
作业
28
复习提问 教学过程 课堂练习 小结
38
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
些面是平的？哪些面是曲的?
(1)
(2)
(3)
(4)
(5)
返回点线面体的20概念
复习提问 教学过程 课堂练习 小结
作业
返回点线面体的21概念
复习提问 教学过程 课堂练习 小结
作业
下面这些立体图形中哪些线是直的？哪些线是曲的?

B
两点之间，线段最短. (线段的基本性质) 线段AB的长度，就是AB两点间的距离.
在纸上画一点A和一点B. 边画边思考:(1)过点A能画出几条直线?
(2)经过A,B两点画直线,能画出几条直线? (3)那么经过三点画直线,能画出几条直线? [小组讨论] 你们能得出什么结论? 结论： 经过一点能画无数条直线，经过两点有一条直线，并且 只有一条直线（两点确定一条直线），经过三点可能画一 条直线，也可能画不出直线.
看想 一一 看想
道车
路站
用用
什什
么么
表表
示示
的的
?
?
………………………..
烛光尖端运动后形成的图形?
拉紧的绳子 刻度尺的边缘
乌鲁木齐
B•
C •
重庆
北京
•A
上海
•D
点：通常用点表示一个物体的位置.例如，在交通图上 用点来表示城市的位置. 表示方法: 用一个大写字母表示．例如：点A.
乌鲁木齐
B•
m
3.下列说法正确的是（ D ） A.两点确定两条直线 B.三点确定一条直线 C.过一点只能作一条直线 D.过一点可以作无数条直线
4.如图，射线PA与PB是同一条射线，则符合题意的图 为（ C ）
A
P
B A
A PB B
A
B P
C
A P
P
B
D
5.如图所示的直线、射线、线段能相交的是（ C ）
D C
1 2
AB，或AB=2AO)
所以点O是线段AB的中点(线段中点的定义).
2.反之，如果已知点O是线段AB的中点，那么就有AO=BO. 这可以用符号语言表示为：
如图，因为点O是线段AB的中点 所以AO=BO(或AO= 1 AB，或AB=2AO) (线段中点的定义).

82
1 直线性的面； 表现规则、平稳、较为理性的视觉效果
第一章 平面构成基本要素
当单个的点在画面中的位置不同产生心理感受 也是不同的。居中会有平静、集中感；偏上时会 有不稳定感，形成自上而下的视觉流程；位置偏 下时，画面会产生安定的感觉，但容易被人们忽 略。位于画面三分之二偏上的位置时，最易吸引 人们的观察力和注意力。
12
一．点的构成
第一章 平面构成基本要素
63
三．面的构成
第一章 平面构成基本要素
用等距离的垂直线和水平线来组成二个正方形， 它的长宽感觉不一样，水平线组成的正方形，给人感 觉稍高些，而垂直线组成的正方形则使人感觉稍微宽 些。
64
三．面的构成
第一章 平面构成基本要素
浅色的显大
深色的显小
65
三．面的构成
第一章 平面构成基本要素
（四）面的构成方法
24
一．点的构成
点在服饰搭配上的应用
第一章 平面构成基本要素
在服装上主要体现在纽扣、蝴蝶结、领结、 耳环、眼镜、配件和面料上点的图案等。
25
一．点的构成
第一章 平面构成基本要素
日本服装大师三宅一生的作品，他就在上衣上装饰 了点状的材料，这些点又和戴的眼镜形成呼应
26
一．点的构成
第一章 平面构成基本要素
(4) 有机形的面，得出柔和、自然、抽象的面的形态
69
三．面的构成
第一章 平面构成基本要素
(5) 偶然形的面，自由、活泼而富有哲理性
70
三．面的构成
第一章 平面构成基本要素
(6) 人造形的面，较为理性的人文特点
71
三．面的构成
面的构成（范例）
第一章 平面构成基本要素

用2个或2个以上相 同的小圆柱拼组大 圆柱。
做一做
随堂小练
1.哪些是用4个 拼成的？在（ ）里画“√”。(教材P71 做一做第1题)
1个
2个
1个
3个
3个
3个
3个
√
√
随堂小练
2.哪两堆可以拼成 第2题)
？连一连。(教材P71做一做
随堂小练
3.用4个相同的 ，你能拼出哪几种不同的长方体？ (教材P71做一做第3题)
探索新知
③用4个相同的小正方体拼组立体图形。
长方体
不规则图形
探索新知
➢ 至少几个相同的小正方体可以拼成一个大正方 体呢？
至少8个相同的小正方体可以拼成 一个大正方体。
探索新知
➢ 用长方体拼一拼 ①用2个相同的小长方体拼组立体图形。
探索新知
②用3个相同的小长方体拼组立体图形。
探索新知
➢ 用圆柱拼一拼
课堂小结
通过这节课的学习，我们认识了长方体、正方体、圆柱 和球及它们的主要特征。
立体图形有特征， 长正柱球各不同。
长长方方长方体 四四方方正方体。 圆柱圆圆粗细同, 球儿滚动本领高。
课堂小结
长方体 正方体
圆柱 球（球体）
课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
长长方方的，有6个 平平的面，面有大有 小。
四四方方的，有6个 平平的面，面的大小 都一样。
探索新知
圆柱 球体(球)
探索新知
立体图形
图形名称
圆柱 球体(球)
特征
直直的，上下一样粗， 两端是圆圆的、平平 的面。
圆圆的，表面是曲面， 可以任意滚动。
探索新知
你能发现什么？

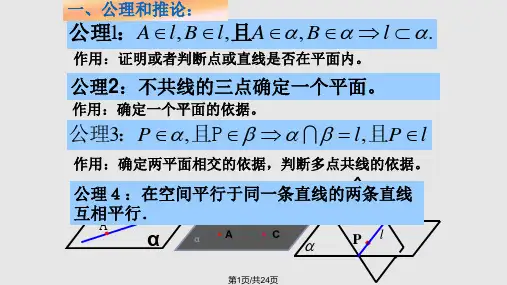
一、公理和推论：
公理1：Al, B l,且A, B l .
作用：证明或者判断点或直线是否在平面内。
公理2：不共线的三点确定一个平面。
作用：确定一个平面的依据。
公理3：P ,且P l,且P l
作用：确定两平面相交的依据，判断多点共线的依据。
公理４：在空间平行于同一条直线的两 条直线
互相A．平行．Bα．
C．如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥平面γ
D．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β
第10页/共24页
4．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（ ） A若l⊥m，m⊂α，则l⊥α
B
B若l⊥α，l∥m，则m⊥α C若l∥α，m⊂α，则l∥m D若l∥α，m∥α，则l∥m
D
第13页/共24页
10．已知m、n为两条不同的直线，α、β为两个不同的平面，则下列命题中正确的是 （）
A．m⊂α，n⊂α，m∥β，n∥β⇒α∥β
D
B．α∥β，m⊂α，n⊂β，⇒m∥n C．m⊥α，m⊥n⇒n∥α
D．n∥m，n⊥α⇒m⊥α
11．对于任意的直线l与平面α，在平面α内必有直线m，使m与l（ ）
垂直,那么该直线与此平面垂直. （线线垂直 线面垂直）；
m ,n
a
mn P
a
a
n
Pm
a m, a n
第5页/共24页
2.判定两平面垂直的方法:
（1）定义法：平面与平面相交成直二面角则面面垂直；
（2）判定定理：如果一个平面经过另一个平面的垂线，
那么这两个平面互相垂直. （线面垂直 面面垂直）；
a a
第6页/共24页

0.03
0.09
0.025 0.25
0.097.5 0.01 . 8
练一练
填一填，把下面的算式转化成除数是整数的除法算式。
4.68÷1.2= 46.8 ÷12 2.38÷0.34= 238 ÷ 52
5.2÷3.2= 52 ÷32 1.61÷0.46= 161 ÷ 46
练一练
算一算，利用所学知识进行下列除法的计算。
售票处
售票处
售票处
1 2 3 4 5
前2
前3 前4
后2
后3 后4
售票处
售票处
售票处
售票处
售票处
售票处
售票处
售票处
售票处
售票处
售票处
从左边起涂色。
涂4个
涂第4个
4号车前面有几辆车? 它的后面是几号车?
和
同样多
３ 和 ３ 同样多 ３＝３
读一读
1 和 1 同样多 2 和 2 同样多 4 和 4 同样多
海滨学校 崔菲菲
长方体 正方体
圆柱 球
举一举，贴一贴，摸一摸，滚一滚
猜谜语
圆圆鼓鼓小淘气，滚来滚去不费力。 正正方方六张脸，平平滑滑一个样。 上下圆圆一样大，放倒一推就滚动。 长长方方六张脸，相对两面一个样。
1、找朋友
长方体 正方体 圆柱 球
2、数一数
( 8 )个 ( 6 )个 ( 3 )个 ( 1 )个
130
0
除数是整数的小数除法
被除数整数部分不够除时，商0，点小数点； 商和被除数小数点位置对齐；除到整数末尾有 余数，添0，继续除。
奶奶编“中国结”，编一个要用0.85m丝绳。
这里有7.65m丝绳。
这些丝绳可以编几个 “中国结”？