第三章2岩石的破坏准则
- 格式：doc
- 大小：523.23 KB
- 文档页数：44
下载文档原格式
合集下载
第3章 岩石力学强度
二、岩石的抗压强度
3、岩石强度的影响因素 物理性质
孔隙率大，强度低； 密度大，强度高。
风化作用
风化对强度影响大，同一种岩石的风化程度越高，其强度越低。
水的作用
水对岩石强度有显著的影响。水对岩石的软化作用对工程极为不利， 特别是水利工程，水库蓄水后，水侵入岩石的孔隙和裂隙，削弱了岩 石颗粒间的连接，使强度降低。 用软化系数表示： Rw S Rw—湿强度；Rd—干强度。 Rd
0
σ σ σ
/ //
///
σ
////
σ
(MPa)
tg f ——摩擦系数。
如将残余强度 τ0 与 σ作直线，可得纯摩强度曲线，。
0 tg
四、 岩石的抗剪强度
2）楔形剪切试验 ①试样：10×10×5cm～30×30×30cm ②方法：用楔形剪切仪，将试样倾斜放在 剪切仪上,在上部加压力p，直至发生破坏。 按力的平衡条件： N P cos P f sin
四、 岩石的抗剪强度
2、抗剪强度的测定
对同一种试样，在不同的
σ下进行多次试验，即可
得到相应的抗剪强度， 绘制曲线τf ~σ ，在σ 不大时(＜10MPa)，为 一直线， 则： c tg
f
τ f(MPa)
τ f~σ
τ τ τ τ
φ///////σ Nhomakorabeaτ 0~
τfσ ~
//
/
此式即为库伦公式， c—凝聚力(MPa)；υ—内摩擦角；
α 2
α 3
α 4
α 5
φ
α
σ
四、 岩石的抗剪强度
2、抗剪强度的测定
3) 三轴压缩试验 三轴压缩试验采用压力机进行。 在岩体工程中，岩体一般处在三向应力状态下，引 用单向受力条件的岩石试验来研究岩石变形、强度 特征是不够的，必须用三轴试验研究岩石在三相受 力条件下的变形及破坏规律。 按应力的组合方式，三轴试验可分为两种：
岩石的强度理论及破坏判据[详细]
![岩石的强度理论及破坏判据[详细]](https://img.taocdn.com/s1/m/b87c145d5ef7ba0d4b733ba7.png)
分析，库仑准则的有效取值范围由图 6-8给出，并可
用方程表示为：
σ3 σ1=σ3
1
f
2
1
f
3
f
2
1
f
2c
P β
3 1
1
1 2
c
1
1 2
c
0
σc / 2
σc
σ1
-σt
A
S
图7-8 σ1－σ3坐标系中的库仑准则的完整强度曲线
在此库仑准则条件下，岩石可能发生以下四种方式的破坏。
(1)当 0 11 11 22时cc，33岩石t属t单轴拉伸破裂； (2)当 1122cc11 c时c，t岩t石3 属3 0双0轴 拉伸破裂；
四、 格里菲斯强度理论
格里菲斯（Griffith ，1920年）认为:脆性材料断 裂的起因是分布在材料中的微小裂纹尖端有拉应力 集中（这种裂纹称之为Griffith裂纹）。
格里菲斯原理认为:当作用力的势能始终保持不 变时，裂纹扩展准则可写为：
(Wd Wc ) 0 C
式中：C为裂纹长度参数；Wd为裂纹表面的表面能； We为储存在裂纹周围的弹性应变能。
1
τ3
2
2α
式中：为t 岩石的单轴抗拉强度σ；0 σ3 t
n 为待定系数。
σ σ
σ
c
利用图 7-10中的关系，有：
σ 3
1 2
(1 3)
1 2
(1
3)
ctg 2
sin 2
1.双向压7缩应4力2圆，2.双向拉压应力圆，
3..双向拉伸应力圆 图7-10 二次抛物型强度包络线
其中：
n( t )
d ctg2
n
d
岩石破坏准则
目前岩石力学领域中,对岩石在单独承受静荷载作用时破坏准则的研究已经比较深透(详情见资料p170-175),对单独承受动载作用时的岩石破坏也取得一定进展(1,19,182-192).上述实验和理论表明,岩石在承受动静和在动、静载荷时，其力学特性和破坏规律有较大差异，岩石破坏准则也有较大差异。
少数学者利用动力三轴试验机进行过加围压的岩石三向抗压试验（19），得到了以三向静压缩不同的结论。
对于同方向的动静组合加载强度的专门研究，目前善无文献记载。
目前就岩石材料低应变率（ɛ*<10−4/s）的破坏准则和高应变率（ɛ*<10−2/s）破坏准则的试验较多且理论分析较为深入，介于这两者中间的中等应变率的破坏准则研究，受到实验条件和技术的限制，显得相对较少。
此前材料破坏准则分为四大类：⑴应力或应变类破坏准则；⑵能量类破坏准则；⑶损伤类破坏准则；⑷经验类破坏准则；
有代表性的能量类破坏准则即形状改变比能理论（第四强度理论），实践证明，对于塑性材料，该理论主要适用于拉压性质相同的情况，对三向等值拉伸无能为力；对于脆性材料，该理论主要适用于三向压应力相近的情况。
由于破坏准则中一般忽略了反映静水压力的体积形变能，故2002年广西大学学报刊登了余熙莹《关于第四强度理论的修正》，提出了用体积变形比能和形状改变比能之和即应变能密度作为材料破坏准则。
分工:XXX。
岩石的破坏准则汇总
岩石的破坏准则岩石的破坏准则对岩石试样的室内及现场试验，可获得岩石试样的强度指标，但对复杂应力状态下的天然岩体，又是如何判断其破坏呢？因此，就必须建立判断岩石破坏的准则（或称强度理论）。
岩石的应力、应变增长到一定程度，岩石将发生破坏。
用来表征岩石破坏条件的函数称为岩石的破坏准则。
岩石在外力作用下常常处于复杂的应力状态，许多试验指出，岩石的强度及其在荷载作用下的性状与岩石的应力状态有着很大的关系。
在单向应力状态下表现出脆性的岩石，在三向应力状态下具有延1岩石的破坏准则2性性质，同时它的强度极限也大大提高了。
岩石的破坏准则许多部门和学者从不同角度提出不同的破坏准则，目前岩石破坏准则主要有：最大正应力理论最大正应变理论最大剪应力理论（H.Tresca）八面体应力理论莫尔理论及库伦准则格里菲思理论（Griffith）伦特堡理论（Lundborg）经验破坏准则3岩石的破坏准则41、最大正应力理论这是较早的一种理论，该理论认为岩石的破坏只取决于绝对值最大的正应力。
即岩石内的三个主应力中只要有一个达到单轴抗压或抗拉强度时，材料就破坏。
适用条件： 单向应力状态。
对复杂应力状态不适用。
写成解析式：破坏岩石的破坏准则52、最大正应变理论该理论认为岩石的破坏取决于最大正应变，即岩石内任一方向的正应变达到单向压缩或拉伸时的破坏数值时，岩石就发生破坏。
则破坏准则为式中 m ax ε——岩石内发生的最大应变值；u ε——单向拉、压时极限应变值；这一破坏准则的解析式为（由广义虎克定律）岩石的破坏准则6R — R t 或R c推出：实验指出，该理论与脆性材料实验值大致符合，对塑性材料不适用。
岩石的破坏准则73、最大剪应力理论（H.Tresca ）该理论认为岩石材料的破坏取决于最大剪应力，即当最大剪应力达到单向压缩或拉伸时的危险值时，材料达到破坏极限状态。
其破坏准则为：在复杂应力状态下，最大剪应力231max σστ-=岩石的破坏准则8单位拉伸或压缩时，最大剪应力的危险值则有 R ≥-31σσ或写成 {}{}{}0)][)][)][221222232231=------R R R σσσσσσ这个理论适用于塑性岩石，不适用于脆性岩石。
岩石破坏准则
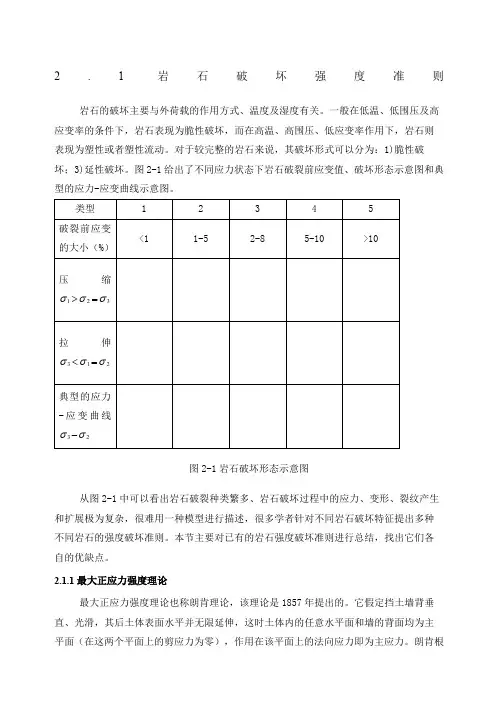
2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下，岩石表现为脆性破坏，而在高温、高围压、低应变率作用下，岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说，其破坏形式可以分为：1)脆性破坏；3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
图2-1岩石破坏形态示意图从图2-1中可以看出岩石破裂种类繁多、岩石破坏过程中的应力、变形、裂纹产生和扩展极为复杂，很难用一种模型进行描述，很多学者针对不同岩石破坏特征提出多种不同岩石的强度破坏准则。
本节主要对已有的岩石强度破坏准则进行总结，找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论，该理论是1857年提出的。
它假定挡土墙背垂直、光滑，其后土体表面水平并无限延伸，这时土体内的任意水平面和墙的背面均为主平面（在这两个平面上的剪应力为零），作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态，应用极限平衡条件，推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时，作用在微分土体上的竖向应力sz 保持不变，而水平向应力sx 逐渐减小，直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ，而最小主应力s3即为主动土压力强度pa 。
根据土的极限平衡理论，当主体中某点处于极限平衡状态时，大主应力1σ和小主应力3σ之间应满足以下关系式：粘性土：213...2tan tan 454522c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪⎝⎭⎝⎭（1）无粘性土231.tan 452ϕσσ⎛⎫︒=- ⎪⎝⎭（2）该理论认为材料破坏取决于绝对值最大的正应力。
因此，作用于岩石的三个正应力中，只要有一个主应力达到岩石的单轴抗压强度或岩石的单轴抗拉强度，岩石便被破坏。
岩石力学第三章：岩石的力学特性及强度准则
常 见 岩 石 的 软 化 系 数
岩 石 名 称
花 岗 岩 闪 长 岩 辉 绿 岩 流 纹 岩
软化系数
0.72～0.97 0.60～0.80 0.33～0.90 0.75～0.95
岩石名称
泥 岩
软化系数
0.40～0.60 0.44～0.54 0.70～0.94 0.75～0.97
泥 灰 岩 石 灰 岩 片 麻岩
岩石名称
抗压强度 (MPa)
100～250
抗拉强 度 (MPa)
7～25
岩石名称
抗压强度 (MPa)
5～100
抗拉强度 (MPa)
2～10
常 见 岩 石 的 抗 压 及 抗 拉 强 度
花岗岩
页 岩
流纹岩
160～300
12～30
粘土岩
2～15
0.3～1
闪长岩
120～280
12～30
石灰岩
40～250
7～20
安山岩
140～300
10～20
白云岩
80～250
15～25
辉长岩
160～300
12～35
板 岩
60～200
7～20
辉绿岩
150～350
15～35
片 岩
10～100
1～10
玄武岩 砾岩 砂 岩
150～300 10～150 20～250
10～30 2～15 4～25
片麻岩 石英岩 大理岩
50～200 150～350 100～250
（二）岩石的水理性质
5．可溶性：是指岩石被水溶解的性能。它与岩石 的矿物成分、水中CO2 含量及水的温度等因素有 关。 6．膨胀性：岩石吸水后体积增大引起岩石结构破 坏的性能称膨胀性。
岩石破坏准则
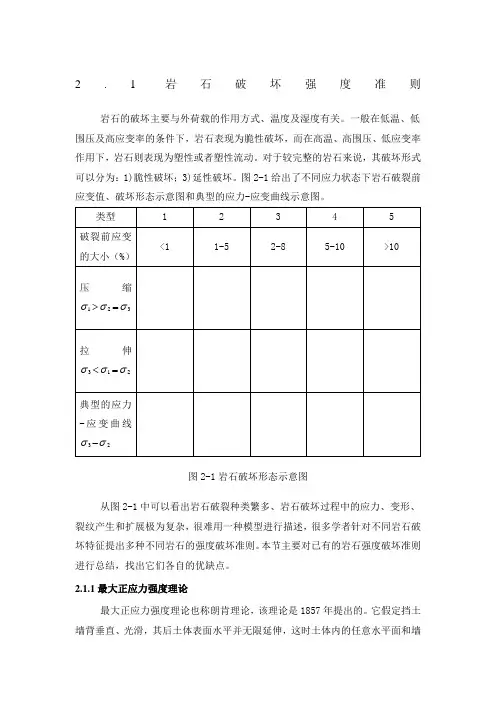
2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下，岩石表现为脆性破坏，而在高温、高围压、低应变率作用下，岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说，其破坏形式可以分为：1)脆性破坏；3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
图2-1岩石破坏形态示意图从图2-1中可以看出岩石破裂种类繁多、岩石破坏过程中的应力、变形、裂纹产生和扩展极为复杂，很难用一种模型进行描述，很多学者针对不同岩石破坏特征提出多种不同岩石的强度破坏准则。
本节主要对已有的岩石强度破坏准则进行总结，找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论，该理论是1857年提出的。
它假定挡土墙背垂直、光滑，其后土体表面水平并无限延伸，这时土体内的任意水平面和墙的背面均为主平面（在这两个平面上的剪应力为零），作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态，应用极限平衡条件，推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时，作用在微分土体上的竖向应力sz 保持不变，而水平向应力sx 逐渐减小，直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ，而最小主应力s3即为主动土压力强度pa 。
根据，当主体中某点处于极限平衡状态时，大主应力1σ和小主应力3σ之间应满足以下关系式：粘性土：213...2tan tan 454522c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪⎝⎭⎝⎭（1）无粘性土231.tan 452ϕσσ⎛⎫︒=- ⎪⎝⎭（2）该理论认为材料破坏取决于绝对值最大的正应力。
因此，作用于岩石的三个正应力中，只要有一个主应力达到岩石的单轴抗压强度或岩石的单轴抗拉强度，岩石便被破坏。
岩石力学第3章 岩石的强度与屈服
12
7)Kim-Lade准则 1984年，Kim和Lade提出了用应力张量的第一、第 三不变量表示的三参数经验强度准则：
8)Johnston准则 1985年，Johnston提出了下述强度准则，用以描述 由粘土到坚硬岩石等不同岩石材料的破坏特征。即
13
9)变形准则 一般来说，岩石的宏观破坏现象可分为两类：即拉 断（拉破）和剪断。但有时岩石的塑性变形也能够破坏 其正常的工作条件，所以广义强度的概念还应该包括对 塑性变形的抗力。
38
39
40
图3.13 弱面的莫尔-库仑破坏准则
41
42
图3.14 以一般应力分量表示的弱面破坏准则
43
44
图3.15 多组弱面时的强度极限曲线
45
(2)弱面最不利的位置
46
图3.16 岩体及弱面强度曲线
47
48
49
图3.17
50
3.4.3 各向异性体的屈服准则 Hill提出了金属材料各向异性的屈服准则。他所提出 的各向异性屈服条件，除了应符合试验资料外，略去各 向异性，应该还原成各向同性的屈服函数。Hill建议的 正交异性体的屈服函数以应力分量表示（正交异性主轴 与坐标轴重合），其屈服函数的形式如下：
11
5)Hoek-Brown准则 1980年，Hoek和Brown为了能够预测岩体特征，而 提出岩体强度经验准则：
6)Yudhbir准则 1983年Yudhbir用灰岩、砂岩、花岗岩及由石膏和 松香混合制成的模拟材料等含有裂隙的122个样品进行 了三轴实验，试图通过试验数据，对不同的经验准则进 行比较，结果发现尽管Hoek和Brown准则对易碎岩石十 分有效，但对塑性岩石却存在一定局限性。因此， Yudhbir提出了一个修正准则：
7)Kim-Lade准则 1984年，Kim和Lade提出了用应力张量的第一、第 三不变量表示的三参数经验强度准则：
8)Johnston准则 1985年，Johnston提出了下述强度准则，用以描述 由粘土到坚硬岩石等不同岩石材料的破坏特征。即
13
9)变形准则 一般来说，岩石的宏观破坏现象可分为两类：即拉 断（拉破）和剪断。但有时岩石的塑性变形也能够破坏 其正常的工作条件，所以广义强度的概念还应该包括对 塑性变形的抗力。
38
39
40
图3.13 弱面的莫尔-库仑破坏准则
41
42
图3.14 以一般应力分量表示的弱面破坏准则
43
44
图3.15 多组弱面时的强度极限曲线
45
(2)弱面最不利的位置
46
图3.16 岩体及弱面强度曲线
47
48
49
图3.17
50
3.4.3 各向异性体的屈服准则 Hill提出了金属材料各向异性的屈服准则。他所提出 的各向异性屈服条件，除了应符合试验资料外，略去各 向异性，应该还原成各向同性的屈服函数。Hill建议的 正交异性体的屈服函数以应力分量表示（正交异性主轴 与坐标轴重合），其屈服函数的形式如下：
11
5)Hoek-Brown准则 1980年，Hoek和Brown为了能够预测岩体特征，而 提出岩体强度经验准则：
6)Yudhbir准则 1983年Yudhbir用灰岩、砂岩、花岗岩及由石膏和 松香混合制成的模拟材料等含有裂隙的122个样品进行 了三轴实验，试图通过试验数据，对不同的经验准则进 行比较，结果发现尽管Hoek和Brown准则对易碎岩石十 分有效，但对塑性岩石却存在一定局限性。因此， Yudhbir提出了一个修正准则：
第三章 岩体的变形与破坏
第三章岩体的变形与破坏变形：不发生宏观连续性的变化，只发生形、体变化。
破坏：既发生形、体变化、也发生宏观连续性的变化。
1．岩体变形破坏的一般过程和特点（1）岩体变形破坏的基本过程及发展阶段①压密阶段（OA段）：非线性压缩变形—变形对应力的变化反应明显；裂隙闭合、充填物压密。
应力-应变曲线呈减速型（下凹型）。
②弹性变形阶段（AB段）：经压缩变形后，岩体由不连续介质转变为连续介质；应力-应变呈线性关系；弹性极限B点。
③稳定破裂发展阶段（BC段）：超过弹性极限（屈服点）后，进入塑性变形阶段。
a．出现微破裂，随应力增长而发展，应力保持不变、破裂则停止发展；b.应变：侧向应变加速发展，轴向应变有所增高，体积压缩速率减缓（由于微破裂的出现）；④不稳定破裂发展阶段（CD段）：微破裂发展出现质的变化：a.破裂过程中的应力集中效应显著，即使是荷载应力保持不变，破裂仍会不断地累进性发展；b. 最薄弱部位首先破坏，应力重分布导致次薄弱部位破坏，直至整体破坏。
“累进性破坏”。
c. 应变：体积应变转为膨胀，轴向及侧向应变速率加速增大；※结构不均匀；起始点为“长期强度”；⑤强度丧失、完全破坏阶段（DE段）：破裂面发展为宏观贯通性破坏面，强度迅速降低，岩体被分割成相互分离的块体—完全破坏。
应重视的问题：①各发展阶段的界限点，尤其是“长期强度”；②空隙压力曲线：a.空隙水压力～体积应变、变形发展阶段；b.工程意义：滑坡、地震等。
（2）岩体破坏的基本形式①张性破坏（图示）；②剪切破坏（图示）：剪断，剪切。
③塑性破坏（图示）。
破坏形式取决于：荷载条件、岩体的岩性及结构特征；二者的相互关系。
①破坏形式与受力状态的关系：a.与围压σ3有关：低围压或负围压—拉张破坏（图示）；中等围压—剪切破坏（图示）；高围压（150MN/m2=1500kg/cm2）—塑性破坏。
b.与σ2的关系：σ2/σ 3 <4（包括σ 2 =σ3），岩体剪断破坏，破坏角约θ=25°；σ2/σ 3 >8（包括σ 2 =σ1）：拉断破坏，破坏面∥σ1，破坏角0°;4≤σ2/σ3≤8：张、剪性破坏，破坏角θ=15°。
岩石的破坏准则
为研究等倾面上的应力，取一由等倾面与三个主应力面围成的四面 体来研究。
N与x、y、z的夹角分别为，且 。 设：，， 则有 设等倾面ABC面积为S，则三个主应力面(，，面)的面积分别为 根据力的平衡条件 , , 推出：，
而 等倾面S上合力： 所以： 另，等倾面S上的法向应力为各分力px、py、pz在N上的投影之和， 即
该值为 直线在轴上的截距，但与实测的Rt有差别，需对＜0时的直线段 进行修正。
岩石破坏的判断条件： ， 破坏
， 极限 ，稳定
6、格里菲思（Griffith）理论
以上各理论都是把材料看作为连续的均匀介质，格里菲思则认为： 当岩石中存在许多细微裂隙，在力的作用下，在缝端产生应力集中，岩 石的破坏往往从缝端开始，裂缝扩展，最后导致破坏。
由于s＝0～1，则 如果令σ1=0，则得到岩体的单轴抗拉强度。 从Rcm和Rtm中可看出，当S=1时，Rcm=Rc为完整岩块，当S=0时， Rtm=Rcm=0为完全破损的岩石。因此，处于完整岩石和完全破损岩石 之间的岩体，其S值在1~0之间。
根据几何关系， ，得出 代入中，得到 另由公式推导：将1、3表示的 和 代入中，导出 或 对求导， 推出： 破坏面与最大主应力面的夹角 而与最大主应力方向的夹角
为）
2）．用主应力1、3表达的强度准则 将 和 的表达式代入 中，
利用关系： 化简得： 当3=0时（单轴压缩）：，
令，则， 当1=0时（单轴抗拉）：
或写成 破坏 稳定
这个理论适用于塑性岩石，不适用于脆性岩石。 该理论未考虑中间主应力的影响。
4、八面体剪应力理论（Von.Mises）
该理论认为岩石达到危险状态取决于八面体剪应力。其破坏准则为
已知单元体三个主应力，， ，取坐标系平行于主应力。作一等倾 面（其法线N与三个坐标轴夹角相同）。八个象限的等倾面构成一个封 闭的正八面体，此八面体上剪应力和法向应力即为八面体应力。
N与x、y、z的夹角分别为，且 。 设：，， 则有 设等倾面ABC面积为S，则三个主应力面(，，面)的面积分别为 根据力的平衡条件 , , 推出：，
而 等倾面S上合力： 所以： 另，等倾面S上的法向应力为各分力px、py、pz在N上的投影之和， 即
该值为 直线在轴上的截距，但与实测的Rt有差别，需对＜0时的直线段 进行修正。
岩石破坏的判断条件： ， 破坏
， 极限 ，稳定
6、格里菲思（Griffith）理论
以上各理论都是把材料看作为连续的均匀介质，格里菲思则认为： 当岩石中存在许多细微裂隙，在力的作用下，在缝端产生应力集中，岩 石的破坏往往从缝端开始，裂缝扩展，最后导致破坏。
由于s＝0～1，则 如果令σ1=0，则得到岩体的单轴抗拉强度。 从Rcm和Rtm中可看出，当S=1时，Rcm=Rc为完整岩块，当S=0时， Rtm=Rcm=0为完全破损的岩石。因此，处于完整岩石和完全破损岩石 之间的岩体，其S值在1~0之间。
根据几何关系， ，得出 代入中，得到 另由公式推导：将1、3表示的 和 代入中，导出 或 对求导， 推出： 破坏面与最大主应力面的夹角 而与最大主应力方向的夹角
为）
2）．用主应力1、3表达的强度准则 将 和 的表达式代入 中，
利用关系： 化简得： 当3=0时（单轴压缩）：，
令，则， 当1=0时（单轴抗拉）：
或写成 破坏 稳定
这个理论适用于塑性岩石，不适用于脆性岩石。 该理论未考虑中间主应力的影响。
4、八面体剪应力理论（Von.Mises）
该理论认为岩石达到危险状态取决于八面体剪应力。其破坏准则为
已知单元体三个主应力，， ，取坐标系平行于主应力。作一等倾 面（其法线N与三个坐标轴夹角相同）。八个象限的等倾面构成一个封 闭的正八面体，此八面体上剪应力和法向应力即为八面体应力。
试证明岩石力学mc准则
试证明岩石力学mc准则
岩石力学中的Mohr-Coulomb准则（简称MC准则）是用来描述岩石在破坏时的应力状态的理论模型。
MC准则假设岩石的破坏是由于剪切应力超过了岩石材料的内聚力而发生的。
具体来说，MC准则假定岩石材料的内聚力是一个与正应力状态相关的函数。
这个函数在应力空间中可以用一条线段来表示，称为正应力线段，其斜率为内摩擦角。
MC准则定义了岩石破坏的极限条件，即剪切应力与正应力之间的关系。
根据MC准则，当岩石体内部的剪切应力超过正应力与摩擦力乘积时，岩石会发生破坏。
这个关系可以用下面的不等式来表示：
τ = σ * tan(φ)
其中，τ是岩石的剪切应力，σ是岩石的正应力，φ是岩石的内摩擦角。
第三章 岩体的变形与破坏
（2）变形过程中所具有的阶段性特征是判断岩体或 地质体演变阶段、预测其发展趋势的重要依据。
（3）变形过程中还包含恒定应力的长期作用下的蠕 变（或流变）。即变形到破坏有时经历一个相当长的 时期，过程中蠕变效应意义重大。岩体的不稳定发展 阶段相当于加速蠕变阶段，进入此阶段的岩体达到最 终破坏已势在必然，仅仅是个时间的问题。判断进入 加速蠕变阶段的变形标志和临界应力状态是一个重要 的课题。
3.1.2 岩体破坏的基本形式
根据岩体破坏机制可将岩体破坏划分为剪性破坏和 张性破坏两类。
岩
剪性破坏
体
破
坏 张性破坏
剪切滑动破坏 剪断破坏
塑性破坏
（a) 拉断破坏；(b)剪断破坏； (c) 塑性破坏
破坏方式影响因素： 荷载条件、岩性、结构及所处的环境特征及配合情况
3.1.2.1 岩体变形破坏形式与受力状态的关系 岩石的三轴实验表明，岩石破坏形式与围压的大小有
（ncr为应力系数）结构面的动摩擦角φk低于其静摩 擦角φs,两者相差的程度与岩石性质、接触面的光滑程 度、温度，充填物的性质，滑移速度，湿度以及振动 状况都有关。某些材料试验表明动、静摩擦角的差别 可以十分悬殊(如铸铁的φs，为48，而其φk值仅为 830′).因而剪切位移一旦起动，由于静、动摩擦相差 悬殊，可出现突跃的剪切位移，即所谓粘滑stick— slip)现象。
第三章 岩体的变形与破坏
3.1 基本概念及研究意义
变形：岩体承受应力，就会在体积、形状或宏观 连续性上发生某种变化（解释）。宏观连续性无明 显变化者称为变形（deformation )。
破坏：如果宏观连续性发生了显著变化的称为破 坏（failure)。
岩体变形破坏的方式与过程既取决于岩体的岩性、 结构，也与所承受的应力状态及其变化有关。
（3）变形过程中还包含恒定应力的长期作用下的蠕 变（或流变）。即变形到破坏有时经历一个相当长的 时期，过程中蠕变效应意义重大。岩体的不稳定发展 阶段相当于加速蠕变阶段，进入此阶段的岩体达到最 终破坏已势在必然，仅仅是个时间的问题。判断进入 加速蠕变阶段的变形标志和临界应力状态是一个重要 的课题。
3.1.2 岩体破坏的基本形式
根据岩体破坏机制可将岩体破坏划分为剪性破坏和 张性破坏两类。
岩
剪性破坏
体
破
坏 张性破坏
剪切滑动破坏 剪断破坏
塑性破坏
（a) 拉断破坏；(b)剪断破坏； (c) 塑性破坏
破坏方式影响因素： 荷载条件、岩性、结构及所处的环境特征及配合情况
3.1.2.1 岩体变形破坏形式与受力状态的关系 岩石的三轴实验表明，岩石破坏形式与围压的大小有
（ncr为应力系数）结构面的动摩擦角φk低于其静摩 擦角φs,两者相差的程度与岩石性质、接触面的光滑程 度、温度，充填物的性质，滑移速度，湿度以及振动 状况都有关。某些材料试验表明动、静摩擦角的差别 可以十分悬殊(如铸铁的φs，为48，而其φk值仅为 830′).因而剪切位移一旦起动，由于静、动摩擦相差 悬殊，可出现突跃的剪切位移，即所谓粘滑stick— slip)现象。
第三章 岩体的变形与破坏
3.1 基本概念及研究意义
变形：岩体承受应力，就会在体积、形状或宏观 连续性上发生某种变化（解释）。宏观连续性无明 显变化者称为变形（deformation )。
破坏：如果宏观连续性发生了显著变化的称为破 坏（failure)。
岩体变形破坏的方式与过程既取决于岩体的岩性、 结构，也与所承受的应力状态及其变化有关。
第3讲-岩石力学-岩石的变形、破坏特征
弹性：一定的应力范围内，物体受外力作用产生变形，而去除 外力后能够立即恢复其原有的形状和尺寸大小的性质。
弹性按其应力和应变关系又可分为两种类型 应力和应变呈直线关系—即线弹性（虎克 型弹性、理想弹性） 应力应变呈非直线的非线性弹性
1.岩石变形的定义
塑性：物体受力后产生变形，在外力去除后不能完全恢复 原状的性质。
岩石的微结构面
微结构面：指存在于矿物颗粒内部或矿物颗粒间的软弱面或 缺陷，包括矿物解理、晶格缺陷、粒间空隙、微裂隙、微层 理及片理面、片麻理面等。
① 降低岩石强度
② 导致岩石力学性质各向异性
1、岩石的组构特征
岩石的主要胶结类型：
基底型：彼此不发生接触的矿物颗粒埋在玻璃体中，这种情况下 胶结程度很高，岩石强度与胶结物有关。
v
r
A
r
o
a
空隙闭合应力：单轴压缩状态下使岩石中的空隙闭合的 最下应力。
2.岩石变形特征
v
r
e
A
B
r
o
a
比例弹性极限或弹性极限：应力-应变曲线保持直线 关系的极限应力
2.岩石变形特征
v
r
p
e
A
C B
r
a
屈服应力：单轴压缩状态下岩石出现塑性变形的极限应力
2.岩石变形特征
ms d V
sat
msat V
m V
2、岩石的物理性质
常见岩石的密度
岩石名称 花 岗 岩 闪 长 岩 辉 长 岩 密度 (g／cm3) 2.52～2.81 2.67～2.96 2.85～3.12 岩石名称 石 灰 岩 白 云 岩 片 麻 岩 密度(g／cm3) 2.37～2.75 2.75～2.80 2.59～3.06
弹性按其应力和应变关系又可分为两种类型 应力和应变呈直线关系—即线弹性（虎克 型弹性、理想弹性） 应力应变呈非直线的非线性弹性
1.岩石变形的定义
塑性：物体受力后产生变形，在外力去除后不能完全恢复 原状的性质。
岩石的微结构面
微结构面：指存在于矿物颗粒内部或矿物颗粒间的软弱面或 缺陷，包括矿物解理、晶格缺陷、粒间空隙、微裂隙、微层 理及片理面、片麻理面等。
① 降低岩石强度
② 导致岩石力学性质各向异性
1、岩石的组构特征
岩石的主要胶结类型：
基底型：彼此不发生接触的矿物颗粒埋在玻璃体中，这种情况下 胶结程度很高，岩石强度与胶结物有关。
v
r
A
r
o
a
空隙闭合应力：单轴压缩状态下使岩石中的空隙闭合的 最下应力。
2.岩石变形特征
v
r
e
A
B
r
o
a
比例弹性极限或弹性极限：应力-应变曲线保持直线 关系的极限应力
2.岩石变形特征
v
r
p
e
A
C B
r
a
屈服应力：单轴压缩状态下岩石出现塑性变形的极限应力
2.岩石变形特征
ms d V
sat
msat V
m V
2、岩石的物理性质
常见岩石的密度
岩石名称 花 岗 岩 闪 长 岩 辉 长 岩 密度 (g／cm3) 2.52～2.81 2.67～2.96 2.85～3.12 岩石名称 石 灰 岩 白 云 岩 片 麻 岩 密度(g／cm3) 2.37～2.75 2.75～2.80 2.59～3.06
岩石破坏应变准则
岩石破坏应变准则引言：岩石是地壳中的主要构成物质，其稳定性直接关系到地质工程的安全性和可持续发展。
岩石在受到外力作用下会发生破坏，因此研究岩石破坏的应变准则对于地质工程的设计和施工具有重要意义。
本文将介绍岩石破坏应变准则的基本概念、分类和应用。
一、岩石破坏应变准则的基本概念岩石破坏应变准则是指岩石在受到外力作用下发生破坏时，所表现出的应变规律和特征。
破坏应变准则是岩石力学研究的基础，它可以用来描述岩石的破坏过程和破坏特征，为工程实践提供理论依据。
二、岩石破坏应变准则的分类根据岩石破坏应变的特点和机制，岩石破坏应变准则可以分为以下几类：1. 弹性破坏准则弹性破坏准则是指岩石在受到外力作用下，当应力达到一定临界值时发生破坏，此时岩石的应变仍然处于弹性范围。
弹性破坏准则适用于岩石的强度较高，且具有较好的韧性的情况，如一些坚硬的岩石。
2. 弹塑性破坏准则弹塑性破坏准则是指岩石在受到外力作用下，当应力达到一定临界值时发生破坏，此时岩石的应变已经进入塑性范围。
弹塑性破坏准则适用于岩石的强度较低，具有较强的延展性和塑性变形能力的情况，如一些软弱的岩石。
3. 脆性破坏准则脆性破坏准则是指岩石在受到外力作用下，当应力达到一定临界值时发生破坏，此时岩石的应变表现为瞬时的破裂和断裂。
脆性破坏准则适用于岩石的强度较高，但缺乏韧性和延展性的情况，如一些脆性的岩石。
三、岩石破坏应变准则的应用岩石破坏应变准则在地质工程中具有广泛的应用价值，主要体现在以下几个方面：1. 工程设计岩石破坏应变准则可以用来评估岩石的破坏特征和破坏模式，为工程设计提供依据。
根据不同的岩石破坏应变准则，可以选择合适的工程方案和施工方法，以确保工程的安全性和可靠性。
2. 施工监测岩石破坏应变准则可以用来监测岩石的变形和破坏过程，及时发现和处理潜在的岩体稳定性问题。
通过对岩石破坏应变的监测和分析，可以采取相应的措施，防止岩体的进一步破坏，保证施工的顺利进行。
岩石破坏准则
精心整理2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下，岩石表现为脆性破坏，而在高温、高围压、低应变率作用下，岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说，其破坏形式可以分为：1)脆性破坏；3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
准则。
本节主要对已有的岩石强度破坏准则进行总结，找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论，该理论是1857年提出的。
它假定挡土墙背垂直、光滑，其后土体表面水平并无限延伸，这时土体内的任意水平面和墙的背面均为主平面（在这两个平面上的剪应力为零），作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态，应用极限平衡条件，推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时，作用在微分土体上的竖向应力sz 保持不变，而水平向应力sx 逐渐减小，直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ，而最小主应力s3即为主动土压力强度pa 。
根据土的极限平衡理论，当主体中某点处于极限平衡状态时，大主应力1σ和小主应力3σ之间应满足以下关系式：粘性土：213...2tan tan 4545c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪（1）（2）2.1.2变，岩石强度条件可以表示为：m εε≤max （3）式中，m ax ε为岩石内发生的最大应变值，可用广义胡克定律求出；m ε为单向压缩或单向拉伸试验时岩石破坏的极限应变值，由实验求得。
对于三轴应力状态时：()[]321max 1σσμσε+-=E（4）对单轴拉伸应力状态时：E1max σε=（5）试验证明，这种强度理论只适用于脆性岩石，不适用于岩石的塑性变形。
《岩石力学教案》课件
《岩石力学教案》PPT课件第一章：岩石力学概述1.1 岩石力学的定义岩石力学的定义和研究对象岩石力学的应用领域1.2 岩石的物理和力学性质岩石的物理性质岩石的力学性质1.3 岩石力学的研究方法实验研究理论分析和数值模拟第二章：岩石的力学行为2.1 岩石的弹性行为弹性模量和泊松比弹性应变和应力2.2 岩石的塑性行为塑性应变和应力岩石的屈服和破坏2.3 岩石的断裂行为断裂韧性和断裂强度断裂准则第三章：岩石的变形和强度3.1 岩石的变形线应变和切应变弹性变形和塑性变形3.2 岩石的强度压缩强度和拉伸强度剪切强度和抗弯强度3.3 岩石的流变行为粘弹性理论和流变模型岩石的长期强度和蠕变特性第四章：岩石力学实验4.1 岩石力学实验方法实验设备和原理实验步骤和数据采集4.2 岩石力学实验案例压缩实验剪切实验弯曲实验4.3 实验结果分析和讨论实验数据的处理和分析实验结果的可靠性和精度第五章：岩石力学在工程中的应用5.1 岩石工程中的岩石力学问题岩体支护和加固设计5.2 岩土工程中的岩石力学应用岩土工程的稳定性分析岩土工程的支护和加固技术5.3 采矿工程中的岩石力学应用矿山压力和岩层控制矿山支护和通风技术第六章：岩石力学数值模拟6.1 数值模拟方法概述有限元方法离散元方法有限差分方法6.2 岩石力学数值模型连续介质模型离散介质模型6.3 数值模拟案例分析岩体稳定性分析岩石破裂过程模拟第七章：岩石力学在地质工程中的应用7.1 地质工程中的岩石力学问题地质灾害防治7.2 地质工程中的岩石力学应用隧道工程基坑工程7.3 地球物理勘探中的岩石力学地震勘探地球物理测井第八章：岩石力学在土木工程中的应用8.1 土木工程中的岩石力学问题大坝和水库岩体稳定性道路和桥梁基础稳定性8.2 土木工程中的岩石力学应用岩体支护和加固岩体锚固技术8.3 地质灾害防治中的岩石力学滑坡防治岩体崩塌防治第九章：岩石力学在采矿工程中的应用9.1 采矿工程中的岩石力学问题矿山压力和岩层控制矿山支护和通风技术9.2 采矿工程中的岩石力学应用地下开采技术露天开采技术9.3 矿山安全与环境保护矿山安全评价矿山环境保护措施第十章：岩石力学的未来发展趋势10.1 岩石力学研究的新理论连续介质力学的发展非连续介质力学的研究10.2 岩石力学研究的新技术先进的测试技术数字图像分析技术10.3 岩石力学在可持续发展中的作用绿色岩石力学可持续岩石工程设计重点和难点解析重点环节1：岩石的物理和力学性质岩石的物理性质包括密度、孔隙度、渗透率等，这些性质对岩石的力学行为有重要影响。
3.2岩石破坏理论强度准则
五、岩石的破坏准则对岩石试样的室内及现场试验，可获得岩石试样的强度指标，但对复杂应力状态下的天然岩体，又是如何判断其破坏呢？因此，就必须建立判断岩石破坏的准则（或称强度理论）。
岩石的应力、应变增长到一定程度，岩石将发生破坏。
用来表征岩石破坏条件的函数称为岩石的破坏准则。
岩石在外力作用下常常处于复杂的应力状态，许多试验指出，岩石的强度及其在荷载作用下的性状与岩石的应力状态有着很大的关系。
在单向应力状态下表现出脆性的岩石，在三向应力状态下具有延性性质，同时它的强度极限也大大提高了。
许多部门和学者从不同角度提出不同的破坏准则，目前岩石破坏准则主要有：最大正应力理论最大正应变理论最大剪应力理论（H.Tresca）八面体应力理论莫尔理论及库伦准则格里菲思理论（Griffith）伦特堡理论（Lundborg）经验破坏准则1、最大正应力理论这是较早的一种理论，该理论认为岩石的破坏只取决于绝对值最大的正应力。
即岩石内的三个主应力中只要有一个达到单轴抗压或抗拉强度时，材料就破坏。
适用条件：单向应力状态。
对复杂应力状态不适用。
写成解析式：破坏2、最大正应变理论该理论认为岩石的破坏取决于最大正应变，即岩石内任一方向的正应变达到单向压缩或拉伸时的破坏数值时，岩石就发生破坏。
则破坏准则为式中ε——岩石内发生的最大应变值；maxε——单向拉、压时极限应变值；u这一破坏准则的解析式为（由广义虎克定律）R —R t或R c推出：实验指出，该理论与脆性材料实验值大致符合，对塑性材料不适用。
3、最大剪应力理论（H.Tresca）该理论认为岩石材料的破坏取决于最大剪应力，即当最大剪应力达到单向压缩或拉伸时的危险值时，材料达到破坏极限状态。
其破坏准则为：在复杂应力状态下，最大剪应力231 max σστ-=单位拉伸或压缩时，最大剪应力的危险值则有 R ≥-31σσ或写成 {}{}{}0)][)][)][221222232231=------R R R σσσσσσ这个理论适用于塑性岩石，不适用于脆性岩石。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
,.五、岩石的破坏准则对岩石试样的室内及现场试验，可获得岩石试样的强度指标，但对复杂应力状态下的天然岩体，又是如何判断其破坏呢？因此，就必须建立判断岩石破坏的准则（或称强度理论）。
岩石的应力、应变增长到一定程度，岩石将发生破坏。
用来表征岩石破坏条件的函数称为岩石的破坏准则。
岩石在外力作用下常常处于复杂的应力状态，许多试验指出，岩石的强度及其在荷载作用下的性状与岩石的应力状态有着很大的关系。
在单向应力状态下表现出脆性的岩石，在三向应力状态下具有延,. 性性质，同时它的强度极限也大大提高了。
,.许多部门和学者从不同角度提出不同的破坏准则，目前岩石破坏准则主要有：最大正应力理论最大正应变理论最大剪应力理论（H.Tresca）八面体应力理论莫尔理论及库伦准则格里菲思理论（Griffith）伦特堡理论（Lundborg）经验破坏准则,.1、最大正应力理论这是较早的一种理论，该理论认为岩石的破坏只取决于绝对值最大的正应力。
即岩石内的三个主应力中只要有一个达到单轴抗压或抗拉强度时，材料就破坏。
适用条件： 单向应力状态。
对复杂应力状态不适用。
写成解析式：0))()((223222221=---R R R σσσ 0))()((223222221≥---R R R σσσ 破坏,.2、最大正应变理论该理论认为岩石的破坏取决于最大正应变，即岩石内任一方向的正应变达到单向压缩或拉伸时的破坏数值时，岩石就发生破坏。
则破坏准则为u εε≥max 式中 m ax ε——岩石内发生的最大应变值；u ε——单向拉、压时极限应变值；这一破坏准则的解析式为（由广义虎克定律）,.R —R t或R c))()((223222221≥---uuuεεεεεε推出：{}{}{}0)]([)]([)]([222132231222321=-+--+--+-RRRσσμσσσμσσσμσ{}{}{}0)]([)]([)]([222132231222321≥-+--+--+-RRRσσμσσσμσσσμσ破坏实验指出，该理论与脆性材料实验值大致符合，对塑性材料不适用。
,.3、最大剪应力理论（H.Tresca ）该理论认为岩石材料的破坏取决于最大剪应力，即当最大剪应力达到单向压缩或拉伸时的危险值时，材料达到破坏极限状态。
其破坏准则为：u ττ≥max在复杂应力状态下，最大剪应力231max σστ-=,.单位拉伸或压缩时，最大剪应力的危险值则有 R ≥-31σσ或写成 {}{}{}0)][)][)][221222232231=------R R R σσσσσσ {}{}{}0)][)][)][221222232231≥------R R R σσσσσσ破坏{}{}{}0)][)][)][221222232231<------R R R σσσσσσ稳定这个理论适用于塑性岩石，不适用于脆性岩石。
该理论未考虑中间主应力的影响。
,.4、八面体剪应力理论（Von.Mises ）该理论认为岩石达到危险状态取决于八面体剪应力。
其破坏准则为已知2σ，3σ坐标轴夹角相同）,.面体上剪应力和法向应力即为八面体应力。
为研究等倾面上的应力，取一由等倾面与三个主应力面围成的四面体来研究。
N 与x 、y 、z 的夹角分别为γβα、、，且 γβα＝＝。
设：l =αcos ，m =βcos ，n =γcos设等倾面ABC 面积为S ，则三个主应力面(1σ，2σ，3σ面)的面积分别为,.根据力的平衡条件∑=0X , ∑=0Y , ∑=0Z推出：⎪⎩⎪⎨⎧⋅⋅=⋅=⋅⋅=⋅=⋅⋅=⋅=∑∑∑γσβσασcos 0cos 0cos 0321S S p Z S S p Y S S p X z y x ， 而 等倾面S 上合力：222z y x p p p p ++=另，等倾面S 上的法向应力为各分力p x 、p y 、p z 在N 上的投影之和，即,.)(1cos cos cos σσσγβασ++=++=p p pS oct ττ≥,.适用条件：塑性，5、莫尔理论及莫尔库伦准则该理论是目前应用最多的一种强度理论。
该理论假设，岩石内某一点的破坏主要取决于它的大主应力和小主应力，即σ1和σ3，而与中间主应力无关。
也就是说，当岩石中某一平面上的剪应力超过该面上的极限剪应力值时，岩石破坏。
而这一极限剪应力值，又是作用在该面上法向压应力的函数，即)(στf=。
这样，我们就可以根据不同的σ1、σ3绘制莫尔应力图。
,.每个莫尔圆都表示达到破坏极限时应力状态。
一系列莫尔圆的包线即为强度曲线)(στf =由此可知，材料的破坏与否，一方面与材料内的剪应力有关，同时也与正应力有关关于包络线：,. 抛物线：软弱岩石双曲线或摆线：坚硬岩石,.直线：当σ＜10MPa 时,.为简化计算，岩石力学中大多采用直线形式：ϕστtg c f ⋅+=c ——凝聚力（MPa ） ϕ——内摩擦角。
该方程称为库伦定律，所以上述方法合称为：莫尔库伦准则。
当岩石中任一平面上 f ττ≥ 时，即发生破坏。
即： ϕσττtg c f ⋅+=≥下面介绍用主应力来表示莫尔库仑准则。
任一平面上的应力状态可按下式计算,.ασσσσσ2cos 223131-++=① ασστ2sin 231-=②α（σ1角。
,. 强度指标与主应力之间关系。
1）c和ϕ值与σ1、σ3和α角关系在σ1~σ3的应力圆上，找出2α的应力点T（TM为半径为231σσ-）则，与直径TM垂直且与圆相切的直线即为ϕστtgc⋅+=,.根据几何关系，οοο902)2180(90-=--=ααϕ，得出 代入ϕστtg c ⋅+=中，得到 )902(ο-⋅-=⋅-=αστϕστtg tg c另由公式推导：将σ1、σ3表示的 σ 和 τ 代入ϕστtg c ⋅+=中，导出对α求导，01=ασd d 推出：245ϕα+=ο破坏面与最大主应力面的夹角,.而与最大主应力方向的夹角2）．用主应力σ1、σ3表达的强度准则 将 σ 和 τ 的表达式代入 ϕστtg c ⋅+=中，ϕασσσσασσtg c ⎥⎦⎤⎢⎣⎡-+++=-2cos 222sin 2313131利用关系：ααϕ2sin )902cos(cos =-=ο ααϕ2cos )902sin(sin -=-=ο化简得：,.当σ3=0时（单轴压缩）：ϕϕσsin 1cos 21-==c R c ，令ϕϕϕsin 1sin 1-+=N ，则，N =ϕσσ31当σ1=0时（单轴抗该值为 )(στf =直线在σ但与实测的R t 有差别，需对σ直线段进行修正。
,. 岩石破坏的判断条件：ϕ>，破坏sin极限ϕ<，稳定sin,.6、格里菲思（Griffith）理论以上各理论都是把材料看作为连续的均匀介质，格里菲思则认为：当岩石中存在许多细微裂隙，在力的作用下，在缝端产生应力集σ1方向成β边壁就开始破裂。
,.1）.任一裂隙的应力。
假定：②二维问题处理，取z σ椭圆参数方程：αcos a x =，αsin b y = 椭圆的轴比为：ab m =椭圆裂隙周壁上偏心角的α的任意点的切向应力 可用弹性力学中英格里斯（Inglis ）公式表示：,.由于裂缝很窄，轴比很小，形状扁平，所以最大应力显然发生在靠近椭圆裂隙的端部，即α很小的部位，当0→α时，αα→sin ，1cos →α又由于m ，α很小，略去高次项，则有 m 为定值，当1σ，2σ，3σ确定时，y σ、xy τ也为定值，则b σ仅随α而变。
这是任一条裂隙沿其周边的切向应力。
,.显然在椭圆周边上，随α不同b σ有不同的值，对α求导。
0222=--xy y xy m m τασατ 推出：xyy y m ττσσα22+±-=,.2）．岩块中的最大切向应力所在的裂隙上面导出了某一条裂隙上的最大切向应力，但在多条裂隙中，哪一条裂隙的b σ 最大？y σ，xy τ与1σ，3σ的关系为：βσσσσσ2cos 223131--+=y ， βσστ2sin 231--=xy代入 m ax ,b σ中，显然m ax ,b σ与β有关，对其求导，便可求得b σ为最大的那条裂隙，即确,.定出β角。
即取 0m ax ,=⋅βσd d m b则，02sin =β， )(22cos 3131σσσσβ+-=①02sin =β，有β＝0或ο90代入m ax ,b σ中，β＝0时， mb 3max ,2σσ= 或 0 β＝ο90时，mb 1max ,2σσ=或0。
共四个可能极值，与σ1平行或垂直的裂隙。
,.②将)(22cos 3131σσσσβ+-=代入 m ax ,b σ中，⎪⎪⎩⎪⎪⎨⎧+--+++=⎥⎦⎤⎢⎣⎡--+±+--+=)(4)()(4)3)(3(4)()(21)()(41)(21312313131312/123123213123131max ,σσσσσσσσσσσσσσσσσσσσσb m共有两个极值，即与σ1斜交裂隙中有两个方向裂隙的切向应力达极值。
因为β＝0或ο90时，12cos =β或－1。
,.因此，与σ1斜交时，必须β≠0或ο90， 即 12cos <β 时 才是与σ1斜交，则要求1)(23131<+-σσσσ 或 0331>+σσ此时，裂隙的最大拉应力为 )(4)(31231max ,σσσσσ+--=b m （*）如果0331<+σσ， 则1)(23131>+-σσσσ，则3σ必为负值（拉应力）此时由12cos ≥β推出12cos =β，即β为0或90°，表明裂隙与σ1平行或正交。
,.因为03<σ，考查β＝0，ο90的极值，则3max ,2σσ=b m （**） 为最大拉应力。
式（*）（**）即为岩石中的m ax ,b m σ达到某一临界值时就会产生破坏。
为了确定m 值，做单轴抗拉试验，使σ3垂直裂隙面（椭圆长轴），则这时的t R -=3σ 推出 t b R m 2max ,-=σ 这说明裂隙边壁最大应力m ax ,b m σ与m 乘积必须满足的关系。
此时，格菲思强度理论的破坏准则为：I. 由（**）式，当0331<+σσ时，t b R m 2max ,-=σ， 则 322σ=-t Rt R -=3σ， 0=β,.II. 由（*）式，当0331>+σσ代入 t b R m 2max ,-=σ， 则有：等于0，处于极限状态；大于0， 破坏； 小于0， 稳定。
,.上面的准则是用σ1、σ3表示的，也可用y σ，xy τ表示 将t b R m 2max ,-=σ 代入 )(122max ,xy y y b mτσσσ+±=中， 222xyy y t R τσσ+±=- 推出：t y xy y R 222+=+±στσ，22224)2(t y t y xy y R R +=+=+σστσ )(42t y t xyR R +=στ 在0<σ时的包线更接近实际。