第五章 分式与分式方程 复习

八下第 五 章 分式与分式方程专题复习【本章知识框架】一、 认识分式1、定义：A 、B 表示两个整式，且B 中含有字母，则把B A 称为分式。

例如：a b 2，-x x -+41x xy2、性质：分子和分母同时乘以或除以一个不为0的整式，分式的值不变，数学语言：a b =m a m b⋅⋅（m )0≠,a b =m a m b ÷÷（m )0≠※ 约分：（1）定义：把一个分式的分子和分母的公因式约去，这种变形称为约分。

（2）约分的关键：提取公因式（当分子分母为多项式时先分解因式）3、运算：（1）乘除法：两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母；两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘（2）加减法：同分母的分式相加减，分母不变，把分子相加减。

异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法法则进行计算（通分，找最小公倍数，当分母为多项式时先分解因式）运算结果形式化成最简分数，分子一定要展开，分母不作要求4、经典题型解法：a 、有无意义：分式有意义的条件：分母不为0分式无意义的条件：分母为0分式值为0的条件：分子为0B 、平方法、换元法、整体代入法、倒数法二、分式方程1、定义：分母中含有未知数的方程2、解法：a 、转化法：将分式方程转化为整式方程。

检验：将所得的根代入最简分母，分母为0，则为增根B 、换元法：主要使方程形式简化3、题型解法：方程有增根： 增根必满足（1）满足化解后的整式方程（2）使分母为零方程无解： 无解必满足 （1）整式方程无解（2）有界但为增根4、实际问题：尽量少设元【本章经典错题再现（10~15道）】选择题1、 若分式112--X X 的值为0，则x 的值为( )A, -1 B, 0 C, 1 D, 1±2、下列分式最简分式是（ ）A 、1212+-X X B 、121-+X X C 、-XY X Y XY X -+-2222 D 、122362+-X X 3、已知311=-Y X ,则代数YXY X Y XY X ---+232的值为（ ） A 、-27 B 、-211 C 、29 D 、43 4、在正数范围内定义一种运算 ＊，其规则为a ＊b=ba 11+,根据这个规则X ＊(X+1)=23的解为（ ） A 、 X=32 B 、X=1 C 、X=-32或1 D 、X=32或-1 填空题1、 当X 为_______，分式622||-+-x x x 的值为零 2、 若分式aa ++13的值为正，则a 的取值范围______________ 3、 不论X 取何值，分式M X X +-221总有意义，则M 的取值范围 解答题1、解方程（1）22-x x =1-x -21 （2）3-x x -621-x =21（3） 42-x x +22+x =x x x 2222-- （4）x x 22+-22-+x x =xx x 2222--4、 计算题：（1） （-3)2b a ÷（2322）b a3、分式化简求值（1）122-x -X ÷12222+++X X X +11-X ,其中X=2(2) (ba b a ba bab a +---++22222)÷b a b a -+,其中a=-2,b=3(3) 若分式2521-n ，51+n 的最简公分母为11.求n 的值 4、应用题（1）某水果店搞促销活动，对某种水果打8折出售，若用60元钱买这种水果，可以比打折前多买3斤，求该种水果打折前的单价是多少？（2）某市为绿化环境计划植树2400棵，实际劳动中每天植树的数量比原计划多20%，结果提前8天完成任务，则原计划每天植树多少【本章巩固练习（10~15道）】选择题1、当x 为任意实数时，下列分式一定有意义（ ）2、A, 21XX + B, 121+-X X C, 121+-X X D, 1||1-+X X 2、若解分式方程X X m X X ++-+2112=X X 1+产生增根，则m 的值是（ ） A 、 -1或者-2 B 、 -1或者2 C 、 1或者2 D 、 1或者-23、若Y a YX 2-X 2a 22-÷aYaX Y X ++2)(的值为5，则a 的值是（A 、 5B 、 -5C 、51D 、-51 4、已知X+Y=43.X-Y=3,则（Y X XY Y X -+-4）(Y X XY Y X +-+4)的值是（ ） A 、 48 B 、23 C 、16 D 、12填空题1、 当m 为___________时，关于x 的方程234222+=-+-X X mX X 无解 2、 当K 为 时，分式方程XX X K X X 5)1(216-++=-有增根。

第五章 《分式方程》一、认识分式考点一：认识分式一般地，用A,B 表示两个整式，A ÷B 可以表示成B A ，如果B 中含有字母，那么称B A 为分式，其中A 称为分式的分子，B 称为分式的分母，对于任意一个分式，分母都不能为零。

考点二：分式的基本性质分式的分子与分母都乘（或除以）同一个不等于零的整式，分式的值不变。

用式子表示为B A =M B M A ∙∙=M B M A ÷÷（A,B,M 是整式，且M ≠0）。

例1 分式x--11可变形为 （ ） A. 11--x B.11+x C.x +-11 D.11-x 考点三：分式的约分根据分式的基本性质，把一个分式的分子和分母的公因式约去，这种变形称为分式的约分。

分子与分母没有公因式（除去1）的分式成为最简分式。

例2 计算12412+-a a 的结果是 。

二、分式的乘除法考点一：分式的乘除法法则1. 两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母。

2. 两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘。

用式子表示为：（1）ac bd c d a b =∙ （2）adbc d c a b c d a b =∙=÷ 考点二：分子和分母都是单项式的分式相除分子和分母都是单项式的分式乘除法的解题步骤是：（1）含有分式除法运算时，先用分式除法法则把分式除法运算变成分式乘法运算；（2）再用分式乘法法则得出积的分式；（3）用分式符号法则确定积的符号；（4）用分式约分法则使积化成最简分式或整式（一般为单项式）。

例1 （1）化简aa a a 112-∙- （2）计算：ab b a 63÷⎪⎭⎫ ⎝⎛-考点三：分子或分母是多项式的分式乘除分子或分母是多项式的分式乘除法的解题步骤是：（1）将原分式中含同一字母的各多项式按降幂（或升幂）排列，在乘除过程中遇到整式则视其为分母为1，分子为这个整式的分式；（2）把各分式中分子或分母里的多项式分解因式；（3）应用分式乘除法法则进行运算得到积的分式；（4）应用分式约分法则使积化成最简分式或整式。

第五章分式与分式方程知识点1：分式的概念1、分式的定义：一般地，用A,B表示两个正式，A÷B可以表示成AB的形式。

如果B中含有字母，那么称AB为分式，其中A称为分式的分子，B称为分式的分母。

分式需要满足的三个条件：（1）是形如AB的式子；（2）A,B都整式；（3）分母B中必须含有字母。

分式有意义的条件：分母不能为0.分式无意义的条件：分母等于0.分式的值为0的条件：分子等于0且分母不等于0.知识点2：分式的性质2、分式的基本性质分式的基本性质：分式的分子与分母都乘（或除以）同一个不等于零的整式，分式的值不变。

字母表示：AB =A·CB·C，AB=A÷CB÷C(C≠0，其中A,B,C均是整式)运用条件：（1）分子和分母要同时做“乘法（或除法）”运算；（2）“乘（或除以）”的对象必须是同一个不等于0的整式。

3、分式的符号法则法则内容：分式的分子、分母与分式本身的符号同时改变其中两个，分式的值不变。

字母表示：AB =−A−B=−−AB=−A−B知识点3：分式的约分与通分4、分式的约分约分：根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分，即A·CB·C =AB（C为整式且C≠0）.约分的方法：如果分式的分子、分母都是单项式，那么直接约去分子、分母的公因式；如果分式的分子、分母中至少有一个多项式，那么先分解因式，再约去分子、分母的公因式。

最简分式：分子与分母没有公因式的分式，叫做最简分式。

5、分式的通分通分：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分。

用字母表示：将AB 和CD通分，AB=A·DB·D，CD=B·CB·D（分母都为B·D）。

通分的步骤：（1）将所有分式的分母化为乘积的形式，当分母为多项式时，应进行因式分解；（2）确定最简公分母，即各分母的所有因式的最高次幂的积；（3）将分子、分母同乘一个因式，使分母变为最简公分母。

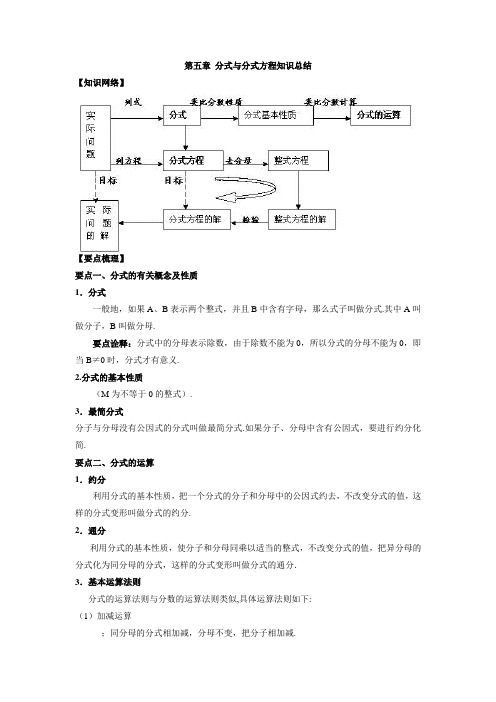
第五章分式与分式方程知识总结【知识网络】【要点梳理】要点一、分式的有关概念及性质1．分式一般地，如果A、B表示两个整式，并且B中含有字母，那么式子叫做分式.其中A叫做分子，B叫做分母.要点诠释：分式中的分母表示除数，由于除数不能为0，所以分式的分母不能为0，即当B≠0时，分式才有意义.2.分式的基本性质（M为不等于0的整式）.3．最简分式分子与分母没有公因式的分式叫做最简分式.如果分子、分母中含有公因式，要进行约分化简.要点二、分式的运算1．约分利用分式的基本性质，把一个分式的分子和分母中的公因式约去，不改变分式的值，这样的分式变形叫做分式的约分.2．通分利用分式的基本性质，使分子和分母同乘以适当的整式，不改变分式的值，把异分母的分式化为同分母的分式，这样的分式变形叫做分式的通分．3．基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下:（1）加减运算；同分母的分式相加减，分母不变，把分子相加减.；异分母的分式相加减，先通分，变为同分母的分式，再加减.（2）乘法运算，其中是整式，.两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.（3）除法运算，其中是整式，.两个分式相除，把除式的分子和分母颠倒位置后，与被除式相乘.（4）乘方运算分式的乘方，把分子、分母分别乘方.4.分式的混合运算顺序先算乘方，再算乘除，最后加减，有括号先算括号里面的.要点三、分式方程1．分式方程的概念分母中含有未知数的方程叫做分式方程．2．分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程．3．分式方程的增根问题增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根---增根.要点诠释：因为解分式方程可能出现增根，所以解分式方程必须验根．验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解.要点四、分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解.。

第五章分式与分式方程一、认识分式知识点一分式的概念1、分式的概念从形式上来看，它应满足两个条件：（1）写成的形式（A、B表示两个整式) （2）分母中含有这两个条件缺一不可2、分式的意义（1）要使一个分式有意义，需具备的条件是（2）要使一个分式无意义，需具备的条件是（3）要使分式的值为0，需具备的条件是知识点二、分式的基本性质分式的分子与分母都乘以（或除以）同一个分式的值不变用字母表示为AB=,A M A A MB M B B M⨯÷=⨯÷（其中M是不等于零的整式）知识点三、分式的约分1、概念：把一个分式的分子和分母中的公因式约去，这种变形称为分式的约分2、依据：分式的基本性质注意：（1）约分的关键是正确找出分子与分母的公因式（2）当分式的分子和分母没有公因式时，这样的分式称为最简分式，化简分式时，通常要使结果成为最简分式或整式。

（3）要会把互为相反数的因式进行变形，如：（x－－y）2=（y－－2)2二、分式的乘除法【巩固训练】1、(2013四川成都)要使分式51x-有意义，则x的取值范围是( )(A)x≠1 (B)x＞1 (C)x＜1 (D)x≠－12、（2013深圳）分式242xx-+的值为0，则x的取值是A．2x=-B．2x=±C．2x=D．0x=3、（2013湖南郴州）函数y =中自变量x的取值范围是（）A． x＞3 B．x＜3 C．x≠3D．x≠﹣34．（2013湖南娄底，7，3分）式子有意义的x的取值范围是（）A．x≥﹣且x≠1B．x≠1C．5．（2013贵州省黔西南州，2，4分）分式的值为零，则x的值为（）A．﹣1 B．0 C．±1 6．（2013广西钦州）当x= 时，分式无意义．7、（2013江苏南京）使式子1+1x-1有意义的x的取值范围是。

8、（2013黑龙江省哈尔滨市）在函数3xyx=+中，自变量x的取值范围是．9、（2013江苏扬州）已知关于x的方程123++xnx=2的解是负数，则n的取值范围为．10、（2013湖南益阳）化简：111xx x---= ．11、（2013山东临沂，6，3分）化简212(1)211a a a a +÷+-+-的结果是（ ）A ．11a - B ．11a +C ．211a -D ．211a +12、 （2013湖南益阳）化简：111x x x ---= ． 13、（2013湖南郴州）化简的结果为（ ）A ．﹣1B ． 1C ．D ．14、（2013湖北省咸宁市）化简+的结果为 ． 15、（2013·泰安）化简分式的结果是（ ）A ．2B ．C ．D ．－216（2011年四川乐山）．若m 为正实数，且13m m-=，221m m-则= 17（2013重庆市(A )）分式方程2102x x-=-的根是（ ）A ．x ＝1B ．x ＝－1C ．x ＝2D ．x ＝－218、（2013湖南益阳）分式方程x x 325=-的解是（ ） A ．x =3B ．x =3-C ．x =34 D ．x =34-19、（2013白银）分式方程的解是（ ）A ． x =﹣2B ． x =1C ． x =2D ． x =320、（2013江苏扬州）已知关于x 的方程123++x nx =2的解是负数，则n 的取值范围为 ． 21．（2013山东临沂）分式方程21311x x x+=--的解是_________________． 22. （2013广东省）从三个代数式：①222b ab a +-，②b a 33-，③22b a -中任意选择两个代数式构造成分式，然后进行化简，并求当a =6，b =3时该分式的值．23、（2013湖北孝感，19，6分）先化简，再求值：，其中，．24．（2013江苏苏州，21，5分）先化简，再求值：23111x x x x -⎛⎫÷+- ⎪--⎝⎭，其中x ＝3－2． 25．（2013贵州安顺，20，10分）先化简，再求值：12a)111(2++÷+-a a a ，其中a =3－1.6． （2013山东德州,18,6分）先化简，再求值：244412222+-÷⎪⎭⎫ ⎝⎛++--+-a a a a a a a a ，其中a =2－1. 26、．（2013湖南永州，19，6分）先化简，再求值:22111121x x x x x x x ++⎛⎫+÷ ⎪---+⎝⎭， 2.x =其中 27．（2013广东珠海，12，6分）解方程：．28、（2013年陕西）（本题满分5分）解分式方程：12422=-+-x xx . 29．（2013山东日照，9，4分）甲计划用若干个工作日完成某项工作，从第三个工作日起，乙加入此项工作，且甲、乙两人工效相同，结果提前3天完成任务，则甲计划完成此项工作的天数是A .8B .7C .6D .530、（2013深圳，8，3分）小朱要到距家1500米的学校上学，一天，小朱出发10分钟后，小朱的爸爸立即去追小朱，并且在距离学校60米的地方追上了他。

第五章 分式与分式方程【学习目标】1、掌握分式的定义、基本性质，会进行分式的运算。

2、会解可化为一元一次方程的分式方程3、会解已知方程有增根时方程中有待定字母的值【学习重难点】重点：分式的运算，解分式方程；难点：分式的通分，分式方程的增根产生的原因。

【学习过程】一、典型问题分析： 问题一：1、下列各式1132x y +，1xy，15a +，4xy -，2x x ，2x x 中，分式的个数是（ ）A. 1个B. 2个C. 3个D. 4个2、在4.5x ， 12x +，21x π+-，732x y -，12233x y z +-，211x x -+中，是分式的有（ ）A. 2个B. 3个C. 4个D. 5个问题二：（1）当x 时，分式121x x -+有意义； （2）当x 时，分式293x x -+的值为零；（3）若分式32x x +-无意义，则x = ； （4）当x 时，分式532x +的值为正数。

问题三：计算：⑴yx xx y x y x +⋅+÷+222)(⑵22224421y xy x y x y x y x ++-÷+-- ⑶224)2222(x x x x x x -⋅-+-+-问题四：解下列分式方程： （1）23=x 3x - （2）12=2x x+3； （3）x 31=x 1(x 1)(x+2)--- （4）224=x 1x 1--问题五：.21322.3132912的值。

有增根，试求的方程、若关于有增根，增根可能是、若分式方程K x x x k x x x x m --=+--=++-二、归纳总结 三、课后作业 四、课后反思。