五年级数学小数除法知识点与习题

知识点一、除数是整数小数除以整数，按整数除法的方法去除。

商的小数点要和被除数的小数点对齐。

整数部分不够除，商0，点上小数点。

如果有余数，要添0再除。

除得的商的哪一数位上不够商，就在那一位上写0占位。

二、除数是小数一看：看清被除数有几位小数。

二移：把除数和被除数的小数点同时向右移动相同的位数（也就是同时扩大相同的倍数），使除数变成整数，（被除数是不是整数不重要，只要扩大相同倍数就行）。

三算：按照除数是整数的小数除法计算进行计算。

a÷b=c（b≠0），b=1时，a=c；b＞1时，a＞c；b＜1时，a＜c三、商的近似数求商的近似值：计算时要比保留的小数多一位。

取商的近似值的方法：“四舍五入”法、保留商的近似值，小数末尾的0不能去掉。

求积的近似值：计算出整个积的值后再去近似值。

四、循环小数1、循环小数的定义：一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

2、循环节的定义：一个循环小数的小数部分，依次不断重复出现的一个数字或者几个数字，叫做这个循环小数的循环节。

如5.33……循环节是3。

7.14545……的循环节是45。

3、循环小数必须满足的条件：①必须是无限小数；②一个数字或者几个数字依次不断重复出现。

4、循环小数的记法：①省略后面的“……”号；②在第一个循环节首尾的数字上分别加点。

5、小数分类：可以分为无限小数和有限小数。

小数部分的位数是有限的小数，叫做有限小数。

小数部分是无限的小数叫做无限小数。

循环小数就是无限小数中的一种。

循环小数一定是无限小数，无限小数不一定是循环小数。

五、解决问题应用题中取商的近似值的方法有：“四舍五入”法、“进一法”和“去尾法”。

在解决问题的时候，要根据题目实际情况选择“进一法”和“去尾法”取商的近似值。

练习题一、填空：1.两个数相除时，如果被除数扩大10倍，要使商不变，除数应（）。

2.计算2.025÷1.47时，先将1.47的小数点向（）移动（）位，使它（），再将2.205的小数点向（）移动（）位，最后按除数是整数的除法进行计算。

小数除法整理及复习知识框架：知识点一：小数除法的意义小数除法的意义：已知两个因数的（ ）与其中的一个因数，求另一个因数的运算。

如：0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3，求另一个因数的运算。

知识点二：小数除以整数的计算方法小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商写上0，点上小数点。

如果有余数，要添0再除。

【练习】58.89÷13 96÷15 0.465÷15 16.32÷51例题1：学校买了13盒白粉笔和10盒彩色粉笔，共付64.5元。

每盒白粉笔2.5元，每盒彩色粉笔多少元？变式练习：一支钢笔的价钱是一支圆珠笔价钱的4倍。

王小东买了一支钢笔和3支圆珠笔，一共花了17.5元。

钢笔和圆珠笔的单价各是多少元？例题2：服装厂做校服。

原来每套服装用布2.2米，现在每套用布节省0.2米。

原来做800套这种服装的布，现在可以做多少套？变式练习：工程队要铺设一条长4.8千米的地下管道，计划用15天完成，实际每天比计划多铺设3.2千米，实际多少天完成任务？变式练习：西平乡修一条长2.1千米的河堤，前15天平均每天修0.086千米。

余下的要9天完成，平均每天修多少千米？1、 小数除以整数*计算法则：按整数除法的法则进行计算，商的 小数点要和被除数的小数点对齐。

2、一个数除以小数 如果有余数，要添0再除。

（整数部分不够除，商0，点上小数点。

（一位一位落数，不够商1就用0占位。

） 与图形 3、商的近似数。

四舍五入法(结合生活实际，具体问题具体分析) 有限小数 4、循环小数：小数 无限不循环小数 无限小数 无限循环小数 5、解决问题小数除法知识点一：除数是小数的除法的计算方法除数是小数的除法的计算方法：先将除数和被除数扩大相同的倍数，使除数变成整数，再按“除数是整数的小数除法”的法则进行计算。

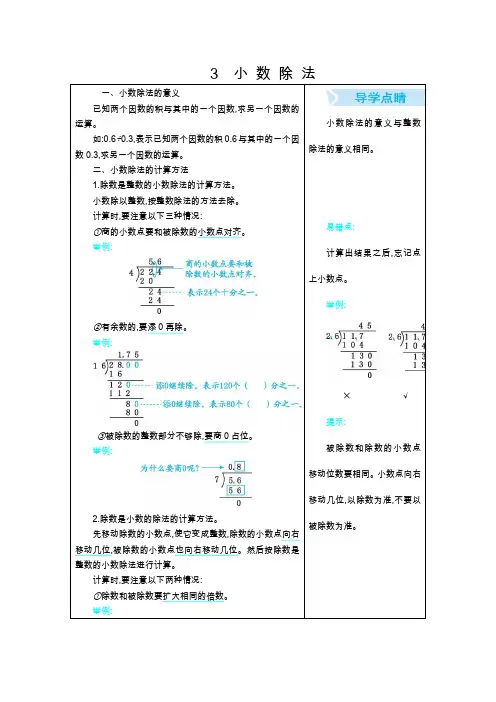
3 小数除法一、小数除法的意义已知两个因数的积与其中的一个因数,求另一个因数的运算。

如:0.6÷0.3,表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。

二、小数除法的计算方法1.除数是整数的小数除法的计算方法。

小数除以整数,按整数除法的方法去除。

计算时,要注意以下三种情况:①商的小数点要和被除数的小数点对齐。

举例:②有余数的,要添0再除。

举例:③被除数的整数部分不够除,要商0占位。

举例:2.除数是小数的除法的计算方法。

先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位。

然后按除数是整数的小数除法进行计算。

计算时,要注意以下两种情况:①除数和被除数要扩大相同的倍数。

举例:小数除法的意义与整数除法的意义相同。

易错点:计算出结果之后,忘记点上小数点。

举例:✕√提示:被除数和除数的小数点移动位数要相同。

小数点向右移动几位,以除数为准,不要以被除数为准。

②被除数的位数不够的,在被除数的末尾用“0”补足。

举例:3.除法中的变化规律。

(1)商不变的性质:被除数和除数同时乘或除以同一个数(0除外),商不变。

(2)除数不变,被除数乘或除以几(0除外),商就乘或除以几。

(3)被除数不变,除数乘或除以几(0除外),商就除以或乘几。

三、商的近似数1.在实际应用中,小数除法中所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。

2.按要求取近似数时,一般情况下用“四舍五入”法,“进一”法、“去尾”法在解决实际问题时选择应用。

3.取商的近似数时,要求保留到哪一位,一定要除到那一位的下一位,然后用“四舍五入”法取近似数。

没有要求时,除不尽的一般保留两位小数。

易错点:没有把被除数和除数的小数点移动相同的位数。

举例:✕√ 易错点:没有把商的小数点与移动后的被除数的小数点对齐。

举例:✕√ 常用的规律:①被除数大于除数,商就大于1;被除数小于除数,商就小于1。

小数除法一、知识梳理二、教学重、难点三、作业完成情况四、典题探究例1填一填（1）除法中，如果除数扩大10倍，要使商不变，被除数也要（ ）。

（2）两个数相除的商是256，被除数是128，那么除数是（ （3）两数相除的商是3.14，被除数扩大10 ）。

例2完成下面的竖式820.8 9 11.73 3.51例3计算（能简算的要简算）10.24÷1.25÷8 126.5×0.25×408.8×（12.5×9.9） 3.79×78＋5.21×78＋78[2.95＋（10.58－3.53）]÷0.25 3.5×4-96.24÷24＋4.01例4 实际应用下面是某水果批发市场两种水果的批发价和零售价：苹果一箱15千克香蕉一箱12千克批发价：每箱63元批发价：每箱54元零售价：每千克5.8元零售价：每千克4.8元（1）每种水果卖出1千克，各盈利多少元？（2）卖出85千克苹果和60千克香蕉，一共可以盈利多少元？五、演练方阵A档（巩固专练）1、判断（1）一个数除以小数，商一定小于被除数。

( ) （2）一个小数除以一个整数，商一定大于被除数。

( ) （3）商的小数点要和被除数的小数点对齐。

( ) （4）5.39••93是一个无限小数。

( ) （5）125÷3的商保留一位有效数字是41.6。

( ) （6）除数扩大到原来的100倍，被除数不变，商扩大10倍。

( ) （7）365÷50=7.3则0.365÷5=0.0073。

( )（8）12.0560560563…是循环小数，循环节是056。

( ) （9）在小数除法中，商不变的性质不适应。

( ) （10）比3.9小且比3.7大的小数只有3.8. ( ) 2、口算0.66÷6= 5.6÷0.8= 7.2÷9= 42÷0.07= 12.5÷5= 5.4÷6= 0.35÷0.5= 0.48÷16= 0.152÷0.8= 0÷0.38= 10000÷0.01= 3.5÷0.007= 3、列竖式计算：210÷1.4= 0.6÷1.5= 13.95÷45=44.8÷1.6= 22.2÷0.33≈ 73.5÷6.7≈4、脱式计算：运用适当的方法6.4÷0.8+5 8.4÷（0.4+0.4） 15.6÷0.02÷310.08÷48+0.25 8.91⨯2÷0.2 0.52÷0.4+0.78÷0.2 5、选择（1）下列数中不是循环小数是（ ）A.3.333B.3.33…C.3.33213333... （2）把15.23的小数点向左移动1位，这个数就（ ） A.扩大10倍 B.缩小10倍 C.大小不变 （3）0.4••82的小数部分第8位上的数字是（ ） A.4 B.2 C.8 （4）得数是9.1的算式是（ ）A.91÷100B.9.1÷100C.91÷10 （5）甲数是100，乙数是0.001，甲数除以乙数的商是（ ） A.10000 B.100000 C.1000000 （6）3.65除以0.99（ ）3.65A.大于B.小于C.等于 （7）最小的两位数是0.05的（ ）倍。

用“四舍五入”法求商的近似值1.7.364保留一位小数约是（），保留两位小数约是（）。

2.7.395保留整数是（）；精确到百分位，要看（）位是否满5，约是（）。

3.一个三位小数，保留两位小数约是7.30，这个三位小数最大是（），最小是（）。

人民币的兑换1.如果一美元换取人民币6.31元，600元人民币大约换取（）（保留两位小数）美元；123美元换取（）元人民币。

2.王叔叔到日本出差，他带了1200元人民币，能兑换多少日元？（100日元兑换人民币7.89元，结果保留两位小数）3.小伟的叔叔到香港旅游时，买了一部手机，折合人民币多少元？（1港元兑换人民币0.81元）4.张阿姨从泰国旅游回来，还剩1500泰铢，能换多少人民币？（100泰铢兑换人民币20.32元）商与被除数的大小关系在○中填“＞”“＜”或“＝”。

7.26÷1○7.26 0.56÷0.99○0.56 12.2÷1.2○12.2 循环小数1.下面哪些是循环小数？0.666… 1.4848… 4.252525 0.1875875…2.无限小数一定比有限小数大。

（）7.循环小数0.396保留两位小数约是（）；2.4666……的循环节是（）。

0.445○0.4 7.34○7.223 3.567○3.567 0.4333○0.43 3.047○3.047 3.785○3.578 6.3.181818……是循环小数，还可以记作（），保留三位小数约是（）。

7.把6.16，6.16，6.16，6.166按从小到大的顺序排列起来是：（）＜（）＜（）＜（）。

应用题1.妈妈将5.9千克绿豆分装在一些小袋中，要全部装完，每个袋子最多可装0.8千克，至少需准备几个袋子？2.每套校服用布2.2米300米布最多能做多少套校服？3.用10千克红豆做豆沙包，一个豆沙包要用0.06千克红豆，最多可以做多少个豆沙包？4.用80米的彩带包扎礼盒，每个礼盒用彩带1.3米，这些彩带可以包扎多少个礼盒？3.两只大熊猫3天吃了 36.12kg 竹子,平均每只大熊猫每天吃了多少千克竹子？4.周老师带了 200 元去买奖品,他先花66.5元买了25 本笔记本,剩下的钱用来买钢笔。

北师大版数学五年级（上册）各单元知识点第一单元小数除法1、除数是整数的小数除法计算法则：①除数是整数的小数除法，按照整数除法的法则去除；②商的小数点要和被除数的小数点对齐；③如果除到被除数的末尾仍有余数，就在余数后面添“0”再继续除。

2、除数是小数的小数除法计算法则：①除数是小数的除法，先移动除数的小数点，使它变成整数；②除数的小数点向右移动几位，被除数的小数点也向右移动几位(位数不够的，在被除数末尾用0补足)；③然后按照除数是整数的小数除法进行计算。

3、在小数除法中的发现：①当除数大于1时，商小于被除数。

如：3.5÷5=0.7②当除数小于1时，商大于被除数。

如：3.5÷0.5=74、小数除法的验算方法：①商×除数=被除数(通用)②被除数÷商=除数③被除数÷除数=商5、商的近似数：①计算时，比要求保留的小数位数多除一位，再根据“四舍五入”法保留小数位数，求出商的近似数。

例如：要求保留一位小数的，商要除到第二位小数就可以停下来；要求保留两位小数的，商除到第三位小数停下来……如此类推。

②在解决实际问题取商的近似数时，要结合实际情况用“去尾”法或者“进一”法。

6、循环小数问题：①小数部分的位数是有限的小数，叫做有限小数。

如：0.37、1.4135等。

②小数部分的位数是无限的小数，叫做无限小数。

如：5.3……、7.145145……等。

③一个数的小数部分，从某位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

(如5.3……、3.12323……、5.7171……)④一个循环小数的小数部分，依次不断重复的数字，叫做小数的循环节。

(如5.333……的循环节是3，4.6767…的循环节是67，6.9258258…的循环节是258)7、用简写循环小数的方法：①只写一个循环节，并在这个循环节的首位和末位上面记一个小圆点。

例如：只有一个数字循环节的，就在这个数字上面记一个小圆点，5.333…写作∙3.5；有两位小数循环节的，就在这两位数字上面记上小圆点，7.4343…写作∙∙3 4.7有三位或以上小数循环的，在首位和末位记上小数点，10.732732…写作∙∙237.108、除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数( 0除外)，商不变。

姓名：五年级数学一：小数除法1.小数除法的意义：与整数除法的意义相同，是已知两个因数的积与其中一个因数，求另个一个因数的运算。

2.小数除法的计算法则：（1）除数是整数：①按照整数除法的法则去除；②商的小数点要和被除数的小数点对齐（重点！）③每一位商都要写在被除数相同数位的上面。

④如果除到末尾仍有余数，在被除数的个位数的右边点上小数点，再在被除数的后面添上“0”继续除，直到除尽为止。

⑤除得的商的哪一数位上不够商，就在那一位上写0占位。

例一：（1）÷8 （2）÷6（3）511÷14 （4）306÷75习题一：列竖式计算。

（1）÷6 （2）÷14（3）6÷15 （4）÷8（2）除数是小数：①先看除数中有几位小数，就把除数和被除数的小数点向右移动相同的位置，使除数变成整数，当被除数数位不够时，用0补足；②然后按照除数是整数的小数除法计算。

例二：（1）÷（2）÷习题二：列竖式计算。

（1）÷（2）21÷3、商不变的规律：被除数扩大a倍（或缩小）除数也扩大（或缩小）a倍，商不变。

简言之，被除数和除数同时扩大或者同时缩小相同的倍数，商不变。

例三：（1）÷=（）÷68 （2）÷18=（）÷18习题三：（1）÷=（）÷48（2）÷=（）÷344、被除数不变，除数扩大（或缩小）a倍，商缩小（或扩大）a倍。

被除数扩大（或缩小a倍，除数不变，商扩大（或缩小）倍。

例四：（1）÷30 = （2）180÷25=÷3 = 18÷25=÷= ÷25习题四：（1）÷2= （2）÷8=÷20= 48÷8=÷200= 480÷8=5、被除数比除数大的，商大于1。

五年级数学小数除法知识点归纳（附习题及解析），一定要给孩子看《小数除法》要点知识1、小数除法的意义：已知两个因数的积与其中的一个因数，求另一个因数的运算。

如：0.6÷0.3表示已知两个因数的积0.6，一个因数是0.3，求另一个因数是多少。

2、小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商0，点上小数点。

如果有余数，要添0再除。

3、除数是小数的除法的计算方法：先将除数和被除数扩大相同的倍数，使除数变成整数，再按“除数是整数的小数除法”的法则进行计算。

注意：如果被除数的位数不够，在被除数的末尾用0补足。

4、在实际应用中，小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数，求出商的近似数。

5、除法中的变化规律：①商不变性质：被除数和除数同时扩大或缩小相同的倍数（0除外），商不变。

②除数不变，被除数扩大（缩小），商随着扩大（缩小）。

③被除数不变，除数缩小，商反而扩大；被除数不变，除数扩大，商反而缩小。

6、(P28)循环小数：一个数的小数部分，从某一位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

循环节：一个循环小数的小数部分，依次不断重复出现的数字。

如6.3232……的循环节是32.简写作6.327.小数部分的位数是有限的小数，叫做有限小数。

小数部分的位数是无限的小数，叫做无限小数。

小数分为有限小数和无限小数。

易错题解析1、9.97÷4.21的商保留两位小数是( )保留整数是（）。

2.37 22.去掉0.25的小数点，就是把这个数扩大（）；把50.4的小数点向左移动两位，就是把它缩小到原来的（）。

100倍百分之一3、125缩小到它的（）是0.125；（）扩大到它的100倍是0.3。

千分之一 0.0034、0.25除以0.15，当商是1.6时，余数是（）;0.79÷0.04,商是19,余数是（）。

五年级数学综合算式专项练习题小数除法一、整体理解小数除法是指将一个小数除以另一个小数的运算。

在小数除法中，我们需要将被除数除以除数，然后得到商。

小数除法涉及到小数点后的运算，需要注意对齐小数点。

二、基础知识回顾在进行小数除法运算之前，我们需要回顾一些基础知识。

1. 小数点的位置在一个数的整数部分后面，小数点表示小数的开始。

小数点的位置决定了小数的大小和精度。

2. 小数的读法小数的读法与整数略有不同。

小数点前面的数是整数，小数点后面的数可以一个个读，也可以连在一起读。

例如，0.25可以读作“零点两五”或者“零点二五”。

3. 小数的比较小数的大小比较需要根据小数点后面的数进行比较。

如果小数点后面的数相同，再比较整数部分的大小。

三、练习题1. 小数除法练习题一将0.8除以0.2，计算商。

解答：首先，将0.8除以0.2，将小数点对齐后进行相除。

4┌────────────────────0.2 │ 0.8- 0.8答案：商为4。

2. 小数除法练习题二将2.25除以0.75，计算商。

解答：将2.25除以0.75，将小数点对齐后进行相除。

3┌───────────────────0.75 │ 2.25- 2.25答案：商为3。

3. 小数除法练习题三将5.6除以0.8，计算商。

解答：将5.6除以0.8，将小数点对齐后进行相除。

7┌────────────────────0.8 │ 5.6- 4.880- 80答案：商为7。

四、总结通过以上的小数除法练习题，我们可以得出以下结论：1. 在小数除法运算中，需要将小数点对齐后进行相除。

2. 小数除法运算的结果是一个小数，可以是有限小数也可以是无限循环小数。

3. 在进行小数除法运算时，需要注意保持数字的对齐和精度。

4. 小数除法是五年级数学中的一个重要知识点，需要进行反复练习和掌握。

希望通过这些练习题，你能更好地理解和掌握小数除法运算，提升自己的数学综合运算能力。

加油！。

课题：小数乘除法复习知识点一、小数乘法考点一：小数乘法运算法则练习:11、计算小数乘法时，先按照算出积，再点；点时，看中一共有几位小数，就从积的起数出几位，点上小数点。

2、计算2.4×0.8，先按整数乘法（）×（）算出积，再看2.4和0.8这两个因数中一共有（）位小数，就从积的右边起数出（）位，点上小数点。

3、 3.15×2.14的积是（）位小数；0.0125×0.8的积是（）位小数。

练习2：给下面各题中的积点上小数点。

0．87 × 0．26= 2 2 6 2 38．7× 0．25= 9 6 7 51．38 × 0．015= 2 0 7 0 449．5×1．2= 5 3 9 4 0考点二：积不变的性质在小数乘法中，一个因数（），另一个因数（），积不变。

练习1：1、根据38×45＝1710，在括号里填上合适的数。

3.8×4.5＝（） 3.8×45＝（） 0.38×450＝（）38×0.45＝（）2、根据794×98＝77812，填出下面各式的得数。

79.4×0.98＝（） 79.4×980＝（） 7.94×0.98＝（）3、根据56×1.3=72.8，直接写出下面各题的结果。

56×13=( ) 0.56×1.3=( ) 5.6×13=( )练习2：根据积不变的性质填空根据96×0.018=1.728写出（）×（）=1.728 ；（）×（）=1.728；考点三：利用乘法运算规律比较大小一个数乘以（）的数积大于这个数；一个数乘以（）的数积等于这个数；一个数乘以（）的数积小于这个数。

练习1：4．8×0．99○4．8 3．05×1．03○3．05 0．78×1○0．78 0．5○ 47× 0．51．2○1．2×1．1 0．95×1．3○1．3 13.76×0.8○13.76 0.2○1.1×0.2考点四：判断选择题汇总 练习1：判断并改正1、一个因数扩大10倍，另一个因数缩小到它的101,积不变。

北师大版五年级上册知识要点第一单元一、精打细算、打扫卫生。

(2)二、谁打电话时间长。

(2)三、商的近似数。

(3)四、小数除法的验算方法 (4)五、循环小数问题。

(4)七、除法中的变化规律 (5)第一单元测试卷及答案 (6)第一单元真题卷及答案 (14)一、精打细算、打扫卫生。

18.9 ÷6 ＝ 3.15（元）计算方法是：除数是整数的小数除法，按照整数除法的法则计算，商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数，就在余数后面添0再继续除。

二、谁打电话时间长。

5.1÷0.3＝17（分）计算方法：除数是小数的除法，先移动除数的小数点，使它变成整数;除数的小数点向右移动几位，被除数的小数点也向右移动几位(位数不够的，在被除数末尾用0补足)，然后按照除数是整数的小数除法进行计算。

在小数除法中的发现：（1）当除数不为0且大于1时，商小于被除数。

（2）当除数不为0且小于1时，商大于被除数。

（3）当除数不为0且等于1时，商等于被除数。

三、商的近似数。

根据要求要保留的小数位数，决定商要除出几位小数，再根据“四舍五入”法保留一定的小数位数，求出商的近似数。

例如：要求保留一位小数的，商除到第二位小数可停下来;要求保留两位小数的，商除到第三位小数停下来……如此类推。

四、小数除法的验算方法①商×除数=被除数(通用) ②被除数÷商=除数五、循环小数问题。

A、小数部分的位数是有限的小数，叫做有限小数。

如，0.37、1.4135等。

B、小数部分的位数是无限的小数，叫做无限小数。

如5.3… 7.145145…等。

C、一个数的小数部分，从某位起，一个数字或者几个数字依次不断重复出现，这样的小数叫做循环小数。

(如5.3…3.12323…5.7171…)D、一个循环小数的小数部分，依次不断重复的数字，叫做小数的循环节。

(如5.333…的循环节是3，4.6767…的循环节是67，6.9258258…的循环节是258)E、用简便方法写循环小数的方法：①只写一个循环节，并在这个循环节的首位和末位上面记一个小圆点。

五年级第三单元《小数除法》整理和复习知识框架：小数除以整数一、基础操练知识点一：小数除法的意义小数除法的意义：已知两个因数的（ ）与其中的一个因数，求另一个因数的运算。

如：0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3，求另一个因数的运算。

知识点二：小数除以整数的计算方法1、小数除以整数*计算法则：按整数除法的法则进行计算，商的小数点要和被 2、一个数除以小数 除数的小数点对齐。

如果有余数，要添0再除。

（整数部分不够除，商0，点上小数点。

（一位一位落数，不够商1就用0占位。

）空间与图形3、商的近似数。

四舍五入法(结合生活实际，具体问题具体分析)有限小数4、循环小数：小数 无限不循环小数 无限小数无限循环小数 5、用计算器探索规律 6、解决问题小数除法小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商写上0，点上小数点。

如果有余数，要添0再除。

【练习】58.89÷13 96÷15 0.465÷15 16.32÷51二、感悟与实践例题1：学校买了13盒白粉笔和10盒彩色粉笔，共付64.5元。

每盒白粉笔2.5元，每盒彩色粉笔多少元？变式练习：一支钢笔的价钱是一支圆珠笔价钱的4倍。

王小东买了一支钢笔和3支圆珠笔，一共花了17.5元。

钢笔和圆珠笔的单价各是多少元？例题2：服装厂做校服。

原来每套服装用布2.2米，现在每套用布节省0.2米。

原来做800套这种服装的布，现在可以做多少套？变式练习：工程队要铺设一条长4.8千米的地下管道，计划用15天完成，实际每天比计划多铺设3.2千米，实际多少天完成任务？变式练习：西平乡修一条长2.1千米的河堤，前15天平均每天修0.086千米。

余下的要9天完成，平均每天修多少千米？三、巩固练习练习1一、口算。

23.6÷10=10÷4=0.36÷3=8.4÷2=40÷50= 6.6÷33 =二、填空。

人教版五年级上册数学第三单元知识点及练习题1.人教版五班级上册数学第三单元学问点1、小数除法的计算方法（1）除法的意义：已知两个因数的积与其中的一个因数，求另一个因数的运算。

（2）小数除以整数的计算方法：小数除以整数，按整数除法的方法去除，商的小数点要和被除数的小数点对齐。

整数部分不够除，商写上0，点上小数点。

假如有余数，要添0再除。

（3）除数是小数的除法的计算方法：先将除数和被除数扩大相同的倍数，使除数变成整数，再按“除数是整数的小数除法”的法则进行计算。

易错点：假如被除数的位数不够，在被除数的末尾用0补足。

2、除法中的变化规律①商不变性质：被除数和除数同时扩大或缩小相同的倍数（0除外），商不变。

②除数不变，被除数扩大，商随着扩大。

③被除数不变，除数缩小，商扩大。

3、商的近似数（1）精确数与近似数①精确数：在日常生活和生产实际所遇到的数中，有时可以得到完全精确的数，他们精确，没有误差。

如：五（1）班有同学46人，这里的46是精确数。

②近似数：由于实际中经常不需要用精确的数描述一个量，或不行能得到精确的数。

如：中国约有13亿人，这里的13就是近似数。

（2）有效数字：一个近似数精确到哪一位，从左边第一个不是零的数算起，到这一位数字上，全部的数字，都叫做这个数的有效数字。

例如：0.6166≈0.62，有两个有效数字：6、2。

（3）求商的近似数：一般先除到比需要保留的小数位数多一位，再根据“四舍五入”法取商的近似值。

易错点：其中小数末尾的“0”不能去掉。

4、循环小数假如除到被除数的末位仍有余数，要在余数后面添“（）”连续除。

假如被除数的整数部分不够除，要先在（）上商0，点上（）后再连续除。

2、55.8÷6，商的高位在（）位上，商比1（）。

5.58÷6，商的高位在（）位上，商比1（）。

二、口算。

4.8÷12＝ 4.5÷15＝8.1÷27＝9.6÷6=18.9÷9＝ 2.8÷4＝18÷3.6= 1.25÷5＝三、列竖式计算下面各题，并用乘法验算。

【关键字】数学第三单元小数除法一：除数是整数的小数除法知识点1. 小数除以整数的计算方法6.75÷5= 46.4÷4 = 30.6÷18 = 29.52÷24= 399÷3.8= 741÷0.95=小结：先按照（）的方法计算，再把商的小数点与被除数的小数点对齐。

口诀：整数除小数，计算并不难，先按整数除，商加小数点。

位置很好找，对齐被除数。

知识点2：除到被除数的末位仍有余数的计算方法（1）30.9÷15= 3.6÷24= 36÷15= 1÷8=（2）已知两个因数的积是1.53，一个因数是18，另一个因数是（）小结：计算除法时，如果除到被除数的末位仍有余数，要在后面（）继续除。

知识点3：被除数的整数部分不够除的计算方法小数除以整数，如果小数的整数部分不够除，就在个位上商0，点上商的小数点后继续除。

小数除以整数，小数部分中某一位不够商1的方法1.26÷14 1.08÷12 0.552÷46 6.84÷38 5.768÷56小结：小数除以整数和整数除法一样，除到哪一位上不够商1时，就在那一位上商0占位知识点4：小数除以整数的计算方法总结及验算小数除以整数，先按（）除法的方法去除，商的小数点要和（）的小数点对齐；整数部分不够除，就要在个位上商（），点上小数点继续除；如果除到被除数的末位仍有余数，就在余数的后面（），再继续除。

验算：可以利用商x除数=被除数，来验算小数除法。

除法算式中商与1的关系1.观察被除数和除数的特点，在商小于1的算式右面划“√”54÷36（）25.4÷42 （）8.4÷7（） 5.06÷6（）15÷16（）小结：被除数不为0时，除数大于被除数，商（）1；除数小于被除数，商（）1.口诀：小数除法并不难，小数点齐是关键。