17年第六章实验计算题训练

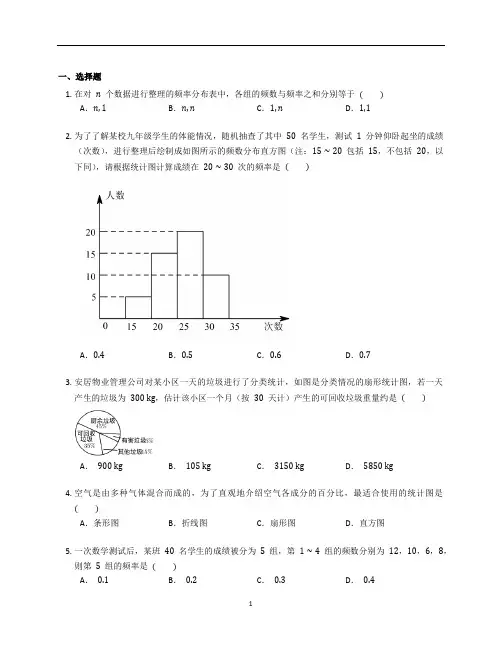
一、选择题1.在对n个数据进行整理的频率分布表中，各组的频数与频率之和分别等于( )A．n,1B．n,n C．1,n D．1,12.为了了解某校九年级学生的体能情况，随机抽查了其中50名学生，测试1分钟仰卧起坐的成绩（次数），进行整理后绘制成如图所示的频数分布直方图（注：15∼20包括15，不包括20，以下同），请根据统计图计算成绩在20∼30次的频率是( )A．0.4B．0.5C．0.6D．0.73.安居物业管理公司对某小区一天的垃圾进行了分类统计，如图是分类情况的扇形统计图，若一天产生的垃圾为300 kg，估计该小区一个月（按30天计）产生的可回收垃圾重量约是( )A．900 kg B．105 kg C．3150 kg D．5850 kg4.空气是由多种气体混合而成的，为了直观地介绍空气各成分的百分比，最适合使用的统计图是( )A．条形图B．折线图C．扇形图D．直方图5.一次数学测试后，某班40名学生的成绩被分为5组，第1∼4组的频数分别为12，10，6，8，则第5组的频率是( )A．0.1B．0.2C．0.3D．0.46.为了鼓励学生课外阅读，学校公布了“阅读奖励”方案，征求了所有学生的意见，根据赞成、反对、无所谓三种意见的人数之比画出扇形统计图，图中α的度数为( )A．36∘B．20∘C．10∘D．无法确定7.如图是北京城镇居民家庭2010−2017年每百户移动电话拥有量折线统计图，根据图中信息，相邻两年每百户移动电话拥有量变化最大的是( )A．2010年至2011年B．2011年至2012年C．2014年至2015年D．2016年至2017年8.黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%，请估计黄石地区1000斤蚕豆种子中不能发芽的大约有( )A．971斤B．129斤C．97.1斤D．29斤9.随着智能手机的普及，“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐，某商场对2019年7−12月中使用这两种手机支付方式的情况进行统计，得到如图所示的折线图，根据统计图中的信息，得出以下四个推断，其中不合理的是( )A．6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多B．6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大C．6个月中11月份使用手机支付的总次数最多D．9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多10.小刚家2017年和2018年的家庭支出情况如图所示，则小刚家2018年教育方面支出的金额比2017年增加了( )A．0.216万元B．0.108万元C．0.09万元D．0.36万元二、填空题11.某快递公司的快递件分为甲类件和乙类件，快递员送甲类件每件收入1元，送乙类件每件收入2元．累计工作1小时，只送甲类件，最多可送30件，只送乙类件，最多可送10件；累计工作2小时，只送甲类件，最多可送55件，只送乙类件，最多可送20件；⋯⋯，经整理形成统计表如下：（1）如果快递员一天工作8小时，且只送某一类件，那么他一天的最大收入为元；（2）如果快递员一天累计送x小时甲类件，y小时乙类件，且x+y=8，x，y均为正整数，那么他一天的最大收入为元．12.北京市2010~2015年高考报名人数统计如图所示．根据统计图中提供的信息，预估2016年北京市高考报名人数约为万人，你的预估理由是．13.如图是我市某连续7天的最高气温与最低气温的变化图，根据图中信息可知，这7天中最大的日温差是∘C．14.为了解全区5000名初中毕业生的体重情况，随机抽测了200名学生的体重，频率分布如图所示（每小组数据可含最小值，不含最大值），其中从左至右前四个小长方形的高依次为0.02，0.03，0.04，0.05，由此可估计全区初中毕业生的体重不小于60千克的学生人数约为人．15.如图，将一个圆分割成三个扇形，若甲、丙两个扇形面积之比为3:2，圆心角∠BOC=120∘，则∠AOC=∘．16.某班学生参加环保知识竞赛，已知竞赛得分都是整数．把参赛学生的成绩整理后分为6小组，画出竞赛成绩的频数分布直方图（如图所示），根据图中的信息，可得成绩高于60分的学生占全班参赛人数的百分率是．17.为了帮助班上的两名贫困学生解决经济困难，班上的20名学生捐出了零花钱，他们的捐款数（单位：元）如下：19，20，25，30，24，23，25，29，27，27，28，28，26，27，21，30，20，19，22，20．班主任老师准备将这组数据制成频数分布直方图，以表彰他们的爱心，制图时先计算最大值与最小值的差：．若取组距为2，则应分成组；若第一组的起点定为18.5，则在26.5∼28.5范围内的频数为．三、解答题18.某中学八年级在新学学期开设了四门校本选修课程：A．轮滑；B．书法；C．舞蹈；D．围棋；要求每名学生必须选择且只能选择其中一门课程，学校随机抽查了部分八年级学生，对他们的课程选择情况进行了统计，并绘制了如图两幅不完整的统计图．请根据统计图提供的信息，解答下列问题：(1) 此次共抽查了名学生；(2) 请通过计算补全条形统计图；(3) 若该校八年级共有900名学生，请估计选择C 课程的有多少名学生．19.新冠肺炎疫情期间，某市防控指挥部想了解自1月20日至2月末各学校教职工参与志愿服务的情况．在全市各学校随机调查了部分参与志愿服务的教职工，对他们的志愿服务时间进行统计，整理井绘制成两幅不完整的统计图表．请根据两幅统计图表中的信息回答下列问题：志愿服务时间(小时)频数A0<x≤30aB30<x≤6010C60<x≤9016D90<x≤12020(1) 本次被抽取的教职工共有名；(2) 表中a=，扇形统计图中“C”部分所占百分比为%；(3) 扇形统计图中，“D”所对应的扇形圆心角的度数为∘；(4) 若该市共有30000名教职工参与志愿服务，那么志愿服务时间多于60小时的教职工大约有多少人？20.某中学举行“庆祝中华人民共和国成立70周年”知识预赛，学生会把成绩x（分）分成五组：A组：50≤x<60；B组：60≤x<70；C组：70≤x<80；D组：80≤x<90，E组：90≤x<100．统计后绘制成如下两个统计图（不完整）．(1) 直接填空：① m的值为．②在图2中，C组的扇形圆心角的度数为．(2) 在图1中，画出60≤x<70所对应的条形图．(3) 若学生会计划从预赛中选拔前30名进入复赛，则进入复赛的成绩应不低于多少分？21.新华社消息：法国教育部宜布，小学和初中于2018年9月新学期开始，禁止学生在校使用手机．为了解学生手机使用情况，包河区某学校开展了“手机伴我健康行”的主题活动，学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，图②的统计图．已知“查资料”的人数为42．(1) 本次抽样调查一共抽取了人；补全条形统计图；(2) 在扇形统计图中，“玩游戏”对应的圆心角的度数为度；(3) 该校共有学生2100人，请估计每周使用手机时间在2小时以上（不含2小时）的人数．22.某区举办科技比赛，某校参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图如图．(1) 该校参加机器人的人数是人；“航模”所在扇形的圆心角的度数是∘．(2) 补全条形统计图．(3) 从全区参加科技比赛选手中随机抽取80人，其中有16人获奖，已知全区参加科技比赛人数共有3215人，请你估算全区参加科技比赛的获奖人数约是多少人？23.图①是某手机生产厂第一季度三个月产量统计图，图②是这三个月的产量与第一季度总产量的比例分布统计图，统计员在制作图①、图②时漏填了部分数据．(1) 该厂二月份生产的手机产量占第一季度的比例为%；(2) 求该厂三月份生产手机的产量；(3) 请求出图②中一月份圆心角的度数．24.某校开展“阳光体育活动”主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳这四种运动项目．为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图所示的条形统计图和扇形统计图．请你结合图中的信息解答下列问题：(1) 样本中喜欢B项目的人数百分比是，其所在扇形统计图中的圆心角的度数是．(2) 把条形统计图补充完整．(3) 已知该校有2000人，根据样本估计全校喜欢乒乓球的人数是多少？25.“校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调査的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题：(1) 接受问卷调查的学生共有人，扇形统计图中“了解”部分所对应扇形的圆心角为度；(2) 请补全条形统计；(3) 若该中学共有学生1200人，估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数．答案一、选择题1. 【答案】A【知识点】频数分布表及直方图2. 【答案】D【知识点】频数分布表及直方图3. 【答案】C【解析】300×35%×30=3150(kg)，该小区一个月（按30天计）产生的可回收垃圾重量约是3150 kg．【知识点】扇形统计图4. 【答案】C【解析】根据题意，得要求直观反映空气的组成情况，即各部分在总体中所占的百分比，结合统计图各自的特点，应选择扇形统计图．【知识点】扇形统计图5. 【答案】A【解析】根据题意得：40−(12+10+6+8)=40−36=4，则第5组的频率为4÷40=0.1．【知识点】数据的分布6. 【答案】A【解析】由图知“无所谓”意见人数占总人数的10%，所以图中α的度数为360∘×10%=36∘．【知识点】扇形统计图7. 【答案】B【解析】观察折线统计图可知：2011年至2012年每百户移动电话拥有量变化最大．【知识点】折线统计图8. 【答案】D【解析】由题意可得，黄石地区1000斤蚕豆种子中不能发芽的大约有：1000×(1−97.1%)= 1000×0.029=29斤．【知识点】用样本估算总体9. 【答案】B【知识点】折线统计图10. 【答案】A【解析】2017年教育方面支出所占的百分比：1−30%−25%−15%=30%，教育方面支出的金额：1.8×30%=0.54（万元）；2018年教育方面支出的金额：2.16×35%=0.756（万元），小刚家2018年教育方面支出的金额比2017年增加了0.756−0.54=0.216（万元）．【知识点】条形统计图、扇形统计图二、填空题11. 【答案】160；180【知识点】统计表12. 【答案】6.53；最近三年下降趋势平稳【解析】答案不唯一，预估理由需包含统计图提供的信息，且支撑预估的数据即可.【知识点】折线统计图、数据变化趋势分析13. 【答案】11【解析】∵由折线统计图可知，周一的日温差=8∘C+1∘C=9∘C；周二的日温差=7∘C+1∘C=8∘C；周三的日温差=8∘C+1∘C=9∘C；周四的日温差=9∘C；周五的日温差=13∘C−5∘C=8∘C；周六的日温差=15∘C−71∘C=8∘C；周日的日温差=16∘C−5∘C=11∘C，∴这7天中最大的日温差是11∘C．【知识点】折线统计图14. 【答案】1500【知识点】频数分布直方图、用样本估算总体15. 【答案】96【知识点】扇形统计图16. 【答案】80%【知识点】频数分布表及直方图17. 【答案】11；6；5【知识点】频数分布表及直方图三、解答题18. 【答案】(2) C 项目的人数为180−46−34−40=60（名）．条形统计图补充为：(3) 估计全校选择C 课程的学生有900×60180=300（名）．【解析】(1) 这次学校抽查的学生人数是40÷80360=180（名）．【知识点】条形统计图、扇形统计图、用样本估算总体19. 【答案】(1) 50(2) 4；32(3) 144(4) 由题意可知：30000×16+2050×100%=21600（人）．∴估计全市志愿服务时间多于60小时的教职工大约有21600人．【知识点】用样本估算总体、扇形统计图20. 【答案】(1) ① 150② 90∘(2) 400×72360=80人，所画条形图如图所示．(3) 由（1）可得E组的人数为：400−40−80−100−150=30人，∴前30名的成绩应不低于90分，即进入复赛的成绩应不低于90分．【解析】(1) ① 40÷36360=400，400×135400=150人．② 360∘×100400=90∘．【知识点】扇形统计图、条形统计图21. 【答案】(1) 105；补全条形统计图，如图所示：=1380（人）．(3) 估计每周使用手机时间在2小时以上（不含2小时）的人数为2100×32+37105答：全校学生2660名学生中每周使用手机时间在2小时以上（不含2小时）的有1380人．【解析】(1) 42÷40%=105（人），3小时以上的人数为：105−(2+16+18+32)=37（人）．(2) 1−(40%+18%+7%)=35%，则“玩游戏”对应的圆心角度数是360∘×35%=126∘．【知识点】扇形统计图、用样本估算总体、条形统计图22. 【答案】(1) 4；90(2) 因为被调查的总人数为6÷25%=24人，所以电子百拼的人数为24−(6+4+6)=8人，补全图形如下：=643人．(3) 估算全区参加科技比赛的获奖人数约是：3215×1680【解析】(1) 该校参加机器人的人数是4，“航模”所在扇形的圆心角的度数是360∘×25%=90∘．【知识点】扇形统计图、用样本估算总体、条形统计图23. 【答案】(1) 34%(2) 该厂第一季度总产量为：1500÷30%=5000（部），5000×36%=1800（部）；答：该厂三月份生产手机为1800部；(3) 360∘×30%=108∘．答：图②中一月份圆心角的度数为：108∘．【解析】(1) 该厂二月份生产的手机产量占第一季度的比例为1−30%−36%=34%；【知识点】扇形统计图、条形统计图24. 【答案】(1) 20%；72∘(2)(3) 2000×44%=880【解析】(1) 1−8%−28%−44%=20%，360∘×20%=72∘．(2) 44÷44%×20%=20．【知识点】用样本估算总体、扇形统计图、条形统计图25. 【答案】(1) 60；90(2) “了解很少”的人数为60−(15+30+5)=10人，补全图形如下：=900(3) 估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数为1200×15+3060人．【解析】(1) 接受问卷调査的学生共有30÷50%=60人，扇形统计图中“了解”部分所对应扇形的圆心角=90∘．为360∘×1560【知识点】条形统计图、扇形统计图、用样本估算总体。

第6章圆周运动练习题一、选择题。

1、如图所示的齿轮传动装置中，主动轮的齿数z1＝24，从动轮的齿数z2＝8，当主动轮以角速度ω顺时针转动时，从动轮的转动情况是()A.顺时针转动，周期为2π3ω B.逆时针转动，周期为2π3ωC.顺时针转动，周期为6πω D.逆时针转动，周期为6πω2、下列关于向心力的说法中正确的是()A．做匀速圆周运动的物体除了受到重力、弹力等力外还受到向心力的作用B．向心力和重力、弹力一样，是性质力C．做匀速圆周运动的物体的向心力即为其所受的合外力D．做圆周运动的物体所受各力的合力一定充当向心力3、如图所示，一个水平大圆盘绕过圆心的竖直轴匀速转动，一个小孩坐在距圆心为r处的P点不动(P未画出)，关于小孩的受力，以下说法正确的是()A.小孩在P点不动，因此不受摩擦力的作用B.小孩随圆盘做匀速圆周运动，其重力和支持力的合力充当向心力C.小孩随圆盘做匀速圆周运动，圆盘对他的摩擦力充当向心力D.若使圆盘以较小的转速转动，小孩在P点受到的摩擦力不变4、如图所示，一根轻杆(质量不计)的一端以O点为固定转轴，另一端固定一个小球，小球以O点为圆心在竖直平面内沿顺时针方向做匀速圆周运动。

当小球运动到图中位置时，轻杆对小球作用力的方向可能()A.沿F1的方向B.沿F2的方向C.沿F3的方向D.沿F4的方向5、关于做匀速圆周运动物体的向心加速度的方向，下列说法中正确的是()A.与线速度方向始终相同B.与线速度方向始终相反C.始终指向圆心D.始终保持不变6、(双选)如图所示，光滑水平面上，质量为m的小球在拉力F作用下做匀速圆周运动。

若小球运动到P点时，拉力F发生变化，下列关于小球运动情况的说法中正确的是()A.若拉力突然变大，小球将沿轨迹Pb做离心运动B.若拉力突然变小，小球将沿轨迹Pb做离心运动C.若拉力突然消失，小球将沿轨迹Pa做离心运动D.若拉力突然变小，小球将沿轨迹Pc做近心运动7、(双选)如图所示，在风力发电机的叶片上有A、B、C三点，其中A、C在叶片的端点，B在叶片的中点。

【对应训练】 5．计算：
(1)
3 （－2）2 －
1 27
×
（－3）2 ＋
196 ×3 －64 ÷
(2)| 5 － 6 |－| 5 －3|－| 6 －4|.
12254 ；
解：(1)－39 (2)2 6 －7
6．已知(x－12)2＝169，(y－1)3＝－0.125，求 x － 2xy －3 4y＋x 的值．
4 25
－|
7 －3|.
(3) 0.3；
解： 7
解：1525
21．解方程： (1)(x－2)3＝64;
解：x＝6
(2)4(3x＋1)2－1＝0. 解：x＝－16 或－12
22．已知实数 x，y 满足 x－2 ＋(y＋1)2＝0，则 x－y 等于( A ) A．3 B．－3 C．1 D．－1
【对应训练】
3 3.
－64
的立方根为_3__－__4____．
4．如果 x＜0，那么 x 的立方根为( A )
A．3 x
B．3 －x
C．－3 x
D．±3 x
四、对实数的有关概念理解不透彻 【例4】下列命题正确的是( D) A．无理数包括正无理数、0和负无理数 B．无理数不是实数 C．无理数是带根号的数 D．无理数是无限不循环小数
2．已知 M＝m－1 m＋6 是 m＋6 的算术平方根， N＝2m－3n＋3 n＋6 是 n＋6 的立方根，试求 M－N 的值．
解：由题意可知 m－1＝2，2m－3n＋3＝3，可得 m＝3，n＝2， 所以 M＝ 9 ＝3，N＝3 8 ＝2，所以 M－N＝3－2＝1
二、实数的非负性 【例 2】若 x2－1 ＋ y＋1 ＝0，求 x2019＋y2020 的值． 分析：由题意可知 x2－1＝0，y＋1＝0，分别求出 x，y， 再代入求值，注意分两种情况．

概率初步真题演练一、选择题1.某校举行“中国梦•我的梦”演讲比赛，需要在初三年级选取一名主持人，共有12名同学报名参加，其中初三（1）班有2名，初三（2）班有4名，初三（3）班有6名，现从这12名同学中随机选取一名主持人，则选中的这名同学恰好是初三（1）班同学的概率是（）A. B. C. D.2.在不透明口袋内有形状、大小、质地完全一样的5个小球，其中红球3个，白球2个，随机抽取一个小球是红球的概率是（）A. B. C. D.3.下列说法正确的是（）A. 袋中有形状、大小、质地完全一样的5个红球和1个白球，从中随机抽出一个球，一定是红球B. 天气预报“明天降水概率10%”，是指明天有10%的时间会下雨C. 某地发行一种福利彩票，中奖率是千分之一，那么，买这种彩票1000张，一定会中奖D. 连续掷一枚均匀硬币，若5次都是正面朝上，则第六次仍然可能正面朝上4.已知袋中有若干个球，其中只有2个红球，它们除颜色外其它都相同．若随机从中摸出一个，摸到红球的概率是，则袋中球的总个数是（）A. 2B. 4C. 6D. 85.在一个不透明的袋子中装有4个红球和3个黑球，它们除颜色外其他均相同，从中任意摸出一个球，则摸出黑球的概率是（）A. B. C. D.6.在英文单词“parallcl“（平行）中任意选择一个字母是“a“的概率为（）A. B. C. D.7.下列事件中，是必然事件的是（）A. 购买一张彩票，中奖B. 通常温度降到0℃以下，纯净的水结冰C. 明天一定是晴天D. 经过有交通信号灯的路口，遇到红灯8.在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是白球的概率为，则黄球的个数为（）A. 2B. 4C. 12D. 169.甲、乙、丙三人站成一排拍照，则甲站在中间的概率是（）A. B. C. D.10.一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4随机摸出一个小球，不放回，再随机摸出一个小球，两次摸出的小球标号的积小于4的概率是（）A. B. C. D.二、填空题11.在一个不透明的袋子中装有除颜色外其他均相同的3个红球和2个白球，从中任意摸出一个球，则摸出白球的概率是______．12.在一个不透明的盒子中，有五个完全相同的小球，把它们分别标号为1，2，3，4，5，随机摸出一个小球，摸出的小球标号为偶数的概率是______ ．13.甲盒装有3个乒乓球，分别标号为：1，2，3；乙盒装有2个乒乓球，分别标号为1，2现分别从每个盒中随机地取出1个球，则取出的两球标号之和为4的概率是______．14.一个口袋中装有10个红球和若干个黄球．在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.4．根据上述数据，估计口袋中大约有______个黄球．15.发芽频率那么这种油菜籽发概率是______ （精确到0.01）．三、解答题16.在一个不透明的口袋里装有白、红、黑三种颜色的小球，其中白球2只，红球1只，黑球1只，它们除了颜色之外没有其它区别，从袋中随机地摸出1只球，记录下颜色后放回搅匀，再摸出第二只球并记录颜色，求两次都摸出白球的概率．17.从甲地到乙地有A1、A2两条路线，从乙地到丙地有B1、B2、B3三条路线，从丙地到丁地有C1、C2两条路线．一个人任意选了一条从甲地到丁地的路线，求他恰好选到B2路线的概率是多少？18.甲、乙两队进行打乒乓球团体赛，比赛规则规定：两队之间进行3局比赛，3局比赛必须全部打完，只要赢满2局的队为获胜队，假如甲、乙两队之间每局比赛输赢的机会相同，且甲队已经赢得了第1局比赛，那么甲队最终获胜的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）19.小明、小林是三河中学九年级的同班同学，在四月份举行的自主招生考试中，他俩都被同一所高中提前录取，并将被编入A、B、C三个班，他俩希望能再次成为同班同学．（1）请你用画树状图法或列举法，列出所有可能的结果；（2）求两人再次成为同班同学的概率．答案和解析【答案】1. D2. C3. D4. D5. B6. C7. B8. B9. B10. C11. 12. 13. 14. 1515. 0.954种情况，∴两次都摸出白球的概率是：=．17. 解：用树状图分析如下：所以P（选到B2路线）==．答：他恰好选到B2路线的概率是．18. 解：根据题意画出树状图如下：一共有4种情况，确保两局胜的有3种，所以，P=．19. 解：（1）画树状图如下：由树形图可知所以可能的结果为AA，AB，AC，BA，BB，BC，CA，CB，CC；（2）由（1）可知两人再次成为同班同学的概率==．【解析】1. 解：∵初三（1）班有2名，初三（2）班有4名，初三（3）班有6名，∴共有12名同学，∵初三（1）班有2名，∴P（初三一班）==；故选D．用初三一班的学生数除以所有报名学生数的和即可求得答案．此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．2. 解：∵共有5个球，其中红球有3个，∴P（摸到红球）=，故选C．用红球的个数除以所有球的个数即可求得抽到红球的概率．此题主要考查概率的意义及求法．用到的知识点为：概率=所求情况数与总情况数之比．3. 解：A、袋中有形状、大小、质地完全一样的5个红球和1个白球，从中随机抽出一个球，一定是红球的概率是，故本选项错误；B、天气预报“明天降水概率10%”，是指明天有10%的概率会下雨，故本选项错误；C、某地发行一种福利彩票，中奖率是千分之一，那么，买这种彩票1000张，可能会中奖，故本选项错误；D、连续掷一枚均匀硬币，若5次都是正面朝上，则第六次仍然可能正面朝上，故本选项正确．故选D．根据概率的意义对各选项进行逐一分析即可．本题考查的是概率的意义，熟知一般地，在大量重复实验中，如果事件A发生的频率mn会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率是解答此题的关键．4. 解：袋中球的总个数是：2÷=8（个）．故选：D．根据概率公式结合取出红球的概率即可求出袋中球的总个数．本题考查了概率公式，根据概率公式算出球的总个数是解题的关键．5. 解：∵在一个不透明的袋子中装有除颜色外其他均相同的4个红球和3个黑球，∴从中任意摸出一个球，则摸出黑球的概率是．故选B．根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数．二者的比值就是其发生的概率的大小．本题考查概率的求法与运用，一般方法为：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．6. 解：单词中共有8个字母，a有两个，所以在英文单词“parallcl“（平行）中任意选择一个字母是“a“的概率==，故选C．可先找出单词中字母的个数，再找出a的个数，用a的个数除以总个数即可得出本题的答案．本题考查的是概率的公式，要求准确找出字母的总数和含n的个数．用到的知识点为：概率=所求情况数与总情况数之比．7. 解：（A）购买一张彩票中奖是随机事件；（B）根据物理学可知0℃以下，纯净的水结冰是必然事件；（C）明天是晴天是随机事件；（D）经过路口遇到红灯是随机事件；故选（B）根据随机事件与必然事件的定义即可求出答案．本题考查随机事件的定义，解题的关键是正确理解随机事件与必然事件，本题属于基础题型．8. 解：设黄球的个数为x个，根据题意得：=，解得：x=4．∴黄球的个数为4．故选：B．首先设黄球的个数为x个，然后根据概率公式列方程即可求得答案．此题考查了概率公式的应用．解此题的关键是设黄球的个数为x个，利用方程思想求解．9. 解：画树状图为：共有6种等可能的结果数，其中甲站在中间的结果数为2，所以甲站在中间的概率==．故选：B．画树状图展示所有6种等可能的结果数，再找出甲站在中间的结果数，然后根据概率公式求解．本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．10. 解：画树状图得：∵共有12种等可能的结果，两次摸出的小球标号的积小于4的有4种情况，∴两次摸出的小球标号的积小于4的概率是：=．故选C．首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的小球标号的积小于4的情况，再利用概率公式求解即可求得答案．此题考查了列表法或树状图法求概率．注意此题是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．11. 解：∵在一个不透明的袋子中装有除颜色外其他均相同的3个红球和2个白球，∴从中任意摸出一个球，则摸出白球的概率是．故答案为．根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数．二者的比值就是其发生的概率的大小．本题考查概率的求法与运用，一般方法为：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．12. 解：∵5个小球中，标号为偶数的有2、4这2个，∴摸出的小球标号为偶数的概率是，故答案为：确定出偶数有2个，然后根据概率公式列式计算即可得解．本题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．13. 解：列树状图得：共有6种等可能的情况，取出的两球标号之和为4的情况有2种，所以概率是．列举出所有情况，看取出的两球标号之和为4的情况占总情况的多少即可．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．14. 解：∵小明通过多次摸球实验后发现其中摸到红色球的频率稳定在0.4，设黄球有x个，∴0.4（x+10）=10，解得x=15．答：口袋中黄色球的个数很可能是15个．在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，先求得红球的频率，再乘以总球数求解．解答此题的关键是要估计出口袋中红色球所占的比例，得到相应的等量关系．15. 解：观格得到这种油菜籽发芽的频率稳095附近，则种油菜发芽概率是0.95，故答为：.95．观察表格得到这油菜发的频率稳定在.95，即可估计出这种油菜的概率．题查利用率估率，从表格中的数确定出这种油菜籽芽的频率是解本题的关键．16. 首先根据题意列出表格，然后表格求得所有等可能的结果与两次都摸出白球的情况，再利用概率公式求解即可求得答案．此题考查的是用列表法或树状图法求概率．注意画树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意此题属于放回实验．17. 用树状图列举出所有情况，看所求的情况占总情况的多少即可．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=，注意本题是放回实验．18. 根据甲队第1局胜画出第2局和第3局的树状图，然后根据概率公式列式计算即可得解．本题考查了用树状图列举随机事件出现的所有情况，并求出某些事件的概率，但应注意在求概率时各种情况出现的可能性务必相同．用到的知识点为：概率=所求情况数与总情况数之比．19. （1）画树状图法或列举法，即可得到所有可能的结果；（2）由（1）可知两人再次成为同班同学的概率．本题涉及列表法和树状图法以及相关概率知识，用到的知识点为：概率=所求情况数与总情况数之比．。

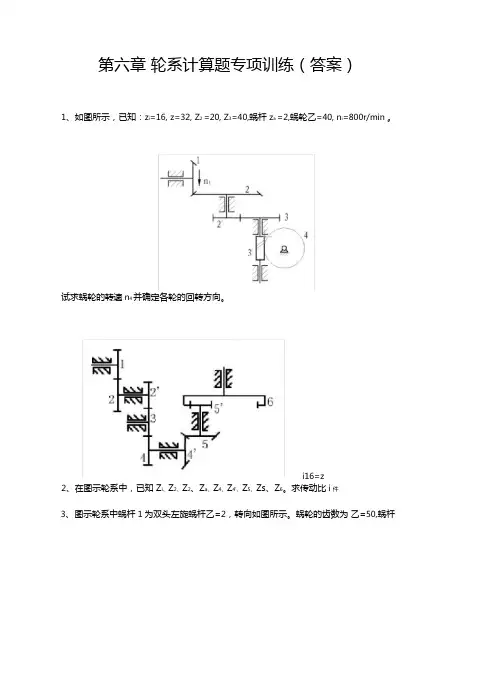
第六章轮系计算题专项训练（答案）1、如图所示，已知：z i=16, z=32, Z2 =20, Z3=40,蜗杆z a =2,蜗轮乙=40, n i=800r/min 。

试求蜗轮的转速n4并确定各轮的回转方向。

i16=z2、在图示轮系中，已知 Z i、Z2、Z2、Z a、Z4、Z4'、Z5、Zs、Z6。

求传动比i件3、图示轮系中蜗杆1为双头左旋蜗杆乙=2，转向如图所示。

蜗轮的齿数为乙=50,蜗杆2为单头右旋蜗杆乙'=1，蜗轮3的齿数为乙=40,其余各轮齿数为Z3' =30, Z 4=20, 乙’=26, Z 5=18, Z 5 =46, Z s=16, Z7=22。

求 i 17。

i17=Z2Z3Z4Z5Z6Z7/Z1Z2,Z3,Z4,Z5,Z6=50*40*20*18*22/2*1*30*26*46= 220.7 4、在习题图8 所示的轮系中，已知z i=15 , z 2=25 , z 2' =15 , z 3=30 , z 3' =15 , z 4=30,Z4 =2 , z 5=60,若m=500 r/min，求齿轮5转速的大小和方向。

（隹=2.5 r/minn5 乙25 30 30 6015 15 15 2n5蔬20° 2.5(r/m)；齿轮5的方向可以画箭头确定。

5、在图示轮系中，已知Z l、Z2、Z2'、Z3、Z4、Z 4'、Z5、Z5'、 Z6。

求传动比i 16。

ZJZ\7,6、如图所示轮系，已知Z i 24, Z2 46, Z223, Z3 48, Z4 35, Z4 20, Z5 48 , O i 为主动轴。

试计算轮系的传动比i i5并确定齿轮5的转动方向。

7、在如图所示的轮系中，已知乙=2 （右旋）,乙=60,乙=15,乙=30, Z5= 15,30,求：（1）该轮系的传动比i i6=?（2）若n1 = 1200 r / min ，求轮6的转速大小和方向?32256]XSE 蝎杆3遍7右旋Tm耀轮2&图示为一蜗杆传动的定轴轮系，已知蜗杆转速 n 1= 750r/min , Z i = 3, Z2 = 60,乙=18,乙=27, Z5 = 20, Z6 = 50,试用画箭头的方法确定Z6的转向，并计算其转速。

一、你还记得什么是频数、什么叫频率、什么叫概率吗试举例说明.二、将一枚硬币抛起，使其自然下落，每抛两次作为一次实验，当硬币落定后，一面朝上，我们叫做“正”，另一面朝上，我们叫做“反”.（1）一次实验中，硬币两次落地后可能出现几种情况（2）做20次实验，根据实验结果，填写下表.结果正正正反反反频数频率（3）根据上表，制作相应的频数分布直方图.（4）经观察，哪种情况发生的频率较大.（5）实验结果为“正反”的频率是多大.（6）5个同学结成一组，分别汇总其中两人，三人，四人，五人的实验数据，得到40次，60次，80次，100次的实验结果，将相应数据填入下表。

次数40次60次80次100次“正反”的频数“正反”的频率（7）依上表，绘制相应的折线统计图.（8）计算“正反”出现的概率.（9）经过以上多次重复实验，所得结果为“正反”的频率与你计算的“正反”的概率是否相近.小知识：在篮球比赛和足球比赛中，人们往往用抛硬币的方法决定由谁先来开球.那么抛硬币后，正面向上和反面向上的几率有多大呢相等吗下面我们来想办法解决这个问题.首先想到的是实验方法.投掷硬币500次记总抛出次数正面向上次正面向上频率§6.1.1频率与概率（次） 数（次） （…%）500225我们得到的是硬币正面向上的频率的百分比.即硬币正面向上的频率.其次我们又想到硬币的正、反面都没有什么特殊性，所以在落下时正面向上和反面向上的可能性相等.所以正面向上与反面向上都有21的可能性，也就是说正面向上的概率是___________.生活中常见一些概率问题的应用，例如彩票.20选5第2003178期中奖号码 05、12、15、16、17 一等奖 6注 18678元 二等奖 1214注 50元 三等奖 19202注5元本期销售额 548538元出球顺序05、15、12、16、17一、掷一枚硬币，落地后，国徽朝上、朝下的概率各是多少二、质地均匀的骰子被抛起后自由落在桌面上，点数为“1”或“3”的概率是多少三、掷两枚硬币，规定落地后，国徽朝上为正，国徽朝下为“反”，则会出现以下三种情况.“正正”“反反”“正反”分别求出每种情况的概率.（1）小刚做法：通过列表可知，每种情况都出现一次，因此各种情况发生的概率均占31. 可能出现正正正反反反§6.1.2频率与概率的情况 概率31 31 31 小敏的做法：第一枚硬币的可能情况第二枚硬币的可能情况正反正 正正 反正 反正反反反通过以上列表，小敏得出：“正正”的情况发生概率为41.“正反”的情况发生的概率为21，“反反”的情况发生的概率为41. （1）以上三种做法，你同意哪种，说明你的理由.（2）用列表法求概率时要注意哪些一、如图（1）是不是所有的随机事件的概率都可以用画树形图或列表的方法来求，试举例说明你的理由.二、图（2）钉落地实验，将图钉抛在地上. （1）观察图钉落地后出现几种状态.（2）猜想哪种情况发生的概率大（3）连续抛掷50次，将实验结果填在下表. 落地状态钉尖朝上钉尖着地频 数 频 率§6.2.1频率与概率（4）实验结果中各种情况发生的概率与你猜想的概率是否相符呢（5）如果班里有50位同学，每人做50次实验共做了2500次实验，请将实验数据汇总，再进一步计算各种情况发生的频率.（6）现在你能估计钉尖着地的概率了吗（7）以上做法是：利用大量的实验数据计算出某一情况发生的频率，再利用此频率来估计这一情况发生的概率，你还能举出生活中利用这一原理求概率的实例吗三、（如下图所示）把一小球从箭头处自由释放，落入一个内有阻碍物的容器中，小球一种情况是落入A槽，一种是落入B槽，你能通过列表法分别算出它们的概率吗一、填空题1.口袋中有2个白球，1个黑球，从中任取一个球，用实验的方法估计摸到白球的概率为_________.2.把一对骰子掷一次，共有_________种不同的结果.3.任意掷三枚均匀硬币，如果把掷出正面朝上记为“上”，掷出正面朝下记为“下”，所有的结果为_________.4.必然事件的概率为_________，不可能事件的概率为_________，不确定事件的概率范围是_________.5.频数和频率都能反映一个对象在实验总次数中出现的频繁程度，我认为：（1）频数和频率间的关系是_________.（2）每个实验结果出现的频数之和等于_________. （3）每个实验结果出现的频率之和等于_________..上学方式 步行 骑车 乘车 “正”字法记录正正正频数 9 频率40%抛掷结果 5次 50次 300次 800次 3200次 6000次 9999次 出现正面的频数 1 31 135 408 1580 2980 5006 出现正面的频率20%62%45%51%%%%（1）由这张频数和频率表可知，机器人抛掷完5次时，得到1次正面，正面出现的频率是20%，那么，也就是说机器人抛掷完5次时，得到_________次反面，反面出现的频率是_________. （2）由这张频数和频率表可知，机器人抛掷完9999次时，得到_________次正面，正面出现的频率是_________.那么，也就是说机器人抛掷完9999次时，得到_________次反面，反面出现的频率是_________. 二、选择题8.给出以下结论，错误的有（ ）①如果一件事发生的机会只有十万分之一，那么它就不可能发生. ②如果一件事发生的机会达到%，那么它就必然发生. ③如果一件事不是不可能发生的，那么它就必然发生. ④如果一件事不是必然发生的，那么它就不可能发生. 个 个 个 个9.一位保险推销员对人们说：“人有可能得病，也有可能不得病，因此，得病与不得病的概率各占§6.2.2频率与概率50%”他的说法（）A.正确B.不正确C.有时正确，有时不正确D.应由气候等条件确定10.某位同学一次掷出三个骰子三个全是“6”的事件是（）A.不可能事件B.必然事件C.不确定事件可能性较大D.不确定事件可能性较小三、解答题11.请制作一个方案说明你在你们班的同学中花“零花钱”属于多的还是少的12.走近你家附近的商店，统计几类主要产品的月销量，制出相应的条形统计图.13.与他人合作掷骰子100次，要求（2）制出条形统计图.（3）计算出各点的概率.（4）有可能再现7点吗它的概率为多少一、有400位同学，其中一定有至少两人生日相同吗若有367位同学呢说说你的理由.二、通过本节实验，你发现50位同学中有至少两位同学出生月日相同的频率占多少，估计这个情况的概率是多少三、通过本节学习，我们发现有些实验估计起来既费时，又费力，可以用摸球实验或其他模拟实验.（1）请再回顾一下我们是怎样将复杂的调查转化成模球实验的（2）请熟悉你的计算器产生随机数字的操作程序.四、取出一副扑克中的红桃A至红桃K共13张牌，牌面朝下放在桌面上，每次摸取一张看后放回，共摸取4次，试用计算器产生的随机数进行摸拟实验.小知识：小威和小丽在同一天过生日，他们班共有50名同学.想一想：这样能说50个人中2个人生日相同的概率为1吗为什么在§这一节我们将来研究怎样调查50个人中2个人生日相同的概率.下面我们来考虑几个类似的问题：1.估计六个人中同属相的概率.2.估计六个人中同星座的概率.§频率与概率在研究这种问题中，要想使估算的概率准确，就必须尽可能多的增加调查对象，这样既费时又费力，想一想有什么方法可以替代做调查来估算概率呢预习下节课的内容。

第6章数据与统计图表综合测试题一、选择题1. 要调查你校学生学业负担是否过重，选用下列哪种方法最恰当（）A．查阅文献资料B．对学生问卷调查C．上网查询D．对校领导问卷调查2. 如图，这是某地2014年和2015年粮食作物产量的条形统计图，请你根据此图判断下列说法合理的是（）A．2015年三类农作物的产量比2014年都有增加B．玉米产量和杂粮产量增长率相当C．2014年杂粮产量是玉米产量的约七分之一D．2014年和2015年的小麦产量基本持平3.（2016•瓯海区一模）为了解初三学生的体育锻炼时间，小华调查了某班45名同学一周参加体育锻炼的情况，并把它绘制成折线统计图．由图可知，一周参加体育锻炼时间等于9小时的人数是（）A．5 B．18 C．10 D．44.随着经济的发展，人们的生活水平不断地提高．如图是西湖景点2009-2011年游客总人数和旅游收入年增长率统计图．已知该景点2010年旅游收入4500万元．下列说法：①三年中该景点2011年旅游收入最高；②与2009年相比，该景点2011年的旅游收入增加[4500×（1+29%）-4500×（1-33%）]万元；③若按2011年游客人数的年增长率计算，2012年该景点游客总人数将达到280×（1+280−255255）万人次，其中正确的个数是（）A．0B．1C．2D．35.（2017•益阳模拟）小明家上个月支出共计800元，各项支出如图所示，其中用于教育上的支出是（）A．232元B．200元C．160元D．80元6. 要反映2015年末嘉兴市各个县（区）常住人口占嘉兴市总人口的比例，宜采用（）A．条形统计图B．折线统计图C．扇形统计图D．频数直方图7. 某校对初三年级1600名男生的身高进行了测量，结果身高（单位：m）在1.58～1.65这一小组的频率为0.4，则该组的人数为（）A．640人B．480 人C．400人D．40人8. 在一篇文章中，“的”、“地”、“和”三个字共出现100次，已知“的”和“地”的频率之和是0.7，那么“和”字出现的频数是（）A．28 B．30 C．32 D．349.某棉纺厂为了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x（单位：mm）的数据分布如下表所示，则棉花纤维长度的数据在16≤x＜32这个范围的频率为（）A．0.8 B．0.7 C．0.4 D．0.210．如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形统计图，（两图都不完整），则下列结论中正确的是（）A．步行人数为30人B．骑车人数占总人数的10%C．该班总人数为50人D．乘车人数是骑车人数的40%二、填空题11. 学习了统计知识后，小明就本班同学的上学方式进行了一次调查统计，他通过采集数据后，绘制一幅不完整的统计图（如图所示）．已知骑车的人数占全班人数的30%，结合图中提供的信息，可得该班步行上学的有人．12. 如图，镇江四月份某日的温度变化情况，则这天中8时到18时的温差为13. （2017春•陆丰市校级月考）如图，A、B、C3个扇形所表示的数据个数的比是2：7：3，则扇形C的圆心角的度数为.14. 在网络上，可以很方便的查阅平顶山市近期某天24小时整点天气预报图，那么这个天气预报图选用的是统计图．15. 将一批数据分成5组，列出频率分布表，其中第一组与第五组的频率之和是0.26，第二与第四组的频率之和是0.55，那么第三组的频率是.16.在大课间活动中，同学们积极参加体育锻炼，小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本绘制如图所示的部分频数分布直方图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图，若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，估计该校学生“一分钟跳绳”成绩优秀的人数为人．三、解答题17．我市某中学为了解该校学生对四种国家一级保护动物的喜爱情况，围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中，你最喜欢哪一种动物？（必选且只选一种）”这一问题，在全校范围内随机抽取部分同学进行问卷调查．根据调查结果绘制成如下不完整的条形统计图．其中最喜欢丹顶鹤的学生人数占被抽取人数的16%；请你根据以上信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？（2）求在被调查的学生中，最喜欢滇金丝猴的学生有多少名？并补全条形统计图；（3）如果全校有1200名学生，请你估计全校最喜欢大熊猫的学生有多少名？18. 某校组织学生排球垫球训练，训练前后，对每个学生进行考核．现随机抽取部分学生，统计了训练前后两次考核成绩，并按“A，B，C”三个等次绘制了如图不完整的统计图．试根据统计图信息，解答下列问题：（1）抽取的学生中，训练后“A”等次的人数是多少？并补全统计图．（2）若学校有600名学生，请估计该校训练后成绩为“A”等次的人数．根据表、图提供的信息，解决以下问题：（1）计算出表中a、b的值；（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？20.初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：（1）在这次评价中，一共抽查了名学生；（2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为度；（3）请将频数分布直方图补充完整；（4）如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？参考答案1~5BDBCB 6~10CABBC11.8 12.15.5℃13. 90°14.折线15.0.19 16.48017.18.19.20.。

第六章第2节《立方根》单元训练题 (7)一、单选题1．下列说法中：①绝对值最小的有理数是1；②任何有理数都有相反数；③任何有理数都有倒数；④立方等于它本身的有理数有3个，其中结论正确的是（ ）A ．②③④B ．①②④C ．只有②④D ．只有①② 2．下列各组数中，互为相反数的是（ ）A ．B ．2-与12-C ．()23-与23-D 3．下列判断正确的是（ ）A 4=±B ．9-的算术平方根是3C ．27的立方根是±3D ．正数a 4．下列各组数，互为相反数的是（ ）A ．3-和13- B C D ．5．下列说法，其中错误的有（ ）9±；3的平方根；③-8的立方根为-2；2=±． A ．1个 B ．2个 C ．3个 D ．4个6．下列等式成立的是（ ）A ．±1B ＝±2C 6D 37．下列说法中，正确的是（ ）A ±3B ．－22的平方根是±2C ．64的立方根是±4D 5的一个平方根8．如图为洪涛同学的小测卷，他的得分应是（ ）A ．25分B ．50分C ．75分D ．100分9=（ ）．A ．-8B ．8C ．-4D ．4 10．下列式子中，运算正确的是（ ）．A ．(29=B 3=±C 2=-D 1-二、解答题11．将一个体积为3125cm 的立方体体积增加V ，而保持立方体的形状不变，则棱长应该增加多少？（用含有V 的代数式表示）；若3875V cm =，则棱长应增加多少厘米？12．计算：213．求下列式中的x 的值（1）23750x -= （2）31(3)42x -=- 14．已知2a-1的平方根为±3，2a+b-1的立方根为2，求a+2b 的平方根15．求满足下列各式的未知数x ：（1）22581x =； （2）26x =（3）3(1)8x -=-16．已知21b +的平方根为±3，321a b ++的立方根为3，求2+a b 的平方根．17．解方程：（1）（x －1）2＝25；（2）3（x －5）3＝－24．18．求下列各式中的x 的值（1）31250x +=（2）2(1)250x +-=19．求下列各式中x 的值（1）2425x =（2）()38327x -=-20．如图，a ，b ，c 是数轴上三个点A 、B 、C 所对应的实数．a b b c ---．21．解方程：（1）2(2)36x -=； （2）3(21)80x -+=．22．解方程：（1）21681x =（2）387290x +=23．观察下列各式，并用所得出的规律解决问题：（1 1.414≈14.14≈141.4≈，……0.1732≈ 1.732≈17.32≈，……由此可见，被开方数的小数点每向右移动______位，其算术平方根的小数点向______移动______位．（2 3.873≈ 1.225≈≈_____≈______．（31=10=100=，……小数点的变化规律是_______________________．（4 2.154≈0.2154≈-，则y =______．24．已知2a-1的算术平方根是5 ， b+2的立方根是2，求a+2b+11的平方根．25．求下列各式中x 的值：（1）2250x -=；（2）()332240x ++=．三、填空题26．若3x +1的平方根为±2，4y -1的立方根为3，则y -2x 的值为____． 27 _______ ；3的立方根是 __________．28．已知：一个正数的两个平方根分别是2a－2和a－4，则这个正数的立方根是_____．29．①12的平方根是______；的立方根是______；③的倒数是______．230=___________【答案与解析】1．C【解析】根据相反数、绝对值、倒数、立方的定义即可得出答案．绝对值最小的数为0，∴①错误；任何有理数都有相反数，②正确；0没有倒数，∴③错误；立方等于本身的数有－1、0、1，∴④正确．故选C ．本题考查了相反数、绝对值、倒数、立方的定义，比较简单．2．C【解析】根据绝对值运算、有理数的乘方运算、立方根、相反数的定义逐项判断即可得．A 、=不是相反数，此项不符题意；B 、2-与12-不是相反数，此项不符题意； C 、()223399,--=-=，则()23-与23-互为相反数，此项符合题意；D 2,2=-=-故选：C ．本题考查了绝对值运算、有理数的乘方运算、立方根、相反数的定义，熟记各运算法则和定义是解题关键．3．D【解析】根据算术平方根、立方根的定义依次判断即可得．解：A 4=，此选项错误；B ．9的算术平方根是3，此选项错误；C ．27的立方根是3，此选项错误；D ．正数a故选：D ．本题主要考查立方根、算术平方根，解题的关键是掌握立方根、算术平方根的定义．4．C【解析】分别化简各项，再根据相反数的定义判断．解：A 、3-和13-不互为相反数，故错误；B ，不互为相反数，故错误；C =-3，互为相反数，故正确；D 、，，不互为相反数，故错误；故选C ．此题主要考查了算术平方根和立方根的定义，以及相反数的含义和求法，要熟练掌握． 5．B【解析】根据平方根的定义和立方根的定义即可判定．解：9，它的平方根是±3，故选项错误；3的平方根，故选项正确；③−8的立方根为−2，故选项正确；2=，故选项错误．故选：B ．本题主要考查了平方根和立方根的概念，要掌握其中的几个特殊数字的特殊性质．如果一个数x 的立方等于a ，即x 的三次方等于a （x 3＝a ），那么这个数x 就叫做a 的立方根，也叫做三次方根．读作“三次根号a”其中，a 叫做被开方数，3叫做根指数．（a 不等于0）如果x 2＝a （a≥0），则x 是a 的平方根．若a ＞0，则它有两个平方根，我们把正的平方根叫a 的算术平方根．若a ＝0，则它有一个平方根，即0的平方根是0，0的算术平方根也是0：负数没有平方根．6．A【解析】分别根据算术平方根、立方根的定义逐一判断即可．A ．书写规范，故本选项符合题意；B.算术平方根只能是正数不能是负数，故本选项不合题意；C.立方根与被开方数符号一致，故本选项符合题意；D.33=27，27的立方根才等于3，故本选项不合题意．故选：A．本题主要考查了算术平方根与立方根的定义，熟练掌握算术平方根的性质是解答本题的关键．7．D【解析】根据平方根、立方根的定义即可判断．3，故错误；B.－22没有平方根，故错误；C.64的立方根是4，故错误；D.5的一个平方根，正确；故选D．此题主要考查平方根、立方根，解题的关键是熟知平方根、立方根的定义．8．C【解析】根据实数的性质和基本运算法则计算即可．解：①2的相反数是-2；②倒数等于本身的数是1和-1；③8的立方根是2；±2；∴有3个是正确的；故选：C本题主要考查实数基本性质和平方根，立方根等基本运算．9．D【解析】求一个数的立方根；4，故选：D．本题考查求一个数的立方根，注意计算的准确性10．D【解析】根据平方根、算术平方根及立方根进行求解即可．A 选项：(23=，不符合题意；B 3=，不符合题意；C 2=，不符合题意：D1=-，符合题意．故选D ．本题主要考查平方根、算术平方根及立方根，熟练掌握平方根、算术平方根及立方根是解题的关键．115（厘米），5（厘米）． 【解析】根据原来与增加后的立方体体积，求出各自的棱长，相减即可得到结果；将875V代入算式，化简求值即可．解：依题意得：棱长应该增加：331251255V （厘米）， 当875V时，3512587551055（厘米）． 此题考查了立方根的应用，熟练掌握立方根的定义是解本题的关键．12．8【解析】进行算术平方根和立方根的计算．解：原式16358=--=．本题考查算术平方根和立方根的计算，解题的关键是掌握算术平方根和立方根的计算． 13．（1）5x =±；（2）1x =．【解析】（1）利用平方根的性质解方程即可得；（2）利用立方根的性质解方程即可得．（1）23750x -=，2375x =，225x =，5x =±；（2）31(3)42x -=-， 3(3)8x -=-，32x -=-，1x =．本题考查了利用平方根和立方根的性质解方程，熟练掌握平方根和立方根的性质是解题关键．14．【解析】根据已知得出2a-1=9，2a+b-1=8，求出a=5，b=-1，求出a+2b 的值，最后求出a+2b 的平方根即可．解：∵2a-1的平方根是±3，2a+b-1的立方根是2， ∴2a-1=9，2a+b-1=8，∴a=5，b=-1，∴a+2b=5-2=3，即a+2b 的平方根是．本题考查了平方根，立方根的应用，关键是得出关于a 、b 的方程组．15．（1）59x =±；（2）x =；（3）x = -1 【解析】（1）根据平方根的定义求解可得；（2）根据平方根的定义求解可得；（3）根据立方根的定义得出x-1=-2，解之可得．解：（1）∵22581x =，∴x =x =59±； （3）∵26x =∴x =（3）∵()318x -=-，∴x-1=-2，则x=-1．本题考查立方根、平方根，解题的关键是掌握立方根和平方根的定义．16．【解析】先根据平方根和立方根的定义列出二元一次方程组，然后求得a 、b 的值，最后代入求2+a b 的平方根即可．解：由题意得：21932127b a b +=⎧⎨++=⎩ 解得64a b =⎧⎨=⎩则2+a b =6+8=14，即2+a b 的平方根为．本题考查了平方根、立方根的定义，灵活运用平方根、立方根的定义是解答本题的关键． 17．（1）x ＝6或−4；（2）x ＝3【解析】（1）根据平方根的定义求解；（2）先变形得到（x−5）3＝8，然后根据立方根的定义得到x−5＝2，再解一次方程．（1）解：（x−1）2＝25，x−1＝±5x ＝6或−4；（2）解：（x−5）3＝−8x−5＝−2x ＝3．本题考查了平方根、立方根，熟练掌握基础知识，若一个数的立方等于a ，那么这个数叫a 的立方18．（1）x=-5；（2）x=4或x=-6【解析】（1）先移项，再根据立方根的定义开立方，即可求出方程的解．（2）先移项，再根据平方根的定义开平方，即可求出方程的解；解：（1）31250x +=∴3-125=x∴x=-5（2）2(1)250x +-=∴2(1)=25+x∴x+1=5±∴x=4或x=-6本题考查了对平方根和立方根的定义的应用，主要考查学生的理解能力和计算能力．19．（1）52x =或52x =-；（2）32x = 【解析】（1）根据平方根定义开方，再求出方程的解即可；（2）根据立方根定义开方，再求出方程的解即可；（1）2425x =， 2254x =， 52x =±， ∴52x =或52x =-； （2）()38327x -=-，()32738x -=-， 332x -=-， ∴32x =． 本题主要考查了立方根、平方根的计算，准确计算是解题的关键．20．-2b-c ．【解析】根据数轴上点的位置判断出绝对值里和根号下式子的符号，利用绝对值的代数意义化简，去括号合并即可得到结果．解：根据题意得：b ＜0，a-b ＞0，a+b ＜0，b-c ＜0，则原式=-b+a-b-a-b+b-c=-2b-c ．此题考查了开平方，开立方绝对值化简运算，判断出绝对值里边式子的正负是解本题的关键． 21．（1）8或-4；（2）12-． 【解析】（1）先直接开平方，然后求出x 的值即可；（2）先移项，再根据立方根的定义先求出2x-1的值，然后求出x 的值即可．解：（1）（x-2）2=36，x-2=6或x-2=-6，x 1=8，x 2=-4；（2）（2x-1）3=-8，2x-1=-2，2x=-1， x=12-． 此题考查了立方根和平方根，熟练掌握立方根和平方根的定义是解题的关键． 22．（1）x=94或x=94-；（2）x=92- 【解析】（1）先移项，然后根据平方根的定义解方程即可；（2）先移项，然后根据立方根的定义解方程即可．解：（1）21681x = 移项，得28116x =解得：x=94或x=94- （2）387290x += 移项，得37298x =-解得：x=92- 此题考查的是利用平方根和立方根解方程，掌握平方根和立方根的定义是解题关键．23．（1）两；右；一；（2）12.25；0.3873；（3）被开方数的小数点向右（左）移三位，其立方根的小数点向右（左）移动一位；（4）-0.01【解析】（1）观察已知等式，得到一般性规律，写出即可；（2）利用得出的规律计算即可得到结果；（3）归纳总结得到规律，写出即可；（4）利用得出的规律计算即可得到结果．解：（1 1.414≈，14.14≈141.4≈，……0.1732≈ 1.732≈17.32≈，……由此可见，被开方数的小数点每向右移动两位，其算术平方根的小数点向右移动一位． 故答案为：两；右；一；（2 3.873≈ 1.225≈12.25≈0.3873≈；故答案为：12.25；0.3873；（31=10=100=，……小数点的变化规律是：被开方数的小数点向右（左）移三位，其立方根的小数点向右（左）移动一位；（4） 2.154≈，0.2154≈-，0.2154≈，0.2154≈-，∴y=-0.01．此题考查了立方根，以及算术平方根，弄清题中的规律是解本题的关键．24．±6【解析】由算术平方根及立方根可求a 、b 的值，然后代入进行求解平方根即可．解：由题意得: 2a-1=25a=13b+2=8b=66∴a+2b+11的平方根是±6．本题主要考查平方根、算术平方根及立方根，熟练掌握平方根、算术平方根及立方根是解题的关键． 25．（1）x=±5；（2）x=-4．【解析】（1）先求出x 2的值，再根据平方根的定义进行解答即可；（2）把（x+2）看作一个整体，求出（x+2）3的值，然后根据立方根的定义进行解答． 解：（1）2250x -=；，∴x 2=25，∴x=±5；（2）()332240x ++=，（x+2）3=-8，∴x+2=-2，∴x=-4．本题考查了利用平方根与立方根求解方程，熟记概念是解题的关键，（2）中把（x+2）看作一个整体是解题的关键．26．5【解析】首先依据平方根和立方根的定义求得x 、y 的值，再代入求值即可．解：∵3x +1的平方根为±2，4y -1的立方根为3， ∴3x +1=4，4y -1=27，∴x =1，y =7，∴y -2x=7-2=5故答案为：5．本题主要考查的是平方根和立方根的定义，熟练掌握相关定义是解题的关键．27． 2a【解析】根据平方根的定义及立方根的定义解答.的平方根是，38a 的立方根是2a ，故答案为：2a.此题考查平方根及立方根的定义，利用定义求一个数的平方根及立方根.28．【解析】根据平方根定义，正数有两个平方根，它们是互为相反数，先求a ,再求这个数，最后求这个数的立方根即可．一个正数的两个平方根分别是2a－2和a－4，2a-2+a-4=0，合并得3a=6，a=2，a-4=2-4=-2，(a-4)2=4，，．本题考查正数的立方根，关键掌握平方根的性质和立方根定义，正数有两个平方根，它们是互为相反数，0的平方根是0，负数没有平方根，会求一个数的立方根．29．± 2【解析】根据平方根，立方根，倒数的定义进行计算即可．解：12的平方根是±8，8的立方根是2；；3故答案为：±2．本题考查了平方根，立方根，倒数，掌握这些知识点是解题关键．30．-3．【解析】，故答案为：-3．本题考查平方根与立方根问题，掌握平方根与立方根的性质，求平方根是应注意先化简，再求平方根是解题关键．。

实验设计与数据处理第六章例题及课后习题答案例题6-8（Ｃ）催化剂种类因素⽔平表⽔平(A)温度/℃(Ｂ)碱⽤量／ｋｇ18085甲28548⼄39055丙Ｌ９（３４）试验号ＡＢＣｙ111115121222713133358421238252231696231259731327783213859332184Ｋ１180210195204Ｋ２210225237207Ｋ３246201204225ｋ１60706568ｋ２70757969ｋ３82676875极差Ｒ228147趋势图⼯作表8060 Array 85709082487555678570甲65⼄79丙68例题6-13(D)废⽔浓度28-9不加Na2CO3浓39-10410-11L8（41×24）试验号A B C D空列得分yi 11111145212222703211225542221165531212856321219574122190842112100 K1115275295295295K2120330310310310K3180K4190k157.568.873.873.873.8k260.082.577.577.577.5k390.0k495.0极差R37.513.8 3.8 3.8 3.8SS2309.375378.12528.12528.12528.125总和T605P=T2/n45753.13⽅差分析表差异源SS df MS F显著性A2309.3753769.79227.3704*B378.1251378.12513.4444*C28.125128.125D28.125128.125误差e28.125128.125误差eΔ84.375328.125F0.05（3,3）9.277F0.01(3,3)29.457F0.05（1,3）10.128F0.01(1,3)34.116280160231001801Ｌ９（３４）试验号ＡＢＣｙ11111 5.321222531333 4.942123 5.452231 6.462312 3.773132 3.983213 3.393321 2.4Ｋ１15.214.612.314.1Ｋ２15.514.712.812.6Ｋ３9.61115.213.6ｋ１5.066667 4.866666667 4.1 4.7ｋ２5.166667 4.9 4.26667 4.2ｋ３3.2 3.666666667 5.066674.53333极差Ｒ1.966667 1.2333333330.966670.5因素主→次优⽅案趋势图⼯作表605.066667804.8666671604.91803.66666715.06666724.2666673 4.1习题6.2⽔平(A)反应温度(B)CU2+与氨⽔质?CuSO4溶液浓度／(g/ml)17001:00.00.12528001:00.50.539001:00.51Ｌ９（３４）试验号ＡＢＣ转换率1111140.262122240.463133361.79ABC A2B2C24212360.155223173.976231291.317313273.528321387.199332197.26Ｋ１142.51173.93218.76211.49Ｋ２225.43201.62197.87205.29Ｋ３257.97250.36209.28209.13ｋ１47.5033333357.976772.9270.497ｋ２75.1433333367.206765.956768.43ｋ３85.9983.453369.7669.71极差Ｒ38.4866666725.4767 6.96333 2.0667因素主→次优⽅案Ｋ１ 4.474.8465.898 5.445Ｋ２ 5.6843.421 3.813 5.01Ｋ３4.4816.368 4.924 4.18ｋ１ 1.491.61533 1.966 1.815ｋ２ 1.8946666671.14033 1.271 1.67ｋ３ 1.4936666672.12267 1.64133 1.3933极差Ｒ0.404666667最终优⽅案A3B2C2习题6.3Ｌ９（３４）试验号ＡＢＣ包合率包合物收率1111112.0161.82122215.8684.313133316.9580.15421238.667.235223113.7177.26623127.2276.5373132 6.5458.61832137.7878.1293321 5.4377.6K12.270840.74943823 1.19055 1.40944K21.392932.090804961 1.53806 1.37318K30.77943 1.602956793 1.71459 1.66057k10.7569470.2498127430.396850.46981k20.464310.6969349870.512690.45773k30.259810.5343189310.571530.55352极差R0.4971370.4471222440.174680.0958因素主→次优⽅案ABC A3B3C1BCA B2C2A1转换率铜粉松密度ABC A1B2C3习题6.4L8（27）试验号A B A×B C空列空列11111112111222312211241222215212121621221272211228221211 K1283282268268276275k26868.2571.7571.7569.7570极差R119191935A*B C A B D因素主→次因素A*B⽔平搭配表A1A2B169.571.5B27264.5习题6-5L8（41×24）试验号A B C D空列得分yi 111111195212222205321122220422211225531212210632121215741221185842112190 K1400810820820820K2445835825825825K3425K4375k1200.0202.5205.0205.0205.0k2222.5208.8206.3206.3206.3k3212.5k4187.5极差R35.0 6.3 1.3 1.3 1.3因素主→次优⽅案习题6-6L 9（34）实验号C C（虚拟）B AD 酸洗时间/min 11111136222123225222313462231221723132168232131992332137K1887476107K2149859169K3787061k129.3333324.666725.333335.667k224.8333328.333330.333323k32623.333320.333极差R-4.5 3.77.015.3因素主→次优⽅案习题6-7L 8（27）试验号A B A×B C A×C B×C 11111112111222312211241222215212121621221272211228221211K14.53 4.17 3.66 3.93 3.5 3.66K23.15 3.514.02 3.75 4.18 4.02k11.1325 1.04250.9150.98250.8750.915k20.78750.8775 1.0050.9375 1.045 1.005极差R1.380.660.36-0.180.680.36因素主→次A BCD或者ABDC A 2B2C2D2或A2B2D2C2DABC D3A3B1C2A A×CB D A×B B×C C 或 A A×C BA1A2C1 1.070.895C2 1.1950.68因素B×C⽔平搭配表B1B2C1 1.020.945C2 1.0650.81习题6-8123456试验号L27（313）A B(A×B)1(A×B)2C(A×C)1 111111121111223111133412221151222226122233713331181333229133333102123121121232312212331132231121422312315223131162312121723122318231231193132132031322121313232223213132332132127332132 K1879800795807796800K2785790807790802792K3732806794799798804极差R147161317612SS1231.6314.5185185211.629616.0741 2.07418.2963总和T2396P=T2/n212622.8⽅差分析表差异源SS df MS F显著性A1231.632615.815218.776**B14.5185227.25926 2.57895AB27.70374 6.92593 2.46053C 2.0740742 1.037040.36842AC28.1481547.03704 2.5D312.51852156.25955.5132**BC56.59259414.1481 5.02632*E107.1852253.592619.0395*F 3.629632 1.814810.64474误差e11.185192 5.59259误差eΔ16.888896 2.81481F0.05（2,6） 5.14F0.01（2,6）10.52F0.05（4,6） 4.53F0.01（4,6）9.15⽔平搭配表B1B2B3C1868891.33333333C29088.6666788.66666667C390.666666786.6666788.66666667A1D1E1B3C1优⽅案习题6-9Ｌ９（３４）试验号ＡＢＣｙ11111 5.321222562312 3.773132 3.983213 3.393321 2.4Ｋ１15.214.612.314.1Ｋ２15.514.712.812.6Ｋ３9.61115.213.6极差Ｒ 5.9 3.7 2.9 1.5SS7.362222 2.962222222 1.602220.38889SST=总和T40.3P=T2/n180.4544⽅差分析表差异源SS df MS F显著性A7.3622222 3.6811118.9314B 2.9622222 1.481117.61714C 1.60222220.80111 4.12误差e0.38888920.19444误差eΔ0.38888920.19444F0.05（2,2）19习题6-10L8（41×24）试验号A B C D空列得分yi 111111195212222205321122220422211225531212210632121215741221185842112190 K1400810820820820K2445835825825825K3425K4375总和T1645P=T2/n338253.1⽅差分析表差异源SS df MS F显著性A1384.3753461.458147.667**B78.125178.12525*C 3.1251 3.1251D 3.1251 3.1251误差e 3.1251 3.125误差eΔ9.3753 3.125F0.05（1,3）10.13F0.01（1,3）34.12F0.05（3,3）9.28F0.01（3,3）29.46习题6-11L9（34）实验号C C（虚拟）B A D酸洗时间/min 111111362112223231133320422123225222313462231221723132168232131992332137 K1887476107K2149859169K3787061SS40.520.666778402.67SST=总和T237P=T2/n6241⽅差分析表差异源SS df MS F显著性A7823918.72B20.66667210.3333 4.96C40.5140.519.44*D402.66672201.33396.64**误差e 4.1666672 2.08333误差eΔ 4.1666672 2.08333F0.05（2,2）19F0.01（2,2）39F0.05（1,2）18.51F0.01（1,2）38.51铜粉松密度2.0080.6931.7691.2961.6132.7751.5421.1151.824包合物收率综合分包合率⾪属0.571180.124120.392 0.9053810.94310.838130.935 0.275170.335410.299 0.718750.725680.722 0.155380.697280.372 0.0963500.058 0.203990.759140.426 00.738910.296D得率/%16527427117327017316226727328268.2570.59时间/minD提取量/mL1 1.012 1.332 1.131 1.062 1.0310.810.7620.563.634.050.90751.01250.42A×B C78910111213(A×C)2(B×C)1D(B×C)2E F抗压强度/kg.cm-2 1111111100 2222222983333333971222333952333111963111222991333222942111333993222111101312312385123123182231231298323131285131212390212323185331223191112331289223112380213213273321321390132132177221332184332113280113221376232121389313232178121313285 788784836791790824794 802800799800804785801 806812761805802787801182875141439719.851943.8519312.511.1912.7407107.2 3.63SST=1795.185 12.3156 1471.88。

《知识与能力训练•物理》八年级上册参考答案（2017秋）第一章机械运动第1节长度和时间的测量（1）自主导学1．km m dm cm mm μm nm m2．量程分度值零刻度线在哪里3．（1）零刻度紧靠（2）正对（或“平视”）（3）（测量）单位4．18.50cm左右5．（1）m （2）cm （3）dm（4）cm（5）dm （6）mm基础练习1．（1）1.25 1250 1.25×109（2）250 2.5×108（3）300 3×107 （4）80 8×1062．15.31cm 18.22cm3．6cm 1cm 3.4 1mm 3.60cm4．C 5．B 6．D提高练习7．C 8．A 9．B 10．C第1节长度和时间的测量（2）自主导学1．秒s h min 60 36002．误差误差减小误差3．多次测量求平均值选用精密的测量工具改进测量方法基础练习1．（1）s （2）min 0.75 2700 （3） 75 4500 （4） 150 2.5 2．99.83．B4．D5．B6．B7．D提高练习8．180 9．A第2节运动的描述自主导学1．位置2．参照物参照物相对基础练习1．运动运动静止运动2．B3．B 4．D提高练习5．A 6．B 7．C 8．A 9．D 10．B第3节运动的快慢（1）自主导学1．快慢路程时间2．m/s km/h 1m/s=3.6km/h3．直线速度4．平均速度基础练习1．（1）5 （2）72 2．30 3．C4．D5．C 6．C7．C提高练习8．D 9．100km/h 10．A 11．A第3节运动的快慢（2）基础练习1．＜2．加速直线匀速直线3．C 4．B提高练习5．甲丙乙6．15 93.37．C 8．B 9．A 10．D 11．C第4节测量平均速度自主导学1．刻度尺停表基础练习1．0.09m/s2．（1）v=s/t（2）变速（3）v3 >v1>v2提高练习3．14．（1）质量（2）在光滑程度相同的情况下，小球在斜面上滚下的平均速度与质量无关第一章测试题一、选择题1．B 2．B 3．D4．C 5．B6．A 7．C 8．C 9．D 10．B11．C 12．B 13．C 14．D 15．D 16．A 17．B 18. B 19．A二、填空题20．0.1cm 3.80cm21．（1）15 （2）1822．东边地平线西边的山23．物体位置的改变变速三、实验题24．（1）v=s/t（2）小减小（3）大（4）0.2 v AB<v AC<v BC四、综合应用题25．5.4m/s26．8m/s27．利用汽车上的速率计和计时设备测量速度和时间来计算长度，利用汽车上的里程表读取长度等第二章声现象第1节声音的产生与传播自主导学1．振动固体液体气体声波真空2．快快340基础练习1．B 2．B3．A4．A 5．D 6．D7．C 8．C 9．C 10．B11．产生传播提高练习12．（1）一般情况下，声音在不同介质中的传播速度不同（2）一般情况下，声音在固体中的传播速度比液体、气体中的大13．介质345 14．C15．B 16．13.98s第2节声音的特性自主导学1．高低振动的快慢高2．强弱振幅3．音调响度音色4．20000 20基础练习1．B2．A 3．C 4．D 5．B 6．A 7．B 8．D 9．D 10．C 11．A 提高练习12．D第3节声的利用自主导学1．回声定位声呐2．能量基础练习1．C 2．A 3．D 4．D 5．D 6．D 7．D 8．B 9．C 10．B提高练习11．（1）高于20000Hz（2）能量（3）真空不能传声（4）3000第4节噪声的危害和控制自主导学1．分贝dB 损害健康人耳刚好能听见2．（1）防止噪声的产生（2）阻断噪声传播（3）防止噪声进入人耳基础练习1．A 2．A 3．D 4．C 5．C 6．C 7．D 8．C提高练习9．B 10．A 11．B 12．B第二章测试题一、选择题1．C 2．C 3．A 4．B 5．D 6．C 7．A 8．C 9．D 10．D11．C 12．B 13．D 14．B 15．D 16．D 17．B 18．B 19．D 20．A 二、非选择题21．响度音调频率22．振动响度音调4Hz 不能23．（1）能（2）逐渐变小（或听不到声音）（3）不能[ 声音的传播需要介质（或声音在真空中不能传播）]（4）空气真空24．低 225．空气锣面停止了振动26．固体快27．超声波能量次声波28．4s 660m29．牛蚊子30．（1）“烟”是以光速传播的，计时员看到“烟”所用的时间极短；而“枪声”是以声速传播的，计时员听到“枪声”所用时间较长。

第六章概率初步一、选择题1.下列说法正确的是（）A. 不可能事件发生的概率为0B. 随机事件发生的概率为C. 概率很小的事件不可能发生D. 投掷一枚质地均匀的硬币1000次，正面朝上的次数一定是500次2.在课外实践活动中，甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率，其实验次数分别为10次、50次、100次，200次，其中实验相对科学的是（）A. 甲组B. 乙组C. 丙组D. 丁组3.下列事件中，是必然事件的是（）A. 两条线段可以组成一个三角形B. 400人中有两个人的生日在同一天C. 早上的太阳从西方升起D. 打开电视机，它正在播放动画片4.在一个布口袋里装有白、红、黑三种颜色的小球，它们除颜色外没有任何区别，其中白球2只，红球6只，黑球4只，将袋中的球搅匀，闭上眼睛随机从袋中取出1只球，则取出黑球的概率是（）A. B. C. D.5.动物学家通过大量的调查估计，某种动物活到20岁的概率为0.8，活到25岁的概率为0.6，则现年20岁的这种动物活到25岁的概率是（）A. 0.8B. 0.75C. 0.6D. 0.486.一个不透明的盒子里有n个除颜色外其他完全相同的小球，其中有9个黄球．每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么估计盒子中小球的个数n为（）A. 20B. 24C. 28D. 307.数学老师将全班分成7个小组开展小组合作学习，采用随机抽签确定一个小组进行展示活动，则第3个小组被抽到的概率是（）A. B. C. D.8.从图中的四张印有汽车品牌标志图案的卡片中任取一张，取出印有汽车品牌标志的图案是中心对称图形的卡片的概率是（）A. B. C. D. 19.如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（）A. B. C. D.10.从正五边形的五个顶点中，任取四个顶点连成四边形，对于事件M，“这个四边形是等腰梯形”．下列推断正确的是()A. 事件M是不可能事件B. 事件M是必然事件C. 事件M发生的概率为D. 事件M发生的概率为二、填空题11.一个盒中装着大小、外形一模一样的x颗白色弹珠和y颗黑色弹珠，从盒中随机取出一颗弹珠，取得白色弹珠的概率是．如果再往盒中放进12颗同样的白色弹珠，取得白色弹珠的概率是，则原来盒中有白色弹珠______ 颗．12.现有50张大小、质地及背面图案均相同的《西游记》任务卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回，洗匀后再抽．通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3．估计这些卡片中绘有孙悟空这个人物的卡片张数约为______ ．13.不透明的布袋里有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，那么从布袋中任意摸出一球恰好为红球的概率是______．14.从数-2，-，0，4中任取一个数记为m，再从余下的三个数中，任取一个数记为n，若k=mn，则正比例函数y=kx的图象经过第三、第一象限的概率是______ ．15.一个均匀的正方体各面上分别标有数字：1、2、3、4、5、6，这个正方体的表面展开图如图所示．抛掷这个正方体，则朝上一面所标数字恰好等于朝下一面所标数字的3倍的概率是______．三、计算题16.全面两孩政策实施后，甲、乙两个家庭有了各自的规划，假定生男生女的概率相同，回答下列问题：（1）甲家庭已有一个男孩，准备再生一个孩子，则第二个孩子是女孩的概率是______；（2）乙家庭没有孩子，准备生两个孩子，求至少有一个孩子是女孩的概率．17.四张扑克牌（方块2、黑桃4、黑桃5、梅花5）的牌面如图l，将扑克牌洗匀后，如图2背面朝上放置在桌面上．小亮和小明设计的游戏规则是两人同时抽取一张扑克牌，两张牌面数字之和为奇数时，小亮获胜；否则小明获胜．请问这个游戏规则公平吗？并说明理由．18.一只口袋中放着3只红球和2只黑球，这两种球除了颜色以外没有任何区别．袋中的球已经搅匀．蒙上眼睛从口袋中取一只球，（1）取出黑球与红球的概率分别是多少？（2）若第一次取出的是一只红球不放回去，第二次取出的是红球的概率是多少？19.在一个不透明的袋中装有5个只有颜色不同的球，其中3个黄球，2个黑球．（1）求从袋中同时摸出的两个球都是黄球的概率；（2）现将黑球和白球若干个（黑球个数是白球个数的2倍）放入袋中，搅匀后，若从袋中摸出一个球是黑球的概率是，求放入袋中的黑球的个数．答案和解析【答案】1. A2. D3. B4. C5. B6. D7. A8. A9. B10. B11. 412. 1513.14.15.16.17. 解：此游戏规则不公平．理由如下：画树状图得：共有12种等可能的结果，其中两张牌面数字之和为奇数的有8种情况，所以P（小亮获胜）==；P（小明获胜）=1-=，因为＞，所以这个游戏规则不公平．18. 解：（1）根据题意得：P（黑球）=；P（红球）=；（2）根据题意得：P（第二次为红球）==．19. 解：（1）画树状图为：共有20种等可能的结果数，其中从袋中同时摸出的两个球都是黄球的结果数为6，所以从袋中同时摸出的两个球都是黄球的概率==；（2）设放入袋中的黑球的个数为x，根据题意得=，解得x=2，所以放入袋中的黑球的个数为2．【解析】1. 解：A、不可能事件发生的概率为0，故本选项正确；B、随机事件发生的概率P为0＜P＜1，故本选项错误；C、概率很小的事件，不是不发生，而是发生的机会少，故本选项错误；D、投掷一枚质地均匀的硬币1000次，是随机事件，正面朝上的次数不确定是多少次，故本选项错误；故选：A．根据不可能事件是指在任何条件下不会发生，随机事件就是可能发生，也可能不发生的事件，发生的机会大于0并且小于1，进行判断．本题考查了不可能事件、随机事件的概念．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．2. 解：根据模拟实验的定义可知，实验相对科学的是次数最多的丁组．故选：D．大量反复试验时，某事件发生的频率会稳定在某个常数的附近，这个常数就叫做事件概率的估计值．考查了模拟实验，选择和抛硬币类似的条件的试验验证抛硬币实验的概率，是一种常用的模拟试验的方法．3. 解：A、两条线段可以组成一个三角形是不可能事件，故A错误；B、400人中有两个人的生日在同一天是必然事件，故B正确；C、早上的太阳从西方升起是不可能事件，故C错误；D、打开电视机，它正在播放动画片是随机事件，故D错误；故选：B．根据必然事件指在一定条件下，一定发生的事件，可得答案．本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．4. 解：根据题意可得：口袋里共有12只球，其中白球2只，红球6只，黑球4只，故从袋中取出一个球是黑球的概率：P（黑球）==，故选：C．根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数．二者的比值就是其发生的概率的大小．本题考查概率的求法与运用．一般方法为：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．5. 解：设共有这种动物x只，则活到20岁的只数为0.8x，活到25岁的只数为0.6x，故现年20岁到这种动物活到25岁的概率为=0.75．故选B．先设出所有动物的只数，根据动物活到各年龄阶段的概率求出相应的只数，再根据概率公式解答即可．考查了概率的意义，用到的知识点为：概率=所求情况数与总情况数之比．注意在本题中把20岁时的动物只数看成单位1．6. 解：根据题意得=30%，解得n=30，所以这个不透明的盒子里大约有30个除颜色外其他完全相同的小球．故选D．根据利用频率估计概率得到摸到黄球的概率为30%，然后根据概率公式计算n的值．本题考查了利用频率估计概率：大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．当实验的所有可能结果不是有限个或结果个数很多，或各种可能结果发生的可能性不相等时，一般通过统计频率来估计概率．7. 解：第3个小组被抽到的概率是，故选：A．根据概率是所求情况数与总情况数之比，可得答案．本题考查了概率的知识．用到的知识点为：概率=所求情况数与总情况数之比．8. 解：在这四个图片中只有第三幅图片是中心对称图形，因此是中心对称称图形的卡片的概率是．故选：A．根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数．二者的比值就是其发生的概率的大小．本题将两个简易的知识点，中心对称图形和概率组合在一起，是一个简单的综合问题，其中涉及的中心对称图形是指这个图形绕着对称中心旋转180°后仍然能和这个图形重合的图形，简易概率求法公式：P（A）=，其中0≤P（A）≤1．9. 解：∵根据轴对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合，白色的小正方形有13个，而能构成一个轴对称图形的有5个情况，∴使图中黑色部分的图形仍然构成一个轴对称图形的概率是：．故选：B．由在4×4正方形网格中，任选取一个白色的小正方形并涂黑，共有13种等可能的结果，使图中黑色部分的图形构成一个轴对称图形的有5种情况，直接利用概率公式求解即可求得答案．此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．也考查了轴对称图形的定义．10. 连接BE，根据正五边形ABCDE的性质得到BC=DE=CD=AB=AE，根据多边形的内角和定理求出∠A=∠ABC=∠C=∠D=∠AED=108°，根据等腰三角形的性质求出∠ABE=∠AEB=36°，求出∠CBE=72°，推出BE∥CD，得到四边形BCDE是等腰梯形，即可得出答案．11. 解：∵取得白色棋子的概率是，可得方程=又由再往盒中放进12颗白色棋子，取得白色棋子的概率是∴可得方程=，组成方程组解得：x=4，y=8故答案为4．根据从盒中随机取出一颗棋子，取得白色棋子的概率是，可得方程=又由再往盒中放进12颗白色棋子，取得白色棋子的概率是可得方程=联立即可求得x的值．本题考查的是概率的求法．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．12. 解：因为通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3，所以估计抽到绘有孙悟空这个人物卡片的概率为0.3，则这些卡片中绘有孙悟空这个人物的卡片张数=0.3×50=15（张）．所以估计这些卡片中绘有孙悟空这个人物的卡片张数约为15张．故答案为15．利用频率估计概率得到抽到绘有孙悟空这个人物卡片的概率为0.3，则根据概率公式可计算出这些卡片中绘有孙悟空这个人物的卡片张数，于是可估计出这些卡片中绘有孙悟空这个人物的卡片张数．本题考查了频率估计概率：用频率估计概率得到的是近似值，随实验次数的增多，值越来越精确．13. 解：∵在不透明的袋中装有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，∴从这不透明的袋里随机摸出一个球，所摸到的球恰好为红球的概率是：=．故答案为：．由在不透明的袋中装有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，直接利用概率公式求解，即可得到任意摸出一球恰好为红球的概率．此题考查了概率公式的应用．解题时注意：概率=所求情况数与总情况数之比．14. 解：从数-2，-，0，4中任取1个数记为m，再从余下，3个数中，任取一个数记为n．根据题意画图如下：共有12种情况，∵正比例函数y=kx的图象经过第三、第一象限，∴k=mn＞0．由树状图可知符合mn＞0的情况共有2种，∴正比例函数y=kx的图象经过第三、第一象限的概率是=．故答案为：．根据题意先画出图形，求出总的情况数，再求出符合条件的情况数，最后根据概率公式进行计算即可．本题考查了概率的知识．用到的知识点为：概率=所求情况数与总情况数之比．15. 解：由图可知1、3相对，2、6相对，4、5相对，那么3朝上或6朝上时，朝上一面所标数字恰好等于朝下一面所标数字的3倍，共有6种情况，则朝上一面所标数字恰好等于朝下一面所标数字的3倍的概率是．根据随机事件概率大小的求法，找准两点：①朝上一面所标数字恰好等于朝下一面所标数字的3倍的情况数目；②所有标法的总数．二者的比值就是其发生的概率的大小．本题考查概率的求法与运用，一般方法为：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．16. 解：（1）第二个孩子是女孩的概率=；故答案为；（2）画树状图为：共有4种等可能的结果数，其中至少有一个孩子是女孩的结果数为3，所以至少有一个孩子是女孩的概率=．（1）直接利用概率公式求解；（2）画树状图展示所有4种等可能的结果数，再找出至少有一个孩子是女孩的结果数，然后根据概率公式求解．本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．17. 先利用树状图展示所有有12种等可能的结果，其中两张牌面数字之和为奇数的有8种情况，再根据概率公式求出P（小亮获胜）和P（小明获胜），然后通过比较两概率的大小判断游戏的公平性．本题考查了游戏公平性：判断游戏公平性需要先计算每个事件的概率，然后比较概率的大小，概率相等就公平，否则就不公平．18. （1）根据5只小球中红球与黑球的个数求出所求概率即可；（2）取出一个红球，口袋中红球与黑球个数都为2，即可求出所求概率即可．此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．19. （1）画树状图展示所有20种等可能的结果数，再找出从袋中同时摸出的两个球都是黄球的结果数，然后根据概率公式求解；（2）设放入袋中的黑球的个数为x，利用概率公式得到=，然后解方程即可．本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．。

5．C
【解析】
负数小于零，零小于正数，两个负数绝对值大的反而小，根据实数的大小比较法则解答.
∵ ，
∴ <
∴ < <0<1，
故选：C.
此题考查实数的大小比较法则，熟记法则是解题的关键.
6．C
【解析】
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【解析】
根据无理数的意义（有理数是指有限小数或无限循环小数）填上即可；根据无理数的意义（无理数是指无限不循环小数）判断即可；分数包括有限小数和无限循环小数和分数）判断即可．
30．实数的大小比较：2__________ ．（填“＞”、“＝”或“＜”）
【答案与解析】
1．B
【解析】
利用立方根的定义，将x的值代入如图所示的流程，取27的立方根为3，为有理数，再次代入，得 ，为无理数符合题意，即为y值．
根据题意，x=27，取立方根得3，3为有理数，再次取3的立方根，得 ，为无理数.符合题意，即输出的y值为 .
本题考查了新定义下的实数运算，解题的关键是明确题意，找出所求问题需要的条件．
16．6－
【解析】
分别进行乘方、平方根与立方根以及绝对值的计算，最后进行实数的加减混合运算即可．
=－1+2－(－3)+2－
=6－ ．
本题主要考查乘方、平方根与立方根以及绝对值的计算，熟记实数的运算法则是解题关键．
17．-7，0， ，-2.55555……，3.01，+9；4.020020002…， ；-7，0，+9； ，-2.55555……，3.01

第六章第3节《实数》单元训练题 (16)一、单选题1．在实数 1.414-，π，3.14，2+ 3.212212221…中，无理数的个数是（ ）个． A ．1B ．2C ．3D ．422的整数部分是a ，小数部分是b b -的值是（ ） A ．5B ．5-C ．3D ．3-3．下列各数：1,7π-，，0.3149,0.313，其中无理数的个数是（ ） A ．4 B ．3 C ．2 D ．14．规定用符号[]x 表示一个实数的整数部分，例如[]3.873=，1=，则1⎤=⎦（ ）A ．5B ．4C ．3D ．2 5．下列实数中，是无理数的为（ ）A ．3.14B ．13C D6．在实数27，2π，3.14，0.3232232223…（相邻两个3之间依次增加一个2）中，无理数有（ ）A ．1个B ．2个C ．3个D ．4个7．下列各数，是无理数的是（ ）．A ．3.14BCD ．3178，0215中，是无理数的是（ ）AB ．0CD ．215二、填空题9|2|π-=________．10．比较大小：|5|-________（填“>”“=”或“<”）11．比较大小：12π-________1- 12．在实数的原有运算法则中，我们补充新运算法则“*”如下：当a≥b 时，a*b=b 2，当a<b 时，a*b=a ，则当()()1*-3*=x x x ______13．在实数π，87，0中，无理数的个数是________个． 14．若[)x 表示大于x 的最小整数，如[)56=，[)1.81-=-，则下列结论中正确的有______（填写所有正确结论的序号）．①[)01=；②33055⎡⎫-=⎪⎢⎣⎭；③[)0x x -<；④[)1x x x <≤+；⑤存在有理数x 使[)0.2x x -=成立．15．实数2-227，π-中属于无理数的是________．16_____74．17．已知5+的整数部分为a ，5-b ，则2ab b +=_________．三、解答题18．计算（113+--（2）321(2)()2-19．计算：（1）132322⎛⎫⨯-⨯-⎪⎝⎭ （2）2291|11232⎛⎫-+--⨯- ⎪⎝⎭20．计算：201()( 3.14)|22π---21．计算：（1()23-．（2）()21183⎤⎛⎫-⨯-⎥ ⎪⎝⎭⎥⎦． 22．教材中的探究：如图，把两个边长为1的小正方形沿对角线剪开，用所得到的4个直角三角形拼成一个面积为2的大正方形．由此，得到了一种能在数轴上画出无理数对应点的方法（数轴的单位长度为1）．（1）阅读理解：图1中大正方形的边长为________，图2中点A 表示的数为________； （2）迁移应用：请你参照上面的方法，把5个小正方形按图3位置摆放，并将其进行裁剪，拼成一个大正方形． ①请在图3中画出裁剪线，并在图3中画出所拼得的大正方形的示意图．②利用①中的成果，在图4的数轴上分别标出表示数－0.5以及 3-+的点，并比较它们的大小．233=，31a b -+的平方根是4±，c 3a b c ++的平方根． 24．计算：（1．（2）()23540.255(4)8⨯--⨯⨯-．25．计算： （1）36 1.754⎛⎫--+ ⎪⎝⎭； （2）()()232524-⨯--÷；（3）()225--．26．对于实数p 、q ，我们用符号max{,}p q 来表示p 、q 两数中较大的数，如：max{1,2}2=．（1）求max{=_______．（2）我们知道，当21m =时，1m =±，利用这种方法解决下面问题，若{}22max (1),4x x -=，求x 的值． 27．小明定义了一种新的运算，取名为⊗运算，按这种运算进行运算的算式举例如下：①（+4）⊗（+2）＝+6；②（﹣4）⊗（﹣3）＝+7；③（﹣5）⊗（+3）＝﹣8；④（+6）⊗（﹣4）＝﹣10；⑤（+8）⊗0＝8；⑥0⊗（﹣9）＝9．问题：（1）请归纳⊗运算的运算法则：两数进行⊗运算时， ；特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算， ．（2）计算：[（﹣2）⊗（+3）]⊗[（﹣12）⊗0]； （3）我们都知道乘法有结合律，这种运算律在有理数的⊗运算中还适用吗？请判断是否适用，并举例验证．28．（1）小明解方程2x 1x a 332-+=-去分母时，方程右边的−3忘记乘6，因而求出的解为x=2，则原方程正确的解为多少？（2）设x ，y 是有理数，且x ，y 满足等式2x 2y 17++=-x-y 的值．29．计算：()214322--⨯-（ 30．计算：（1）(23)(41)----；（2）1111115()13()3()555-⨯-+⨯--⨯-；（3）2(2)|1|-+；（4）311()()(2)424-⨯-÷-．【答案与解析】1．D【解析】无理数常见的三种类型（1）开不尽的方根；（2）特定结构的无限不循环小数；（3）含有π的绝大部分数，如2π．−1.414是有限小数，是无理数，π是无理数，3.14无限循环小数是有理数，2+是无理数，3.212212221…是无限不循环小数是无理数，故选：D．本题主要考查的是无理数的认识，掌握无理数的常见类型是解题的关键．2．C【解析】2的整数部分和小数部分，然后代入，计算可得答案．解：∵3＜4，∴1＜2-2的整数部分是a=1-2的小数部分是-3，b-3)3=．故选：C．此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．3．C【解析】根据无理数是无限不循环小数，可得答案．解：17，133是分数，属于有理数；0.3149，0.3是有限小数，属于有理数；7=是整数，属于有理数；无理数有-π，2个，故选：C．本题考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．4．B【解析】1的范围，再根据范围求出即可．解：∵34<<∴415<+<1的整数部分为4∴1⎤=⎦ 4故选：B．此题考查的是求无理数的整数部分，掌握实数比较大小的方法是解决此题的关键．5．C【解析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．A.3.14是有限小数，属于有理数；B.13是分数，属于有理数；3，是整数，属于有理数.故选：C．此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．6．C【解析】先将可以化简的化简，再依据无理数的形式去判断即可，无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．实数27，2π，3.14，0.3232232223…（相邻两个3之间依次增加一个2）中无理数是2π，0.3232232223…（相邻两个3之间依次增加一个2）． 故选C ．本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．7．C【解析】根据无理数的定义判断即可．解：A 选项：3.14是有理数，故A 错误；B 2=是有理数，故B 错误；C 是无理数，故C 正确；D 选项：317是有理数，故D 错误． 故选C ．本题考查了无理数的概念，熟记无理数的定义，掌握无理数的常见形式是解题关键．8．A【解析】根据无理数是无限不循环小数，可得答案．0215， 故选：A ．此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．9． 1.14-【解析】先计算算术平方根、化简绝对值，再计算实数的加减法即可得．原式()3.142ππ=---， 3.142ππ=--+，1.14=-，故答案为： 1.14-．本题考查了算术平方根、绝对值、实数的加减运算，熟练掌握各运算法则是解题关键． 10．>【解析】先求出|5|-=5，，再比较即可．因为|5|-=5，，5>-5，所以|5|->故答案为：>．考核知识点：实数大小比较．求出绝对值和算术平方根是关键．11．<【解析】利用估值比较法322π>>，再利用不等式的性质3，不等式两边都乘以-1，不等式方向改变2π-<，最后利用不等式性质1，不等式两边都加1，不等号方向不变即可确定大小．∵322π>322<，∴2π>，∴2π-<，∴12π-<1．故答案为：<．本题考查无理数的比较大小问题，掌握不等式的性质，会用不等式的性质比较大小，用估值法比较大小是解题关键．122【解析】根据题中所给的运算法则进行求解即可；∵当a≥b 时，a*b=2b ，当a ＜b 时，a*b=a∴ 当 ，=2，∴) 2，2．本题是新定义的问题，解决此类问题的关键是按题中的规定去运算即可；13．2【解析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．由无理数的定义可知，π是无理数．故答案为：2．此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．14．①④⑤【解析】根据题意[)x 表示大于x 的最小整数，结合各项进行判断即可得出答案．解：①[)01=，根据[)x 表示大于x 的最小整数，故正确； ②33055⎡⎫-=⎪⎢⎣⎭，应该等于333215555⎡⎫-=-=⎪⎢⎣⎭，故错误； ③[)0x x -<，当x=0.5时，[)10.5=0.50x x -=-＞，故错误；④[)1x x x <≤+，根据定义可知[)x x <，但[)x 不会超过x+1，所以[)1x x x <≤+成立，故正确； ⑤当x=0.8时，[)1-0.8=0.2x x -=，故正确．故答案为：①④⑤．本题主要考查了对题意的理解，准确的理解题意是解决本题的关键．15，π-【解析】根据无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，找出无理数的个数．3=-，在2-227，π-，这5， π-，这2个数，，π-． 本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．16．＜【解析】2.5，再比较大小即可．∵5＜6.25，2.5，∴27<，7474<． 故答案为：＜本题考查了实数比较大小，熟练掌握无理数的估算是解题的关键．17．37-【解析】的大小，推出7＜5+＜8，求出a ，同理求出253<-<，求出b ，代入求出即可． 解：∵479<<，∴23<<，32-<<-∴758<+<，253<-<，∴7a =，523b =-=-∴()(237337ab b b a b +=+=+=-故答案为：37-此题考查了无理数的大小的应用，关键是确定5+和5-18．（1）4；（2）36-【解析】（1）实数的混合运算，先化简绝对值，然后再计算；（2）实数的混合运算，注意先算乘方，然后再算乘除，最后算加减．解：（113-1-=4（2）321(2)()2-=184434-⨯-⨯- =3213---=36-本题考查实数的混合运算，掌握运算顺序和计算法则正确计算是解题关键．19．（1）32；（2） 【解析】（1）直接利用有理数混合运算法则计算得出答案；（2）原式先计算乘方，再计算乘法运算，进而算加减运算即可求出值．（1）原式=6-3×32=6-92=32；（2）原式＝-1-23×152． 本题主要考查了有理数和实数的混合运算，正确掌握运算法则是解题关键．20．【解析】直接利用负指数幂的性质以及零指数幂的性质和绝对值的性质分别化简得出答案．解：原式＝4﹣1+．此题主要考查了负指数幂的性质以及零指数幂的性质和绝对值的性质，正确化简各数是解题关键．21．（1）11；（2）-10【解析】（1）首先计算乘方、开方，然后从左向右依次计算，求出算式的值是多少即可．（2）首先计算乘方、开方和括号里面的运算，然后计算括号外面的乘法，求出算式的值是多少即可．解：（1()23- 539=-+11=．（2）()21183⎤⎛⎫-⨯-⎥ ⎪⎝⎭⎥⎦ ()211839⎛⎫=-⨯- ⎪⎝⎭ ()5189=⨯- 10=﹣．此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．22．（1（2）①见解析；②见解析， 30.5-+-【解析】（1）设正方形边长为a ，根据正方形面积公式，结合平方根的运算求出a 值，则知结果； （2） ① 根据面积相等，利用割补法裁剪后拼得如图所示的正方形；②由题（1，然后在数轴上以-3为圆心，以大正方形的边长为半径画弧交数轴的右方与一点M ，再把N 点表示出来，即可比较它们的大小．解：设正方形边长为a ，∵a 2=2，∴a=，，；（2）解：①裁剪后拼得的大正方形如图所示：②设拼成的大正方形的边长为b ，∴b 2=5，∴在数轴上以-3为圆心，以大正方形的边长为半径画弧交数轴的右方与一点M ，则M 表示的数为-3+-0.5的N 点在M 点的右方，∴比较大小：30.5-+<-．本题主要考查平方根与算术平方根的应用及实数的大小比较，熟练掌握平方根与算术平方根的意义及实数的大小比较是解题的关键．23．5±【解析】3=求出a 的值，根据3a +b -1的平方根是±4求出b 的值，根据c 求出c 的值，把求得的值代入a +b +3c ，然后求出入a +b +3c 的平方根即可.3=，∴219a -=，解得：5a =，∵31a b +-的平方根是4±，∴15116b +-=，解得：2b =，∵c 67<< ∴6c =，∴3521825a b c ++=++=∴3a b c ++的平方根是5±本题考查了算术平方根的意义，平方根的意义，无理数的估算，熟练掌握算术平方根的意义、平方根的意义、夹逼法估算无理数的值是解答本题的关键．24．（1）6；（2）70．【解析】（1）首先计算算术平方根、立方根，然后进行加减计算即可；（2）首先计算乘方、乘法，最后进行加减计算即可．解：（1=4-(-2)=6．（2）()23540.255(4)8⨯--⨯⨯- =()()5160.255648⨯--⨯⨯-=1080-+=70．本题考查了实数的混合运算，正确理解算术平方根、立方根性质及乘方法则，确定运算顺序是关键．25．（1）182；（2）22；（3【解析】（1）先去括号，同时将小数化为分数，再计算加减法；（2）先计算乘方，再计算乘除法，最后计算加减法；（3）先计算乘方和绝对值，再计算加减法. （1）36 1.754⎛⎫--+ ⎪⎝⎭=336144++ =182； （2）()()232524-⨯--÷=()4584⨯--÷=20+2=22；（3）()225--=4-（此题考查运算能力，掌握有理数的加减法计算法则，乘方的计算法则，实数的绝对值化简，有理数的混合运算法则是解题的关键.26．（1）（2）x 的值为2或1-．【解析】(1)根据定义，比较两个数的大小即可；(2)根据定义，分类进行大小比较，并建立方程求解即可.（1）<∴>∴max{=（2）{}22max (1),4x x -=，①当22(1)x x -<时，24x =，2x =±（由题意，负值舍去）， ∴2x =；②当22(1)x x ->时，2(1)4x -=，12x -=±，13x =（不符合题意，舍去），21x =-，∴1x =-．综上：x 的值为2或1-．本题考查了新定义问题，实数的大小比较，分类思想，利用平方根解方程，根据定义，把问题转化为实数的大小比较是解题的关键.27．（1）同号得正，异号得负，并把绝对值相加；都得这个数的绝对值；（2）﹣17；（3）适用，举例验证见解析【解析】（1）根据示例得出，两数进行⊗运算时，同号得正，异号得负，并把绝对值相加．特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，都得这个数的绝对值；（2）根据⊗运算的运算法则进行计算即可；（3）举例即可做出结论．解：（1）根据示例得出，两数进行⊗运算时，同号得正，异号得负，并把绝对值相加；特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，都得这个数的绝对值．故答案为：同号得正，异号得负，并把绝对值相加；都得这个数的绝对值；（2）[（﹣2）⊗（+3）]⊗[（﹣12）⊗0]＝（﹣5）⊗（+12）＝﹣17；（3）结合律仍然适用．例如[（﹣3）⊗（﹣5）]⊗（+4）＝（+8）⊗（+4）＝+12，（﹣3）⊗[（﹣5）⊗（+4）]＝（﹣3）⊗（﹣9）＝+12，所以[（﹣3）⊗（﹣5）]⊗（+4）＝12＝（﹣3）⊗[（﹣5）⊗（+4）．故结合律仍然适用．本题考查了新定义下的有理数的加减运算，正确理解新定义运算法则是解题的关键．28．（1）x＝−13；（2）（2）x-y的值为9或-1.【解析】（1）将错就错把x＝2代入计算求出a的值，即可确定出正确的解；（2）根据题意可以求得x、y的值，从而可以求得x−y的值．（1）把x＝2代入2（2x−1）＝3（x＋a）−3中得：6＝6＋3a−3，解得：a＝1，代入方程得：2x1x13 32-+=-，去分母得：4x−2＝3x＋3−18，解得：x＝−13；（2）∵x、y 是有理数，且 x，y 满足等式2x2y17++=-∴22174x yy⎧+=⎨=-⎩，解得，54xy=⎧⎨=-⎩或54xy=-⎧⎨=-⎩，∴当x＝5，y＝−4时，x−y＝5−（−4）＝9，当x＝−5，y＝−4时，原式＝−5−（−4）＝−1．故x-y的值为9或-1.此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．也考查了实数．29．31．【解析】利用实数的混合运算法则计算得出答案．解：原式=4+9⨯12-(2)2⎡⎤⨯-⎢⎥⎣⎦=4+9⨯[]2+1=4+9⨯3=4+27=31．本题主要考查了实数的运算，正确化简各数是解题的关键．30．（1）4；（2）-11；（3；（4）16 -．【解析】（1）直接利用有理数的加减运算法则计算得出答案；（2）逆用分配律，直接提取公因数-115，进而计算得出答案；（3）直接利用绝对值和立方根的性质分别化简得出答案；（4）直接利用有理数的混合运算法则计算得出答案．解：（1）(23)(41)----15=-+4=；（2）原式11()(5133) 5=-⨯-+-1155=-⨯11=-；（3）原式413=--=（4）原式314429 =-⨯⨯16=-．本题主要考查了实数运算，正确化简各数是解题的关键．。

三、计算题3
代入T＝298.15K：
k298.15＝7.222×10-6
298.15K时，分解10％所需时间为：
t0.9＝14589h
三、计算题4
A K k1 X X k2 A K X k3K G
－ dcA dt
k1cAcK
k2cX
dcX dt
k1cAcK k2cX
t 39.23(min)
三、计算题5
ln k1 Ea,1 ( 1 1 )
k1'
R T1 T1'
ln 4 Ea,1 ( 1 1 ) R 310 298
Ea,1 88.728(kJ / mol)
ln
k2 k2'
Ea,2 R
1 ( T2

1 T2'
)
ln 2 Ea,2 ( 1 1 ) R 310 298
带入数据，得：T2＝366.1K 再带入阿伦尼乌斯公式，得： k1 /k2＝0.5879
故所需时间t＝10/0.5879＝17(mim）
三、计算题2
H＋为催化剂，故
dcA dt

k AcA
c H

KcA
K kAcH
因为半衰期与A的初始浓度无关，故：α＝1
pH 5;
t1/ 2
k3cX

0

cX
=
k1cAcK k2 k3
－ dcA dt
k1cAcK
k2
k1cAcK k2 k3

k1k3 k2 k3
cAcK
k2 ? k3
－ dcA dt

k1k3 k2

湘教版七年级数学下册 第6章 数据的分析6．2 方差 同步练习题1．在方差计算公式：s 2＝110[(x 1－15)2＋(x 2－15)2＋…＋(x 10－15)2]中，10、15分别表示( )A ．数据的个数和方差B ．平均数和数据的个数C ．数据的个数和平均数D ．数据的方差和平均数2．某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参加比赛．为此，九(1)班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是96分，甲的成绩的方差是0.2，乙的成绩的方差是0.8，根据以上数据，下列说法正确的是( )A ．甲的成绩比乙的成绩稳定B ．乙的成绩比甲的成绩稳定C ．甲、乙两人的成绩一样稳定D ．无法确定甲、乙的成绩谁更稳定3．某工厂为了选拔1名车工参加直径为5mm 精密零件的加工技术比赛．随机抽取甲、乙两名车工加工的5个零件．现测得的结果如下表．平均数依次为x 甲、x 乙，方差依次为s 2甲、s 2乙，则下列关系中完全正确的是( )A.x 甲＜x 乙，s 2甲＜s 2乙B ．x 甲＝x 乙，s 2甲＜s 2乙C.x 甲＝x 乙，s 2甲＞s 2乙 D ．x 甲＞x 乙，s 2甲＞s 2乙4．若要对一射击运动员最近5次训练成绩进行统计分析，判断他的训练成绩是否稳定，则需要知道他这5次训练成绩的( ) A ．中位数 B ．平均数 C ．众数D ．方差5．从总体中抽取一部分数据作为样本去估计总体的某种属性．下面叙述正确的是( )A ．样本容量越大，样本平均数就越大B．样本容量越大，样本的方差就越大C．样本容量越大，样本的极差就越大D．样本容量越大，对总体的估计就越准确6．2014年8月26日，第二届青奥会将在南京举行，甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备．在某天“110米跨栏”训练中，每人各跑5次，据统计，他们的平均成绩都是13.2秒，甲、乙、丙、丁的成绩的方差分别是0.11，0.03，0.05,0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是( )A．甲B．乙C．丙D．丁7．如果一组数据x1，x2，…，xn的方差是3，则另一组数据x1＋5，x2＋5，…，xn＋5的方差是( )A．3 B．8C．9 D．148．已知一组数据：3、4、5、6、5、7.那么这组数据的方差是( )A.53B．12C．43D．239．已知一组数据1、2、3、4、5的方差为2，则另一组数据11、12、13、14、15的方差为.10．在射击比赛中，某运动员的6次射击成绩(单位：环)为：7、8、10、8、9、6，计算这组数据的方差为.11．一组数据按从小到大的顺序排列为1,2,3，x,4,5，若这组数据的中位数为3，则这组数据的方差是.12．一组数据按从小到大的顺序排列为1,2,3，x,4,5，若这组数据的中位数为3，则这组数据的方差是.13．已知一组数据的方差是s2＝120[(x1－3)2＋(x2－3)2＋…＋(x20－3)2]，则这组数据的数据个数是个，这组数据的平均数是.14．若甲、乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为S2甲＝1.5，S2乙＝2.5，则芭蕾舞团参加演出的女演员身高更整齐(填“甲”或“乙”)．15．我市射击队为了从甲、乙两名运动员中选出一名运动员参加省运动会比赛，组织了选拔测试，两人分别进行了五次射击，成绩(单位：环)如下：则应选择运动员参加省运动会比赛．16．求数据8,9,10,11,12的方差．17．甲、乙两台机床生产同种零件，10天出的次品分别是：甲：0,1,0,2,2,0,3,1,2,4；乙：2,3,1,2,0,2,1,1,2,1.请你根据计算判断哪台机床的性能较好？18．已知一个样本1、2、3、x、5，它的平均数是3.求这个样本的方差．19．已知一组数据x1，x2，…，x6的平均数为1，方差为53.(1)求x21＋x22＋…＋x26；(2)若在这组数据中加入另一个数据x7，重新计算，平均数无变化，求这7个数据的方差(结果用分数表示)．。

初中数学七年级下册第六章数据与统计图表专项练习（2021-2022浙教考试时间：90分钟，总分100分）班级：__________ 姓名：__________ 总分：__________一、单选题（10小题，每小题3分，共计30分）1、2018年1～4月我国新能源乘用车的月销售情况如图所示，则下列说法错误．．的是（）A．1月份销售为2.2万辆B．从2月到3月的月销售增长最快C．4月份销售比3月份增加了1万辆D．1～4月新能源乘用车销售逐月增加2、对某市某社区居民最爱吃的鱼类进行问卷调查后（每人选一种），绘制成如图所示统计图．已知选择鲳鱼的有40人，那么选择黄鱼的有（）A．20人B．40人C．60人D．80人3、2017年12月8日，以“[数字工匠]玉汝于成，[数字工坊]溪达四海”为主题的2017一带一路数学科技文化节•玉溪暨第10届全国三维数字化创新设计大赛（简称“全国3D大赛”）总决赛在玉溪圆满闭幕．某学校为了解学生对这次大赛的了解程度，在全校1300名学生中随机抽取部分学生进行了一次问卷调查，并根据收集到的信息进行了统计，绘制了下面两幅统计图．下列四个选项错误的是（）A．抽取的学生人数为50人B．“非常了解”的人数占抽取的学生人数的12%C．a=72°D．全校“不了解”的人数估计有428人4、要调查安顺市中学生了解禁毒知识的情况，下列抽样调查最适合的是（）A．在某中学抽取200名女生B．在安顺市中学生中抽取200名学生C．在某中学抽取200名学生D．在安顺市中学生中抽取200名男生5、为了解中学300名男生的身高情况，随机抽取若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图(如图)．估计该校男生的身高在169.5cm～174.5cm之间的人数有（）A．12 B．48 C．72 D．966、甲、乙两超市在1月至8月间的盈利情况统计图如图所示，下面结论不正确的是（）A．甲超市的利润逐月减少B．乙超市的利润在1月至4月间逐月增加C．8月份两家超市利润相同D．乙超市在9月份的利润必超过甲超市7、下列调查中，最适合采用全面调查（普查）方式的是（）A．对重庆市初中学生每天阅读时间的调查B．对端午节期间市场上粽子质量情况的调查C．对某批次手机的防水功能的调查D．对某校九年级3班学生肺活量情况的调查8、在下列四项调查中，方式正确的是()A．了解本市中学生每天学习所用的时间，采用全面调查的方式B．为保证运载火箭的成功发射，对其所有的零部件采用抽样调查的方式C．了解某市每天的流动人口数，采用全面调查的方式D．了解全市中学生的视力情况，采用抽样调查的方式9、九年级一班同学根据兴趣分成 A、B、C、D、E 五个小组，把各小组人数分布绘制成如图所示的不完整统计图．则 D 小组的人数是（）A．10 人B．l1 人C．12 人D．15 人10、新区四月份第一周连续七天的空气质量指数（AQI）分别为：118，96，60，82，56，69，86，则这七天空气质量变化情况最适合用哪种统计图描述（）A．折线统计图B．扇形统计图C．条形统计图D．以上都不对二、填空题（5小题，每小题4分，共计20分）1、去年某市有9万名初中毕业生参加升学考试，为了了解这9万名考生的数学成绩，从中取2000名考生数学成绩进行统计分析．在这个抽样中，总体是________，个体是________，样本是________，样本容量是________．2、牛奶里含有丰富的营养成分，某品牌牛奶所含营养成分如图所示．若同学们每天喝一支200克的这种牛奶，则能补充的蛋白质为________克．3、在数据25，23，21，29，28，25，22，26，28，26，26，27，25，21，29中，范围在2527（包括前边的数，不包括后边的数）这一组的频数是________．4、某班将安全知识竞赛成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%、12%、40%、28%，第五组的频数是8，则：①该班有50名同学参赛；②第五组的百分比为16%；③成绩在70﹣80分的人数最多；④80分以上的学生有14名，其中正确的个数有 __个．5、某校对七年级学生进行“综合素质”评价，评价结果分为A，B，C，D，E五个等级．根据收集的评价结果绘制了如图所示的统计图，已知图中从左到右的五个长方形的高之比为2:3:3:1:1，评价结果为“A”的学生有68名，则该校七年级学生共有___________．三、解答题（5小题，每小题10分，共计50分）1、某校对全校2600名学生进行“新冠防疫知识”的教育活动，从中抽取部分学生进行测试，成绩评定按从高分到低分排列分为A、B、C、D四个等级，绘制了图（1）、图（2）两幅不完整的统计图，请结合图中所给信息解答下列问题：（1）求本次抽查的学生共有多少人？（2）将两幅统计图补充完整．（3）求扇形统计图中“B”等级所对应的扇形圆心角的度数．（4）估计全校得“D”等级的学生有多少人？2、今年是中国共产党建党100周年，某校七年级开展“学党史，诵经典”主题诗歌诵比赛，评选出一、二、三等奖若干名．现随机抽取部分获奖学生的情况进行统计，绘制成如下统计图（均不完整）．请你根据给出的信息完成下列问题：（1）本次统计抽取的获奖学生人数是多少？（2）补全条形统计图，并求出扇形统计图中二等奖的圆心角度数；（3）若本次比赛七年级有120名学生获奖，估计其中有多少人获三等奖？3、判断下面这些抽样调查选取样本的方式是否合适，并说明理由．（1）为了了解某厂家生产的零件质量，在其生产线上每隔300个零件抽取1个检查；（2）为了了解某城市全年的降水情况，随机调查该城市某月的降水量．4、为配合“禁烟”行动，某校组织同学们在我市某社区开展了“你最支持哪种戒烟方式”的问卷调查，征求市民的意见，并将调查结果整理后制成了如下两个不完整的统计图：（1）根据以上信息，把条形统计图补充完整（并标注人数）；（2）在统计图中，表示“强制戒烟”方式的扇形的圆心角为多少度？（3）假定该社区有1万人，请估计该社区大约有多少人支持采取“警示戒烟”这种戒烟方式？5、2020年冬季达州市持续出现雾霾天气．某记者为了了解“雾霾天气的主要成因”，随机调查了该市部分市民，并对调查结果进行整理，绘制了尚不完整的统计图表．请根据图表中提供的信息解答下列问题：（1）填空：m＝，n＝，扇形统计图中E组所占的百分比为%；（2）若该市人口约有200万人，请你估计其中持D组“观点”的市民人数．（3）治污减霾，你有什么建议？---------参考答案-----------一、单选题1、D【详解】【分析】观察折线统计图，一一判断即可.【解答】观察图象可知：A. 1月份销售为2.2万辆,正确.B. 从2月到3月的月销售增长最快,正确.C.4.3 3.31-=， 4月份销售比3月份增加了1万辆，正确.D. 1～4月新能源乘用车销售先减少后增大.故错误.故选D.【点评】考查折线统计图，解题的关键是看懂图象.2、D【分析】扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．用整个圆的面积表示总数（单位1），用圆的扇形面积表示各部分占总数的百分数．【详解】解：鱼类总数：40÷20%＝200（人），选择黄鱼的：200×40%＝80（人），故选D．【点睛】本题考查的是扇形统计图．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键；扇形统计图直接反映部分占总体的百分比大小．3、D【详解】【分析】利用统计图中的信息逐项进行判断即可得解.【详解】抽取的总人数为6+10+16+18=50（人），故A正确，不符合题意；“非常了解”的人数占抽取的学生人数的650=12%，故B正确，不符合题意；α=360°×1050=72°，故C正确，不符合题意；全校“不了解”的人数估计有1300×1850=468（人），故D错误，符合题意，故选D．【点睛】本题考查了条形统计图、扇形统计图等知识，读懂统计图，从中找到必要的信息是解题的关键．4、B【详解】分析：根据具体情况正确选择普查或抽样调查方法，并理解有些调查是不适合使用普查方法的．要选择调查方式，需将普查的局限性和抽样调查的必要性结合起来具体分析．详解：要调查安顺市中学生了解禁毒知识的情况，就对所有学生进行一次全面的调查，费大量的人力物力是得不尝失的，采取抽样调查即可．考虑到抽样的性别差异和学校差异，所以应在安顺市中学生中随机抽取200名学生．故选B．点睛：本题考查了抽样调查和全面调查，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．5、C【详解】解:根据图形，身高在169.5cm～174.5cm之间的人数的百分比为：12100%=24%6+10+16+12+6，∴该校男生的身高在169.5cm～174.5cm之间的人数有300×24%＝72(人)．故选C．6、D【分析】根据折线图中各月的具体数据对四个选项逐一分析可得．【详解】A、甲超市的利润逐月减少，此选项正确，不符合题意；B、乙超市的利润在1月至4月间逐月增加，此选项正确，不符合题意；C、8月份两家超市利润相同，此选项正确，不符合题意；D、乙超市在9月份的利润不一定超过甲超市，此选项错误，符合题意，故选D．【点睛】本题主要考查折线统计图，折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．7、D【详解】A、对重庆市初中学生每天阅读时间的调查，调查范围广适合抽样调查，故A错误；B、对端午节期间市场上粽子质量情况的调查，调查具有破坏性，适合抽样调查，故B错误；C、对某批次手机的防水功能的调查，调查具有破坏性，适合抽样调查，故C错误；D、对某校九年级3班学生肺活量情况的调查，人数较少，适合普查，故D正确；故选D．8、D【详解】分析：由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．详解：A、了解本市中学生每天学习所用的时间，调查范围广适合抽样调查，故A不符合题意；B、为保证运载火箭的成功发射，对其所有的零部件采用全面调查的方式，故B不符合题意；C、了解某市每天的流动人口数，无法普查，故C不符合题意；D、了解全市中学生的视力情况，采用抽样调查的方式，故D符合题意；故选D．点睛：本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．9、C【分析】从条形统计图可看出 A 的具体人数，从扇形图找到所占的百分比，可求出总人数，然后结合 D所占的百分比求得 D小组的人数．【详解】总人数=510%=50（人），D 小组的人数=50×86.4360=12（人）），故选C．【点睛】本题考查了条形统计图、扇形统计图、用样本估计总体，读懂统计图，从不同的统计图中找到必要的信息进行解题是关键.10、A【分析】根据统计图的特点进行分析可得：扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．【详解】解：由题意得，要描述这七天空气质量变化情况最适合用折线统计图．故选A．【点睛】此题根据扇形统计图、折线统计图、条形统计图各自的特点，熟练掌握三种统计图的特点是解答本题的额关键．二、填空题1、9万名考生的数学成绩每名考生的数学成绩被抽出的2000名考生的数学成绩 2000 【分析】根据抽样中总体、个体、样本以及样本容量的概念解答即可．【详解】根据题意，在这个抽样中，总体是9万名考生的数学成绩，个体是每名考生的数学成绩，样本是被抽出的2000名考生的数学成绩，样本容量是2000．故答案为：9万名考生的数学成绩；每名考生的数学成绩；被抽出的2000名考生的数学成绩；2000．【点睛】本题主要考查了对抽样中总体、个体、样本以及样本容量的理解，属于基础题，掌握总体、个体、样本以及样本容量的概念是解题关键．2、12【分析】根据扇形统计图的数据直接求解即可．【详解】⨯=2006%12故答案为：12【点睛】本题考查的是扇形统计图的概念，理解概念是解题的关键．3、6【分析】根据频数的定义：每个对象出现的次数求解即可．【详解】解：由题意知：范围在25～27这一组的频数是6，故答案为：6．【点睛】本题考查了频数的定义，属于基础问题．4、3【分析】根据频数分布直方图中每一组内的频率总和等于1，可得出第五组的百分比，又因为第五组的频数是8，即可求出总人数，根据总人数即可得出80分以上的学生数，从而得出正确答案．【详解】解：第五组所占的百分比是：1﹣4%﹣12%﹣40%﹣28%＝16%，故②正确；则该班有参赛学生数是：8÷16%＝50（名），故①正确；从直方图可以直接看出成绩在70～80分的人数最多，故③正确；80分以上的学生有：50×（28%+16%）＝22（名），故④错误；其中正确的个数有①②③，共3个；故答案为：3．【点睛】本题考查了数据的统计分析，根据频率分布直方图得出正确信息是解题关键.5、340【分析】用A 的学生有68名除以A 等级人数所占比例即可得．【详解】解： “综合素质”评价结果为“A ”的学生所占比例为：21233115=++++， ∴该校七年级学生共有：1683405÷=（名）， 故答案为：340．【点睛】本题主要考查频数分布直方图，从频率分布直方图可以清楚地看出数据分布的总体态势，但是从直方图本身得不出原始的数据内容．三、解答题1、（1）120人；（2）见解析；（3）144°；（4）260人【分析】（1）由A 等级人数及其所占百分比可得总人数；（2）总人数乘以C 等级百分比求出其人数，再根据四个等级人数之和等于总人数求出D 等级人数，继而分别用B 、D 等级人数除以总人数求出其所占百分比即可补全图形；（3）用360°乘以样本中B 对应的百分比即可；（4）用总人数乘以样本中D 等级人数所占百分比即可．【详解】解：（1）本次抽查的学生人数为24÷20%＝120（人）；（2）C 等级人数为120×30%＝36（人），D 等级人数为120﹣（24+48+36）＝12（人），B等级人数所占百分比为48÷120×100%＝40%，D等级人数所占百分比为12÷120×100%＝10%，补全图形如下：（3）扇形统计图中“B”等级所对应的扇形圆心角的度数为360°×40%＝144°；（4）估计全校得“D”等级的学生有2600×10%＝260（人）．【点睛】此题主要考查统计调查的应用没解题的关键是熟知条形统计图与扇形统计图的特点．2、（1）40；（2）图见解析，108°；（3）72人【分析】（1）根据条形图可得一等奖人数为4人，根据扇形图可得一等奖所占百分比为10%，根据频率公式即可求解；（2）根据样本容量减去一等奖，二等奖人数可三等奖人数即可补全条形图如图，然后求出二等奖所占百分比，利用360°×二等奖百分比便可求出扇形圆心角；（3）先求出样本的百分比，然后用样本的百分比乘以年级总数即可．【详解】解：（1）∵一等奖人数为4人，一等奖所占百分比为10%，本次统计随机抽取部分获奖学生人数为4÷10%=40人；（2）三等奖人数为40-4-12=24，补全条形图如图，∵二等奖所占百分比为12÷40×100%=30%，∴扇形统计图中二等奖的圆心角度数360°×30%=108°；（3）∵样本中获三等奖的百分比为24÷40×100%=60%，∴本次比赛七年级有120名学生中获三等奖人数为120×60%=72人．【点睛】本题考查条形统计图与扇形统计图获取信息，样本容量，补画条形图，求扇形圆心角，用样本的百分比含量估计总体中的数量，习题难度适中，能灵活运用统计知识是解题关键．3、（1）比较合适，可以保证样本的广泛性和代表性；（2）不合适，用某月的降水量代表全年的降水量不具有代表性【分析】根据调查应具有代表性分析解答．【详解】解：（1）比较合适，可以保证样本的广泛性和代表性；（2）不合适，用某月的降水量代表全年的降水量不具有代表性．【点睛】此题考查调查样本的选取，掌握样本的选取应具有代表性的特点是解题的关键．4、（1）见解析；（2）144°；（3）3500人【分析】（1）在条形统计图中找出“代替品戒烟”人数为30人，在扇形统计图中所占的百分比为10％，求出随机调查的总人数，由总人数及“药物戒烟”所占的百分比，“警戒戒烟”所占的百分比，求出各自的人数，补全条形统计图即可；（2）“强制戒烟”的人数为120人，总人数为300人，求出所占的百分比，再乘以360 即可；（3）先求出样本中支持“警戒戒烟”这种方式所占的百分比，再利用样本估计总体即可得出答案．【详解】（1）如图所示：（2）调查的人数=30÷10%=300（人），“强制戒烟”方式的扇形的圆心角=（120÷300）×100%×360°=144°；（3）支持“警示戒烟”方式的人数=（1-10%-15%-40%）×10000=3500（人），答：该社区大约有3500人支持采取“警示戒烟”这种戒烟方式．【点睛】本题考查条形统计图、扇形统计图以及用样本估计总体，根据统计图，找出有用信息是解题的关键．5、（1）400，100，15；（2）60万人；（3）见解析【分析】（1）根据A的人数除以BA所占的百分比，求得总人数，总人数乘以B的百分比可得m，总人数减去其余各组人数之和可得n，用E组人数除以总人数可得答案；（2）根据全市总人数乘以D类所占比例，可得答案；（3）根据以上图表提出合理倡议均可．【详解】解：（1）本次调查的总人数为80÷20%＝400（人），则B组人数m＝400×10%＝40（人），C组人数n＝400﹣（80+40+120+60）＝100（人），∴扇形统计图中E组所占的百分比为（60÷400）×100%＝15%；（2）200×120400＝60（万人），答：估计其中持D组“观点”的市民人数有60万人；（3）由上面的统计可知，造成“雾霾”的主要原因是“工厂造成的污染”和“汽车尾气排放”．倡议关停重污染企业，加大对工厂排污的监管和处罚；倡议大家尽量乘坐公共交通工具出行，减少汽车尾气的排放．【点睛】本题主要考查了扇形统计图，统计表，能从图形中获取准确信息是解题的关键．。

P(S 2<9.1) = P (〃-1W (25-l)x9.1-6-< =p{x 2(24)< 36.4} = 1 一 p{/ (24) 2 36.4} >1.叫=P« 10注144i=l 〉=户{/(10)>16} = 0.1 X-a X-a 习题六1.设总体X 〜N(〃,6),从中抽取容量为25的一个样本，求样本方差尸小于9.1的概率. 解X 〜N(/,6),由代世〜/(〃-1),于是 cf1-0.05 = 0.95.io2.设乂偿2，・・撰|。

是取自正态总体N(0,0.32)的样木，试求P Zx ：>1.44}./=i解：由—;—〜事(〃)，于是3. 设总体X 〜Ng),X\,X".,X“是取自总体X 的一个样本,X 为样本均值，试问样本容 量〃分别为多大时，才能使以下各式成立，(1) E 伊—此)匕0.1; (2) E (|x-r/|)<0.1; (3) P(|7-«| < 1} > 0.95.— 4 X-a 解(1)因为X 〜N(Q ,-),所以一〜N(0,l),从而 n 4V n1 X C X /-) A=事后注办=方"「标=寿"3 所以 〃-4)=金£ =貉 <0.1, 从而 n>~ =254.7,故〃 > 255.a N(0,l),所以24 =一".1,所以〃 240.n I 2P^X-a 所以 > 0.975,而S （1.96） =0.975,从而—>1.96, n > 15.37,故〃 > 16.解(1)3S 2 b /⑶， （2）P {|X -H |<0.250-}= 6. (3)因为4, 已知总体X 〜N(10,S),＜7为未知,乂偿2法3，匕总体X 的一个样本,X 、$2分别为样本 均值和样本方差(D 构造一个关于京的统计量吃使得E ⑶;(2)设s = 1.92,求使尸｛-。