材料力学惯性矩ppt

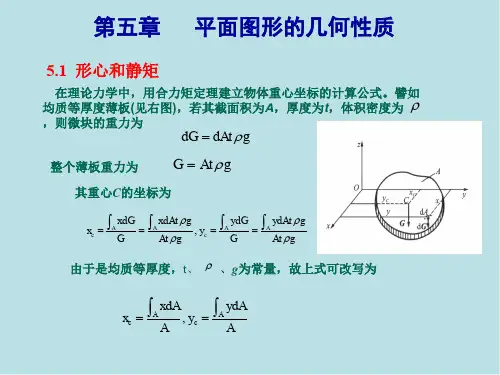
1、静矩（求形心）⎰=AZ ydA S⎰=Ay zdA SSz 、Sy 分别定义为图形对z 轴和y 轴的静矩，也称为图形对z 轴和y 轴的一次矩。

平面图形的静矩是对某一坐标而言的，同一图形对不同的坐标轴，其静矩也就不同。

静矩的数值可能为正值，可能为负值，也可能为零。

静矩的量纲是长度的三次方。

静矩用来求平面图形的形心坐标：A zdAz A ydAy AA⎰⎰==对于规则的形状，可以将其划分为若干个规则的简单图形，通过组合求的形心。

212211212211A A z A z A z A A y A y A y ++=++=注：A 为简单图形的面积（空心面积可以为负值），y 、z 为简单图形的形心坐标值2、惯性矩⎰⎰==Ay AZ dAz I dAy I 22Iz 、Iy 分别定义为图形对z 轴和y 轴的惯性矩，也称为图形对z 轴和y 轴的二次轴矩。

惯性矩始终为正值，惯性矩的量纲是长度的四次方。

计算步骤123222332202202bh bx dx x b x bdx dA z I h h Ay =⨯=⨯=⨯⨯==⎰⎰⎰左图三角形面积对z轴的惯性矩1243)()(44322hyhydyyyhydyyhI hhz=-=-=⨯-=⎰⎰右图关于z轴的惯性矩为左图的四倍34hIz=惯性距的平行移轴定理：有了它规则形状的物体就不用通过积分来求惯性矩了，省时省力(但精准度差了一些)截面图形对某轴的惯性矩，等于它对该轴平行的形心轴的惯性矩，加上两轴间距离的平方乘以截面面积。

A a I I xc x 2+=Ix ——截面图形对目标轴的惯性矩（目标轴：组合图形的形心轴） Ixc ——截面图形对形心轴的惯性矩（注意理解：此处的形心轴是指划分的规则截面的形心轴）a ——两轴之间的距离 A ——截面图形的面积3、极惯性矩图形对于任意一对互相垂直的轴的惯性矩之和，等于它对该两轴交点的极惯性矩。

I p=I z+I y4、惯性积在平面图形的坐标（x ，y ）处，取微面积dA ，遍及整个图形面积的积分⎰=AyzyzdA I ，定义为图形对y ，z 轴的惯性积。

静矩，惯性矩，极惯性矩等问题静矩（截面一次矩）：微元面积（把微元面积视为垂直于图形的力）对坐标轴的矩的积分，即微元面积与微元到坐标轴距离的乘积的积分。

应用：1形心：图形几何形状的中心。

若将微元面积视为垂直于图形平面的力，则形心即为合力的作用点。

利用平衡力系求得。

下式中Yc和Zc就是图形的形心坐标静矩与坐标轴有关，同一平面内对不同坐标轴有不同的静矩，可以为正，也可以为负。

它的量纲是长度的三次方。

对于通过形心的坐标轴，图形静矩等于零。

静矩和形心相互关联，知道其中一个就可求出另一个。

静矩的力学意义是：如果截面上作用有均匀分布载荷，其值以单位面积上的量表示，则载荷对于某个轴的合力矩就等于分布载荷乘以截面对该轴的静矩。

静矩是求截面形心和计算截面内各点剪应力的必要数据。

2：静矩在材料力学中主要应用于弯曲剪应力的计算，考虑剪应力平行于剪力，并且剪应力在截面宽度方向上均匀分布，此时，矩形截面，工字梁，圆截面的剪应力的表达式为：τ=QS/Ib，这里Q为剪力，S为距离中性面y以外面积对中性轴的静矩，b为截面的宽度，I为截面对中性轴的惯性矩。

3：求解静定结构的位移的单位载荷法，当研究对象为线弹性体的时候，即为莫尔定理，或者莫尔积分。

在求解莫尔积分的时候，被积函数中有一个函数为线性函数的时候，便可以采用莫尔积分图乘法。

原理是当被积函数一个为线性函数的时候，该函数可以表示为x*tan(θ)，而tan(θ)对于莫尔积分来讲是常数，可以提到积分号以外，因此，原来的积分便可以表示为x与另一个函数相乘的积分，而其物理意义即为该函数曲线围成的曲面面积到y轴的静矩，所以该积分的解可以由该曲面的面积乘以形心的x坐标。

因此对于原始积分来讲需要乘以tan(θ)，所以莫尔积分的图乘法的结果是曲线面积乘以形心的纵坐标。

惯性矩（截面二次矩）：微元面积（把微元面积视为垂直于图形的力）对到坐标轴距离的平方的积分。

极惯性矩（截面二次极矩）：对某点的极惯性矩为该微元面积对到该点距离的平方的积分。

材料力学惯性矩材料力学是研究物质内部力的作用和变形规律的一门学科，而惯性矩则是材料力学中非常重要的一个概念。

在工程实践中，我们经常需要计算和应用惯性矩来分析和设计结构。

因此，对于材料力学惯性矩的理解和掌握是非常必要的。

首先，我们来了解一下惯性矩的概念。

惯性矩是描述物体抵抗转动的能力的物理量，它与物体的质量和形状密切相关。

惯性矩的大小取决于物体的质量分布和旋转轴的位置。

在工程中，我们通常需要计算关于惯性矩的一些参数，比如转动惯量、极转动半径等，以便进行结构设计和分析。

其次，惯性矩的计算方法有很多种，根据不同的情况可以采用不同的计算公式。

比如对于一般的平面图形，我们可以利用基本的几何学知识来计算其惯性矩；对于复杂的三维结构，我们则需要运用积分或者数值计算的方法来求解。

在实际工程中，我们经常会遇到各种各样的结构和形状，因此掌握多种计算方法是非常重要的。

另外，惯性矩的计算还需要考虑材料的弹性模量和截面的形状。

对于不同的材料和截面形状，其惯性矩的计算方法也会有所不同。

比如对于矩形截面和圆形截面，它们的惯性矩计算公式就是不同的。

因此，在实际工程中，我们需要根据具体情况选择合适的计算方法，并结合材料的力学性能参数来进行计算。

最后，惯性矩的应用非常广泛，不仅可以用于结构设计和分析，还可以用于动力学和振动学的研究。

比如在机械设计中，我们需要计算零件的惯性矩来确定其转动惯量，从而分析其转动特性；在航天航空领域，惯性矩也是非常重要的参数，它关系到飞行器的稳定性和控制性能。

总之，材料力学惯性矩是工程领域中非常重要的概念，它涉及到结构设计、力学分析、动力学和振动学等多个领域。

掌握惯性矩的计算方法和应用技巧，对于工程师来说是非常必要的。

希望本文的介绍能够帮助大家更好地理解和应用惯性矩的知识。

截面惯性矩编辑同义词截面矩一般指截面惯性矩计算公式编辑常见截面的惯性矩公式矩形b*h^3/12 其中：b—宽；h—高三角形b*h^3/36 其中：b—底长；h—高圆形π*d^4/64 其中：d—直径圆环形π*D^4*(1-α^4)/64; α=d/D 其中：d—内环直径；D—外环直径惯性矩编辑惯性矩I=质量X垂直轴二次）the moment of inertiacharacterize an object's angular acceleration due to torque.静矩静矩（面积X面内轴一次）把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx= ydF。

截面惯性矩截面惯性矩（I=面积X面内轴二次）截面惯性矩：the area moment of inertiacharacterized an object's ability to resist bending and is required to calculate displacement.截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix= y↑2dF。

截面极惯性矩截面极惯性矩（Ip=面积X垂直轴二次）。

扭转惯性矩Ip: the torsional moment of inertia极惯性矩the polar moment of inertia截面各微元面积与各微元至垂直于截面的某一指定轴线二次方乘积的积分Ip= P↑2dF。

a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.相互关系截面惯性矩和极惯性矩的关系截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩Ip=Iy+Iz。