六年级数学竞赛上册奥数高思第1讲：计算综合二(20200403194556)

六年级拔尖数学目录第1讲定义新运算第2讲简单的二元一次不定方程第3讲分数乘除法计算第4讲分数四那么混合运算第5讲估算第6讲分数乘除法的计算技巧第7讲简单的分数应用题〔1〕第8讲较复杂的分数应用题〔2〕第9讲阶段复习与测试〔略〕第10讲简单的工程问题第11讲圆和扇形第12讲简单的百分数应用题第13讲分数应用题复习第14讲综合复习〔略〕第15讲测试〔略〕第16讲复杂的利润问题〔2〕第一讲 定义新运算在加.减.乘.除四那么运算之外，还有其它许多种法那么的运算。

在这一讲里，我们学习的新运算就是用“ #〞“*〞“Δ〞等多种符号按照一定的关系“临时〞规定的一种运算法那么进展的运算。

例1：如果A*B=3A+2B ，那么7*5的值是多少？例2：如果A#B 表示3B A + 照这样的规定，6#〔8#5〕的结果是多少？例3：规定YX XY Y X +=∆ 求2Δ10Δ10的值。

例4：设M*N 表示M 的3倍减去N 的2倍，即M*N=3M-2N（1） 计算〔14 *10〕*6（2） 计算 〔58*43〕 *〔1 *21〕例5：如果任何数A 和B 有A ¤B=A ×B-〔A+B 〕求〔1〕10¤7〔2〕〔5¤3〕¤4〔3〕假设2¤X=1求X例6：设P ∞Q=5P+4Q ，当X ∞9=91时，1/5∞〔X ∞ 1/4〕的值是多少？例7：规定X*Y=XY Y AX +，且5*6=6*5那么〔3*2〕*〔1*10〕的值是多少？例8：▽表示一种运算符号，它的意义是））（（A Y A X XY Y X +++=∇11 3211212112=+++=∇））（（A 那么20218▽2021=？稳固练习1、2▽3=2+22+222=246； 3▽4=3+33+333+3333=3702；按此规那么类推（1） 3▽2 〔2〕5▽3〔3〕1▽X=123，求X 的值2、1△4=1×2×3×4；5△3=5×6×7计算〔1〕〔4△2〕+〔5△3〕 〔2〕〔3△5〕÷〔4△4〕3、如果A*B=3A+2B，那么〔1〕7*5的值是多少？〔2〕〔4*5〕*6 〔3〕〔1*5〕*〔2*4〕4、如果A>B，那么｛A，B｝=A；如果A<B，那么｛A，B｝=B；试求〔1〕｛8，0.8｝〔2〕｛｛1.9，1.901｝1.19｝5、N为自然数，规定F〔N〕=3N-2 例如F〔4〕=3×4-2=10试求：F〔1〕+F〔2〕+F〔3〕+F〔4〕+F〔5〕+……+F〔100〕的值6、如果1=1！1×2=2！1×2×3=3！……1×2×3×4×……×100=100!那么1！+2！+3！+……+100！的个位数字是几？〔第四届小学生“迎春杯〞数学决赛试题〕7、假设“+、-、×、÷、=、〔〕〞的意义是通常情况，而式子中的“5”却相当于“4”。

在进行加减法计算时，“先计算括号中的部分，再从左往右依次计算”是基本的运算法则．但除此之外，还有许多运算技巧，熟练掌握各种运算技巧可以使你算得更快更准．“凑整法”是最常用的巧算方法，就是在计算时优先计算可以得到整十、整百、整千的部分，从而达到巧算的目的．要想凑出整十，两个数的末位相加应该得0，这样的情况除了00+，55+，46+．同学们在做题时要注意观察各+，28+，37+外，还有19加数的个位，看能不能找到合适的凑法．除了加法可以凑整以外，减法同样可以凑整，个位相同的两个数相减后便能得到整十的数．在进行加减法混合运算时，经常会遇到能够巧算的数不在一起的情况，这时候就需要通过调整运算顺序，把能巧算的放在一起先算．但需要注意的是，在调整的过程中，每个数都必须带着自己左边的符号一起移动，这种调整可以形象地称作“带符号搬家”．如果搬家的是算式中的第一个数，前面没有符号，在这个数之前添上一个加号即可．分析 （1）通过个位凑十来配对，但其中以1和9结尾的都分别有2个，应该如何配对呢？（2）加法配对看末位，减法应该如何配对？练习1.（1）计算：36973264168103+++++；（2）计算：24681925323922241234−++−+．除了“带符号搬家”可以调整运算次序外，“脱括号”与“添括号”也是改变运算顺序的常用手段．加减法算式中“脱括号”要遵循下面的规则：括号前面是加号，脱去括号不变号；括号前面是减号，脱去括号变符号．分析 去掉括号会变成什么样？练习2.（1）计算：()()12323454567−−−−；（2）（2（2）计算：()()437200836353−−+−． 小笑话从前，山东省有个大军阀，他横行霸道，却不学无术，经常闹笑话．一次会议开始时，他想点点名，了解一下哪些人来了，哪些人没来．可是，他一看到会的人数比较多，点名很费事．于是这个不学无术的军阀就想了一个“办法”．他认为没有来的人总是少数，只要知道哪些人没来，来的人不用一一点名，也会清楚了．于是他便大声地叫道：“没有来的人举手!”他这么喊过之后，到会的人面面相觑，都感到莫名其妙．上面只是一个小笑话，但是其实这个军阀运用了数学中“补数”的思想，只要知道了没到的人数，再用总人数减去没到的人数就可以了，只是他脱离了实际，结果闹了笑话．其实补数是速算和心算时一个重要的概念．比如，在计算45798−时，可以把98看成1002−来计算，()4579845710024571002359−=−−=−+=．在运用补数进行巧算的时候要注意补数前的符号到底是加还是减．分析 把题目中接近整百整十的数都变成补数的形式，应该怎么变？练习3.（1）计算：999999999++；（2）计算：23452993981198−−−．前面学习了“脱括号”的巧算方法，其实“添括号”也是一个重要的技巧，“添括号”与“脱括号”类似，同样要注意：括号前面是加号，添上括号不变号；（2）当然，这里所说的“括号前面”是指要添上的括号之前，而要改变的符号是新括号里的那些符号．分析 题（1）中全都是减号，在什么位置添上括号可以简化计算？题（2）中有加有减，有哪些数之间是可以凑整的？练习4.（1）计算：379131588742−−−−；（2）计算：9811451813235577+−−+−．最后我们来看两个与数字特点有关的计算：分析 仔细观察每一问里的数字都有什么特点？试着利用这些特点进行巧算．练习5. 计算：（1）714147471555++−；（2）1827364554637281+−+−+−+．（2（2）例题5本讲知识点汇总一、通过末位找到凑整的关系：加法末位和为10，减法末位相同．二、脱括号、添括号的原则：括号前面是加号，脱去/添上括号不变号；括号前面是减号，脱去/添上括号变符号．三、巧用补数：对于靠近整十整百整千的数，可以先用那些整的进行计算，再计算它们的补数．四、把每个数位分开计算．作业1. 计算：2589127175373289−++++．2. 计算：()()62235778600457−−−−．−−−．3.计算：100197396298−−−+．4.计算：3579862138734234++−．5.计算：334343433111。

小学奥数基础教程(六年级)第1讲比较分数的大小第2讲巧求分数第3讲分数运算的技巧第4讲循环小数与分数第5讲工程问题(一)第6讲工程问题(二)第7讲巧用单位“1”第8讲比和比例第9讲百分数第10讲商业中的数学第11讲圆与扇形第12讲圆柱与圆锥第13讲立体图形(一)第14讲立体图形(二)第15讲棋盘的覆盖第16讲找规律第17讲操作问题第18讲取整计算第19讲近似值与估算第20讲数值代入法第21讲枚举法第22讲列表法第23讲图解法第24讲时钟问题第25讲时间问题第26讲牛吃草问题第27讲运筹学初步（一）第28讲运筹学初步（二）第29讲运筹学初步（三）第30讲趣题巧解第一讲比较分数的大小同学们从一开始接触数学，就有比较数的大小问题。

比较整数、小数的大小的方法比较简单，而比较分数的大小就不那么简单了，因此也就产生了多种多样的方法。

对于两个不同的分数，有分母相同，分子相同以及分子、分母都不相同三种情况，其中前两种情况判别大小的方法是：分母相同的两个分数，分子大的那个分数比较大；分子相同的两个分数，分母大的那个分数比较小。

第三种情况，即分子、分母都不同的两个分数，通常是采用通分的方法，使它们的分母相同，化为第一种情况，再比较大小。

由于要比较的分数千差万别，所以通分的方法不一定是最简捷的。

下面我们介绍另外几种方法。

1.“通分子”。

当两个已知分数的分母的最小公倍数比较大，而分子的最小公倍数比较小时，可以把它们化成同分子的分数，再比较大小，这种方法比通分的方法简便。

如果我们把课本里的通分称为“通分母”，那么这里讲的方法可以称为“通分子”。

2.化为小数。

这种方法对任意的分数都适用，因此也叫万能方法。

但在比较大小时是否简便，就要看具体情况了。

3.先约分，后比较。

有时已知分数不是最简分数，可以先约分。

4.根据倒数比较大小。

5.若两个真分数的分母与分子的差相等、则分母（子）大的分数较大；若两个假分数的分子与分母的差相等，则分母（子）小的分数较大。

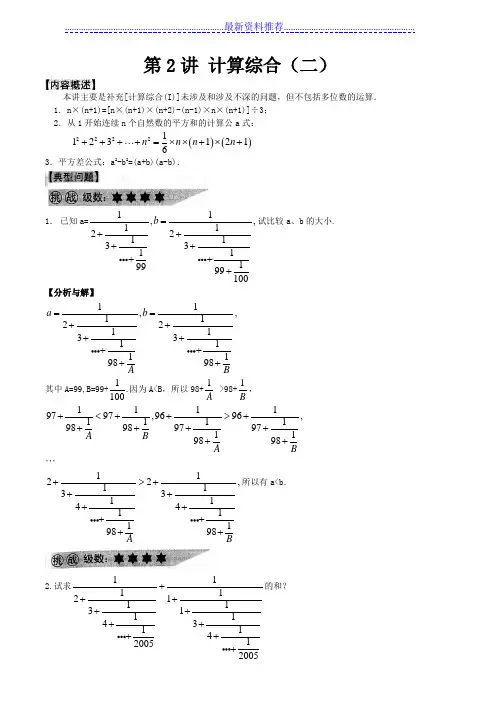
第2讲计算综合（二）本讲主要是补充[计算综合(I)]未涉及和涉及不深的问题，但不包括多位数的运算． 1．n×(n+1)=[n×(n+1)×(n+2)-(n-1)×n×(n+1)]÷3；2．从1开始连续n个自然数的平方和的计算公a式：()()222211231216n n n n++++=⨯⨯+⨯+3．平方差公式：a2-b2=(a+b)(a-b)．1．已知a=11,,112211331119999100b=+++++++试比较a、b的大小.【分析与解】11,,1122113311119898a bA B==++++++++其中A=99,B=99+1.100因为A<B，所以98+1A>98+1B，11119797,9696,111198989797119898A BA B+<++>+++++++1122,1133114411119898A B+>+++++++++所以有a<b．2.试求11112111311143114120052005++++++++++的和？【分析与解】记1,131412005x=+++则题目所要求的等式可写为：11,1211xx++++而11111.122211xx x xx++=+=+++++所以原式的和为1．评注：上面补充的两例中体现了递推和整体思想．2．试求1+2+3+4+…4+100的值?【分析与解】方法一：利用等差数列求和公式，(首项+末项)×项数÷2=(1+100)×100÷2=5050．方法二：倒序相加，1+ 2+ 3+ 4+ 5+… 97+ 98+ 99+ 100100+ 99+ 98+ 97+ 96+…4+ 3+ 2+ 1,上下两个数相加都是101，并且有100组，所以两倍原式的和为101×100，那么原式的和为10l×100 ÷2=5050．方法三：整数裂项(重点)，原式=(1×2+2×2+3×2+4×2+…+100×2)÷2=[]122(31)3(42)4(53)100(10199)2⨯+⨯-+⨯-+⨯-++⨯-÷=(12⨯23+⨯12-⨯34+⨯23-⨯45+⨯34-⨯10010199100++⨯-⨯)2÷=1001012⨯÷=5050.3．试求l×2+2×3+3×4+4×5+5×6+…+99×100．【分析与解】方法一：整数裂项原式=(1×2×3+2×3×3+3×4×3+4×5×3+5×6×3+…+99×100×3)÷3=[1×2×3+2×3×(4-1)+3×4×(5-2)+4×5×(6-3)+5×6×(7-4)+…+99×100×(101-98)]÷3(123⨯⨯234+⨯⨯123-⨯⨯345+⨯⨯234-⨯⨯456+⨯⨯345-⨯⨯567+⨯⨯456-⨯⨯99100101 9899100++⨯⨯-⨯⨯)3991001013331011003333100333300.÷=⨯⨯÷=⨯⨯=⨯=方程二：利用平方差公式12+22+32+42+…+n2=2(1)(21).6n n nn⨯+⨯+=原式：12+l+22+2+32+3+42+4+52+5+…+992+99=12+22+32+42+52+…+992+1+2+3+4+5+…+99=991001999910062⨯⨯⨯+=328350+4950=333300．5．计算下列式子的值：0.1×0.3+0.2⨯0.4+0.3×0.5+0.4×0.6+…+9.7×9.9+9.8⨯10.0【分析与解】这个题看上去是一个关于小数的问题，实际上我们可以先把它们变成整数，然后再进行计算．即先计算1×3+2⨯4+3×5+4⨯6+…+97⨯99+98×100。

《华数奥赛教材(6年级)》目录
上册
第一讲速算与巧算（一）
第二讲速算与巧算（二）
第三讲估算
第四讲计数问题（一）
第五讲计数问题（二）
第六讲分数与百分数（一）
第七讲分数与百分数（二）
第八讲圆的面积
第九讲圆的面积及综合问题
第十讲工程问题（一）
第十一讲工程问题（二）
第十二讲整除问题
第十三讲余数问题
《华数奥赛教材(6年级)》目录
下册
第一讲比和比例（一）
第二讲比和比例（二）
第三讲立体图形的计算（一）
第四讲立体图形的计算（二）
第五讲列方程解应用题（一）
第六讲列方程解应用题（二）
第七讲不定方程
第八讲逻辑推理问题
第九讲行程问题
第十讲时钟问题
第十一讲观察与归纳
第十二讲周期性问题
综合练习（一）综合练习（二）综合练习（三）综合练习（四）综合练习（五）综合练习（六）综合练习（七）综合练习（八）。

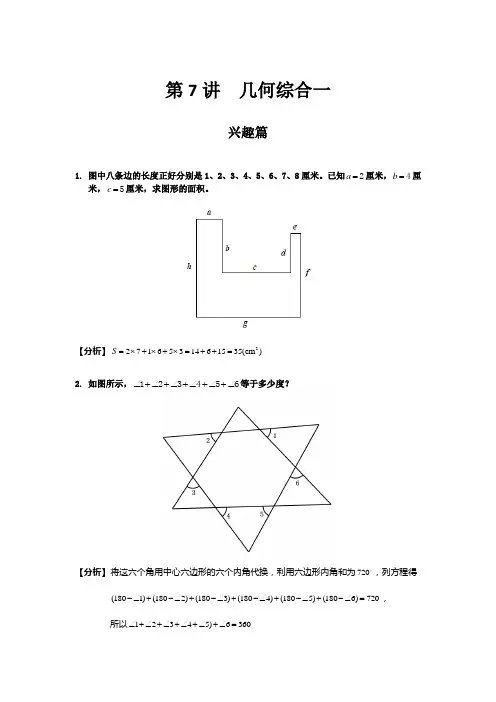
第7讲几何综合一兴趣篇1. 图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米。

已知a=2厘米，b=4厘米，c=5厘米，求图形的面积。

【分析】2S=⨯+⨯+⨯=++=2716531461535(cm)2. 如图所示，∠+∠+∠+∠+∠+∠123456等于多少度？【分析】将这六个角用中心六边形的六个内角代换，利用六边形内角和为720，列方程得(1801)(1802)(1803)(1804)(1805)(1806)720-∠+-∠+-∠+-∠+-∠+-∠=，所以12345)6360∠+∠+∠+∠+∠+∠=3. 如图，平行四边形ABCD 的周长为75厘米。

以BC 为底时高是14厘米，以CD 为底时高是16厘米。

求平行四边形ABCD 的面积。

【分析】 75237.5BC CD +=÷=,根据面积相等，底的比与高的比成反比例，所以:16:148:7BC CD ==,因此37.5(87)820BC =÷+⨯=,平行四边形ABCD 的面积是2014280⨯=平方厘米4. 如图所示，一个边长为1米的正方形被分成4个小长方形，它们的面积分别是310平方米、25平方米、15平方米和110平方米。

已知图中的阴影部分是正方形，那么它的面积是多少平方米？【分析】 1251110CH HD ==,因此23CH =,13HD =,3310245AE EB ==,所以37AE =,47EB =,因此2353721FG =-=,那么它的面积是252521441⎛⎫= ⎪⎝⎭平方米5. 如图，红、黄、绿三块大小一样的正方形纸片，放在一个正方体盒内，它们之间相互重叠。

已知露在外面的部分中，红色的面积是20，黄色的面积是14，绿色的面积是10。

那么，正方体盒子的底面积是多少？绿黄红【分析】 将黄色纸片推到左边，则每块纸片露出的形状如右上图.黄、绿两色的面积之和保持14+10=24不变，则在右图中这两块面积相等，均为24212÷=.根据公式可知，空白处面积=黄⨯绿÷红=1212207.2⨯÷=，则正方形盒底面积是7.212122051.2+++=.6. 如图，在三角形ABC 中，IF 和BC 平行，GD 和AB 平行，HE 和AC 平行。

第1讲 分数数列计算内容概述建立抵消的思想，特别是灵话运用裂项的方法求解一些分数数列的计算问题．典型问题兴趣篇1．计算：⋅⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯1091981871761651541431321211 2．计算：⋅⨯++⨯+⨯+⨯99972752532312 3．计算：⋅⨯++⨯+⨯+⨯100981861641421 4．计算：.90172156142130120112161+++++++ 5．计算：⋅+++++97001130170128141 6．计算：⋅⨯++⨯+-⨯++⨯+-⨯+1091099898878776766565 7．计算：⋅+-+-+-+-901972175615421330112091276523 8．计算：⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯10099982543243223212 9．计算：⋅++++++240239210209201912116521 10．计算：⋅+⨯-⨯⨯+⨯-⨯+⨯-)911()911()311()311()211()211(拓展篇1．计算：⋅⨯++⨯+⨯+⨯+⨯+⨯200820071651541431321211 2．计算：⋅⨯++⨯+⨯+⨯+⨯101983141131183853523 3．计算：⋅⨯-⨯+⨯-⨯+⨯-⨯1311241192097167512538314 4．计算：;90117721155611342111301920171215613211)1(++++++++ ⋅⨯-⨯-⨯+⨯++⨯+⨯-⨯-⨯+⨯+⨯-⨯-⨯+⨯42408241398040387839377611920108189716861475126410538426314)2( 5．计算：)10921()921(10)4321()321(4)321()21(3)21(121++++⨯++++++++⨯+++++⨯+++⨯+ 6．计算：⋅++++++83975939231137.计算：⋅⨯⨯++⋅⨯⨯+⨯⨯+⨯⨯10097999810798746541328.计算：⋅+++++++++++++++206421864216421421219.计算：⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯504948154314321321110.计算：⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯109811543643253214 11.计算：⋅-⨯⨯⋅-⨯-)9911()311()211(222 12.计算：⋅⨯+⨯⨯⨯+⨯⨯+⨯⨯+)2009200711()5311()4211()3111(超越篇1.计算：⋅⨯++⨯+++⨯++⨯+201920191918191832322121222222222.计算：.1201201181181414121222222222⋅-++-+++-++-+3.已知算式)19189()17168()542()321(+⨯+⨯⨯+⨯+ 的结果是一个整数，那么它的末两位数字是多少？4.计算：⋅⨯⨯++⨯⨯+⨯⨯+⨯⨯201918375437432532135.计算：!10099!43!32!21++++ （最后结果可以用阶乘表示）6.已知22226411019181,81++++==B A ，请比较A 和B 的大小。

第1讲计算综合（一）繁分数的运算，涉及分数与小数的定义新运算问题，综合性较强的计算问题．1．繁分数的运算必须注意多级分数的处理，如下所示:甚至可以简单地说：“先算短分数线的，后算长分数线的"．找到最长的分数线,将其上视为分子,其下视为分母．2．一般情况下进行分数的乘、除运算使用真分数或假分数，而不使用带分数．所以需将带分数化为假分数．3．某些时候将分数线视为除号，可使繁分数的运算更加直观．4．对于定义新运算,我们只需按题中的定义进行运算即可．5．本讲要求大家对分数运算有很好的掌握，可参阅《思维导引详解》五年级［第1讲循环小数与分数]．1．计算：71147 182621358 1333416⨯+⨯-÷【分析与解】原式=712372317 461224 1488128 131233+⨯=⨯=-2．计算：【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199．于是，我们想到改变运算顺序，如果分子与分母在5199后的两个数字的运算结果一致，那么作为被除数的这个繁分数的值为1；如果不一致，也不会增加我们的计算量．所以我们决定改变作为被除数的繁分数的运算顺序．而作为除数的繁分数，我们注意两个加数的分母相似,于是统一通分为1995×0.5．具体过程如下：原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+ =5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯- =199320.41()19950.5+÷⨯=0.410.5÷=1143．计算：1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734．计算:已知=181111+12+1x+4=，则x 等于多少? 【分析与解】方法一:1118x 68114x 112x 7111+11148x 62+214x 1x+4+====+++++++ 交叉相乘有88x+66=96x+56,x=1．25．方法二：有11131118821x 4+==+++，所以18222133x 4+==++；所以13x 42+=，那么x =1。

第一讲:分数的速算与巧算教学目标本讲知识点属于计算大板块内容，分为三个方面系统复习和学习小升初常考计算题型.1、 裂项：是计算中需要发现规律、利用公式的过程，裂项与通项归纳是密不可分的，本讲要求学生掌握裂项技巧及寻找通项进行解题的能力2、 换元：让学生能够掌握等量代换的概念，通过等量代换讲复杂算式变成简单算式。

3、 循环小数与分数拆分：掌握循环小数与分数的互化，循环小数之间简单的加、减运算，涉及循环小数与分数的主要利用运算定律进行简算的问题． 4、通项归纳法通项归纳法也要借助于代数，将算式化简，但换元法只是将“形同”的算式用字母代替并参与计算，使计算过程更加简便，而通项归纳法能将“形似”的复杂算式，用字母表示后化简为常见的一般形式． 知识点拨一、裂项综合 （一）、“裂差”型运算 (1)对于分母可以写作两个因数乘积的分数，即1a b⨯形式的，这里我们把较小的数写在前面，即a b <，那么有1111()a b b a a b=-⨯- (2)对于分母上为3个或4个连续自然数乘积形式的分数，即：1(1)(2)n n n ⨯+⨯+，1(1)(2)(3)n n n n ⨯+⨯+⨯+形式的，我们有：1111[](1)(2)2(1)(1)(2)n n n n n n n =-⨯+⨯+⨯+++1111[](1)(2)(3)3(1)(2)(1)(2)(3)n n n n n n n n n n =-⨯+⨯+⨯+⨯+⨯++⨯+⨯+裂差型裂项的三大关键特征：（1）分子全部相同，最简单形式为都是1的，复杂形式可为都是x(x 为任意自然数)的，但是只要将x 提取出来即可转化为分子都是1的运算。

（2）分母上均为几个自然数的乘积形式，并且满足相邻2个分母上的因数“首尾相接” （3）分母上几个因数间的差是一个定值。

（二）、“裂和”型运算：常见的裂和型运算主要有以下两种形式：（1）11a b a b a b a b a b b a+=+=+⨯⨯⨯ （2）2222a b a b a b a b a b a b b a +=+=+⨯⨯⨯ 裂和型运算与裂差型运算的对比：裂差型运算的核心环节是“两两抵消达到简化的目的”，裂和型运算的题目不仅有“两两抵消”型的，同时还有转化为“分数凑整”型的，以达到简化目的。

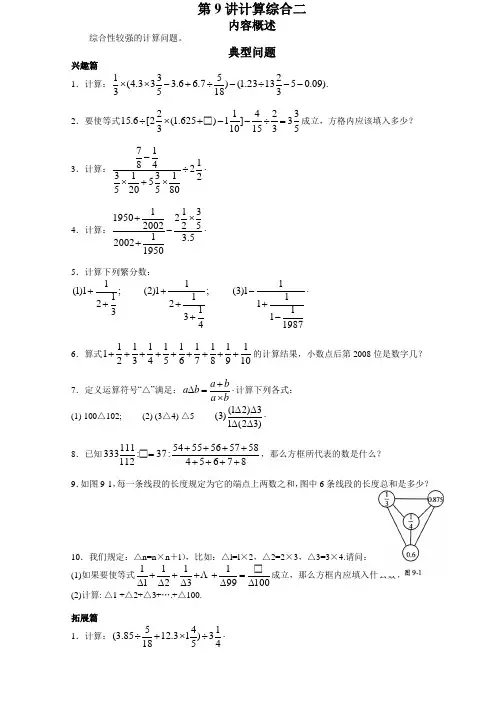
第9讲计算综合二内容概述综合性较强的计算问题。

典型问题兴趣篇1．计算：).09.05321323.1()1857.66.35333.4(31--÷-÷+-⨯⨯2．要使等式53332154]1011) □625.1(322[6.15=÷--+⨯÷成立，方格内应该填入多少？3．计算：⋅÷⨯+⨯-212805520541874．计算：⋅⨯-++5.353212195020022002119505．计算下列繁分数：;31211)1(++;431211)2(+++⋅-+-198711111)3(6．算式10191817161514131211+++++++++的计算结果，小数点后第2008位是数字几？7．定义运算符号“△”满足：⋅⨯+=∆ba ba b a 计算下列各式： (1) 100△102; (2) (3△4) △5⋅∆∆∆∆)32(13)21()3(8．已知876545857565554:37 □:112111333++++++++=，那么方框所代表的数是什么？9．如图9-1，每一条线段的长度规定为它的端点上两数之和，图中6条线段的长度总和是多少？10．我们规定：△n=n ×n ＋l ），比如：△l=l ×2，△2=2×3，△3=3×4.请问： (1)如果要使等式100□991312111∆=∆++∆+∆+∆ 成立，那么方框内应填入什么数？ (2)计算: △1 +△2+△3+….+△100.拓展篇1．计算：⋅÷⨯+÷413)5413.1218585.3(2．计算：⋅÷÷-+⨯8721654333113612141873．计算：).19956.15.019954.01993(22.550276951922.510939519+⨯⨯÷+--+4．我们规定：符号“O ”表示选择两数中较大数的运算，例如：3.5 O 2.9= 2.9 O3.5=3.5．符号“△”表示选择两数中较小数的运算，例如：3.5△2.9 =2.9△3.5=2.9．请计算：⋅∆+⨯∆)25.2104235()3.0 ○31()4.0 ○384155()3323625.0(5．计算：⋅+⨯+++-++⨯++)975753357579()531135975753357579135531()531135975753357579()975753357579135531(6．算式2004)1311211111019181716151413121(⨯+++++++++++计算结果的小数点后第2004位数字是多少？7．古埃及人计算圆形面积的方法是：将直径减去直径的91，然后再平方．由此看来，古埃及人认为圆周率л等于多少？（结果精确到小数点后两位数字）8．(1)将下面这个繁分数化为最简真分数： (2)若下面的等式成立，工应该等于多少？;21314151+++⋅=+++1184112111x 9．已知符号“*”表示一种运算，它的含义是：))(1(11*A b a ab b a +++=，已知413*2=，那么：(1)A 等于多少？ (2)计算⋅++++)100*99()6*5()4*3()2*1(10.已知19991100211001110001,200019991651431211++++=⨯++⨯+⨯+⨯=B A 比较A 和B 的大小，并计算出它们的差．11.根据图9-2中5个图形的变化规律，求第99个图形中所有圆圈（实心圆圈与空心圆圈）的个数．12.定义：)11()311()211()111(1nn na +⨯⨯+⨯+⨯+=(1)求出20010021,,,a a a a 的大小； (2)计算：⋅+++++10043211004321a a a a a超越篇1.⋅-++⨯----⨯2141121117331311227331393766)43322(17412．真分数27a化为小数后，如果小数点后连续2004个数字之和是8684，那么a 可能等于多少？3．定义运算“Ω”满足：304.)]1([2,1=Ω+-Ω⨯=Ω=Ωm a n a n a a a 已知②①。

第一讲比赛中的推理快*布，这定我找体仟 老算抄来的比我们 高出臥进了不少球叽 駅近矗思、IT 罗.工林三所守校之间锻 行了一轮足竦骼环翌- 刚比完・小豪盛皓大 案带回* .战fti rK4rSf BL・■社KVteI■yA**kHf7n#>n这一讲我们学习的主要内容是与比赛有关的逻辑推理问题. 这些问题有各种不同的形式：有分析对阵情况的，有计算各队积分的，有利用积分排名的，甚至还有讨论进球数、失球数的•不同类型的问题我们应该用不同的方法来处理.在逻辑推理中，特别有用的方法是画示意图或表格，这种方法相信大家并不陌生，用它来分析比赛问题，能够让我们对比赛的情况更为直观明了.例题1」 ..................... …一…. ...... . .... . ........ ..编号为1、2、3、4、5、6的同学进行围棋比赛，每2个人都要赛1盘.现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号一样，那么编号为6的同学赛了几盘？「分析」为了让问题更加直观，我们可以画出一个示意图，用6个点来表示这6个同学•如果两个同学之间比赛过，则把对应的两个点用实线连起来，如果没比赛过，则用虚线连起来.A、B、C、D、E五所小学，每所小学派出1支足球队，共5支足球队进行友谊比赛•不同学校间只比赛1场，比赛进行了若干天后，A校的队长发现另外4支球队赛过的场数依次为4、3、2、1.问：这时候A校的足球队已赛过的场数?例题2———— ... —I，每天同A、B、C、D、E、F六个国家的足球队进行单循环比赛（即每队都与其他队赛一场）时在3个场地各进行一场比赛，已知第一天B对D，第二天C对E,第三天D对F，第四天B对C•那么第五天与A队比赛的是那个队？A B C D E F1D B2E C3F D4C B5「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第二列从上到下依次表示A在5天中分别遇到的对手，第三列表示B在5天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什么特点？练习五个国家足球队A、B、C、D、E进行单循环比赛，每天进行两场比赛，一队轮空.已知第一天比赛的是A与D , C轮空；第二天A与B比赛，E轮空；第三天A与E比赛；第四天A与C比赛；B与C的比赛在B与D的比赛之前进行.那么C与E在哪一天比赛？例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？时在3个场地各进行一场比赛，已知第一天B 对D ，第二天C 对E ,第三天D 对F ，第四天「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与B 对C •那么第五天与A 队比赛的是那个队？A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？时在3个场地各进行一场比赛，已知第一天B 对D ，第二天C 对E ,第三天D 对F ，第四天「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与B 对C •那么第五天与A 队比赛的是那个队？A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？时在3个场地各进行一场比赛，已知第一天B 对D ，第二天C 对E ,第三天D 对F ，第四天「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与B 对C •那么第五天与A 队比赛的是那个队？A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？时在3个场地各进行一场比赛，已知第一天B 对D ，第二天C 对E ,第三天D 对F ，第四天「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与B 对C •那么第五天与A 队比赛的是那个队？A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场） ，每天同 时在3个场地各进行一场比赛，已知第一天 B 对D ，第二天C 对E ,第三天D 对F ，第四天C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？B 对C •那么第五天与A 队比赛的是那个队？A1 2 3 45 B C DEC BD E B CF「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场） ，每天同 时在3个场地各进行一场比赛，已知第一天 B 对D ，第二天C 对E ,第三天D 对F ，第四天C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？B 对C •那么第五天与A 队比赛的是那个队？A1 2 3 45 B C DEC BD E B CF「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场） ，每天同 时在3个场地各进行一场比赛，已知第一天 B 对D ，第二天C 对E ,第三天D 对F ，第四天C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？B 对C •那么第五天与A 队比赛的是那个队？A1 2 3 45 B C DEC BD E B CF「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第 二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一 天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场） ，每天同时在3个场地各进行一场比赛，已知第一天 B 对D ，第二天C 对E ,第三天D 对F ，第四天 C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？B 对C •那么第五天与A 队比赛的是那个队？A 1 2 3 45 B C DEC BD EBC F 「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示 B 在 5 天中遇到的对手，依 此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场） ，每天同时在3个场地各进行一场比赛，已知第一天 B 对D ，第二天C 对E ,第三天D 对F ，第四天 C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？B 对C •那么第五天与A 队比赛的是那个队？A 1 2 3 4 5BC DE C BD EBCF「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示 B 在 5 天中遇到的对手，依此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与例题 2C 比赛；B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛？A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛（即每队都与其他队赛一场） ，每天同 时在3个场地各进行一场比赛，已知第一天 B 对D ，第二天C 对E ,第三天D 对F ，第四天 「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示•如图，第二列从上到下依次表示 A 在 5 天中分别遇到的对手，第三列表示 B 在 5 天中遇到的对手，依 此类推•观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什 么特点？练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛，每天进行两场比赛，一队轮空.已知第一天比赛的是 A 与D , C 轮空；第二天 A 与B 比赛，E 轮空；第三天 A 与E 比赛；第四天 A 与 B 对C •那么第五天与A 队比赛的是那个队？ A1234 5 B C D E C BD E B C F。

第一讲比赛中的推理这一讲我们学习的主要内容是与比赛有关的逻辑推理问题．这些问题有各种不同的形式：有分析对阵情况的，有计算各队积分的，有利用积分排名的，甚至还有讨论进球数、失球数的．不同类型的问题我们应该用不同的方法来处理．在逻辑推理中，特别有用的方法是画示意图或表格，这种方法相信大家并不陌生，用它来分析比赛问题，能够让我们对比赛的情况更为直观明了．例题1编号为1、2、3、4、5、6的同学进行围棋比赛，每2个人都要赛1盘．现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号一样，那么编号为6的同学赛了几盘？「分析」为了让问题更加直观，我们可以画出一个示意图，用6个点来表示这6个同学．如果两个同学之间比赛过，则把对应的两个点用实线连起来，如果没比赛过，则用虚线连起来．练习1A、B、C、D、E五所小学，每所小学派出1支足球队，共5支足球队进行友谊比赛．不同学校间只比赛1场，比赛进行了若干天后，A校的队长发现另外4支球队赛过的场数依次为4、3、2、1．问：这时候A校的足球队已赛过的场数？例题2A、B、C、D、E、F六个国家的足球队进行单循环比赛（即每队都与其他队赛一场），每天同时在3个场地各进行一场比赛，已知第一天B对D，第二天C对E，第三天D对F，第四天B对C．那么第五天与A队比赛的是那个队？A B C D E F1 D B2 E C3 F D4 C B5「分析」题目的条件比较多，如何才能看清楚呢？我们可以用下面的表格来表示．如图，第二列从上到下依次表示A在5天中分别遇到的对手，第三列表示B在5天中遇到的对手，依此类推．观察表格，这个表格的每行有几个字母？每列有几个字母？每行、每列的字母有什么特点？练习2五个国家足球队A、B、C、D、E进行单循环比赛，每天进行两场比赛，一队轮空．已知第一天比赛的是A与D，C轮空；第二天A与B比赛，E轮空；第三天A与E比赛；第四天A与C比赛；B与C的比赛在B与D的比赛之前进行．那么C与E在哪一天比赛？例题3甲、乙、丙、丁四个同学进行象棋比赛，每两人都比赛一场，比赛规定胜者得2分，平局各得1分，输者得0分．请问：（1）一共有多少场比赛？（2）四个人最后得分的总和是多少？（3）如果最后结果甲得第一，乙、丙并列第二，丁最后一名，那么乙得了多少分？「分析」（1）每两人之间都比赛一场，总比赛场数就是从四个人中挑出两人的方法数；（2）比赛的胜负情况有很多种可能？那么总分也有很多种可能吗？大家考虑一下每场比赛，比赛双方的得分之和就知道了；（3）乙、丙最后的分数一样，由于总分是固定的，这个相同的分数既不能太大，也不能太小，那么会是多少呢？练习3有A、B、C、D四支足球队进行单循环比赛，每两队都比赛一场．比赛规定：胜一场得2分，平局各得1分，负一场得0分．全部比赛结束后，A、B两队的总分并列第一名，C队第二名，D队第三名，C队最多得多少分？例题44支足球队进行单循环比赛，即每两队之间都比赛一场．每场比赛胜者得3分，负者得0分，平局各得1分．比赛结果，各队的总得分恰好是4个连续的自然数．问：输给第一名的队的总分是多少？「分析」4支球队之间一共比赛了多少场？所有比赛的总分最多是多少，最少是多少？你能由此推断出各队的得分吗？练习4甲、乙、丙、丁4个队举行足球单循环赛．规定：每场比赛胜者得3分，负者得0分，平局各得1分．已知：（1）比赛结束后4个队的得分都是奇数；（2）甲队总分超过其他各队，名列第一；（3）乙队恰有两场平局，并且其中一场是与丙队平局．那么丁队得了多少分？例题5A、B、C、D四个足球队进行循环比赛，赛了若干场后，A、B、C三队的比赛情况如下：场数胜平负进球失球A 3 2 1 0 2 0B 2 1 1 0 4 3C 2 0 0 2 3 6D问：D赛了几场？D所参与的各场比赛的比分分别是什么？「分析」对于整个表格来说总进球数等于总失球数．总胜场应当等于总负场，平局数为偶数场．另外表格中的A很特别，两胜一平却只进两个球，这说明什么呢？例题6A 、B、C、D、E五位同学分别从不同的途径打听到五年级那位获得数学竞赛第一名的同学的情况：A打听到的：姓李，是女同学，13岁，东城区；B打听到的：姓张，是男同学，11岁，海淀区；C打听到的：姓陈，是女同学，13岁，东城区；D打听到的：姓黄，是男同学，11岁，西城区；E打听到的：姓张，是男同学，12岁，东城区．实际上该同学的情况在上面都出现过，而且这五位同学的消息都仅有一项正确，那么第一名的同学应该是哪个区的，今年多少岁呢？「分析」每个同学打听到的消息都只有一项正确，可谓相当的少！5420⨯=个判断，一共才5个正确的，其中关于姓氏、性别、年龄、地区的判断各有几项是正确的呢？课堂内外足球世界杯世界杯（World Cup，FIFA World Cup），世界足球锦标赛是世界上最高荣誉、最高规格、最高水平的足球比赛，与奥运会并称为全球体育两大顶级赛事，是影响力、转播覆盖率很高的全球体育盛事．世界杯是全球各个国家最梦寐以求的神圣荣耀，哪一支国家足球队能得到它，就是名正言顺的世界第一．整个世界都会为之疯狂沸腾，世界杯上发挥出色的球员都会被该国家奉为民族英雄永载史册，所以它亦代表了各个足球运动员的终极梦想．世界杯每四年举办一次，任何国际足联会员国（地区）都可以派出代表队报名参加这项赛事．世界杯的奖杯为大力神杯，它采用意大利人加扎尼亚的设计方案——两个大力士双手举起地球的设计方案．这个造形象征着世界第一运动的规模．该杯高36.8厘米，重6.175公斤，其中4.97公斤的主体由纯金铸造．底座由两层孔雀石构成，珍贵无比．1974年第十届世界杯赛，德国队作为冠军第一次领取了该杯．国际足联规定新杯为流动奖品，不论哪个队获得多少冠军，也不能永久占有此杯．在大力神杯的底座下面有能容纳镌刻17个冠军队名字的铭牌——可以持续使用到2038年．世界杯32支队伍，在小组赛阶段进行的是单循环比赛，16强阶段进行的是淘汰赛，积分规则是3分制．大力神杯作业：1.A、B、C、D四支球队进行足球比赛，每两队都要比赛一场．已知A、B、C三队的成绩分别是：A队二胜一负，B队二胜一平，C队一胜二负．那么D队的成绩是什么？2.6名同学进行象棋比赛，每两人都比赛一场，比赛规定胜者得2分，平局各得1分，输者得0分．请问：（1）一共有多少场比赛？（2）6个人最后得分的总和是多少？（3）得分最高的三名同学的分数之和最多是多少？3.六个人参加乒乓球比赛，每两人之间都要比赛一场，胜者得2分，负者得0分，没有平局．比赛结束时发现，有两人并列第二名，两人并列第五名．那么第一名和第四名各得了多少分？4.足球甲A联赛共有12个足球俱乐部参加，实行主客场双循环赛制，即任何两队分别在主场和客场各比赛一场，胜一场得3分，平一场各得1分，负一场得0分，在联赛结束后按积分的高低排出名次．那么，在积分榜上第一名与第二名的积分差距最多可达多少分？5.A、B、C、D四个足球队进行循环比赛，赛了若干场后，A、B、C三队的比赛情况如下：问：D赛了几场？D所参与的各场比赛的比分分别是什么？第一讲 比赛中的推理例1． 答案：3详解：5号已经赛过5盘，说明他和其他5个人都已经赛过了．而1号只赛了一盘，所以1号这一盘是同5号赛的，他同其他四个人都没有赛过，如图1所示．再看4号，他赛过4盘，且同1号没有赛过，所以4号赛过的同学是除1号以外的4个人．而2号只赛过两盘，所以2号只同5号、4号赛过，如图2所示．3号赛过3盘，而且他同1号、2号没有赛过，那么同3号赛过的就是4号、5号和6号，如图3所示．于是我们知道同6号赛过的有3号、4号和5号．他赛了3盘．例2． 答案：B 详解：如图4，列出表格后发现，每行、每列各有6个字母，而且同一行或列的6个字母互不相同，只需用这一原则把表格补充完整即可．首先可以确定（2，D ）处应填A ．这是因为第2行已经有E 和C ，第4列已经有D 、B 和F ，所以这一个格不能填这些字母，只能填A ．由于第二天A 与D 比赛，那么对应地（2，A ）处也应填D ．第二天余下的一场就是B 对F ，因而（2，B ）处应填F ，（2，F ）处应填B ．我们用类似的方法推理各行、列，最终把整个表格填出来，得到图5．于是，第五天与A 比赛的球队是B ．例3．答案：6；12；3 详解：（1）6；（2）12；（3）3．（1）详解：从四个人中选出两人，有246C 种方法．每两人之间比赛一场，那么一共就有6场比赛；（2）详解：不论胜负还是平局，每场比赛两人得分之和都是2分．一共6场比赛，所以四个人最号5号图135号图2号5号图3后得分的总和就是2612⨯=分；（3）详解：四个人得分之和是12分，甲得分最高，丁得分最低，而乙、丙得分相同．如果乙、丙得分是4分，则甲得分超过4分，这三人的得分之和已经超过12分，与题意矛盾．因此乙、丙得分最多是3分．如果乙、丙得分是2分，则丁最多得了1分，而甲至少得了122217---=分．但是连胜3场也只能得6分，不可能达到7分，因此乙、丙得分至少是3分．所以乙、丙得分就是3分．例4． 答案：4详解：如果比赛分出胜负，那么双方得分之和就是3分；如果平局，双方得分之和就是2分．4支球队之间要进行246C =场比赛，所以总分就要在12分和18分之间． 由题意，四支球队的得分是4个连续的自然数．而四个连续自然数的和可能是：01236+++=，123410+++=，234514+++=，345618+++=，…… 在12分和18分之间的只有14和18．如果是3分、4分、5分、6分，总分是18分，那么每场比赛都分出了胜负，但这是不可能的（大家自己想想这是为什么）．所以四个连续的分数为2分、3分、4分、5分．于是第一名得5分，只能是1胜2平；第二名得4分，只能是1胜1平1负；第三名得3分，可能是1胜2负，也可能是3平；第四名得2分，只能是2平1负．其中只有第三名的比赛结果有两种情况．综合考虑第一名、第二名、第四名的胜负情况：他们一共有2胜5平2负．由于总胜场数与总负场数相同，所以第三名只能是3平．容易画出四支队之间的比赛胜负关系，如图6所示．因此输给了第一名的只有第二名，他得了4分．例5．答案：3，A :D =1:0，B :D =4:3，C :D=3:5详解：首先A 两场胜场均为1比0胜出，平局为0比0，而且一定是A 以1比0胜C ，同样以1比0胜D ，0比0平B ，而B 胜的那场胜场以4:3胜出，C 的负场以3比5败北，所以不能是B 胜C ，那么一定是B 胜D ，D 胜C ，所以，D 参加了3场比赛．分别是A :D =1:0，B :D =4:3，C :D=3:5．例6．答案：海淀区，12岁详解：5420⨯=个判断，一共才5个正确的，可以推断出第一名同学的姓名、性别、年龄、城区，分别有1项、2项、1项、1项是正确的．先来看性别，有2项正确，那么第一名是女同学；再来看年龄，2个人说是13岁，2个人说是11岁，只有1个人说是12岁，由于只有1项消息正确，则第一名是12岁；再看城区，3人说东城区，1人说海淀区，1人说西城区，那么第一名在海淀区或者西城区；类似地，可以分析出第一名同学姓李，或姓陈，或姓黄．综合考虑第一名同学的姓名与城区，就很容易判断出唯一的答案：姓黄，是女同学，12岁，海淀区．第一名 1胜2平第二名 1胜1平1负第三名 3平第四名 2平1负图6练习答案：练习1答案：赛2场简答：连线，从胜得最多的和胜得最少的队伍入手分析．练习2答案：第五天简答：列表分析，用*表示轮空，可得下图．练习3答案：3简答：四人总得分是12分，其中C 的分数肯定小于1234÷=分，所以得分不多于3分．四人分别得4分、4分、3分、1分是容易构造出来的，所以C 队得分最多就是3分．练习4答案：3简答：先推断出各队得分分别为7分、5分、3分、1分，然后分析胜负情况即可．图1作业：6. 答案：一平二负．简答：B 队有一平，只可能平D ，所以对A 、C 是二胜．于是A 的两胜是赢了C 和D ．故C 的一胜是胜D ，于是D 的成绩是一平二负．7. 答案：（1）15；（2）30；（3）24．简答：（1）；（2）；（3）．8. 答案：10；4．简答：并列第五名的两人至少要各赢1场，所以第四名至少要赢2场，并列第二名至少要各赢3场，第一名至少要赢4场．，而一共要进行15场比赛，所以只能是第一名赢5场得10分，第四名赢2场得4分．9. 答案：46． 简答：第一名要积分多，最好是要22场全胜，得66分．剩下的11支球队还要比赛（场），每场比赛两队合起来至少得2分，于是剩下11队总共至少得220分．因此得分最多的队伍至少有分，当这11队全平时，第二名只能得20分，因此分差最大为46分．10. 答案：2；A 与D 是1:0、B 与D 是1:0．简答：由A 全胜，且进球数为3，可知A 与其他三队的比分都是1:0．B 赛了三场，且两胜一负，所以B 胜C ，而C 只比了两场，进球数为0，所以B 与C 的比分是3:0；而B 与D 只能是1:0．2201120÷= 2112110C ⨯= 12232414⨯++⨯+= 303224-⨯= 15230⨯=2615C =。