测度与概率(第2版)第二章部分作业
- 格式:pdf
- 大小:7.33 MB
- 文档页数:18
![概率论与数理统计第二章习题参考答案]](https://uimg.taocdn.com/02a7d8de6f1aff00bed51ebf.webp)

第二章习题与答案同学们根据自己作答的实际情况,并结合总正误率和单个题目正误统计以及答案解析来总结和分析习题!!!标红表示正确答案标蓝表示解析1、为掌握商品销售情况,对占该地区商品销售额60%的10家大型商场进行调查,这种调查方式属于( )。
A普查B抽样调查【解析:抽取一部分单位进行调查;习惯上将概率抽样(根据随机原则来抽取样本)称为抽样调查】C重点调查【解析:在调查对象中选择一部分重点单位进行调查的一种非全面调查】D统计报表2、人口普查规定标准时间是为了()。
A确定调查对象和调查单位B避免资料的重复和遗漏。
C使不同时间的资料具有可比性D便于登记资料【解析:规定时间只是为了统计该时间段内的人口数据,没有不同时间数据对比的需要】3、对一批灯泡的使用寿命进行调查,应该采用( )。
A普查 B重点调查 C典型调查D抽样调查4、分布数列反映( )。
A总体单位标志值在各组的分布状况B总体单位在各组的分布状况【解析:课本30页1.分布数列的概念一段最后一句】C总体单位标志值的差异情况D总体单位的差异情况5、与直方图比较,茎叶图( )。
A没有保留原始数据的信息B保留了原始数据的信息【解析:直方图展示了总体数据的主要分布特征,但它掩盖了各组内数据的具体差异。
为了弥补这一局限,对于未分组的原始数据则可以用茎叶图来观察其分布。
课本P38】C更适合描述分类数据D不能很好反映数据的分布特征6、在累计次数分布中,某组的向上累计次数表明( )。
A大于该组上限的次数是多少B大于该组下限的次数是多少C小于该组上限的次数是多少【解析:向上累计是由变量值小的组向变量值大的组累计各组的次数或频率,各组的累计次数表明小于该组上限的次数或百分数共有多少。
课本P33】D小于该组下限的次数是多少7、对某连续变量编制组距数列,第一组上限为500,第二组组中值是750,则第一组组中值为 ( )。
A. 200B. 250C. 500D. 300【解析:组中值=下限+组距/2=上限+组距/2】8、下列图形中最适合描述一组定量数据分布的是( )。

概率论第二章习题答案习题1:离散型随机变量及其分布律设随机变量X表示掷一枚公正的六面骰子得到的点数。
求X的分布律。
解答:随机变量X的可能取值为1, 2, 3, 4, 5, 6。
由于骰子是公正的,每个面出现的概率都是1/6。
因此,X的分布律为:\[ P(X=k) = \frac{1}{6}, \quad k = 1, 2, 3, 4, 5, 6 \]习题2:连续型随机变量及其概率密度函数设随机变量Y表示从标准正态分布中抽取的数值。
求Y的概率密度函数。
解答:标准正态分布的概率密度函数为高斯函数,其形式为:\[ f(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}}, \quad -\infty < y < \infty \]习题3:随机变量的期望值已知随机变量X的分布律为:\[ P(X=k) = p_k, \quad k = 1, 2, ..., n \]求X的期望值E(X)。
解答:随机变量X的期望值定义为:\[ E(X) = \sum_{k=1}^{n} k \cdot p_k \]习题4:随机变量的方差继续使用习题3中的随机变量X,求X的方差Var(X)。
解答:随机变量X的方差定义为期望值的平方与每个值乘以其概率之和的差:\[ Var(X) = E(X^2) - (E(X))^2 \]其中,\( E(X^2) = \sum_{k=1}^{n} k^2 \cdot p_k \)习题5:二项分布设随机变量X表示n次独立伯努利试验中成功的次数,每次试验成功的概率为p。
求X的分布律和期望值。
解答:X服从参数为n和p的二项分布。
其分布律为:\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0, 1, ..., n \]X的期望值为:\[ E(X) = np \]结束语:以上是概率论第二章的一些典型习题及其解答。



概率论第二版习题答案概率论是一门研究随机事件发生规律的数学学科,它在现代科学和工程领域中具有广泛的应用。
而对于学习概率论的学生来说,习题是检验理解和掌握程度的重要途径。
本文将为读者提供《概率论第二版》习题的答案,帮助读者更好地理解和应用概率论知识。
第一章:概率论的基本概念1. 什么是随机试验?随机试验是指在相同的条件下,可以重复进行,但每次结果不确定的试验。
例如抛硬币、掷骰子等。
2. 什么是样本空间?样本空间是随机试验所有可能结果的集合。
例如抛硬币的样本空间为{正面,反面}。
3. 什么是事件?事件是样本空间的子集,表示随机试验的某种结果。
例如抛硬币出现正面朝上可以表示为事件A。
第二章:概率的公理化定义1. 什么是概率?概率是用来描述随机事件发生可能性大小的数值,通常用P(A)表示事件A发生的概率。
2. 概率的公理化定义有哪些?概率的公理化定义包括非负性公理、规范性公理和可列可加性公理。
非负性公理要求概率值必须大于等于0;规范性公理要求样本空间的概率为1;可列可加性公理要求对于不相容事件的概率,可以通过将它们的概率相加来计算。
3. 什么是条件概率?条件概率是指在已知事件B发生的条件下,事件A发生的概率,用P(A|B)表示。
计算条件概率时,需要使用条件概率公式:P(A|B) = P(A∩B) / P(B)。
第三章:随机变量及其分布1. 什么是随机变量?随机变量是随机试验结果的数值表示,它可以是离散的(如掷骰子的点数)或连续的(如测量体重的结果)。
2. 什么是概率质量函数(PMF)?概率质量函数是离散随机变量的概率分布函数,用于描述每个可能取值的概率。
例如,掷骰子的点数为随机变量X,其PMF为P(X=k) = 1/6,其中k为1到6的整数。
3. 什么是概率密度函数(PDF)?概率密度函数是连续随机变量的概率分布函数,用于描述随机变量取值的概率密度。
例如,测量体重的结果为随机变量X,其PDF为f(x) = 1/(σ√(2π)) * e^(-(x-μ)²/(2σ²)),其中μ为均值,σ为标准差。

解答题:离散型特例规律:90年代强调实际应用!21cn 更强调混合计算! 1,1989(4)已知X,Y 变量联合分布如下:①X 与Y 边缘分布?②X+Y 的分布-------------------------- 难度级别低! 解:边缘分布件上表!2,1990(4)甲乙两人独立射击两次,甲命中率为0.2,乙命中率为0.5,X,Y 分别表示甲、乙两人的命中次数,试求X,Y 联合概率分布。
难度级别低! 注:实质上,依题意得X ~B(2,0.2),Y ~B(2,0.5),均为二项分布。
可得边缘分布,再依据X,Y 边缘分布可得到联合分布!20028.02.0C =0.64; 11128.02.0C =0.32; 02228.02.0C =0.04; 3,1994(4)假设随机变量X1,X2,X3,X4相互独立同分布P(Xi=0)=0.6,P(Xi=1)=0.4,(i-1,2,3,4),求行列式4321X X X X 的概率分布。
难度级别中!注:考虑X1,X2,X3,X4都只有0,1两种取值,行列式的值仅有几种,分别计算。
记ξ=4321X X X X ,X=Xi 中的0的个数,则ξ=0:P(X=4)=44C 0.640.40=0.64, P(X=3)=34C 0.630.41,P(X=2,ξ=0)=4*0.620.42, P(X=0)=04C 0.600.44,ξ=1: P(X=2,ξ=1)=1*0.620.42, P(X=2,ξ=1)=2*0.610.43,ξ=-1: P(X=2,ξ=-1)=1*0.620.42, P(X=2,ξ=-1)=2*0.610.43, 其分布可由具体概率之和相加即可。
答案略4,1999数学4—已知随机变量ξ,η概率分布如下,而且P(ξ·η=0)=1 η~ -1 0 1 ξ~ 0 11/4 1/2 1/4 1/2 1/2 难度级别中! 求①ξ与η的联合分布;②ξ、η是否独立?③上述随机变量函数的分布∵P(ξ·η=0)=1,∴P(ξ·η≠0)=0,∴上表成立。

(2)正态分布N (µ, σ 2 ;(3)对数正态分布LN (µ, σ 2 .解:(1)因 X 服从区间 (a, b上的均匀分布,则0.5 = P{ X ≤ x0.5 } = P{a < X ≤ x0.5 } = 故中位数x0.5 = a + 0.5(b − a = (2)因 X 服从正态分布N (µ, σ 2 ,x0.5 − a ,b−a a+b ; 2 x −µ⎛x −µ⎞ =0,则 0.5 = P{ X ≤ x0.5 } = F ( x0.5 = Φ⎜ 0.5 ⎟,即0.5 σ ⎝ σ ⎠故中位数 x0.5 = µ;(3)因 X 服从对数正态分布LN (µ, σ 2 ,有 ln X 服从正态分布 N (µ, σ 2 ,ln x0.5 − µ ⎛ ln x0.5 − µ ⎞ =0,则0.5 = P{ X ≤ x0.5 } = P{ln X ≤ ln x0.5 } = F (ln x0.5 = Φ⎜⎟,即σ σ ⎝⎠故中位数 x0.5 = e µ. 4.设 X ~ Ga (α , λ ,对 k = 1, 2, 3,求µ k = E (X k 与ν k = E [X − E (X ] k.解:因Ga (α , λ 的密度函数为⎧λα α −1 − λ x ⎪ x e , x ≥ 0, p X ( x = ⎨ Γ(α ⎪ x < 0. ⎩0, 由正则性知∫ +∞ +∞ +∞ Γ(α λα α −1 − λ x x e dx = 1 ,可得∫ x α −1 e −λ x dx = α ,0 Γ(α λ 0 故µ1 = ∫ 0 x⋅ λα α −1 − λ x λα+ ∞ α −λ x λα Γ(α + 1 α x e dx = x e dx = ⋅ = ;λ Γ(α Γ(α ∫0 Γ(α λα +1 λα α −1 −λ x λα + ∞ α +1 − λ x λα Γ(α + 2 α (α + 1 e = ⋅ = x e dx = x dx ;Γ(α Γ(α ∫0 Γ(α λα + 2 λ2 λα α −1 − λ x λα + ∞ α + 2 −λ x λα Γ(α + 3 α (α + 1(α + 2 e = ⋅ = x e dx = x dx ;Γ(α Γ(α ∫0 Γ(α λα + 3 λ3 µ2 = ∫ µ3 = ∫ +∞ 0 x2 ⋅ +∞ 0 x3 ⋅ ν 1 = E [X − E (X ] = 0;α (α + 1 α 2 α − 2 = 2 ;λ2 λ λ α (α + 1(α + 2 α (α + 1 α α 3 2α .3 2 − ⋅ + = ν 3 =E[ X − E ( X ]3 = µ 3 − 3µ 2 µ1 + 2µ13 = λ λ3 λ2 λ3 λ3 5.设X ~ Exp(λ,对 k = 1, 2, 3, 4,求µ k = E (X k 与ν k = E [X − E (X ] k ,进一步求此分布的变异系数、偏ν 2 = E[ X − E ( X ] 2 = µ 2 − µ12 = 度系数和峰度系数.解:因 X 的密度函数为⎧λ e − λ x , x ≥ 0, p X ( x = ⎨ x < 0. ⎩0, 41且 k 为正整数时,∫ 故µ1 = ∫ +∞ 0 +∞ 0 x k −1 e − λ x dx = +∞ Γ(k λ k = (k − 1! λk 1 ,; x ⋅ λ e −λ x dx = λ ∫ 0 x e −λ x dx = λ ⋅ λ 2 = 2! 1 λ = = = µ 2 = ∫ x 2 ⋅ λ e −λ x dx = λ ∫ x 2 e −λ x dx = λ ⋅ 0 0 +∞ +∞ 2 λ λ 3 λ2 6 ;;;µ 3 = ∫ x 3 ⋅ λ e − λ x dx = λ ∫ x 3 e − λ x dx = λ ⋅ 0 0 +∞ +∞ 3! 4 λ3 24 µ 4 = ∫ x 4 ⋅ λ e −λ x dx = λ ∫ x 4 e −λ x dx = λ ⋅ 0 0 +∞ +∞ 4! λ 1 5 λ4 ν 1 = E [X − E (X ] = 0;ν 2 = E[ X − E ( X ] 2 = µ 2 −µ12 = 2 λ 2 − 1 λ 2 = λ2 6 3 ;ν 3 = E[ X − E ( X ]3 = µ 3 − 3µ 2 µ1 + 2µ13 = λ −3 2 λ 2 ⋅ 1 λ 4 +2 −4 1 λ 6 3 = ⋅ 1 2 λ3 ;ν 4 = E[ X − E ( X ] 4 = µ 4 − 4 µ 3 µ1 + 6µ 2µ12 − 3µ14 = 变异系数C v ( X = 24 λ λ 3 λ +6 2 λ 2 ⋅ 1 λ 2 −3 1 λ 4 = 9 λ3 ; Var( X E( X =2;= ν2 =1; µ1 偏度系数β 1 = ν3 (ν 2 3 / 2 峰度系数β 2 = ν4 −3=9−3=6.(ν 2 2 6.设随机变量 X 服从正态分布 N (10, 9,试求 x0.1 和 x0.9.x − 10 ⎛ x − 10 ⎞解:因F ( x 0.1 = Φ⎜ 0.1 = 1.2816 ,故 x0.1 = 6.1552;⎟ = 0.1 ,得− 0.1 3 3 ⎝⎠ x − 10 ⎛ x − 10 ⎞又因F ( x 0.9 = Φ⎜ 0.9 = 1.2816 ,故 x0.9 = 13.8448.⎟ = 0.9 ,得0.9 3 3 ⎝⎠ x − 10 x 0.1 − 10 = 1.28 ,故 x0.1 = 6.16; 0.9 = 1.28 ,故 x0.9 = 13.84)3 3 7.设随机变量 X 服从双参数韦布尔分布,其分布函数为(或查表可得− m ⎧⎪⎪⎛ x⎞⎫⎟⎜ F ( x = 1 − exp ⎨− ⎜⎟⎬, η ⎭⎪⎩⎝⎠⎪ x>0,其中η > 0, m > 0.试写出该分布的 p 分位数 xp 的表达式,且求出当m = 1.5, η = 1000 时的 x0.1 , x0.5 , x0.8 的值.⎧⎪⎛ xp 解:因F ( x p = 1 − exp⎨− ⎜⎜η ⎪⎩⎝故x p = η[−ln(1 − p ] m ; 1 ⎞⎟⎟⎠ m ⎫⎪⎬= p,⎪⎭ 42当m = 1.5, η = 1000 时, x 0.1 = 1000(− ln 0.9 1 1.5 1 = 223.0755 ; x 0.5 = 1000(− ln 0.5 1 1.5 = 783.2198 ;x 0.8 = 1000(− ln 0.2 1.5 = 1373.3550 . 8.自由度为 2 的χ 2 分布的密度函数为p ( x = 1 −2 e , 2 x x>0,试求出其分布函数及分位数x0.1 , x0.5 , x0.8 .解:设 X 服从自由度为 2 的χ 2 分布,当 x < 0 时,F (x = P{X ≤ x} = P (∅ = 0,当x ≥ 0 时,F ( x = P{ X ≤ x} = ∫ 故 X 的分布函数为 x ⎧ − ⎪1 − e2 , x ≥ 0, F ( x = ⎨⎪ x < 0. ⎩0, x − − 1 −2 e du = (− e 2 = 1 − e 2 ; 2 0 u u x x 0 因 F (x p = 1 − e − xp 2 = p ,有xp = −2 ln (1 − p,故x0.1 = −2 ln 0.9 = 0.2107;x0.5 = −2 ln 0.5 = 1.3863;x0.8 = −2 ln 0.2 = 3.2189. 9.设随机变量 X 的分布密度函数 p(x 关于 c 点是对称的,且 E (X 存在,试证(1)这个对称点 c 既是均值又是中位数,即 E (X = x0..5 = c;(2)如果 c = 0,则xp = −x1 − p .证:设 f (x = p (x + c,因 p (x 关于 c 点对称,有 f (x 为偶函数,(1)E ( X = ∫ xp( xdx = ∫ ( x − c p ( xdx + ∫ cp( xdx = ∫ up (u + cdu + c = ∫ uf (u du + c −∞ −∞ −∞ −∞ −∞ +∞ +∞ +∞ +∞ +∞ = 0 + c = c;因 f (x 为偶函数,有∫ 则F (c = ∫ c −∞ 0 −∞ 0 f ( xdx = 1 +∞ f ( xdx = 0.5 ,2 ∫− ∞ 0 p( x dx = ∫ p (u + cdu = ∫ −∞ −∞ f (u du = 0.5 ,可得 x0..5 = c;故 E (X = x0..5 = c;(2)如果 c = 0,有 p (x 为偶函数,则 F (x p = ∫ xp −∞ p ( xdx = ∫ −xp +∞ p(−u ⋅ (−du = ∫ +∞ −xp p(u du = 1 − ∫ −xp −∞ p(u du = 1 − F (− x p = p ,可得 F (−xp = 1 − p,故−xp = x1 − p ,即xp = −x1 − p . 10.试证随机变量 X 的偏度系数与峰度系数对位移和改变比例尺是不变的,即对任意的实数a, b (b ≠ 0, Y = a + b X 与 X 有相同的偏度系数与峰度系数.证:因 Y = a + bX,有 E (Y = E (a + bX = a + bE (X ,可得Y − E (Y = a + b X − a − bE (X = b[X − E (X ],则ν 2 (Y = E [Y − E (Y ]2 = E{b2[X − E (X ]2} = b2 E [X − E (X ]2 = b2ν 2 (X ,ν 3 (Y = E [Y − E (Y ]3 = E{b3[X − E (X ]3} = b3 E [X − E (X ]3 = b3ν 3 (X ,ν 4 (Y = E [Y − E (Y ]4 =E{b4[X − E (X ]4} = b4 E [X − E (X ]4 = b4ν 4 (X ,故偏度系数β 1 (Y = ν 3 (Y [ν 2 (Y ] 3/ 2 = b 3ν 3 ( X [b ν 2 ( X ] 2 3/ 2 = b 3ν 3 ( X b [ν 2 ( X ] 3 3/ 2 = ν 3 (X [ν 2 ( X ]3 / 2 = β1 ( X ; 43峰度系数β 2 (Y = b 4ν 4 ( X b 4ν 4 ( X ν 4 (Y ν (X−3 = − 3 = −3= 4 − 3 = β2(X .2 2 2 4 2 [ν 2 (Y ] [b ν 2 ( X ] b [ν 2 ( X ] [ν 2 ( X ] 2 11.设某项维修时间 T(单位:分)服从对数正态分布LN (µ, σ 2 .(1)求 p 分位数 tp;(2)若µ =4.127,求该分布的中位数;(3)若µ = 4.127,σ = 1.0364,求完成 95%维修任务的时间.解:(1)因 T 服从对数正态分布LN (µ, σ 2 ,有 ln T 服从正态分布 N (µ, σ 2 ,ln t p − µ ⎛ ln t p − µ ⎞⎟则p = P{T ≤ t p } = P{ln T ≤ ln t p } = Φ⎜ = up ,ln tp = µ + σ ⋅ up,⎜σ ⎟,即σ ⎝⎠故tp = e µ +σ ⋅u p ;(2)中位数 t0.5 = e µ +σ ⋅u0.5 = e 4.1271+0 = 61.9979 ;(3)t0.95 = e µ +σ ⋅u0.95 = e4.1271+1.0364×1.6449 = 340.9972 . 12.某种绝缘材料的使用寿命 T(单位:小时)服从对数正态分布LN (µ, σ 2 .若已知分位数 t0.2 = 5000 小时,t0.8 = 65000 小时,求µ和σ.解:因 T 服从对数正态分布LN (µ, σ 2 ,有 ln T 服从正态分布N (µ, σ 2 ,由第 11 题可知t p = e µ +σ ⋅u p ,则t0.2 = e µ +σ ⋅u0.2 = e µ−0.8416σ = 5000 ,t0.8 = e µ +σ ⋅u0.8 = e µ +0.8416σ = 65000 ,可得µ − 0.8416σ = ln 5000 = 8.5172,µ + 0.8416σ = ln 65000 = 11.0821,故µ = 9.7997,σ =1.5239. 13.某厂决定按过去生产状况对月生产额最高的 5%的工人发放高产奖.已知过去每人每月生产额 X(单位:千克)服从正态分布 N (4000, 602 ,试问高产奖发放标准应把生产额定为多少?解:因 X 服从正态分布 N (4000, 602 ,x − 4000 ⎛ x − 4000 ⎞ = u0.95 = 1.6449 ,则0.95 = P{ X ≤ x0.95 } = F ( x0.95 = Φ⎜0.95 ⎟,即 0.95 60 60 ⎝⎠故高产奖发放标准应把生产额定为 x0.95 = 4000 + 60 ×1.6449 = 498.6940 千克. 44。

概率论与数理统计第二章习题答案[])()()()()式,有利用(显然)()(则若))(()()(从而)()()()(的可加性,有:互不相容,因此由概率与而)(则解:AB P A P AB A P B A P A AB AB A P B A P A B B P A P B A P B A P B P B A B P A P B A B B A B A A B -=-=-⊂-=-⊄-=--+=-=--=⊂**.132)(1)()()(1)()()()|()4(2.05.01.0)()()|()3(25.04.01.0|)2(8.0)1(.2=--=--=========-+=B P AB P A P B P B A P B P B A P B A P A P AB P A B P B P AB P B A P AB P B P A P B A P )()()()()()()(解:7.0)(1)|()4(4.0)(1)|()3(72.0)()()()()()()()()2(3.0)()|(1.3=-==-==⋅-+=-+===A P B A P B P A B P B P A P B P A P AB P B P A P B A P A P B A P )解:(时成立。
第一个等号在)()()()()(”成立时“当)()(”成立时“)(当)()()()()()()(解:B A B P A P B A P A P AB P A AB A B B A P A P B A A AB P B A P B P A P AB P B P A P B A P ⊂+≤≤≤∴⊂=⊂≤∴⊂==≥+∴-+= 0.4.32)()()(,91)().()(),()()()(,),()(.5======A P B P A P B A P B P A P B P A P B P A P B A B A B A B A P B A P 可推出结合独立性以及又由题意可得:一些简单计算可得式及再由对立事件的概率公都是独立的,从而有:与事件以及与是独立的可知,事件根据事件解:根据题意可得:..21)(.21)()(3)(3)()(2,)()(2)()()()(2).(43)(,41)(.169)(3)(3)()()()()()()()(1.62222由于要画图,反例略是不正确题中要求证明是注解:有反例可以说明从而有于是由于)(舍去或者所以)解:(<≤-≤-⊂-=-+====-=+---++=A P A P A P A P A P A P C B A B A A P A P AB P B P A P B A P A P A P A P A P ABC P BC P AC P AB P C P B P A P C B A P)()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()解:(C P B A P C P B A P C P B P A P C B A P C B A P C P AB P C P B P A P ABC P C AB P B A P C P AB P B P A P C P B P A P B P A P C P C P B P A P C P B P C P A P ABC P BC P AC P BC AC P C B A P ⋅-=⋅=⋅⋅==-⋅=⋅⋅===-+=-+=-+=-+==][][3][2][][][1.7832.03.06.04.04.04.06.0)()()()()(3.06.0200100)/(4.06.0150100)/(6.020*******.8=⨯⨯+⨯+=++===⨯==⨯======B A C P A B P A P C B A P D P B A C P A B P A P D C B A )(“击中目标”米处射击击中”“相距米处射击击中”“相距米处射击击中”“相距解:设2112632112|31812|6)2(185|8)1(.9222222222222111111111=++++=========== )()()()()()()(”“点数和大于“点数和为奇数”)()()()()(”“点数和为“点数和为偶数”解:B P B A P B A P A P B A P A B P B A A P B P A P B A P A B P B A.535443321)()()(-1)(-15360160126047514131413141513151413151413151.10=⨯⨯-====+-=⨯⨯+⨯-⨯-⨯-++=+---++=======C P B P A P C B A P C B A P ABC P BC P AC P AB P C P B P A P C B A P C P B P A P C B A )(另解:)()()()()()()()()(,)(,)(“丙破译密码”“乙破译密码”“甲破译密码”解:61|1011|.11110=====)()()()()()(解:B P AB P B A P C A P AB P A B P1025515510530520|.12C C C C C A B P A P AB P B A ⋅⋅=⋅===)()()(球各半”“第二次取出的黄、白球”“第一次取出的全是黄解:cb a ac b a c b b a b A A A P A A P A P A A A P A A A 2||32.13213121321321++⋅+++⋅+=⋅====)()()()(次取白球”“第次取黄球”“第“第一次取黄球”解:161013616101474113161013469677036937067||21610147469667067|12.1421121121212121211212121=-=-==⋅+⋅=+=+==⋅=====)()()()()()()()()()()()()()()(“被退货”次抽到次品”“第“第一次抽到次品”解:A A P D P A A P A P A A P A P A A P A A P A A A A P A A P A P A A P D A A493297%4.1153)]|(1[)()()|()|()3(73%4.153%1)()()|()|()2(%4.152%253%1||1525330001800%2|%1|.15111111122112121=-⋅-===⨯===⨯+⨯=+⋅=======B A P A P B P B A P A B P A P B P B A P A B P B P B A P B P B A P A P B P B P B A P B A P A )()()()()()()(,)()(,)(“次品”解:17.00545.005.09.01)()()|(1)|(1)|()2(0545.00095.0045.095.001.005.09.0)()]|(1[05.09.0)()|()()|()()1(05.0)(99.0)|(9.0|.16=⨯-=-=-==+=⨯+⨯=-+⨯=+======B P A P A B P B A P B A P A P A B P A P A B P A P A B P B P A P A B P A B P B A )(“某方法检验为次品”“次品”,解:5000380500018020035000180025000180180%630003000535000200%10200020005250001.17=+===∴=⨯=⨯=⨯=⨯)()()()()(,女生选修会计人数女生人数:,男生选修会计人数)男生人数:(解:C P B P A P0006.07519.0%3%981||27519.0%97%1%3%98%3%98||%97%1%3%98]|1[%3%98||1%99|%98|%3.18=⨯-===⨯+⨯⨯==⨯+⨯=-+⨯=+======)()()()()()()()()()()()()()()()()()()(,)(,)(“患有肺癌”光查肺癌”,“用解:A P B P B A P A B P A P B P B A P A B P B P B A B P B A P B P B A P A P B A P B A P B P B X A6896863.001.07.0)02.01((7.0)02.01()()|()()|()()|()|(01.0)|(,02.0)|(3.0)(,7.01010.19=⨯+⨯-⨯-=+=========A P A B P A P A B P A P A B P B A P A B P A B P A P A P B B A A )(”“收到”,“收到”,“发送”,“发送解:968.0)|()|()|()4(032.0)|()|(1)|()3(242.062.03.05.0)()()|()|()2(726.062.05.09.0)()()|()|(62.02.01.03.05.05.09.0)()|()()|()()|()()1(1.0)|(5.0)|(9.0)|(2.0)(3.0)(5.0)(2000.202121213222111332211321321321=+==--==⨯===⨯===⨯+⨯+⨯=++===========B A P B A P B A A P B A P B A P B A P B P A P A B P B A P B P A P A B P B A P A P A B P A P A B P A P A B P B P A B P A B P A B P A P A P A P B A A A 台以上”“卖出“滞销”,“一般”,“畅销”,解:75.04.013.0432.0211.04100|]||[|]||[|]||[3(4.05.0511)(3.05.05143)|(2.05.05121)|(1.01015.05141|05.00||25.0]14321410[515115141510|||1.215522115432111552211=⨯+⨯+⨯+⨯+⨯=++⋅+⋅===⨯==⨯==⨯===⨯=====++++=⨯++⨯+⋅=+++==)()()()()()()(再次出现字面”))()()()()()()()()()()()()()(“字面”解:A B P A B C P A B P A B C P A B P A B C P C P C A B P A B P A B P A B P A P B P B A P A B P B P B A P B P B A P B P B A P A P A458.014.0141.06.036.02.0)()|()()|()()|()(14.07.05.04.0)()(41.07.05.06.07.05.04.03.05.04.0\)()()()()()()()()()()()()()(36.07.05.06.03.05.06.03.05.04.0.2233221132133213213213213213213213213212321321321323213213213213211321321=⨯+⨯+⨯=++==⨯⨯===⨯⨯+⨯⨯+⨯⨯=++=++===⨯⨯+⨯⨯+⨯⨯=++=++=========A P A B P A P A B P A P A B P B P C C C P A P C P C P C P C P C P C P C P C P C P C C C P C C C P C C C P C C C C C C C C C P A P C P C P C P C P C P C P C P C P C P C C C P C C C P C C C P C C C C C C C C C P A P C C C B A A A )()()()()()()()()()()()()()(“丙射击”“乙射击”,“甲射击”,“飞机被击落”“三人击中”“两人击中”,“一人击中”,解:设独立的。

测度与概率第二版教学设计一、教材简介本教学设计针对《测度与概率》第二版(作者:周勇,出版社:高等教育出版社)这一教材进行。
该教材主要介绍测度论的相关概念及其在概率论中的应用。
二、教学目标1.理解和掌握测度论的基本概念,如测度、可测集、完全可测、Lebesgue测度等;2.掌握测度论在概率论中的应用,如随机变量、期望、条件概率、大数定律、中心极限定理等;3.能够运用测度论和概率论知识解决实际问题。
三、教学内容及安排第一章测度空间1.1 测度空间的概念1.2 测度空间的性质1.3 测度空间的例子教学方法:讲授 + 讨论第二章可测函数和可积函数2.1 可测函数2.2 相关定理2.3 可积函数第三章 Lebesgue测度3.1 Lebesgue测度的概念3.2 Lebesgue测度的性质3.3 Lebesgue可积函数教学方法:讲授 + 练习第四章随机变量4.1 随机变量的概念和分类4.2 随机变量函数的分布4.3 分布函数教学方法:讲授 + 讨论第五章期望5.1 期望的定义及性质5.2 切比雪夫不等式和Markov不等式5.3 Fatou引理和Lebesgue收敛定理教学方法:讲授 + 练习第六章条件概率6.1 条件概率的概念与性质6.2 独立性与无后效性6.3 贝叶斯公式第七章大数定律与中心极限定理7.1 大数定律7.2 中心极限定理7.3 证明教学方法:讲授 + 讨论四、教学评价方法1.平时出勤情况2.课堂参与情况3.期中、期末测验4.作业及其准确度5.自主学习情况五、教学资源1.化学与材料科学学院教学楼2.教学用书:《测度与概率》第二版3.录音笔、投影仪4.网络资源:自建教学网络平台,可供学生在线学习和练习六、教学实施本教学设计应由专业教师授课,推荐采用课堂讲授和小组讨论相结合的方式,以便更好地理解和掌握教材内容。
学生在听课的同时应积极参与讨论和练习,并按时完成作业和测验。
学生可在自主学习期间针对课堂中的难点和疑点进行互相探讨和学习。
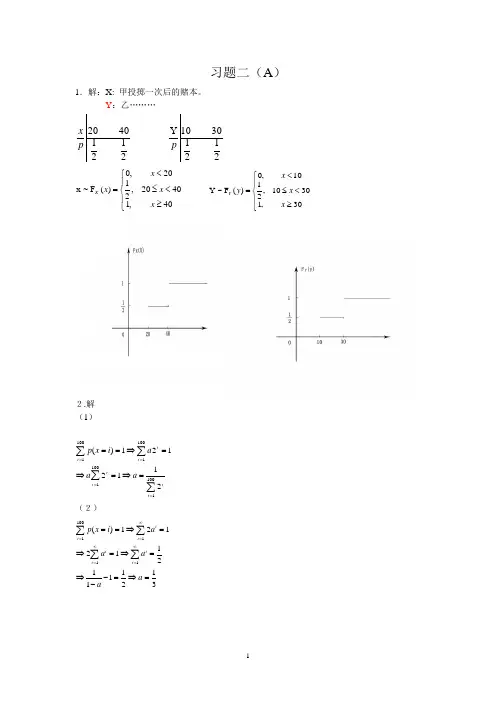
习题二(A )1.解:X: 甲投掷一次后的赌本。
Y :乙……… 21214020p x 21213010Y p ⎪⎩⎪⎨⎧≥<≤<=40,14020,2120,0)(F ~x x x x x X ⎪⎩⎪⎨⎧≥<≤<=30,13010,2110,0)(F ~Y x x x y Y2.解(1)∑∑∑∑=====⇒=⇒=⇒==10011001100110012112121)(i ii i i i ia a a i x p(2)31211112112121)(1110011=⇒=--⇒=⇒=⇒=⇒==∑∑∑∑∞=∞==∞=a a a a ai x p i i i i i i i3.解 21 51 101512 0 25X --p 4.解(1)X:有放回情形下的抽取次数。
P (取到正品)=107C C 11017=P (取到次品)=103 107)103( 107)103( 107 103,107i 3 2 1X 1-i 2 ⋅p(2)Y:无放回情形下。
778192103 87 92103 97 103 1074 3 2 1 Y ⋅⋅⋅⋅⋅⋅p5.解54511)5(1)3(1)3P(=-=-=-=-≤-=->X p X p X 542)P(X 0)P(X )2()33()3X P(==+=+-==<<-=<X p X p 107)5()2()3()1()21P(2)1()21X P(=-=+==-<+>=-<++>+=>+X p X p X p X p X X p6.解(1)根据分布函数的性质11)1()(2lim 1lim 1=⇒=⇒=++→→A Ax F x F x x (2))5.0()8.0()8.05.0(F F X P -=≤<225.08.0-==0.39 7.解:依据分布满足的性质进行判断: (1)+∞<<∞-x单调性:+∞<<<⇒<x x F x F x x 0).()(2121在时不满足。
概率论第二版习题答案概率论是一门研究随机现象的数学分支,它在统计学、金融学、工程学等多个领域都有广泛的应用。
第二版的概率论教材通常会在第一版的基础上进行修订和补充,以反映最新的研究成果和教学方法。
以下是一些概率论习题的答案示例,这些答案仅供参考,具体习题的答案可能会根据教材的不同而有所变化。
第一章:概率空间1. 习题1:描述一个概率空间的基本元素。
- 答案:一个概率空间由三个基本元素组成:样本空间(Ω),事件集合(F),以及概率测度(P)。
样本空间包含了所有可能的结果,事件集合是样本空间的子集,概率测度为每个事件分配一个介于0和1之间的实数,表示事件发生的可能性。
2. 习题2:证明如果事件A和事件B互斥,那么P(A∪B) = P(A) +P(B)。
- 答案:由于A和B互斥,即A∩B = ∅,根据概率测度的性质,P(A∪B) = P(A) + P(B) - P(A∩B)。
由于A和B互斥,P(A∩B) = 0,因此P(A∪B) = P(A) + P(B)。
第二章:随机变量及其分布1. 习题1:定义离散型随机变量和连续型随机变量。
- 答案:离散型随机变量是其取值可以列举的随机变量,其概率分布可以用概率质量函数来描述。
连续型随机变量是其取值无法一一列举的随机变量,其概率分布可以用概率密度函数来描述。
2. 习题2:如果X是一个随机变量,求E(X)和Var(X)。
- 答案:期望E(X)是随机变量X的平均值,定义为E(X) = ∑x *P(X = x)(对于离散型随机变量)或E(X) = ∫x * f(x) d x(对于连续型随机变量)。
方差Var(X)是随机变量X的离散程度的度量,定义为Var(X) = E[(X - E(X))^2]。
第三章:多维随机变量及其分布1. 习题1:描述联合分布函数和边缘分布函数的关系。
- 答案:联合分布函数给出了两个或多个随机变量同时取特定值的概率,而边缘分布函数是通过对联合分布函数进行积分或求和得到的,它给出了单个随机变量的分布。
第二章练习题(答案)一、单项选择题1.已知连续型随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤+<=ππx x b kx x x F ,10,0,0)( 则常数k 和b 分别为 ( A )(A )0,1==b k π (B )π1,0b k = (C )0,21==b k π (D )π21,0==b k . 2.下列函数哪个是某随机变量的分布函数 ( A )A. f (x )={xa e −x 22a,x ≥01, x <0(a >0); B. f (x )={12cosx, 0< x <π0, 其他C. f (x )={cosx, −π2< x <π20, 其他D. f (x )={sinx, −π2< x <π20, 其他3.若函数()f x 是某随机变量X 的概率密度函数,则一定成立的是 ( C ) A. ()f x 的定义域是[0,1] B. ()f x 的值域为[0,1] C. ()f x 非负 D. ()f x 在(,)-∞+∞内连续4. 设)1,1(~N X ,密度函数为)(x f ,则有( C ) A.{}{}00>=≤X P X P B. )()(x f x f -= C. {}{}11>=≤X P X P D. )(1)(x F x F --=5. 设随机变量()16,~μN X ,()25,~μN Y ,记()41-<=μX P p ,()52+>=μY P p ,则正确的是 ( A ).(A )对任意μ,均有21p p = (B )对任意μ,均有21p p < (C )对任意μ,均有21p p > (D )只对μ的个别值有21p p = 6. 设随机变量2~(10,)X N ,则随着的增加{10}P X ( C )A.递增B.递减C.不变D.不能确定7.设F 1(x )与F 2(x )分别为随机变量X 1、X 2的分布函数,为使F (x )=aF 1(x )-bF 2(x )是某一随机变量的分布函数,在下列给定的多组数值中应取 ( A )A . a =53, b =52-; B . a =32, b =32;C . 21-=a , 23=b ; D . 21=a , 23-=b .8.设X 1与X 2是任意两个相互独立的连续型随机变量,它们的概率密度函数分别为f 1(x )和f 2(x ),分布函数分别为F 1(x )和F 2(x ),则 ( D ) (A) f 1(x )+f 2(x ) 必为某个随机变量的概率密度; (B )f 1(x )•f 2(x ) 必为某个随机变量的概率密度; (C )F 1(x )+F 2(x ) 必为某个随机变量的分布函数; (D) F 1(x ) •F 2(x ) 必为某个随机变量的分布函数。