高中数学人教A版必修2《空间直角坐标系》讲义

高中数学《空间直角坐标系》教案11新人教A版必修2（优秀范文五篇）第一篇：高中数学《空间直角坐标系》教案11 新人教A版必修24.3.1 空间直角坐标系教案教学要求：使学生能通过用类比的数学思想方法得出空间直角坐标系的定义、建立方法、以及空间的点的坐标确定方法。

教学重点：在空间直角坐标系中，确定点的坐标教学难点：通过建立适当的直角坐标系，确定空间点的坐标教学过程：一.复习准备：1.提问：平面直角坐标系的建立方法，点的坐标的确定过程、表示方法？2.讨论：一个点在平面怎么表示？在空间呢？二、讲授新课：1.空间直角坐标系：如图，OBCD-D,A,B,C,是单位正方体.以A为原点，分别以OD,OA，OB的方向为正方向，建立三条数轴x轴.y轴.z轴。

这时建立了一个空间直角坐标系Oxyz.1）叫做坐标原点2）x 轴，y轴，z轴叫做坐标轴.3）过每两个坐标轴的平面叫做坐标面。

2.右手表示法：令右手大拇指、食指和中指相互垂直时，可能形成的位置。

大拇指指向为x轴正方向，食指指向为y轴正向，中指指向则为z轴正向，这样也可以决定三轴间的相位置。

3.有序实数组1）空间一点M的坐标可以用有序实数组(x,y,z)来表示，有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标，记作M(x,y,z)（x叫做点M的横坐标，y叫做点M的纵坐标，z叫做点M的竖坐标思考：原点O的坐标是什么？讨论:空间直角坐标系内点的坐标的确定过程。

例题1：在长方体OBCD-D,A,B,C,中，OA=3,oC=4,OD,=2.写出D，C,A，B,四点坐标.（建立空间坐标系→写出原点坐标→各点坐标）讨论：若以C点为原点，以射线BC、CD、CC1 方向分别为ox、oy、oz轴的正半轴，建立空间直角坐标系，那么，各顶点的坐标又是怎样的呢？（得出结论：不同的坐标系的建立方法，所得的同一点的坐标也不同。

）4.练习：V-ABCD为正四棱锥，O为底面中心，若AB=2，VO=3，试建立空间直角坐标系，并确定各顶点的坐标。

人教版高一数学必修二《空间直角坐标系》说课稿一、教材分析1. 教材内容概述本节课的教材内容是《空间直角坐标系》。

在高中数学必修二的学习中，这一章节是非常重要的基础内容，它为学生提供了进一步理解和掌握三维空间中直角坐标系的基本概念和性质的机会。

2. 教材知识结构教材围绕着以下几个主要知识点展开教学：•点的坐标与向量•空间直角坐标系•直线的方程与旋转•平面的方程与选点•空间图形的平移和旋转通过这些知识点的学习，学生能够理解并掌握在三维空间中描述点、直线和平面的方法，同时能够运用所学知识解决相关问题。

3. 学生特点分析本节课所面对的学生对象为高一学生。

他们正处于数学知识的初步学习阶段，基本熟悉了平面直角坐标系的概念和性质。

但对于空间直角坐标系和相关知识仍存在一定的陌生感。

因此，需要通过本课程的教学，引导学生逐步理解和掌握空间直角坐标系的概念和运用方法。

二、教学目标1. 知识与能力目标•理解空间直角坐标系的概念和性质•掌握点、直线和平面在空间直角坐标系中的表示方法•能够解决与空间直角坐标系相关的简单几何问题2. 过程与方法目标•培养学生观察、分析和解决问题的能力•培养学生合作学习和团队合作的能力•提高学生对数学概念的形象化理解和运用能力3. 情感态度和价值观目标•培养学生对数学的兴趣和热爱•培养学生思维的逻辑性和严谨性•培养学生独立思考和解决问题的能力三、教学重点和难点1. 教学重点•理解空间直角坐标系的概念和性质•能够正确表示点、直线和平面在空间直角坐标系中的位置关系•运用所学知识解决与空间直角坐标系相关的简单几何问题2. 教学难点•理解空间直角坐标系三维空间的特点和表示方法•掌握直线和平面的方程表示方法•能够准确应用空间直角坐标系解决几何问题四、教学过程设计1. 导入与概念解释为了让学生了解本节课的重要性，我们可以通过以下问题引导学生思考：•什么是空间直角坐标系？•空间直角坐标系有什么特点和作用？通过提问和学生的回答，引起学生对空间直角坐标系的兴趣，并激发他们运用此概念解决问题的欲望。

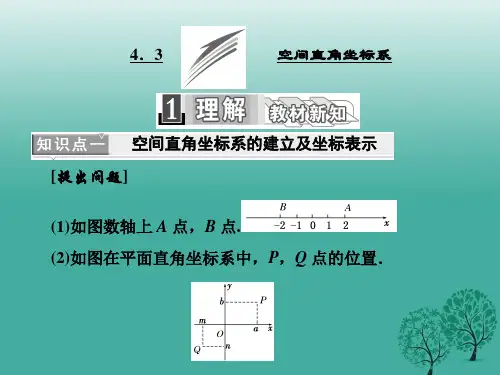
4.3 空间直角坐标系[核心必知]1．预习教材，问题导入根据以下提纲，预习教材P134～P137，回答下列问题．(1)平面直角坐标系由两条互相垂直的数轴组成，设想空间直角坐标系由几条数轴组成？其相对位置关系如何？提示：三条交于一点且两两互相垂直的数轴．(2)建立了空间直角坐标系以后，空间中任意一点M对应的三个有序实数如何找到呢？提示：如图所示，设点M是空间的一个定点，过点M分别作垂直于x轴、y轴和z轴的平面，依次交x轴，y轴和z轴于点P、Q和R.设点P、Q和R在x轴、y轴和z轴上的坐标分别是x，y和z，那么点M就对应唯一确定的有序实数组(x，y，z)．(3)设点P1(x1，y1，z1)，P2(x2，y2，z2)在xOy平面上的射影分别为M、N.①M、N的坐标是什么？点M、N之间的距离如何？②若直线P1P2是xOy平面的一条斜线，点P1，P2间的距离如何？提示：①M(x1，y1,0)，N(x2，y2,0)；|MN|＝x1－x22＋y1－y22.②如图，在Rt△P1HP2中，|P1H|＝|MN|＝x1－x22＋y1－y22，根据勾股定理，得|P1P2|＝|P1H|2＋|HP2|2＝x1－x22＋y1－y22＋z1－z22.2．归纳总结，核心必记(1)空间直角坐标系及相关概念①空间直角坐标系：从空间某一定点引三条两两垂直，且有相同单位长度的数轴：x轴、y轴、z轴，这样就建立了空间直角坐标系Oxyz.②相关概念：点O叫做坐标原点，x轴、y轴、z轴叫做坐标轴．通过每两个坐标轴的平面叫做坐标平面，分别称为xOy平面、yOz平面、zOx平面．(2)右手直角坐标系在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系．(3)空间一点的坐标空间一点M的坐标可以用有序实数组(x，y，z)来表示，有序实数组(x，y，z)叫做点M 在此空间直角坐标系中的坐标，记作M(x，y，z)．其中x叫点M的横坐标，y叫点M的纵坐标，z叫点M的竖坐标．(4)空间两点间的距离公式①点P(x，y，z)到坐标原点O(0,0,0)的距离，|OP|＝x2＋y2＋z2.②任意两点P1(x1，y1，z1)，P2(x2，y2，z2)间的距离，|P1P2|＝x1－x22＋y1－y22＋z1－z22.[问题思考](1)给定的空间直角坐标系下，空间任意一点是否与有序实数组(x，y，z)之间存在唯一的对应关系？提示：是．给定空间直角坐标系下，空间给定一点其坐标是唯一的有序实数组(x，y，z)；反之，给定一个有序实数组(x，y，z)，空间也有唯一的点与之对应．(2)空间两点间的距离公式对在坐标平面内的点适用吗？提示：适用．空间两点间的距离公式适用于空间任意两点，对同在某一坐标平面内的两点也适用．[课前反思]通过以上预习，必须掌握的几个知识点．(1)怎样建立空间直角坐标系？如何确定空间一点的坐标？；(2)空间两点间的距离公式是什么？怎样用？.(1)如图数轴上A点、B点．(2)如图在平面直角坐标系中，P、Q点的位置．(3)下图是一个房间的示意图，我们如何表示板凳和气球的位置？[思考1] 上述(1)中如何确定A、B两点的位置？提示：利用A、B两点的坐标2和－2.[思考2] 上述(2)中如何确定P、Q两点的位置？提示：利用P、Q两点的坐标(a，b)和(m，n)．[思考3] 对于上述(3)中，空间中如何表示板凳和气球的位置？提示：可借助于平面坐标系的思想建立空间直角坐标系，如图示．讲一讲1．建立适当的坐标系，写出底边长为2，高为3的正三棱柱的各顶点的坐标．(链接教材P135—例1)[尝试解答] 以BC的中点为原点，BC所在的直线为y轴，以射线OA所在的直线为x 轴，建立空间直角坐标系，如图．由题意知，AO＝32×2＝3，从而可知各顶点的坐标分别为A(3，0,0)，B(0,1,0)，C(0，－1,0)，A1(3，0,3)，B1(0,1,3)，C1(0，－1,3)．空间中点P坐标的确定方法(1)由P点分别作垂直于x轴、y轴、z轴的平面，依次交x轴、y轴、z轴于点P x、P y、P z，这三个点在x轴、y轴、z轴上的坐标分别为x、y、z，那么点P的坐标就是(x，y，z)．(2)若题所给图形中存在垂直于坐标轴的平面，或点P在坐标轴或坐标平面上，则要充分利用这一性质解题．练一练1．如图所示，V­ABCD是正棱锥，O为底面中心，E，F分别为BC，CD的中点．已知|AB|＝2，|VO|＝3，建立如图所示空间直角坐标系，试分别写出各个顶点的坐标．解：∵底面是边长为2的正方形，∴|CE|＝|CF|＝1.∵O点是坐标原点，∴C(1,1,0)，同样的方法可以确定B(1，－1,0)，A(－1，－1,0)，D(－1,1,0)．∵V在z轴上，∴V(0,0,3)．讲一讲2．在空间直角坐标系中，点P(－2,1,4)．(1)求点P关于x轴的对称点的坐标；(2)求点P关于xOy平面的对称点的坐标；(3)求点P关于点M(2，－1，－4)的对称点的坐标．[尝试解答] (1)由于点P关于x轴对称后，它在x轴的分量不变，在y轴、z轴的分量变为原来的相反数，所以对称点为P1(－2，－1，－4)．(2)由于点P关于xOy平面对称后，它在x轴、y轴的分量不变，在z轴的分量变为原来的相反数，所以对称点为P2(－2,1，－4)．(3)设对称点为P3(x，y，z)，则点M为线段PP3的中点，由中点坐标公式，可得x＝2×2－(－2)＝6，y＝2×(－1)－1＝－3，z＝2×(－4)－4＝－12，所以P3(6，－3，－12)．(1)求空间对称点的规律方法空间的对称问题可类比平面直角坐标系中点的对称问题，要掌握对称点的变化规律，才能准确求解．对称点的问题常常采用“关于谁对称，谁保持不变，其余坐标相反”这个结论．(2)空间直角坐标系中，任一点P(x，y，z)的几种特殊对称点的坐标如下：①关于原点对称的点的坐标是P1(－x，－y，－z)；②关于x轴(横轴)对称的点的坐标是P2(x，－y，－z)；③关于y轴(纵轴)对称的点的坐标是P3(－x，y，－z)；④关于z轴(竖轴)对称的点的坐标是P4(－x，－y，z)；⑤关于xOy坐标平面对称的点的坐标是P5(x，y，－z)；⑥关于yOz坐标平面对称的点的坐标是P6(－x，y，z)；⑦关于xOz坐标平面对称的点的坐标是P7(x，－y，z)．练一练2.保持本解中的点P不变，(1)求点P关于y轴的对称点的坐标；(2)求点P关于yOz平面的对称点的坐标；(3)求点P关于点N(－5,4,3)的对称点的坐标．解：(1)由于点P关于y轴对称后，它在y轴的分量不变，在x轴、z轴的分量变为原来的相反数，故对称点的坐标为P1(2,1，－4)．(2)由于点P关于yOz平面对称后，它在y轴、z轴的分量不变，在x轴的分量变为原来的相反数，故对称点的坐标为P2(2,1,4)．(3)设所求对称点为P3(x，y，z)，则点N为线段PP3的中点，由中点坐标公式，可得－5＝－2＋x2，4＝1＋y2，3＝4＋z2，即x＝2×(－5)－(－2)＝－8，y＝2×4－1＝7，z＝2×3－4＝2，故P3(－8,7,2).(1)已知数轴上A点的坐标2，B点的坐标－2.(2)已知平面直角坐标系中P(a，b)，Q(m，n)．[思考1] 如何求数轴上两点间的距离？提示：|AB|＝|x1－x2|＝|x2－x1|.[思考2] 如何求平面直角坐标系中P、Q两点间距离？提示：d＝|PQ|＝a－m2＋b－n2.[思考3] 若在空间中已知P1(x1，y1，z1)，P2(x2，y2，z2)，如何求|P1P2|?提示：与平面直角坐标系中两点的距离求法类似．讲一讲3．已知点A(－4，－1，－9)，B(－10,1，－6)，C(－2，－4，－3)，试判断△ABC的形状．[尝试解答]|AB|＝－4＋2＋－1－2＋－9＋2＝49＝7，|BC|＝－10＋2＋＋2＋－6＋2＝98＝72，|AC|＝－4＋2＋－1＋2＋－9＋2＝49＝7，则|AB|＝|AC|，且|AB|2＋|AC|2＝|BC|2，所以△ABC为等腰直角三角形．求空间两点间的距离时，一般使用空间两点间的距离公式，应用公式的关键在于建立适当的坐标系，确定两点的坐标．确定点的坐标的方法视具体题目而定，一般说来，要转化到平面中求解，有时也利用几何图形的特征，结合平面直角坐标系的知识确定．练一练3．已知两点P(1,0,1)与Q(4,3，－1)．(1)求P、Q之间的距离；(2)求z轴上的一点M，使|MP|＝|MQ|.解：(1)|PQ|＝－2＋－2＋＋2＝22.(2)设M(0,0，z)，由|MP|＝|MQ|，得12＋02＋(z－1)2＝42＋32＋(z＋1)2，∴z＝－6.∴M(0,0，－6)．——————————[课堂归纳·感悟提升]—————————————1．本节课的重点是了解右手直角坐标系及有关概念，掌握空间直角坐标系中任意一点的坐标的含义，会建立空间直角坐标系，并能求出点的坐标，理解空间两点间距离公式的推导过程和方法，掌握空间两点间的距离公式及其简单应用．难点是空间直角坐标系的建立及求相关点的坐标、空间两点间距离公式及其简单运用．2．本节课要重点掌握的规律方法(1)空间直角坐标系中点的坐标的确定方法，见讲1.(2)求空间中对称点坐标的规律，见讲2.(3)空间两点间距离公式的应用，见讲3.3．本节课的易错点是空间中点的坐标的确定，如讲1.课下能力提升(二十六) [学业水平达标练]题组1 空间直角坐标系的建立及坐标表示 1．点(2,0,3)在空间直角坐标系中的( ) A ．y 轴上 B ．xOy 平面上 C ．xOz 平面上 D ．第一象限内解析：选C 点(2,0,3)的纵坐标为0，所以该点在xOz 平面上．2．在空间直角坐标系中，点P (4,3，－1)关于xOz 平面的对称点的坐标是( ) A ．(4，－3，－1) B ．(4,3，－1) C ．(3，－4,1) D ．(－4，－3,1)解析：选A 过点P 向xOz 平面作垂线，垂足为N ，则N 就是点P 与它关于xOz 平面的对称点P ′连线的中点，又N (4,0，－1)，所以对称点为P ′(4，－3，－1)．3．已知A (3,2，－4)，B (5，－2,2)，则线段AB 中点的坐标为________． 解析：设中点坐标为(x 0，y 0，z 0)，则x 0＝3＋52＝4，y 0＝2－22＝0，z 0＝－4＋22＝－1，∴中点坐标为(4,0，－1)． 答案：(4,0，－1)4．点P (1,2，－1)在xOz 平面内的射影为B (x ，y ，z )，则x ＋y ＋z ＝________. 解析：点P (1,2，－1)在xOz 平面内的射影为B (1,0，－1)，∴x ＝1，y ＝0，z ＝－1，∴x ＋y ＋z ＝1＋0－1＝0.答案：05．如图，在长方体ABCD ­A 1B 1C 1D 1中，E ，F 分别是棱BC ，CC 1上的点，|CF |＝|AB |＝2|CE |，|AB |∶|AD |∶|AA 1|＝1∶2∶4.试建立适当的坐标系，写出E ，F 点的坐标．解：以A 为坐标原点，射线AB ，AD ，AA 1的方向分别为正方向建立空间直角坐标系，如图所示．分别设|AB |＝1，|AD |＝2，|AA 1|＝4，则|CF |＝|AB |＝1，|CE |＝12|AB |＝12，所以|BE |＝|BC |－|CE |＝2－12＝32.所以点E 的坐标为⎝ ⎛⎭⎪⎫1，32，0，点F 的坐标为(1,2,1)．6．如图，在空间直角坐标系中，BC ＝2，原点O 是BC 的中点，点D 在平面yOz 内，且∠BDC ＝90°，∠DCB ＝30°，求点D 的坐标．解：过点D 作DE ⊥BC ，垂足为E .在Rt △BDC 中，∠BDC ＝90°，∠DCB ＝30°，BC ＝2，得|BD |＝1，|CD |＝3，∴|DE |＝|CD |sin 30°＝32，|OE |＝|OB |－|BE |＝|OB |－|BD |cos 60°＝1－12＝12， ∴点D 的坐标为⎝ ⎛⎭⎪⎫0，－12，32.题组2 空间两点间的距离7．(2016·长春高一检测)已知点A (x,1,2)和点B (2,3,4)，且|AB |＝26，则实数x 的值是( )A ．－3或4B ．6或2C ．3或－4D ．6或－2 解析：选D 由题意得x －2＋－2＋－2＝26，解得x ＝－2或x ＝6.8．在空间直角坐标系中，正方体ABCD ­A 1B 1C 1D 1的顶点A 的坐标为(3，－1,2)，其中心M 的坐标为(0,1,2)，则该正方体的棱长为________．解析：由A (3，－1,2)，中心M (0,1,2)， 所以C 1(－3,3,2)．正方体体对角线长为|AC 1|＝[3－－2＋－1－2＋－2＝213，所以正方体的棱长为2133＝2393.答案：2393[能力提升综合练]1．在长方体ABCD ­A 1B 1C 1D 1中，若D (0,0,0)、A (4,0,0)、B (4,2,0)、A 1(4,0,3)，则对角线AC 1的长为( )A ．9 B.29 C ．5 D ．2 6解析：选B 由已知求得C 1(0,2,3)，∴|AC 1|＝29.2．点A (1,2，－1)，点C 与点A 关于面xOy 对称，点B 与点A 关于x 轴对称，则|BC |的值为( )A ．2 5B ．4C ．2 2D ．27解析：选B 点A 关于面xOy 对称的点C 的坐标是(1,2,1)，点A 关于x 轴对称的点B 的坐标是(1，－2,1)，故|BC |＝－2＋＋2＋－2＝4.3．△ABC 在空间直角坐标系中的位置及坐标如图所示，则BC 边上的中线的长是( )A. 2 B ．2 C. 3 D ．3解析：选C BC 的中点坐标为M (1,1,0)，又A (0,0,1)， ∴|AM |＝12＋12＋－2＝ 3.4．在空间直角坐标系中，一定点P 到三个坐标轴的距离都是1，则该点到原点的距离是( )A.62B. 3C.32 D.63解析：选A 设P (x ，y ，z )，由题意可知⎩⎪⎨⎪⎧x 2＋y 2＝1，y 2＋z 2＝1，x 2＋z 2＝1，∴x 2＋y 2＋z 2＝32，∴x 2＋y 2＋z 2＝62.5．在空间直角坐标系中，点(－1，b,2)关于y 轴的对称点是(a ，－1，c －2)，则点P (a ，b ，c )到坐标原点O 的距离|PO |＝________.解析：点(－1，b,2)关于y 轴的对称点是(1，b ，－2)，所以点(a ，－1，c －2)与点(1，b ，－2)重合，所以a ＝1，b ＝－1，c ＝0，所以|PO |＝12＋－2＋02＝ 2.答案： 26．在棱长为1的正方体ABCD ­A 1B 1C 1D 1中，F 是BD 的中点，G 在棱CD 上，且|CG |＝14|CD |，E 为C 1G 的中点，则EF 的长为________．解析：建立如图所示的空间直角坐标系，D 为坐标原点，由题意，得F ⎝ ⎛⎭⎪⎫12，12，0，C 1(0,1,1)，C (0,1,0)，G ⎝⎛⎭⎪⎫0，34，0，则E ⎝ ⎛⎭⎪⎫0，78，12.所以|EF |＝⎝ ⎛⎭⎪⎫0－122＋⎝ ⎛⎭⎪⎫78－122＋⎝ ⎛⎭⎪⎫12－02＝418. 答案：4187．如图所示，在长方体ABCD ­A 1B 1C 1D 1中，|AB |＝|AD |＝3，|AA 1|＝2，点M 在A 1C 1上，|MC 1|＝2|A 1M |，N 在D 1C 上且为D 1C 中点，求M 、N 两点间的距离．解：如图所示，分别以AB 、AD 、AA 1所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系．由题意可知C (3,3,0)，D (0,3,0)， ∵|DD 1|＝|CC 1|＝|AA 1|＝2，∴C 1(3,3,2)，D 1(0,3,2)，A 1(0,0,2)． ∵N 为CD 1的中点，∴N ⎝ ⎛⎭⎪⎫32，3，1. M 是A 1C 1的三分之一分点且靠近A 1点，∴M (1,1,2)． 由两点间距离公式， 得|MN |＝⎝ ⎛⎭⎪⎫32－12＋－2＋－2＝212. 8．如图所示，直三棱柱ABC ­A 1B 1C 1中，|C 1C |＝|CB |＝|CA |＝2，AC ⊥CB ，D ，E 分别是棱AB ，B 1C 1的中点，F 是AC 的中点，求DE ，EF 的长度．解：以点C 为坐标原点，CA 、CB 、CC 1所在直线为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系． ∵|C 1C |＝|CB |＝|CA |＝2，∴C (0,0,0)，A (2,0,0)，B (0,2,0)，C 1(0,0,2)，B 1(0,2,2)， 由中点坐标公式可得，D (1,1,0)，E (0，1,2)，F (1,0,0)， ∴|DE |＝－2＋－2＋－2＝5，|EF |＝－2＋－2＋－2＝ 6.11。