第8讲 模数转换器ADC

adc模数转换器原理
ADC模数转换器是一种将模拟信号转换为数字信号的电路。

它将连续的模拟信号转换为离散的数字信号，通过采样和量化的过程来实现。

首先，采样是指在连续的模拟信号上，以一定的时间间隔取样，得到一系列离散的采样值。

这样做的目的是将连续的模拟信号转换为离散的信号。

然后，量化是指对采样得到的离散信号进行编码，将其转换为数字形式。

在量化的过程中，将信号分为若干个区间，每个区间都用一个数字表示。

这个数字通常是二进制形式，所以转换器输出的是一系列二进制代码。

采样和量化过程之后，转换器会产生一系列二进制代码。

这些二进制代码通常被存储在数字寄存器或者RAM中，以便处理
和传输。

在ADC的实现中有多种不同的技术，例如逐次逼近型ADC、闪存型ADC和积分型ADC等。

每种技术都有其优势和适用
场景，选择合适的ADC技术取决于应用需求和性能要求。

总结来说，ADC模数转换器通过采样和量化的过程，将连续
的模拟信号转换为离散的数字信号，使得模拟信号能够被数字系统处理和传输。

模数转换器（ADC）原理及分类解析在仪器仪表系统中，常常需要将检测到的连续变化的模拟量如：温度、压力、流量、速度、光强等转变成离散的数字量，才能输入到计算机中进行处理。

这些模拟量经过传感器转变成电信号（一般为电压信号），经过放大器放大后，就需要经过一定的处理变成数字量。

实现模拟量到数字量转变的设备通常称为模数转换器（ADC），简称A/D。

通常情况下，A/D转换一般要经过取样、保持、量化及编码4个过程。

取样是将随时间连续变化的模拟量转换为时间离散的模拟量。

取样过程示意图如图11.8.1所示。

图（a）为取样电路结构，其中，传输门受取样信号S(t)控制，在S(t)的脉宽τ期间，传输门导通，输出信号vO(t)为输入信号v1,而在（Ts-τ）期间，传输门关闭，输出信号vO(t)=0。

电路中各信号波形如图（b）所示。

图11.8.1 取样电路结构(a)图11.8.1 取样电路中的信号波形(b)通过分析可以看到，取样信号S(t)的频率愈高，所取得信号经低通滤波器后愈能真实地复现输入信号。

但带来的问题是数据量增大，为保证有合适的取样频率，它必须满足取样定理。

取样定理：设取样信号S(t)的频率为fs，输入模拟信号v1(t)的最高频率分量的频率为fimax，则fs与fimax必须满足下面的关系fs ≥2fimax，工程上一般取fs>(3～5)fimax。

将取样电路每次取得的模拟信号转换为数字信号都需要一定时间，为了给后续的量化编码过程提供一个稳定值，每次取得的模拟信号必须通过保持电路保持一段时间。

取样与保持过程往往是通过取样-保持电路同时完成的。

取样-保持电路的原理图及输出波形如图11.8.2所示。

图11.8.2 取样-保持电路原理图图11.8.2 取样-保持电路波形图电路由输入放大器A1、输出放大器A2、保持电容CH和开关驱动电路组成。

电路中要求A1具有很高的输入阻抗，以减少对输入信号源的影响。

为使保持阶段CH上所存电荷不易泄放，A2也应具有较高输入阻抗，A2还应具有低的输出阻抗，这样可以提高电路的带负载能力。

adc模数转换器原理模数转换器（ADC）是一种非常重要的电子电路，它可以将模拟信号转换为数字信号，以便电路中的微处理器可以对其进行处理。

随着科技的发展，ADC的性能也在不断提高，可以提供更多功能和性能，以满足不断变化的需求。

本文将重点介绍ADC的工作原理，以及其在现有技术中的应用。

ADC的基本原理是将模拟信号（如模拟电压或电流）转换成数字信号，然后通过串行数据总线将其传送到微处理器其他部分。

ADC的类型主要分为抽样-持续转换（SAR）和按位逐次抽样（S&S）两种，其中SAR类型ADC更加常用。

SAR类型ADC的工作原理主要是将电路中的输入信号反复地采样，并使用内部电压参考或外部电压参考进行比较，以确定最终输出值。

采样率和参考电压是控制转换精度的关键因素，采样率越高，参考电压越精准，最终转换的精度就越高。

此外，随着科技的发展，ADC的性能也在不断提高。

近年来，ADC 技术可以实现多种性能，如低功耗、高动态范围、高采样率和高精度等功能。

通过不断的技术进步，ADC已经可以用于传感器、医疗影像、音频应用、声纳应用、无线通信和军事应用等多个领域。

最后，ADC技术也取得了很大的发展，能够为上述应用提供更优质的服务。

例如，最新的ADC技术可以实现低功耗、高转换速率和极高的精度，以满足当今快速变化的应用需求。

综上所述，ADC模数转换器是一种关键电路，它可以将模拟信号转换为数字信号，以便电路中的微处理器可以对其进行处理。

它的原理是采样-持续转换，依靠内部或外部参考电压进行比较，以确定最终输出值，并可用于多种应用场合，比如传感器、音频应用等。

由于技术的不断进步，ADC可以实现低功耗、高转换速率和极高的精度，以满足现有应用的需求。

adc模数转换器原理模数转换器（ADC）是一种电子设备，它可以将模拟信号转换成数字信号。

它是一种把模拟信号转换成数字系数的技术，它主要应用在测量、仪器仪表和计算机等领域。

ADC可以将模拟信号（电压或电流）转换成数字信号。

ADC由一组电路组成，它可以将一个模拟量转换成一组数字。

ADC的研究历史可以追溯到机器数字技术的早期，直到有可能的研究者开始提出不同的模拟/数字转换器（ADC）设计概念。

现代ADC 可以追溯到1907年，当时广为人知的英国物理学家Sir Oliver Lodge 提出了一种模拟/数字转换器，它可以将模拟信号转换成数字信号。

常见的ADC通常包括模拟前端、采样持续系统和数字控制环节。

模拟前端过滤有效信号，以帮助维持模拟输入的频率，而采样持续系统使用所谓的“咆哮器”（Ramp Generator）来测量模拟输入的平均电平，而数字控制环节则使用电路来得出最终的数字序列。

此外，一些采用复杂技术的ADC还可能包括多种数字前端，以便在低速率下获得更高精度的测量结果。

ADC技术的发展也使ADC能够以较高的速度工作，这种技术就是多维ADC。

多维ADC的好处是：它可以在一个时钟周期内进行多路信号采样，并且在测量中可以获得更高的精度.多维ADC对应用非常有用，因为它可以提供更高的精度和更快的采样延迟。

除了多维ADC之外，还有另一种类型的ADC，即“混合信号ADC”。

该技术可以将模拟部分转换成数字信号，从而实现特定类型的信号处理，混合信号ADC通常由两个独立的子系统组成：数字信号处理子系统和ADC子系统。

数字信号处理子系统可以实现信号的初始处理，而ADC子系统则可以将模拟信号转换成数字信号，以便进行更精确的处理。

总的来说，ADC模数转换器可以满足各种应用场合的需求，它在测量、仪器仪表和计算机等领域均有广泛的应用。

此外，ADC技术的不断进步也使得它具有更高的精度和速度，能够满足多种不同的应用需求。

模数和数模转换器（ADC和DAC）工作原理为了能够使用数字电路处理模拟信号,必须把模拟信号转化成相应的数字信号,方能送入数字系统进行处理.同时也要把处理后得到的数字信号在转换成相应的模拟信号,作为最后的输出.我们把前一种从模拟信号到数字信号的转换叫做模-数转换,或简称A/D;把后一种从数字信号到模拟信号的转换叫做数-模转换,或简称D/A.同时把A/D或D/A 转换的电路叫做模数转换器(简称ADC)或数模转换器(简称DAC)主要分成以下几个部分：1、取样：取样（也称采样）是将时间上连续变化的信号，转换为时间上离散的信号，即将时间上连续变化的模拟量转换为一系列等间隔的脉冲，脉冲的幅度取决于输入模拟量。

2、保持：模拟信号经采样后，得到一系列样值脉冲。

采样脉冲宽度一般是很短暂的，在下一个采样脉冲到来之前，应暂时保持所取得的样值脉冲幅度，以便进行转换。

因此，在取样电路之后须加保持电路。

3、量化：将采样后的样值电平归化到与之接近的离散电平上，这个过程称为量化。

4、编码：把量化的结果用代码表示出来，称为编码。

这些代码就是A/D转换的输出结果。

模拟信号数字化需要注意两个问题：①每秒钟需要采集多少个信号样本，也就是采样频率(fs)是多少，②每个信号样本的比特数b/s(bit per sample)应该是多少，也就是量化精度。

根据奈奎斯特理论（Nyquist theory），采样频率的高低是由模拟信号本身的最高频率决定的。

奈奎斯特理论指出，采样频率不应低于模拟信号最高频率的两倍，这样就能把以数字表达的信号还原成原来的信号，这叫做无损数字化（lossless digitization）。

采样定律用公式表示为fs ≥ 2f或者T s ≤ T/2其中f为被采样信号的最高频率，T为被采样信号的最低周期，fs 称为采样频率，Ts为采样间隔。

如下图，图中的正弦曲线代表原始音频曲线；填了颜色的方格代表采样后得到的结果，二者越吻合说明采样结果越好。

模数转换器（ADC）：精度与分辨率区别详述 在与使用模数转换器(ADC) 的系统设计人员进行交谈时，我最常听到的一个问题就是： 你的16位ADC的精度也是16位的吗？ 这个问题的答案取决于对分辨率和精度概念的基本理解。

尽管是两个完全不同的概念，这两个数据项经常被搞混和交换使用。

 今天的文章详述了这两个概念间的差异。

我们将在一系列帖子中深入研究造成ADC不准确的主要原因。

 ADC的分辨率被定义为输入信号值的最小变化，这个最小数值变化会改变数字输出值的一个数值。

对于一个理想ADC来说，传递函数是一个步宽等于分辨率的阶梯。

然而，在具有较高分辨率的系统中（≥16位），传输函数的响应将相对于理想响应有一个较大的偏离。

这是因为ADC以及驱动器电路导致的噪声会降低ADC的分辨率。

 此外，如果DC电压被施加到理想ADC的输入上并且执行多个转换的话，数字输出应该始终为同样的代码（由图1中的黑点表示）。

现实中，根据总体系统噪声（也就是包括电压基准和驱动器电路），输出代码被分布在多个代码上（由下面的一团红点表示）。

系统中的噪声越多，数据点的集合就越宽，反之亦然。

图1中显示的是一个中量程DC输入的示例。

ADC传递函数上输出点的集合通常被表现为ADC数据表中的DC柱状图。

 图1：ADC传递曲线上ADC分辨率和有效分辨率的图示 图1中的图表提出了一个有意思的问题。

如果同样的模拟输入会导致多个数字输出，那幺对于ADC分辨率的定义仍然有效吗？是的，前提是我们只考虑ADC的量化噪声。

然而，当我们将信号链中所有的噪声和失真计算在内时，正如等式(1) 中所显示的那样，ADC的有效无噪声分辨率取决于输出代码分布(NPP)。

 在典型ADC数据表中，有效位数(ENOB) 间接地由AC参数和信噪失真比(SINAD) 指定，可使用方程式2计算得出： 下面，考虑一下图1中的输出代码簇（红点）不是位于理想输出代码的中央，而是位于远离黑点的ADC传递曲线上的其他位置（如图2中所示）。

模数转换器ADC_综述随着数字技术，特别是计算机技术的飞速发展普及，在现代控制、通讯及检测领域中，对信号的处理广泛采用了数字计算机技术。

由于系统的实际处理对象往往都是一些模拟量（如温度、压力、位移、图像等），要使计算机或数字仪表能识别和处理这些信号，必须首先将这些模拟信号转换成数字信号。

这样，就需要一种能将模拟信号转换为数字信号的电路，即模数转换电路(Analog to Digital Converter, ADC)。

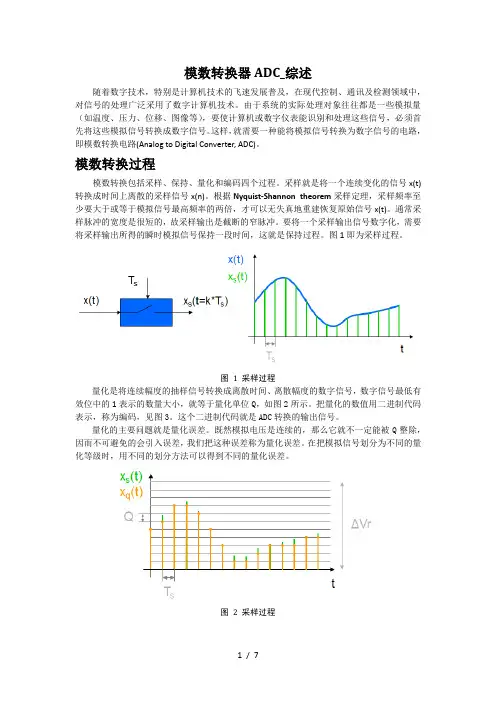
模数转换过程模数转换包括采样、保持、量化和编码四个过程。

采样就是将一个连续变化的信号x(t)转换成时间上离散的采样信号x(n)。

根据Nyquist-Shannon theorem采样定理，采样频率至少要大于或等于模拟信号最高频率的两倍，才可以无失真地重建恢复原始信号x(t)。

通常采样脉冲的宽度是很短的，故采样输出是截断的窄脉冲。

要将一个采样输出信号数字化，需要将采样输出所得的瞬时模拟信号保持一段时间，这就是保持过程。

图1即为采样过程。

图 1 采样过程量化是将连续幅度的抽样信号转换成离散时间、离散幅度的数字信号，数字信号最低有效位中的1表示的数量大小，就等于量化单位Q，如图2所示。

把量化的数值用二进制代码表示，称为编码，见图3。

这个二进制代码就是ADC转换的输出信号。

量化的主要问题就是量化误差。

既然模拟电压是连续的，那么它就不一定能被Q整除，因而不可避免的会引入误差，我们把这种误差称为量化误差。

在把模拟信号划分为不同的量化等级时，用不同的划分方法可以得到不同的量化误差。

图 2 采样过程图 3 编码过程要提高ADC的精度，可以通过提高采样间隔Ts和分辨率Q来实现。

实际中，输入模拟信号的频率由于存在无限次谐波，因此要在采样前加入抗混叠滤波器，该滤波器与采样频率的关系一般为：f s ≈ (3…5)*f filter。

图4描述了这一过程。

图 4 加入抗混叠滤波器模数转换技术是现实各种模拟信号通向数字世界的桥梁，作为将模拟信号转换成数字信号的模数转换技术主要有以下几种。

adc模数转换过程
ADC（Analog-to-Digital Converter，模数转换器）是一种将模拟信号转换为数字信号的电子元件。

其工作原理是通过采样、保持、量化和编码等步骤，将连续的模拟信号转换为离散的数字信号。

具体来说，ADC的转换过程可以分为以下四个步骤：
1.抗混叠滤波：为了防止高频信号在采样过程中产生混叠，需要在模拟信
号输入到ADC之前进行抗混叠滤波，以确保输入信号的频率在采样频
率的两倍以下。

2.采样保持：采样是将连续的模拟信号转换为离散的过程。

采样后，模拟
信号的幅度和相位可能会发生变化，因此需要在采样后使用采样保持电
路来保持模拟信号的幅度和相位不变。

3.量化：量化是将连续的模拟信号转换为离散的数字信号的过程。

量化的
基本原理是将模拟信号的幅度范围划分为若干个离散的等距区间，然后
将模拟信号映射到这些区间中的某一个。

4.编码：编码是将量化后的数字信号转换为适合存储和传输的格式的过
程。

常见的编码方式有二进制编码、BCD编码和Gray编码等。

以上就是ADC模数转换的基本过程。

在实际应用中，不同类型的ADC可能会采用不同的技术和方法来实现这些步骤。

模数转换器(ADC)的几种主要类型现在的软件无线电、数字图像采集都需要有高速的A/D采样保证有效性和精度，一般的测控系统也希望在精度上有所突破，人类数字化的浪潮推动了A/D转换器不断变革，而A/D转换器是人类实现数字化的先锋。

A/D转换器发展了30多年，经历了多次的技术革新，从并行、逐次逼近型、积分型ADC，到近年来新发展起来的∑-Δ型和流水线型ADC，它们各有其优缺点，能满足不同的应用场合的使用。

逐次逼近型、积分型、压频变换型等，主要应用于中速或较低速、中等精度的数据采集和智能仪器中。

分级型和流水线型ADC主要应用于高速情况下的瞬态信号处理、快速波形存储与记录、高速数据采集、视频信号量化及高速数字通讯技术等领域。

此外，采用脉动型和折叠型等结构的高速ADC，可应用于广播卫星中的基带解调等方面。

∑-Δ型ADC主应用于高精度数据采集特别是数字音响系统、多媒体、地震勘探仪器、声纳等电子测量领域。

下面对各种类型的ADC作简要介绍。

1．逐次逼近型逐次逼近型ADC是应用非常广泛的模/数转换方法，它包括1个比较器、1个数模转换器、1个逐次逼近寄存器（SAR）和1个逻辑控制单元。

它是将采样输入信号与已知电压不断进行比较，1个时钟周期完成1位转换，N位转换需要N个时钟周期，转换完成，输出二进制数。

这一类型ADC的分辨率和采样速率是相互矛盾的，分辨率低时采样速率较高，要提高分辨率，采样速率就会受到限制。

优点：分辨率低于12位时，价格较低，采样速率可达1MSPS；与其它ADC相比，功耗相当低。

缺点：在高于14位分辨率情况下，价格较高；传感器产生的信号在进行模/数转换之前需要进行调理，包括增益级和滤波，这样会明显增加成本。

2．积分型ADC积分型ADC又称为双斜率或多斜率ADC，它的应用也比较广泛。

它由1个带有输入切换开关的模拟积分器、1个比较器和1个计数单元构成，通过两次积分将输入的模拟电压转换成与其平均值成正比的时间间隔。

何谓ADC—全方位学习模数转换器（ADC）在电子领域中模拟技术是被公认的最难的技术，众多资深的模拟工程师无一不是从百上千次的实践中不断学习，不断摸索。

但是作为初级的模拟工程师呢?如何能够快速的上手并在模拟技术领域快速的成长呢?电子发烧友网作为电子行业的网站为上百万工程师提供电子资讯及电子技术资料及方案，帮助更多的工程师成长。

本文针对模拟工程师的必备知识-模数转换器(ADC)进行了知识整理与讲解，让大家较全面的学习ADC的知识。

什么是ADC,ADC是什么意思adc: Analog-to-Digital Converter的缩写,意思是模/数转换器。

实现把模拟信号转变为数字量的设备称为模—数(A/D)转换器，简称ADCADC(A/D转换器)在ADC转换器中，一般经过采样、保持、量化和编码这四个步骤来完成从模拟量到数字量的转换。

(1)采样与保持(2)量化与编码数字信号最低有效位的1即1LSB所代表的数量就是这个最小数量单位，称为量化单位，用Δ表示。

将采样输出电压用最小单位的整数倍来表示，这个过程就叫量化。

将量化的结果用代码表示出来的过程就称为编码。

编码输出的结果就是A/D转换器的输出。

A/D转换电路方式模—数转换器根据其工作原理大致分为并行式和并/串式A/D、逐次逼近式、双积分式和计数比较式A/D等几种形式。

逐次逼近式A/D由电压比较器、D/A转换器、逐次逼近寄存器(SAR)和控制逻辑等组成。

ADC0808/0809IN0～IN7：模拟量输入脚;ADDA、ADDB、ADDC：通道地址输入端。

CLOCK：时钟输入端。

ALE：地址锁存允许端。

START：启动脉冲输入端。

EOC：转换结束信号端。

OE：允许输出端。

D7～D0引脚：转换所得8位数据在这8个管脚上输出，D7是最高位，D0是最低位。

UCC：电源正极输入端，接+5 V。

GND：地端，电源负极接至该端。

UREF(+)和UREF(-)：分别为基准电压UREF的高电平端和低电平端。