当前位置：文档之家 › 数字信号处理第四章习题

数字信号处理第四章习题

  • 格式：doc
  • 大小：146.00 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

数字信号处理课后习题答案(全)1-7章

数字信号处理课后习题答案(全)1-7章
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
（6） y(n)=x(n2)
令输入为
输出为
x(n－n0)
y′(n)=x((n－n0)2) y(n－n0)=x((n－n0)2)=y′(n) 故系统是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n2)+bx2(n2) =aT［x1(n)］+bT［x2(n)］
第 1 章 时域离散信号和时域离散系统
题4解图（一）
第 1 章 时域离散信号和时域离散系统
题4解图（二）
第 1 章 时域离散信号和时域离散系统
题4解图（三）
第 1 章 时域离散信号和时域离散系统
(4) 很容易证明： x(n)=x1(n)=xe(n)+xo(n)
上面等式说明实序列可以分解成偶对称序列和奇对称序列。 偶对称序列可 以用题中(2)的公式计算， 奇对称序列可以用题中(3)的公式计算。
（2） y(n)=x(n)+x(nN+1)k 0
（3） y(n)= x(k)
（4） y(n)=x(n－nn0)n0
（5） y(n)=ex(n)
k nn0
第 1 章 时域离散信号和时域离散系统
解：（1）只要N≥1， 该系统就是因果系统， 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M， 则|y(n)|≤M， （2） 该系统是非因果系统， 因为n时间的输出还和n时间以 后（（n+1）时间）的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
=2x(n)+x(n－1)+ x(n－2)
将x(n)的表示式代入上式， 得到 1 y(n)=－2δ(n+2)－δ(n+1)－0.5δ(2n)+2δ(n－1)+δ(n－2)

数字信号处理课后答案+第4章(高西全丁美玉第三版)

数字信号处理课后答案+第4章(高西全丁美玉第三版)

6*． 按照下面的IDFT算法编写MATLAB语言 IFFT程 序， 其中的FFT部分不用写出清单， 可调用fft函数。 并分 别对单位脉冲序列、 矩形序列、 三角序列和正弦序列进行 FFT和IFFT变换， 验证所编程序。
解： 为了使用灵活方便， 将本题所给算法公式作为函 数编写ifft46.m如下： %函数ifft46.m %按照所给算法公式计算IFET function xn=ifft46(Xk， N) Xk=conj(Xk)； %对Xk取复共轭 xn=conj(fft(Xk， N))/N； %按照所给算法公式计算IFFT 分别对单位脉冲序列、 长度为8的矩形序列和三角序列 进行FFT， 并调用函数ifft46计算IFFT变换， 验证函数 ifft46的程序ex406.m如下：
快速卷积时， 需要计算一次N点FFT（考虑到H(k)= DFT［h(n)］已计算好存入内存）、 N次频域复数乘法和 一次N点IFFT。 所以， 计算1024点快速卷积的计算时间Tc 约为
Fs <
1024 = 15 625 次 /秒 65536 × 10−6
Fs 15625 = = 7.8125 kHz 2 2
1 x ( n) = IDFT[ X ( k )] = [DFT[ X * ( k )]]* N
%程序ex406.m %调用fft函数计算IDFT x1n=1； %输入单位脉冲序列x1n x2n=［1 1 1 1 1 1 1 1］； %输入矩形序列向量x2n x3n=［1 2 3 4 4 3 2 1］； %输入三角序列序列向量x3n N=8； X1k=fft(x1n， N)； X2k=fft(x2n， N)； X3k=fft(x3n， N)； %计算x1n的N点DFT %计算x2n的N点DFT %计算x3n的N点DFT

《现代数字信号处理》第4章习题答案

《现代数字信号处理》第4章习题答案

（a）试求
AR（2）模型的系数 a2
=
⎡⎣1, a2 (1), a2 (2)T
⎤⎦
（表示为 w0 ,
σ
2 w
和
P
的函数形式。）
（b）求AR（2）模型对应的反射系数Γ1和Γ2。
（c）当 σ
2 w
→
0
时，AR（2）参数和反射系数的极限值是多少？
解：(a)
rx (0) =
P
+
σ
2 w
,
rx (1) =
P cosω0,
{ } E
ei− (n) x∗ (n − k )
=
E
⎧⎪⎡ ⎨⎢
x
(
n
− i) +
i
∑ ai∗
(
j)
x(n
−i
+
j)⎤⎥ ⋅
x∗
(n
−
k )⎫⎪⎬
⎪⎩⎣
j =1
⎦
⎪⎭
i
= rx (k − i) + ∑ ai∗ ( j) rx (k − i + j) j =1
=
⎡ ⎢rx
(i
−
k
)
+
i
∑ ai
(
j)
rx
1 6
2 3
⎤ ⎥ ⎦
，
且：
b
(0)
=
rx
(
0)
+
a
(1)
rx
(1)
+
a
(
2)
rx
(
2)
=
1
−
1 6
×
1 2
−
2 3

数字信号处理(Digital Signal Processing)智慧树知到课后章节答案2023年

数字信号处理(Digital Signal Processing)智慧树知到课后章节答案2023年

数字信号处理（Digital Signal Processing）智慧树知到课后章节答案2023年下聊城大学聊城大学绪论单元测试1.声音、图像信号都是（）。

A:二维信号 B:一维信号 C:确定信号 D:随机信号答案:随机信号第一章测试1.序列的周期为（）。

A:7 B:7 C:14 D:14答案:142.序列的周期为（）。

A:10 B:10 C:8 D:8答案:103.对于一个系统而言，如果对于任意时刻n0，系统在该时刻的响应仅取决于此时刻及此时刻以前时刻的输入系统，则称该系统为____系统。

（）A:线性 B:因果 C:稳定 D:非线性答案:因果4.线性移不变系统是因果系统的充分必要条件是______。

（）A:n<0,h(n)=0 B:n>0,h(n)=0 C:n>0,h(n)>0 D:n<0,h(n)>0答案:n<0,h(n)=05.要想抽样后能够不失真的还原出原信号，则抽样频率必须，这就是奈奎斯特抽样定理。

（）A:等于2倍fm B:小于等于2倍fm C:大于2倍fm D:大于等于2倍fm答案:大于等于2倍fm6.已知x(n)=δ(n),其N点的DFT[x(n)]=X(k),则X(N-1)= 1。

（）A:对 B:错答案:对7.相同的Z变换表达式一定对应相同的时间序列。

（）A:对 B:错答案:错8.滤波器设计本质上是用一个关于z的有理函数在单位圆上的特性来逼近所有要求的系统频率特性。

（）A:错 B:对答案:对9.下面描述中最适合离散傅立叶变换DFT的是（）A:时域为离散周期序列，频域也为离散周期序列 B:时域为离散有限长序列，频域也为离散有限长序列 C:时域为离散序列，频域也为离散序列 D:时域为离散无限长序列，频域为连续周期信号答案:时域为离散有限长序列，频域也为离散有限长序列10.巴特沃思滤波器的幅度特性必在一个频带中（通带或阻带）具有等波纹特性。

（）A:错 B:对答案:错第二章测试1.N＝1024点的DFT，需要复数相乘次数约（）。

数字信号处理第4章习题解答教材

数字信号处理第4章习题解答教材


DFT [x2 (n)]

DFT {Im[ w(n )]}

1 j Wop (k )

1 2j
[W
((k )) N
W
* (( N

k )) N
]RN
(k)
解：由题意 X k DFT xn，Y k DFT y n 构造序列 Z k X k jY k 对Z k 作一次N点IFFT可得序列z n z(n) IDFT Z k
Re[w(n)] j Im[w(n)]
Wep (k) Wop (k)
由x1(n) Re[w(n)]得
X1(k) DFT[x1(n)] DFT{Re[w(n)]} Wep (k)

1 2
[W
((k
))
N
W *((N

k ))N
]RN
(k)
由x2 (n) Im[w(n)]得
X 2 (k )
(2) 按频率抽取的基-2FFT流图
同样共有L = 4级蝶形运算，每级N / 2 = 8个蝶形运算
基本蝶形是DIT 蝶形的转置
X m1(k )
X m1( j)
WNr
-1
X m (k ) Xm( j)
每个蝶形的两节点距离为2Lm ，即从第一级到 第四级两节点距离分别为8，4，2，1。
系数WNr的确定：r (k )2 2m1 即k的二进制左移m 1位补零
3. N=16 时，画出基 -2 按时间抽取法及按频率抽取法 的 FFT 流图（时间抽取采用输入倒位序，输出自然数 顺序，频率抽取采用输入自然顺序，输出倒位序）。
解： 自然序
倒位序
0 0000 0000 0 1 0001 1000 8 2 0010 0100 4 3 0011 1100 12 4 0100 0010 2 5 0101 1010 10 6 0110 0110 6 7 0111 1110 14

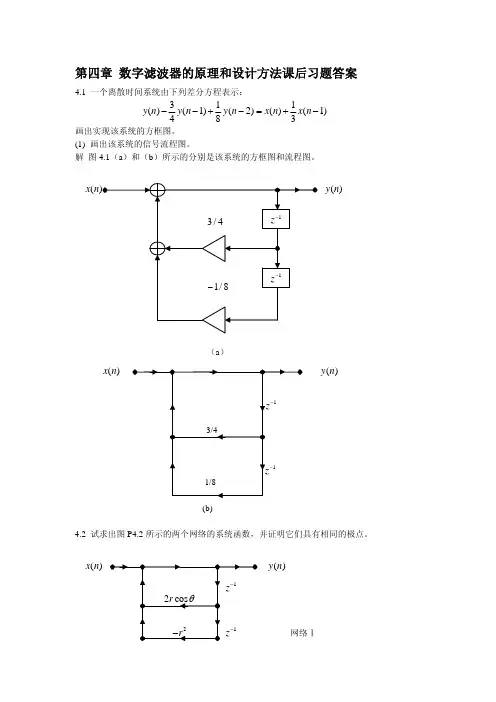
数字信号处理 答案 第四章

数字信号处理 答案 第四章

z −1
r sin θ
− r sin θ r cos θ
y ( n)
z −1
网络Ⅱ 解 网络Ⅰ：根据信号流程图写出差分方程
y (n) = 2r cos θ y (n − 1) − r 2 y (n − 2) + x(n)
由差分方程得系统函数
H1 ( z ) =
Y ( z) 1 = X ( z ) 1 − 2r cos θ z −1 + r 2 z −1 1 )(rz −1 − e jθ )
（4）并联型
x ( n)
z −1
1/4 10/3
-7/3
y ( n)
z −1
1/2 将系统函数写成部分分式形式
H ( z) =
−7 / 3 10 / 3 + 1 −1 1 1− z 1 − z −1 4 2
4.4 用直接Ⅰ型和直接Ⅱ型结构实现以下系统函数； (1)
H(z)=
−5 + 2 z −1 − 0.5 z −2 1 + 3z −1 + 3z −2 + z −3
3z 3 + 2 z 2 + 2 z + 5 (2) H(x)=0.8 3 z + 4 z 2 + 3z + 2
解 (1)根据系统函数写出差分方程
y (n) + 3 y (n − 1) + 3 y (n − 2) + y (n − 3) = −5 x(n) + 2 x(n − 1) − 0.5 x(n − 2)
可见网络Ⅰ和网络Ⅱ具有相同极点。 4.3 一个因果线性离散系统由下列差分方程描述：
3 1 1 y(n)- y(n-1)+ y(n-2)=x(n)+ x(n-1) 4 8 3

数字信号处理习题集(附答案)

数字信号处理习题集(附答案)
解：
因为
所以
9．序列 ，其4点DFT 如下图所示。现将 按下列（1），（2），（3）的方法扩展成8点，求它们8点的DFT？（尽量利用DFT的特性）
（1）
（2）
（3）
解：（1）
（2）
（3）
10．设 是一个2N点的序列，具有如下性质：
另设 ，它的N点DFT为 ，求 的2N点DFT 和 的关系。
解： 推导过程略
（2）设 的长度N为偶数，且有 ，求 。
解：（1）因n为奇数时 ，故
，
另一方面
因此
所以
按照上式可画出 的图形，如图5.34所示。
16．计算下列有限长序列 的DFT，假设长度为N。
（1）
（2）
解：（1）
(2)
17．长度为8的有限长序列 的8点DFT为 ，长度为16的一个新序列定义为
0
试用 来表示 。
解：
解：
3．已知 则 的
4点循环卷积为（）。
解：
证明题：
4．试证N点序列 的离散傅立叶变换 满足Parseval恒等式
证：
5． 是一个离散傅里叶变换对，试证明离散傅里叶变换的对称性：
证明略。
6． 长为N的有限长序列， 分别为 的圆周共轭偶部及奇部，也即
证明：
证
7．若
证： （1）
（2）
由（2） ，将 互换，则有
（1）
（2）
（3）
【解】（1）
（2）假定 和 的变换分别为 和 ，则
所以
（3）
8．求下列序列的时域离散傅里叶变换
， ，
解：
三、离散时间系统系统函数
填空题：
1．设 是线性相位FIR系统，已知 中的3个零点分别为1，0.8，1+j，该系统阶数至少为（）。

数字信号处理第四章附加习题及答案-new

数字信号处理第四章附加习题及答案-new

第四章附加题1. 请推导出三阶巴特沃思低通滤波器的系统函数，设1/c rad s Ω=。

解：幅度平方函数是：2261()()1A H j Ω=Ω=+Ω令： 22s Ω=- ,则有：61()()1a a H s H s s -=- 各极点满足121[]261,26k j k s ek π-+==所得出的6个 k s 为：15==j es 2321321jes j +-==π12-==πj e s 2321343jes j --==π2321354j es j -==π2321316j es j +==π15==j e s 2321321je s j +-==π12-==πj e s 2321343je s j --==π2321354j es j -==π2321316j es j +==π122))()(()(233210+++=---=s s s k s s s s s s k s H a 1221)(23+++==s s s s H a 代入s=0时, ,可得,故:1=)s (H a 10=k2. 设计一个满足下列指标的模拟Butterworth 低通滤波器，要求通带的截止频率6,p f kHz =，通带最大衰减3,p A dB =，阻带截止频率12,s f kHz =，阻带的最小衰减25s A dB =，求出滤波器的系统函数。

解： 2,2s s p p f f ππΩ=Ω= 0.10.1101lg 101N 2lg()s pA A sp⎛⎫- ⎪-⎝⎭≥ΩΩ=4.15取N=5，查表得H(p)为：221()(0.6181)( 1.6181)(1)H p p p p p p =+++++因为3,p A dB =所以c p Ω=Ω[]52222()()0.618 1.618cs p c c c c c c H s H p s s s s s =Ω=Ω=⎡⎤⎡⎤+Ω-Ω+Ω-Ω+Ω⎣⎦⎣⎦3. 设计一个模拟切比雪夫低通滤波器，要求通带的截止频率 f p =3kHz ，通带衰减要不大于0.2dB ，阻带截止频率 f s = 12kHz ，阻带衰减不小于 50dB 。

数字信号处理(程佩青)第四章 习题

数字信号处理(程佩青)第四章 习题
所以
6
6
T = T1 + T2 = 0.013824s
4-2
1.注意输入,输出,蝶形结,旋转因子 注意输入,输出,蝶形结, 注意输入 2.注意每 一级有多少蝶形单元 注意每 3.旋转因子求解时有何特殊方法 旋转因子求解时有何特殊方法 4.蝶形单元的输入与输出是在时域还是 蝶形单元的输入与输出是在时域还是 在频域? 在频域?
看出:第m级的系数为W , k = 0,1 2
结论:每由后向前( 由 结论:每由后向前(m由M-->1级)推进一级, 级 推进一级, 则此系数为后级系数中偶数序号的那一半. 则此系数为后级系数中偶数序号的那一半.
试求出N=64时用 时用DIT共有多少级,每级有多 共有多少级, 试求出 时用 共有多少级 少个蝶形单元, 少个蝶形单元 6 并写出每一级的旋转因子. 解:N = 64 = 2,并写出每一级的旋转因子.
m = 5,旋转因子为W ,W ,W ,W 共16个
0 64 2 64 4 64 30 64
m = 6, 旋转因子为W ,W ,W ,W 共32个
0 64 1 64 2 64 31 64
�
第四章 习题
直接DFT的运算量和FFT DFT的运算量和FFT的运算量 4-1 直接DFT的运算量和FFT的运算量
解:
(1)直接计算 复乘所需时间
T1 = 5 ×106 × N 2 = 5 ×106 × 5122 = 1.31072 s
复加所需时间
T2 = 0.5 ×106 × N × ( N 1) = 0.5 ×106 × 512 × ( 512 1) = 0.130816s
-1 -1
0 W16
2 W16 3 W16 4 -1 W16 5 -1 W16

数字信号处理知到章节答案智慧树2023年上海健康医学院

数字信号处理知到章节答案智慧树2023年上海健康医学院

数字信号处理知到章节测试答案智慧树2023年最新上海健康医学院第一章测试1.如果连续时间信号是最高截止频率为的带限信号，采样频率为_______可不失真地恢复原连续时间信号。

参考答案:2.由模拟信号采样得到的序列，模拟角频率Ω与序列的数字域频率参考答案:线性3.在连续系统中，正弦信号是周期信号，其周期与频率呈_______关系。

参考答案:2π/w4.在离散时间系统中，最常用的是_______。

参考答案:线性非移变系统5.线性非移变系统的性质不包括_______。

参考答案:0-1 率6.由于序列是离散的，故在序列运算中不存在微积分运算。

（）参考答案:对7.采样频率太高会产生太大的数据量，使运算时间延长，设备成本增加。

（）参考答案:对8.系统满足可加性或齐次性，即为线性系统。

（）参考答案:错9.任何序列都可以表示成单位脉冲序列移位加权和的形式。

（）参考答案:对10.两个线性非移变系统级联后构成一个线性移变系统。

（）参考答案:错第二章测试1.Z 变换是从_______直接引申出来的一种变换方法。

参考答案:拉普拉斯2.当序列是一个（）序列时，双边Z变换和单边Z变换是相等的。

参考答案:因果3.Z 变换是关于 Z 的无穷多项的幂级数的_______。

参考答案:和4.的Z变换是_______。

参考答案:5.的 Z 变换收敛域是_______。

参考答案:|z|>|a|6.Z 变换等价于序列的傅里叶变换。

（）参考答案:错7.收敛域包含∞是因果序列的Z变换得特征。

参考答案:对8.根据序列的 Z 变换求对应序列的运算称之为逆 Z 变换。

（）参考答案:错9.的Z变换等于1。

参考答案:对10.对于求解同样的逆 Z 变换，因选择的方法不同，得到结果序列的分段点不同，实际数值上二者是等价的。

（）参考答案:对第三章测试1.时域的连续周期对应于频域的（）。

参考答案:非周期离散2.序列x1（n）的长度为4，序列x2（n）的长度为3，则它们线性卷积的长度是（），5点圆周卷积的长度是（）。

中国科学院刘艳老师现代数字信号处理第四章上机作业

中国科学院刘艳老师现代数字信号处理第四章上机作业

1、假设一平稳随机信号为()()()0.81x n x n w n =−+，其中)(n w 是均值为0，方差为1的白噪声，数据长度为1024。

（1）、产生符合要求的)(n w 和)(n x ；（2）、给出信号x(n)的理想功率谱；（3）、编写周期图谱估计函数，估计数据长度N=1024及256时信号功率谱，分析估计效果。

（4）、编写Bartlett 平均周期图函数，估计当数据长度N=1024及256时，分段数L 分别为2和8时信号)(n x 的功率谱，分析估计效果。

一、一、解题思路解题思路w(n)可以通过随机序列randn(1,N)来产生，x(n)可以通过对w(n)滤波产生（由递推式可得系统的传递函数），也可以直接由递推式迭代产生。

由于线性系统的输出功率谱等于输入功率谱乘以传递函数模的平方，X(n)可以看做w(n)通过一线性系统的输出，H(z)=1/(1-0.8z)。

所以x(n)的理想功率谱P(ejw)=σw2|H(ejw)|2。

周期图方法：直接对观测数据做FFT变换，变换的结果取模的平方再除以数据长度，作为估计的功率谱。

256个观测点时可以对原观测数据以4为间隔提取得到。

Bartlett法：将L组独立的观测数据分别求周期图，再将L个周期图求平均作为信号的功率谱估计。

L组数据可以通过对原观测数据以L为间隔提取得到。

二、二、MATLAB MATLAB MATLAB实现程序及注解实现程序及注解clear all;clear;close all;Fs=500;%采样率N=1024;%观测数据w=sqrt(1)+randn(1,N);%0均值,方差为1的白噪声,长度1024x=[w(1)zeros(1,N-1)];%初始化x(n),长度1024,x(1)=w(1)for i=2:Nx(i)=0.8*x(i-1)+w(i);%迭代产生观测数据x(n)end%%%%%%%%%%%%%%%%%%%%%理想功率谱%%%%%%%%%%%%%%%%%%%%[h,w1]=freqz(x);figure,plot(w1*500/(2*pi),10*log10(abs(h).^2));grid on;title('理想功率谱');xlabel('频率');ylabel('功率db');%%%%%%%%%%%%%%%%%%%%%周期图法%%%%%%%%%%%%%%%%%%%%%%1024个观测点Pxx=abs(fft(x)).^2/N;%周期图公式Pxx=10*log10(Pxx(index+1));%化为dbfigure;plot(k,Pxx);grid on;title('周期图1024点');xlabel('频率');ylabel('功率db');%周期图256个观测点x1=x(1:4:N);Pxx1=abs(fft(x1,1024)).^2/N;figure;plot(k,Pxx1);grid on;title('周期图256点');xlabel('频率');ylabel('功率db');%%%%%%%%%%%%%%%Bartlett平均周期图,N=1024%%%%%%%%%%%%%%%%%%%分段L=2L=2;x_21=x(1:L:N);x_22=x(2:L:N);Pxx_21=abs(fft(x_21,1024)).^2/length(x_21);Pxx_22=abs(fft(x_22,1024)).^2/length(x_22);Pxx_2=(Pxx_21+Pxx_22)/L;figure;subplot(2,2,1),plot(k,10*log10(Pxx_2(index+1)));grid on;title('N=1024,L=2');xlabel('频率');ylabel('功率db');%分段L=8L1=8;x3=zeros(L1,N/L1);%产生L1行,N/L1列的矩阵用以存储分组的数据for i=1:L1x3(i,:)=x(i:L1:N);%将原始数据分为8组endPxx3=zeros(L1,1024);%产生L1行,1024列矩阵用以存储分组的周期图for i=1:L1Pxx3(i,:)=abs(fft(x3(i,:),1024)).^2/length(x3(i,:));%分别求周期图,结果保存在Pxx3中,FFT长度为1024endfor i=1:1024Pxx3_m(i)=sum(Pxx3(:,i))/L1;%求平均endsubplot(2,2,2),plot(k,10*log10(Pxx3_m(index+1)));grid on;title('N=1024,L=8');xlabel('频率');ylabel('功率db');%%%%%%%%%%%%%%%Bartlett平均周期图,N=256,求法同上%%%%%%%%%%%%%%分段L=2,分别计算周期图,再取平均x=x(1:4:N);L2=2;x_31=x(1:L2:length(x));x_32=x(2:L2:length(x));Pxx_31=abs(fft(x_31,1024)).^2/length(x_31);Pxx_32=abs(fft(x_32,1024)).^2/length(x_32);Pxx_3=(Pxx_31+Pxx_32)/L2;subplot(2,2,3),plot(k,10*log10(Pxx_3(index+1)));grid on;title('N=256,L=2');xlabel('频率');ylabel('功率db');%分段L=8L3=8;x4=zeros(L3,length(x)/L3);for i=1:L3x4(i,:)=x(i:L3:length(x));%将原始数据分为8组endPxx4=zeros(L3,1024);for i=1:L3Pxx4(i,:)=abs(fft(x4(i,:),1024)).^2/length(x4(i,:));%分别求周期图,FFT长度为1024endfor i=1:1024Pxx4_m(i)=sum(Pxx4(:,i))/L3;%求平均endsubplot(2,2,4),plot(k,10*log10(Pxx4_m(index+1)));grid on;title('N=256,L=8');xlabel('频率');ylabel('功率db');三、实验结果理想功率谱图如图1-1所示图1-1理想功率谱图1024点的周期图以及256点的周期图分别如图1-2、1-3所示图2-21024点的周期图图2-3256点的周期图Bartlett平均周期图法的相应图像如图1-4所示图1-4Bartlett平均周期图法的相应图像四、实验结果分析由图1-2、1-3可以看出，周期图法得到的功率谱估计，谱线的起伏较大，即估计所得的均方误差较大。

数字信号处理第4章部分习题详解

数字信号处理第4章部分习题详解
其中 ni 、 k i 都是二进制数。
)( 2 k1 k0 ) n1k0 ( 2 n 2 n3 级间旋转因子 W16 。 W16
4
22 n1 2n2 n3 23 n0
0000 1000 0100 1100 0010 1010 0110 1110 0001 1001 0101 1101 0011 1011 0111 1111 x(0) x(8) x(4) -j x(12) x(2) x(10) x(6) -j x(14) x(1) x(9) x(5) -j x(13) x(3) x(11) x(7) x(15) -j -1 -1 -1 -1 -1 -1 -1 -1
nk X (k ) x(n)WN n 0 N 1

1
1
n3 0 n2 0 1
x(n n n n )W
n1 0 1 n0 0 1 0 1 2 3 0 1 2 3
1
1
1
( 23 n0 2 2 n1 2 n2 n3 )( 23 k3 2 2 k 2 2 k1 k0 ) 16
3
n1 0

3
3 n1 ( 4 k1 k 0 ) x(n0 n1 )W4n0 k 0 W16 n 0 0
n1k0 X 1 (n1k0 ) W16 W4n1k1 X 2 (k1k0 ) n1 0
n1 k 0 其中 W16 是级间旋转因子。

n3 0 n 2 0 1 1

n1 0
1 n3 ( 2 2 k 2 2 k1 k 0 ) x(n0n1n2n3 )W2n0 k 0 W4n1k 0 W2n1k1 W8n2 ( 2 k1 k 0 ) W2n2 k 2 W16 W2n3 k3 n 0 0

数字信号处理课后习题Ch4

数字信号处理课后习题Ch4

= ( n−2 α )π sin[( n − α ) wc ] sin[( n − α ) w0] 因为 h(n)=hd (n)W R (n)= hd(n) R N (n) 所以（1）当 N 为奇数时 h（n）= { (0 ≤ n ≤ N − 1) ; 0 , 其他 （2）当 N 为偶数时 h（n）的表达式与 N 为奇数时相同 （3）若采用汉明窗设计 h(n)= h d (n)W(n) = ( n−2 α )π sin[( n − α ) wc ] sin[( n − α ) w0] [0.54-0.46cos (
N ⎧ 2 1 ⎪ H (ω ) = b ( n ) c o s [ω ( n − )] ∑ ⎪ 2 n =1 ∴ ⎨ ⎪ N b (n ) = 2 h ( − 1 + n) ⎪ 2 ⎩
∴ （1）当 N 为奇数时
2
sinωc (n − α ) ⎧ RN (n), 0 ≤ n ≤ N − 1 ⎪2cosω0 (n-α ) π (n − α ) h( n) = ⎨ ⎪0, 其他 ⎩
（2）当 N 为偶数时 h(n)的表达式与 N 为奇数时的相同； （3）若用汉明窗设计
h( n) = hd (n)ω (n) = 2 cos ω0 ( n − α ) sin ωc ( n − α ) 2π n [0.54 − 0.46 cos( )]RN (n) π (n − α ) N −1
(1 ).h d ( n ) = =
1 2π
∫
2π 0
H d (e
jω
)e
jn ω
dω
1 π + ω c − j ( ω − π ) α jn ω e e dω 2 π ∫π − ω c π +ωc 1 = e jπ α ∫ e j ( n −α )ω d ω π −ω c 2π 1 1 = e jπ α e j ( n − α ) ω 2π j ( n − α ) 1 e jπ α [e = 2π j ( n − α )

数字信号处理(第三版)教程及答案第4章

数字信号处理(第三版)教程及答案第4章

第 4 章 时域离散系统的网络结构及数字信号处理的实现
4.3 按照系统函数或者差分方程画系统流图
按照系统函数设计系统的实现方法主要依据的是系统函 数的特点和要求， 画出系统流图， 然后根据流图设计用硬 件或软件进行实现。 系统的网络结构有很多， 但最基本的是FIR和IIR网络结 构。 这两类结构各有特点。 FIR结构一般没有反馈回路， 单 位脉冲响应是有限长的， 系统稳定， 但相对IIR结构， FIR 结构的频率选择性不高， 换句话说， 要求频率选择性高时， 要求FIR有很高的阶数。
N / 2 −1
H ( z) =
∑
n =0
h(n)[ z − n ± z − ( N − n −1) ]
N为偶数
第 4 章 时域离散系统的网络结构及数字信号处理的实现
H ( z) =
( N −1) / 2 −1
∑
n=0
h(n)[ z − n
N −1 − − ( N − n −1) ±z ] + h( )z 2
第 4 章 时域离散系统的网络结构及数字信号处理的实现
N
Ak H ( z) = C + ∑ 1 − p k z −1 k =1
式中, pk是极点l， C是常整数， Ak是展开式中的系数。 一 般pk、 Ak都是复数。 为了用实数乘法， 将共轭成对的极点 放在一起， 形成一个二阶网络， 公式为
bk 0 + bk1 z H k ( z) = 1 + a k1 z −1 + a k 2 z − 2
−1
第 4 章 时域离散系统的网络结构及数字信号处理的实现
上式中的系数均是实数。 总的系统函数为
H ( z) = C + ∑ H k ( z)

数字信号处理习题集

数字信号处理习题集

数字信号处理习题集数字信号处理习题集第⼀章习题1、已知⼀个5点有限长序列，如图所⽰，h (n )=R 5(n )。

（1）⽤写出的()n δ()x n 函数表达式；（2）求线性卷积*。

()y n =()x n ()hn 2、已知x (n )=(2n +1)[u (n +2)-u (n -4)],画出x (n )的波形，并画出x (-n )和x (2n )的波形。

3、判断信号是否为周期信号，若是求它的周期。

3()sin 73x n n ππ??=+4、判断下列系统是否为线性的，时不变的，因果的，稳定的？（1），（2）2()(3)y n x n =-0()()cos()y n x n n ω=5、已知连续信号。

()2sin(2),3002a x t ft f Hz ππ=+=（1）求信号的周期。

()a x t （2）⽤采样间隔T=0.001s 对进⾏采样，写出采样信号的表达式。

()a x t ?()a xt （3）写出对应于的时域离散信号的表达式，并求周期。

?()a xt ()x n 6、画出模拟信号数字处理的框图，并说明其中滤波器的作⽤。

第⼆章习题1、求下列序列的傅⽴叶变换。

（1），（2）11()333nx n n ??=-≤ ?[]2()()()n x n a u n u n N =--2、已知理想低通滤波器的频率响应函数为：为整数，000(),0j n j e H e n ωωωωωωπ-?≤≤?=? <≤??cc 求所对应的单位脉冲响应h (n )。

3、已知理想⾼通滤波器的频率响应函数为：，求所对应0()1j H e ωωωωωπ≤≤=<≤??cc 的单位脉冲响应h (n )。

4、已知周期信号的周期为5,主值区间的函数值=,求该周期信号的()(1)n n δδ+-离散傅⾥叶级数和傅⾥叶变换.5、已知信号的傅⽴叶变换为，求下列信号的傅⽴叶变换。

()x n ()j X e ω（1）（2）(3)x n -*()x n -6、已知实因果信号如图所⽰，求和。

数字信号处理第四章作业

数字信号处理第四章作业

求线性卷积，并比较它们的运算量。
k
(b) z k ak , k=0,1„,N-1.a 为实数， a 0 。 (c) (a)和(b)两者都行。 (d) (a)和(b)都不行，即线性调频 z 变换不能计算 H(z)在 z 为实数时的取样。 10. (第四章习题 13)设对列长 N=64 及列长 L=48 的两序列用(1)直接计算法，(2)快速卷积法
数字信号处理第四章作业数字信号处理数字信号处理试卷数字信号处理第三版数字信号处理pdf数字信号处理期末试卷matlab数字信号处理数字信号处理教程数字信号处理实验报告数字信号处理第四版
数字信号处理第四章作业
1. ( 第四章习题 1) 如果一台通用计算机的速度为平均每次复乘需要 100us,每次复加需要 20us， 今用来计算 N=1024 点的 DFT[x(n)],问直接运算需要长时间， 用 FFT 运算需多少时间？ 2. (第四章习题 2)把 16 点序列 x(0) x(1) „x(15)排成反序序列。 3. (第四章习题 4)试用基-2 按时间抽取与按频率抽取法分别作出 N=16 时的信号流图。 4. (第四章习题 5)试画出 4 点按时间抽取的 FFT 算法流程图，要求利用本书图 4-8 的蝶形， 具有反序的输入序列，自然顺序的输出序列，并且表示成“原位”计算。 5. (第四章习题 6)重排题 5 的流图，使它仍然符合“原位”计算，但要有自然顺序输入，反 序输出。 6. (第四章习题 8)推导 N=16 时，基-4FFT 公式，并画出流图，就运算量的多少（不计 i, j 的运算量）与基-2 情况作比较。 7. (第四章习题 9)画出 8 点分裂基 L 型运算流图，计算其复数乘法次数，并与基 -2 和基-4 法 进行比较。 8. (第四章习题 10)已知 X(k)和 Y(k)分别是两个 N 点实序列 x(n)和 y(n)的 DFT 为提高运算效 率，试设计用一次 N 点 IFFT 来从 x(k)和 y(k)求 x(n)和 y(n)。 9. (第四章习题 12)在下列说法中选择正确的结论。线性调频 z 变换可以用来计算一个有限长 序列 h(n)在 z 平面实 z 轴上诸点{zk}的 z 变换 H（z） ，使 (a) z k a , k=0,1„,N-1.a 为实数， a 1 。

数字信号处理教程第四章练习题

数字信号处理教程第四章练习题

数字信号处理教程第四章练习题一、单选题1、直接计算N点DFT所需的复数乘法次数与( D)成正比。

A、NB、N2C、N3D、Nlog2N2、基-2FFT算法的基本运算单元为(A)。

A、蝶形运算B、卷积运算C、相关运算D、延时运算3、在N=32的按时间抽取法FFT运算流图中,从x(n)到X(k)需(B)级蝶形运A、4B、5C、6D、34、如图所示的运算流图符号是( B)基2FFT 算法的蝶形运算流图符号。

A、按频率抽取B、按时间抽取C、A、B都是D、A、B都不是5、如何将无限长序列和有限长序列进行线性卷积(D)。

A、直接使用线性卷积计算B、使用FFT计算C、使用循环卷积计算D、采用分段卷积可采用重叠相加法二、多选题1、用FFT算法计算DFT所需的复数乘法次数为(),复数加法次数为(AD)。

A、N/2log2NB、N/4log2NC、Nlog2N/2D、Nlog2N2、快速傅里叶变换的特点是(BCD)。

A、线性计算B、蝶形计算C、原位计算D、码位计算3、利用的哪些性质可以减少DFT的运算量(ACD)。

A、周期性B、循环性C、对称性D、可约性4、采用FFT算法用DFT计算线性卷积的方法有(AD)A、重叠相加法B、重叠相减法C、重叠去除法D、重叠保留法三、填空题1、快速傅里叶变换算法可以分为两大类,分别是(时域抽取法)、(频域抽取法)。

2、若对序列x(n)作1024点的DIT-FFT运算,则FFT运算中总需要的复数乘法次数(5120)。

四、判断题1、时域抽取法基2 FFT算法中不能实现原位计算。

(×)2、按频率抽取的基-2 FFT算法中,输入顺序为自然排列,输出为倒序排。

(√)3、按时间抽取的FFT算法运算量等于按频率抽取的FFT算法运算量。

(√)4、重叠相加法求线性卷积也是利用圆周卷积法代替线性卷积,用FFT算法求得。

(√)。

数字信号处理-第4章习题

数字信号处理-第4章习题

习题四4.1 用窗函数法设计一线性相位FIR 高通滤波器，通带边界频率为0.6π，阻带边界频率为0.4π，要求阻带衰减不小于40dB ，窗函数从矩形窗、汉宁窗、海明窗和布莱克曼窗中选取，且要求滤波器的阶数最小。

求出该滤波器的单位脉冲响应h (n )的解析式。

解 求理想高通滤波器的边界频率n ω和过渡带宽ω∆:0.60.40.522c rn ωωππωπ++≈== 0.60.40.2c r ωωωπππ∆=-=-=选择窗函数和窗口长度。

阻带衰减不小于40dB ，因此选择汉宁窗。

根据过渡带宽求窗口长度N 和线性相位延迟常数α:6.20.231N Nππ=⇒= 1152N α-== 根据理想边界频率n ω和线性相位延迟常数α，求理想单位脉冲响应d ()h n :[][]()()d sin ()sin ()1()()d d 21n n n j n j n n n n n n h n e e n ωπωαωαπωαπαωαπαωωπωαπ----⎧---≠⎪⎪-⎡⎤=+=⎨⎢⎥⎣⎦⎪-=⎪⎩⎰⎰ 窗函数与理想单位脉冲响应相乘，即可得到线性相位FIR 高通滤波器的单位脉冲响应:[][]sin (15)sin (15)0.50.50.5cos ()15()15(15)0.515N n n n R n n h n n n ππππ⎧---⎡⎤⎛⎫-⋅⋅≠⎪ ⎪⎢⎥=-⎝⎭⎨⎣⎦⎪=⎩0,1,2,,30n =⋅⋅⋅6kHz ，阻带边界频率为2kHz 和8kHz ，采样频率为20kHz ，要求阻带衰减不小于50dB ，窗函数从矩形窗、汉宁窗、海明窗和布莱克曼窗中选取，且要求滤波器的阶数最小。

求出该滤波器的单位脉冲响应h (n )的解析式。

解 求理想带通滤波器的边界频率1ω、2ω和过渡带宽ω∆:12121212112212221120.4 , 20.620.2 , 20.80.3 , 0.7220.2c c c c s s r r r r s sc r c r r c c r f ff f f ff f ωππωππωππωππωωωωωπωπωωωωωπ========++≈=≈=∆=-=-= 选择窗函数和窗口长度。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章习题4.1 (a) By expanding the equation()()[]()⎥⎦⎤⎢⎣⎡==⎰--∞→∞→2200021T T Ft j T xx T xx dt e t x T E lim F P E lim F 00πΓ taking the expected value, and finally taking the limit as ∞→0T ,show that the right-hand side converges to )(f xx Γ.(b) Prove that2102211)(1)(∑∑-=---+-==N n fn j fm j N N m xx en x N e m r ππ.4.2 For zero-mean, jointly Gaussian random variables, X 1, X 2, X 3, X 4, itis well known that)()()()()()()(3241423143214321X X E X X E X X E X X E X X E X X E X X X X E ++=. Use this result to derive the mean-square value of ()m r xx and the variance, given by()[][]()()()[]∑∞-∞=+-+-≈n xx xx xx xx m n m n n m N N m r γγγ*22varwhich is defined as[][][]22(()(var m r E m r E m r xx xx xx -=. 4.3 By use of the expression for the fourth joint moment for Gaussianrandom variables, show that(a)()()[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡+++=2212122121421)(sin )(sin )(sin )(sin 1f f N N f f f f N N f f f P f P E x xx xx ππππσ (b)[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡++=2212122121421)(sin )(sin )(sin )(sin )()(cov f f N N f f f f N N f f f P f P x xx xx ππππσ(c)[]⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛+=242sin 2sin 1)(var f N fN f P x xx ππσ under the condition that the sequence ()n x is a zero-mean white Gaussian noise sequence with variance 2x σ.4.4 Generalize the results in Problem 4.3 to a zero-mean Gaussian noiseprocess with power density spectrum )(f xx Γ, as given by()[]()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+Γ=222sin 2sin 1var f N fN f f P xx xx ππ (Hint: Assume that the colored Gaussian noise process is the output of a linear system excited by white Gaussian noise.)4.5 Show that the periodogram values at frequencies,1,1,0,/-==L k L k f k given by (4.1.35), can be computed by passing the sequence through a bank of L IIR filters, where each filter has an impulse response )()(/2n u e n h N nk j k π-= and then computing the magnitude-squared value of the filter outputs at n=N. Note that each filter has a pole on the unit circle at the frequency f k .4.6 The Bartlett method is used to estimate the power spectrum of asignal x(n). We know that the power spectrum consists of a single peak with a 3 dB bandwidth of 0.01 cycle per sample, but we do not know the location of the peak.(a) Assuming that N is large, determine the value of M=N/K so thatthe spectral window is narrower than the peak.(b) Explain why it is not advantageous to increase M beyond thevalue obtained in part (a).4.7 The N-point DFT of a random sequence x(n) is ∑-=-=10/2)()(N n N nk j e n x k X π.Assume that E[x(n)]=0 and E[x(n)x(n+m)]=)(2m w δσ (in other words,x(n) is a white noise process).(a) Determine the variance of X(k).(b) Determine the autocorrelation of X(k).4.8 An AR(2) process is described by the difference equation)()2(81.0)(n n x n x ω+-=, where w(n) is a white noise process withvariance 2ωσ.(a) Determine the parameters of the MA(2), MA(4), and MA(8)models that provide a minimum mean-sequare error fit to thedata x(n).(b) Plot the true spectrum and those of the MA (q), q=2,4,8spectra and compare the results. Comment on how well theMA(q) models approximate the AR (2) process.4.9 An MA (2) process is described by the difference equation )2(81.0)()(-+=n n n x ωω, where w(n) is a white noise process withvariance 2ωσ.(a) Determine the parameters of the AR(2), AR(4), and AR(8)models that provide a minimum mean-square error fit to the data x(n).(b) Plot the true spectrum and those of the AR(p), p=2,4,8, andcompare the results. Comment on how well the AR(p) modelsappoximate the MA (2) process.4.10 The autocorrelation sequence for an AR process x(n) ismxx m ⎪⎭⎫ ⎝⎛=41)(γ (a) Determine the difference equation for x(n)(b) Is your answer unique? If not, give any other possiblesolutions.4.11 Suppose that we represent an ARMA(p,q) process as a cascade ofan MA(q) followed by an AR(p) model. The input-output equation for the MA(q) model is ∑=-=qk k k n w b n v 0)()(, where w(n) is a whitenoise process. The input-output equation for the AR(p) model is∑==-+pk k n v k n x a n x 1)()()((a) By computing the autocorrelation of v(n), show thatq m d b b m mq k m w m k k w vv ≤≤==∑-=+0)(022σσγ(b) Show that 1)()(00=+=∑=a k m a m pk vx k vv γγ4.12 Suppose that the AR(2) process in Problem 4.8 is corrupted by anadditive white noise process v(n) with variance 2v σ. Thus, we havey(n)=x(n)+v(n)(a) Determine the difference equation for y(n) and thusdemonstrate that y(n) is an ARMA(2,2) process. Determinethe coefficients of the ARMA process.(b) Generalize the result in part (a) to an AR(p) process∑=+--=pk k n w k n x a n x 1)()()( and )()()(n v n x n y +=.4.13 The harmonic decomposition problem considered by Pisarenko maybe expressed as the solution to the equationa a a Γa H w yy H 2σ=The solution for a may be obtained by minimizing the quadratic form a Γa yy H subject to the constraint that a a H =1. The constraint can be incorporated into the performance index by means of a Lagrange multiplier. Thus the performance index becomes()a a a Γa H yy H 1-+=λζ.By minimizing ζ with respect to a , show that this formulation is equivalent to the Pisarenko eigenvalue problem given in (4.4.9), with the Lagrange multiplier playing the role of the eigenvalue. Thus,show that the minimum of ζ is the minimum eigenvalue 2w σ.4.14 The autocorrelation of a sequence consisting of a sinusoid withrandom phase in noise is)(2cos )(21m m f P m w xx δσπγ+=where 1f is the frequency of the sinusoidal, P its power, and 2w σthe variance of the noise. Suppose that we attempt to fit an AR(2) model to the data.(a) Determine the optimum coefficients of the AR(2) model as afunction of 2w σ and 1f .(b) Determine the reflection coefficients 1K and 2K correspondingto the AR(2) model parameters.(c) Determine the limiting values of the AR(2) parameters and (1K ,2K )as 02→w σ.4.15 This problem involves the use of cross-correlation to detect a signalin noise and estimate the time delay in the signal. A signal x(n) consists of a pulsed sinusoid corrupted by a stationary zero-mean white noise sequence. That is, 10),()()(0-≤≤+-=N n n w n n y n x ,where )(n w is the noise with variance 2w σ and the signal is⎩⎨⎧-≤≤=otherwise M n n A n y ,010,cos )(0ω. The frequency 0ω is known, but the delay 0n , which is a positiveinteger, is unknown, and is to be determined by cross-correlating x(n) with y(n). Assume that 0n M N +>. Let∑-=-=10)()()(N n xy n x m n y m rdenote the cross-correlation sequence between x(n) and y(n). In the absence of noise, this function exhibits a peak at delay 0n m =. Thus,0n is determined with no error. The presence of noise can lead toerrors in determining the unknown delay.(a) For 0n m =, determine ()[]0n r E xy . Also, determine thevariance ()[]0var n r xy , due to the presence of the noise. In bothcalculations, assume that the double-frequency term averages to zero. That is, 0/2ωπ>>M .(b) Determine the signal-to-noise ratio, defined as []{}[])(var )(020n r n r E SNR xy xy = (c) What is the effect of the pulse duration M on the SNR?。