五年级几何体的表面积与体积的计算

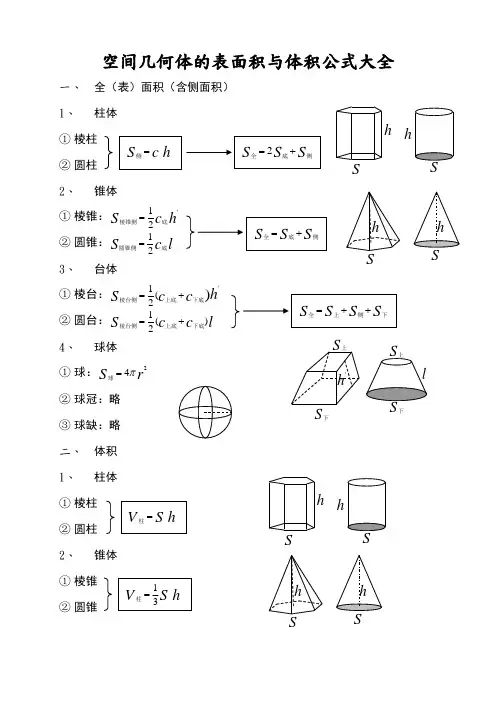
空间几何体的表面积与体积公式大全一、 全（表）面积（含侧面积） 1、柱体① 棱柱② 圆柱 2、锥体①棱锥：h c S ‘底棱锥侧21=② 圆锥：l c S 底圆锥侧21=3、 台体① 棱台：h c c S)(21‘下底上底棱台侧+=②圆台：l c c S )(21下底上底棱台侧+=4、 球体① 球：r S 24π=球 ② 球冠：略 ③ 球缺：略 二、 体积 1、柱体① 棱柱 ② 圆柱 2、锥体① 棱锥 ② 圆锥3、① 棱台 ② 圆台 4、球体① 球：r V 334π=球② 球冠：略 ③ 球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高h '计算；而圆锥、圆台的侧面积计算时使用母线l 计算。

三、 拓展提高 1、祖暅原理：（祖暅：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的。

2、阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是r 2的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的32。

分析：圆柱体积：r r h S V r 3222)(ππ=⨯==圆柱圆柱侧面积：r h cS r r 242)2(ππ=⨯==圆柱侧因此：球体体积：r r V 3334232ππ=⨯=球 球体表面积：r S 24π=球通过上述分析，我们可以得到一个很重要的关系（如图）+ =即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和 3、台体体积公式公式： )(31S SS S h V 下下上上台++=证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD 。

延长两侧棱相交于一点P 。

设台体上底面积为S 上，下底面积为S 下高为h 。

易知：PDC ∆∽PAB ∆，设h PE 1=， 则h h PF +=1由相似三角形的性质得：PFPEAB CD =即：hh hSS +=11下上(相似比等于面积比的算术平方根)整理得：SS h S h 上下上-=1又因为台体的体积=大锥体体积—小锥体体积 ∴h S S S h h S h h S V 下上下上下台）（31)(313131111+-=-+=代入：SS h S h 上下上-=1得：hS S S SS h S V 下上下上下上台31)(31+--=即：)(3131)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(31S SS S h V 下下上上台++=4、球体体积公式推导分析：将半球平行分成相同高度的若干层（层n ），n 越大，每一层越近似于圆柱，+∞→n 时，每一层都可以看作是一个圆柱。

体积和表面积的关系与运算一、体积与表面积的定义1.体积：物体所占空间的大小。

2.表面积：物体表面的总面积。

二、体积与表面积的计算公式1.立方体的体积公式：V = a³（a为立方体的边长）2.立方体的表面积公式：S = 6a²三、体积与表面积的运算关系1.体积与边长的关系：体积随边长的增加而增加。

2.表面积与边长的关系：表面积随边长的增加而增加。

四、体积与表面积的单位1.体积的单位：立方米（m³）、立方分米（dm³）、立方厘米（cm³）等。

2.表面积的单位：平方米（m²）、平方分米（dm²）、平方厘米（cm²）等。

五、体积与表面积的换算1.1立方米（m³）= 1000立方分米（dm³）2.1立方米（m³）= 1000000立方厘米（cm³）3.1平方米（m²）= 100平方分米（dm²）4.1平方米（m²）= 10000平方厘米（cm²）六、常见几何体的体积与表面积公式1.圆柱体的体积公式：V = πr²h（r为圆柱的底面半径，h为圆柱的高）2.圆柱体的表面积公式：S = 2πrh + 2πr²3.圆锥体的体积公式：V = (1/3)πr²h（r为圆锥的底面半径，h为圆锥的高）4.圆锥体的表面积公式：S = πr² + πrl（l为圆锥的母线长）5.球的体积公式：V = (4/3)πr³（r为球的半径）6.球的表面积公式：S = 4πr²七、体积与表面积的实际应用1.计算物体的体积和表面积，以便了解物体的大小和形状。

2.在制作和包装物体时，计算体积和表面积，以节省材料和空间。

3.在建筑设计中，计算建筑物的体积和表面积，以确定建筑材料的需求量和建筑物的外观。

八、体积与表面积的拓展1.立体图形的体积和表面积的计算。

长方体、正方体【教学目标】1.长方体与正方体的的认识；2.长方体与正方体的棱长、表面积和体积的计算公式的理解性记忆与运用；3.培养学生的空间想象能力.【教学重点】1.长方体与正方体的表面积和体积的计算公式的理解性记忆与运用;2.培养学生的空间想象能力.【教学难点】1.长方体与正方体的表面积和体积的计算公式的理解性记忆与运用；2.培养学生的空间想象能力。

【教学内容】本讲内容从我们熟悉的平面扩展到了三维立体空间,培养学生的空间想象能力，同学生要记住知识是有限的，但想象力是无限的。

①长方体表面积：若长方体的长、宽、高分别为a、b、c,那么可得：长方体的表面积：S长方体＝2（ab＋bc＋ac)；如右图，长方体共有六个面（每个面都是长方形）,八个顶点,十二条棱。

在六个面中,两个对面是全等的,即三组对面两两全等。

②正方体的表面积：我们也可以称其为立方体，它是一种特殊的长方体，它的六个面都是正方形．如果它的棱长为a，那么可得:正方体的表面积：S正方体=6a2；如右图，正方体共有六个面（每个面都是全等的正方形），八个顶点，十二条棱．板块一：长方体与正方体的棱长例1、填空1．0.08立方米=（）升=( ）毫升3。

8升=（）升（)毫升6.47升=( ）毫升=（）立方分米415平方厘米=（）平方米10020立方分米=（）立方米20升=（）立方米9.08立方分米=（）升=( ）毫升0。

08立方米=( ）毫升例2、填空1）长方体有_______个面,都是_______形，也有可能相对的面是_________形，相对的两个面的面积___________。

2）正方体有_____个面，都是_______形,面积都_______，正方体的长、宽、高都______.3）两个面相交的_______叫做棱，长方体有_____条棱,相对的_____条棱______。

正方体有_____条棱,这些棱的长度都_________。

4)如图，长方体的长是___________，宽是_____________，高是______________,12条棱长的和是_________。

几何体的表面积与体积计算教案一、引言几何体的表面积与体积是数学中常见的计算问题，掌握其计算方法对于几何学的学习至关重要。

通过本教案的学习，学生将能够准确计算不同几何体的表面积与体积，并且理解其中的计算原理与方法。

二、教学目标1. 理解几何体表面积与体积的概念；2. 能够运用适当的公式计算不同几何体的表面积与体积；3. 培养学生的观察力、分析能力和解决实际问题的能力；4. 培养学生的团队合作意识和交流能力。

三、教学内容与教学步骤1. 立方体的表面积与体积计算- 引导学生观察立方体的特点，并引导他们思考立方体表面积与体积之间的关系。

- 告诉学生立方体的表面积公式为：表面积 = 6 ×边长的平方，体积公式为：体积 = 边长的立方。

- 给学生提供几个立方体的边长数据，让他们根据公式计算并填写表面积和体积。

2. 圆柱体的表面积与体积计算- 引导学生观察圆柱体的特点，并引导他们思考圆柱体表面积与体积之间的关系。

- 告诉学生圆柱体的表面积公式为：表面积= 2π × 半径 ×（半径 + 高度），体积公式为：体积= π × 半径的平方 ×高度。

- 给学生提供几个圆柱体的半径和高度数据，让他们根据公式计算并填写表面积和体积。

3. 锥体的表面积与体积计算- 引导学生观察锥体的特点，并引导他们思考锥体表面积与体积之间的关系。

- 告诉学生锥体的表面积公式为：表面积= π × 半径 ×（半径 + 斜高），体积公式为：体积= 1/3 × π × 半径的平方 ×高度。

- 给学生提供几个锥体的半径、斜高和高度数据，让他们根据公式计算并填写表面积和体积。

4. 教学总结与拓展- 让学生总结本节课所学的不同几何体的表面积与体积公式，并核对计算结果的准确性。

- 给学生拓展更多几何体计算的例子，让他们尝试自主解决问题并运用所学的知识。

四、教学评价与反馈在教学过程中，可以通过以下方式对学生进行评价与反馈：1. 课堂练习：设计一些实用题目让学生运用所学的知识进行计算，并即时给予反馈。

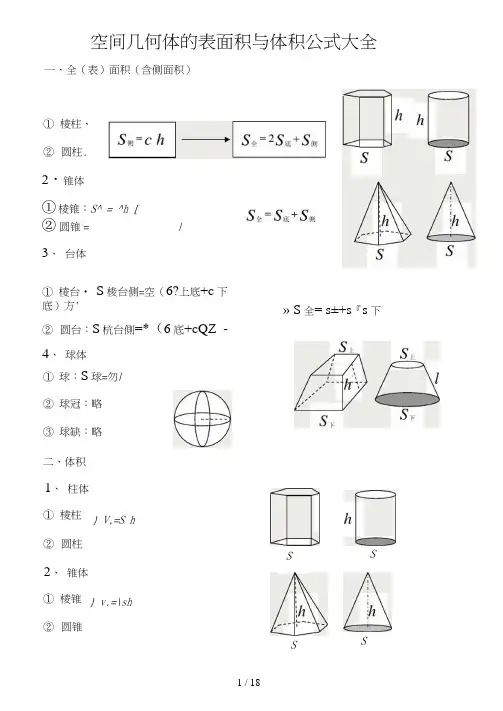
空间几何体的表面积与体积公式大全一、全（表）面积（含侧面积）①棱柱、②圆柱.2・锥体①棱锥：S^ = ^h [②圆锥:= /3、台体①棱台• S梭台侧=空（6?上底+c下底）方'» S全= s±+s『s下②圆台：S杭台側=*（6底+cQZ -4、球体①球：S球=勿/②球冠：略③球缺：略二、体积1、柱体①棱柱} V,=S h②圆柱S S 2、锥体①棱锥} v.=\sh②圆锥S S3、 台体V 台肓//（S 匕+ JS 上S F + S 下）台=齐方（厂上+Jr 上厂下+厂下） 4、 球体①球：V 球② 球冠：略VyT/③ 球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高力计算；而圆锥、圆台的 侧面积计算时使用母线/计算。

三、拓展提高1、 祖眶原理：（祖璀：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的。

2、 阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2厂的圆柱形容器内装一个最大 的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的？。

①棱台 ②圆台丿分析：圆柱体积：V H1 = s h =（^r）x2r = 2^/圆柱侧面积：S叭削= c/z = （2岔）X2广=4兀/2 彳4 彳因lit :球体体积：|/厅=—x2/r^ =_龙厂球体表面积：S球=4兀厂通过上述分析，我们可以得到一个很重要的关系（如图）即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：几冷〃（S上+、恳瓦+ S』证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD。

延长两侧棱相交于一点P 0设台体上底面积为Si，下底面积为S下高为// °易知：\PDCs 型AB，设卩£ =人，则Pf+h由相似三角形的性质得：孚=袋AB PF即：（相似比等于面积比的算术平方根）、用hi整理得：人=尺刃又因为台体的体积二大锥体体积一小锥体体积u台=§s下（九+力r s上人人（S下-S上）+§s下方即：（、瓦+丫瓦）+扣下力=|/z $ + 应7+S卜）4、球体体积公式推导分析：将半球平行分成相同高度的若干层（兀层），〃越大，每一层越近似于圆柱'"T -HZ）时»每一层都可以看作是一个圆柱。

球的体积与表面积球是一种立体几何体，具有很多特点和属性。

其中，体积和表面积是球的两个重要参数，用于描述球的大小和形态。

本文将详细介绍球的体积和表面积的计算方法，并探讨一些与球相关的实际问题。

一、球的体积球的体积表示了球所占据的空间大小。

对于一个给定的球，其体积可以通过以下公式计算得出：V = (4/3)πr³其中V表示球的体积，π是一个数学常数，约等于3.14159，r表示球的半径。

通过上述公式，我们可以轻松计算出球的体积。

例如，假设球的半径为5cm，那么根据上述公式，可以得到球的体积为：V = (4/3)π(5)³ ≈ 523.6cm³二、球的表面积球的表面积表示了球的外部覆盖面积。

同样，对于一个给定的球，其表面积可以通过以下公式计算得出：A = 4πr²其中A表示球的表面积，π是一个数学常数，约等于3.14159，r表示球的半径。

通过上述公式，我们可以轻松计算出球的表面积。

例如，假设球的半径为5cm，那么根据上述公式，可以得到球的表面积为：A = 4π(5)² ≈ 314.16cm²三、球体积与表面积的关系从球的体积和表面积的计算公式可以看出，球的体积与半径的立方成正比，而表面积与半径的平方成正比。

这意味着球的体积和表面积都与球的半径密切相关。

当球的半径增大时，其体积和表面积也会增大。

例如，当半径由5cm增加到10cm时，根据上述公式计算可以得到新球的体积为：V = (4/3)π(10)³ ≈ 4188.8cm³同时，新球的表面积为：A = 4π(10)² ≈ 1256.64cm²可以看出，新球的体积和表面积较原来的球都有所增大。

这一点在实际应用中十分重要，例如在建筑设计、物体容器容量计算等方面都会涉及到。

四、实际应用举例球的体积和表面积在现实生活中有着广泛的应用，下面举几个例子说明其重要性：1. 建筑设计：在建筑设计中，对于球形结构（如球形穹顶、球形体育馆等），需要计算球的体积和表面积，以合理规划结构和空间。

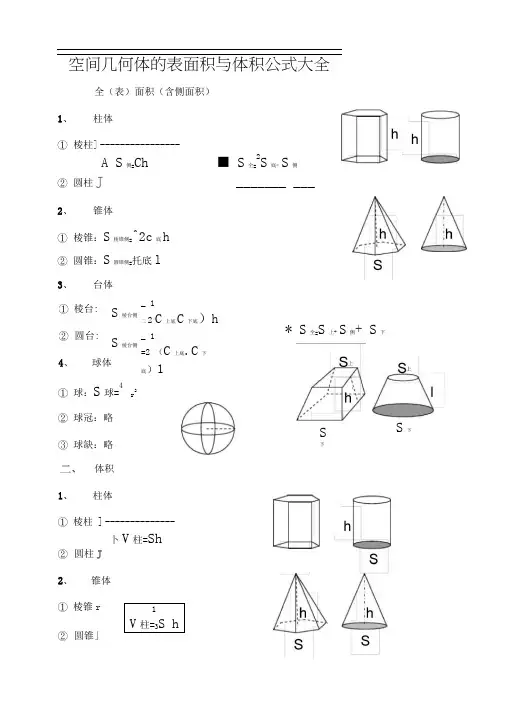
空间几何体的表面积与体积公式大全全（表）面积（含侧面积）1、柱体①棱柱]----------------A S侧=Ch ■ S全=2S底* S侧②圆柱J _______ ___2、锥体①棱锥：S棱锥侧=^2c底h②圆锥：S圆锥侧=托底l3、台体①棱台:②圆台:S棱台侧S棱台侧_ 1二2（C上底C下底）h_ 1=2 （C上底.C下底）1* S全=S上+ S侧+ S下4、球体①球：S球=4r2②球冠：略③球缺：略S下S下体积1、柱体①棱柱]--------------卜V柱=Sh②圆柱J2、锥体①棱锥r②圆锥」1V柱=3S h3、台体1①棱台］V台=gh （S上NS上S^ +S下）②圆台J V圆台=3兀h （r上+Q r上r下+ r下）4、球体①球：V球=4二r'②球冠：略③球缺：略说明：棱锥、棱台计算侧面积时使用侧面的斜高h计算；而圆锥、圆台的侧面积计算时使用母线I计算。

三、拓展提高1、祖暅原理：（祖暅：祖冲之的儿子）夹在两个平行平面间的两个几何体，如果它们在任意高度上的平行截面面积都相等，那么这两个几何体的体积相等。

最早推导出球体体积的祖冲之父子便是运用这个原理实现的2、阿基米德原理：（圆柱容球）圆柱容球原理：在一个高和底面直径都是2r的圆柱形容器内装一个最大的球体，则该球体的全面积等于圆柱的侧面积，体积等于圆柱体积的-。

3分析：圆柱体积：V圆柱=Sh =（二「2）2r=2^r'圆柱侧面积：S圆柱侧=C h =（2 r） 2r = 4二「因此：球体体积：V球=2 2二J=4二r33 3球体表面积：S球=4 r2即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式：V台=1h （S上+ S下）证明：如图过台体的上下两底面中心连线的纵切面为梯形ABCD 延长两侧棱相交于一点P设台体上底面积为S上,下底面积为S下P 高为h。

易知：PDC s .>PAB ,设PE = h i，则PF =h i h由相似三角形的性质得:CD PEAB PFA整理得：h 1 ： =S上hPS 下-VS上又因为台体的体积=大锥体体积一小锥体体积1 11 1 二V台=3S 下(h 1h K3S 上h^3h 1(S下一S上) 下h代入：h= i S 上芬得: V台=3胪L(S下—S"3S 下hJS下3*SrS31 ___ I ------ ------ 1即: V 台=3 S上h (S下S上)3S下人二 V 台=3h （S 上S 上S 下S下）球体体积公式推导即：ShiS 下-h lh （相似比等于面积比的算术平方根）1 ______________=3h (S上S 上S 下S下)4、分析：将半球平行分成相同高度的若干层（ n 层），n 越大，每一层越近似于圆柱，n “ •「时，每一层都可以看作是个圆柱。

几何体积与表面积的数学知识点全面解读在我们的数学学习中，几何体积与表面积是非常重要的概念。

无论是在解决实际问题，还是在进行理论推导中，都离不开对它们的理解和运用。

接下来，让我们一起深入探讨这一有趣且实用的数学领域。

首先，我们来聊聊什么是几何体积。

简单来说，体积就是一个几何体所占空间的大小。

比如说，一个长方体盒子，它能装多少东西，这个“多少”就是体积。

对于常见的几何体，如长方体，其体积计算公式为：体积＝长×宽×高。

如果一个长方体的长是 5 厘米，宽是 3 厘米，高是 2 厘米，那么它的体积就是 5×3×2 ＝ 30 立方厘米。

正方体是一种特殊的长方体，所有棱长都相等，所以正方体的体积＝棱长×棱长×棱长。

圆柱体的体积＝底面积×高。

底面积＝π×半径²，所以圆柱体体积＝π×半径²×高。

圆锥体的体积是与它等底等高圆柱体体积的三分之一，即圆锥体体积＝ 1/3×底面积×高。

接下来，我们再看看表面积。

表面积指的是几何体表面的总面积。

长方体的表面积＝（长×宽＋长×高＋宽×高）×2。

还是拿刚才那个长方体举例，长 5 厘米，宽 3 厘米，高 2 厘米，表面积就是（5×3 ＋5×2 ＋ 3×2）×2 ＝ 62 平方厘米。

正方体的表面积＝棱长×棱长×6。

圆柱体的表面积由侧面积和两个底面积组成。

侧面积＝底面圆的周长×高，底面圆的周长＝2×π×半径，所以圆柱体表面积＝2×π×半径×高＋2×π×半径²。

圆锥体的表面积＝底面积＋侧面积。

侧面积＝π×半径×母线（母线是顶点到底面圆周上一点的距离）。

几何体的表面积体积计算公式平面图形名称符号周长C和面积S正方形 a—边长 C＝4aS＝a^2长方形a和b－边长 C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a^2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角 S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角 S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长 S＝Dd/2＝a^2sinα梯形a和b－上、下底长h－高m－中位线长 S＝(a+b)h/2＝mh圆r－半径d－直径 C＝πd＝2πrS＝πr^2＝πd^2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr^2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数 S＝r^2/2·(πα/180-sinα) ＝r^2arccos[(r-h)/r] - (r-h)(2rh-h^2)1/2＝παr^2/360 - b/2·[r^2-(b/2)^2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径 S＝π(R^2-r^2)＝π(D^2-d^2)/4椭圆D－长轴d－短轴 S＝πDd/4立方图形名称符号面积S和体积V正方体 a－边长 S＝6a^2V＝a^3长方体a－长b－宽c－高 S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高 V＝Sh棱锥S－底面积h－高 V＝Sh/3棱台S1和S2－上、下底面积h－高 V＝h[S1+S2+(S1S2)^1/2]/3拟柱体S1－上底面积S2－下底面积S0－中截面积h－高 V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积 C＝2πrS底＝πr^2S侧＝ChS表＝Ch+2S底V＝S底h＝πr^2h空心圆柱R－外圆半径r－内圆半径h－高 V＝πh(R^2-r^2)直圆锥r－底半径h－高 V＝πr^2h/3圆台r－上底半径R－下底半径h－高 V＝πh(R^2＋Rr＋r^2)/3球r－半径d－直径 V＝4/3πr^3＝πd^3/6球缺h－球缺高r－球半径a－球缺底半径 V＝πh(3a^2+h^2)/6 ＝πh^2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高 V＝πh[3(r1^2＋r2^2)+h^2]/6圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径 V＝2π2Rr^2＝π2Dd^2/4桶状体D－桶腹直径d－桶底直径h－桶高 V＝πh(2D^2＋d^2)/12 (母线是圆弧形,圆心是桶的中心)V＝πh(2D^2＋Dd＋3d^2/4)/15 (母线是抛物线形)。

圆台棱台表面积体积公式圆台和棱台都是常见的几何体形状，它们的表面积和体积是计算几何学中的重要内容。

下面将介绍圆台和棱台的表面积和体积公式，并对其进行拓展。

一、圆台的表面积和体积公式：1. 表面积公式：圆台的表面积由两部分组成：底面的面积和侧面的面积。

底面的面积为圆的面积，侧面的面积由圆台的斜高、底半径和侧面的弧长决定。

圆台的表面积公式如下：表面积 = 圆的底面积 + 侧面积= πr1^2 + π(r1 + r2)l其中，r1为圆台的底半径，r2为圆台的顶半径，l为圆台的斜高。

2. 体积公式：圆台的体积由底面积和高度决定。

圆台的体积公式如下：体积 = 1/3 ×圆的底面积×高度= 1/3 ×πr1^2 × h其中，r1为圆台的底半径，h为圆台的高度。

二、棱台的表面积和体积公式：1. 表面积公式：棱台的表面积由底面的面积、顶面的面积和侧面的面积组成。

底面和顶面的面积分别为底面的面积和顶面的面积，侧面的面积由棱台的高度和棱长决定。

棱台的表面积公式如下：表面积 = 底面积 + 顶面积 + 侧面积= 底面积 + 顶面积 + 边长×高度× 2其中，底面积和顶面积由底面和顶面的形状决定，边长为棱台的底边长，高度为棱台的高度。

2. 体积公式：棱台的体积由底面积和高度决定。

棱台的体积公式如下：体积 = 1/3 ×底面积×高度其中，底面积由底面的形状决定，高度为棱台的高度。

拓展：除了圆台和棱台，还有许多其他几何体的表面积和体积公式。

例如，圆柱的表面积由底面积和侧面积组成，体积由底面积和高度决定。

球体的表面积和体积公式也存在。

此外，对于复杂的几何体，可以通过分解成简单的几何体来计算表面积和体积。

五年级几何体的表面积与体积的计算(可以直接使用，可编辑实用优秀文档，欢迎下载）空间与图形教师辅导讲义——立体图形的知识与应用知识要点长方体、正方体、圆柱体、圆锥体的表面积及体积1．表面积：物体表面面积的总和，叫做物体的表面积。

表面积通常用S 表示。

常用面积单位是平方千米、平方米、平方分米、平方厘米。

2．体积：物体所占空间的大小，叫做物体的体积。

体积通常用V 表示。

常用体积单位是立方米、立方分米、立方厘米。

3．容积：箱子、油桶、仓库等所能容纳物体的体积，叫做它们的容积或容量。

常用容积单位是升、毫升。

4．体积与容积单位之间的换算：1立方分米=l 升，1立方厘米=l 毫升。

5．体积和容积的异同点 容积的计算方法跟体积的计算方法相同，但要从容器的里面量长、宽、高，而计算体积要从物体的外面量长、宽、高。

计量体积用体积单位，计量容积除了用体积单位外，还可以用容积单位升和毫升。

6. 立体图形的表面积、侧面积和体积计算公式相同点不同点 面棱顶点面的特点 面的大小 棱长 长方体6个12条8个6个面一般都是长方形，也可能有两个相对的面是正方形相对的面的面积相等每一组互相平行的四条棱的长度相等正方体6个12条8个6个面都是相等的正方形6个面的面积都相等12条棱长的长度都相等精典题型分析1、一个零件形状大小如下图：算一算，它的体积是多少立方厘米，表面积是多少平方厘米。

（单位：厘米）练习：学校生物小组做了一个昆虫箱（如图）。

昆虫箱的上、下、左、右面是木板，前、后面装纱网。

①制作这样一个昆虫箱，至少需要多少平方厘米的木板？②制作这样一个昆虫箱，至少需要多少平方厘米的纱网？2、在一个长15分米，宽12分米的长方体水箱中，有10分米深的水。

如果在水中沉入一个棱长为30厘米的正方体铁块，那么，水箱中水深多少分米？练习1：一个长方体的玻璃缸内有一些水，水面距离上沿0.6分米（如图）。

准备在缸内放入一块体积是60立方分米的假山石（假山石能全部浸在水中），水会溢出吗？如果会溢出，溢出多少立方分米？练习2：一个正方体玻璃容器，从里面量棱长是2dm。

几何体的表面积与体积问题之前已经学过空间几何体的相关概念，知道什么是多面体什么是旋转体。

然后它们之间的一系列转化也已经了解，那么我们知不知道这些几何体的表面积或者是体积怎么求，本节课主要就是学习这块的内容。

在初中我们已经知道圆柱的体积是底面积乘以高，然后圆锥的体积需要乘以31。

所以这边我们先要了解一些其它的几何体的表面积和体积。

1．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面 展开图侧面 积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧 ＝π(r ＋r ′)l2.空间几何体的表面积与体积公式名 称 几何体 表面积体 积柱体 (棱柱和圆柱)S 表面积＝S 侧＋2S 底 V ＝S 底h 锥体 (棱锥和圆锥)S 表面积＝S 侧＋S 底V ＝13S 底h台体 (棱台和圆台)S 表面积＝S 侧 ＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h 球S ＝4πR 2V ＝43πR 3一些总结1．辨明两个易误点(1)求组合体的表面积时，要注意各几何体重叠部分的处理．(2)底面是梯形的四棱柱侧放时，容易和四棱台混淆，在识别时要紧扣定义，以防出错． 2.求空间几何体体积的常用方法(1)公式法：直接根据相关的体积公式计算．(2)等积法：根据体积计算公式，通过转换空间几何体的底面和高使得体积计算更容易，或是求出一些体积比等．(3)割补法：把不能直接计算体积的空间几何体进行适当的分割或补形，转化为可计算体积的几何体1．如图，一个空间几何体的正(主)视图、侧(左)视图、俯视图均为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为( )A ．1B ．12C.13D ．16D [解析] 由三视图可知，该几何体为三棱锥，V ＝13Sh ＝13×12×1×1×1＝16，故选D ．2.(2015·高考陕西卷)一个几何体的三视图如图所示，则该几何体的表面积为( ) A ．3π B ．4π C ．2π＋4D ．3π＋4D [解析] 由几何体的三视图可知，该几何体为半圆柱，直观图如图所示． 表面积为2×2＋2×12×π×12＋π×1×2＝4＋3π.主要的难点在于如何由三视图来转化为原来的几何体，然后进而求解几何体的表面积和体积。

五年级上册数学表面积和体积公式全文共四篇示例，供读者参考第一篇示例：数学是一门让许多学生都头疼的学科，尤其是对于小学五年级的学生来说，学习面积和体积公式可能会让他们感到困惑。

只要掌握了正确的方法和技巧，这些概念其实并不难理解。

今天，我们就来详细地学习一下五年级上册数学中关于表面积和体积的公式。

我们来看一下什么是表面积和体积。

简单来说，表面积是指一个物体外部的总面积，而体积则是指一个物体内部所占据的空间。

在日常生活中，我们经常会遇到需要计算表面积和体积的问题，比如购买家具时需要计算柜子的表面积，或者装水时需要计算容器的体积等等。

接下来，我们来学习一下常见的几何图形的表面积和体积公式。

首先是长方形和正方形。

长方形的表面积公式为S=2(l+w)，其中l为长，w为宽；体积公式为V=l×w×h，其中h为高。

正方形的表面积公式为S=4a^2，其中a为边长；体积公式为V=a^3。

以上就是五年级上册数学中关于表面积和体积的常见公式。

通过不断练习和掌握这些公式，相信大家一定可以轻松解决相关问题。

数学虽然有些难，但只要坚持下去，就一定能够取得优异的成绩。

希望本文对大家有所帮助，祝愿大家在学习数学的道路上一帆风顺！第二篇示例：五年级上册数学课程涉及到表面积和体积的公式，这是一个非常重要的概念，能够帮助我们计算和理解各种形状的物体。

表面积和体积是几何学中的两个重要概念，分别表示物体的外表面积和内部空间大小。

在这篇文章中，我们将详细介绍五年级上册数学课程中涉及到的一些表面积和体积的公式，帮助学生更好地理解和掌握这些知识。

让我们来介绍一下表面积的概念。

表面积是指一个物体的外表面的总面积，通常用单位面积（如平方厘米或平方米）来表示。

在五年级上册数学课程中，学生将学习如何计算不同形状物体的表面积，比如长方形、正方形、圆柱体等。

对于不同形状的物体，我们可以使用不同的公式来计算其表面积。

让我们来看看长方形的表面积公式。

正方体表面积和体积的公式
正方体是一种非常常见的几何体，它的六个面都是正方形，每个角都是直角，边长相等。

正方体的表面积和体积是我们在学习几何学时必须掌握的基本概念。

我们来看正方体的表面积公式。

正方体的表面积是指正方体六个面的总面积。

由于正方体的六个面都是正方形，所以每个面的面积都是边长的平方。

因此，正方体的表面积公式为：表面积 = 6 × 边长 × 边长 = 6 × 边长²。

接下来，我们来看正方体的体积公式。

正方体的体积是指正方体所占的空间大小。

由于正方体的六个面都是相等的正方形，所以正方体的体积公式为：体积 = 边长 × 边长 × 边长 = 边长³。

正方体的表面积和体积公式是非常基础的几何学知识，但是它们在我们的日常生活中却有着广泛的应用。

比如，在建筑工程中，我们需要计算房间的体积，以确定需要多少材料来建造房间。

在制造箱子或包装物品时，我们需要计算箱子的表面积，以确定需要多少纸板来制造箱子。

在计算机图形学中，我们需要计算三维物体的体积和表面积，以确定需要多少计算资源来渲染这些物体。

正方体的表面积和体积公式是我们在学习几何学时必须掌握的基本概念。

它们不仅在学术领域有着广泛的应用，而且在我们的日常生活中也有着重要的作用。

因此，我们应该认真学习和掌握这些公式，
以便在需要时能够灵活运用。

计算五棱柱的体积和表面积五棱柱是一种具有五个面的多面体，其中两个面是正五边形，其余三个面是矩形。

要计算五棱柱的体积和表面积，我们需要了解其几何特征以及相应的计算公式。

下面将分别介绍五棱柱的体积和表面积计算方法。

一、计算五棱柱的体积五棱柱的体积是指该几何体所占的三维空间的容积大小。

根据几何定律，我们知道计算五棱柱体积的公式为：体积 = 底面积 ×高度。

五棱柱的底面是一个正五边形，而其高度是从底面到顶面的直线距离。

为了计算体积，我们需要先计算出底面积和高度。

1. 计算底面积正五边形的面积计算公式为：底面积 = (5 ×边长^2) / (4 × tan(π/5))。

其中，边长是正五边形的边长，π是圆周率，tan(π/5)是五边形内角的正切值。

2. 计算高度五棱柱的高度可以通过测量底面中心到顶面的垂直距离得到。

3. 计算体积将计算出的底面积和高度代入体积公式，即可得到五棱柱的体积。

二、计算五棱柱的表面积五棱柱的表面积是指该几何体表面的总面积大小。

它由底面积、顶面积和侧面积三部分组成。

计算五棱柱的表面积需要分别计算这三部分的面积并求和。

1. 计算底面积和顶面积由前面提到的计算底面积的公式可知，底面积即为正五边形的面积。

2. 计算侧面积五棱柱的侧面是由三个矩形组成的，而矩形的面积计算公式为：侧面积 = 底边长 ×高度。

在五棱柱中，底边长即为正五边形的边长，而高度可以通过测量底面中心到顶面的垂直距离得到。

3. 计算表面积将底面积、顶面积和侧面积三部分的面积相加，即可得到五棱柱的表面积。

总结：计算五棱柱的体积和表面积时，我们首先需要计算底面积和高度，然后根据相应的公式进行计算。

体积的计算公式为体积 = 底面积 ×高度，表面积的计算公式为表面积 = 底面积 + 顶面积 + 侧面积。

根据这些计算公式，我们可以准确计算出五棱柱的体积和表面积。

体积与表面积之练习题计算几何体的体积和表面积在几何学中，计算物体的体积和表面积是非常重要的任务。

对于不同形状的几何体，我们需要掌握不同的计算方法。

本文将通过练习题的方式，帮助读者巩固对体积和表面积的计算方法的理解和掌握。

一、长方体的体积和表面积计算长方体是最基本的几何体之一，其具有长方形的底面和平行于底面的六个矩形侧面。

下面我们来计算一个长方体的体积和表面积。

例题1：一个长方体的长、宽、高分别为6cm、4cm、3cm，求其体积和表面积。

解：首先计算体积。

长方体的体积公式为V = 长 ×宽 ×高。

代入已知的数值，可得V = 6cm × 4cm × 3cm = 72cm³。

接下来计算表面积。

长方体的表面积公式为A = 2(长 ×宽 + 长 ×高+ 宽 ×高)。

代入已知的数值，可得A = 2(6cm × 4cm + 6cm × 3cm +4cm × 3cm) = 120cm²。

所以该长方体的体积为72cm³，表面积为120cm²。

二、圆柱体的体积和表面积计算圆柱体是一个底面为圆，侧面为平行于底面的矩形的几何体。

下面我们来计算一个圆柱体的体积和表面积。

例题2：一个圆柱体的底面直径为10cm，高为8cm，求其体积和表面积（取π ≈ 3.14）。

解：首先计算体积。

圆柱体的体积公式为V = πr²h，其中r为底面半径，h为高。

底面直径为10cm，那么半径为r = 10cm/2 = 5cm。

代入已知的数值，可得V = 3.14 × (5cm)² × 8cm = 628cm³。

接下来计算表面积。

圆柱体的表面积公式为A = 2πrh + 2πr²。

代入已知的数值，可得A = 2 × 3.14 × 5cm × 8cm + 2 × 3.14 × (5cm)² =376cm²。

球锥的体积与表面积计算方法球锥是由一个球面和一个锥面组成的几何体。

在计算球锥的体积和表面积时，我们需要分别计算球面的面积和锥面的面积，然后将两者相加即可得到球锥的总体积和总表面积。

首先，我们来计算球面的面积。

球面的面积公式为：S1 = 4πr²其中，S1表示球面的面积，r表示球的半径。

根据题目要求，我们已经知道球锥的底面是一个圆球，假设其半径为r。

因此，球面的面积即为底面圆球的表面积。

接下来，我们计算锥面的面积。

锥面的面积公式为：S2 = πrL其中，S2表示锥面的面积，r表示底面圆球的半径，L表示球锥的母线长度。

母线是连接球锥顶点与底面圆心的直线。

现在，我们已经知道了球锥的底面圆球的半径r，接下来需要计算母线的长度L。

根据题目没有给出具体的数据，我们可以假设球锥的高为h，然后利用勾股定理计算母线的长度。

根据勾股定理，我们可以得到：L² = r² + h²通过求根运算，可以解出母线长度L。

然后，我们就可以根据锥面的面积公式计算锥面的面积S2。

最后，我们将球面的面积S1和锥面的面积S2相加，即可得到球锥的总表面积：ST = S1 + S2同理，我们可以计算球锥的体积。

球锥的体积公式为：V = (1/3)S1h其中，V表示球锥的体积，S1表示球面的面积，h表示球锥的高度。

综上所述，计算球锥的体积与表面积的方法为：1. 已知底面圆球半径r和球锥高度h，首先计算球面的面积S1，公式为S1 = 4πr²。

2. 根据球锥高度h和底面圆球半径r计算母线长度L，公式为L² =r² + h²，通过求根运算得出L。

3. 计算锥面的面积S2，公式为S2 = πrL。

4. 计算球锥的总表面积ST，公式为ST = S1 + S2。

5. 计算球锥的体积V，公式为V = (1/3)S1h。

通过以上计算步骤，我们可以准确计算出球锥的体积和表面积。

在实际应用中，这些计算方法对于工程建设、物理学等领域都有着重要的意义。