[趣味数学] 韩信点兵

趣味数学教案-韩信点兵一、教学目标：1. 让学生了解并掌握“韩信点兵”的基本方法和技巧。

2. 培养学生的逻辑思维能力和解决问题的能力。

3. 提高学生学习数学的兴趣，感受数学的趣味性和实用性。

二、教学内容：1. “韩信点兵”的背景故事介绍。

2. “韩信点兵”的基本方法和步骤。

3. “韩信点兵”在实际生活中的应用。

三、教学重点与难点：1. 教学重点：让学生掌握“韩信点兵”的基本方法和技巧。

2. 教学难点：如何引导学生运用“韩信点兵”解决实际问题。

四、教学方法：1. 讲授法：讲解“韩信点兵”的背景故事、基本方法和步骤。

2. 案例分析法：分析“韩信点兵”在实际生活中的应用案例。

3. 实践操作法：让学生分组进行“韩信点兵”的实践操作，培养学生的动手能力。

五、教学准备：1. 教学课件：包括“韩信点兵”的背景故事、方法步骤、实际应用案例等。

2. 教学素材：准备一些关于“韩信点兵”的实际问题，用于课堂练习和拓展。

3. 分组标志：用于学生分组实践操作。

教案一、导入（5分钟）1. 讲述“韩信点兵”的背景故事，引发学生兴趣。

2. 提问：同学们听说过“韩信点兵”吗？你们认为“韩信点兵”是一种什么方法？二、基本方法讲解（10分钟）1. 讲解“韩信点兵”的基本方法和步骤。

2. 通过举例，让学生理解并掌握“韩信点兵”的原理。

三、实际应用案例分析（10分钟）1. 分析“韩信点兵”在实际生活中的应用案例。

2. 让学生思考：如何将“韩信点兵”应用于生活中的问题解决？四、实践操作（10分钟）1. 将学生分成若干小组，每组选择一个实际问题进行“韩信点兵”的操作实践。

2. 教师巡回指导，解答学生疑问。

五、总结与拓展（5分钟）1. 对本节课的内容进行总结，强调“韩信点兵”的方法和技巧。

2. 提出一些拓展问题，激发学生进一步探索的兴趣。

教学反思：通过本节课的教学，学生是否掌握了“韩信点兵”的基本方法和技巧？他们在实际操作中是否能够灵活运用？对于教学中的难点，学生是否能够理解并解决实际问题？这些问题都值得我们反思和改进。

简介：韩信点兵又称为中国剩余定理，乃由于相传汉高祖刘邦问大将军韩信统御兵士多少，韩信答说，每3人一列余1人、5人一列余2人、7人一列余4人、13人一列余6人……。

刘邦茫然而不知其数。

韩信点兵是一个很有趣的猜数游戏，随便抓一把蚕豆粒，假若3个一数余1粒，5个一数余2粒，7个一数余2粒，那么所抓的蚕豆有多少粒?这类题目看起来是很难计算的，可是中国古时却流传着一种算法，它的名称也很多，宋朝周密叫它「鬼谷算」，又名「隔墙算」；杨辉叫它「剪管术」；而比较通行的名称是「韩信点兵」。

最初记述这类算法的是一本名叫「孙子算经」的书，后来在宋朝经过数学家秦九韶的推广，又发现了一种算法，叫做「大衍求一术」，流传到西洋以后，外国化称它是「中国剩余定理」，在数学史上是极有名的问题。

至于它的算法，在「孙子算经」上就已经有了说明：“凡三三数之剩一，则置七十；五五数之剩一，则置二十一；七七数之剩一，则置十五”，而且还流传着这么一首歌诀：三人同行七十稀，五树梅花廿一枝，七子团圆正半月，除百零五便得知。

这就是韩信点兵的计算方法，《孙子算经》中给出了其中关键的步骤是：但在《孙子算经》中并没有说明求乘数的方法，直到1247年宋代数学家秦九韶在《数书九章》中才给出具体求法：70是5与7最小公倍的2倍，21、15分别是3与7、3与5最小公倍数的1倍。

秦九韶称这2、1、1的倍数为“乘率”，求出乘率，就可知乘数，意思是说：凡是用3个一数剩下的余数，将它用70去乘（因为70是5与7的倍数，而又是以3去除余1的），5个一数剩下的余数，将它用21去乘（因为21是3与7的倍数，又是以5去除余1的），7个一数剩下的余数，将它用15去乘（因为15是3与5的倍数，又是以7去除余1的），最后将70、5、15这些数加起来，若超过105，就再减掉105，所得的数便是原来的数了。

根据这个道理，你就可以很容易地把前面一个题目列成算式：1×70＋2×21＋2×15－105＝142－105＝37。

簡介：韓信點兵又稱為中國剩餘定理，乃由於相傳漢高祖劉邦問大將軍韓信統御兵士多少，韓信答說，每3人一列餘1人、5人一列餘2人、7人一列餘4人、13人一列餘6人……。

劉邦茫然而不知其數。

韓信點兵是一個很有趣的猜數遊戲，隨便抓一把蠶豆粒，假若3個一數餘1粒，5個一數餘2粒，7個一數餘2粒，那麼所抓的蠶豆有多少粒?這類題目看起來是很難計算的，可是中國古時卻流傳著一種算法，它的名稱也很多，宋朝周密叫它「鬼谷算」，又名「隔牆算」；楊輝叫它「剪管術」；而比較通行的名稱是「韓信點兵」。

最初記述這類算法的是一本名叫「孫子算經」的書，後來在宋朝經過數學家秦九韶的推廣，又發現了一種算法，叫做「大衍求一術」，流傳到西洋以後，外國化稱它是「中國剩餘定理」，在數學史上是極有名的問題。

至於它的算法，在「孫子算經」上就已經有了說明：“凡三三數之剩一，則置七十；五五數之剩一，則置二十一；七七數之剩一，則置十五”，而且還流傳著這麼一首歌訣：三人同行七十稀，五樹梅花廿一枝，七子團圓正半月，除百零五便得知。

這就是韓信點兵的計算方法，《孫子算經》中給出了其中關鍵的步驟是：但在《孫子算經》中並沒有說明求乘數的方法，直到1247年宋代數學家秦九韶在《數書九章》中才給出具體求法：70是5與7最小公倍的2倍，21、15分別是3與7、3與5最小公倍數的1倍。

秦九韶稱這2、1、1的倍數為“乘率”，求出乘率，就可知乘數，意思是說：凡是用3個一數剩下的餘數，將它用70去乘（因為70是5與7的倍數，而又是以3去除餘1的），5個一數剩下的餘數，將它用21去乘（因為21是 3與 7的倍數，又是以5去除餘1的），7個一數剩下的餘數，將它用15去乘（因為15是3與5的倍數，又是以 7去除餘 1的），最後將70、5、15這些數加起來，若超過105，就再減掉105，所得的數便是原來的數了。

根據這個道理，你就可以很容易地把前面一個題目列成算式：1×70＋2×21＋2×15－105＝142－105＝37。

韩信点兵的故事及数学知识
韩信点兵的故事是一个著名的数学问题，它在中国古代数学史上占有重要地位。

这个故事描述的是韩信在点兵时，通过利用余数的方法来判断士兵的数量。

故事背景是秦朝末年，楚汉相争时期。

韩信作为刘邦的部下，需要点兵迎战。

他让士兵们每排站3人，结果多出2名；每排站5人，结果多出3名；每排站7人，结果多出2名。

通过这一系列条件，韩信得知了总共有1073名士兵。

这个问题的核心是利用余数来判断士兵的数量。

当士兵们每排站3人时，多出2人，即士兵总数除以3的余数是2。

同样地，当每排站5人时，多出3人，即士兵总数除以5的余数是3。

当每排站7人时，多出2人，即士兵总数除以7的余数是2。

因此，我们可以使用中国剩余定理来解决这个问题。

中国剩余定理是指在整数系中，给定一组线性同余方程（组），存在一个整数n，使得n对这组同余方程（组）的余数均为0。

在这个问题中，我们可以设士兵总数为n，那么n对3、5、7的余数分别为2、3、2。

因此，我们可以得到一组线性同余方程：
n ≡ 2 (mod 3)
n ≡ 3 (mod 5)
n ≡ 2 (mod 7)
通过解这组方程，我们可以得到士兵的总数为1073。

这个故事展示了数学在古代中国的广泛应用。

通过数学方法来解决实际问题，不仅体现了数学的实用性，也展示了古代中国在数学领域的卓越成就。

[兴趣数学] 韩信点兵民间故事《韩信点兵》：韩信是汉高祖刘邦手下的大将，他勇敢善战，智谋超群，为汉朝的兴成立下了卓越的功绩。

听说韩信的数学水平也特别高明，他在点兵的时候，为了保住军事机密，不让仇敌知道自己队伍的实力，先令士兵从 1 至3 报数，而后记下最后一个士兵所报之数；再令士兵从 1 至5 报数，也记下最后一个士兵所报之数；最后令士兵从 1 至7 报数，又记下最后一个士兵所报之数；这样，他很快就算出了自己队伍士兵的总人数，而仇敌则一直没法弄清他的队伍终究有多少名士兵。

比方，已知军队人数大体在1000-1100 左右，假如1-3 报数余2 人，1-5 报数余 3 人，1-7 报数余 2 人，则韩信马上知道总人数1073 人。

汉军原来就服气自己的统帅，这一来更相信韩信是“仙人下凡”、“神机秒术”于。

是每次出战都士气大振，常常大获全胜。

把韩信点兵问题再换个更简单的说法，就是说，有个数除 3 余2，除 5 余3，除7 余2，问你这个数字最小是几？也可以给定一个范围，问你是几。

这种问题，纠结应当怎么下手解决呢？关于这样的问题，要先察看，能否存在规律，假如切合必定的规律，则能够经过简单口诀来实现；假如没有规律，那么就要经过一些特别方法办理。

一、有规律问题的解法重要口诀：和同加和，差同减差，余同取余，最小公倍加先来谈谈最后一句，最小公倍加，意思是，不论什么状况，先把最小公倍数求出来，这个是作为基础。

而后依据不一样情况进行鉴别，怎样持续办理。

（一）和同加和意思是，假如不一样被除数和余数的和相同，那么就把这个和，加到最小公倍数上。

例：一个数除 5 余3，除 6 余2，除7 余1解题思路：5、6、7 的最小公倍数是210 ，因为5＋3＝6＋2 ＝7＋1＝8，因此这个数最小就是8，其他知足条件的数字是210 的倍数＋8，比方218 、428⋯⋯（二）差同减差意思是，假如不一样被除数和余数的差相同，那么就把这个差，用最小公倍数减掉。

趣味数学教案-韩信点兵一、教学目标：1. 让学生了解并掌握“韩信点兵”的基本方法和原理。

2. 培养学生的逻辑思维能力和解决问题的能力。

3. 激发学生对数学的兴趣，提高学生的学习积极性。

二、教学内容：1. 韩信点兵的背景故事介绍。

2. 韩信点兵的方法和步骤讲解。

3. 韩信点兵的应用练习。

三、教学重点与难点：1. 教学重点：韩信点兵的方法和步骤。

2. 教学难点：如何灵活运用韩信点兵解决实际问题。

四、教学准备：1. 准备相关背景故事资料。

2. 准备韩信点兵的练习题。

五、教学过程：1. 导入：讲述韩信点兵的背景故事，引发学生兴趣。

2. 新课讲解：讲解韩信点兵的方法和步骤，让学生理解和掌握。

3. 练习环节：让学生运用韩信点兵的方法解决实际问题，巩固所学知识。

六、教学策略：1. 采用问题驱动的教学方法，引导学生主动探究韩信点兵的解题方法。

2. 通过小组合作、讨论交流的方式，提高学生的合作能力和沟通能力。

3. 利用信息技术辅助教学，展示韩信点兵的动画演示，增强学生的直观感受。

七、教学评价：1. 课堂练习：观察学生在练习中的表现，评估学生对韩信点兵方法的掌握程度。

2. 学生互评：鼓励学生之间相互评价，提高学生的自我认知和反思能力。

3. 课后反馈：收集学生的课后反馈，了解学生在课堂外的应用情况。

八、教学延伸：1. 组织学生进行数学竞赛，运用韩信点兵的方法解决竞赛题目。

2. 邀请家长参与亲子活动，共同探讨韩信点兵在生活中的应用。

3. 鼓励学生进行数学研究，深入挖掘韩信点兵的原理和拓展应用。

九、教学反思：在教学过程中，及时反思教学方法的有效性，根据学生的反馈调整教学策略。

关注学生的个体差异，因材施教，使每位学生都能在课堂上得到有效的提升。

十、教学计划：1. 课时安排：本课题计划安排4课时完成。

3. 课后作业：布置相关练习题，巩固学生对韩信点兵方法的掌握。

重点和难点解析一、教学目标：在制定教学目标时，需关注如何将韩信点兵的原理与实际应用相结合，以培养学生的逻辑思维能力和解决问题的能力。

【叙事】韩信点兵有趣的数学题作文600字韩信是中国历史上著名的军事将领，他智勇双全，在军事战争中屡建奇功。

而韩信点兵这个故事，更是为我们展示了他非凡的智慧和计算能力。

下面就让我们一起来看看，韩信点兵的有趣数学题吧。

韩信首先让士兵们排成10行100列的队伍，然后他对他们说：“第一排报数！”这时站在第一排的士兵依次报数：“1，2，3，……，100。

”然后韩信说：“三百步内报到者留下，其他人走开。

”接着他让第二排的士兵报数：“1，2，3，……，100。

”然后又让第三排的士兵报数：“1，2，3，……，100。

”如此循环直至最后一排报数完毕。

韩信便可以轻易地知道留下的士兵是否1000人了，而且他还知道了具体是哪些士兵留下的。

这是如何做到的呢？这就是一个有趣的数学题。

我们知道1000可以被表示为10x100，其中x是一个正整数。

每次让一排士兵报数后，韩信就可以知道留下的士兵数目，只要对1000除以这个数目并取余数，就可以知道留下的是哪些士兵。

比如当韩信让第一排士兵报数后，余数是0时，就可以知道留下的士兵是1,2,3,……,100。

然后当让第二排士兵报数后，余数是0时，则可以知道仍然留下的是101,102,……,200。

以此类推，韩信可以依次得知每排士兵中留下的人数和具体是哪些士兵，最终就可以得知留下的士兵数目是否达到了1000。

这个数学题虽然看似简单，但却蕴含了非常深刻的数学含义。

通过这个数学题，我们不仅可以锻炼自己的算术能力，还可以体会到数学在现实生活中的应用价值。

这个有趣的数学题也向我们展示了韩信这位古代将军非凡的智慧和严谨的思维方式。

通过韩信点兵的有趣数学题，我们不仅可以感受到古代将军的智慧，还可以学到一些有趣的数学知识。

希望我们在平时的学习生活中也能遇到更多有趣的数学问题，从中获得更多的乐趣。

1.鬼谷算
我国汉代有位大将，名叫韩信。

他每次集合部队只要求部下先后按1~3、1~5、1~7报数，然后再报告一下各队每次报数的余数，他就知道到了多少人。

他的这种巧妙算法，人们称为鬼谷算，也叫隔墙算，或称为韩信点兵，外国人还称它为“中国剩余定理”。

比如，一篮鸡蛋，三个三个地数余一，五个五个地数余二，七个七个地数余三，篮子里至少是52个鸡蛋。

算式是什么?
2.下图所示的图形绕哪一点旋转多少度后能与自身重合?
【分析】图1是个正三角形，每个角都是60°，有三条对称轴，每两个对称轴之间是120°，所以，图1绕点O旋转120°能与自身重合。

同理，图2有五条对称轴，相邻两条对称轴的夹角是72°，所以，图2绕中心点旋转72°后能与自身重合。

【答案】图1绕点O旋转120°能与自身重合。

图2绕中心点旋转72°后能与自身重合。

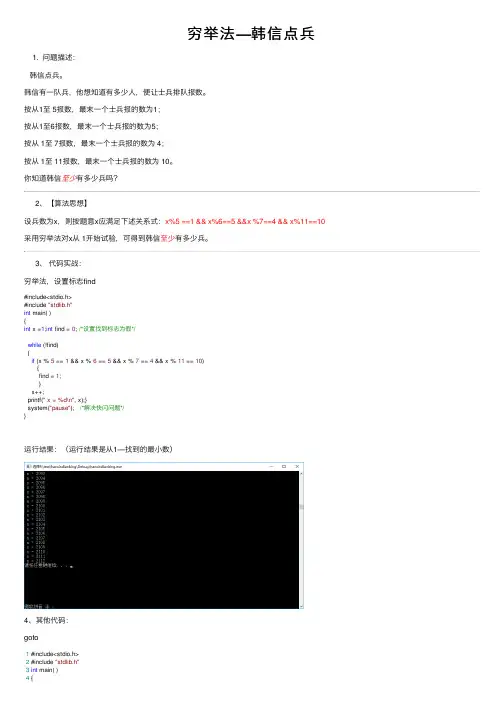
穷举法—韩信点兵1. 问题描述：韩信点兵。

韩信有⼀队兵，他想知道有多少⼈，便让⼠兵排队报数。

按从1⾄ 5报数，最末⼀个⼠兵报的数为1；按从1⾄6报数，最末⼀个⼠兵报的数为5；按从 1⾄ 7报数，最末⼀个⼠兵报的数为 4；按从 1⾄ 11报数，最末⼀个⼠兵报的数为 10。

你知道韩信⾄少有多少兵吗？2、【算法思想】设兵数为x，则按题意x应满⾜下述关系式：x%5 ==1 && x%6==5 &&x %7==4 && x%11==10采⽤穷举法对x从 1开始试验，可得到韩信⾄少有多少兵。

3、代码实战：穷举法，设置标志find#include<stdio.h>#include "stdlib.h"int main( ){int x =1;int find = 0; /*设置找到标志为假*/while (!find){if (x % 5 == 1 && x % 6 == 5 && x % 7 == 4 && x % 11 == 10){find = 1;}x++;printf(" x = %d\n", x);}system("pause"); /*解决快闪问题*/}运⾏结果：（运⾏结果是从1—找到的最⼩数）4、其他代码：goto1 #include<stdio.h>2 #include "stdlib.h"3int main( )4 {5int x ;6for(x=1; ;x++)7 {8if(x % 5 == 1 && x % 6 == 5 && x % 7 == 4 && x % 11 == 10 ) 9 { printf("最⼩值是x= %d\n ",x);10goto end;11 }12 }13 end:;14 system("pause");15 }break语句执⾏代码1 #include<stdio.h>2 #include "stdlib.h"3int main( )4 {5int x ;6for(x=1; ;x++)7 {8if(x % 5 == 1 && x % 6 == 5 && x % 7 == 4 && x % 11 == 10 ) 9 { printf("最⼩值是x= %d\n ",x);10break;11 }12 }1314 system("pause");15 }结果相同，不再赘述。

韩信点兵教学目标：一、让学生在故事中学会带余除法的算法，掌握剩余定理。

二、帮助学生开拓逻辑思维，提前掌握用未知数列方程。

三、在学习中玩，在玩中学习，让学生体验到学习的快乐。

教学重点：剩余定理，带余除法教学难点：多方程解未知数课前准备：教学PPT教学步骤：一、韩信点兵汉高祖刘邦曾问大将韩信：“你看我能带多少兵？”韩信斜了刘邦一眼说：“你顶多能带十万兵吧！”汉高祖心中有三分不悦，心想：你竟敢小看我！“那你呢？”韩信傲气十足地说：“我呀，当然是多多益善啰！”刘邦心中又添了三分不高兴，勉强说：“将军如此大才，我很佩服。

现在，我有一个小小的问题向将军请教，凭将军的大才，答起来一定不费吹灰之力的。

”韩信满不在乎地说：“可以可以。

”刘邦狡黠地一笑，传令叫来一小队士兵隔墙站队，刘邦发令：“每三人站成一排。

”队站好后，小队长进来报告：“最后一排只有二人。

”“刘邦又传令：“每五人站成一排。

”小队长报告：“最后一排只有三人。

”刘邦再传令：“每七人站成一排。

”小队长报告：“最后一排只有二人。

”刘邦转脸问韩信：“敢问将军，这队士兵有多少人？”韩信脱口而出：“二十三人。

”刘邦大惊，心中的不快已增至十分，心想：“此人本事太大，我得想法找个岔子把他杀掉，免生后患。

”一面则佯装笑脸夸了几句，并问：“你是怎样算的？”韩信说：“臣幼得黄石公传授《孙子算经》，这孙子乃鬼谷子的弟子，算经中载有此题之算法.二、唐僧师徒摘桃子一天，唐僧命徒弟悟空、八戒、沙僧三人去花果山摘些桃子。

不长时间，徒弟三人摘完桃子高高兴兴回来。

师父唐僧问：你们每人各摘回多少个桃子？八戒憨笑着说：师父，我来考考你。

我们每人摘的一样多，我筐里的桃子不到100个，如果3个3个地数，数到最后还剩1个。

你算算，我们每人摘了多少个？沙僧神秘地说：师父，我也来考考你。

我筐里的桃子，如果4个4个地数，数到最后还剩1个。

你算算，我们每人摘了多少个？悟空笑眯眯地说：师父，我也来考考你。

【叙事】韩信点兵有趣的数学题作文600字韩信是中国历史上著名的军事将领，他的智谋和谋略被后人传颂不衰。

而他点兵的故事更是被人津津乐道。

今天，我们就来讲一讲这个有趣的故事。

相传在韩信年轻的时候，他曾经在一个军队里做过一个小小的官，他非常聪明能干，服务得很受人喜欢。

有一天，他奉命点兵，要准备军队出征。

韩信想出了一个非常有趣的数学题来点兵。

他把所有的士兵分成了三队，并对他们说：“这三队士兵的数量之积等于三千，现在我给你们一个数学题，你们分组，每组的数量之积等于这个数学题的答案，请看谁能最快的分组。

”士兵们听了之后，都纷纷掐指算计，可是没一个人会算，韩信心中暗喜，因为他知道，这个数学题并不是那么容易的。

不久，一名精明的士兵走了出来，他说：“我知道了，大人，我来说答案，第一队有三百人，第二队有三十人，第三队有十人，这样的话，就能满足你所说的条件了。

”韩信听了之后，点点头，对这名士兵说：“不错，你很聪明，确实符合我的要求。

”其他士兵听了之后，也都纷纷拍手称快，因为他们一开始也都纷纷掐指算计，也都算不出来。

韩信点兵的故事就这样传了下来，后来人们把这个故事当成数学题来讲解，这个数学题也因此而闻名遐迩。

这个故事给我们留下了很深的启发，不仅能引起我们对数学的兴趣，同时也启发了我们要善于运用数学的思维方式来解决生活中的问题。

这个故事还告诉我们一个道理，那就是智慧是无穷的，只要肯动脑筋，人人都可以想出办法来解决难题。

正所谓“智者乐水，仁者乐山”，只要我们努力去学习，用心去思考，就一定可以找到解决问题的方法。

韩信的点兵故事给我们留下了很深的启发，用数学题来点兵，不仅展现了韩信的聪明智慧，也让我们对数学题增加了更多的兴趣。

相信通过这个故事，我们可以更深入地了解到数学的魅力，也可以更好地学习数学知识。

初中数学趣味题目大全之韩信点兵韩信点兵韩信是我国汉代著名的大将，曾经统率过千军万马，他对手下士兵的数目了如指掌。

他统计士兵数目有个独特的方法，后人称为“韩信点兵”。

他的方法是这样的，部队集合齐后，他让士兵1、2、3－－1、2、3、4、5－－1、2、3、4、5、6、7地报三次数，然后把每次的余数再报告给他，他便知道部队的实际人数和缺席人数。

他的这种计算方法历史上还称为“鬼谷算”，“隔墙算”，“剪管术”，外国人则叫“中国剩余定理”。

有人用一首诗概括了这个问题的解法：三人同行七十稀，五树梅花廿一枝，七子团圆月正半，除百零五便得知。

这意思就是，第一次余数乘以70，第二次余数乘以21，第三次余数乘以15，把这三次运算的结果加起来，再除以105，所得的除不尽的余数便是所求之数（即总数）。

例如，如果3个3个地报数余1，5个5个地报数余2，7个7个地报数余3，则总数为52。

算式如下：1×70＋2×21＋3×15＝157157÷105＝1 (52)一般说来，“教师”概念之形成经历了十分漫长的历史。

杨士勋（唐初学者，四门博士）《春秋谷梁传疏》曰：“师者教人以不及，故谓师为师资也”。

这儿的“师资”，其实就是先秦而后历代对教师的别称之一。

《韩非子》也有云：“今有不才之子……师长教之弗为变”其“师长”当然也指教师。

这儿的“师资”和“师长”可称为“教师”概念的雏形，但仍说不上是名副其实的“教师”，因为“教师”必须要有明确的传授知识的对象和本身明确的职责。

下边给同学们出一道题，请用“韩信点兵法”算一算。

唐宋或更早之前，针对“经学”“律学”“算学”和“书学”各科目，其相应传授者称为“博士”，这与当今“博士”含义已经相去甚远。

而对那些特别讲授“武事”或讲解“经籍”者，又称“讲师”。

“教授”和“助教”均原为学官称谓。

前者始于宋，乃“宗学”“律学”“医学”“武学”等科目的讲授者；而后者则于西晋武帝时代即已设立了，主要协助国子、博士培养生徒。

《韩信点兵的数学故事》小朋友们，今天我要给你们讲一个特别有趣的数学故事，叫韩信点兵。

韩信呀，是古代一位很厉害的将军。

有一次，他带着士兵们出去打仗。

打完仗回来，他想知道自己到底带了多少士兵。

他让士兵们先排成 3 人一排，结果多了 2 个人；再排成 5 人一排，多了 3 个人；最后排成7 人一排，又多了 2 个人。

这可把大家难住了。

但是韩信可聪明啦！他想了一会儿，就知道士兵的数量了。

我来给你们举个例子啊。

比如说，我们先从 3 人一排多 2 个人开始想。

可能是5 个、8 个、11 个……那再结合 5 人一排多 3 个人，7 人一排多 2 个人，一点点去试，最后就能找到答案啦。

小朋友们，你们觉得韩信是不是很厉害呀？《韩信点兵的数学故事》小朋友们，咱们来讲讲韩信点兵的故事哟！韩信带着好多好多士兵去打仗。

打完仗了，他想数数有多少人。

他让士兵们 3 个 3 个地站一排，哎呀，多了 2 个；又让 5 个 5 个地站一排，多了3 个；再让7 个7 个地站一排，还是多了 2 个。

这可把大家给难坏了。

不过，韩信可聪明着呢！他就坐在那里想啊想。

比如说，我们先从少一点的数字开始猜。

3 人一排多 2 个，可能是 5 个，那再看看 5 人一排合不合适。

就这样一点点去试，最后就能知道到底有多少士兵啦。

小朋友，要是让你们来猜，能猜得出来吗？《韩信点兵的数学故事》小朋友们，今天来讲韩信点兵的好玩故事。

韩信这位大将军，打完仗要数士兵。

他让士兵 3 个一排，多 2 个；5 个一排，多 3 个；7 个一排，多 2 个。

这可咋整呢？咱们来想想啊，比如从10 个人开始试。

10 个不行，那15 个，还不行。

就这样一直试。

韩信可厉害啦，他一直想一直想，终于想到答案啦。

我再给你们举例，假如先猜20 个人，看看符合不符合条件。

不符合就再换个数字。

小朋友们，你们觉得这个故事有趣不？。

韩信点兵数学题韩信是中国历史上著名的将领之一，他在数学方面也非常突出。

他曾提出了一道著名的问题，被称为“韩信点兵数学题”。

这道题可以用一个简单的数学算法来解决，下面我们就来详细讲解。

问题描述韩信在战斗中遇到了一支敌军。

他想要知道敌军究竟有多少兵力，于是他派人去数敌军的军营。

不过，他的间谍只能在外面听取军营内的人数。

听了一阵之后，间谍回来汇报说：“将军，我数了三次，每次听到的数字分别是3、5和7，而且这些数字之和是78。

”这时，韩信突然想到，敌军的兵力究竟是多少呢？问题分析假设敌军的兵力为x，那么我们可以列出以下的等式：3x ≡ 2 (mod 3)5x ≡ 3 (mod 5)7x ≡ 4 (mod 7)这里，≡ 指的是模等于，也就是两个数除以模数后的余数相等。

我们可以发现，所有的式子右边都有一个共同的模数，也就是3、5和7的乘积，即105。

在这个等式组中，我们要找到一个数x，使得对于每个等式，都满足模等于的条件。

欧拉定理为了解决这类问题，我们可以利用欧拉定理。

欧拉定理表示：如果两个数a和m互质（即它们没有公因数），那么a^φ(m) ≡ 1 (mod m)。

其中，φ(m)表示小于或等于m的正整数中，与m互质的数的个数。

在我们的问题中，3、5和7互质。

所以我们可以求解方程组中每个等式的解。

解题过程首先，我们需要根据欧拉定理来计算φ(m)。

φ(3) = 3 - 1 = 2φ(5) = 5 - 1 = 4φ(7) = 7 - 1 = 6接下来，我们将每个等式的模数m换成105，并根据欧拉定理来求解。

3^2 ≡ 1 (mod 3)5^4 ≡ 1 (mod 5)7^6 ≡ 1 (mod 7)然后，我们可以得到以下的等式：3x ≡ 2 (mod 105)5x ≡ 3 (mod 105)7x ≡ 4 (mod 105)接下来，我们可以计算这些等式的解。

对于第一个等式，我们可以得到x ≡ 35 (mod 105)。

韩信点兵问题韩信点兵问题又称“中国剩余定理”或“孙子定理”。

这种问题好多老师的讲解方法很笨拙，同学们做起来也很吃力，不少好学生在考试时，用了大量的时间研究这道题，为了提高我们的解题速度及正确率，现将我的经验和解题技巧提供给大家。

这类问题的解法根据是：1、如果被除数增加除数的若干倍，除数不变，那么余数不变。

例如：19÷7=2 (5)（19+2×7）÷7=4 (5)2、如果被除数扩大若干倍，除数不变，那么余数也扩大同样的倍数。

例如：20÷9=2 (2)（20×3）÷9=6 (6)例1、一个数除以5余3，除以6余4，除以7余1.求适合这些条件的最小数。

【5，6】=30 因为30÷7=4……2 不余1，要想余数为1，就得将余数2扩大4倍，即被除数扩大4倍，得30×4=120，所以120除以7余1。

【5，7】=35 因为 35÷6=5……5 ，要想余数为4，就得将余数5扩大2倍，那么被除数30就得扩大2倍，即35×2=70所以70÷6余4.【6，7】=42 因为42÷5=8……2 要想符合题中要求余3的话，余数2就得扩大4倍，即被除数扩大4倍，得42×4=168，168除以5余3.现找到的符合题中条件的一个数为：120+70+168=358 ，但不是最小的数，要想最小，就得减去除数5、6、7的最小公倍数，直到不够减为止。

【5，6，7】=210 ， 358-210=148 ，所以答案为148完整的算式为：【5，6】=30 30÷7=4……2 30×4=120【5，7】=35 35÷6=5……5 35×2=70【6，7】=42 42÷5=8……2 42×4=168【5，6，7】=210120+70+168=358 358-210=148答：符合条件的最小的数是148.注：也可能会出现四个除数，不管有几个除数，都是用其它几个数的最小公倍数除以另外一个数，再找符合该条件的余数的被除数。

【叙事】韩信点兵有趣的数学题作文600字韩信是中国古代著名的将军，他在军事谋略上颇有造诣。

有一次，他要临近激战，需要点兵进行兵力统计。

韩信并不善于算术，但他却想出了一个有趣的数学题来点兵。

韩信在一片空旷的草地上，让士兵排成一行，编号从1开始。

然后，他让士兵按照一定的规则报数，最后根据报数的情况进行点兵。

规则非常简单，规定了两个数字m和n。

韩信让第一个士兵报数1，然后第二个士兵报数2，依次类推，每个士兵报的数比前一个士兵的数大1。

当某个士兵的报数等于m时，他必须走到一边。

接下来，新的一轮开始，剩下的士兵继续报数，但是从上一个走到一边的士兵的下一个士兵开始报到1。

当某个士兵的报数等于n时，他也必须走到一边。

韩信说：“我将按照这个规则点兵，剩下的士兵的编号就是我们的兵力。

请问，m和n 的值分别是多少？”士兵们静静地听着，又是兴奋又是紧张，开始思考这道数学题。

他们将问题分为两个部分来考虑。

第一轮过后所有走到一边的士兵的数量等于m-1，所以剩下的士兵的编号就是m。

然后，第二轮过后所有走到一边的士兵的数量等于n-1，所以剩下的士兵的编号就是n。

为了求解这个问题，士兵们首先要找到一个满足条件的m值。

他们开始尝试不同的m 值，并根据这个值模拟士兵们的报数过程。

如果最后剩下的士兵的编号和m值相同，并且又满足n-1的条件，那么这个m值就是我们要找的答案。

士兵们通过反复尝试，终于找到了一个满足条件的m值。

接下来，士兵们推理出了这个m值的特性。

他们发现，当m=4时，剩下的士兵编号为18。

进一步分析，剩下的士兵们可以组成一个等差数列，差为4。

而对于n-1的条件，士兵们也通过模拟推理出了最终的答案。

士兵们充满自豪地向韩信报告了他们找到的答案，他们充分展示了自己在数学方面的智慧和创造力。

韩信听完后，赞叹不已，并对士兵们表示了由衷的敬意。

他们的努力不仅解决了问题，还展示出团队合作和创新的精神。

这个有趣的数学题让我们了解到，数学不仅只是一门学科，更是一种思维方式。