统计学_ 贾俊平 -中国人民大学出版社_第五版
- 格式:doc
- 大小:2.84 MB
- 文档页数:87
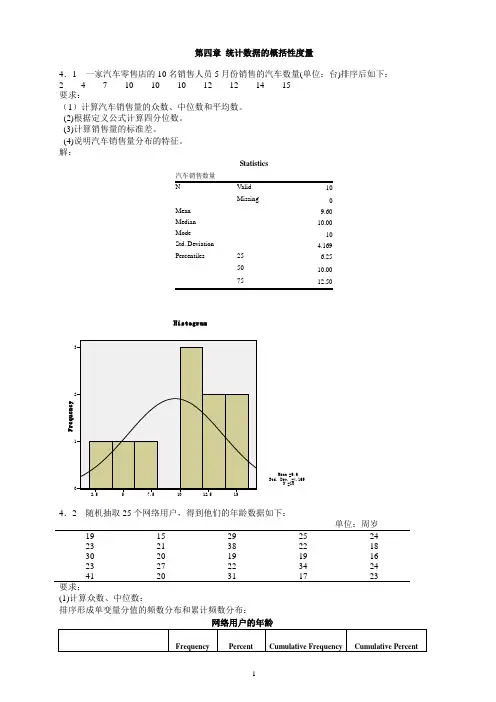
第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。

第9章 分类数据分析一、思考题1.简述列联表的构造与列联表的分布。
答:列联表是由两个以上的变量进行交叉分类的频数分布表。
列联表的分布可以从两个方面看,一个是观察值的分布,又称为条件分布,每个具体的观察值就是条件频数;一个是期望值的分布。
2.用一张报纸、一份杂志或你周围的例子构造一个列联表,说明这个调查中两个分类变量的关系,并提出进行检验的问题。
答:对三个生产厂甲、乙、丙提供的学习机的A、B、C三种性能进行质量检验,欲了解生产厂家同学习机性能的质量差异是否有关系。
抽查了450部学习机次品,整理成为如表9-2所示的3×3列联表。
表9-2根据抽查检验的数据表明:次品类型与厂家(即哪一个厂)生产是无关的(即是相互独立的)。
建立假设:H0:次品类型与厂家生产是独立的,H1:次品类型与厂家生产不是独立的。
可以计算各组的期望值,如表9-3所示(表中括号内的数值为期望值)。
表9-3 各组的期望值计算表所以2222(2017)(4033)(7058)9.821173358χ---=+++=…。
而自由度等于(R -1)(C -1)=(3-1)×(3-1)=4,若以0.01的显著性水平进行检验,查χ2分布表得20.01(4)13.277χ=。
由于220.019.821(4)13.277χχ=<=,故接受原假设H 0,即次品类型与厂家生产是独立的。
3.说明计算2χ统计量的步骤。
答:计算2χ统计量的步骤:(1)用观察值o f 减去期望值e f ;(2)将(o f -e f )之差平方;(3)将平方结果2)(e o f f -除以e f ;(4)将步骤(3)的结果加总,即得:22()o e ef f f χ-=∑。
4.简述ϕ系数、c 系数、V 系数的各自特点。
答:(1)ϕ相关系数是描述2×2列联表数据相关程度最常用的一种相关系数。
它的计算公式为:ϕ,式中,∑-=ee of f f 22)(χ;n 为列联表中的总频数,也即样本量。

4.2(1)众数:19;23中位数:23 平均数:24(2)四分位数:Q L 位置=425=6.25.所以Q L =19+0.25^0=19 Q U 位置=475=18.75,所以Q U =25+2^0.75=26.5(3)标准差:6.65 (4)峰度0.77,偏度1.08 4.3(1)茎叶图Frequency Stem & Leaf 1.00 5. 5 3.00 6. 678 5.00 7. 13488 (2) 平均数:7,标准差0.71 (3)第一种方式的离散系数x s v s ==2.797.1=0.28 第二种方式的离散系数xs v s ==771.0=0.10 所以,第二种排队方式等待时间更集中。
(4)选择第二种,因为平均等待的时间短,而且等待时间的集中程度高 4.5.甲企业总平均成本nf Mx ki ii∑==1=3406600=19.41(元) 乙企业总平均成本nf Mx ki ii∑==1=(元)29.183426255=所以甲企业的总平均成本比乙企业的高,原因是甲企业高成本的产品B 生产的产量比乙企业多,所以把总平均成本提高了。
4.6计算数据如表:利润总额的平均数nf Mx ki ii∑==1=(万元)67.42612051200= 利润总额标准差()nx x f *2∑-=σ= (万元)99.1151201614666==σ 峰态系数6479.03352.23)99.115(120851087441643)(4414—=-=-⨯=--=∑=ns f x MK ki ii偏态系数313)(ns f x MSK ki ii∑=-==2057.0)99.115(120)67.426(3513=⨯-∑=i iif M4.8对于不同的总体的差异程度的比较采用标准差系数,计算如下:%3.8605===x s v s 男; %10505===x s v s 女 (1)女生的体重差异大,因为离散系数大;(2)以磅为单位,男生的平均体重为132.6磅,标准差为11.05磅;女生的平均体重为110.5磅,标准差为11.05磅%33.86.13205.11===x s v s 男%105.11005.11===x s v s 女 (3)156065=-=-=s x x z i i ,所以大约有68%的人体重在55kg~65kg 之间;(4)255040=-=-=s x x z i i ,所以大约有95%的女生体重在40kg~60kg 之间。




第4章 数据的概括性度量一、单项选择题1.一组数据中出现频数最多的变量值称为( )。
A.众数B.中位数C.四分位数D.平均数【答案】A【解析】众数是一组数据中出现次数最多的变量值。
众数主要用于测度分类数据的集中趋势。
一般情况下,只有在数据量较大的情况下,众数才有意义。
2.下列关于众数的叙述,不正确的是( )。
A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响【答案】C【解析】众数是一组数据中出现次数最多的变量值。
众数主要用于测度分类数据的集中趋势,当然也适用于作为顺序数据以及数值型数据集中趋势的测度值。
一般情况下,只有在数据量较大的情况下,众数才有意义。
一组数据可能存在多个众数,由于众数是一个位置代表值,因此它不受数据中极端值的影响。
3.一组数据排序后处于中间位置上的变量值称为( )。
A.众数B.中位数C.四分位数D.平均数【答案】B【解析】中位数是一组数据排序后处于中间位置上的变量值。
中位数将全部数据等分成两部分,每部分包含50%的数据,一部分数据比中位数大,另一部分则比中位数小。
4.一组数据排序后处于25%和75%位置上的值称为( )。
A.众数B.中位数C.四分位数D.平均数【答案】C【解析】四分位数也称四分位点,它是一组数据排序后处于25%和75%位置上的值。
四分位数是通过3个点将全部数据等分为4部分,其中每部分包含25%的数据。
5.非众数组的频数占总频数的比例称为( )。
A.异众比率B.离散系数C.平均差D.标准差【答案】A【解析】异众比率是指非众数组的频数占总频数的比例。
主要用于衡量众数对一组数据的代表程度。
6.四分位差是( )。
A.上四分位数减下四分位数的结果B.下四分位数减上四分位数的结果C.下四分位数加上四分位数D.四分位数与上四分位数的中间值【答案】A【解析】四分位差也称内距或四分间距,它是上四分位数与下四分位数之差。
四分位差反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中;其数值越大,说明中间的数据越分散。


统计学(第五版)贾俊平课后习题答案(完整版)第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。

《统计学》分章习题及答案(贾俊平,第五版)主编:杨群目录习题部分 (2)第1章导论 (3)第2章数据的搜集 (4)第3章数据的整理与显示 (5)第4章数据的概括性度量 (6)第5章概率与概率分布 (9)第6章统计量及其抽样分布 (10)第7章参数估计 (11)第8章假设检验 (12)第9章分类数据分析 (13)第10章方差分析 (15)第11章一元线性回归 (17)第12章多元线性回归 (19)第13章时间序列分析和预测 (22)第14章指数 (25)答案部分 (29)第1章导论 (29)第2章数据的搜集 (29)第3章数据的图表展示 (29)第4章数据的概括性度量 (30)第5章概率与概率分布 (31)第6章统计量及其抽样分布 (32)第7章参数估计 (32)第8章假设检验 (33)第9章分类数据分析 (33)第10章方差分析 (35)第11章一元线性回归 (35)第12章多元线性回归 (37)第13章时间序列分析和预测 (38)第14章指数 (40)习题部分第1章导论一、单项选择题1.指出下面的数据哪一个属于分类数据()A.年龄B.工资C.汽车产量D.购买商品的支付方式(现金、信用卡、支票)2.指出下面的数据哪一个属于顺序数据()A.年龄B.工资C.汽车产量D.员工对企业某项制度改革措施的态度(赞成、中立、反对)3.某研究部门准备在全市200万个家庭中抽取2000个家庭,据此推断该城市所有职工家庭的年人均收入,这项研究的统计量是()A.2000个家庭B.200万个家庭C.2000个家庭的人均收入D.200万个家庭的人均收入4.了解居民的消费支出情况,则()A.居民的消费支出情况是总体B.所有居民是总体C.居民的消费支出情况是总体单位D.所有居民是总体单位5.统计学研究的基本特点是()A.从数量上认识总体单位的特征和规律B.从数量上认识总体的特征和规律C.从性质上认识总体单位的特征和规律D.从性质上认识总体的特征和规律6.一家研究机构从IT从业者中随机抽取500人作为样本进行调查,其中60%的人回答他们的月收入在5000元以上,50%的回答他们的消费支付方式是使用信用卡。
统计学第五版(贾俊平)课后题答案第4章 数据的归纳性气宇(1)众数:100=M 。
中位数:5.5211021=+=+=n 中位数位置,1021010=+=e M 。
平均数:6.91096101514421==++++==∑= nxx ni i。
(2)5.24104===n Q L 位置 ,5.5274=+=LQ 。
5.7410343=⨯==n Q U 位置,1221212=+=U Q 。
(3)2.494.156110)6.915()6.914()6.94()6.92(1)(222212==--+-++-+-=--=∑= n x xs ni i(4)由于平均数小于中位数和众数,所以汽车销售量为左偏散布。
(1)从表中数据能够看出,年龄出现频数最多的是19和23,所以有两个众数,即190=M 和230=M 。
将原始数据排序后,计算的中位数的位置为:13212521=+=+=n 中位数位置,第13个位置上的数值为23,所以中位数23=e M 。
(2)25.64254===n Q L 位置,19)1919(25.019=-⨯+=L Q 。
75.184253=⨯=位置U Q ,56.252-7257.052=⨯+=)(U Q 。
(3)平均数242560025231715191==++++==∑= n xx ni i。
65.61251062125)2423()2417()2415()2419(1)(222212=-=--+-++-+-=--=∑= n x xs ni i(4)偏态系数:()08.165.6)225)(125(242533=⨯---=∑i x SK 。
峰态系数:[]77.065.6)325)(225)(125()125()24(3)24()125(254224=⨯-------+=∑∑i i x x K 。
(5)分析:从众数、中位数和平均数来看,网民年龄在23~24岁的人数占多数。
由于标准差较大,说明网民年龄之间有较大不同。
第1章 导 论一、单项选择题1.指出下面的变量哪一个属于分类变量?( )A.年龄B.工资C.汽车产量D.购买商品时的支付方式(现金、信用卡、支票)【答案】D【解析】分类变量是指观测结果表现为某种类别的变量。
题中D项购买商品时的支付方式分为三类:现金、信用卡和支票,因此属于分类变量。
ABC三项均属于数值型变量。
2.指出下面的变量哪一个属于顺序变量?( )A.年龄B.工资C.汽车产量D.员工对企业某项改革措施的态度(赞成、中立、反对)【答案】D【解析】顺序变量又称为有序分类变量,观测结果表现为某种有序类别的变量。
C项员工对企业某项改革措施的态度按顺序依次表现为:赞成、中立、反对三种,因此属于顺序变量。
ABD三项均属于数值型变量。
3.指出下面的变量哪一个属于数值型变量?( )A.年龄B.性别C.企业类型D.员工对企业某项改革措施的态度(赞成、中立、反对)【答案】A【解析】数值型变量又称为定量变量,观测结果表现为数字的变量。
A项生活费支出的观测结果表现为数字的变量,因此为数值型变量。
BD项均为顺序变量,C项为分类变量。
4.某研究部门准备在全市200万个家庭中抽取2000个家庭,推断该城市所有职工家庭的年人均收入。
这项研究的总体是( )。
A.2000个家庭B.200万个家庭C.2000个家庭的人均收入D.200万个家庭的总收入【答案】B【解析】总体是指包含所研究的全部个体(数据)的集合,它通常由所研究的一些个体组成。
题中的总体为200万个家庭。
5.某研究部门准备在全市200万个家庭中抽取2000个家庭,推断该城市所有职工家庭的年人均收入。
这项研究的样本是( )。
B.200万个家庭C.2000个家庭的总收入D.200万个家庭的人均收入【答案】A【解析】样本是指从总体中抽取的一部分元素的集合。
题中的样本为2000个家庭。
6.某研究部门准备在全市200万个家庭中抽取2000个家庭,推断该城市所有职工家庭的年人均收入。
by _kiss-ahuang3.1为评价家电行业售后服务得质量,随机抽取了由100个家庭构成得一个样本。
服务 质量得等级分别表示为:A ・好:B .较好;C -般:D ・较差;E 、差。
调査结果如卞:B E CC AD C B AE D A C B C D E C E E A D B C C A E D C B B A C D E A B D D C C B C E D B C C B C D A C B C D E C E B B E C C A D C B A E B A C E E A B D D C AD B C C AE D C B CBCEDBCCBC要求:U)指出上而得数据属于什么类型。
顺序数据(2) 用Excel 制作一张频数分布表。
用数据分析一一直方图制作:—— (3)绘制一张条形图仮映评价等级得分布。
——用数据分析一一直方图制作:16 17 32 21 14(4) 绘制评价等级得帕累托图0 逆序排序后,制作累计频数分布表:接收频数频率(知累讣频率(知第二部分:直方图DBAC 接收40緊20E接收E D C B AC 32 32 32 B 21 21 53D 17 17 70 E16 16 86 A14141003・2某行业管理局所属40个企业2002年得产品销售收入数据如下: 152 124 129 H6 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 9788123115H9138112146113126要求:(1)根摇上而得数据进行适当得分组,编制频数分布表,并计算出累积频数与累积频率。
1、确定组数:2 +髓-罟十蹤心2心2、 确定组距:组距=(最大值-最小值)+组数={152-87)4-6=10. 83,取103、 分组频数表(2)按规世,销售收入在125万元以上为先进企业,115-125万元为良好企业,105〜115万 元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业进行■频数 T 一累计频率(%)分组。
贾俊平统计学第5版视频精讲!贾俊平《统计学》(第5版)精讲班【教材精讲+考研真题串讲】讲师:孙玉奎/谷小冉目录说明:本课程共包括27个高清视频(共42课时)。
序号名称1 第1章导论2 第2章数据的搜集(1)3 第2章数据的搜集(2)4 第3章数据的图表展示(1)5 第3章数据的图表展示(2)6 第4章数据的概括性度量(1)7 第4章数据的概括性度量(2)8 第5章概率与概率分布(1)9 第5章概率与概率分布(2)10 第6章统计量及其抽样分布11 第7章参数估计(1)12 第7章参数估计(2)13 第8章假设检验(1)14 第8章假设检验(2)15 第8章假设检验(3)16 第9章分类数据分析17 第10章方差分析(1)18 第10章方差分析(2)19 第11章一元线性回归(1)20 第11章一元线性回归(2)21 第12章多元线性回归(1)22 第12章多元线性回归(2)23 第13章时间序列分析和预测(1)24 第13章时间序列分析和预测(2)25 第13章时间序列分析和预测(3)26 第14章指数(1)27 第14章指数(2)内容简介本课程是贾俊平《统计学》(第5版)网授精讲班,为了帮助参加研究生招生考试指定考研参考书目为贾俊平《统计学》(第5版)的考生复习专业课,我们根据教材和名校考研真题的命题规律精心讲解教材章节内容。
【辅导内容】(1)精讲教材核心考点。
按照教材篇章结构,讲解教材的重难知识点。
(2)串讲名校考研真题。
通过分析历年考研真题,梳理命题规律和特点,分析名校考研真题出题思路。
考虑到课时的需要以及相关知识点的难易程度,对于一些简单的、考试不易涉及的知识点,本课程不予以讲述或一带而过,故建议在学习本课程之前提前复习一遍教材。
注:本课程的学员可以下载电子版讲义打印学习。
【讲师简介】孙玉奎,中央财经大学统计学博士,圣才教育独家签约讲师,主要讲授《统计学》、《商务经济统计学》等,常年从事统计类考研、统计师考试的辅导工作,并参与编写统计学类考研等辅导书,具有扎实的理论基础和实践经验,能将统计学知识寓于生活学习中的生动事例,通俗易懂。